Model Heterogeneous Federated Learning for Intrusion Detection
-
摘要:
针对模型异构和代理数据稀缺问题, 提出模型异构的联邦学习入侵检测(model heterogeneous federated learning for intrusion detection, MHFL-ID)框架。首先, MHFL-ID根据模型异同对节点进行分组, 将结构相同的模型分到同一组; 其次, 在组内采用以组长为中心的同构聚合方法, 根据目标函数投影值选取组长, 并引导组内节点的优化方向以提升全组模型能力; 最后, 在组间采用基于知识蒸馏的异构聚合方法, 不需要代理数据就能用局部平均软标签和全局软标签传递异构模型中的知识。在NSL-KDD和UNSW-NB15这2个数据集上进行了对比实验, 与当前先进方法相比, MHFL-ID框架及所提方法能有效解决联邦学习中模型异构聚合的问题, 在准确率方面也取得了较好结果。
Abstract:Aiming at the problem of model heterogeneity and agent data scarcity, a model heterogeneous federated learning for intrusion detection (MHFL-ID) framework was proposed. First, MHFL-ID groups nodes according to model similarities and differences, that is, models with the same structure were grouped into the same group. Second, the group leader centered isomorphic aggregation method was used to select the group leader according to the projection value of the objective function and guide the optimization direction of the nodes in the group to enhance the modeling capability of the whole group model. Finally, the heterogeneous aggregation method based on knowledge distillation was used between groups to transfer knowledge in heterogeneous models with local average soft label and global soft label without proxy data. Comparative experiments on two datasets, NSL-KDD and UNSW-NB15, show that MHFL-ID framework and the proposed method can effectively solve the problem of heterogeneous model aggregation in federated learning and achieve better results in terms of accuracy.
-
随着网络领域的快速发展和网络攻击技术的不断更新,网络安全已成为人们关注的主要问题之一。为了解决这个问题,人们提出了许多抵御网络攻击的技术。入侵检测就是网络防御技术的一个重要分支[1]。入侵检测通过检查网络流量来判断是否有入侵现象[2]。入侵检测技术可以分为异常检测和误用检测两大类,主要由三部分组成:数据采集模块、入侵检测分析模块和状态响应模块。传统的入侵检测技术并不完善,普遍具有误诊、提取特征不准确、智能程度不高等缺点[3]。
为了解决上述问题,许多学者提出了基于深度学习的入侵检测方案。它可以在没有过多的人为干预情况下,自动提取网络流量中的特征,从而判断流量是否正常。例如:Wang等[4]提出一种基于深度残差卷积神经网络的入侵检测方案。该方案在提高入侵检测准确率的同时又能避免梯度消失或梯度爆炸。Althubiti等[5]提出基于长短期记忆网络的入侵检测方案。该方案最大的优点是可以对已知和未知入侵进行分类和预测。Imamverdiyev等[6]提出基于高斯-伯努利型受限玻尔兹曼机的入侵检测方案。该方案为了提高检测精度,在模型的可见层和隐藏层之间增加了7层,并且通过对所提模型的超参数进行优化,获得了准确的检测结果。此外,李贝贝等[7]提出基于深度强化学习的工业物联网入侵检测系统。侯海霞[8]提出基于深度学习的入侵检测方法和模型。许聪源[9]提出基于深度学习的网络入侵检测方法研究。
虽然基于深度学习的入侵检测方案提高了入侵检测的准确率和智能化程度,但基于深度学习的入侵检测训练往往需要大量的训练数据[10]。然而,由于数据保护法案的出台和个人隐私的意识提高,想获取大量的入侵检测训练数据越来越困难。
因此,为了解决训练数据不足的问题,许多学者开始研究基于联邦学习的入侵检测。联邦学习的入侵检测不仅有效地保护了节点的隐私,而且还通过中央服务器的协调、聚合提高了节点的检测能力[10]。Zhao等[11]提出面向长短期记忆模型的联邦学习入侵检测算法。在这个算法中,每个节点都会部署一个长短期记忆模型,节点根据本地数据训练本地模型,并将模型参数上传到中央服务器。最后,中央服务器执行模型参数聚合,形成一个新的全局模型,将其分发给节点。将以上步骤不断循环,直到完成入侵检测模型的训练。Qin等[12]提出基于特征选择和联邦学习的入侵检测框架。该框架根据攻击类型的特点增强检测模型,同时,从网络流量特征中选择有效的特征集。首先,针对不同的攻击类别,利用贪心算法选择入侵检测准确率较高的特征; 然后,在联邦学习中,服务器根据确定的节点特征生成多个全局模型。该框架在入侵检测数据集上进行了仿真实验。实验结果表明,该框架有效地提高了节点的精度。
Nguyen等[13]提出将联邦学习用于基于异常检测的入侵检测系统中,可以有效地聚合行为档案,从而应对新出现的未知攻击,并且将该系统配备在30多个物联网中,对其进行了评估。实验结果表明,该系统可以快速(257 ms)且精准(95.6%的检测率)识别恶意攻击。Li等[14]提出针对工业网络安全的联邦学习入侵检测模型,该模型将卷积神经网络和门控循环单元融合在一起。在这个联邦学习入侵检测框架中,允许多个参与者共同构建一个全面的入侵检测模型。此外,还设计了一个基于密码系统的安全通信协议,用来保护模型参数的隐私。
尽管基于联邦学习的入侵检测方法受到了学界和工业界的广泛关注和应用,但是它仍然面临很多挑战,模型异构就是它的众多挑战之一[15]。模型异构通常指的是,在联邦学习的入侵检测中,节点的模型种类和结构不同。模型的不同导致联邦学习无法聚合节点模型,使得节点不能学习到分散数据中的知识。
为了解决基于联邦学习的入侵检测中模型异构的问题,许多学者提出了异构的联邦学习方案。Li等[16]提出基于知识蒸馏的异构联邦学习算法。该方法利用模型输出的软标签进行知识蒸馏,取代了模型的聚合,从而解决了异构模型的联邦聚合问题。Shen等[15]提出联邦相互学习,并设置了一个模因模型,节点的模因模型与服务器的模型相同。服务器采用同构模型的聚合方式,将节点本身的模型与模因模型进行相互知识蒸馏学习。Li等[17]提出模型和统计异质性算法,该算法同时考虑了联邦学习中的模型异构和数据异质性的问题。模型和统计异质性算法可以用于不同架构的节点模型,并且对节点之间数据不同的分布有很强的健壮性。Arivazhagan等[18]提出个性化层的联邦学习,这种方法将深度学习网络人为地划分为基础层和个性层。基础层能够提取公共的特征,个性化层能够提取本地特征。本地的模型训练完成后,节点只发送模型的基础层给服务器。服务器收到所有节点的基础层后,对这些基础层进行聚合。
因此,本文受知识蒸馏[19]的启发提出模型异构的联邦学习入侵检测(model heterogeneous federated learning for intrusion detection, MHFL-ID)框架。MHFL-ID在没有代理数据集的情况下,应用组内同构聚合和组间异构聚合2种不同的聚合方法来解决模型异构问题和提高基于联邦学习的入侵检测的准确率。
1. 相关工作和背景
1.1 联邦学习
随着联邦学习技术的不断发展,它可以分为横向联邦学习、纵向联邦学习、联邦迁移学习[20]。横向联邦学习也被称为按样本划分的联邦学习,可以应用于联邦学习的各个参与方的数据集有相同的特征空间和不同的样本空间的场景。纵向联邦学习是由在数据集上具有相同的样本空间、不同的特征空间的参与方所组成的联邦学习。联邦迁移学习在不损害用户隐私的情况下共享知识,并使互补的知识能够在数据联合中跨域传输,从而使目标域能利用源域的标签构建灵活有效的模型。
横向联邦学习根据用户的维度对数据集水平分割,提取用户相同、数据不同的特征。通过上述特征对齐的方法,横向联邦学习扩展了数据集。例如:在2个不同的区域有2个提供相同服务的参与者,用户来自各自区域,重叠很少。因为业务一样,所以用户的特征是一样的。在这种场景下,可以使用横向联邦学习训练参与者的模型,这样不仅可以增加训练样本,还可以提高模型的准确性。
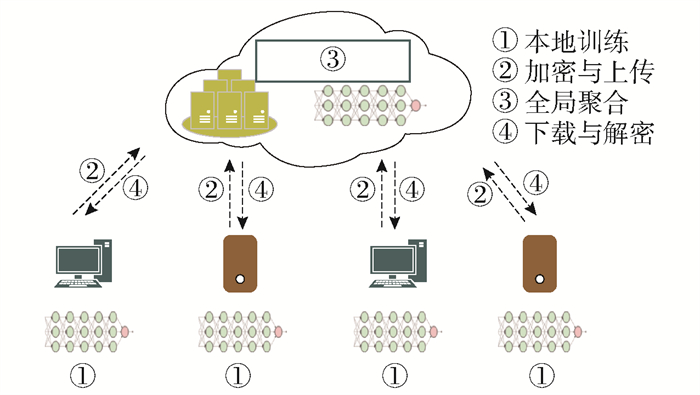
横向联邦学习的框架如图 1所示,整个联邦过程可以分为本地训练、加密与上传、全局聚合、下载与解密[20]。图 1中横向联邦学习单个节点的本地训练的损失函数为
$$ \min L_m({{\boldsymbol{W}}})=\frac{1}{D_m} \sum\limits_{i=1}^{D_m} l\left(f\left(x_i ; {{\boldsymbol{W}}}\right), y_i\right) $$ (1) 式中:f(xi; W)为节点m的预测值,xi为输入样本的特征值,W为权重向量;yi为真实的标签;Dm为节点m拥有的数据个数。横向联邦学习框架的全局聚合整体损失函数为
$$ L({{\boldsymbol{W}}})=\min \sum\limits_{m=1}^M \frac{D_m}{M} L_m({{\boldsymbol{W}}}) $$ (2) 式中M为联邦学习中所有节点的数据个数总和。本文提出的MHFL-ID主要应用领域是横向联邦学习。
谷歌提出利用横向联邦学习为安卓本地用户建立公共模型。本地用户可以不断地将模型参数上传到安卓云上,也可以不断地从安卓云上下载公共模型来提升本地模型的能力[21]。文献[21]采用差分隐私和安全聚合来保证整个框架的安全。Kim等[22]提出区块链的横向联邦学习体系结构。该体系结构利用共识机制可以在本地数据分散的情况下,交换和验证本地模型的更新。Smith等[23]提出多任务的横向联邦学习。多任务的横向联邦学习不仅可以允许多个参与方一起完成工作,还可以在保证安全和隐私的情况下提高原有机制的容错能力。
1.2 知识蒸馏
为了提高深度学习模型的训练效率,Hinton等[24]提出知识蒸馏的方法。知识蒸馏的最初目的是压缩深度学习模型。一个层数较多的教师模型经过训练以后,将知识传递给学生模型。提前训练好的教师模型如图 2所示,根据
$$ P_i=\frac{\exp \left(Z_i / T\right)}{\sum\limits_{i=1}^N \exp \left(Z_i / T\right)} $$ (3) 输出软标签。式中:Pi为教师模型每个类别输出的概率;Zi为每个类别的输出值;N为类别个数;T为温度值,T=1时,就是标准的Softmax()函数。T越大,Pi的分布就越平滑,分布的熵也越大。学生的软标签公式为
$$ q_i=\frac{\exp \left(Z_i / T\right)}{\sum\limits_{i=1}^N \exp \left(Z_i / T\right)} $$ (4) 式中qi为学生模型每个类别输出的概率。
学生模型的损失函数包含教师-学生知识蒸馏的损失和学生自己训练的损失两部分。教师-学生知识蒸馏的损失公式为
$$ L_{\mathrm{s}}=\sum\limits_{i=1}^N P_i \lg q_i $$ (5) 学生自己训练的损失公式为
$$ L_{\mathrm{h}}=-\sum\limits_{i=1}^N c_i \lg q_i $$ (6) 式中ci为在第i类上的真实值,ci∈{0,1},正标签取1,负标签取0。学生总的损失公式为
$$ L=\alpha L_{\mathrm{h}}+\beta L_{\mathrm{s}} $$ (7) 式中α和β分别是关于Lh和Ls的权重参数。实验发现,当β权重较小时,能产生较好的效果,这是一个经验性的结论[25]。
Seo等[26]提出联邦学习蒸馏框架,应用渐近分析方法揭示了该框架的工作原理。该框架和联邦学习的对比结果说明它的准确性和通信效率都高于联邦学习。此外,Seo等还将该框架广泛地应用于各种场景来说明它的普适性。Kim等[22]以意译者为教师网络模型,以翻译者为学生模型。教师网络通过无监督的学习训练获取教师网络的意译信息。学生网络的翻译人员提取学生因素,并通过翻译教师的意译信息提高自身的能力。也就是说,学生经过公共数据集模仿教师的行为,通过这一行为学习到教师网络模型中的知识。这些知识使得学生模型的泛化能力得到提高。泛化能力的提高使得学生能够检测更多的异常样本。Chen等[27]采用注意力分配的机制将教师层的中间知识匹配到相应的学生层,这是一种跨层的蒸馏方法。注意力机制可以使教师模型的知识更好地匹配学生模型。通过多层、跨层的蒸馏使学生模型获取的知识更加丰富,从而与教师模型中的知识更加接近。这样,学生模型的泛化能力和拟合能力都会得到提升。
2. MHFL-ID框架
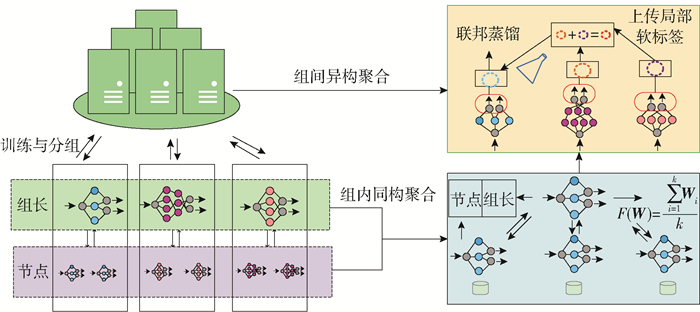
MHFL-ID的整体框架如图 3所示,它主要由3个子模块组成,即训练与分组、组内同构聚合和组间异构聚合。图 3中:F (W)为平均聚合的权重矩阵函数;Wi表示节点i的权重矩阵;k代表组中的节点个数。假设在训练与分组中,异构模型的联邦学习入侵检测共有n个节点,这n个节点有一部分节点的模型是同构的,另一部分节点的模型是异构的。节点根据本地数据训练模型。训练完成后,节点将模型的权重矩阵上传到服务器,服务器根据模型权重矩阵的异同对节点进行分组。
在组内同构聚合中,本文将召回率和精准率作为优化函数模型中的双目标函数。优化函数模型的理想解为 V =(1, 1),并且把模型获取的实际值投影到 V上。节点将投影值发送给服务器,服务器以投影值的大小为标准对节点排序,并将排序结果下发给所有的节点,排名第1的节点为本组的组长。组长拥有2个功能:一个是对组内的节点进行组内同构聚合,另一个是负责本地模型的训练与更新。也就是说,服务器对节点分组与排序,节点组长对节点进行同构聚合。
在组间异构聚合中,组长在完成组内同构聚合以后,使用本地模型计算每一类的平均软标签,即局部平均软标签。当服务器收到所有节点的软标签后,计算所有节点每一类的平均软标签,得到全局平均软标签,然后,服务器下发给组长。组长根据全局软标签和本地真实标签进行知识蒸馏。本文提出的组间异构聚合相比已有的异构聚合算法可以在没有代理数据集的情况下完成异构聚合。组间异构聚合不仅更贴合现实的异构联邦学习入侵检测使用场景,而且还提高了入侵检测的准确率。
2.1 训练与分组
在现实的联邦学习入侵检测系统中,节点的深度学习模型往往是异构的。卷积神经网络不仅可以处理高维数据,而且还可以快速提取数据中的特征。因此,在MHFL-ID中,本文把异构的卷积神经网络作为节点的深度学习模型。每一个节点都会根据本地数据进行训练,然后将节点结构信息上传到服务器,服务器对节点分组。分组之后是组内同构聚合和组间异构聚合。
卷积神经网络由输入层、隐藏层和输出层组成[28]。隐藏层分为卷积层、池化层和全连接层[29-31]。卷积层由多个卷积核组成,它们的功能是提取输入数据的特征。池化层的作用是对卷积层输出的特征图进行特征选择和信息过滤,卷积神经网络中输出层的上游通常是全连接层。对于图像分类问题,输出层使用逻辑函数或归一化指数函数输出分类标签。
卷积神经网络进行前向传播的公式为
$$ {\boldsymbol{u}}^l=f\left({\boldsymbol{x}}^{l-1} \times {\boldsymbol{W}}^{l-1}+{\boldsymbol{b}}^{l-1}\right) $$ (8) 式中:x代表l-1层的输出;b为神经元的偏置;f()表示一个激活函数,激活函数的种类多种多样,如sigmoid()、ReLU()和双曲正切函数。通过训练神经元,最后得到一组权重参数和偏置参数。深度学习模型中的参数使输入和输出得到某种函数映射[30]。
反向传播的计算过程如下:首先,定义一个损失函数。本文中的损失函数是交叉熵函数,数学公式为
$$ L\left({\boldsymbol{W}}, {\boldsymbol{b}}, y_i^{\mathrm{p}}, y_i^{\mathrm{l}}\right)=\sum\limits_{i=1}^N-y_i^{\mathrm{p}} \lg y_i^{\mathrm{t}} $$ (9) 式中:yip为卷积神经网络预测值;yit为数据的真实值;i为第i个节点;N为数据集中样本的个数。然后,反向传播根据梯度下降法寻找损失函数的最小值。$ \frac{\partial L}{\partial W_{i, j}^l} $表示误差项对Wi, jl的偏导,$ \frac{\partial L}{\partial b_i^l} $表示误差项对bil的偏导。Wi, jl表示第l层的节点j与第l+1层的节点i的连接权重参数,bil是第l+1层的节点i的偏置。它们的更新公式为
$$ \left\{\begin{array}{l} W_{i, j}^l=W_{i, j}^l-\eta \times \frac{\partial L}{\partial W_{i, j}^l} \\ b_i^l=b_i^l-\eta \times \frac{\partial L}{\partial b_i^l} \end{array}\right. $$ (10) 式中η表示的学习率。值得注意的是,这里的误差项被定义为
$$ E_i^{n_1}=-\left(y_i^{\mathrm{t}}-u_i^{n_1}\right) \times f\left(y_i^{{\mathrm{p}}, n_1}\right)^{\prime} $$ (11) 式中n1代表卷积神经网络层数。
分组的整个过程分为3个步骤:第1步是节点上传自身的权重矩阵,并且服务器根据节点上传的权重矩阵对节点进行分组;第2步是服务器广播组内节点的分组情况;第3步是组内节点确认组长。分组的具体过程如下:首先,节点进行初始化和本地训练,并把模型的种类上传到服务器。然后,服务器对模型进行分组。分组完成后,服务器告知节点的分组情况。最后,节点与组内组长确认。分组把同构模型分到同组,异构模型分到不同的组。组内使用同构聚合获取结构相同的节点知识,组间使用异构聚合获取结构不同的节点知识。总之,分组方法可以尽可能地获取节点数据中的知识,提高节点模型的检测准确率和框架的整体性能。
2.2 组内同构聚合
组内同构聚合构建了一个双目标函数模型。双目标函数模型属于多目标函数模型中的一种[28]。多目标的函数模型定义公式为
$$ \min F({\boldsymbol{x}})=\left(f_1({\boldsymbol{x}}), \cdots, f_{M-1}({\boldsymbol{x}}), f_M({\boldsymbol{x}})\right) $$ (12) 式中:x为一个决策空间,$ {\boldsymbol{x}} \in \mathbb{R}^n $,x ∈(x1, x2, …, xn);M为多目标函数模型中函数的个数;f1(x), …, fM(x)相互矛盾。在本文中,选取召回率R和精准率P作为函数模型的目标函数,它们的值组成模型解S。因为这2个目标函数相互矛盾,所以它们无法同时达到最大,模型的解只能尽可能地接近理想解。因此,本文设置了一个理想解V =(1, 1),将其作为函数模型解的标准。为了衡量和选取函数模型的解,通过将模型获取的实际解投影到理想解来计算投影值E。E越大,表示模型的性能越好;E越小,表示模型的性能越差。E的计算公式为
$$ E=\cos \langle{\boldsymbol{D}}, {\boldsymbol{V}}\rangle|{\boldsymbol{D}}| $$ (13) 当计算完所有节点的E后,节点将E上传到服务器。服务器根据E对组内节点进行排序,并将排序结果告知所有节点。组内节点收到消息以后确认组长。
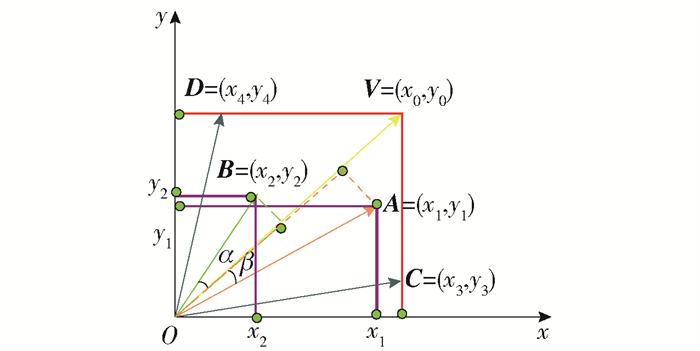
为了更好地说明组内同构聚合选拔组长的过程,以图 4为例进行详述。从图中可以看出,x坐标轴代表的是模型获取的R,y坐标轴代表的是P。坐标系内有 A、B、V共3个解,解 A优于解 B。假设理想解的坐标为 V =(x0, y0),一个模型获取的实际解的坐标为 A =(x1, y1),另一个模型获取实际解的坐标为 B =(x2, y2)。从图中可以发现,A在 V上的投影长度为L1,B在 V上的投影长度为L2。它们的长度大小用坐标表示为
$$ \left\{\begin{array}{l} L_1=\cos <{\boldsymbol{V}}, {\boldsymbol{A}}>|{\boldsymbol{A}}|=\frac{x_0 x_1+y_0 y_1}{\sqrt{x_0^2+y_0^2}} \\ L_2=\cos <{\boldsymbol{V}}, {\boldsymbol{B}}>|{\boldsymbol{B}}|=\frac{x_0 x_2+y_0 y_2}{\sqrt{x_0^2+y_0^2}} \end{array}\right. $$ (14) 从计算的结果可以得到,L1与L2分母相同,分子的大小取决于各自解与理想解的向量内积。因为解 A的内积大于解 B的内积,所以计算结论与从图 4观察的结论相同,即L1>L2。
值得注意的是,在坐标系中长方形覆盖的区域就是模型获取解的范围。在这个范围内,存在 C =(x3, y3)与 D =(x4, y4)是关于直线$ y=\frac{y_0}{x_0} \times x $对称。因为解 C与解 D是对称的,所以它们在 V =(x0, y0)的投影长度是相等的。当发生这种情况,MHFL-ID采取顺序靠前的节点作为组长。
组长的一个重要功能是承担组内节点的同构聚合。组内的聚合公式为
$$ {\boldsymbol{W}}_0=\frac{{\boldsymbol{W}}_1+{\boldsymbol{W}}_2+\cdots+\alpha {\boldsymbol{W}}_q+\cdots+{\boldsymbol{W}}_k}{k} $$ (15) 式中:W0为聚合之后的组长权重矩阵;q为组内E值最大的节点序号;α∈(1.0,1.5],α根据不同的模型、数据挑选合适值。在MHFL-ID中,α超过1.5时往往造成模型崩溃,出现这种情况的原因是模型的梯度会消失或者爆炸。从式(15)可以看出,组长的权重矩阵乘了一个大于1的常数因子,这会使组内同构聚合时,MHFL-ID通过改变组长的系数引导组内节点的优化方向。节点的优化方向与组长的优化方向越靠近,组内节点的准确率就越高,MHFL-ID框架的整体性能就会越高效。
2.3 组间异构聚合
1) 计算局部软标签
MHFL-ID的损失函数可以表示为
$$ \min \limits_{{\boldsymbol{W}}_1, {\boldsymbol{W}}_2, \cdots, {\boldsymbol{W}}_M} \sum\limits_{m=1}^M \frac{D_m}{n} L_m\left({\boldsymbol{W}}_m\right) $$ (16) 式中:Wm为节点m的模型权重矩阵;n为所有数据的个数。因为,在MHFL-ID中 W1, W2,…,WM结构不同,所以不能用式(2)进行聚合求解,只能用式(16)。组长根据
$$ \min L=\frac{1}{D_m} \sum\limits_{i=1}^{D_m} L\left(f\left(x_i ; {\boldsymbol{W}}_j\right), y_i\right) $$ (17) 计算节点的损失。式中:L为交叉熵损失函数;f(xi; Wj)为节点模型的预测值,Wj为节点j的模型的权重矩阵,1≤j≤m;yi为节点的真实标签。
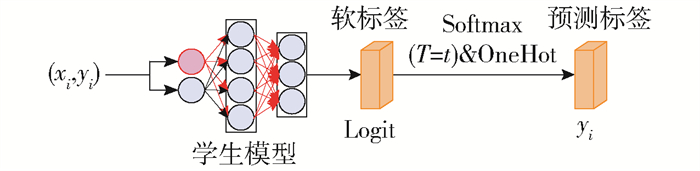
预测标签与软标签之间的关系如图 5所示。图中:logit=f(xi;Wm),是这个网络的倒数第2层输出;$ \tilde{y}_i $=OneHot(Softmax(lg r));预测标签是最后一层的输出。假设节点j中本地数据集Dj共有C类,每一类的平均软标签计算公式为
$$ p_{j\_{\mathrm{a}}, y_h}=\frac{\sum\limits_{\left(x_i, y_h\right)} \lg r_{i h}}{C_h}, \forall\left(x_i, y_h\right) \in D_{j, y_h} $$ (18) 式中:pj_a, yh为新的节点传来的类h的平均软标签;lg rih为类h中每一个样本的软标签; Ch代表类h中样本的个数。
2) 计算全局软标签
节点的局部软标签传递到服务器的时间不同,因此,服务器需要储存节点传递的局部软标签。假设服务器接收到的所有局部软标签S={Sy1, Sy2, …, Syc},Syh代表种类h的平均软标签,1≤h≤c,c为类别总数。当服务器接收到新的节点传来的平均软标签后,根据
$$ S_{y_h} \leftarrow S_{y_h} \cup p_{j\_{\mathrm{a}}, y_h} $$ (19) 把它并到软标签的集合。当服务器接收到所有节点的局部软标签后,服务器根据
$$ p_{{\mathrm{g}}\_{\mathrm{a}}, y_h}=\frac{\sum\limits_{j=1}^e p_{j\_{\mathrm{a}}, y_h}}{e} $$ (20) 计算出全局软件标签。式中:pg_a, yh为类h的全局平均软标签;e为异构模型的联邦学习入侵检测框架中模型的个数。服务器将所有的类的平均软标签计算一遍,得到集合U={pg_a, y1, pg_a, y2, …, pg_a, yc}。
在本文中,组长模型为知识蒸馏中教师模型,本地模型为学生模型。在异构模型的联邦学习入侵检测中,服务器将集合U下发给每一个组长。组长的损失公式为
$$ L_{\mathrm{s}}=\alpha L_{\mathrm{s}}+\beta L_{\mathrm{h}} $$ (21) 式中:Lh为组长模型的预测值与真实标签的损失函数;Ls为组长模型的预测值与服务器集合U的损失函数。Lh的计算公式为
$$ L_{\mathrm{h}}=\sum\limits_{i=1}^c l_i^{\mathrm{g}} \operatorname{CrossEntropy}\left(q_i^{\mathrm{g}}\right) $$ (22) 式中:qig为组长模型在第i类的输出值;lig为真实标签在第i类上的值。Ls的计算公式为
$$ L_{\mathrm{s}}=\sum\limits_{i=1}^c\left(p_{i {\rm{g}} \_{\mathrm{a}}, y_h}-q_i^{\mathrm{g}}\right)^2 $$ (23) 式中pig_a, yh表示yh类的全局平均软标签上的第i类的预测值。在组长的损失函数中,α和β是2个常量参数,根据经验,本文设置2个参数值都为1。
组间异构聚合克服了现有方法必须要用代理数据集的缺点,通过局部的平均软标签和全局的平均软标签传递异构模型间的知识。组间异构聚合借鉴了知识蒸馏的思想,用软标签代替模型获取的知识,对每个类的全局平均软标签进行不同的温度蒸馏,然后将它带入组长的损失函数中来规则化节点的模型参数。
2.4 时间复杂度分析
假设在异构模型的联邦学习入侵检测中,共有M类节点,每类节点的个数分别为N1, N2, …, Nk,每类的参数分别为p1, p2, …, pk,pi为其中任意一个类的参数,i=1, 2, …, k, 传递一个参数的时间为t(本文认为传递到组长和服务器的时间相等)。传统的联邦学习算法需要将所有的节点模型上传到服务器,将类型相同的模型进行聚合。传统方法所耗费的通信时间的计算公式为
$$ T_1=\left(N_1 \times p_1+N_2 \times p_2+\cdots+N_k \times p_k\right) \times t $$ (24) 式中:T1为所有模型的参数上传到服务器节点所需要的时间;Ni×pi为这类模型的参数总量。本文提出的方法只需要将组内节点模型的参数上传到组长,组长上传类的平均软标签。本文方法所耗费的通信时间的计算公式为
$$ T_2=T_4+T_3 $$ (25) 式中T4为节点模型上传到组长的通信时间,计算公式为
$$ \begin{gathered} T_4=\left[\left(N_1-1\right) \times p_1+\left(N_2-1\right) \times\right. \\ \left.p_2+\cdots+\left(N_k-1\right) \times p_k\right] \times t \end{gathered} $$ (26) 式中:Ni-1为第i组中除去组长剩余节点的个数,1≤i≤k。
T3为组长上传局部平均软标签和下载全局软标签个数,计算公式为
$$ T_3=2 \times(k \times c) \times t $$ (27) 式中c代表输出的类别总数。c∈[100,102],而p1∈[104, 107],因此,T3相对于T4几乎为0。由此可得,T2≈T4。综上,节省的通信时间的计算公式为
$$ T=T_1-T_2 \approx T_1-T_4=\left(P_1+P_2+\cdots+P_k\right) \times t $$ (28) 因此,节省的时间占原来方法的比例为
$$ \eta=\frac{T}{T_1}=\frac{\left(P_1+P_2+\cdots+P_k\right)}{\left(N_1 \times p_1+N_2 \times p_2+\cdots+N_k \times p_k\right)} $$ (29) 通过以上分析可以看出,本文算法的通信效率提高了η。因为二者模型的训练时间是一样的,所以时间复杂度从需要的通信时间角度分析即可。
MHFL-ID的框架如算法1所示。K1代表组的个数,K3代表组内节点的个数。整个算法主要分为两部分:第1部分是节点依据算法2进行本地训练,第2部分是算法1进行组内聚和组间聚。组内的损失函数是交叉熵函数,通过计算得到召回率R和精准率P。这2个函数值组成解 D,并投影到理想解上。由此计算出E,并对E进行排序,选出组长。组长将局部软标签传递给服务器,服务器计算得到全局软标签。组长根据全局软标签进行模型优化。
算法1 MHFL-ID
初始化系统参数:设置参数T、K1、K3、α和 V。
1) 循环;
2) 迭代次数更新t=t+1;
3) 根据算法2进行本地训练;
4) 通过判断服务器节点的异同进行分组;
5) 循环;
6) for K0=1 ∶1 ∶K1
7) for K2 =1 ∶1 ∶K3
8) 根据式(13)计算投影值,上传到服务器;
9) end for
10) 服务器对节点的投影值排序,并选出组长;
11) 组长根据式(15)完成组内同构聚合;
12) 组长根据式(18)计算局部平均软标签;
13) end for
14) 循环
15) for K0=1 ∶1 ∶K1
16) for K2=1 ∶1 ∶K1
17) 组长收集局部软标签;
18) end for
19) 根据式(20)计算全局软标签;
20) end for
21) 循环
22) for K0=1 ∶1 ∶K1×K3
23) 则根据式(21)~(23)计算损失函数
24) end for
25) 直到算法收敛,收敛条件是t>T;
算法2 卷积神经网络的本地训练
初始化系统参数:训练数据集、测试数据集。
1) for K0=1 ∶1 ∶K1×K3
2) 模型根据式(8)前向传播,根据式(9)计算损失函数;
3) 根据式(10)(11)进行反向传播;
4) end for
3. 实验
将MHFL-ID框架在2个公开的数据集上与4种不同的算法进行比较来验证它的优越性。这些比较的算法分别是联邦学习的入侵检测、基于组内聚合的联邦学习入侵检测、基于知识蒸馏的异构联邦学习[16]和个性化层的联邦学习[18]。
首先,本文为了验证提出的组内聚合的效果,将联邦学习的入侵检测与基于组内聚合的联邦学习入侵检测对比,后者比前者增加了组内聚合。然后,为了验证单独的组间聚合的效果,本文将基于组内聚合的入侵检测与本文提出的MHFL-ID进行对比,后者只比前者增加了组间聚合。最后,将MHFL-ID与2个异构联邦学习算法(基于知识蒸馏的异构联邦学习和个性化层的联邦学习)进行对比来验证本文框架的整体性能。
3.1 实验设置
1) 实验环境。MHFL-ID使用的服务器操作系统是Ubuntu-18.04.5-LTS。服务器共有4块GPU。GPU的型号是英伟达的GeForce RTX 3070,内存大小为7 982 MB。MHFL-ID框架的实验环境是PyTorch,使用的语言是Python。
2) 实验数据。本文通过NSL-KDD和UNSWNB15这2个公开的数据集验证MHFL-ID框架的性能。
NSL-KDD是在KDDCup99上进行改进得到的数据集。KDDCup99数据集是一个模拟美国空军局域网的网络数据集。它的模拟时间长达9个星期。KDDCup99数据集中每一条记录都有41个固定的特征属性和1个类标签,共42个属性。在41个固定的特征属性中,32个属性为连续型,9个特征属性为离散型。它被分成具有标识的训练数据和未加标识的测试数据。在训练数据集中包含了1种正常类型的数据和22种攻击类型的数据,另外,有14种攻击只出现在测试数据集中。改进的地方主要有以下几方面:1) 因为NSL-KDD数据集的训练集中不含有大量重复的记录,所以分类器不会偏向数量更多的记录。2) NSL-KDD数据集的测试集设置更加合理,使得检测率更为准确。3) 每个层级的攻击数据所占的比例与原数据集中的记录百分比成反比。因此,深度学习的分类率变化幅度更大,这使得对深度学习的准确评估更有效。4) 训练和测试中的记录数量设置是合理的,因此,NSL-KDD数据集比KDDCup99数据集消耗的计算资源更少。
UNSW-NB15数据集包含了9种攻击、49个特征和2 540 044条数据。9种攻击分别是Fuzzers、Analysis、Backdoors、DoS、Exploits、Generic、Reconnaissance、Shellcode和Worms。特征的类型分别为整数类型、浮点型、二进制类型、时间戳。其中,在训练集中共有175 341条记录,在测试集中共有82 332条记录。
本文把NSL-KDD数据集均匀地划分为10份。这10份随机分给10个节点,每个节点按照3 ∶1 ∶1的比例把本地数据集划分为训练数据集、测试数据集、验证数据集。UNSW-NB15数据集分为训练数据集和测试数据集。本文将这两部分数据集均匀地划分为10份,然后随机分给节点,本文中任何算法的数据划分都是以此为根据。
3) 模型设置。MHFL-ID共有5个不同种类的卷积神经网络,每种类型有2个节点模型,共10个节点模型,模型的具体设置如表 1所示。联邦学习框架中共包含10个节点。5个种类的卷积神经网络的卷积层数分别为2、3、4、5、6,它们还有1个池化层和3个全连接层。池化层使用的函数是F.max_pool2d(),连接层的连接函数是nn.Liner(),使用的激活函数是ReLU(),损失函数用的是交叉熵函数和L1范式损失函数。
表 1 模型参数Table 1. Model parameter模型 模型1 模型2 模型3 模型4 模型5 卷积层 [1, 6, 2, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] 卷积层 [6, 16, 3, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] 卷积层 [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] 卷积层 [32, 64, 2, 1, 0] [32, 64, 2, 1, 0] [32, 64, 2, 1, 0] 卷积层 [64, 128, 2, 1, 0] [64, 128, 2, 1, 0] 卷积层 [128, 128, 2, 1, 0] 全连接层 [144, 512] [288, 512] [576, 256] [512, 256] [128, 64] 全连接层 [512, 256] [512, 256] [256, 128] [256, 128] [64, 32] 全连接层 [256, 10] [256, 10] [128, 10] [128, 10] [32, 10] 4) 评价指标。为了评价框架的有效性,本文从4个指标进行评价。这4个指标分别是准确率A、P、R及精确率和召回率的调和平均数F1。A是最常用、最直观的性能指标,它反映了总体分类结果的准确性,计算公式为
$$ A=\frac{T_{\mathrm{P}}+T_{\mathrm{n}}}{T_{\mathrm{P}}+T_{\mathrm{n}}+F_{\mathrm{P}}+F_{\mathrm{n}}} $$ (30) 式中:Tp为正确预测正分类的个数;Fp为错误预测正分类的个数;Tn为正确预测负分类的个数;Fn为错误预测负分类的个数。
R表示的是预测对的正分类样本占所有正分类样本的比例,计算公式为
$$ R=\frac{T_{\mathrm{p}}}{T_{\mathrm{p}}+F_{\mathrm{n}}} $$ (31) P表示的是预测为正的样本中有多少是真正的正样本,计算公式为
$$ P=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{P}}} $$ (32) F1是通过P和R计算得到的。当F1变大时,P和R同时变大,计算公式为
$$ F_1=\frac{2 \times P \times R}{P+R} $$ (33) 因此,本文将联邦学习之后的所有模型的指标进行平均,得出一次联邦学习之后的平均值,4个指标都是这样处理。
3.2 对比算法
3.2.1 组内对比算法
为了增强联邦学习入侵检测整体框架的检测能力,本文提出了组内聚合的联邦学习入侵检测。组内聚合的联邦学习入侵检测使用双目标函数选择组长,然后在聚合时增加组长权重,提高框架整体的检测能力。联邦学习入侵检测与组内聚合联邦学习入侵检测使用的数据集都是NSL-KDD和UNSW-NB15,划分为10个小数据集,随机分配给节点,使用的参数也是一样。
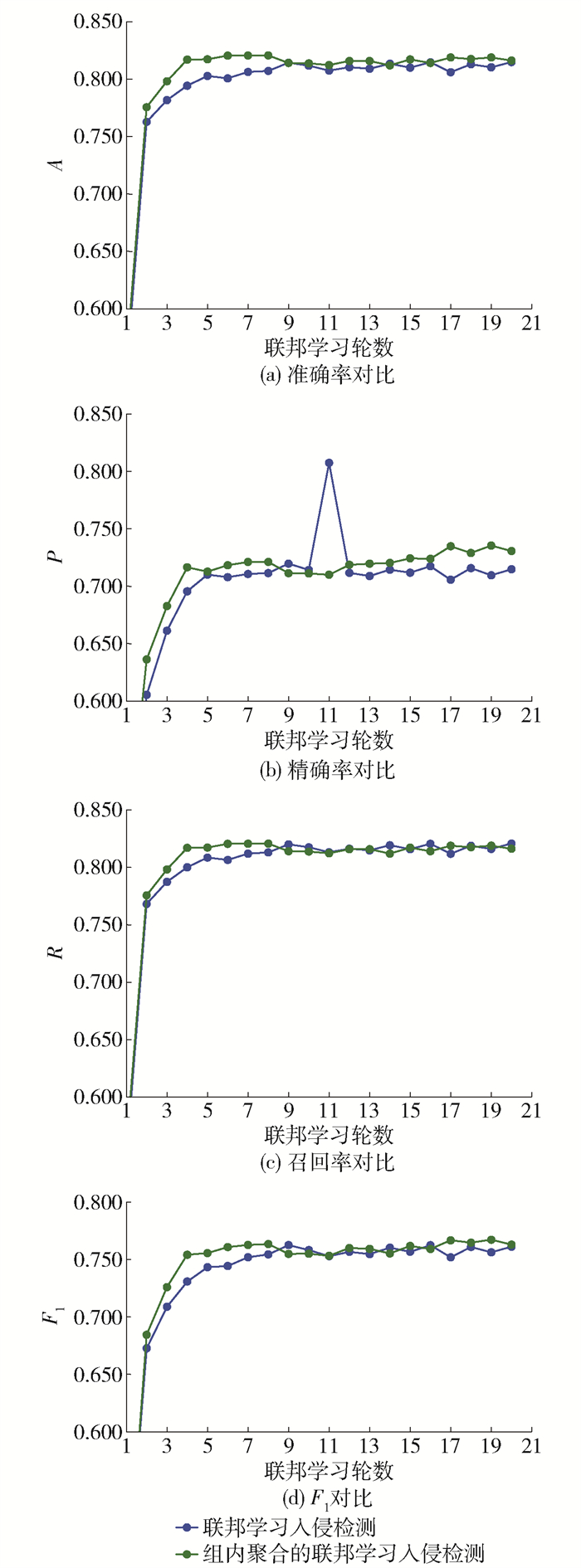
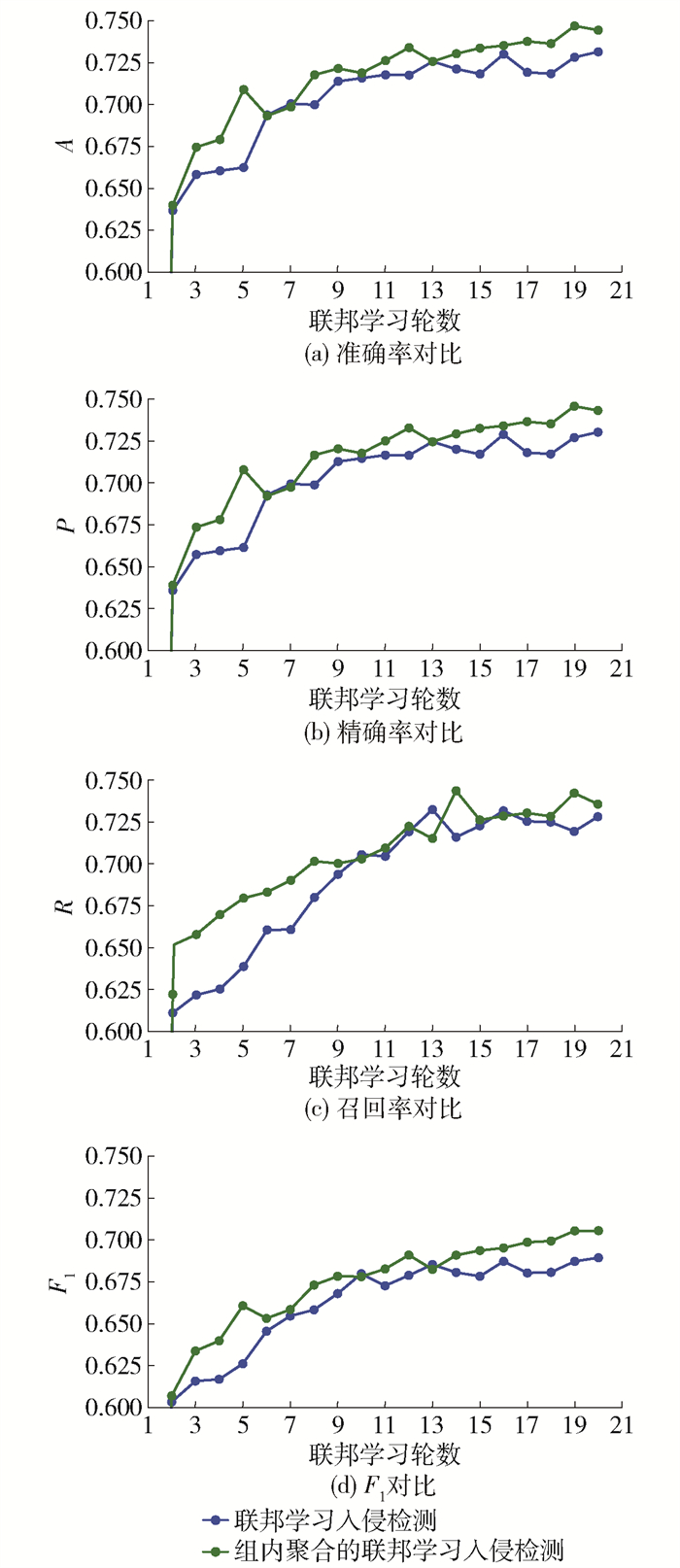
从图 6(a)可以观察到在第2~9轮,组内聚合的联邦学习入侵检测获取的A与联邦学习入侵检测相比优势比较明显,其中相差最大的是第4轮,相差2.27%。第9~20轮优势逐渐减弱,但从整个趋势来看,组内聚合的联邦学习入侵检测优于联邦学习入侵检测。由图 6(b)可知,在第11~20轮,组内聚合的联邦学习入侵检测获取的P与联邦学习入侵检测相比优势逐渐增加,然后,又逐渐减弱,到第17轮最大相差2.92%,到第20轮相差1.59%。由图 6(c)可知,在第2~8轮,组内聚合的联邦学习入侵检测优于联邦学习入侵检测。分析图 6(d),在第2~8轮,组内聚合的联邦学习入侵检测获取的F1大于联邦学习入侵检测获取的F1。由图 7(a)~7(b)可知,组内聚合的联邦学习入侵检测获取的A和P大于联邦学习的入侵检测获取的A和P。由图 7(c)可知:在第2~8轮,组内聚合的联邦学习入侵检测比联邦学习入侵检测有较大的优势;在第9~18轮二者交替领先。在第19~20轮,组内聚合的联邦学习入侵检测领先。在图 7(d)中,除了第7轮和第13轮联邦学习入侵检测获取的F1接近组内聚合的联邦学习入侵检测获取的F1,剩下的轮数,组内聚合的联邦学习入侵检测以较为明显的优势优于联邦学习入侵检测。
对图 6进行分析,可以得到组内聚合的联邦学习入侵检测优于联邦学习入侵检测,虽然优势比较小,但是整体上优于后者。由图 7可知,联邦学习入侵检测算法优于独立模型的入侵检测且优势较为明显。
综上,不管是NSL-KDD数据集,还是UNSW-NB15数据集,都验证了组内聚合的联邦学习入侵检测优于联邦学习入侵检测。其原因是,组内聚合的联邦学习入侵检测使用双目标函数选取组长,全面地考虑了节点学习到的知识。在聚合时,扩大组长的参数,使得组内节点模型朝着组长的方向进行优化。组内聚合的联邦学习入侵检测与联邦学习入侵检测相比只增加了本文提出的组内聚合,但是组内聚合的联邦学习入侵检测却优于联邦学习入侵检测,说明组内聚合提高了框架的性能。组内聚合也可以和其他的算法进行组合来提高整体框架的性能。
3.2.2 组间对比
MHFL-ID在组内聚合的基础上,采用无数据的组间异构聚合。无数据的组间异构聚合可以获取异构节点的知识,扩大使用场景。首先,它的组长计算出局部软标签,并将其上传到服务器,服务器对组长的局部软标签求平均,然后分发给组长。它和组内聚合的联邦学习入侵检测使用的数据集都是NSL-KDD和UNSW-NB15,划分为10个小数据集,随机分配给节点,使用的参数也是一样的。
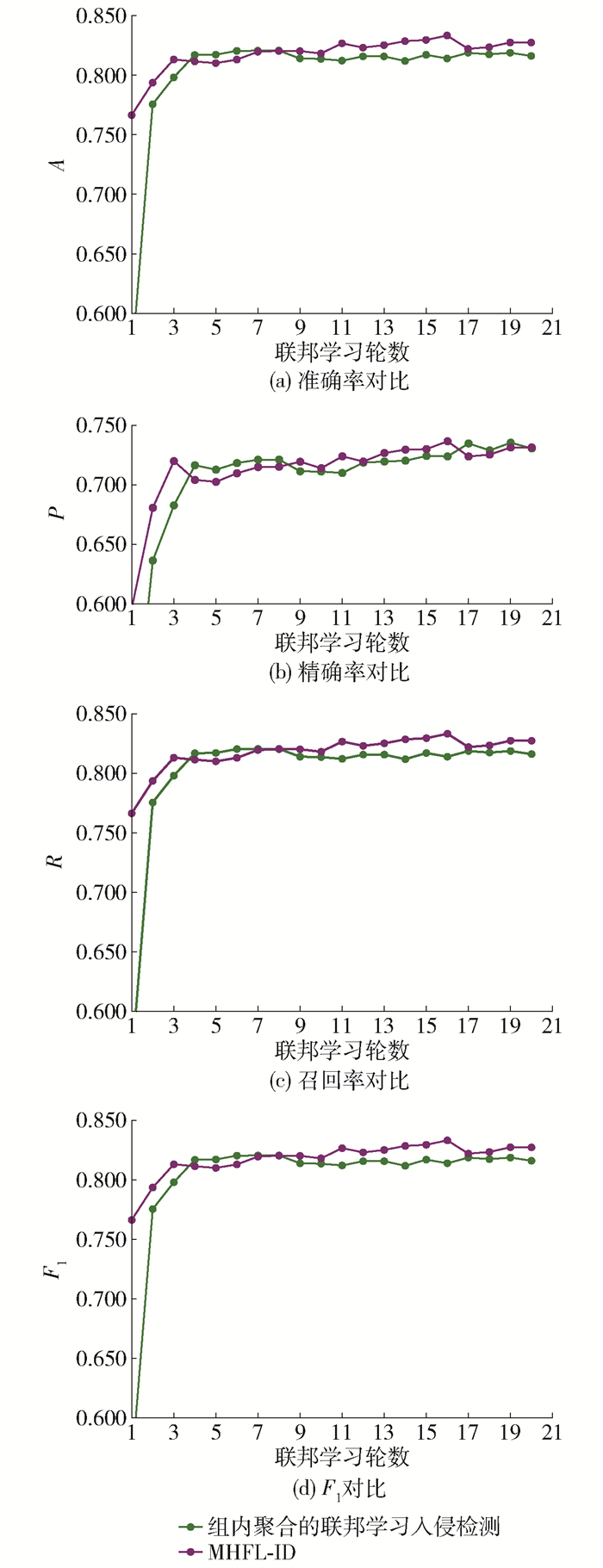
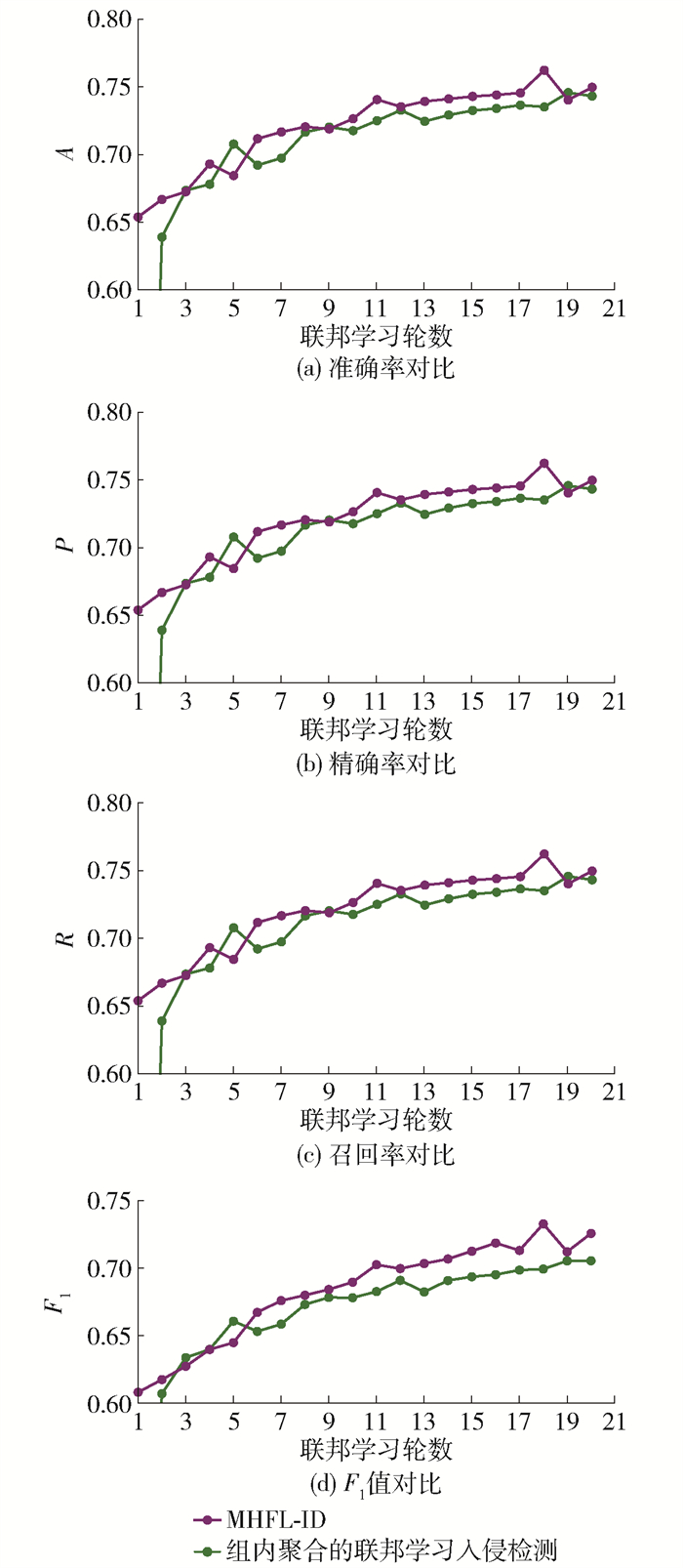
图 8~9是组内聚合的联邦学习入侵检测和MHFL-ID在NSL-KDD和UNSW-NB15这2个数据集上的4个指标。
由图 8(a)可知,在第10~20轮,MHFL-ID以较小的优势优于组内聚合的联邦学习入侵检测。由图 8(b)可知:它在第3~8轮,劣于组内聚合的联邦学习入侵检测;在第9~15轮,优于组内聚合的联邦学习入侵检测;在第17~18轮,劣于组内聚合的联邦学习入侵检测;在第19~20轮几乎持平。由图 8(c)可知,在第11~20轮,MHFL-ID获取的R大于组内聚合的联邦学习入侵检测获取的R。观察图 8(d),在第11~20轮,它获取的F1大于组内聚合的联邦学习入侵检测获取的F1。由图 9(a)可知,在第12~20轮,联邦学习入侵检测优于组内聚合的联邦学习入侵检测且在第18轮的优势最大。由图 9(b)可知,在第12~18轮,联邦学习入侵检测优于组内聚合的联邦学习入侵检测,在第19轮劣于它,在第20轮再次超过。由图 9(c)可知,在第5~20轮,除了在第14轮组内聚合的联邦学习入侵检测获取的R稍微高于MHFL-ID,剩余的轮数中MHFL-ID都高于组内聚合的联邦学习入侵检测。由图 9(d)可知,在第6~20轮,MHFL-ID优于组内聚合的联邦学习入侵检测,最大优势在第18轮。
从图 8、9分析可得,MHFL-ID在NSL-KDD数据集和UNSW-NB15数据集上优于组内聚合的联邦学习入侵检测且在UNSW-NB15数据集上优势更加明显一些。它只比组内聚合的联邦学习入侵检测多增加了一个组间异构聚合,但是框架整体的入侵检测的准确率却得到提升,这说明组间异构是有效的。
3.2.3 模型异构的联邦学习算法对比
将MHFL-ID和2个异构联邦学习算法进行对比,这2个异构联邦学习算法分别是个性化层的联邦学习[18]和基于知识蒸馏的联邦学习模型[16]。对浅层的卷积层聚合的原因是浅层的神经层提取的是本地数据的共同特征,深层的网络提取的是本地数据个性化的特征。基于知识蒸馏的联邦学习模型的思想是用软标签代表模型获取的知识。训练完成后,将模型的软标签上传到服务器,服务器对所有节点的软标签进行聚合,并将聚合之后的软标签下发给所有节点。节点以收到的软标签为数据标签进行模型优化。
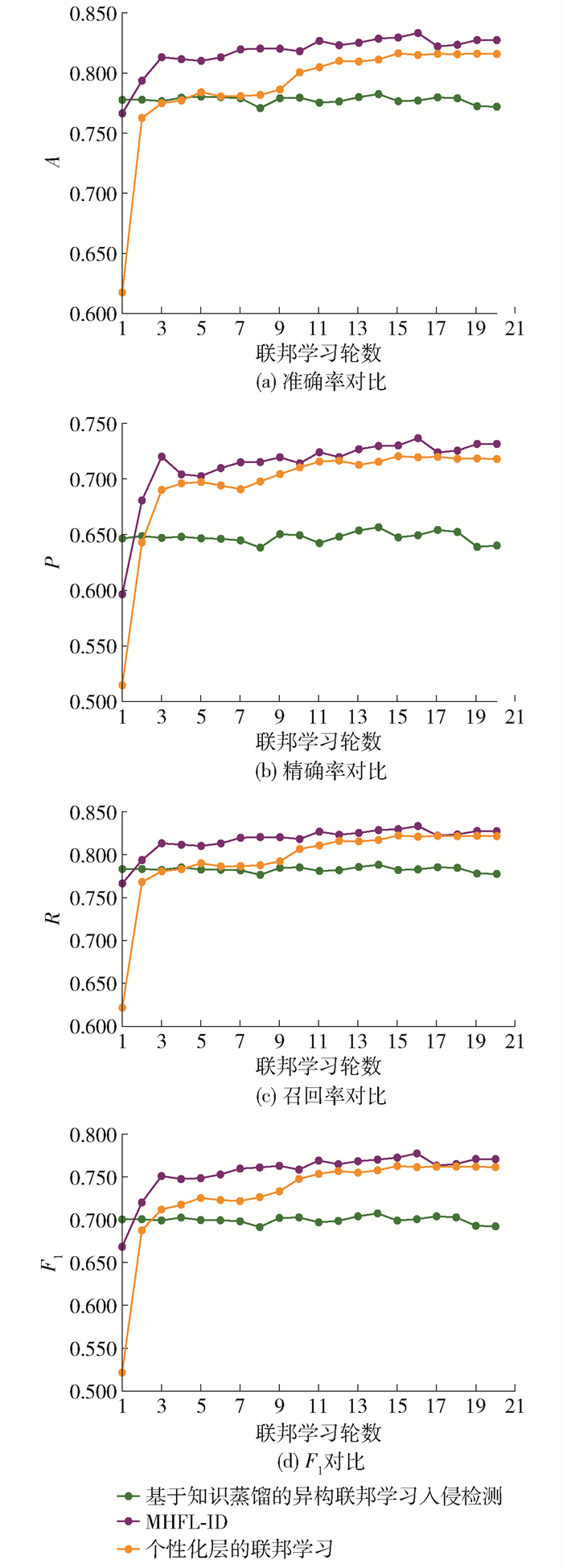
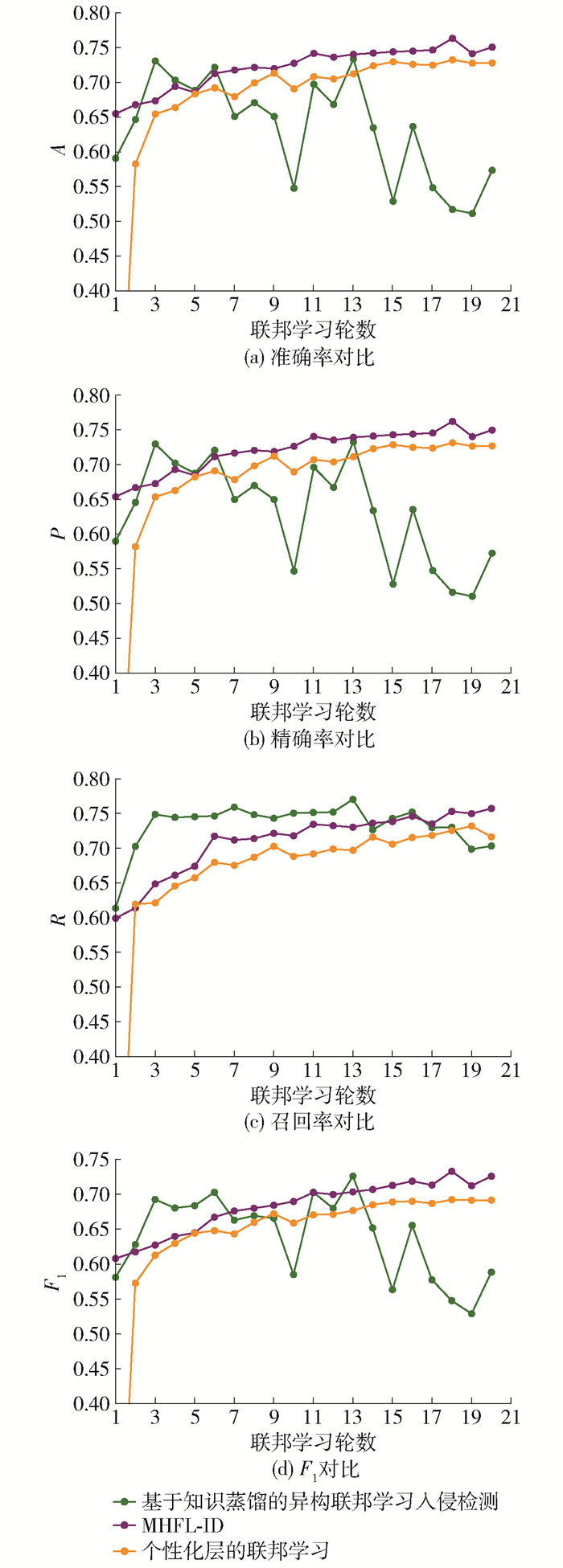
图 10、11是3个异构的联邦学习算法在NSL-KDD和UNSW-NB15数据集上获取的4个指标对比。
由图 10(a)可知:在第2~9轮,MHFL-ID以较为明显的优势优于其他2个算法;在第10~20轮,优势逐渐减弱,但始终优于其他算法。个性化层的联邦学习入侵检测在NSL-KDD数据集上获取的A劣于本文算法,优于知识蒸馏的联邦学习入侵检测。在图 10(a)中知识蒸馏的联邦学习入侵检测在第2~9轮与个性化层的联邦学习入侵检测较为接近,在第10~20轮与本文算法和知识蒸馏的联邦学习入侵检测相差较大。由图 10(b)可知,在第12~20轮,MHFL-ID优于其他2个异构的联邦算法。个性化层的联邦学习入侵检测以较大的优势优于知识蒸馏的联邦学习入侵检测。知识蒸馏的联邦学习入侵检测算法获取的P是最小的。由图 10(c)可知,在第2~16轮MHFL-ID优于其他2个算法,在第17~20轮MHFL-ID以很小的优势优于个性化层的联邦学习入侵检测。知识蒸馏的联邦学习入侵检测在第2~9轮很接近,但是在第10~20轮以后明显落后于个性化层的联邦学习入侵检测,并且差距有逐渐增加的趋势。由图 10(d)可知:在第2~20轮,MHFL-ID优于其他2个算法;在第3~20轮,个性化层的联邦学习入侵检测优于知识蒸馏的联邦学习入侵检测。
由图 11(a)(b)可知:在第6~20轮,本文算法优于其他2个异构联邦学习算法;知识蒸馏的联邦学习入侵检测在第1~3轮上升很快;第3轮个性化层的联邦学习入侵检测达到最大,优于其他2个算法,但是在第4~20轮,它呈现波动下降且波动幅度较大。由图 11(c)可知:在第2~14轮,个性化层的联邦学习入侵检测在UNSW-NB15上获取的R大于其他的2个算法,本文算法排第2;在第14~17轮,个性化层的联邦学习入侵检测与MHFL-ID几乎重合,这说明二者获取的R几乎相同;在第18~20轮,MHFL-ID排第1。由图 11(d)可知,MHFL-ID在第2~16轮优于其他2个算法,在第17轮与个性化层的联邦学习入侵检测几乎持平,在第18~20轮又排第1。知识蒸馏的联邦学习入侵检测获得的F1与其他2个算法相差较大。
由图 10、11可知,MHFL-ID在NSL-KDD、UNSW-NB15数据集上的表现优于其他2个算法。MHFL-ID通过组内聚合增强了组内节点模型获取组内知识的能力,通过组间聚合增强了获取不同组内知识的能力,当获取的知识越多,入侵检测的准确率也就越高。此外,它通过节点-组长-服务器这样的三级架构,降低了通信开销,扩大了框架的应用场景。
4. 结论
1) 针对联邦学习入侵检测中节点模型的异构问题,提出MHFL-ID框架。MHFL-ID首先对节点进行分组,降低了异构联邦学习入侵检测的聚合难度,在提高节点检测准确率的同时降低了节点与服务器的通信开销,减小了服务器的储存压力。
2) 为了加强组内聚合效果,提出一种以组长为中心的组内同构聚合方法。同构聚合使用双目标函数模型优化方法选拔组长,通过改变组长的系数引导组内节点的优化方向。节点的优化方向与组长的优化方向越靠近,组内节点的准确率就越高。
3) 为了解决组间异构的聚合,本文在没有代理数据集的情况下,提出基于知识蒸馏的异构聚合方法。组间异构聚合首先计算组长每一类的局部平均软标签;然后,对所有组长的局部平均软标签再次平均得到全局平均软标签;最后,将全局平均软标签下发给组长,指导组长进行知识蒸馏。组间异构聚合在不用公有数据集的场景下,不仅解决了组间异构聚合,还提高了入侵检测的准确率和通信效率。
-
表 1 模型参数
Table 1 Model parameter
模型 模型1 模型2 模型3 模型4 模型5 卷积层 [1, 6, 2, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] [1, 6, 2, 1, 1] 卷积层 [6, 16, 3, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] [6, 16, 2, 1, 0] 卷积层 [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] [16, 32, 2, 1, 0] 卷积层 [32, 64, 2, 1, 0] [32, 64, 2, 1, 0] [32, 64, 2, 1, 0] 卷积层 [64, 128, 2, 1, 0] [64, 128, 2, 1, 0] 卷积层 [128, 128, 2, 1, 0] 全连接层 [144, 512] [288, 512] [576, 256] [512, 256] [128, 64] 全连接层 [512, 256] [512, 256] [256, 128] [256, 128] [64, 32] 全连接层 [256, 10] [256, 10] [128, 10] [128, 10] [32, 10] -
[1] XIE Y L, FENG D, HU Y C, et al. Pagoda: a hybrid approach to enable efficient real-time provenance based intrusion detection in big data environments[J]. IEEE Transactions on Dependable and Secure Computing, 2020, 17(6): 1283-1296. doi: 10.1109/TDSC.2018.2867595
[2] MARTEAU P F. Random partitioning forest for point-wise and collective anomaly detection-application to network intrusion detection[J]. IEEE Transactions on Information Forensics and Security, 2021, 16: 2157-2172. doi: 10.1109/TIFS.2021.3050605
[3] TIDJON L N, FRAPPIER M, MAMMAR A. Intrusion detection systems: a cross-domain overview[J]. IEEE Communications Surveys and Tutorials, 2019, 21(4): 3639-3681. doi: 10.1109/COMST.2019.2922584
[4] WANG W P, WANG Z R, ZHOU Z F, et al. Anomaly detection of industrial control systems based on transfer learning[J]. Tsinghua Science and Technology, 2021, 26(6): 821-832. doi: 10.26599/TST.2020.9010041
[5] ALTHUBITI S, NICK W, MASON J, et al. Applying long short-term memory recurrent neural network for intrusion detection[C]//SoutheastCon 2018. Piscataway, NJ: IEEE, 2018: 1-5.
[6] IMAMVERDIYEV Y, ABDULLAYEVA F. Deep learning method for denial of service attack detection based on restricted Boltzmann machine[J]. Big Data, 2018, 6(2): 159-169. doi: 10.1089/big.2018.0023
[7] 李贝贝, 宋佳芮, 杜卿芸, 等. DRL-IDS: 基于深度强化学习的工业物联网入侵检测系统[J]. 计算机科学, 2021, 48(7): 47-54. LI B B, SONG J R, DU Q Y, et al. DRL-IDS: deep reinforcement learning based intrusion detection system for industrial Internet of things[J]. Computer Science, 2021, 48(7): 47-54. (in Chinese)
[8] 侯海霞. 基于深度学习的入侵检测方法和模型[D]. 北京: 北京邮电大学, 2021. HOU H X. Deep learning based intrusion detection method and model[D]. Beijing: Beijing University of Posts and Telecommunications, 2021. (in Chinese)
[9] 许聪源. 基于深度学习的网络入侵检测方法研究[D]. 杭州: 浙江大学, 2019. XU C Y. Research of network intrusion detection method based on deep learning[D]. Hangzhou: Zhejiang University, 2019. (in Chinese)
[10] AGRAWAL S, SARKAR S, AOUEDI O, et al. Federated learning for intrusion detection system: concepts, challenges and future directions[J]. Computer Communications, 2022, 195: 346-361. doi: 10.1016/j.comcom.2022.09.012
[11] ZHAO R J, YIN Y, SHI Y, et al. Intelligent intrusion detection based on federated learning aided long short-term memory[J]. Physical Communication, 2020, 42: 101157. doi: 10.1016/j.phycom.2020.101157
[12] QIN Y, MASAAKI K. Federated learning-based network intrusion detection with a feature selection approach[C]//2021 International Conference on Electrical, Communication, and Computer Engineering. Piscataway, NJ: IEEE, 2021: 1-6.
[13] NGUYEN T D, MARCHAL S, MIETTINEN M, et al. DÏoT: a federated self-learning anomaly detection system for IoT[C]//2019 IEEE 39th International Conference on Distributed Computing Systems. Piscataway, NJ: IEEE, 2019: 756-767.
[14] LI B B, WU Y H, SONG J R, et al. DeepFed: federated deep learning for intrusion detection in industrial cyber-physical systems[J]. IEEE Transactions on Industrial Informatics, 2021, 17(8): 5615-5624. doi: 10.1109/TII.2020.3023430
[15] SHEN T, ZHANG J, JIA X K, et al. Federated mutual learning[EB/OL]. [2021-09-17]. https://arxiv.org/abs/2006:16765.
[16] LI D L, WANG J P. Heterogenous federated learning via mode distillation[EB/OL]. [2021-03-31]. https://arxiv.org/abs/1910.03581v1.
[17] LI Y Y, ZHOU W, MI H B, et al. FedH2L: federated learning with model and statistical heterogeneity[EB/OL]. [2021-07-27]. https://arxiv.org/abs/2101.11296.
[18] ARIVAZHAGAN M G, AGGARWAL V, SINGH A K, et al. Federated learning with personalization layers[EB/OL]. [2021-12-02]. https://arxiv.org/abs/1912.00818.
[19] WANG L, YOON K J. Knowledge distillation and student-teacher learning for visual intelligence: a review and new outlook[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(6): 3048-3068. doi: 10.1109/TPAMI.2021.3055564
[20] IMTEAJ A, THAKKER U, WANG S Q, et al. A survey on federated learning for resource-constrained IoT devices[J]. Internet of Things Journal, 2022, 9(1): 1-24. doi: 10.1109/JIOT.2021.3095077
[21] McMAHAN H B, MOORE E, RAMAGE D, et al. Federated learning of deep networks using model averaging[EB/OL]. [2021-05-08]. https://arxiv.org/abs/1602.05629v1.
[22] KIM J, PARK S, KWAK N. Paraphrasing complex network: network compression via factor transfer[C]//Proceedings of 32nd Conference on Neural Information Processing System. New York: ACM, 2018: 2765-2774.
[23] SMITH V, CHIANG C K, SANJABI M, et al. Federated multi-task learning[EB/OL]. [2021-05-10]. https://arxiv.org/abs/1705.10467.
[24] HINTON G, VINYALS O, DEAN J. Distilling the knowledge in a neural network[EB/OL]. [2021-05-10]. https://arxiv.org/abs/1503.02531.
[25] GOU J P, YU B S, MAYBANK S J, et al. Knowledge distillation: a survey[J]. International Journal of Comput Vision, 2021, 129: 1789-1819. doi: 10.1007/s11263-021-01453-z
[26] SEO H, PARK J, OH S, et al. Federated knowledge distillation[EB/OL]. [2021-03-31]. https://arxiv.org/abs/2011.02367.
[27] CHEN D F, MEI J P, ZHANG Y, et al. Cross-layer distillation with semantic calibration[C]//Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence. Palo Alto, CA: IAAA, 2021, 35(8): 7028-7036.
[28] GYSEL P, PIMENTEL J, MOTAMEDI M, et al. Ristretto: a framework for empirical study of resource-efficient inference in convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5784-5789. doi: 10.1109/TNNLS.2018.2808319
[29] SUI X D, ZHENG Y J, WEI B Z, et al. Choroid segmentation from optical coherence tomography with graph-edge weights learned from deep convolutional neural networks[J]. Neurocomputing, 2017, 237: 332-341. doi: 10.1016/j.neucom.2017.01.023
[30] ZHOU X J, GAO Y, LI C J, et al. A multiple gradient descent design for multi-task learning on edge computing: multi-objective machine learning approach[J]. IEEE Transactions on Network Science and Engineering, 2022, 9(1): 121-133. doi: 10.1109/TNSE.2021.3067454
[31] CINTRA R J, DUFFNER S, GARCIA C, et al. Low-complexity approximate convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(12): 5981-5992. doi: 10.1109/TNNLS.2018.2815435
-
期刊类型引用(2)
1. 胡大强,张志磊,康艳,吴纯璐. 联邦学习环境下异构数据集的软件缺陷预测性能提升策略——以通信效率和隐私保护为中心的实证研究. 无线互联科技. 2024(15): 82-85+96 .  百度学术
百度学术
2. 杨绍卿,张钰,邓宝松. 改进SVM实现的无人集群网络入侵检测框架. 智能安全. 2024(03): 45-53 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: