Sufficient Condition for Global Attractivity of a Class of Hopfield Neural Networks With S-distributed Delays
-
摘要:
研究了一类具有S分布时滞的Hopfield神经网络的全局吸引性问题. 首先，通过常微分方程比较原理和适当的迭代证明了系统解的有界性，再通过一类非线性代数方程组和迭代技巧得到了平衡点全局吸引的一个充分条件. 最后，通过数值模拟验证了结论的有效性.
Abstract:Global attractivity of a class of Hopfield neural networks with S-distributed delays was studied in this paper. Based on a class of nonlinear algebraic equations and some computational techniques in M-matrix, a sufficient condition for global attractivity of the equilibrium of a class of Hopfield neural networks with S-distributed delays was obtained. Numerical simulations were given to illustrate validity of the result.
-
近年来, Hopfield神经网络[1-3]的理论成果在联想记忆和最优化计算等方面有了广泛的应用, 因此对于Hopfield神经网络的研究越来越多地引起了人们的关注[4-7]. 在Hopfield神经网络的常微分方程模型被提出之后, 学者们就将有限时滞和无穷时滞引入到模型中, 以求更精确地模拟现实世界的现象. 而时滞的出现会很大程度地影响神经网络的动力学性质, 使网络的性质变得更加复杂.
在文献[3]中, 一类具有有限时滞的Hopfield神经网络
$$ \begin{gathered} C_{i} \dot{u}_{i}(t)=-\frac{1}{R_{i}} u_{i}(t)+\sum\limits_{j=1}^{N} T_{i j} f_{j}\left(u_{j}\left(t-\tau_{j}\right)\right) \\ (i=1,2, \cdots, n) \end{gathered} $$ (1) 被提出, 并对系统(1)的线性化系统进行了稳定性分析. 此外, 亦有许多学者对上述系统的动力学性质进行了研究, 给出了在不同条件下系统(1)的平衡点全局渐近稳定的判据[4, 8]. 而相比具有有限时滞的系统，含有无穷时滞的系统在一定程度上更能准确地描述神经元之间实际的相互作用. 因此，无穷时滞被引入到Hopfield神经网络中.
Gopalsamy等[4]研究了具有无穷时滞的Hopfield神经网络系统
$$ \begin{gathered} \dot{U}_{i}(t)=-b_{i} U_{i}(t)+ \\ \sum\limits_{j=1}^{n} a_{i j} f_{j}\left(\mu_{j} \int_{-\infty}^{t} K_{i j}(t-s) U_{j}(s) \mathrm{d} s\right)+F_{i}(t) \\ (i=1,2, \cdots, n) \end{gathered} $$ (2) 并给出了解存在和解趋向于平衡点的判据. 在文献[9-10]中, 对于满足不同条件的激励函数, 通过Lyapunov泛函方法给出了系统(2)的平衡点与滞量无关的全局渐近稳定的充分条件. 而对于其他具有无穷时滞的神经网络的动力学性质亦有诸多学者进行了深入的研究. Liao等[11]通过构造合适的Lyapunov泛函给出了具有有限和无穷时滞的Cohen-Grossberg神经网络系统的平衡点全局吸引的判据. Zhao等[12]利用Lyapunov方法和线性矩阵不等式技术给出了一类双向联想记忆神经网络正不变集和全局指数吸引集存在的一些代数准则, 并对全局指数吸引域作出了估计. 赵洪涌等[13]给出了一类具有分布时滞的双向联想记忆神经网络的平衡态一致稳定和全局渐近稳定的充分条件. 钟守铭等[14]对细胞神经网络进行了研究, 给出了平衡点全局渐近稳定的几个判据. 此外, 廖晓峰等[15-16]对2类带连续分布时滞的神经网络在具有强核和弱核的情况下的渐近稳定性进行了研究. 然而, 对于系统(2), 亦有学者考虑其具有S分布时滞的动力学性质. 邓瑾等[17]、马亚锋等[18]给出了系统(2)具有S分布时滞的不变集、吸引集和全局渐近稳定性的判据. 而谌红美等[19]则利用Banach不动点定理, 通过构造Lyapunov泛函, 结合Hardy不等式和推广的Halanay时滞微分不等式, 给出了一类具有S分布时滞的细胞神经网络全局指数稳定的充分条件. 再有，卢文联等[20]研究了一类具有S分布的递归神经网络(亦称Grossberg-Hopfield神经网络)殆周期解的存在唯一性和全局稳定性. 此外, 还有许多学者对具有S分布时滞的神经网络进行了大量的研究[21-27]. 然而在以上的研究中更多地是通过构造合适的Lyapunov函数或泛函的方法来得到系统的稳定性质, 但是事实上构造Lyapunov函数或泛函并不是一件容易的事. 本文考虑具有S分布时滞的Hopfield神经网络系统
$$ \begin{gathered} \dot{x}_{i}(t)=-a_{i} x_{i}(t)+ \\ \sum\limits_{j=1}^{n} b_{i j} \int_{-\infty}^{0}\left[\mathrm{~d} K_{i j}(s)\right] f_{j}\left(x_{j}(t+s)\right) \\ (i=1,2, \cdots, n) \end{gathered} $$ (3) 式中：t≥0；ai、bij是实值常数；Kij(s)是(-∞, 0]上的单调不减的有界变差函数；函数fj(u)在(-∞, ∞)上是连续可微的.
系统(3)的初始条件为
$$ \begin{aligned} x_{i}(s)=& \varphi_{i}(s)(-\infty<s \leqslant 0) \\ &(i=1,2, \cdots, n) \end{aligned} $$ (3) 式中初始函数φi(s)(i=1, 2, …，n)在(-∞, 0]上是连续的, 并且存在α>0使得
$$ \int_{-\infty}^{0} \mathrm{e}^{-\alpha \theta}\left|\mathrm{d} K_{i j}(\theta)\right|<\infty $$ 受文献[5-7]的启发, 本文利用常微分方程比较原理和一种迭代技巧证明了系统解的有界性, 并基于M-矩阵理论和一类非线性代数方程组给出了系统(3)的平衡点全局吸引的一个充分条件.
1. 主要结论及证明
对系统(3)做一些假设. 假设系统(3)满足下列条件：
条件1 ai>0 (i=1, 2, …，n).
条件2 $2 f_{i}(0)=0, \left|f_{i}(u)\right| \leqslant Q_{i}\left(u \in \mathbb{R}, Q_{i}\right. $为正常数, i=1, 2, …，n).
条件3 $ \quad f_{i}^{\prime}(u)>0(u \in \mathbb{R})$, 且$0 <\bar{f}_{i}(u) < u(u>0) $, 其中
$$ \bar{f}_{i}(u)=\max \left\{f_{i}(u),-f_{i}(-u)\right\} $$ $$ (u>0, i=1,2, \cdots, n) $$ 条件4 $ \int_{-\infty}^{0} \mathrm{~d} K_{i j}(s)=1(i, j=1, 2, \cdots, n)$.
引理1 如果条件1~4成立, 那么系统(3)的任意解(x1(t), x2(t), …，xn(t))T有
$$ \limsup \limits_{t \rightarrow+\infty} \left|x_{i}(t)\right| \leqslant M_{i} $$ (i=1, 2, …，n), 其中非负常数Mi(i=1, 2, …，n)满足非线性代数方程组
$$ M_{i}= \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}\right) $$ $$ (i=1,2, \cdots, n) $$ 证明：由条件2和4以及系统(3)可得
$$ \begin{gathered} D^{+}\left|x_{i}(t)\right|=\operatorname{sgn}\left\{x_{i}(t)\right\} \dot{x}_{i}(t)= \\ \operatorname{sgn}\left\{x_{i}(t)\right\}\left(-a_{i} x_{i}(t)+\right. \\ \sum\limits_{j=1}^{n} b_{i j} \int_{-\infty}^{0}\left[\mathrm{~d} K_{i j}(s)\right] f_{j}\left.\left(x_{j}(t+s)\right)\right) \leqslant \\ -a_{i}\left|x_{i}(t)\right|+\sum\limits_{j=1}^{n}\left|b_{i j}\right| \int_{-\infty}^{0}\left[\mathrm{~d} K_{i j}(s)\right] \mid f_{j}\left(x _ { j } \left(t+\right.\right.\\ s))\mid\leqslant-a_{i}\left| x_{i}(t)\right|+\sum\limits_{j=1}^{n}\left| b_{i j} \right| \int_{-\infty}^{0}\left[\mathrm{~d} K_{i j}(s)\right] Q_{j} \leqslant\\ -a_{i}\left|x_{i}(t)\right|+\sum\limits_{j=1}^{n}\left|b_{i j}\right| Q_{j} \end{gathered} $$ (i=1, 2, …，n). 由此根据常微分方程比较原理得到
$$ \limsup \limits_{t \rightarrow \infty}\left|x_{i}(t)\right| \leqslant \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| Q_{j}=M_{i}^{(0)} $$ (i=1, 2, …，n). 因此对于任意充分小的正常数η>0, 存在一个充分大的T0=T0(η)>0使得当t>T0时, 有
$$ \left|x_{i}(t)\right| \leqslant M_{i}^{(0)}+\eta $$ (i=1, 2, …，n). 因此, 由条件3和系统(3)可得
$$ \begin{gathered} D^{+}\left|x_{i}(t)\right| \leqslant-a_{i}\left|x_{i}(t)\right|+ \\ \sum\limits_{j=1}^{n}\left|b_{i j}\right| \int_{-\infty}^{0}\left[\mathrm{~d} K_{i j}(s)\right]\left|f_{j}\left(x_{j}(t+s)\right)\right| \leqslant \\ -a_{i}\left|x_{i}(t)\right|+\sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(\int_{-\infty}^{T_{0}-t}\left[\mathrm{~d} K_{i j}(s)\right] \cdot\right. \\ \left|f_{j}\left(x_{j}(t+s)\right)\right|+\int_{T_{0}-t}^{0}\left[\mathrm{~d} K_{i j}(s)\right]\left.\left|f_{j}\left(x_{j}(t+s)\right)\right|\right) \leqslant\\ -a_{i}\left|x_{i}(t)\right|+\sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(\int_{-\infty}^{T_{0}-t}\left[\mathrm{~d} K_{i j}(s)\right] Q_{j}+\right. \\ \int_{T_{0}-t}^{0}\left[\mathrm{~d} K_{i j}(s)\right] \bar{f}_{j}\left.\left(M_{j}^{(0)}+\eta\right)\right)<-a_{i}\left|x_{i}(t)\right|+ \\ \sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(r_{i j}(t)+\bar{f}_{j}\left(M_{j}^{(0)}+\eta\right)\right) \end{gathered} $$ (i=1, 2, …，n), 其中
$$ r_{i j}(t)=\int_{-\infty}^{T_{0}-t}\left[\mathrm{~d} K_{i j}(s)\right] Q_{j} $$ (i, j=1, 2, …，n). 根据条件4容易知道
$$ \lim \limits_{t \rightarrow+\infty} r_{i j}(t)=\lim \limits_{t \rightarrow+\infty} \int_{-\infty}^{T_{0}-t}\left[\mathrm{~d} K_{i j}(s)\right] Q_{j}=0 $$ (i, j=1, 2, …，n). 根据常微分方程比较原理得到
$$ \begin{gathered} \left|x_{i}(t)\right| \leqslant \mathrm{e}^{-a_{i}\left(t-T_{0}\right)}\left|x_{i}\left(T_{0}\right)\right|+ \\ e^{-a_{i} t} \int_{T_{0}}^{t} \mathrm{e}^{a_{i} s}\left[\sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(r_{i j}(s)+\bar{f}_{j}\left(M_{j}^{(0)}+\eta\right)\right)\right] \mathrm{d} s \end{gathered} $$ (t>T0, i=1, 2, …，n). 对不等号右端的积分项应用洛必达法得到
$$ \begin{gathered} \lim \limits_{t \rightarrow+\infty} \mathrm{e}^{-a_{i} t} \int_{T_{0}}^{t} \mathrm{e}^{a_{i} s}\left[\sum _ { j = 1 } ^ { n } | b _ { i j } | \left(r_{i j}(s)+\right.\right. \\ \left.\left.\bar{f}_{j}\left(M_{j}^{(0)}+\eta\right)\right)\right] \mathrm{d} s= \\ \lim \limits_{t \rightarrow+\infty} \frac{1}{a_{i} \mathrm{e}^{a_{i} t}} \mathrm{e}^{a_{i} t}\left[\sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(r_{i j}(t)+\bar{f}_{j}\left(M_{j}^{(0)}+\eta\right)\right)\right]= \\ \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}^{(0)}+\eta\right) \end{gathered} $$ (i=1, 2, …，n). 由此不等式成立
$$ \begin{gathered} \limsup \limits_{t \rightarrow+\infty}\left|x_{i}(t)\right| \leqslant \lim \limits_{t \rightarrow+\infty}\left(\mathrm{e}^{-a_{i}\left(t-T_{0}\right)}\left|x_{i}\left(T_{0}\right)\right|+\right.\\ \left.\mathrm{e}^{-a_{i} t} \int_{T_{0}}^{t} \mathrm{e}^{a_{i s}}\left(\sum\limits_{j=1}^{n}\left|b_{i j}\right|\left(r_{i j}(s)+\bar{f}_{j}\left(M_{j}^{(0)}+\eta\right)\right)\right) \mathrm{d} s\right)= \\ \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}^{(0)}+\eta\right) \end{gathered} $$ (i=1, 2, …，n). 令η→0, 得到
$$ \limsup \limits_{t \rightarrow \infty}\left|x_{i}(t)\right| \leqslant \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}^{(0)}\right)=M_{i}^{(1)} \leqslant M_{i}^{(0)} $$ (i=1, 2, …，n). 重复以上过程, 得到一个满足
$$ \begin{gathered} \limsup \limits_{t \rightarrow \infty}\left|x_{i}(t)\right| \leqslant \frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}^{(k)}\right)= \\ M_{i}^{(k+1)} \leqslant M_{i}^{(k)} \end{gathered} $$ (4) (i=1, 2, …，n; k=1, 2, …)的非负的单调不增的收敛序列{Mi(k)}(i=1, 2, …，n; k=1, 2, …). 令
$$ \lim \limits_{k \rightarrow \infty} M_{i}^{(k)}=M_{i} $$ (i=1, 2, …，n), 那么对式(4)令k→∞, 就得到
$$ \limsup \limits_{t \rightarrow+\infty} \left|x_{i}(t)\right| \leqslant M_{i} $$ (i=1, 2, …，n), 并且
$$ M_{i}=\frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}\right) $$ (i=1, 2, …，n). 引理1证毕.
引理2[28] 令
$$ Z^{n \times n}=\left\{\left(f_{i j}\right)_{n \times n} \mid f_{i j} \leqslant 0, i \neq j, i, j=1,2, \cdots, n\right\} $$ 并且F=(fij)n×n∈Zn×n, 则下面2个命题等价:
1) F的所有主子式非负.
2) 如果x≠0并且y=Fx, 那么存在下脚标i使得xi≠0，并且xiyi≥0.
定理1 如果条件1~4成立, 且矩阵$\hat{\boldsymbol{B}} $满足引理2中的条件1)或2), 那么系统(3)的平衡点(0, 0, …，0)T是全局吸引的. 其中$\hat{\boldsymbol{B}}=\left(\hat{b}_{i j}\right)_{n \times n}, \hat{b}_{i i}=a_{i}-\left|b_{i i}\right|, \hat{b}_{i j}=-\left|b_{i j}\right|(i \neq j ; i, j=1, 2, \cdots, n) $.
证明：假设Mi≥0(i=1, 2, …，n), 并且满足非线性代数方程组
$$ \begin{gathered} M_{i}=\frac{1}{a_{i}} \sum\limits_{j=1}^{n}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}\right) \\ (i=1,2, \cdots, n) \end{gathered} $$ (5) 先来证明Mi(i=1, 2, …，n)不可能同时大于零. 假设Mi(i=1, 2, …，n)同时大于零, 那么由条件3和式(5)得到
$$ M_{i} a_{i}<\sum\limits_{j=1}^{n}\left|b_{i j}\right| M_{j} $$ (i=1, 2, …，n). 可以写成矩阵形式
$$ -\hat{\boldsymbol{B}} \boldsymbol{M}<0 $$ (6) 式中M=(M1, M2, …，Mn)T>0. 令x=M>0且$ y= - \hat{\boldsymbol{B}} \boldsymbol{M} $. 那么根据引理2, 存在下脚标i使得
$$ M_{i} y_{i}=M_{i}\left(-\sum\limits_{j=1}^{n} \hat{b}_{i j} M_{j}\right) \geqslant 0 $$ 这便和式(6)矛盾. 因此Mi(i=1, 2, …，n)不可能同时大于零.
不失一般性, 假设Mn=0, 那么带有n个未知量Mi(i=1, 2, …，n)的非线性代数方程组(5)就退化为带有n-1个未知量Mi(i=1, 2, …，n-1)的非线性代数方程组
$$ M_{i}=\frac{1}{a_{i}} \sum\limits_{j=1}^{n-1}\left|b_{i j}\right| \bar{f}_{j}\left(M_{j}\right) $$ (i=1, 2, …，n-1). 再重复上面的讨论，一定存在某个k(1≤k≤n-1)使得Mk=0. 不失一般性，可以假设Mn-1=0. 再次重复上面的过程, 就得到M2=M3=…=Mn-1=0, 并且有
$$ M_{1}=\frac{1}{a_{1}}\left|b_{11}\right| \bar{f}_{1}\left(M_{1}\right) $$ 如果b11=0, 那么显然M1=0. 如果b11≠0并且M1>0, 那么由条件3得到
$$ \left(a_{1}-\left|b_{11}\right|\right) M_{1}<0 $$ 这便和a1-|b11|≥0矛盾. 因此
$$ M_{1}=M_{2}=\cdots=M_{n}=0 $$ 再由引理1, 得到
$$ \lim \limits_{t \rightarrow+\infty} x_{i}(t)=0 $$ (i=1, 2, …，n). 这就说明系统(3)的平衡点(0, 0, …，0)T是全局吸引的.
2. 数值模拟与结论
考虑一维系统
$$ \dot{x}(t)=-x(t)+b \int_{-\infty}^{0}\left[\operatorname{de}^{s}\right] \tanh (x(t+s)) $$ (7) 式中b是常数.
首先，讨论系统(7)的平衡点. 将x(t)=c(c为常数)带入系统(7)得
$$ c=b \tanh c $$ 根据双曲正切函数的性质, 得到
1) 若b≤1, 则系统(7)只有一个零平衡点.
2) 若b>1, 则系统(7)有3个平衡点, 1个正平衡点, 1个零平衡点, 1个负平衡点.
其次，分析系统(7)的渐近稳定性. 当b=0时, 系统(7)退化为常微分方程, 根据常微分方程理论知(7)的平衡点是渐近稳定的. 当b≠0时, 系统(7)的线性化系统的特征方程为
$$ \lambda+1-b \int_{-\infty}^{0} \mathrm{e}^{(\lambda+1) s} \mathrm{~d} s=0 $$ (8) 将λ=α+iβ代入到式(8)并将实虚部分离得
$$ \begin{gathered} \alpha+1-b \int_{-\infty}^{0} \mathrm{e}^{(\alpha+1) s} \cos (\beta s) \mathrm{d} s+ \\ \mathrm{i}\left(\beta-b \int_{-\infty}^{0} \mathrm{e}^{(\alpha+1) s} \sin (\beta s) \mathrm{d} s\right)=0 \end{gathered} $$ (9) 由式(9), 得到特征方程(8)的根的情况:
1) 当α+1≤0时, 特征方程(8)无根.
2) 当α+1>0且β≠0时, 特征方程(8)无根.
3) 当α+1>0且β=0且b < 0时, 特征方程(8)无根.
4) 当α+1>0且β=0且b>0时, 特征方程(8)有一个单根$\lambda=-1+\sqrt{b} $.
根据以上分析, 当特征方程(8)的根只具有负实部时, 即0 < b < 1时, 系统(7)的零解是渐近稳定的[29]. 综上所述，当0≤b < 1时, 系统(7)的零解是渐近稳定的.
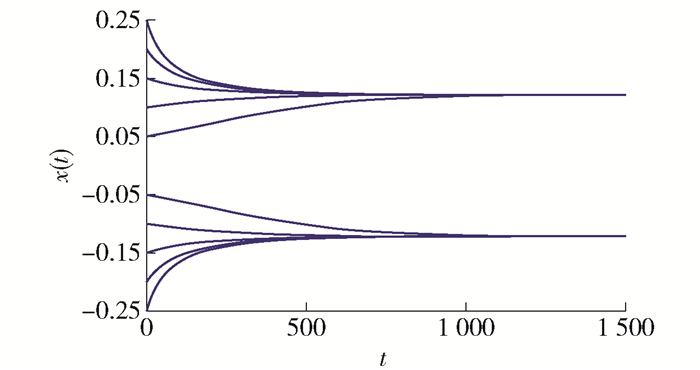
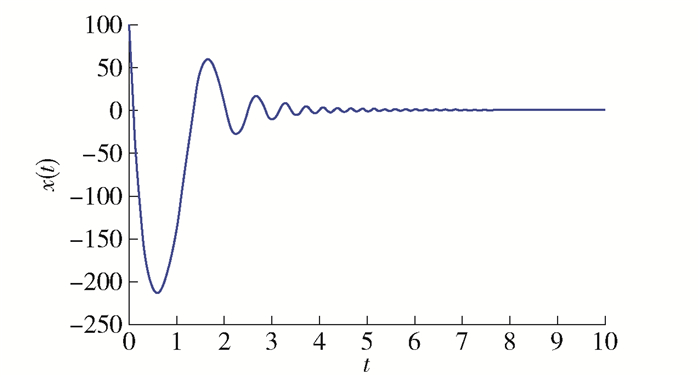
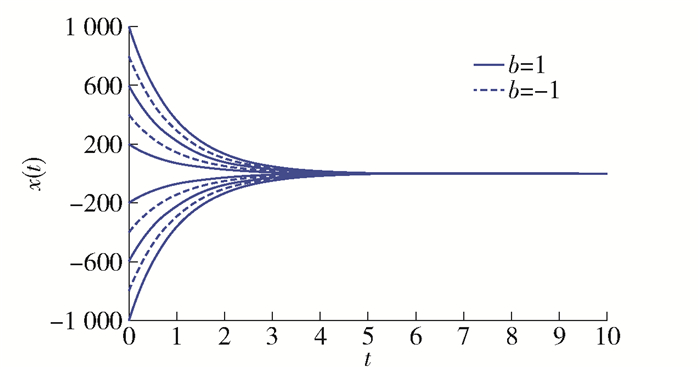
最后，通过数值模拟的结果来说明定理1的有效性. 容易看出系统(7)满足条件1~4, 且$\hat{\boldsymbol{B}}= (1-|b|) $. 而矩阵$ \hat{\boldsymbol{B}}$满足引理2中的条件1)或2)当且仅当|b|≤1. 因此由定理1知, 如果|b|≤1, 那么系统(7)的平衡点是全局吸引的. 事实上, 图 1表明, 当满足|b|≤1的条件时, 系统(7)唯一的平衡点是全局吸引的, 这说明了定理1是有效的. 图 2说明, 当b>1时, 系统(7)的解趋向于2个非零的位置, 而不再收敛到零平衡点. 实际上, 当b>1时, 系统(7)不再只有唯一的零平衡点, 而是衍生出另外的一正一负2个非零平衡点, 图 2中的解曲线实际上分别趋向于2个非零平衡点. 而图 3表明, 当b取得很小时, 系统(7)唯一的平衡点也是全局吸引的. 本文并未从理论上证明当b < -1时, 系统(7)唯一的平衡点是全局吸引的, 但大量的数值模拟显示当b取得更小时, 系统(7)在不同初始函数条件下的解曲线仍旧趋向于唯一的平衡点.
![]()
图 1 当b=1、b=-1时, 系统(7)对于不同初始函数的解Figure 1. Solution of system (7) corresponding to different initial functions when b=1 or b=-1![]()
图 2 当b=1.01时, 系统(7)对于不同初始函数的解Figure 2. Solution of system (7) corresponding to different initial functions when b=1.01![]()
图 3 当b=-1 000且初始函数φ=100时, 系统(7)的解Figure 3. Solution of system (7) when b=-1 000 and initial function φ=100 -
![]()
图 1 当b=1、b=-1时, 系统(7)对于不同初始函数的解
Figure 1. Solution of system (7) corresponding to different initial functions when b=1 or b=-1
![]()
图 2 当b=1.01时, 系统(7)对于不同初始函数的解
Figure 2. Solution of system (7) corresponding to different initial functions when b=1.01
-
[1] HOPFIELD J J. Neuralnetworks and physical systems with emergent collective computational abilities[J]. Proc Nat Acad Sci U S A, 1982, 79(8): 2554-2558. doi: 10.1073/pnas.79.8.2554
[2] HOPFIELD J J. Neurons with graded response have collective computational properties like those of two-state neurons[J]. Proc Nat Acad Sci U S A, 1984, 81(10): 3088-3092. doi: 10.1073/pnas.81.10.3088
[3] MARCUS C M, WESTERVELT R M. Stability of analog neural networks with delay[J]. Phys Rev A(3), 1989, 39(1): 347-359. http://www.onacademic.com/detail/journal_1000036026618710_18ec.html
[4] GOPALSAMY K, HE X. Stability in asymmetric Hopfield nets with transmission delays[J]. Phys D, 1994, 76(4): 344-358. doi: 10.1016/0167-2789(94)90043-4
[5] MA W B, HARA T, TAKEUCHI Y. Stability of a 2-dimensional neural network with time delays[J]. J Biol Systems, 2000, 8(2): 177-193. doi: 10.1142/S0218339000000110
[6] ZHANG S, MA W B, KUANG Y. Necessary and sufficient conditions for global attractivity of Hopfield-type neural networks with time delays[J]. Rocky Mountain J Math, 2008, 38(5): 1829-1840. http://www.researchgate.net/profile/Yang_Kuang2/publication/238880199_Necessary_and_Sufficient_Conditions_for_Global_Attractivity_of_Hopfield-Type_Neural_Networks_with_Time_Delays/links/00b49535714225846b000000
[7] MA W B, SAITO Y, TAKEEUCHI Y. M-matrix structure and harmless delays in a Hopfield-type neural network[J]. Appl Math Lett, 2009, 22(7): 1066-1070. doi: 10.1016/j.aml.2009.01.025
[8] 王林山, 徐道义. Hopfield型时滞神经网络的稳定性分析[J]. 应用数学和力学, 2002, 23(1): 59-64. doi: 10.3321/j.issn:1000-0887.2002.01.008 WANG L S, XU D Y. Stability analysis of Hopfield neural networks with time delay[J]. Appl Math Mech, 2002, 23(1): 59-64. (in Chinese) doi: 10.3321/j.issn:1000-0887.2002.01.008
[9] 周冬明, 曹进德. 一类具有连续分布时滞模型的稳定性[J]. 生物数学学报, 1998, 13(3): 292-295. doi: 10.3969/j.issn.1001-9626.1998.03.003 ZHOU D M, CAO J D. Stability of a class of continuously distributed delays model[J]. J Biomath, 1998, 13(3): 292-295. (in Chinese) doi: 10.3969/j.issn.1001-9626.1998.03.003
[10] 曹进德. 具有连续分布时滞模型的稳定性分析[J]. 工程数学学报, 2000, 17(1): 7-11. doi: 10.3969/j.issn.1005-3085.2000.01.002 CAO J D. Stability analysis of a continuously distributed delay model[J]. J Engrg Math, 2000, 17(1): 7-11. (in Chinese) doi: 10.3969/j.issn.1005-3085.2000.01.002
[11] LIAO X F, LI C D. Global attractivity of Cohen-Grossberg model with finite and infinite delays[J]. J Math Anal Appl, 2006, 315(1): 244-262. doi: 10.1016/j.jmaa.2005.04.076
[12] ZHAO Z H, JIAN J G. Positive invariant sets and global exponential attractive sets of BAM neural networks with time-varying and infinite distributed delays[J]. Neurocomputing, 2014, 142(1): 447-457. doi: 10.1016/j.neucom.2014.03.050
[13] 赵洪涌, 徐道义. 具有分布时滞的双向联想记忆神经网络稳定性分析[J]. 四川大学学报(自然科学版), 2001, 38(4): 65-67. https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX200104002.htm ZHAO H Y, XU D Y. Stability analysis of bidirectional associative memory neural networks with distributed delays[J]. Journal of Sichuan University (Natural Science Edition), 2001, 38(4): 65-67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX200104002.htm
[14] 钟守铭, 黄廷祝, 黄元清. 具有无穷时滞的细胞神经网络的稳定性分析[J]. 电子学报, 2001, 29(5): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU200105014.htm ZHONG S M, HUANG T Z, HUANG Y Q. The stability analysis of cellular networks with infinite delay[J]. Acta Electronica Sinica, 2001, 29(5): 1-4. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU200105014.htm
[15] 廖晓峰, 王炎, 吴中福, 等. 连续分布时延点格神经网络的稳定性[J]. 计算机研究与发展, 1999, 36(10): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ199910004.htm LIAO X F, WANG Y, WU Z F, et al. Stability of cellular neural networks with continuously distributed delay[J]. Journal of Computer Research and Development, 1999, 36(10): 1-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ199910004.htm
[16] 廖晓峰, 吴中福, 王康, 等. 带分布时延神经网络: 从稳定到振荡再到稳定的动力学现象[J], 电子与信息学报, 2001, 23(7): 687-692. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX200107009.htm LIAO X F, WU Z F, WANG K, et al. A switch form stability to oscillation back to stability for neural network with distributed delay[J]. Journal of Electronics and Information Technology, 2001, 23(7): 687-692. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX200107009.htm
[17] 邓瑾, 王林山, 徐道义. 具有S-型分布时滞的Hopfield神经网络模型的渐近行为[J]. 四川大学学报(自然科学版), 2004, 41(1): 19-23. doi: 10.3969/j.issn.0490-6756.2004.01.005 DENG J, WANG L S, XU D Y. Asymptotic behaviour of Hopfield neural networks with S-type distributed delays[J]. Journal of Sichuan University (Natural Science Edition), 2004, 41(1): 19-23. (in Chinese) doi: 10.3969/j.issn.0490-6756.2004.01.005
[18] 马亚锋, 王林山. S-分布时滞静态神经网络模型的不变集和吸引集[J]. 黑龙江大学学报(自然科学版), 2006, 23(4): 506-508. https://www.cnki.com.cn/Article/CJFDTOTAL-HLDZ200604022.htm MA Y F, WANG L S. Invariant and attracting sets of static neural networks with S-type distributed time delays[J]. Journal of Heilongjiang University (Natural Science), 2006, 23(4): 506-508. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HLDZ200604022.htm
[19] 谌红美, 王林山. 具有S分布时滞细胞神经网络的全局指数稳定性[J]. 中国海洋大学学报, 2012, 42(3): 96-100. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201203016.htm CHEN H M, WANG L S. Global exponential stability of cellular neural networks with S-distributed delays[J]. Periodical of Ocean University of China, 2012, 42(3): 96-100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201203016.htm
[20] 卢文联, 陈天平. 时滞神经网络殆周期解的全局稳定性[J]. 中国科学A辑数学, 2005, 35(7): 774-784. https://www.cnki.com.cn/Article/CJFDTOTAL-JAXK200507004.htm LU W L, CHEN T P. Global stability of almost periodic solutions of delayed neural networks[J]. Science China Mathematics, 2005, 35(7): 774-784. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JAXK200507004.htm
[21] 孙小淇, 王林山. S-分布时滞的随机Hopfield神经网络的稳定性[J]. 中国海洋大学学报, 2016, 46(10): 139-142. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201610019.htm SUN X Q, WANG L S. Stability of stochastic Hopfield neural network with S-type distributed delays[J]. Periodical of Ocean University of China, 2016, 46(10): 139-142. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201610019.htm
[22] 李延波, 王汝凉. S-分布时滞反应扩散Hopfield神经网络稳定性[J]. 哈尔滨理工大学学报, 2010, 15(2): 63-66. doi: 10.3969/j.issn.1007-2683.2010.02.016 LI Y B, WANG R L. Stability of reaction-diffusion Hopfield neural networks with S-type distributed delays[J]. Journal of Harbin University of Science and Technology, 2010, 15(2): 63-66. (in Chinese) doi: 10.3969/j.issn.1007-2683.2010.02.016
[23] 刘芳, 王林山. S-分布时滞随机高阶Hopfield神经网络的均方指数稳定性[J]. 河北师范大学学报(自然科学版), 2015, 39(4): 287-293. https://www.cnki.com.cn/Article/CJFDTOTAL-HBSZ201504004.htm LIU F, WANG L S. The mean square exponential stability of stochastic high order Hopfield neural networks with S-type distributed time delays[J]. Journal of Hebei Normal University(Natural Science Edition), 2015, 39(4): 287-293. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBSZ201504004.htm
[24] 刘博瑞, 王林山. S分布时滞静态递归神经网络周期解的存在与全局指数稳定性[J]. 中国海洋大学学报, 2010, 40(7): 159-162. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201007031.htm LIU B R, WANG L S. Existence and global exponential stability of periodic solution for static recurrent neural networks with S-type distributed delays[J]. Periodical of Ocean University of China, 2010, 40(7): 159-162. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201007031.htm
[25] 郗远霞, 王林山. 多重S-分布时滞二阶Hopfield神经网络的全局指数稳定性[J]. 滨州学院学报, 2012, 28(3): 18-25. doi: 10.3969/j.issn.1673-2618.2012.03.004 XI Y X, WANG L S. Global exponential stability of second-order Hopfield neural networks with multiple S-type distributed time delays[J]. Journal of Binzhou University, 2012, 28(3): 18-25. (in Chinese) doi: 10.3969/j.issn.1673-2618.2012.03.004
[26] 马成荣. 高阶S-分布时滞细胞神经网络的全局鲁棒指数稳定性[J]. 华东师范大学学报(自然科学版), 2011(5): 12-20. doi: 10.3969/j.issn.1000-5641.2011.05.003 MA C R. Global robust exponential stability of high-order cellular neural networks with S-type distributed delays[J]. Journal of East China Normal University(Natural Science), 2011(5): 12-20. (in Chinese) doi: 10.3969/j.issn.1000-5641.2011.05.003
[27] 马成荣, 周凤燕, 高华. 具有S-分布时滞BAM神经网络的全局指数稳定性[J]. 生物数学学报, 2012, 27(4): 717-729. https://www.cnki.com.cn/Article/CJFDTOTAL-SWSX201204019.htm MA C R, ZHOU F Y, GAO H. Global exponential stability of BAM neural networks with S-type distributed delays[J]. J Biomath, 2012, 27(4): 717-729. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWSX201204019.htm
[28] BERMAN A A, PLEMMONS J. Nonnegative matrices in the mathematical sciences[C]//Computer Science and Applied Mathematics. New York-London: Academic Press, 1979: 1-161.
[29] KOLMANOVSKⅡ V, MYSHKIS A. Applied theory of functional differential equations[C]//Mathematics and its Applications 85. Dordrecht: Kluwer Academic Publishers Group, 1992: 1-198.
-
期刊类型引用(2)
1. 韩佳澎，周立群. 一类比例时滞细胞神经网络ω-周期解的全局多项式稳定性. 天津师范大学学报(自然科学版). 2025(01): 1-6 . 
百度学术
2. 高丽丽，潘玉荣，夏福全. 脉冲时滞G-Hopfield神经网络的稳定性分析. 宿州学院学报. 2024(12): 6-12 . 百度学术
其他类型引用(2)
下载:
计量
- 文章访问数: 119
- HTML全文浏览量: 7
- PDF下载量: 58
- 被引次数: 4
