Finite Element Modeling of Temperature Distribution During Temperature-controlled Radiofrequency Ablation of Liver Tumor
-
摘要:
为了提高肝肿瘤射频温控消融温度分布的预测精度，建立了具有比例积分（proportional integral，PI）反馈控制器的射频消融温度分布仿真模型，并且研究了有限元模型中不同传热方程（Pennes和Hyperbolic生物传热方程）对温度分布的影响.首先，利用单电极热消融仪对离体猪肝进行温控射频消融实验，电极针尖稳态温度设定为90℃，消融时间为600 s，并利用测温针获得各测温点的热消融数据.然后，建立具有PI控制器的肝肿瘤温控射频消融有限元模型，其中PI控制器通过反馈调节电压源来使针尖温度与实测数据保持一致，传热方程分别采用基于非傅里叶传热规律的Hyperbolic方程和基于傅里叶传热规律的Pennes方程，生物组织电导率和导热率选用温度依赖性函数.最后，通过仿真温度和实测温度进行对比验证.结果表明，相比于Hyperbolic方程，采用Pennes方程的仿真模型具有较高的精度，各测温点的仿真温度与实验结果之间的标准偏差、平均误差和最大误差的均值分别为0.78、1.46、2.90℃.因此，基于PI控制器和Pennes生物传热方程的肝肿瘤温控射频消融有限元模型能够有效地预测热消融温度.
-
关键词:
- 肝肿瘤 /
- 温控射频消融 /
- 比例积分(PI)反馈控制器 /
- Pennes方程 /
- Hyperbolic方程
Abstract:To improve the temperature prediction accuracy of liver tumor radiofrequency ablation (RFA), a temperature distribution model with a proportional integral (PI) feedback controller was established. Furthermore, the influences of different heat transfer equations (Pennes and Hyperbolic equations) on temperature distribution in simulation models were studied. First, a single-electrode RFA ablator was used to perform RFA experiments on ex vivo pig livers. The steady-state temperature of the electrode tip was set to 90℃, the ablation time was 600 s, and the ablation data of the temperature measurement points was obtained by using thermometers. Second, a finite element model was constructed in combination with a PI controller. The PI controller dynamically adjusted the voltage source to maintain the tip temperature consistent with the experimental data. Hyperbolic equation based on the non-Fourier heat transfer law and Pennes equation based on the Fourier heat transfer law were investigated. Temperature-dependent functions for the electrical conductivity and thermal conductivity of the biological tissue were employed. Finally, the simulation data was verified by comparison with the measured temperatures. Results show that compared with Hyperbolic equation, the simulation model using Pennes equation achieves higher prediction accuracy. The mean values of the standard deviation, the average error and the maximum error between the simulations and the measurements are 0.78, 1.46 and 2.90℃, respectively. Therefore, the finite element model based on PI controller and Pennes bio-heat transfer equation can effectively predict RFA temperatures.
-
随着微创技术的发展，射频消融术(radiofrequency ablation，RFA)已被广泛地用于治疗肝肿瘤疾病.相比于传统的外科切除术，非开放式的RFA具有微创、安全、适应症广、并发症少、术后恢复快和费用低等优点[1-3].特别是对于肿瘤多发或肿瘤位于不可切除部位的患者而言，消融技术已成为行之有效的手段[4]. RFA装置通常包括射频消融仪、消融电极针和负电极板，其通过由交变电流(350~500 kHz)[5]产生的热量来杀灭肿瘤细胞.根据控制模式，射频消融仪可分为温控型、功率控制型和阻抗控制型.目前，临床中较常用的是温控型射频消融仪，其根据电极针尖的预设温度对输出功率进行补偿调节以获得恒定的中心温度，因此在整个消融过程中电压是不断变化的[6].
RFA的治疗效果主要取决于热凝固区对肿瘤组织的适形覆盖(具有5~10 mm的安全边界)[7].在热消融手术过程中，难以实时地获取热凝固区的形状和尺寸，因此可通过建立精准的温度分布仿真模型来预测热消融过程中的靶组织凝固状况.仿真模型的求解方法、电压源的设置和生物传热方程的选择对预测精度具有至关重要的作用.数值求解方法主要包括有限差分法、有限元法、边界法和MonteCarlo法等，其中有限元法能够有效地计算RFA问题的近似解.在电压源方面，有些学者为了简化温度分布仿真模型，将电压源设置为固定值[8]，但仿真结果存在较大误差；另外有些学者尝试利用PI算法控制电压源来建立RFA有限元模型[9-10]，研究表明与采用固定电压相比，基于PI控制器的电压源模式具有较小的仿真误差.生物传热方程主要包括基于傅里叶传热规律的Pennes方程和基于非傅里叶传热规律的Hyperbolic方程，目前肝肿瘤的RFA温度分布仿真模型大多采用Pennes传热方程[10-13].
为了提高温度仿真的精度，本研究基于RFA-I型温控射频消融仪(北京博莱德光电技术开发有限公司)和离体猪肝实验建立了具有PI反馈调节的RFA温度分布有限元模型，建模过程利用Comsol Multiphysics软件(COMSOL Inc.，Palo Alto，CA，USA)来实现.离体猪肝温控RFA中所采用的消融针为单针直线型电极.本文还进一步通过研究不同传热模式(Pennes方程和Hyperbolic方程)对有限元仿真结果的影响建立了具有较高预测精度的温度分布仿真模型.
1. 材料与方法
1.1 实验装置
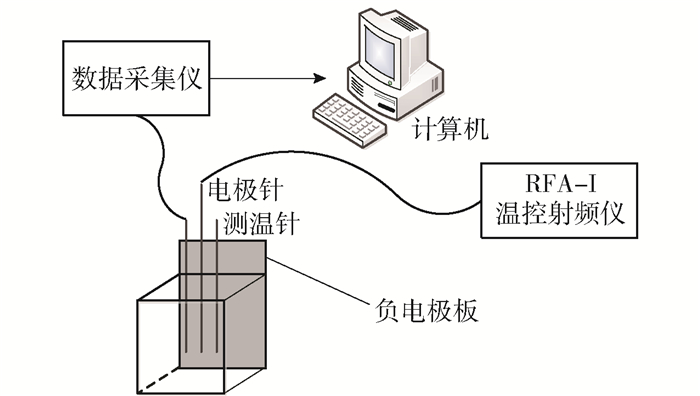
本研究的离体猪肝温控RFA实验平台包括RFA-I型温控射频消融仪、RFA0115型射频消融电极针、负电极板、多路数据采集装置(34970A; Agilent Technologies Inc., Santa Clara, CA, USA)、测温针、实验模具和新鲜的离体猪肝等，其中RFA-I、消融电极针、猪肝组织和负电极板构成闭合回路，如图 1所示. RFA-I型温控射频消融仪的工作频率为330 kHz，最大输出功率为200 W，中心治疗温度分为80、85、90和95 ℃ 4个水平；RFA0115型消融电极针由电极针尖、灌注部分和绝缘杆构成.电极针的长度为150 mm，工作部分电极直径为2.2 mm，消融范围为25 mm×40 mm.
1.2 离体猪肝的射频消融实验
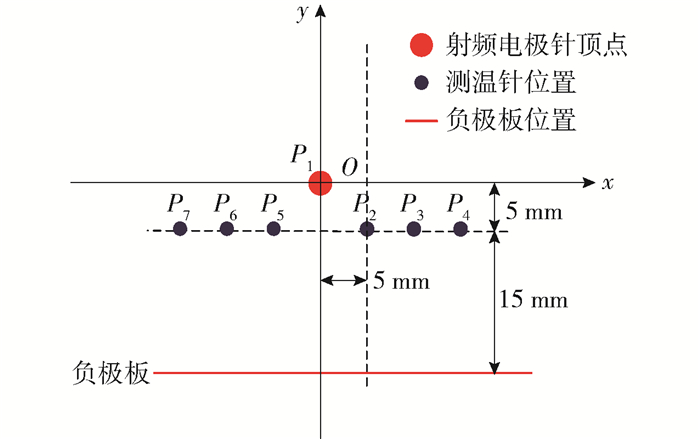
RFA实验材料为新鲜的离体猪肝，每块猪肝组织被切割成70 mm×65 mm×40 mm. RFA-I型温控射频消融仪的参数设置如下：中心温度为90 ℃，温升速率为25 ℃/min，消融时间为600 s.环境温度为20 ℃，电极针平行于负电极板并且插入猪肝组织内的深度为40 mm，电极针尖(P1)与负极板的竖直距离为20 mm，6个测温点(P2、P3、P4、P5、P6和P7)对称地分布于消融电极针两侧，如图 2所示.
![]()
图 2 电极针、测温针和负极板位置Figure 2. Position illustrations of electrode needle, thermometers and negative plate2. RFA温度分布的有限元仿真
2.1 几何建模
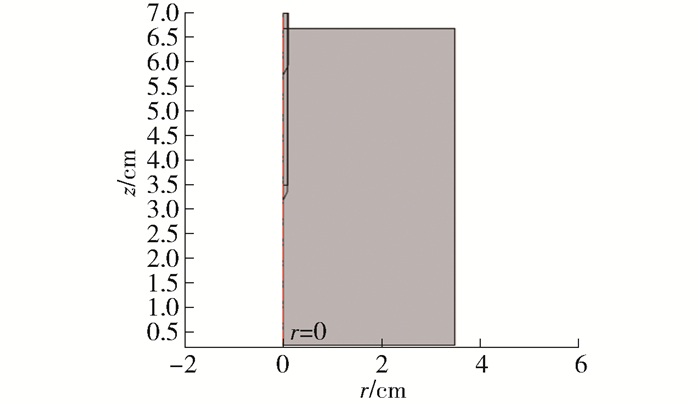
为了提高有限元模型的计算效率，建立离体猪肝的二维轴对称模型，其中射频电极针被设置为对称轴，电极针尖P1坐标为(0 mm，32.5 mm)，猪肝组织宽度和高度分别为35、65 mm，如图 3所示.
2.2 生物传热建模
有限元仿真模型利用生物传热方程计算组织内的热量传递.目前常用的传热方程主要包括Hyperbolic方程[14]和Pennes方程[15].为了研究传热方程对仿真结果的影响，本研究对这2种方程分别进行了有限元建模.
Hyperbolic方程适用于较高频率下的极端传热情况，其可考虑到组织内部热传递存在的弛豫时间τ(热能量传递到组织内部最近单元所需的特征时间，肝脏组织中τ=16 s) [16]. Hyperbolic方程的表达式为
$$ \begin{array} [c]{c} \frac{\partial^{2} T}{\partial t^{2}}({\mathop x\limits_ \sim }, y, z, t) +\frac{1}{\tau} \frac{\partial T}{\partial t}({\mathop x\limits_ \sim }, y, z, t)-\frac{k}{\rho c \tau} \Delta T({\mathop x\limits_ \sim }, y, z, t)=\\ \frac{1}{\rho c \tau} q_{\mathrm{r}}({\mathop x\limits_ \sim }, y, z, t)+\frac{1}{\rho c} \frac{\partial q_{\mathrm{r}}}{\partial t}({\mathop x\limits_ \sim }, y, z, t) \end{array} $$ (1) 式中：T(${\mathop x\limits_ \sim }$, y, z, t)为特定点在t时刻的温度，℃；τ为弛豫时间，s；ρ为密度，kg/m3；c为比热容，J/(kg·K)；k为导热率，W/(m·K)；qr为电磁热源.
Pennes生物传热方程考虑了血流和生物代谢活动的影响，其表达式简单，是最经典、应用最广泛的传热模型. Pennes方程的表达式为
$$ \rho c \frac{\partial T}{\partial t}=\nabla(k \nabla T)-\rho_{\mathrm{b}} c_{\mathrm{b}} \omega_{\mathrm{b}}\left(T-T_{\mathrm{b}}\right)+Q_{\mathrm{m}}+Q_{\mathrm{hs}} $$ (2) 式中：T为组织温度，℃；Tb为动脉血液温度，℃；t为消融时间，s；ρ为组织密度，kg/m3；c为比热容，J/(kg·K)；ωb为血液灌注率，s－1；Qm为代谢生热率，W/m3；Qhs为由RFA发生器产生的热量，W/m3.
本研究是基于离体猪肝实验进行的，忽略血液灌注和代谢生热，Pennes生物传热方程可简化为
$$ \rho c \frac{\partial T}{\partial t}=k \nabla^{2} T+Q_{\mathrm{hs} } $$ (3) 2.3 初始值和边界条件
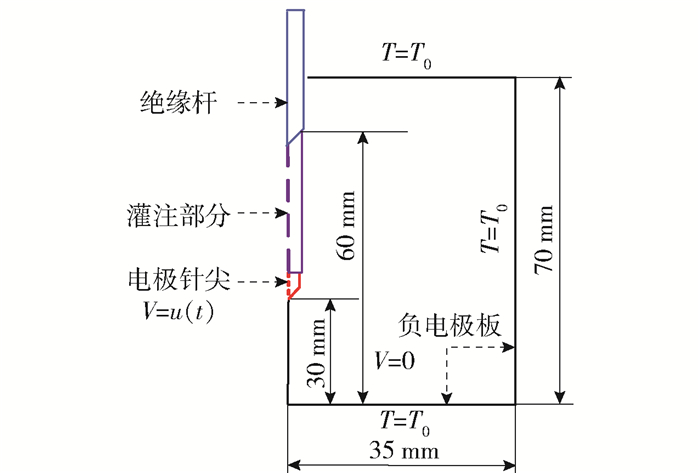
在RFA的有限元模型中，组织的初始温度、电极针尖的初始温度和测温针的初始温度被设定为环境温度
$$ T=T_{0}=20^{\circ} \mathrm{C}, t=0 $$ (4) 初始时刻的电压值为零，有限元模型中的电极针尖和接地边界的电压可由
$$ V=\left\{\begin{array}{l} {u(t), t>0} , \;\;消融电极针尖\\ {0}, \;\; \qquad \qquad 负电极板 \end{array}\right. $$ (5) 表示，式中u(t)为随时间变化的电压，由PI控制器控制.RFA有限元模型中电极针尖和猪肝组织的电边界和热边界条件如图 4所示.
2.4 基于PI控制器的反馈电压源设置
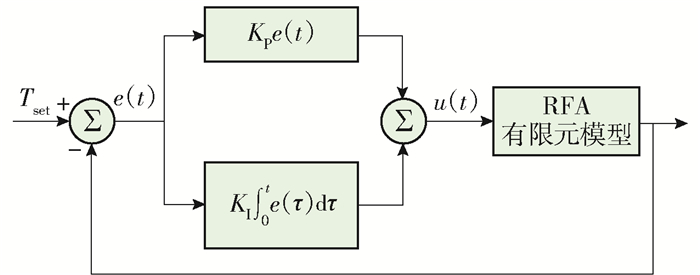
基于电极针尖设定温度Tset和电极针尖实测值T，采用PI控制器获得电极针尖处的电压，u(t)可以表示为
$$ u(t)=K_{\mathrm{p}} e(t)+K_{1} \int_{0}^{t} e(\tau) \mathrm{d} \tau $$ (6) 式中：e(t)为电极针尖实测值T与电极针尖设定温度Tset之间的差值；KP和KI分别表示比例系数和积分系数.基于PI控制器的电压源的反馈控制流程如图 5所示.
2.5 模型参数的设置
研究表明，在实际RFA过程中，离体猪肝组织的特性参数随着温度而改变[17].为了提高温度分布仿真模型的预测精度，生物组织的σ和k参数选取温度依赖性函数.消融电极针以及离体猪肝的热物性参数和电参数如表 1、2所示.
表 1 RFA电极针的热物性参数和电参数Table 1. Thermal and electrical properties of RFA electrode模型 材料 σ/(S·m-1) k/(W·(m·K)-1) ρ/(kg·m-3) c/(J·(kg·K)-1) 针尖 Ni-Ti 1×108 18 6 450 840 灌注部分 不锈钢 4×106 71 21 500 132 绝缘杆 聚氨酯 1×10-5 0.026 70 1 045 表 2 离体猪肝组织的热物性参数和电参数Table 2. Thermal and electrical properties of ex vivo pig liver就离体猪肝组织而言，则有σref=0.2 (S/m)[17]，kref=0.52 (W/(m·K))[17]，Tref=20 ℃，即
$$ \sigma(T)=0.2+0.004\left(T-T_{\mathrm{ref}}\right) $$ (7) $$ k(T)=0.52+0.001 \;3\left(T-T_{\mathrm{ref}}\right) $$ (8) 3. 结果
3.1 离体猪肝RFA结果
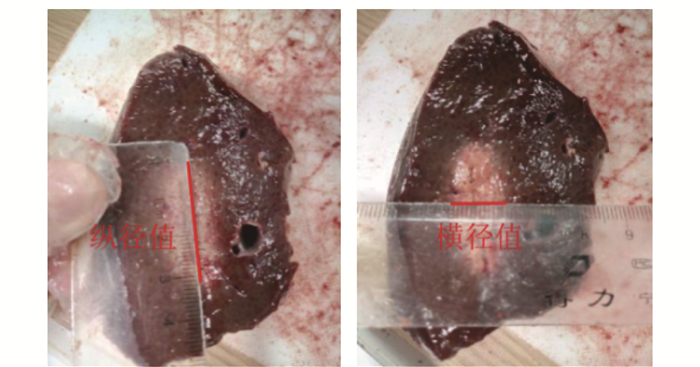
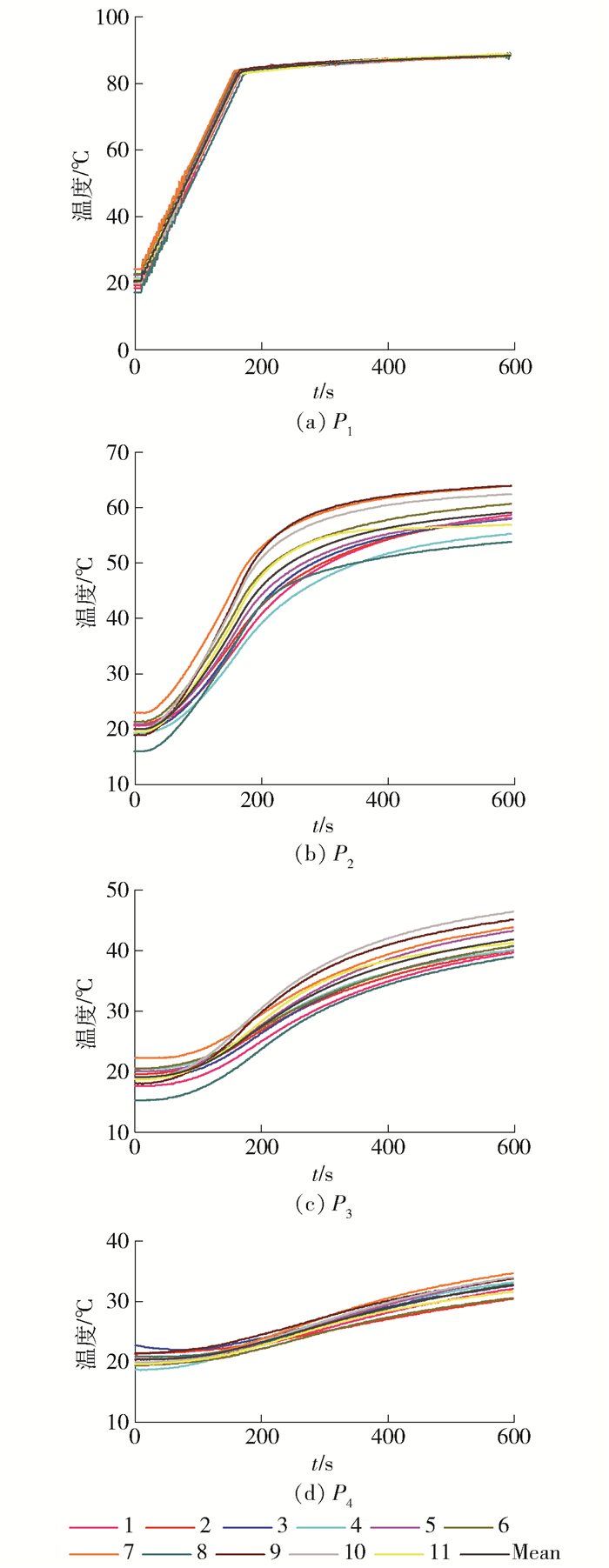
本研究针对21例离体猪肝进行温控射频消融实验，每例实验后沿着平行于射频电极针的方向切开，观察热凝固区内是否存在血管.剔除存在血管的实验组别，共获得11例可用数据(实验序号分别为1~11). 图 6为温控射频消融实验所获得的离体猪肝组织的热凝固区剖面图.热凝固区呈椭圆形状，其面积用S表示；沿电极针方向的凝固区尺寸为纵径值(2a)，与电极针垂直的凝固区尺寸为横径值(2b). 表 3为11例猪肝RFA凝固区的剖面横纵径值和面积大小，所有数据均采用平均值±标准差(Mean±SD)的形式表示.由于测温点P2、P3、P4和P5、P6、P7关于电极针对称，所以仅给出了P1、P2、P3、P4点的温升曲线图，如图 7所示，并对每个测温点的温度求平均值以表示该点的实验结果.
表 3 离体猪肝RFA热凝固区的横纵径值和面积Table 3. Transverse and longitudinal diameters and areas of RFA coagulation zone实验组 2a/mm 2b/mm S/mm2 1 34 14 374 2 36 12 339 3 33 11 285 4 32 12 302 5 28 12 264 6 30 13 306 7 32 15 377 8 40 13 408 9 37 13 378 10 36 12 339 11 38 13 388 Mean±SD 34.2±3.6 12.7±1.1 342±47 ![]()
图 7 离体猪肝温控射频消融实验温升曲线Figure 7. Temperature-rising curves of ex vivo pig livers in temperature-controlled RFA experiments3.2 有限元仿真结果
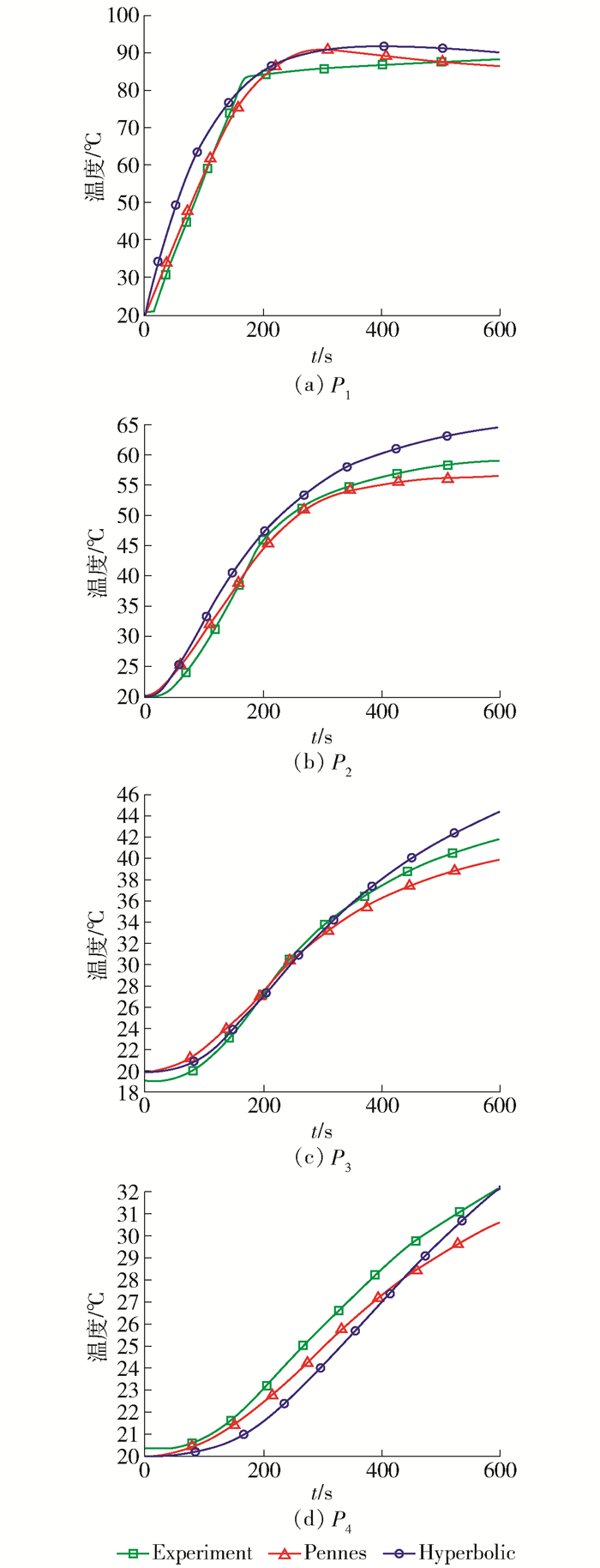
本研究基于针尖实测温度T和预设温度Tset的差值并采用PI控制器来反馈调节RFA有限元仿真中的电压源，PI控制的系数是基于离体实验数据采用试错法获得的[18].由于在离体猪肝实验中测得针尖电极的平均温度为88 ℃，如图 7所示，因此Tset=88 ℃.还研究了采用不同生物传热方程的有限元仿真结果，其中基于Hyperbolic和Pennes生物传热方程的有限元模型的最佳PI系数如表 4所示，不同测温点的温升对比曲线如图 8所示.
表 4 PI反馈控制器的参数设置Table 4. Parameter settings of PI feedback controller参数 Hyperbolic Pennes KP 0.24 0.17 KI 0.003 0.004 5 T/℃ 88 88 ![]()
图 8 基于PI反馈控制电压源的温升曲线图Figure 8. Temperature-rising curves using PI feedback controller从图 8可以看出，在采用Hyperbolic传热方程的情况下，距针尖较近的点(如P2和P3点)的仿真温度高于实测温度，远场点P4处的仿真温度低于实测温度.此外，消融过程中测温点P1、P2和P3的温度值高于采用Pennes传热方程情况下的温度. 表 5列出了采用不同传热方程的有限元仿真结果与实验值之间的误差，其中采用Pennes方程时各测温点温度的仿真结果和实验值之间的标准偏差、平均值和最大误差的均值分别为0.78、1.46、2.90 ℃；采用Hyperbolic方程时标准偏差、平均值和最大误差的均值分别为1.13、2.21、4.36 ℃.结果表明，相比于Hyperbolic方程，基于Pennes方程的各测温点的仿真温度更加符合实际情况.
表 5 基于不同生物传热模型的仿真误差的比较Table 5. Comparison of simulation temperature errors based on different bio-heat transfer models测温点 标准偏差/℃ 平均误差/℃ 最大误差/℃ P H P H P H P1 1.55 1.87 2.40 3.62 5.49 7.74 P2 0.67 1.43 1.43 3.33 2.60 5.32 P3 0.47 0.67 1.12 0.86 1.95 2.59 P4 0.45 0.56 0.88 1.04 1.55 1.79 均值 0.78 1.13 1.46 2.21 2.90 4.36 注：P表示Pennes方程，H表示Hyperbolic方程. 4. 结论
1) 基于离体猪肝消融实验建立了具有PI反馈控制器的肝肿瘤RFA温度分布有限元仿真模型，研究表明，PI控制器能够精确地调节有限元仿真模型中的电压变化.
2) 研究了Pennes生物传热方程和Hyperbolic生物传热方程对RFA仿真模型的影响，相比于非傅里叶传热模式，基于Pennes生物传热方程的温控射频消融有限元仿真模型具有较高的预测精度.
3) 在后续研究中，可基于人体肝脏的CT图像构建真实的肝脏几何模型，在有限元模型中加入血液灌注项，并结合动物活体实验，获得适用于人体肝脏的温控射频消融有限元模型.
-
![]()
图 2 电极针、测温针和负极板位置
Figure 2. Position illustrations of electrode needle, thermometers and negative plate
![]()
图 7 离体猪肝温控射频消融实验温升曲线
Figure 7. Temperature-rising curves of ex vivo pig livers in temperature-controlled RFA experiments
![]()
图 8 基于PI反馈控制电压源的温升曲线图
Figure 8. Temperature-rising curves using PI feedback controller
表 1 RFA电极针的热物性参数和电参数
Table 1 Thermal and electrical properties of RFA electrode
模型 材料 σ/(S·m-1) k/(W·(m·K)-1) ρ/(kg·m-3) c/(J·(kg·K)-1) 针尖 Ni-Ti 1×108 18 6 450 840 灌注部分 不锈钢 4×106 71 21 500 132 绝缘杆 聚氨酯 1×10-5 0.026 70 1 045 
下载: 导出CSV
表 3 离体猪肝RFA热凝固区的横纵径值和面积
Table 3 Transverse and longitudinal diameters and areas of RFA coagulation zone
实验组 2a/mm 2b/mm S/mm2 1 34 14 374 2 36 12 339 3 33 11 285 4 32 12 302 5 28 12 264 6 30 13 306 7 32 15 377 8 40 13 408 9 37 13 378 10 36 12 339 11 38 13 388 Mean±SD 34.2±3.6 12.7±1.1 342±47
下载: 导出CSV
表 4 PI反馈控制器的参数设置
Table 4 Parameter settings of PI feedback controller
参数 Hyperbolic Pennes KP 0.24 0.17 KI 0.003 0.004 5 T/℃ 88 88
下载: 导出CSV
表 5 基于不同生物传热模型的仿真误差的比较
Table 5 Comparison of simulation temperature errors based on different bio-heat transfer models
测温点 标准偏差/℃ 平均误差/℃ 最大误差/℃ P H P H P H P1 1.55 1.87 2.40 3.62 5.49 7.74 P2 0.67 1.43 1.43 3.33 2.60 5.32 P3 0.47 0.67 1.12 0.86 1.95 2.59 P4 0.45 0.56 0.88 1.04 1.55 1.79 均值 0.78 1.13 1.46 2.21 2.90 4.36 注：P表示Pennes方程，H表示Hyperbolic方程.
下载: 导出CSV
-
[1] 罗洪艳, 黄维, 潘进洪, 等.射频消融建模仿真的研究进展[J].激光杂志, 2014, 35(1):1-4. http://d.old.wanfangdata.com.cn/Periodical/jgzz201401001 LUO H Y, HUANG W, PAN J H, et al. Recent progress in modeling and simulation of radio frequency ablation[J]. Lasernal, 2014, 35(1):1-4. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jgzz201401001
[2] HAEMMERICH D, CHACHATI L, WRIGHT A S, et al. Hepatic radiofrequency ablation with internally cooled probes:effect of coolant temperature on lesion size[J]. IEEE Transactions on Biomedical Engineering, 2003, 50(4):493-500. doi: 10.1109/TBME.2003.809488
[3] POULOU L S, BOTSA E, THANOU I, et al. Percutaneous microwave ablation vs radiofrequency ablation in the treatment of hepatocellular carcinoma[J]. World Journal of Hepatology, 2015, 7(8):1054-1063. doi: 10.4254/wjh.v7.i8.1054
[4] 王笑茹, 高宏建, 吴水才, 等.肝肿瘤射频消融温度场仿真技术研究综述[J].中国医疗设备, 2018, 33(6):108-114. doi: 10.3969/j.issn.1674-1633.2018.06.029 WANG X R, GAO H J, WU S C, et al. Review of simulation techniques for radiofrequency ablation of liver tumor[J]. China Medical Equipment, 2018, 33(6):108-114. (in Chinese) doi: 10.3969/j.issn.1674-1633.2018.06.029
[5] CHEN X, LIU H P, LI M, et al. Advances in non-surgical management of primary liver cancer[J]. World Journal of Gastroenterology, 2014, 20(44):16630-16638. doi: 10.3748/wjg.v20.i44.16630
[6] JIN C, HE Z, LIU J. MRI-based finite element simulation on radiofrequency ablation of thyroid cancer[J]. Computer Methods and Programs in Biomedicine, 2014, 113(2):529-538. doi: 10.1016/j.cmpb.2013.12.007
[7] AHMED M, BRACE C L, LEE JR F T, et al. Principles of and advances in percutaneous ablation[J]. Radiology, 2011, 258(2):351-369. doi: 10.1148/radiol.10081634
[8] 刘鹏飞, 刘济全, 段会龙.基于真实解剖模型的心脏导管射频消融有限元仿真[J].中国生物医学工程学报, 2012, 31(4):532-538. doi: 10.3969/j.issn.0258-8021.2012.04.009 LIU P F, LIU J Q, DUAN H L. Finite element modeling simulation of cardiac radiofrequency catheter ablation based on heart chamber anatomy[J]. Chinese Journal of Biomedical Engineering, 2012, 31(4):532-538. (in Chinese) doi: 10.3969/j.issn.0258-8021.2012.04.009
[9] 黄维, 罗洪艳, 潘进洪, 等.构建基于肝脏CT图像的温控射频消融仿真模型[J].中国介入影像与治疗学, 2014, 11(8):532-536. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjryxyzlx201408016 HUANG W, LUO H Y, PAN J H, et al. Construction of temperature-controlled RFA simulation model based on liver CT images[J]. Chinese Journal of Interventional Imaging and Therapy, 2014, 11(8):532-536. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjryxyzlx201408016
[10] DUAN B, WEN R, FU Y, et al. Probabilistic finite element method for large tumor radiofrequency ablation simulation and planning[J]. Medical Engineering and Physics, 2016, 38(11):1360-1368. doi: 10.1016/j.medengphy.2016.08.007
[11] 王笑茹, 高宏建, 吴水才, 等.温控射频消融温度场仿真模型参数敏感性分析[J].中国医疗设备, 2017, 32(9):23-28. http://d.old.wanfangdata.com.cn/Periodical/ylsbxx201709006 WANG X R, GAO H J, WU S C, et al. Parametric sensitivity analysis of simulation model for temperature-controlled radiofrequency ablation temperature field[J]. China Medical Equipment, 2017, 32(9):23-28. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/ylsbxx201709006
[12] SINGH S, REPAKA R. Numerical study to establish relationship between coagulation volume and target tip temperature during temperature-controlled radiofrequency ablation[J]. Electromagnetic Biology and Medicine, 2018, 37(1):13-22. doi: 10.1080/15368378.2017.1422262
[13] HAEMMERICH D, WEBSTER J G. Automatic control of finite element models for temperature-controlled radiofrequency ablation[J]. Biomedical Engineering Online, 2005, 4(1):42-49. doi: 10.1186/1475-925X-4-42
[14] LÍPEZ-MOLINA J A, RIVERA M J, TRUJILLO M, et al. Assessment of hyperbolic heat transfer equation in theoretical modeling for radiofrequency heating techniques[J]. The Open Biomedical Engineering Journal, 2008, 2(1):22-27. doi: 10.2174/1874120700802010022
[15] PENNES H H. Analysis of tissue and arterial blood temperatures in the resting human forearm[J]. Journal of Applied Physiology, 1948, 1(2):93-122. doi: 10.1152/jappl.1948.1.2.93
[16] MOLINA J A L, RIVERA M J, TRUJILLO M, et al. Thermal modeling for pulsed radiofrequency ablation:analytical study based on hyperbolic heat conduction[J]. Medical Physics, 2009, 36(4):1112-1119. doi: 10.1118/1.3085824
[17] ROSSMANN C, HAEMMERICH D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures[J]. Critical Reviews in Biomedical Engineering, 2014, 42(6):467-492. doi: 10.1615/CritRevBiomedEng.2015012486
[18] ZHANG B, MOSER M A J, ZHANG E M, et al. A new approach to feedback control of radiofrequency ablation systems for large coagulation zones[J]. International Journal of Hyperthermia, 2017, 33(4):367-377. doi: 10.1080/02656736.2016.1263365
[19] ZHANG M, ZHOU Z, WU S, et al. Simulation of temperature field for temperature-controlled radio frequency ablation using a hyperbolic bioheat equation and temperature-varied voltage calibration:a liver-mimicking phantom study[J]. Physics in Medicine and Biology, 2015, 60(24):9455-9471. doi: 10.1088/0031-9155/60/24/9455
-
期刊类型引用(6)
1. 贾宇桐，周阿武，赵琛，张岩，张更新，谢亚勃，李建荣. MOF基单原子催化剂用于CO_2还原的研究进展. 北京工业大学学报. 2024(02): 216-229 . 
本站查看
2. 于笑笑，巢艳红，刘海燕，朱文帅，刘植昌. D-A共轭聚合强化光电性能及光催化CO_2转化. 化工进展. 2024(01): 292-301 . 百度学术
3. 谢林华，刘玉辉，李茹霞，吕佳澳，谢亚勃，李建荣. 缺陷型巯基功能化MOF的制备及其重金属离子吸附性能. 北京工业大学学报. 2024(10): 1151-1161 . 本站查看
4. 王忠冬，储巍巍，顾嘉，李为民. 对甲氧基肉桂酸甲酯合成研究进展. 精细石油化工进展. 2023(01): 39-43 . 百度学术
5. 陈红梅，杨泽群，陈搏实，李敏瑜，李海龙. CO_2与NO~-_2/NO~-_3电催化合成尿素研究进展. 能源环境保护. 2023(03): 88-97 . 百度学术
6. 施秋杰，王吴韬，王成成，段世雄，张呈旭. 钌基双金属聚酞菁电催化析氧性能研究. 贵金属. 2023(02): 43-49 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
- 被引次数: 14
