Visco-elasto-plasitc Constitutive Model for Unsaturated Soils
-
摘要:
非饱和土变形是随时间发展的，为了描述非饱和土随时间变化的长期变形行为，本文建立了非饱和土黏弹塑性模型.在已有的非饱和土率无关模型的基础上，考虑应变率对变形和强度影响，建立了一个非饱和土率相关的黏弹塑性模型.根据试验结果，应变率越大，屈服应力则越大，将屈服应力表示为应变率的函数，给出率相关影响的加载湿陷屈服面.利用一致性条件，给出了一维条件下非饱和土的增量方程.对模型进行数值分析，对模型基本行为进行预测.将模型退化饱和条件和率无关2种情形，利用已有的试验结果对模型进行了验证，结果表明模型可以用于预测非饱和土的蠕变行为.
Abstract:It is necessary to build a visco-elasto-plasitc constitutive model for unsaturated soils, because soils deform over time. Based on existed rate independent constitutive model, a rate dependent model which considers the influence of strain rate on soil behavior is developed. Previous test data indicated that the preconsolidate stress increased with the strain rate. Accordingly, the strain rate was included in the hardening equation, and thus the loading collapse yield surface was rate dependent. The one-dimensional constitutive equation of unsaturated soil was then obtained with the help of consistency condition. The model was used to compare with the existing test data. The model simulations show the model behaviors. The model was used to predicted experimental data for the degenerated cases included saturated condition and rate independent condition. Results show a good consistency.
-
Keywords:
- unsaturated soil /
- visco-elastoplasticity /
- constitutive model
-
土体受力变形是一个随时间发展而不断变化的过程，最终会达到一种相对稳定或破坏的状态.这种时间相关性，称之为黏性.土体的强度与其加载速率密切相关，土体的应力、应变和强度之间存在着显著的率相关性.率效应对黏土的应力-应变行为、超静孔隙水压力及其抗剪强度有很大的影响.根据土体的应力-应变-应变率关系建立相应的率相关模型、分析土体率相关特性已经成为近几十年广泛开展的研究课题.一维等速率试验、三轴不排水情况下的控制加载速率剪切试验是广大学者进行应变率效应研究的主要手段[1-2].
自提出土体具有黏塑性以来，国内外学者已经建立了大量的相关本构模型[3-9].基于建立模型所依据的不同理论，现有模型主要有3类：基本元件模型、基于蠕变特性的经验-半经验本构模型和基于塑性理论的弹黏塑性本构模型.基本元件模型是以胡克弹簧、牛顿黏壶和圣维南刚塑性体3种基本元件不同的串联或并联组合模拟土体的弹黏塑性特征，具有表达直观、简单，物理意义较明确的特点.但由于元件自身的特点，它们的不同组合并不能描述土体率相关的非线性特征.经验性或半经验性模型是在总结、归纳大量试验结果的基础上建立起来的本构模型.这类模型常常受到边界条件和加载条件的限制，通用性稍差.
弹黏塑性理论以经典塑性理论为基础，主要研究屈服面、关联准则和硬化规律随时间的变化关系，衍生出过应力理论模型和非稳态流动面模型.当前，广泛采取的方法是在塑性理论中考虑黏性对屈服面的贡献，建立应力-应变-应变率的屈服面模型或塑性应变与时间的关系.过应力理论[10]认为，利用动态加载面来判别是否有黏性产生，将动态加载面与静态加载面之差定义为过应力函数，只有当动态加载面在静态屈服面之外时，土体才会产生黏塑性变化.随后发展出采用势函数代替动态加载函数的方法，势函数的求取是该模型的关键.非稳态流动面理论是对无黏性弹塑性理论的发展，其在经典弹塑性理论的基础上引入一个与时间相关的应变函数因子，用以反映屈服面随时间的变化，从而建立起应力-应变与时间的关系.非稳态流动面理论与过应力理论在表观上有诸多相似之处，但两者所依据的流动法则和考虑时间的函数不同.
尽管目前已发展了大量率相关模型，但这些模型主要是针对饱和土，现阶段非饱和土黏性问题的研究太少，非饱和土本构模型研究也主要集中在率无关弹塑性模型方面[11].实际上非饱和土中由于涉及到孔隙气水的流动，其变形受时间影响很大，此外在多场耦合作用下，不同响应特征时间各不相同，率效应的研究对土体行为有重要影响[12].针对非饱和土率相关问题进行研究，建立相关的本构模型具有重要意义. Oka等[13]基于过应力理论建立了一个非饱和土的弹黏塑性模型. Pereira等[14]在非饱和土巴塞罗那(BBM)模型的基础上，将应变率影响引入模型中，建立一个简单的非饱和土率相关模型.
本文将在已有的非饱和土率无关模型的基础上，考虑应变率对非饱和土的影响，在模型中引入应变率，以考虑其对屈服应力、变形和强度的影响，建立一个率相关的弹黏塑性模型.随后对模型进行数值分析，以说明模型的率相关行为.
1. 模型建立
1.1 模型的基本变量
本节将采用Bishop有效应力$\widetilde{{{\sigma }_{ij}}}$和修正吸力$\widetilde{s}$为基本应力变量来建立模型，分别表示为
$$ \widetilde {{\sigma _{ij}}} = \overline {{\sigma _{ij}}} + s{S_{\rm{r}}}{\delta _{ij}} $$ (1) $$ \widetilde s = ns $$ (2) 式中：σij为净应力；s为基质吸力；Sr为饱和度；n为孔隙率.
模型的固相部分对应的土体变形分解为弹性和黏塑性2部分，即
$$ {\rm{d}}\varepsilon {\rm{ = d}}{\varepsilon ^{\rm{e}}} + {\rm{d}}{\varepsilon ^{{\rm{vp}}}} $$ (3) 式中:dεe代表弹性应变增量；dεvp代表黏塑性应变增量.
弹性关系可以表示为
$$ {\rm{d}}\varepsilon _{\rm{v}}^{\rm{e}} = \frac{\kappa }{{v\widetilde p}}{\rm{d}}\tilde p = \frac{1}{K}{\rm{d}}\tilde p $$ (4) 式中：$\tilde p$为平均有效应力；εve为弹性体应变；v为比体积；κ为弹性常数；K=(${v\widetilde p}$)/κ为弹性体积模量.
土水特征曲线采用简化双线性形式，假设边界线饱和度的变化为弹塑性，其斜率为λw，扫描线上只有弹性变化，其斜率为κw，饱和度的变化表示为
$$ {\rm{d}}{S_{\rm{r}}} = {\rm{d}}S_{\rm{r}}^{\rm{e}} + {\rm{d}}S_{\rm{r}}^{\rm{p}} $$ (5) 其中液相饱和度的弹性变化可以表示为
$$ {\rm{d}}S_{\rm{r}}^{\rm{e}} =-\frac{{{\kappa _{\rm{w}}}{\rm{d}}\widetilde s}}{{\widetilde s}} $$ (6) 当吸力发生屈服时，塑性饱和度增量为
$$ {\rm{d}}S_{\rm{r}}^{\rm{p}} =-\left( {{\lambda _{\rm{w}}}-{\kappa _{\rm{w}}}\frac{{{\rm{d}}\widetilde s}}{{\widetilde s}}} \right) $$ (7) 1.2 率效应的引入
加载湿陷屈服面是建立非饱和土本构模型的关键，它给出了屈服应力随吸力变化的关系.考虑不同因素对屈服应力的影响，可一般表示为
$$ {p_{\rm{c}}}\left( {X, s} \right) = {p_{{\rm{c0}}}}{p_{{\rm{cX}}}}\left( X \right){p_{{\rm{cw}}}}\left( s \right) $$ (8) 式中:pc0为饱和土的先期固结压力；X为硬化参数；pcX(X)为与X有关的屈服应力；pcw(s)为与s有关的屈服应力.
通常选择能够反映应力历史的塑性变形作为模型硬化方程的硬化参数.固相硬化方程中，首先选择塑性体应变作为硬化参数.此外，在耦合弹黏塑性模型中，由于液相变形对固相屈服有影响，因此，固相硬化应包含液相变形因素.但研究指出吸力不能作为一个硬化参数，此外，加载湿陷屈服面(LC)给出的吸力作用也无法反映干湿循环出现的滞回效应.而塑性饱和度可以反映液相饱和度的变化历史，在率无关模型中一般选用塑性体变和塑性饱和度作为硬化参数，即
$$ {p_{{\rm{cX}}}}\left( {\varepsilon _{\rm{v}}^{\rm{p}}, S_{\rm{r}}^{\rm{p}}} \right) = \exp \left( {{K_{\rm{s}}}\varepsilon _{\rm{v}}^{{\rm{vp}}}} \right)\exp \left( {-{k_{{\rm{sw}}}}{K_{\rm{w}}}} \right)S_{\rm{r}}^{\rm{p}} $$ (9) 式中
$$ \begin{array}{l} \;{K_{\rm{s}}} = v/\left( {\lambda-k} \right)\\ {K_{\rm{w}}}{\rm{ = }}1{\rm{/}}\left( {{\lambda _{\rm{w}}}-{k_{\rm{w}}}} \right) \end{array} $$ 式中：ksw为耦合系数；λ为正常固结线斜率.
屈服应力与吸力的关系可参考已有模型给出[15]
$$ {p_{{\rm{cw}}}}\left( s \right) = 1 + \phi \left[{{{\left( {\tilde s/{s_{\rm{a}}}} \right)}^\theta }-1} \right] $$ (10) 式中：sa为进气值；ϕ和θ为拟合参数.
已有研究表明，黏土的加载速率对土体变形和强度有重要影响，根据试验结果，加载速率越大，土体的先期固结压力也越大[16-17]，朱启银等[18]概括了17种黏土等速率试验结果，发现在一定应变率范围内归一化先期固结压力与加载速率成正比，应变率越大、屈服应力越高.因此，可将饱和土先期固结压力表示为应变率的函数[19-20]，即
$$ {p_{{\rm{c}}0}} = {p^{\rm{r}}}{\left( {\frac{{{{\dot \varepsilon }_{\rm{v}}}}}{{\dot \varepsilon _{\rm{v}}^{\rm{r}}}}} \right)^{\beta \left( s \right)}} $$ (11) 式中:pr为与参考应变率${\dot \varepsilon _{\rm{v}}^{\rm{r}}}$对应的先期固结压力；β(s)计算公式为
$$ \beta \left( s \right) = \beta \left( 0 \right)-bs $$ (12) 式中：b反映了吸力对β(0)的影响；β(0)为饱和土的先期固结压力与应变率函数关系的斜率，其大小为次固结系数与λ的比值.
将式(9)~(11)代入式(8)，即可得到最终LC屈服方程的表达式
$$ \begin{array}{l} {p_{\rm{c}}} = {p^{\rm{r}}}{\left( {\frac{{{{\dot \varepsilon }_{\rm{v}}}}}{{\dot \varepsilon _{\rm{v}}^{\rm{r}}}}} \right)^{\beta \left( s \right)}}\left\{ {1 + \phi \left[{{{\left( {\frac{{\tilde s}}{{{s_{\rm{a}}}}}} \right)}^\theta }-1} \right]} \right\} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\exp \left( {{K_{\rm{s}}}\varepsilon _{\rm{v}}^{\rm{p}}} \right)\exp \left( { -{k_{{\rm{sw}}}}{K_{\rm{w}}}S_{\rm{r}}^{\rm{p}}} \right) \end{array} $$ (13) 式(13)表明固相硬化方程与塑性体应变${\varepsilon _{\rm{v}}^{\rm{p}}}$、应变率${{{\dot \varepsilon }_{\rm{v}}}}$和塑性饱和度${S_{\rm{r}}^{\rm{p}}}$相关.
1.3 增量本构方程
为了简化，这里采用相关联流动法则确定非饱和土中固相的黏塑性应变增量，表示为
$$ {\rm{d}}\varepsilon _{\rm{v}}^{{\rm{vp}}} = \delta {\phi _{\rm{s}}}\frac{{\partial {f_{\rm{s}}}}}{{\partial \tilde p}} $$ (14) 对于塑性加载而言，利用一致性条件，硬化方程和流动法则代入，并对其进行求解，可得出黏塑性体变增量为
$$ {\rm{d}}\varepsilon _{\rm{v}}^{{\rm{vp}}} = \frac{1}{{{K_{\rm{s}}}}}\left( {\frac{{{\rm{d}}\tilde p}}{{\tilde p}}-{k_{{\rm{sw}}}}\frac{{{\rm{d}}\tilde s}}{{\tilde s}}-\beta \tilde p\frac{{{\rm{d}}{{\dot \varepsilon }_{\rm{v}}}}}{{{{\dot \varepsilon }_{\rm{v}}}}}} \right) $$ (15) 将式(4)(15)代入式(3)中，即可得到总的体变表达式为
$$ {\rm{d}}{\varepsilon _{\rm{v}}} = \left( {\frac{1}{K} + \frac{1}{{{K_{\rm{s}}}\tilde p}}} \right){\rm{d}}\tilde p-\frac{{{k_{{\rm{sw}}}}}}{{{K_{\rm{s}}}}}\frac{1}{{\tilde s}}{\rm{d}}\tilde s-\frac{{\beta \tilde p}}{{{K_s}{{\dot \varepsilon }_{\rm{v}}}}}{\rm{d}}{{\dot \varepsilon }_{\rm{v}}} $$ (16) 式中：dεv表示总的体应变增量；${\rm{d}}{{\dot \varepsilon }_{\rm{v}}}$表示体变率增量.式(16)表明土体的体变不仅与外力和吸力的变化有关，还与时间相关，利用该式可以对土体的黏塑性行为进行模拟.
2. 数值模拟
本节将利用已有试验来对模型进行数值分析.模型涉及到的参数主要有3类：
1) 饱和土相关参数，即λ、κ，此类参数可利用饱和土固结试验来获得.
2) 非饱和土相关参数，其中LC屈服面参数ϕ、θ通过非饱和土控制吸力的等向固结试验来获得；土水特征曲线参数λw、κw通过干湿循环试验来获得；耦合系数ksw则需通过上述2种试验相互组合来获得.
3) 率相关参数β(0)、b和pr，需要采用控制不同吸力条件下的蠕变试验来获得.
已有的试验大多针对饱和土，很少非饱和土时间效应的试验，所以接下来将模型退化为饱和土率相关(即s=0)和非饱和土率无关(即${{\dot \varepsilon }_{\rm{v}}}$=0)2种情形进行验证，并对率相关行为进行模拟.
2.1 饱和土(s=0)的数值模拟
首先选择Batiscan原状黏土的等向加载试验结果[21]来验证模型预测的合理性.该试验针对饱和土(即s=0)展开，模型参数如表 1所示[21].
表 1 模型参数及初始条件Table 1. Model parameters参数类型 参数取值 传统参数 λ=1.25, κ=0.037 应变率参数 pr=125 kPa
$\dot \varepsilon _{\rm{v}}^{\rm{r}}$=5×10-5/s
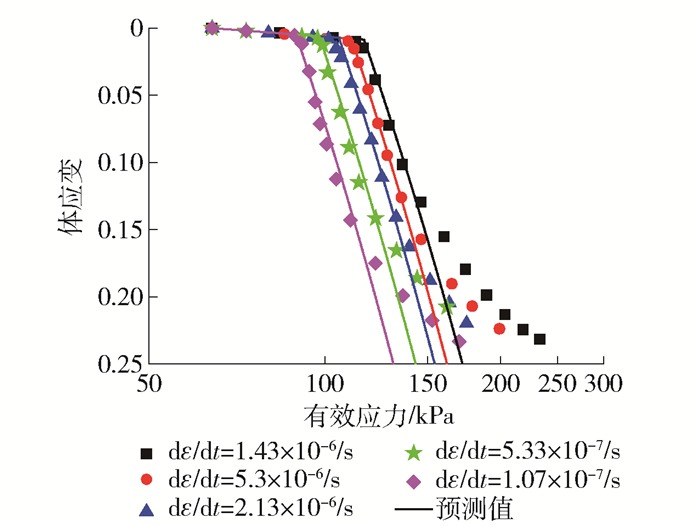
β(0)=0.04初始体积 v=2.92 图 1中，应变率越大，先期固结压力越大，两者存在正比关系.当应变率增大相同的倍数时，先期固结压力的增加量基本相同.在体应变小于15%时，二者具有较好的吻合性，尤其是应变率对先期固结压力的影响与试验结果相一致，但是当应变大于15%时，二者开始出现较为明显的差异性.这是由于原状黏土中普遍存在结构性，而本文在建立模型时，没有考虑到原状黏土的结构性，因此对前期应力应变特征具有较好的拟合性，而对次固结阶段中黏土结构性的影响反映较差.当应变率越大时，结构性的表现越明显，这种差异性出现越早.
![]()
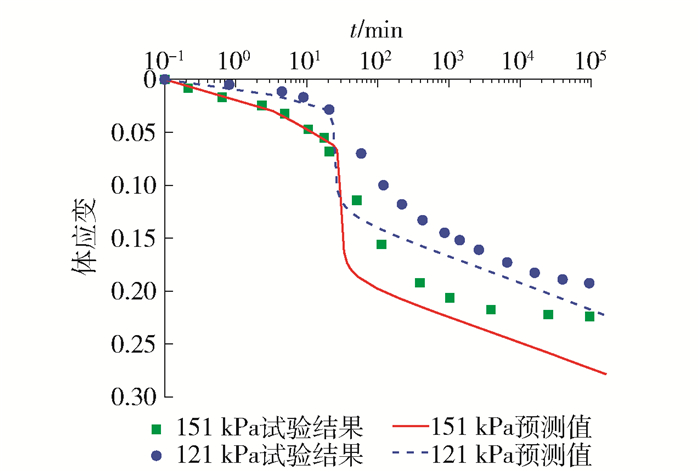
图 1 不同应变率下有效应力与体应变Figure 1. Relationship between volumetric strain and effective stress for saturated soils图 2中给出了饱和土(s=0)时不同应力水平下土体体变与时间关系的模拟结果.在2种应力下计算结果均表现了蠕变收敛的趋势，应力应变趋势与试验结果一致.但当应变不断增大时，模拟计算的变形随时间快速发展，黏滞性表现不明显.总体上来看，主要是由于模型未考虑原状黏土的结构性及固结过程中的耦合作用.同时，模型中采用的次固结系数是常数，与实际并不相符，这也对预测结果产生了一定的影响.通过对次固结系数进行简单的非线性修正(具体方法为取次固结系数是时间的函数)可以得到更符合试验结果的预测曲线[22].
2.2 非饱和土的数值模拟
接下来选择Sharma[23]给出的不同吸力(100 kPa和300 kPa)下的试验结果进行分析.根据试验结果确定模型相关参数取值列于表 2中.
表 2 模型参数及初始条件Table 2. Model parameters参数类型 参数取值 传统参数 λ=0.37, κ=0.03 LC参数 ϕ=0.45, θ=0.6 流体参数 λw=0.2, κw=0.015 耦合系数 ksw=0.6 初始应力 pc0=17 kPa, sa=0.77 kPa 初始饱和度 Sr1=0.65, Sr2=0.57, Sr3=0.5 初始体积 v1=2.31, v2=2.27, v3=2.26 由于缺少部分试验，以下模拟只能在Sharma[23]给出的试验结果的基础上对模型率相关模拟的弹塑性参数进行标定，给出假设的率相关参数β(0)=0.06、b=0.000 05、pr=17 kPa.
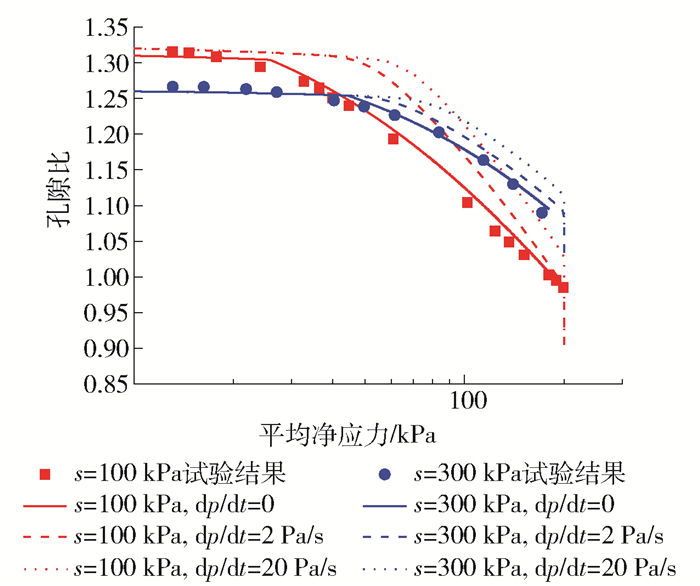
图 3给出了吸力分别为100 kPa和300 kPa时，不同加载速率的土体的孔隙比与净应力的预测曲线.试验结果取自Sharma[23]，当不考虑应变率影响，即dp/dt=0时，预测曲线与实测结果完全相符.在吸力作用下，土体的初始比体积随吸力增大而减小，屈服应力随吸力增加而变大，体积变化量随吸力增大而减小，反映了吸力对模型硬化的影响.
![]()
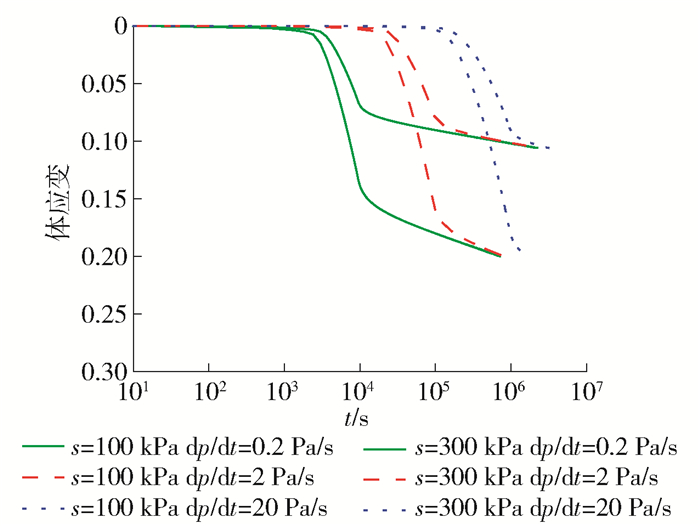
图 3 不同吸力、不同加载速率下孔隙比与应力的关系Figure 3. Relationship between void ratio and net stress under different suction and stress rate应力率增大，相应的应变率也会随之增大. 图 3中，当加载速率增大时，土体的先期固结压力明显增大，表明了加载速率对土体屈服的影响作用.当净应力达到200 kPa时，保持不变，土体产生了明显的蠕变变化趋势，如图 4所示.此外，吸力增大后，加载速率增大所引起的屈服应力的增大略有减小，这与应变率参数β的改变有关.总体而言，模型能够描述非饱和土相关的应力-应变-强度之间的变化趋势，从而验证模型的合理性.
![]()
图 4 不同吸力、不同加载速率下体变与时间的关系Figure 4. Relationship between volumetric strain and time under different suction and stress rate3. 结论
1) 本文提出了一个非饱和土弹黏塑性的本构模型.模型采用修正吸力和有效应力作为应力状态变量，考虑了先期固结压力与应变率在对数空间内存在正比关系，在硬化方程中引入了应变率的影响因素.整个模型中共含有10个模型参数，均可通过试验获得.
2) 将模型分别退化为饱和土率相关模型和非饱和土率无关模型，通过与已有试验数据的对比，从侧面验证了模型的合理性，同时给出相同吸力下不同应变率的率相关模拟结果.
3) 在等向固结压缩试验中模型能够很好反映应变率效应，对黏土的先期固结压力的率相关性取得了较好的模拟结果，无论是饱和土还是非饱和土其先期固结压力随着应变率的增大或应力加载率增大而增大.同时模型还可以预测停止加载后土体的蠕变行为，模拟结果在蠕变阶段表现出线性特征，如果对参数β进行修正则可以得到更好模拟结果.
-
![]()
图 1 不同应变率下有效应力与体应变
Figure 1. Relationship between volumetric strain and effective stress for saturated soils
![]()
图 3 不同吸力、不同加载速率下孔隙比与应力的关系
Figure 3. Relationship between void ratio and net stress under different suction and stress rate
![]()
图 4 不同吸力、不同加载速率下体变与时间的关系
Figure 4. Relationship between volumetric strain and time under different suction and stress rate
表 1 模型参数及初始条件
Table 1 Model parameters
参数类型 参数取值 传统参数 λ=1.25, κ=0.037 应变率参数 pr=125 kPa
$\dot \varepsilon _{\rm{v}}^{\rm{r}}$=5×10-5/s
β(0)=0.04初始体积 v=2.92 
下载: 导出CSV
表 2 模型参数及初始条件
Table 2 Model parameters
参数类型 参数取值 传统参数 λ=0.37, κ=0.03 LC参数 ϕ=0.45, θ=0.6 流体参数 λw=0.2, κw=0.015 耦合系数 ksw=0.6 初始应力 pc0=17 kPa, sa=0.77 kPa 初始饱和度 Sr1=0.65, Sr2=0.57, Sr3=0.5 初始体积 v1=2.31, v2=2.27, v3=2.26
下载: 导出CSV
-
[1] AUGUSTESEN A, LIINGAARD M, LADE P. Evaluation of time-dependent behavior of soils[J]. International Journal of Geomechanics, 2004, 34(3):137-156. https://www.researchgate.net/publication/248877161_Evaluation_of_Time-Dependent_Behavior_of_Soils
[2] 尹振宇, 朱启银, 朱俊高.软黏土蠕变特性试验研究:回顾与发展[J].岩土力学, 2013, 34(增刊2):1-17. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2013S2002.htm YIN Z Y, ZHU Q Y, ZHU J G. Experimental investigation on creep behavior of soft clays:review and development[J]. Rock and Soil Mechanics, 2013, 34(Suppl 2):1-17. (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2013S2002.htm
[3] LIINGAARD M, AUGUSTESEN A, LADE P. Characterization of models for time-dependent behavior of soils[J]. International Journal of Geomechanics, 2004, 4(3):157-177. doi: 10.1061/(ASCE)1532-3641(2004)4:3(157)
[4] 王者超, 乔丽苹.土蠕变性质及其模型研究综述与讨论[J].岩土力学, 2011(8):2251-2260. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytlx201108003&dbname=CJFD&dbcode=CJFQ WANG Z C, QIAO L P. A review and discussion on creep behavior of soil and its models[J]. Rock and Soil Mechanics, 2011(8):2251-2260. (in Chinese) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytlx201108003&dbname=CJFD&dbcode=CJFQ
[5] 殷建华.等效时间和岩土材料的弹粘塑性模型[J].岩石力学与工程学报, 1999, 18(2):6-10. http://en.cnki.com.cn/Article_en/CJFDTotal-YSLX902.001.htm YIN J H. Equivalent time and elastic visco-plastic modelling of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(2):6-10. (in Chinese) http://en.cnki.com.cn/Article_en/CJFDTotal-YSLX902.001.htm
[6] 袁静, 龚晓南, 益德清.岩土流变模型的比较研究[J].岩石力学与工程学报, 2001, 20(6):772-779. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200106004 YUAN J, GONG X N, YI D Q. Comparison study on rheological constitutive models[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6):772-779. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200106004
[7] YAO Y P, KONG L M, HU J. An elastic-viscous-plastic model for overconsolidated clays[J]. Science China(Technological Sciences), 2013(2):441-457. doi: 10.1007/s11431-012-5108-y
[8] 孔令明, 罗汀, 姚仰平.率相关本构模型的临界状态描述[J].岩土力学, 2015, 36(9):2442-2450. http://www.cnki.com.cn/Article/CJFDTotal-YTLX201509003.htm KONG L M, LUO T, YAO Y P. Description of critical state for rate-dependent constitutious models[J]. Rock and Soil Mechanics, 2015, 36(9):2442-2450. (in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-YTLX201509003.htm
[9] 尹振宇.软黏土流变理论及应用[M].上海:同济大学出版社, 2016. [10] PERZYNA P. On the constitutive equations for work-hardening and rate sensitive plastic materials[J]. Proc Vibration Problems, 1964, 12:281-290. http://www.ams.org/mathscinet-getitem?mr=163510
[11] 刘艳, 赵成刚, 蔡国庆, 等.非饱和土力学理论的研究进展[J].力学与实践, 2015, 37(4):457-465. doi: 10.6052/1000-0879-15-008 LIU Y, ZHAO C G, CAI G Q, et al. Research development of unsaturated soil mechanics[J]. Mechanics in Engineering, 2015, 37(4):457-465. (in Chinese) doi: 10.6052/1000-0879-15-008
[12] 刘艳, 赵成刚, 蔡国庆.理性土力学与热力学[M].北京:科学出版社, 2016. [13] OKA F, KODAKA T, KIMOTO S. An elasto-viscoplastic model and multiphase coupled FE analysis for unsaturated soil[C]//The Fourth International Conference on Unsaturated Soils. Carefree, Arizona: ASCE, 2006: 2039-2050. https://www.researchgate.net/publication/268591152_An_Elasto-Viscoplastic_Model_and_Multiphase_Coupled_FE_Analysis_for_Unsaturated_Soil?ev=prf_cit
[14] PEREIRA J, DE GENNARO V. On the time-dependent behaviour of unsaturated geomaterials[C]//The Fifth International Conference on Unsaturated Soils. Barcelona: CRC Press, 2010, 2: 921-925. https://www.researchgate.net/publication/47398486_On_the_time-dependent_behaviour_of_unsaturated_geomaterials
[15] 刘艳, 韦昌富, 赵成刚, 等.一个高饱和度非饱和土的本构模型[J].岩土力学, 2013, 34(8):2189-2194. http://d.wanfangdata.com.cn/Periodical_ytlx201308014.aspx LIU Y, WEI C F, ZHAO C G, et al. A constitutive model of unsaturated soils with high saturation[J]. Rock and Soil Mechanics, 2013, 34(8):2189-2194. (in Chinese) http://d.wanfangdata.com.cn/Periodical_ytlx201308014.aspx
[16] YIN J H, GRAHAM J. Elastic viscoplastic modelling of the time-dependent stress-strain behaviour of soils[J]. Canadian Geotechnical Journal, 1999, 36(4):736-745. doi: 10.1139/t99-042
[17] YIN Z Y, KARSTUNEN M. Modelling strain-rate-dependency of natural soft clays combined with anisotropy and destructuration[J]. Acta Mechanica Solida Sinica, 2011, 24(3):216-230. doi: 10.1016/S0894-9166(11)60023-2
[18] 朱启银, 尹振宇, 朱俊高, 等.软黏土加载速率效应特性试验研究:进展与趋势[J].岩土力学, 2014, 35(1):7-24. http://www.oalib.com/paper/5020957 ZHU Q Y, YIN Z Y, ZHU J G, et al. Progress and trend of experimental investigation on rate-dependent behavior of soft clays[J]. Rock and Soil Mechanics, 2014, 35(1):7-24. (in Chinese) http://www.oalib.com/paper/5020957
[19] DE GENNARO V, PEREIRA J M, GUTIERREZ M. On the viscoplastic modelling of porous chalks[J]. Italian Geotechnical Journal, 2009(1):44-64. https://www.researchgate.net/publication/47398461_On_the_viscoplastic_modelling_of_porous_chalks
[20] DE GENNARO V, PEREIRA J M. A viscoplastic constitutive model for unsaturated geomaterials[J]. Computers and Geotechnics, 2013, 54(Suppl C):143-151. https://www.sciencedirect.com/science/article/pii/S0266352X13000979
[21] YIN Z Y, WANG J. A one-dimensional strain-rate based model for soft structured clays[J]. Science China(Technological Sciences), 2012(1):90-100. doi: 10.1007/s11431-011-4513-y
[22] 李冬. 非饱和土率相关本构模型研究[D]. 北京: 北京交通大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10004-1017090559.htm LI D. Study on rate dependent constitutive model for unsaturated soils[D]. Beijing: Beijing Jiaotong University, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10004-1017090559.htm
[23] SHARMA R S. Mechanical behaviour of unsaturated highly expansive clays[D]. Oxford: University of Oxford, 1998. https://www.researchgate.net/publication/35723474_Mechanical_behaviour_of_unsaturated_highly_expansive_clays
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
