城际轨道交通列车长期户外运动,有时甚至在恶劣环境下运行,车轮表面会产生许多缺陷,这使得轮轨接触状态变得极其复杂,若车轮表面产生裂纹和缺陷,则会使其表面产生交变载荷,持续高速的运行将使车轮踏面缺陷更加恶化,也会使材料特性、轮轨表面硬度发生变化,并且磨耗的车轮对高速动车组运行的稳定性以及使用寿命构成了严重的威胁 . 在修复过程中,不落轮车床对车轮的修复加工与普通数控车床不一样,由于车轮踏面加工的特殊性,使得在不落轮车床加工过程中需要调节浮动装置“跟随”车轮踏面的变化,以此来提供足够的摩擦动力驱使车轮的旋转,在车削过程中,很显然摩擦力矩要大于等于切削抗力力矩,否则将会导致车轮的“堵转”现象,这将会产生机床振动不稳定,反过来影响车削加工精度和加工的稳定性 .

在不落轮车床车削振动的影响下,车削车轮将会产生动态厚度的变化,因此车削工艺系统将在一个动态激励力下完成列车车轮的修复加工 . 在车削加工中,不但车轮转速和工艺参数对车轮修复加工产生影响,而且不落轮车床的刚度系数、阻尼系数、车削刚度系数、方向系数等多参数对车削工艺系统的影响也是至关重要的,都在不同程度上造成了车削加工不稳定现象 . 因此近年来国内外许多学者对于车削加工方面进行了长时间的研究,已经对实际车削加工中避免和抑制车削加工稳定性问题起了指导性作用 . 朱立达等 ^{[ 1]} 基于正交车铣复合车削,运用解析法建立了颤振稳定域的模型 . Ding等 ^{[ 2]} 运用全离散方法推导车削稳定性理论,有效降低了车削加工的时间 . 李金华等 ^{[ 3]} 用切削稳定性叶瓣图包含切削速度和极限切削宽度来表示切削稳定性条件,从稳定状态到开始出现颤振时的切削宽度的临界值,直接反映加工系统动态性能的优劣 . 梁睿君等 ^{[ 4]} 通过有限元方法获得工件的各阶段颤振稳定域预测图 . Kersting等 ^{[ 5]} 通过把薄壁零部件化简为解耦后的谐振单元,研究变化位置对颤振稳定域的影响 . Alan等 ^{[6 - 7]} 利用测试并分析得到主轴 -刀具系统刀尖点的频响函数,进一步研究车削状态下不发生颤振稳定性条件 . 张勇等 ^{[ 8]} 利用MATLAB/Simulink软件对二自由度车削再生颤振模型进行数值仿真,从能量补充的角度分析了系统的极限切削宽度,但在模型中没有综合考虑切削参数对再生颤振的影响,也没有进行试验验证 . 于俊一 ^{[ 9]} 基于涡合型颤振模型基础上研究了机床主轴刚度方位对切削稳定性的影响 . Zhang等 ^{[ 10]} 在铣削颤振稳定性建模与分析中,还考虑了再生效应和模态耦合,进行了颤振试验验证稳定性的影响因子 . Siddhpura等 ^{[ 11]} 分析了切削颤振对切削稳定性的影响,并分析了颤振预测与监控的试验方法和颤振抑制的方法等 . 韩贤国等 ^{[ 12]} 在车削过程中研究了受轴向三维动态切削力工件的稳定性,在考虑了被加工轴的直径和质量变化的影响,建立了车削轴的振动力学模型 .

国内外许多学者的研究成果对车削加工的稳定性具有一定的指导性意义,但是大多数研究成果只是停留在工件转速和单个车削参数方面对车削工艺系统的影响,对车削加工考虑多参数影响下的不落轮车削加工稳定性的研究还是很少的 . 针对不落轮车床结构的复杂性及列车车轮踏面加工轨迹的独特性,在其加工过程中车削系统工艺参数的变化直接影响车轮踏面加工的稳定性问题,本文首先建立了以动态车削力作为激励下车削系统的动力学模型,然后通过分析模型找到车削工艺参数对车削工艺系统的影响规律,得到了主轴转速、刚度系数、刀具几何参数等对车削颤振系统稳定性的影响规律 . 分析表明通过调节这些参数可以有效地控制车削加工中的稳定性,从而可以有效地提高加工效率和精度 . 本文所建的模型及分析结论将为不落轮车床车削加工车轮表面质量和加工效率的提高具有一定的指导意义 .

1 不落轮车床车削振动的数学模型

1.1 不落轮车床车削加工过程

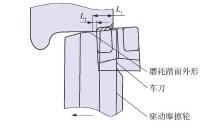
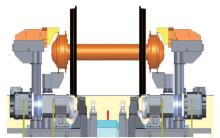
不落轮车床车削加工示意图如 图1所示 .

图  1  不落轮车床车削加工示意图

Figure  1.  Underfloor wheelsets lathe’s turning processing

下载: 全尺寸图片 幻灯片

在工作情况下,由 图2可知,不落轮车床的驱动装置与列车轮对保持接触而且始终有传动力的作用,若开始修复时长度为 L ₁,加工时 L ₁减少到 L ₂,如此继续下去, L ₂将继续减小,最后摩擦轮架带着驱动摩擦轮由旧踏面到新踏面上继续加工,这样就能够保证恒定的传动摩擦扭矩进行传动和精密的定位 . 由于车削加工过程中,车轮由旧踏面过渡到新踏面上,踏面的形状的不规则变化,影响了车削工艺系统参数的变化,刀具刀尖的轨迹就会在径向发生变化而影响车削抗力的大小,这样就会使得车削工艺系统产生再生型车削振动,影响车削加工的稳定性 .

图  2  刀具车削加工示意图

Figure  2.  Turning process of the tool

下载: 全尺寸图片 幻灯片

1.2 建立车削系统多参数动力学模型

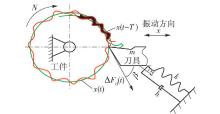
图3为建立再生型车削振动系统动力学模型,并对 图2所示的加工模型进行简化:

1) 不落轮车床的刀架系统是车削系统的最薄弱环节 .

2) 车削系统由于颤振而产生的作用力和阻尼力分别与振动位移和振动速度成正比 .

3) 车削厚度变化是由再生效应引起的 .

图  3  再生颤振系统动力学模型

Figure  3.  Regenerative chatter system’s dynamics model

下载: 全尺寸图片 幻灯片

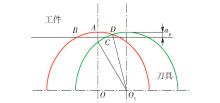
设前后2(转)次车削厚度重叠系数为 u,如 图4所示 . 根据几何关系可得

u= $\begin{array}{c}\frac{\mathit{CD}}{\mathit{AB}}\end{array}$

设 x( t-T)为上一转车削轮径刀具的振动位移, x( t)为本转车削轮径刀具的振动位移,则本转车削厚度变化量为

a( t) =ux( t-T) -x( t)(1)

式中: x( t)为本次车削振动振幅,mm; x( t-T)为前一转振动的振幅,mm .

图  4  相邻2次车削的重叠系数

Figure  4.  Turning overlap coefficient

下载: 全尺寸图片 幻灯片

动态车削力Δ F _d( t)为

Δ F _d( t) =k _c b[ ux( t-T) -x( t)] (2)

式中: b为不落轮轮对加工的宽度,mm; k _c为单位车削宽度下的车削刚度系数,N/mm ² .

根据 图3所示,建立动力学模型,其运动方程可以表示为

m $\begin{array}{c}\stackrel{··}{q}\end{array}$ ( t) +c $\begin{array}{c}\stackrel{·}{q}\end{array}$ ( t) +kq( t) =Δ F _d( t)cos( β-α) (3)

式中: m为车削系统的等效质量,N·s ²/mm; C为车削系统的等效阻尼,N·s/mm; k为车削系统的等效刚度,N/mm; α为主振动方向与刀具振动方向的夹角; β为动态车削抗力振动方向与刀具振动方向的夹角 .

根据 图3,有 x=qcos α,代入式(3)得

m $\begin{array}{c}\stackrel{··}{x}\end{array}$ ( t) +c $\begin{array}{c}\stackrel{·}{x}\end{array}$ ( t) +kx( t) =Δ F _d( t)cos( β-α)cos α (4)

设cos( β-α)cos α=h, h简称为方向系数,它是与车削抗力和主振方向有关的参数,将 h代入式(4)得

$\begin{array}{c}\stackrel{··}{x}\end{array}$ ( t) +2 ξω _n $\begin{array}{c}\stackrel{·}{x}\end{array}$ ( t) +ω ² x( t) =Δ F _d( t) $\begin{array}{c}\frac{h}{m}\end{array}$ (5)

式中: ξ= $\begin{array}{c}\frac{c}{2m{\omega }_n}\end{array}$ 为振动系统等效阻尼系数; ω _n = $\begin{array}{c}\sqrt[]{\frac{k}{m}}\end{array}$ 为振动系统的固有频率,rad/s .

综上所述,多参数车削系统动力学模型为

$\begin{array}{c}\stackrel{··}{x}\end{array}$ ( t) +2 ξω _n $\begin{array}{c}\stackrel{·}{x}\end{array}$ ( t) + $\begin{array}{c}{\omega }_n^2\end{array}$ x( t) = $\begin{array}{c}\frac{h{\omega }_n^2{k}_{c}b}{k}\end{array}$ [ ux( t-T) -x( t)] (6)

1.3 车削系统稳定性极限分析

现在研究车削系统处于临界稳定状态下的振动,为此假设本次车削刀具系统的振动振幅

$\begin{array}{c}\left\{\begin{array}{c}x\left(t\right)=\mathit{Asin}\left(\mathit{\omega t}\right)\\ \stackrel{·}{x}\left(t\right)=\mathit{A\omega cos}\left(\mathit{\omega t}\right)\end{array}\right.\end{array}$ (7)

则前一次车削刀具的振动振幅为

x( t-T) =Asin( ωt-ωT) =x( t)cos( ωT) - $\begin{array}{c}\frac{\mathit{sin}\left(\mathit{\omega T}\right)}{\omega }\end{array}\begin{array}{c}\stackrel{·}{x}\end{array}$ ( t) (8)

式中: A为振动振幅,mm; ω为振动频率,rad/s .

把式(7)(8)代入式(6)进行拉式变换得

s ² +[2 ξω _n + $\begin{array}{c}\frac{\mathit{Ku}}{\omega }\end{array}$ sin( ωT)] s+ $\begin{array}{c}{\omega }_n^2\end{array}$ -Kucos( ωT) +K=0 (9)

令 s=σ+i ω,振动系统的稳定性是由方程的根 s的大小决定:

1) σ<0 处于稳定状态;

2) σ=0 处于临界稳定状态;

3) σ>0 处于不稳定状态 .

对于情况2) σ=0,即 s=i ω,则可以求出车削宽度 b _lim . 将 s=i ω代入式(9),令 λ=ω/ω _n,并将 K= $\begin{array}{c}\frac{h{\omega }_n^2{k}_{c}b}{k}\end{array}$ 代入整理得

1 -λ ² +2 ξλi= $\begin{array}{c}\frac{h{k}_{c}b}{k}\end{array}$ [ ucos( ωT) -1 -usin( ωT) i] (10)

若保证式(10)成立,则要求等式两边的实部和虚部分别相等,即

$\begin{array}{c}\left\{1-{\lambda }^2=-\frac{h{k}_c{b}_{\mathit{lim}}}{k}\left[1\right.-\mathit{ucos}\left(\mathit{\omega T}\right)]2\mathit{\xi \lambda }=-\frac{h{k}_c{b}_{\mathit{lim}}}{k}\mathit{usin}(\mathit{\omega T})\right.\end{array}\mathit{}$ (11)

上述方程联立得

b _lim =- $\begin{array}{c}\frac{k(1-{\lambda }^2)}{k_{c}h\left[1\right.-\mathit{ucos}\left(\mathit{\omega T}\right)]}\mathit{}\end{array}$ (12)

由式(11)化简得

$\begin{array}{c}\sqrt[]{u^2[1+(\frac{1-{\lambda }^2}{2\mathit{\xi \lambda }}\left){}^2\right]}\end{array}$ sin( ωT+ϕ) =1 (13)

其中

tan φ= $\begin{array}{c}\frac{2\mathit{\xi \lambda }}{1-{\lambda }^2}\end{array}$

sin( ωT+ϕ) = $\begin{array}{c}\frac{1}{\sqrt[]{u^2[1+(\frac{1-{\lambda }^2}{2\mathit{\xi \lambda }}\left){}^2\right]}}\end{array}$

ωT=arcsin( $\begin{array}{c}\frac{2\mathit{\xi \lambda }}{u\sqrt[]{{\left(2\right.\mathit{\xi \lambda })}^2+(1-{\lambda }^2{)}^2}}\end{array}$ ) -arctan( $\begin{array}{c}\frac{2\mathit{\xi \lambda }}{1-{\lambda }^2}\end{array}$ ) +2 jπ ( j=0,1,2,…)(14)

又因为 T=60 /N代入式(14)整理得

N= $\begin{array}{c}\frac{60\lambda {\omega }_n}{\mathit{arcsin}[\frac{2\mathit{\xi \lambda }}{u\sqrt[]{{\left(2\right.\mathit{\xi \lambda })}^2+(1-{\lambda }^2{)}^2}}-\mathit{arctan}(\frac{2\mathit{\xi \lambda }}{1-{\lambda }^2}\left)\right]+2\mathit{j\pi }}\end{array}\mathrm{}$ (15)

把式(14)代入式(12)得

b _lim =- $\begin{array}{c}\frac{k(1-{\lambda }^2)}{k_{c}h\{1-\mathit{ucos}[\mathit{arcsin}\left(\frac{2\mathit{\xi \lambda }}{u\sqrt[]{{\left(2\right.\mathit{\xi \lambda })}^2+(1-{\lambda }^2{)}^2}}\right)+2\mathit{j\pi }-\mathit{arctan}\left(\frac{2\mathit{\xi \lambda }}{1-{\lambda }^2}\right)\left]\right\}}\end{array}\mathit{}$ (16)

由以上推导得到不落轮车床车削振动的数学方程,如果知道振动过程中的各参数的大小,就可以通过图表形式描绘出这些动力学参数对不落轮轮对车削稳定性的影响关系 .

2 稳定性极限数值仿真与动力学参数影响分析

本文研究的是某不落轮车床车削加工,其实际加工测得的车削工艺系统动力学参数如 表1所示,来推导多参数对不落轮车削加工的稳定性影响 .

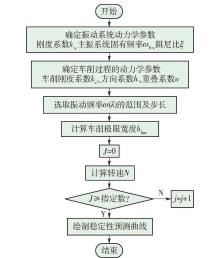
表  1  车削系统动力学参数

Table  1.  Turning system’s dynamics parameters

参数	数值
车削系统的刚度系数 k/(N·mm -1)	10945
系统的固有频率 ω n /(rad·s -1)	500π
系统的阻尼比 ξ	0 .07
振动系统方向系数 h	0 .5
车削刚度系数 k c /(N·mm -2)	10032
重叠系数 u	0 .5

下载: 导出CSV 

| 显示表格

根据不落轮车床车削系统稳定性极限分析表明:在实际加工前,对系统的动力学参数进行识别,由式(15)(16)可以求得极限车削宽度 b _lim,实现对车削系统稳定性进行预测,其预测流程如 图5所示 .

图  5  求解稳定性极限预测流程

Figure  5.  Stability limit topredict flow chart

下载: 全尺寸图片 幻灯片

根据稳定性流程 图5所示,首先识别车削过程的动力学参数车削刚度系数 k _c、方向系数 h和重叠系数 u以及振动系统动力学参数,主振动系统固有频率 ω _n、阻尼比 ξ、刚度系数 k并选取振动频率 ω( λ)的范围及步长,然后选择不同的 j值( j≥0),计算不同的转速 N下对应的极限车削宽度 b _lim,最后可绘制车削系统稳定性预测图 .

图  6  车削系统参数 N-b _lim的关系

Figure  6.  N-b _lim relationship of turning system parameters

下载: 全尺寸图片 幻灯片

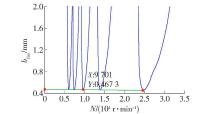
图6为得到的模拟仿真的预测图,每一个 j值对应一个耳廓线,该线即为不同的转速 N下对应的极限稳定车削宽度 b _lim . 对于耳廓线的上部分区域 σ>0,系统处于不稳定状态,也是加工的不稳定区域,将会发生强烈的车削振动,于是在加工过程应该尽量避免这个区域,以免影响加工精度;耳廓线图下部就是实部 σ<0,系统的稳定状态,也是车削区域的稳定区;同理,在所有曲线的最低点连成一条线,则得到( b _lim) _min =0 .4673mm,在直线下方,就是绝对稳定区 . 而直线以上与耳廓线以下的区域,只有特别的条件下,才有可能成为稳定的车削区域,即条件稳定区 .

由 图6知,随着主轴转速加大,极限车削宽度基本上不变,而耳廓线开口区域增大,不稳定区域有增大趋势 .所以在极限车削宽度大于车削宽度情况下,通过加大主轴转速,就可以保证快速的稳定加工 .

3 不落轮车床车削系统动力学参数对稳定性影响的仿真研究

不落轮车床车削加工过程一方面与机床结构、刀具结构和工件本身结构、材质等有关,另一方面还受加工过程动态参数的影响,因此对不落轮车床加工过程的稳定性的分析,需要考虑车削系统各种动力学参数( k、 k _c、 ω _n、 u、 h、 ζ)影响 . 上述车削系统稳定性关系式(15)(16)以及稳定性都是建立在不落轮轮对车削系统动力学参数( k、 k _c、 ω _n、 u、 h、 ζ)一定的基础上的,因此可以根据式(15)(16),分别以 k、 k _c、 ω _n、 u、 h、 ζ为变量,进行仿真模拟车削系统稳定性,从而可以得出影响不落轮车削稳定性因子的趋势及敏感性 .

3.1 重叠系数 u对稳定性的影响

不落轮轮对车削过程中振纹再生效应产生了车削颤振,再生效应的大小与重叠系数 u的大小有直接的关系,因此它是影响车削系统颤振稳定性的一个重要因素 . 其重叠系数 u计算公式为

u=1 - $\begin{array}{c}\frac{\mathit{sin}{k}_r·\mathit{sink}{\text{'}}_r}{\mathit{sin}(k_r+k{\text{'}}_r)}\end{array}$ · $\begin{array}{c}\frac{f_e}{p}\end{array}\mathrm{}$ (17)

式中: k _r为车刀主偏角; k' _r为车刀副偏角; f _e为进给量; p为车削深度 .

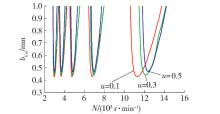
通过式(17)知,0 <u<1,如 表2所示, 图7为根据式(15)(16)模拟仿真得到的 b _lim -N,在保证 表2中其他参数不变的情况下,通过改变重叠系数 u的大小,求证对不落轮车削加工过程中稳定性的影响大小 .

表  2  重叠系数 u变化表

Table  2.  Overlap coefficient u change chart

k/(N·mm - 1)	ω n /(rad·s -1)	ξ	h	k c /(N·mm -2)	u
10945	500π	0 .07	0 .5	10032	0 .1
					0 .3
					0 .5

下载: 导出CSV 

| 显示表格

图  7  u的变化对车削稳定性 N-b _lim的影响

Figure  7.  Change of u for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

从 图7知,随着重叠系数 u值增大,稳定性阈图线略有右移趋势,不落轮轮对极限切削最小值和耳廓线开口大小基本上不变,所以改变 u值对系统稳定性的控制调节作用很小,因此在加工中可以不予考虑重叠系数的变化,这也是与实际加工中相符的 .

3.2 刚度系数 k对稳定性的影响

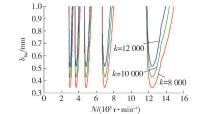
根据式(16)可知,稳定极限切削宽度 b _lim与主振系统刚度系数 k成正比,如 表3所示 . 也即随着 k的增加, b _lim随之变大,系统的稳定性也增强 . 图8为在其他参数相同的条件下, k 取不同值(分别取 12、10、8kN/mm)时,通过模拟仿真得到的车削颤振稳定性 b _lim -N关系曲线 .

表  3  刚度系数 k变化表

Table  3.  Stiffness coefficient k change chart

k/(N·mm -1)	ω n /(rad·s -1)	ξ	h	k c /(N·mm -2)	u
12000
1000	500π	0 .07	0 .5	10032	0 .5
8000

下载: 导出CSV 

| 显示表格

由 图8可知,通过改变刚度系数可以有效地增大最小极限切削宽度和绝对稳定区域,而耳廓开口形状略微减小,不落轮轮对切削系统更容易达到车削稳定状态 . 这也证明了模型建立的正确性和准确性 .

图  8  k的变化对车削稳定性 N-b _lim的影响

Figure  8.  Change of k for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

3.3 车削系统固有频率 ω _n对稳定性的影响

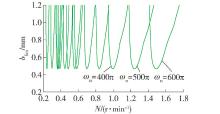
一般情况下,在车削加工过程中,外加激励的振动频率和不落轮工艺系统的固有频率接近时,一般是略大,此时易产生共振,由 λ= $\begin{array}{c}\frac{\omega }{{\omega }_n}\end{array}$ 从式(15)(16)知,不落轮轮对车削系统稳定性与频率比 λ有关,如 表4所示 . 图9为在其他条件不变的条件下,当 ω _n取不同值时,通过数值仿真得到 b _lim -N关系曲线 .

表  4  固有频率 ω _n变化表

Table  4.  Natural frequency ω _n change chart

k/(N·mm -1)	ω n /(rad·s - 1)	ξ	h	k c /(N·mm - 2)	u
	400π
10945	500π	0 .07	0 .5	10032	0 .5
	600π

下载: 导出CSV 

| 显示表格

由 图9可知,通过加大 ω _n的值,条件稳定区域变大,改变主轴转速的条件下可以提高稳定区域的大小,对不落轮轮对车削加工具有一定的经济作用 .

图  9  ω _n的变化对车削稳定性 N-b _lim的影响

Figure  9.  Change of ω _n for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

3.4 方向系数 h对稳定性的影响

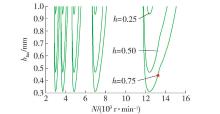
由上文cos( β-α)cos α=h可知,方向系数 h也是影响切削加工的另一个重要因素,如 表5所示 . 而根据式(16)可知,极限车削宽度 b _lim随 h的增大而减小 . 图10为其他条件不变的情况下, h分别取 0 .25、 0 .50、0 .75时模拟出的 b _lim -N关系曲线 .

表  5  方向系数 h的变化表

Table  5.  Direction coefficient h change chart

k/(N·mm - 1)	ω n /(rad·s - 1)	ξ	u	k c /(N·mm -2)	h
					0 .25
10945	500π	0 .07	0 .5	10032	0 .50
					0 .75

下载: 导出CSV 

| 显示表格

由 图10可知,在其他参数不变的情况下,随着方向系数 h的减小,稳定性极限车削宽度的最小值在增大幅度很凸显,所以在不落轮轮对车削加工中略微改变方向系数的值就可以很容易达到车削稳定状态,也就是最敏感因子,此值对本文切削加工中更具有使用价值 .

图  10  h的变化对车削稳定性 N-b _lim的影响

Figure  10.  Change of h for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

3.5 阻尼比 ξ对车削加工稳定性的影响

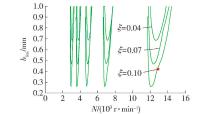
在车削加工中,阻尼是消耗加工能量的机理,它的存在可能会减小外加激励对不落轮轮对车削振动的影响,由式(16)知,极限车削宽度 b _lim与车削系统阻尼比 ξ密切相关,如 表6所示 . 图11为模拟仿真 .

图  11  ξ的变化对车削稳定性 N-b _lim的影响

Figure  11.  Change of ξ for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

表  6  阻尼系数 ξ的变化表

Table  6.  Damping coefficient ξ change chart

k/(N·mm -1)	ω n /(rad·s - 1)	h	u	k c /(N·mm 2)	ξ
					0 .04
10945	500π	0 .5	0 .5	10032	0 .07
					0 .10

下载: 导出CSV 

| 显示表格

由 图11可知,在其他参数不变的情况下,随着车削系统阻尼系数的增大,耳廓线的形状基本上不变,而稳定性极限车削宽度极限值减小幅度很大,即更难达到稳定车削状态,这在车削加工中需要着重注意的因子,通过调节阻尼系数可以有效地控制切削加工中的振动区域和稳定区域的范围 .

3.6 车削刚度系数 k _c对稳定性的影响

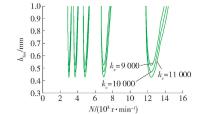
车削刚度系数本身与工件材料、刀具材料、刀具几何参数以及车削参数有着密切的关系,如 表7所示 . 根据式(16)可知,稳定性极限车削宽度 b _lim与车削刚度系数 k _c成反比 . 图12是根据式(16),在其他条件一定时, k _c 取不同值(分别为11、10、9kN/mm ),通过计算机模拟仿真得到的车削颤振稳定性 b _lim -N关系曲线 .

表  7  车削刚度系数 k _c的变化表

Table  7.  Turning stiffness coefficient k _c change chart

k/(N·mm -1)	ω n /(rad·s -1)	h	u	ξ	k c /(kN·mm -2)
					11
10945	500π	0 .5	0 .5	0 .07	10
					9

下载: 导出CSV 

| 显示表格

从 图12知,在其他参数不变的情况下,随着车削系统车削刚度的减小,开口大小基本上不变,稳定性极限车削宽度略微增大趋势,但是并不是特别明显,在车削加工中,可以调节车削刚度系数来达到稳定车削状态,同时也带来了成本的增加 .

图  12  k _c的变化对车削稳定性 N-b _lim的影响

Figure  12.  Change of k _c for turning stability N-b _lim

下载: 全尺寸图片 幻灯片

通过对振动稳定性因素的研究将有助于改善不落轮轮对的加工精度和效率,从而有效地提高了轮对运行的寿命和列车的平稳性 . 本论文的研究对今后的不落轮车床车削加工稳定性方面具有一定的指导意义 .

4 结论

1) 通过不落轮轮对车削加工的振动模型建立了车削振动的微分方程,并通过模拟仿真证明了模型的正确性 . 分析稳定性极限预测图,得到多参数是共同决定稳定区域和振动区域大小的关键因素;结果表明随着多参数的变化,稳定区域和振动区域的大小成反比例增长趋势 .

2) 分析了振动动力学参数对不落轮车削振动稳定性的影响 . 确定各参数对不落轮轮对车削稳定性的影响比重关系,分析表明:车削系统刚度系数的增大、方向系数的减小、车削刚度的减小,使得稳定极限车削宽度增加,更易达到车削稳定状态,三者中方向系数为最敏感因子;而阻尼比系数的减小使得极限车削宽度减小,造成车削加工更难达到稳定状态 . 通过理论推导和数值仿真,得到极限切削宽度 b _lim =0 .4673mm,通过调节这些影响因子,可以有效地改变切削宽度极限值和切削稳定域 .

3) 应用本文提供的数学模型分析了不落轮车削加工稳定性影响因子,并在实际加工中的到了应用,针对不落轮车削加工提出了一些建议,具有较高的工程实际意义 .