No-reference VMAF Video Quality Assessment Model Based on Multi-mode Bilinear Pooling and Temporal Pooling Aggregation
-
摘要:
为了解决在实际应用过程中很难获取到原始视频信息的问题，提出了一种无参考的视频多方法评估融合(video multimethod assessment fusion, VMAF)预测模型. 首先，采用一种基于多模双线性池化的卷积神经网络结构建立视频帧级的无参考VMAF预测模型，用于对失真视频帧的VMAF分数进行预测；其次，采用3种不同的时间池化方法对失真视频帧的VMAF预测分数分别进行聚合，将结果融合后得到一个质量特征向量；最后，采用nu-支持向量回归(nu support vector regression, NuSVR)的方法建立质量特征向量与视频VMAF分数之间的映射关系模型. 该模型不需要原始视频信息就可以预测失真视频的VMAF分数，具有应用价值. 实验结果表明，提出的模型可以获得较高的预测精度.
Abstract:To solve the problem that it is difficult to obtain the original video information in the practical applications, a no-reference video multimethod assessment fusion (VMAF) prediction model was proposed in this paper. First, the VMAF scores of distorted video frames were predicted by adopting a frame level no-reference VMAF prediction model, which was established by a convolutional neural network based on multi-mode bilinear pooling operation. Second, the quality feature vector was obtained by fusing the aggregation results of the VMAF prediction scores of the distorted video frames by three different temporal pooling methods. Finally, the nu support vector regression (NuSVR) method was adopted to establish the mapping relationship model between the quality feature vector and the VMAF score of the video. The important application value is demonstrated that the proposed model can predict the VMAF score of the distorted videos without the original video information. Experimental results show that the proposed model can obtain higher prediction accuracy.
-
视频质量评价是计算机视觉、图像处理等领域的经典问题. 视频在压缩、传输等环节中会引入各种失真，导致视频质量的下降，影响用户的观看体验质量(quality of experience, QoE). 为了评估视频压缩处理算法的性能，优化系统资源的配置，需要对视频质量进行准确的评价.
视频质量评价可分为主观评价和客观评价[1]. 其中主观评价方法依靠人观看待测视频的打分去评估视频质量，是最为准确、可靠的质量评价方法，但是，该方法通常受测试环境和实验人员数量等客观因素影响，具有很大的局限性，不能满足实际应用需求. 客观评价则是通过建立数学模型对待测视频进行打分，但是常常无法准确反映出用户观看视频的主观体验. 近年来，能够与主观评价保持一致的客观质量评价方法受到了工业界和学术界的广泛关注，成为现阶段视频质量评价的研究热点.
视频多方法评估融合(video multimethod assessment fusion, VMAF)是美国Netflix公司于2016年推出的一种视频质量客观评价指标[2]. VMAF采集了大量的主观打分数据作为训练集，采用不同的质量评估方法对视频质量进行度量，然后采用支持向量回归(support vector regression, SVR)进行融合，使得VMAF可以保留每种质量评估方法的优势. 相比于峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性(structural similarity, SSIM)[3]等视频质量客观评价准则，VMAF指标更加接近于主观感受，可以与用户的主观评价保持一致. 实验结果表明，与PSNR相比，采用VMAF作为视频质量评价指标，在人眼感知质量相当的情况下，视频编码码率可以节约30%左右. 因此，VMAF自推出以来就受到了工业界的广泛关注.
虽然VMAF指标比较符合用户的主观感知，但是现在的VMAF指标是一种全参考的评价方法. 在实际应用中，人们往往很难获取到原始视频的信息. 为此，本文提出了一种无参考的VMAF预测模型. 该模型采用“帧级得分预测+时间池化聚合”的方式，分为两阶段进行建模：1) 利用自建的数据集，建立了一种基于多模双线性池化[4]的失真视频帧级VMAF预测模型，用于对视频帧的VMAF分数进行预测；2) 采用3种时间池化方法对预测的视频帧VMAF分数分别进行聚合，构成质量特征向量，采用nu-支持向量回归(nu support vector regression, NuSVR)的方法建立质量特征向量与VMAF预测分数之间的映射模型，用于对失真视频的VMAF分数进行预测. 实验结果表明，采用本文提出的无参考VMAF评价指标，无需原始视频参考信息就可以对视频质量进行准确的评价.
1. 视频质量评价算法
目前视频质量评价建模普遍采用2种思路：
第1种是采用“时空特征提取+回归”的思路. 该类方法首先提取视频的时空特征，然后采用SVR、深度神经网络(deep neural network, DNN)等方式建立特征参数与视频得分之间的映射关系. 文献[5]在码流域采用整数余弦变换(integer cosine transform, ICT)系数的统计信息表示视频的空间纹理信息，采用运动向量的统计信息表示视频的时间复杂度，结合量化参数(quantization parameter, QP)形成特征向量，最后采用DNN的方法对特征向量进行回归，得到视频打分预测模型. 文献[6]将相邻帧的帧差图在离散余弦变换(discrete cosine transform, DCT)域进行统计分析，提取运动一致性度量、全局运动度量和视频抖动特征，并采用自然图像质量评估(natural image quality evaluator, NIQE)[7]方法对图像质量进行评估，作为对空间信息的一种补充特征，最后采用SVR的方法对特征进行回归. 文献[8]采用预训练的卷积神经网络(convolutional neural network, CNN)提取视频的深度特征，设计了手工特征来表示视频的清晰度变化，作为视频的时间特征，最后采用DNN的方法进行特征回归.
第2种是采用“帧级得分预测+时间池化”的思路. 该类方法通常采用图像质量评价(image quality assessment, IQA)方法预测每个视频帧的打分，然后在时间维度上进行池化聚合，得到视频质量打分模型. 文献[9]利用现有的深度无参考图像质量评估(deep blind image quality assessment, DeepBIQA)模型[10]学习视频帧的时空视觉感知特征，得到视频的单帧打分；然后利用卷积神经聚合网络(convolutional neural aggregation network, CNAN) 学习每个视频帧得分的权重，通过各帧得分的加权平均得到视频的质量打分. 文献[11]采用预训练的CNN模型提取视频帧的空间特征，然后利用门控循环单元(gate recurrent unit, GRU)网络学习视频的长时间特征，进而获得视频的各帧打分，最后采用时间池化[12]将视频各帧分数聚合为视频质量打分.
为了将视频的帧级得分合并，得到视频级得分，目前研究人员已经提出多种时间池化策略. 总的来说，目前的池化策略可以分为以下3种不同的类型：
1) 基于数值统计的时间池化方法. 此类方法是最简单有效的时间合并算法，在多个无参考VQA模型中得到广泛使用. 常见的有简单平均池化(mean pooling, Mpooling)[13]、谐波均值池化[14]等等. 以Q表示视频级得分，N表示视频的总帧数，qn表示第n帧的帧分数，其中Mpooling的公式为
$$ Q=\frac{1}{N} \sum\limits_{n=1}^{N} q_{n} $$ (1) 2) 考虑质量较差的帧对视频感知质量的影响. 此类方法以公认的观念为基础，着重强调时间维度质量差的帧的影响. 常见的有百分数池化[15]和视频质量池化(video quality pooling, VQpooling)[16]. 其VQpooling是一种自适应的空间和时间池化策略. 对于时间池化策略而言，其根据分数采用k均值聚类将视频帧分为高质量GH和低质量GL两组，然后采用
$$ Q=\frac{\sum\limits_{n \in G_{\mathrm{L}}} q_{n}+\omega \sum\limits_{n \in G_{\mathrm{H}}} q_{n}}{\left|G_{\mathrm{L}}\right|+\omega\left|G_{\mathrm{H}}\right|} $$ (2) 合并得到视频最终分数. 式中：|GL|和|GH|分别是GL和GH的基数；权重占比ω=(1-ML/MH)2，ML和MH分别是集合GL和GH中分数的平均值.
3) 考虑记忆效应对视频感知质量的影响. 由于视频的最终接受者是用户，对于用户记忆效应的考虑也是感知质量度量的重要方面. 常见的有时间磁滞池化(temporal hysteresis pooling, THpooling)[12]、首因效应和近因效应[17]. 其中THpooling是受用户对时变视频质量的判断中观察到的磁滞效应启发而来. 将用户在第n帧对过去的质量的记忆ln表示为过去视频帧分数的最小值，即
$$ l_{n}= \begin{cases}q_{n}, & n=1 \\ \min\limits _{k \in \kappa_{\text {prev }}}\left\{q_{n}\right\}, & n>1\end{cases} $$ (3) 式中κprev={max(1, n-τ), …, n-2, n-1}表示要考虑的视频帧的索引，τ是一个超参数. 对于当前的质量记忆mn表示为
$$ m_{n}=\sum\limits_{j=1}^{J} v_{j} \omega_{j}, J=\left|\kappa_{\text {next }}\right| $$ (4) 式中：κnext={n, n+1, …, min(n+τ, N)}表示要考虑的视频帧索引；ωj表示高斯加权函数的下降部分；vj表示v=sort({qk}, k∈Knext)的第j帧. 最后，将记忆质量与当前质量合并，得到包含磁滞效应的实际质量，并采用简单平均池化得到视频最终分数.
$$ q_{n}^{\prime}=\alpha m_{n}+(1-\alpha) l_{n} $$ (5) $$ Q=\frac{1}{N} \sum\limits_{n=1}^{N} q_{n}^{\prime} $$ (6) 式中：q′n为包含磁滞效应的第n帧的帧分数；α为超参数，用于平衡当前质量和记忆质量的权重.
时间池化策略可以有效地将视频帧分数聚合为视频分数，但是现在常用的时间池化方法都只是针对某一种时间感知效应所设计的. 文献[18]将多种池化方式结合起来使用，充分发挥各种池化方法的优势，取得了比单一时间池化方式更好的结果.
2. 提出的无参考VMAF视频质量评价模型
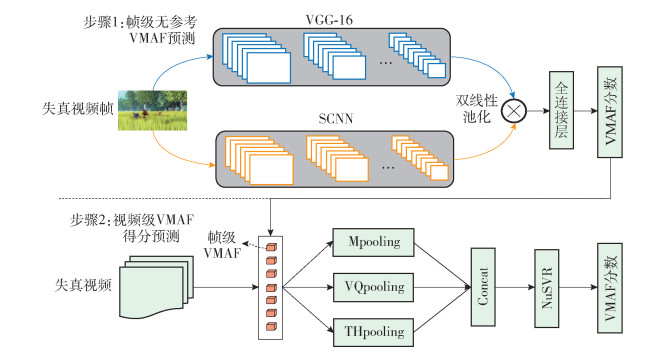
本文采用“帧级得分预测+时间池化聚合”的方式建立无参考VMAF模型，整体结构如图 1所示. 建模过程包括2个核心部分：首先，采用一种基于多模双线性池化的CNN结构，用于建立帧级的无参考VMAF评价模型，在无参考视频信息的情况下，可以对失真视频帧的VMAF分数进行预测；然后，采用3种不同的时间池化方法对失真视频帧的VMAF预测分数进行聚合，得到视频的质量特征向量；最后，采用NuSVR对质量特征向量进行回归，得到失真视频的VMAF预测模型. 下面将分别介绍2个部分的实现细节.
![]()
图 1 提出的无参考VMAF预测模型整体框架Figure 1. Overall framework of proposed no-reference VMAF prediction model2.1 失真视频帧的VMAF打分预测模型
本文采用一种基于多模双线性池化的卷积神经网络结构来建立帧级VMAF分数预测模型，如图 1中步骤1所示. 网络的输入是失真视频帧，输出则是该视频帧的VMAF预测分数. 通过训练该网络可以建立失真视频帧与该帧VMAF预测分数之间的映射模型，从而在无需参考视频信息的情况下，对失真视频帧的VMAF分数进行预测. 其中整个网络结构包括VG G- 16[19]和SCNN两个CNN，2个网络的层数分别是16层和14层.失真视频帧分别被送入2个网络中，将每个网络最后一个卷积层的输出特征提取出来，并将SCNN的输出进行上采样到与VG G- 16的输出具有相同的尺寸，然后采用多模双线性池化将2个特征进行融合，作为失真视频帧的深度特征.
假设采用VG G- 16和SCNN提取的失真视频帧I在位置l处的2个特征分别为fA(l, I)和fB(l, I)，双线性池化过程就是先把同一位置l处的2个特征进行双线性融合(相乘)后，得到矩阵
$$ \boldsymbol{b}(\boldsymbol{l}, \boldsymbol{I})=\boldsymbol{f}_{A}^{\mathrm{T}}(\boldsymbol{l}, \boldsymbol{I}) \boldsymbol{f}_{B}(\boldsymbol{l}, \boldsymbol{I}) $$ (7) 对所有位置的b(l, I) 进行Sum pooling操作，得到矩阵
$$ \boldsymbol{\xi}(\boldsymbol{I})=\sum\limits_{l} \boldsymbol{b}(\boldsymbol{l}, \boldsymbol{I}) $$ (8) 最后把矩阵ξ(I) 张成一个向量，表示为
$$ \boldsymbol{x}=\operatorname{vec}(\boldsymbol{\xi}(\boldsymbol{I})) $$ (9) 对x进行矩归一化和L2归一化操作，得到融合后的特征
$$ \boldsymbol{y}=\operatorname{sign}(\boldsymbol{x}) \sqrt{|\boldsymbol{x}|} $$ (10) $$ \mathit{\boldsymbol{z}}{\rm{ = }}\mathit{\boldsymbol{y}}{\rm{/}}{\left\| \mathit{\boldsymbol{y}} \right\|_2} $$ (11) 众所周知，在处理复杂任务时，DNN的层数越多，则往往性能越好，但这是以大规模的训练样本数据作为支撑的. 如果训练数据集的规模不足，在训练层数较多的DNN时常会出现过拟合现象，导致网络性能难以令人满意，而轻型CNN的结构简单，但是特征提取表达能力往往不足.
考虑到本文自建的数据集规模有限，本文采用一种基于多模双线性池化的CNN结构，可以充分利用2个轻型CNN提取的特征，获得更具表达能力的深度特征. 双线性池化融合后的特征 z 进一步用于回归操作，建立无参考VMAF模型.
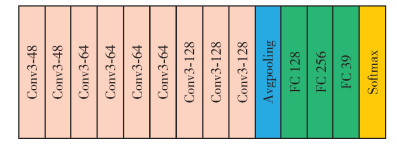
本文采用“预训练+微调”的方式对网络进行训练. 其中，VG G- 16在ImageNet数据集[20]上进行预训练，SCNN则采用Waterloo Exploration数据集[21]和PASCAL VOC数据集[22]合并的数据集进行预训练. SCNN的网络结构如图 2所示. 整个网络共有14层，包括9个卷积层、1个池化层、3个全连接层和1个Softmax层，并且9个卷积层均使用了3×3的卷积核尺寸.
为了对模型参数进行微调，本文采集了大量的数据，自行建立了VMAF数据集. 首先，利用失真视频和相应的原始参考视频获得各个失真视频帧以及整个视频的VMAF真实分数. 然后，将失真视频帧和相应的VMAF真实分数一一对应，作为一个训练样本对，构成训练数据集. 利用该数据集对网络参数进行微调，得到优化后的网络模型.
在对失真视频帧进行预测时，将失真视频帧输入到训练好的网络中，输出即为该帧的VMAF预测分数. 这样，在无需参考视频信息的情况下，就可以对失真视频帧的VMAF分数进行预测，得到一种无参考的VMAF打分模型.
2.2 失真视频的VMAF打分预测
现有的一些对于视频帧分数进行时间池化的方法都是通过统计数据或先验知识驱动的，有多种实现方式，并且不同的方法可能会捕获到视频中包含的不同信息. 比如：Mpooling用于对视频帧的质量进行平均；VQpooling考虑了质量比较差的视频帧对视频整体分数的影响；THpooling则考虑的是用户在观看视频时出现的磁滞效应等. 可以预期的是不同的池化方法具有不同的性能，在不同的数据集上的表现也会有所差异，不同的池化结果之间具有一定的互补性. 因此，如图 1中步骤2所示，本文将各个失真视频帧的VMAF预测分数分别采用3种时间池化方法进行聚合，将结果合并后形成一个质量特征向量，然后利用NuSVR建立该特征向量与视频VMAF分数之间的回归模型，用于对视频的VMAF分数进行预测.
质量特征向量的构建可以表示为
$$ \boldsymbol{F}=C\left(q_{1}, q_{2}, q_{3}\right) $$ (12) 式中：C表示concat级联操作；q1、q2、q3分别表示采用不同时间池化方法对失真视频帧进行处理得到的结果.
Mpooling、VQpooling和THpooling分别针对视频帧质量的波动程度、较差的视频帧对整体质量的影响和用户观看视频时出现的磁滞效应等因素进行表征，因此， F 可以看作是对失真视频的质量进行表达. 接下来，本文采用NuSVR建立质量特征向量 F 和视频VMAF预测分数之间的回归模型，用于对失真视频的VMAF分数进行预测.
2.3 失真视频帧的VMAF打分预测模型
NuSVR[23]是支持向量机(support vector machines, SVM)中的一种回归模型. 对于给定的失真视频集合{(xi, yi)，i=1, 2, …, n}，其中：n为失真视频的数量；xi表示输入的每个失真视频的质量特征向量；yi表示每个视频的真实的VMAF分数. 在实际操作中，NuSVR的优化问题可以转变为一个拉格朗日函数的鞍点求解问题，具体表述为
$$ \begin{gathered} \min _{\alpha, \alpha^{*}} \frac{1}{2} \sum\limits_{i, j=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right)\left(\alpha_{j}^{*}-\alpha_{j}\right) k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)- \\ \sum\limits_{i=1}^{n} y_{i}\left(\alpha_{i}^{*}-\alpha_{i}\right) \end{gathered} $$ (13) $$ \begin{gathered} \text { s.t. } \sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right)=0, \alpha_{i}^{*}, \alpha_{i} \in\left[0, \frac{c}{n}\right] ; \\ i=1, 2, \cdots, n \\ \sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}+\alpha_{i}\right)=c v \end{gathered} $$ 式中：k(xi, xj)为径向基核函数；c为惩罚变量；v用于控制支持向量数量和训练误差. 上述问题的最优解α、α*和相应的偏置项b，可以用于预测视频的VMAF分数. 对于输入的视频质量特征X，VMAF的预测分数可以由
$$ \hat{Q}=f(\boldsymbol{X})=\sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right) k\left(\boldsymbol{X}_{i}, \boldsymbol{X}\right)+b $$ (14) 计算获得.
3. 实验结果与分析
3.1 数据集和性能评价指标
为了验证所提出的无参考VMAF视频质量评价模型的有效性，本文在2个公开的视频数据集上进行了实验，即WaterlooSQoE-Ⅲ数据集[24]和LIVE-NFLX-Ⅱ数据集[25]. WaterlooSQoE-Ⅲ数据集包含20个原始高质量视频，其内容包括人物、植物、自然风光等不同类型. 这些视频以11个固定码率进行编码，在6种自适应码率算法和13种具有代表性的网络环境下生成了450个失真视频. LIVE-NFLX-Ⅱ数据集则包含纪录片、动画、游戏等15个不同类型的原始视频. 原始视频根据内容驱动的动态优化器进行码率编码，在4种客户端码率自适应算法和7种不同移动网络条件下生成了420个失真视频. 利用数据集中的失真视频和原始参考视频，分别计算各个视频帧和视频的VMAF真实分数，构建VMAF数据集，用于进行模型性能的验证.
为了评估模型的性能，采用2个评估指标：皮尔森线性相关系数(Pearson's linear correlation coefficient, PLCC)和斯皮尔曼秩相关系数(Spearman rank-order correlation coefficient, SROCC). 采用PLCC表示预测精度，采用SROCC评估预测单调性. 2个指标的数值越高，则表示模型的预测性能越好，具体的计算公式分别为
$$ V_{\mathrm{PLCC}}=\frac{\sum\limits_{i=1}^{n}\left(y_{p i}-\bar{y}_{p}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(y_{p i}-\bar{y}_{p}\right)^{2}\left(y_{i}-\bar{y}\right)^{2}}} $$ (15) $$ V_{\mathrm{SROCC}}=1-\frac{6 \sum\limits_{i=1}^{n} d_{i}^{2}}{n\left(n^{2}-1\right)} $$ (16) 式中：di为第i个视频的预测分数和真实分数之间的等级差异量；ypi和yi分别为第i个视频的预测分数和真实分数$\bar{y}_{p}$和$\bar{y}$分别为预测平均值和真实平均值；n为测试集中视频的个数.
3.2 实验参数设置
本文方法包括失真视频帧级VMAF分数预测和视频级VMAF分数预测2个部分. 2个部分训练时采用的参数如下：1) 在失真视频帧级VMAF分数预测阶段，为了获取更优越的性能，本文采用自建的VMAF数据集对网络进行了微调. 在微调过程中，初始学习率设置为1×10-3，训练批次为64，迭代次数为50. 2) 在视频级VAMF分数预测阶段，为了训练NuSVR回归模型，将失真视频数据集随机切分为2个子集，其中，80%用于训练，20%用于测试. 采用了Mpooling、VQpooling和THpooling三种池化方法获取视频的质量特征向量，用于建立无参考VMAF模型.
3.3 时间池化方法对模型性能的影响
为了研究不同的时间池化方法对建模精度的影响，本文分别对Mpooling、VQpooling和THpooling三种时间池化方法进行了对比实验，如表 1所示，可以看出：
表 1 不同时间池化方法的性能比较Table 1. Performance comparison of different temporal pooling methods池化方法 WaterlooSQoE-Ⅲ LIVE-NFLX-Ⅱ VPLCC VSROCC VPLCC VSROCC VQpooling 0.855 8 0.912 0 0.900 8 0.903 6 THpooling 0.872 1 0.925 6 0.918 3 0.910 4 Mpooling 0.891 0 0.933 4 0.918 9 0.913 2 VQpooling+THpooling+Mpooling 0.911 1 0.933 3 0.926 4 0.913 3 1) 对于3种时间池化方法来说，在2个数据集上，Mpooling均可以获得最优的性能，这与数据集中大多数视频的质量波动不太剧烈有关.
2) 与采用单一的时间池化方法相比，采用3种时间池化方法相结合的方式可以获得更优的性能，这也说明3种池化方法结合起来可以实现信息互补.
3) 3种池化方法的结果在WaterlooSQoE-Ⅲ数据集上的准确度低于在LIVE-NFLX-Ⅱ数据集上的结果，其原因是WaterlooSQoE-Ⅲ数据集中视频的失真模式更加复杂.
4) 首先，不同的时间池化方法会捕获到视频中包含的不同信息；其次，VSROCC衡量的是预测分数和真实分数的秩序相关性，并不表示预测的准确度. 在WaterlooSQoE-Ⅲ数据集上之所以采用Mpooling获得的VSROCC略优于合并模型，原因在于该数据集中的视频失真模式复杂，视频分数分布范围大，更容易预测视频的秩序相关性，因此，可以获得最高的VSROCC，此时，在合并的模型中VQpooling和THpooling补充的信息不足以继续提升预测结果的VSROCC，更多地是提升预测结果的准确度VPLCC. 可以看到，在2个数据集上合并模型的VSROCC相比于Mpooling分别提升了-0.01%和0.01%，而准确度指标VPLCC分别提升了2.01%和0.75%.
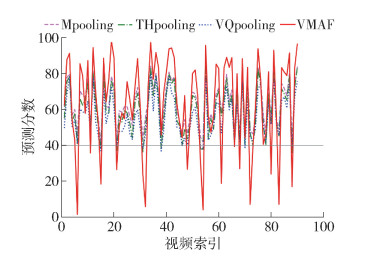
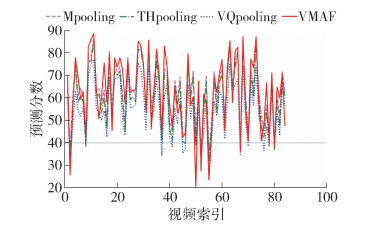
由表 1可知，在3种池化方法中Mpooling可以获得最优的性能，这表明Mpooling适用于大多数情况. 为了证明在合并模型中VQpooling和THpooling会对Mpooling方法有补充作用，给出了单独采用3种时间池化方法在2个数据集上的实验结果，如图 3、4所示. 可以看出，在失真视频的真实VMAF分数低于40时，VQpooling或THpooling可以获得比Mpooling更好的性能. 这是由于在视频质量较差时，VQpooling仅考虑了质量较差的帧的影响，THpooling仅考虑了用户观看视频时的记忆效应，而Mpooling则没有对视频中质量较差帧的影响予以考虑.
![]()
图 3 3种池化方法在WaterlooSQoE-Ⅲ数据集上的实验结果Figure 3. Experimental results of three pooling methods on the WaterlooSQoE-Ⅲ dataset![]()
图 4 3种池化方法在LIVE-NFLX-Ⅱ数据集上的实验结果Figure 4. Experimental results of three pooling methods on the LIVE-NFLX-Ⅱ dataset3.4 不同建模方法的性能对比
为了验证不同建模方法对模型精度的影响，本文分别采用决策树、NuSVR等8种浅层机器学习方法进行建模，其中质量特征向量是通过采用3种时间池化方法相结合的方式得到的. 实验对比结果如表 2所示.
表 2 不同建模方法的模型精度对比Table 2. Comparison of model accuracy of different modeling methods建模方法 WaterlooSQoE-Ⅲ LIVE-NFLX-Ⅱ VPLCC VSROCC VPLCC VSROCC 决策树 0.866 7 0.906 6 0.919 3 0.890 8 自适应增强回归 0.875 8 0.928 3 0.921 1 0.911 4 K近邻回归 0.874 1 0.916 9 0.919 6 0.903 7 随机梯度下降 0.879 2 0.927 4 0.918 2 0.916 8 岭回归 0.880 2 0.929 1 0.919 1 0.914 0 套索回归 0.898 3 0.939 6 0.917 7 0.912 3 随机森林 0.882 8 0.919 0 0.941 4 0.916 9 NuSVR 0.911 1 0.933 3 0.926 4 0.913 3 由表 2可以看出，在WaterlooSQoE-Ⅲ数据集上，采用NuSVR可以得到更优的性能，而在LIVE-NFLX-Ⅱ数据集上，采用随机森林进行建模可以得到更优的性能，这在一定程度上与2个数据集包含不同的失真模式相关. 折中考虑，本文选择NuSVR作为建模方法. 在WaterlooSQoE-Ⅲ数据集上VPLCC和VSROCC分别达到了91.11%、93.33%，在LIVE-NFLX-Ⅱ数据集上分别达到92.64%、91.33%. 实验结果充分说明，本文提出的无参考VMAF模型可以获得较高的预测精度.
4. 结论
1) 提出了一种基于“帧级得分预测+视频级时间池化聚合”的无参考VMAF预测模型. 首先，采用一种基于多模双线性池化的CNN结构，用于对视频帧的无参考VMAF得分进行预测；然后，分别采用3种时间池化方法对视频帧分数进行聚合，得到视频的质量特征向量；最后，采用NuSVR对质量特征向量进行回归.
2) 在实际应用中，由于很难获取原始视频的信息，而提出的模型不需要原始视频信息就可以预测出视频的VMAF分数，因此，具有重要的应用价值. 实验结果表明，本文提出的模型可以获得较高的预测精度.
3) 在QoE建模过程中，视频的质量是一个重要的影响因素. 因此，在下一步的工作中，将尝试把无参考的VMAF模型应用于QoE建模，进而评估用户观看视频的主观感受体验.
-
![]()
图 1 提出的无参考VMAF预测模型整体框架
Figure 1. Overall framework of proposed no-reference VMAF prediction model
![]()
图 3 3种池化方法在WaterlooSQoE-Ⅲ数据集上的实验结果
Figure 3. Experimental results of three pooling methods on the WaterlooSQoE-Ⅲ dataset
![]()
图 4 3种池化方法在LIVE-NFLX-Ⅱ数据集上的实验结果
Figure 4. Experimental results of three pooling methods on the LIVE-NFLX-Ⅱ dataset
表 1 不同时间池化方法的性能比较
Table 1 Performance comparison of different temporal pooling methods
池化方法 WaterlooSQoE-Ⅲ LIVE-NFLX-Ⅱ VPLCC VSROCC VPLCC VSROCC VQpooling 0.855 8 0.912 0 0.900 8 0.903 6 THpooling 0.872 1 0.925 6 0.918 3 0.910 4 Mpooling 0.891 0 0.933 4 0.918 9 0.913 2 VQpooling+THpooling+Mpooling 0.911 1 0.933 3 0.926 4 0.913 3 
下载: 导出CSV
表 2 不同建模方法的模型精度对比
Table 2 Comparison of model accuracy of different modeling methods
建模方法 WaterlooSQoE-Ⅲ LIVE-NFLX-Ⅱ VPLCC VSROCC VPLCC VSROCC 决策树 0.866 7 0.906 6 0.919 3 0.890 8 自适应增强回归 0.875 8 0.928 3 0.921 1 0.911 4 K近邻回归 0.874 1 0.916 9 0.919 6 0.903 7 随机梯度下降 0.879 2 0.927 4 0.918 2 0.916 8 岭回归 0.880 2 0.929 1 0.919 1 0.914 0 套索回归 0.898 3 0.939 6 0.917 7 0.912 3 随机森林 0.882 8 0.919 0 0.941 4 0.916 9 NuSVR 0.911 1 0.933 3 0.926 4 0.913 3
下载: 导出CSV
-
[1] DINGQUAN L I, TINGTING J, MING J. Recent advances and challenges in video quality assessment[J]. ZTE Communications, 2019, 17(1): 3-11.
[2] LI Z, AARON A, KATSAVOUNIDIS I, et al. Toward a practical perceptual video quality metric[R/OL]. [2021-02-24]. http://techblog.netflix.com/2016/06/toward-practical-perceptual-video.html.
[3] WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. doi: 10.1109/TIP.2003.819861
[4] ZHANG W, MA K, YAN J, et al. Blind image quality assessment using a deep bilinear convolutional neural network[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 30(1): 36-47.
[5] 李晨昊, 卓力, 李嘉锋. 基于内容的H. 264无参考视频质量评价模型[J]. 测控技术, 2019, 38(1): 106-110, 135. https://www.cnki.com.cn/Article/CJFDTOTAL-IKJS201901023.htm LI C H, ZHUO L, LI J F. Content-based H. 264 non-reference video quality evaluation model[J]. Measurement and Control Technology, 2019, 38(1): 106-110, 135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-IKJS201901023.htm
[6] SAAD M A, BOVIK A C, CHARRIER C. Blind prediction of natural video quality[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1352-1365. doi: 10.1109/TIP.2014.2299154
[7] MITTAL A, SOUNDARARAJAN R, BOVIK A C. Making a "completely blind" image quality analyzer[J]. IEEE Signal Processing Letters, 2012, 20(3): 209-212.
[8] AHN S, LEE S. No-reference video quality assessment based on convolutional neural network and human temporal behavior[C]//Asia-Pacific Signal and Information Processing Association Annual Summit and Conference. Piscataway: IEEE, 2018: 1513-1517.
[9] KIM W, KIM J, AHN S, et al. Deep video quality assessor: from spatio-temporal visual sensitivity to a convolutional neural aggregation network[C]// Proceedings of the European Conference on Computer Vision. Piscataway: IEEE, 2018: 219-234.
[10] KIM J, KIM W, LEE S. Deep blind image quality assessment by learning sensitivity map[C]//International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2018: 6727-6731.
[11] LI D, JIANG T, JIANG M. Quality assessment of in-the-wild videos[C]//Proceedings of the 27th ACM International Conference on Multimedia. New York: ACM, 2019: 2351- 2359.
[12] SESHADRINATHAN K, BOVIK A C. Temporal hysteresis model of time varying subjective video quality[C]//International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2011: 1153-1156.
[13] MITTAL A, SAAD M A, BOVIK A C. A completely blind video integrity oracle[J]. IEEE Transactions on Image Processing, 2015, 25(1): 289-300.
[14] LI Z, BAMPIS C, NOVAK J, et al. VMAF: the journey continues[R/OL]. [2021-02-24]. https://medium.com/netflix-techblog/vmaf-the-journey-continues-44b51ee9ed12.
[15] CHEN C, IZADI M, KOKARAM A. A perceptual quality metric for videos distorted by spatially correlated noise[C]//Proceedings of the 24th ACM International Conference on Multimedia. New York: ACM, 2016: 1277-1285.
[16] PARK J, SESHADRINATHAN K, LEE S, et al. Video quality pooling adaptive to perceptual distortion severity[J]. IEEE Transactions on Image Processing, 2012, 22(2): 610-620.
[17] MURDOCK B B Jr. The serial position effect of free recall[J]. Journal of Experimental Psychology, 1962, 64 (5): 482-488. doi: 10.1037/h0045106
[18] TU Z, CHEN C J, CHEN L H, et al. A comparative evaluation of temporal pooling methods for blind video quality assessment[C]//International Conference on Image Processing. Piscataway: IEEE, 2020: 141-145.
[19] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. [2021-01-21]. https://arxiv.org/abs/1409.1556vl.
[20] DENG J, DONG W, SOCHER R, et al. ImageNet: a large-scale hierarchical image database[C]//IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2009: 248-255.
[21] MA K, DUANMU Z, WU Q, et al. Waterloo exploration database: new challenges for image quality assessment models[J]. IEEE Transactions on Image Processing, 2016, 26(2): 1004-1016.
[22] EVERINGHAM M, VAN GOOL L, WILLIAMS C K I, et al. The pascal visual object classes (VOC) challenge[J]. International Journal of Computer Vision, 2010, 88(2): 303-338. doi: 10.1007/s11263-009-0275-4
[23] CHANG C C, LIN C J. Training v-support vector regression: theory and algorithms[J]. Neural Computation, 2002, 14(8): 1959-1977. doi: 10.1162/089976602760128081
[24] DUANMU Z, REHMAN A, WANG Z. A quality-of-experience database for adaptive video streaming[J]. IEEE Transactions on Broadcasting, 2018, 64(2): 474-487. doi: 10.1109/TBC.2018.2822870
[25] BAMPIS C G, LI Z, KATSAVOUNIDIS I, et al. Towards perceptually optimized end-to-end adaptive video streaming[EB/OL]. [2021-01-21]. https://arxiv.org/abs/1808.03898.
-
期刊类型引用(1)
1. 胡安康. 基于光流改进的视频虚拟试衣. 智能计算机与应用. 2023(12): 114-119 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 242
- HTML全文浏览量: 22
- PDF下载量: 61
- 被引次数: 2
