电动汽车(electric vehicle，EV)作为一种环保、高效的交通工具，具有显著的环境优势，大力发展EV对我国实现碳中和和碳达峰的“双碳目标”具有重要意义^[1]。与此同时，传统的内燃机汽车面临着环境污染、能源过度消耗等诸多挑战。各国政府采取措施限制内燃机汽车的使用^[2]，鼓励出行用户使用清洁能源的交通工具。如挪威计划到2025年停止内燃机汽车的销售；英国计划到2030年停止销售内燃机汽车，到2035年停止销售混动汽车；法国计划到2040年停止销售内燃机汽车；德国则预计在2050年完全过渡到电动汽车阶段；美国加利福尼亚州也计划到2035年停止销售内燃机汽车；中国计划到2035年新能源汽车占新车销量的37.5%以上。

与传统的快速/超级充电站相比，换电站(battery swapping station，BSS)具有快速、安全、灵活以及环保的优势和潜力，对新能源汽车的发展有积极的推动作用^[3]。以色列公司Better Place于2011年3月部署了首座现代商用BSS，美国Tesla也于2013年进入换电领域。纯电动汽车的使用数量、用户的充电习惯、电价制定、换电设施的兼容性以及用户满意度等成为BSS发展面临的重大挑战^[4]。中国蔚来汽车(NIO)于2018年5月推出首座BSS，到2023年5月，NIO在中国建设了超过1 400座BSS。其中，NIO推出的第三代BSS配备了21个电池组，每天可更换408块电池。国内建设BSS的知名企业还包括国家电网、奥动新能源、宁德时代、东风、第一科技、亿纬锂能、博中等^[5]。其中，长安汽车和奥动新能源公司均预计到2025年部署10 000座BSS，NIO预计到2025年部署4 000座BSS。

目前参与换电服务市场的EV品牌越来越多，且许多公司只支持特定类型的EV换电^[6]。考虑换电技术的持续发展和成本效益问题，吕应龙^[7]针对BSS的选址、规模和运营策略展开深入研究，旨在找到BSS的最佳位置、配置和充电/服务计划，以提高运营商的投资回报率(return on investment，ROI)和用户对换电服务的满意度。Jing等^[8]采用5个整数线性规划确定BSS的数量、位置以及规模，以达到最小化系统总投资的目的，同时追求最佳配置，包括充电设施类型和电池库存。Mak等^[9]采用二阶混合整数二次规划描述了电池库存和EV用户之间的供求关系，以最小化建设和配置BSS的成本为目标。Zhang等^[10]考虑用户的出行行为，采用通用的Bender分解算法和来自出租车车队的真实数据，提出了一个估算BSS位置和规模的模型。高赐威等^[11]提出一个考虑社会、地理和电力系统因素的最佳BSS选址和规模的成本效益模型。用户的充电行为受日行驶里程分布、EV用户的出行习惯等因素的影响，为了更加准确地预测EV到达BSS的时间和剩余电量，许多研究借助车辆行为、行驶里程等统计数据结合Monte Carlo方法进行分析^[12-13]。此外，合理制定电价以及在BSS中合理配置电池的数量^[14]均可以有效影响用户的充电行为，进而促进电网负荷平衡，优化能源利用，降低成本，减少碳排放，推动电动汽车的普及和可持续性发展^[15-16]。卢志平等^[17]提出一个由政府、汽车制造商和换电运营商三方参与的决策博弈模型，求解出补贴政策前后各方的最优电价、适当的补贴比例以及电池配比等关键决策变量。张昌华等^[18]建立了基于车主用车习惯和电池充电管理策略的数学模型，并结合Monte Carlo模型计算电池数量、充电控制策略等因素对换电裕度的影响。Xu等^[19]和Adler等^[20]通过交通流分析和EV路径的非线性算法确定BSS中所需备用电池组数量。

EV用户在BSS中的排队时间是影响用户换电体验的重要因素^[21]，在制定BSS优化策略时需要重点考虑。Tan等^[22-23]提出一种考虑竞争率和换电时间的混合排队网络模型，以阻塞概率来评估BSS的性能，同时通过对BSS系统中所需的最少电池组数量的研究，验证了相较于充电设施，用户的平均等待时间对电池的数量更为敏感。Sun等^[24]运用排队理论，考虑EV到达BSS的时间、状态和充电时间等因素，利用Monte Carlo方法模拟出最优的充电策略。但以上研究都没有考虑到不同类型的电动汽车和电池之间的服务兼容性对用户换电体验和BSS规划的影响。

为了量化共享换电资源对EV用户排队时间和BSS建设成本的价值，搭建一个仿真器对不同规模EV和BSS渗透率下的用户换电排队时间和将排队时间保持在期望阈值内所需的换电站数量进行估算。为保证仿真结果的准确性，仿真参数选取NIO的BSS位置和运行数据，并将NIO品牌下EV用户的换电模式和空间-时间分布作为输入。

1.   仿真方法

为了量化多个EV品牌共享BSS对换电用户排队时间和BSS建设成本的影响，提出一个连续仿真的仿真器。该仿真器基于连续仿真方法，以适应需要跟踪电池的荷电状态(state of charge, SOC)，即当前电池电量与电池总容量的比例持续变化的要求。与基于事件的仿真侧重于事件之间的顺序和影响不同，连续仿真适用于描述系统状态在时间上的连续变化^[25]，通过固定仿真时间步长运行并在每个时间步长结束时更新系统状态。

1.1   排队论模型

排队论是一个强大的计算工具，能够计算出不同场景下充电用户的排队时间，作为本文量化共享BSS收益的理论基础。排队系统的定义如下。

BSS：设置2座BSS为区域内相邻位置，每座BSS目前只服务特定类型的EV。假设每座BSS均被2种类型的EV品牌共享，站内可分别创建一个统一的队列系统，有换电需求的EV用户将考虑不同BSS中的队列长度选择特定的换电站。

EV到达：假设EV到达BSS的时间分布为泊松分布，到达率为λ。可通过标准的车辆交通监控技术确定。

服务时长：即换电时长(包括进入BSS停车的时间)遵循指数分布。将平均服务时长记为D，则单位时间内每座BSS的平均服务率为μ=1/D。

换电系统模型是一个M/M/s排队系统^[26]，属于经典的排队模型。该系统包括s座BBS，且各BSS工作相互独立，服务率相同。上述假设是在排队论研究中通常采用的，有助于分析和理解系统的行为。

根据排队论^[26]，每座BSS的服务强度为ρ=λ/μ，表示换电站的繁忙程度。当ρ/s≤1时，系统服务车辆数为0的概率p₀为

期望排队长度L_q为

站内的期望EV数量L为

排队系统的期望逗留时间W为

排队系统的期望等待时间W_q为

假设2个品牌的EV可共享2座BSS，则所定义的换电排队系统为M/M/2队列。否则，系统有2个M/M/1队列。进一步假设每座BSS每小时可以服务10辆车，且平均每小时有8辆电动汽车到达BSS。根据式(1)~(5)，可以计算这2种场景的排队关键指标。结果如表 1所示。

表  1  排队论的分析结果

Table  1.  Analytic results of the model

场景	λ	μ	s	L	Lq	Ws	Wq
M/M/1	8.0	10.0	2.0	4.0	3.2	30.0	24.0
M/M/2	8.0	10.0	1.0	3.6	2.8	16.7	10.7

下载: 导出CSV 

| 显示表格

计算结果显示，共享BSS可显著提高换电服务效率。例如，2个不同品牌进行BSS共享相较于独立运行可以使所有接受服务的EV用户的平均排队时间从24.0 min减少到10.7 min。虽然这一评估是基于简化模型中的某些假设，但为BSS共享的优势提供了理论依据。下面通过基于实际数据的仿真来深入研究BSS的共享问题。

1.2   数据采集与分析

仿真对象选择覆盖城市中255个站点的大型BSS网络，利用NIO在上海的BSS网络中的真实数据，其中包括截至2023年4月12日的NIO品牌105座BSS的信息。从数据库中提取每座BSS的位置和运行数据，包括历史EV用户到达BSS的时间、开始和结束时的SOC以及其他能够反映用户出行特征的关键指标。分析上述指标的模式和分布以生成仿真的相关输入，使仿真能够有效反映真实情况。

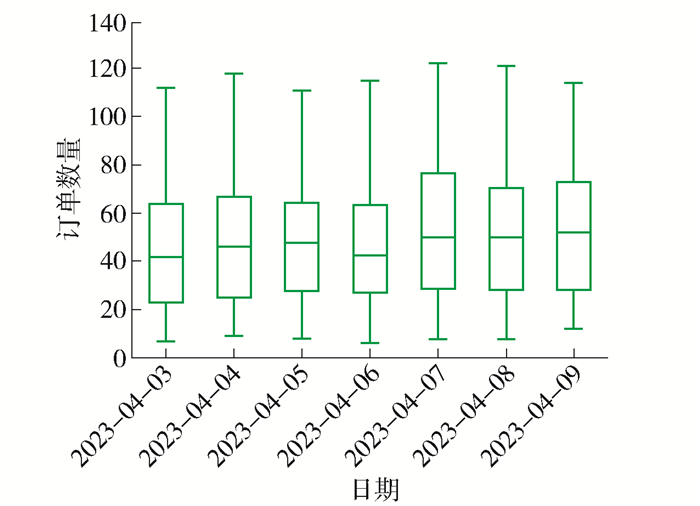
选取NIO在上海BSS网络中的105座BSS运行数据，得到4月份BSS在一周内服务的换电EV数量的分布情况，如图 1所示。多数BSS每天的服务频次集中在20~60次，但处于较繁忙地区的BSS每天的换电服务频次多达130次。此外，换电服务频次中位数为40~50次，表明BSS每天服务的换电EV数量远远低于其服务能力，BSS的利用率存在极大的提升空间。

图  1  2023年4月一周各站订单数分布

Figure  1.  NIO distributions of order numbers of different stations in a whole week of April, 2023

下载: 全尺寸图片 幻灯片

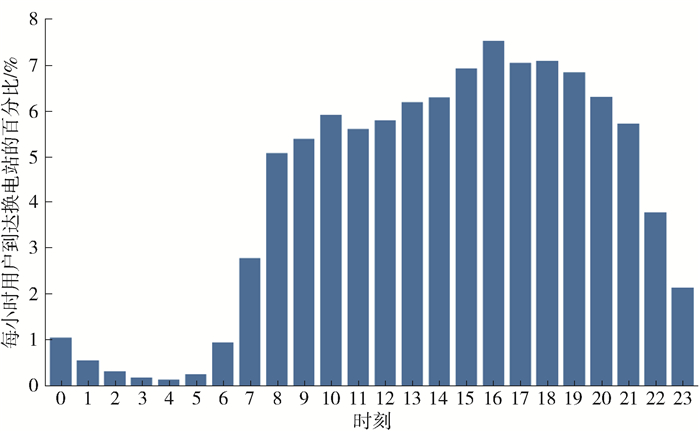
根据NIO 2023年1月至4月的运营数据可得EV用户每小时到达BSS的概率分布，如图 2所示。例如，BSS在凌晨0点到1点之间的服务的EV数量占每日总EV数量的1%，即如果一座BSS在一天内服务100辆EV，其中有1辆EV的换电行为发生在凌晨0点到1点之间。数据显示，晚上9:00之后BSS服务的EV数量大幅下降。高峰时段出现在下午4点至5点之间，获取该时段内EV用户一天到达BSS的时间分布对计算仿真中EV用户到达BSS的时间起着至关重要的作用。

图  2  用户每小时到达的概率分布

Figure  2.  Distribution of customer arrivals in each hour

下载: 全尺寸图片 幻灯片

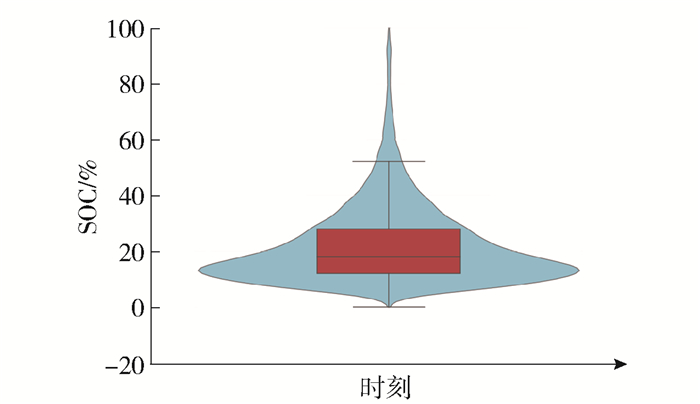
电池的初始荷电状态和最终荷电状态决定了BSS需要提供的负荷量和换电持续时间。通常情况下，当电池的SOC不低于90%时就可以参与换电服务^[27]，故本文假设电池SOC达到90%以上才能参与换电服务。初始SOC的分布如图 3所示，中位数在18%左右，说明EV用户在剩余电量接近该值时开始产生充电需求。该分布将作为仿真中EV到达BSS的初始SOC的输入。

图  3  到达换电站时的EV剩余电量分布

Figure  3.  Distribution of battery SOC at the beginning of swapping service

下载: 全尺寸图片 幻灯片

1.3   仿真框架

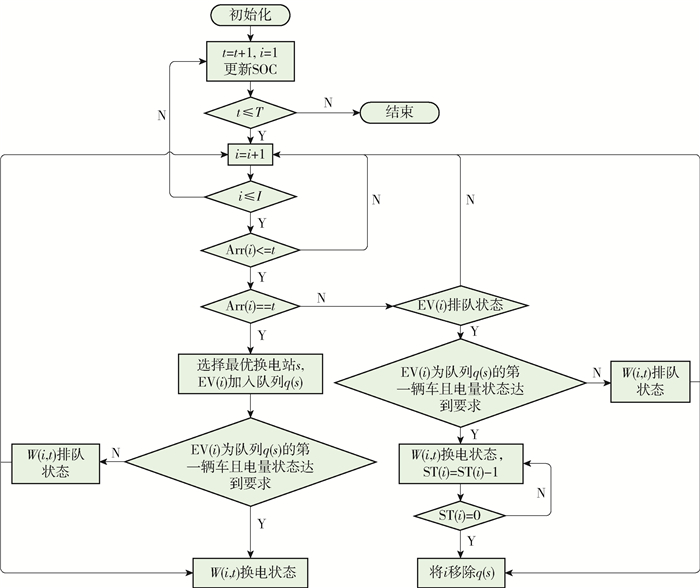
所提仿真器的流程如图 4所示。在整个仿真过程中，连续仿真每辆电动汽车的不同状态(排队、交换、离开)时每座BSS的EV用户排队状态，以及BSS内每个电池组的SOC。表 2为流程图中涉及的符号及其意义。

图  4  仿真流程

Figure  4.  Simulation workflow

下载: 全尺寸图片 幻灯片

表  2  仿真流程图中的参数

Table  2.  Parameters in the simulation flowchart

符号	含义
Arr	车辆i到达换电站的时间
ST	电池换电的剩余时间
W	车辆的状态，W∈[排队，换电，离开]
i	车辆检索，i=1, 2, …, I
q	车辆所在队列列表
s	车站检索，s=1, 2, …, S
t	时间检索，t=1, 2, …, T

下载: 导出CSV 

| 显示表格

仿真中EV到达BSS的时间遵循图 2中的分布，每小时内的时间段是随机的。EV到达BSS时的剩余SOC分布如图 3所示。EV的初始索引i=0，时间的初始索引t=0。单辆EV的排队时间和每座BSS的初始队列均为空列表。电池参与换电服务的SOC阈值设置为90%，模拟时间步长设置为1 min。

为了仿真EV的换电过程，对一天内每个时间步长和每辆EV进行迭代，通过EV到达换电站的时间(Arr)与当前时间(t)的关系确定EV的状态:

1) 如果t在Arr之前，则表明EV尚未到达BSS，此时研究下一辆车。

2) 如果t=Arr，表示EV刚刚到达BSS。遵循选站策略将EV添加到相应的BSS的队列中。若是队列中的第一辆车，将分析该EV的换电过程。

3) 如果t在Arr之后，有2种可能。EV可能已经完成了换电服务并离开了BSS，或者仍然处于排队状态。如果是前者，继续研究下一辆车。如果是后者，则将剩余的服务时间减少一个时间步长。当剩余服务时间为0时，将EV从队列中移除。

在每个时间步长结束时，考虑每个模块的充电功率更新BSS中电池组的SOC。只有当SOC高于阈值时才允许电池交换；否则，车辆必须等待。

该仿真过程的一个重点是为每辆EV选择进行换电服务的BSS。该过程要考虑3个方面，首先，BSS必须位于EV行驶的目标区域内；其次，BSS必须配置有换电EV所需的电池类型，在BSS共享模式下，假设电池组是通用的；最后，根据队列长度和BSS中电池组的状态计算排队等待时间，从而将车辆分配给所有可用BSS中等待时间最短的。

2.   仿真结果

所提仿真器使用软件Python3.9.12从零开始开发，通过仿真EV用户的换电过程，获取EV用户的排队时间，以评估不同场景下BSS的建设成本和EV用户的换电体验。仿真基于NIO二代站，站内可以容纳13个电池组，每个充电模块具有40 kW的功率容量，假设电池容量为75 kW ·h。

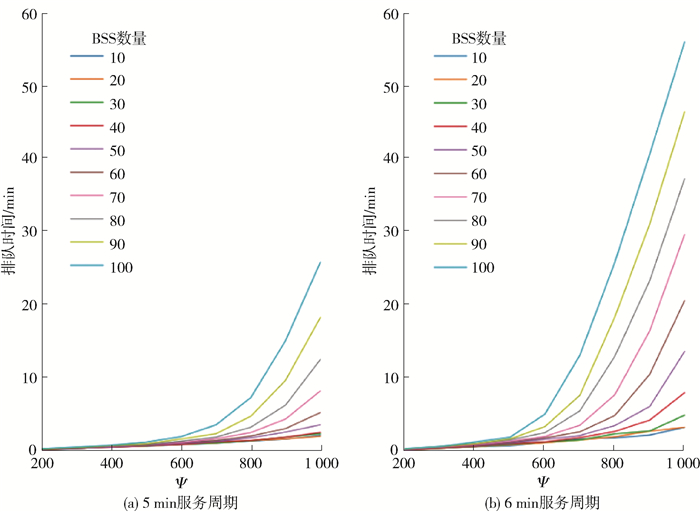
许多因素都会影响排队时间，例如EV和BSS的数量、可用的电池组、充电功率、电池尺寸、换电服务时间等。为了进行敏感度分析，本文将其中几个影响因素作为确定值，针对单一品牌的BSS系统进行研究，分析BSS数量、EV数量和服务时间对用户排队时间的影响。仿真时引入一个变量，即“EV与BSS的数量比率”，表示平均每座BSS可以服务的EV数量，在本文中使用Ψ表示。BSS的数量从10到100不等，步长为10，而Ψ的范围从200到1 000不等，步长为100。图 5(a)和(b)分别表示EV换电服务时长为5 min和6 min时，用户的排队时间随BSS和EV数量的变化有所改变。随着Ψ的增加，BSS每天服务的EV数量越多，用户的排队时间越长，且用户的排队时间随Ψ的增加并不是线性的。例如，在图 5(b)中，当有100座BSS，且Ψ＞600时，用户的排队时间急剧增加。从成本效益的角度来看，在达到这个转折点之前限制Ψ是明智的。

图  5  不同车站数目及Ψ下的排队时间

Figure  5.  Queuing time with different numbers of BSSs and Ψ

下载: 全尺寸图片 幻灯片

当固定Ψ时，排队时间随着BSS数量的增加而增加。例如，在图 5(a)中，当Ψ=800，且有100座BSS时，用户的排队时间为8 min；而当Ψ=800，有90座BSS时，用户的排队时间为5 min。这种增长主要是因为服务的换电EV数量的不平衡随着BSS数量的增加而变得更加明显。假设BSS最初建在繁忙地区，然后往空闲地区扩展，随着BSS和EV数量的增加，繁忙的BSS可能需要服务更多的EV进行换电，导致BSS服务EV数量的不平衡。BSS建设初期允许较大的Ψ值，不会显著增加用户的排队时间。随着EV数量的增加，需要更多的BSS来抵消换电服务负荷失衡的影响。

对比图 5(a)和(b)可知，随着换电服务时间的减少，用户的排队时间显著减少。在服务时间为5 min的情况下，100座BSS可以支持70 000辆EV，且用户的排队时间小于5 min；而在服务时间为6 min的情况下，只能支持60 000辆车。该情况下建议换电服务提供商减少服务持续时间，以提高BSS的使用效率。搭建的仿真器中将换电服务时间设置为6 min。

下文中以“共享”模式表示EV品牌共享换电站，“不共享”模式表示EV品牌均独立运营的情况。分析“共享”模式和“不共享”模式下，随着BSS数量和EV数量的变化，用户平均排队时间的动态变化。在“照常营业”(business as usual，BAU)的情况下，2个品牌在“不共享”模式下，限制每个品牌的EV只能在指定的BSS进行换电。在“共享”模式下，假设2个品牌的EV均可以进入目标区域内的任何一座BSS。考虑到2个EV品牌可能处于不同的发展阶段，给出下面2种换电场景。

场景1：该场景下，X品牌已经成立了几年，拥有稳定的EV市场和BSS数量，而Y品牌刚刚进入新能源市场，且处于建设BSS的初期。本文进一步探索Y品牌在不同发展阶段，两EV品牌EV用户的平均排队时间在“共享”模式和“不共享”模式下的变化情况，从而量化共享BSS对处于稳定发展阶段的EV品牌和新兴EV品牌用户平均排队时间的影响。

场景2：X品牌和Y品牌的BSS和EV数量相近，且数量同步增加。分析该场景下将用户排队时间控制在特定阈值内所需要的BSS数量。以此评估相同排队时间下，共享BSS对换电资源利用率的影响，阐明通过BSS共享在不同场景中实现效率提高和资源优化的优势。

在场景1中假设X品牌在城市中运营100座BSS，总共服务80 000辆EV(Ψ=800)。Y品牌的BSS从10座增加到100座，以10座为单位递增，Ψ的值以100为单位从100增加到1 000。根据仿真计算结果，对应所需要Y品牌的BSS数量分别为10、50、80、100座，如图 6所示。实线表示“共享”模式下的用户平均排队时间，虚线表示BSS在“不共享”模式下的用户平均排队时间。由于X品牌下的EV和BSS数量保持不变，因此在“不共享”模式下，X品牌EV用户的平均排队时间固定为20 min。

图  6  Y品牌用户的平均排队时间在不同Ψ下的变化

Figure  6.  Variation in average queue time for users of Brand Y at different station proportions

下载: 全尺寸图片 幻灯片

如图 6(a)所示，当品牌Y建设10座BSS时，两品牌在“共享”模式下能够显著减少品牌X用户的平均排队时间。同时，Y品牌的平均排队时间略有增加。在图 6(a)和(b)中，2条实线基本保持在2条虚线之间，这表明，虽然共享BSS在减少品牌X用户的平均排队时间的同时增加了品牌Y用户的平均排队时间，但是整体系统的效率仍然是有所提升的。

随着品牌Y的BSS数量的增加，图 6(c)和(d)中突出显示的部分，实线与虚线的位置关系表明“共享”模式下2个品牌用户的平均排队时间相较于“不共享”模式均有所减少。此时，共享BSS对2个品牌都是有利的。然而，随着Y品牌车辆的持续增长，由于Y品牌消耗了X品牌的换电资源，“共享”模式下X品牌用户的平均排队时间超过了“不共享”模式。对于换电资源紧张的品牌，在图中突出显示阶段寻求与其他品牌的资源共享能够有效减少用户排队时间，提升用户的换电体验。

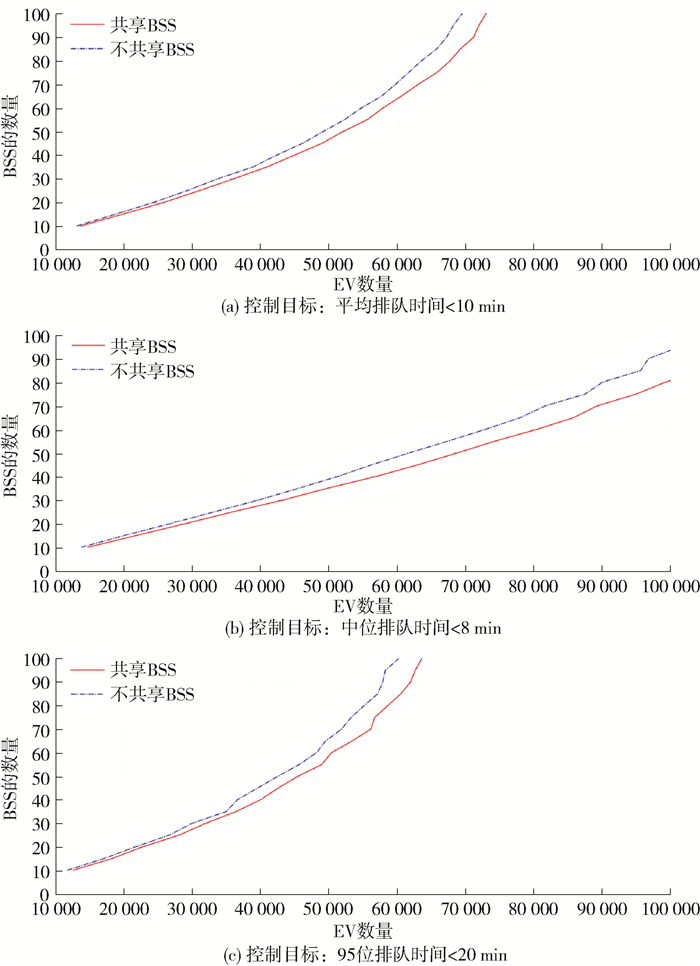
场景2中针对不同的控制目标进行模拟，分析平均值、中位数和95位值，以确定服务特定数量的EV换电时所需的最小BSS数量。其中平均值和中位数表示多数EV用户的换电体验，而95位值表示有最坏换电体验的用户比例。

如图 7(a)所示，维持用户平均排队时间为10 min所需的BSS数量与EV数量之间呈非线性关系。随着车辆数量的增加，需要更多的BSS，主要是由于EV之间的服务负载不平衡。“共享”模式下显著减少了所需BSS的数量。例如，当服务60 000辆EV，并将用户的平均排队时间限制在10 min时，“不共享”模式下需要70座BSS。“共享”模式下每个品牌需要建设63座，减少10%的BSS数量。

图  7  实现不同控制目标的最小BSS数量

Figure  7.  Minimum number of BSSs to achieve different control targets

下载: 全尺寸图片 幻灯片

从运营方的角度，应该重点关注换电体验最差的EV用户。图 7(c)展示了将P95状态用户的排队时间维持在20 min内所需的最少BSS数量。“不共享”模式下，当EV数量达到60 000辆时，每个品牌必须建设100座BSS。在“共享”模式下，只需要建设83座BSS，即“共享”模式下能够节省17座BSS的建设和运营成本。

3.   结论

本文对BSS系统下EV用户的排队时间进行了研究。对NIO汽车品牌下BSS的实际位置和运行数据进行分析，以相关统计数据趋势为依据生成相关仿真参数，以此开发了一个连续的仿真器来量化各种场景下的用户排队时间，探索不同品牌之间共享BSS的收益和成本，得出以下结论：

1) 换电服务时长是影响换电用户平均排队时间的关键因素之一。合理设置换电服务时长能够有效提高换电服务效率，提升用户换电满意度。

2) 共享BSS可以减少不同EV品牌用户的平均排队时间，并有助于减少将用户排队时间保持在期望阈值内所需的BSS数量。

多个电动汽车品牌之间共享BSS资源可以减少用户换电排队时间，显著提升客户体验，同时能够提升BSS的利用率，减少建设成本。此外，共享实践的成功实施需要标准化协议、电池组尺寸，以及制造商和服务提供商之间的充分合作以应对服务负载不平衡、电池组互换性以及服务兼容性对客户体验影响等挑战，继而推动电动汽车充电基础设施的持续改进和提高客户满意度。