Study on Mechanical Properties of Disconnectable Coupling Joint With Steel Wedges (DCJS) Under Eccentric Load
-
摘要:
为了解决钢楔式活络端在偏心荷载作用下工作机理的研究相对较少的问题, 该文定量研究钢楔式活络端的抗弯性能, 首先建立经过试验结果验证的有限元模型, 然后通过数值分析的方法, 系统研究偏心载荷作用下钢楔式活络端的变形和受力机理, 并对钢楔式活络端的抗弯性能进行参数化分析, 基于参数分析结果, 建立适用于钢楔式活络端的弯矩-转角模型。研究结果显示: 钢楔式活络端的抗弯性能随偏心距、钢楔高度和中肋板高度的增加而降低, 随钢楔长度、钢楔宽度、槽钢厚度和钢管壁厚的增加而增加, 同时本文所建立的弯矩-转角模型能够准确地预测钢楔式活络端的弯矩-转角曲线、初始抗弯刚度和塑性抗弯承载力。
Abstract:To quantitatively study the flexural performance of the disconnectable coupling joint with steel wedges (DCJS), the validated finite element model was established based on the test results of the DCJSs. Subsequently a series of finite element models were used to systematically study the deformation and force mechanism of the DCJS under eccentric load. The flexural performance of the DCJDs was analyzed through the parameterization method. Based on the outcomes of the parametric study, the moment-rotation model was established for DCJS. Results show that the flexural performance of the DCJS decreases with the increase of eccentricity, wedge height and midrib height, and increases with the increase of wedge length, wedge width, channel thickness and tube wall thickness. Meanwhile, the moment-angle curve, initial flexural stiffness and plastic flexural capacity of the DCJS can be accurately predicted by the moment-rotation model.
-
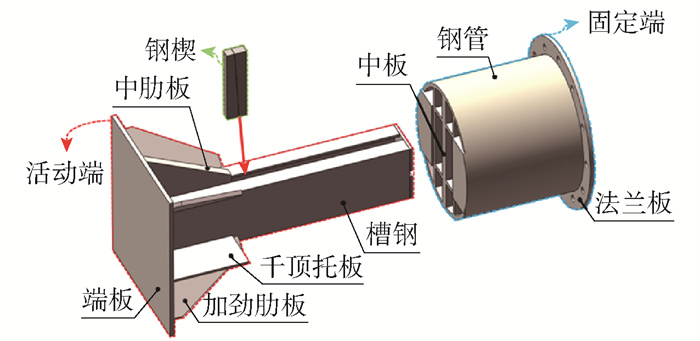
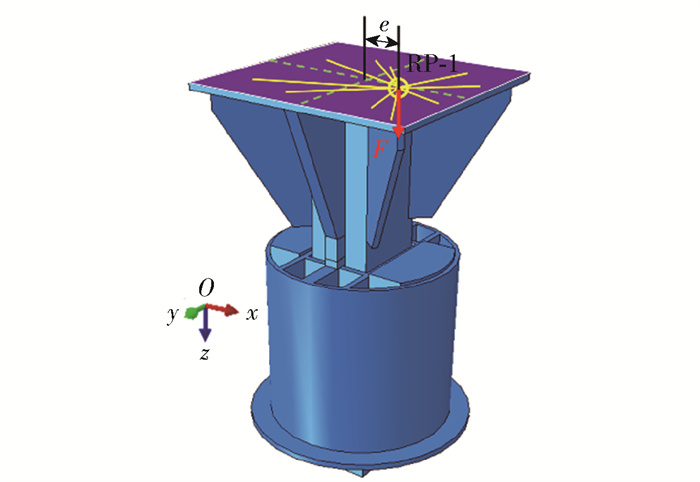
钢楔式活络端是设置钢支撑端部连接钢支撑和围护结构的重要节点，起调节钢支撑长度和施加预加轴力的作用。在地铁基坑施作过程中，由于施工质量或钢支撑架设工序等问题，钢楔式活络端通常受到偏心荷载的作用。这容易使钢支撑局部屈曲甚至失稳破坏，降低其承载性能，如图 1所示。因此钢楔式活络端在偏心荷载作用下的抗弯性能对钢支撑的整体稳定性影响较大。
目前关于钢楔式活络端的研究多集中于承载性能方面。张明聚等[1-3]通过试验方法研究钢楔式活络端的力学性能，分析破坏形态、荷载-位移曲线和应变演化过程。熊栋栋等[4]监测钢楔式活络端预加轴力的保持性能，指出由于偏心荷载的影响，活络端的实际承载性能低于设计值。在活络端偏心受压承载性能的研究方面已有一些相关研究。孙九春等[5]通过数值模拟和理论计算的方法研究偏心距对矩形钢板式活络端承载性能的影响。张明聚等[6]开展双排楔活络端的抗弯性能研究，指出为避免活络端整体失稳，偏心距不得大于端板外表面中心点到箱型体外边缘间的距离。苑媛[7]、张明聚等[8]通过试验方法研究螺栓紧固型楔式(bolt fasten wedge，BFW)活络端在偏心荷载作用下的力学性能，研究结果表明，偏心荷载作用下BFW活络端初始压缩刚度降低明显。Lui等[9]拟合了一种针对半刚性节点的多参数弯矩-转角模型。Wu等[10]拟合了一个三参数指数模型来描述顶底角钢半刚性连接和带有腹板角钢的顶底角钢半刚性连接的弯矩-转角曲线。Ang等[11]拟合了一个幂函数的四参数弯矩-转角模型。施刚等[12]提出一种计算钢结构梁柱半刚性端板连接转动变形的方法，该方法能够较准确计算弯矩-转角全过程曲线。目前关于钢楔式活络端的研究多集中于承载性能的研究，而关于钢楔式活络端在偏心荷载作用下工作机理的研究相对较少。同时，对于作为钢支撑体系中半刚性节点的钢楔式活络端，有必要对其抗弯性能进行定量研究，并提出适用于钢楔式活络端的弯矩-转角计算模型。
基于此，本文首先建立基坑工程钢支撑体系中钢楔式活络端的有限元模型，开展轴心受压的数值模拟，将计算结果与活络端试验结果对比分析，进而验证所建立的钢楔式活络端数值模型的准确性和可靠性；其次，通过该数值模型研究偏心荷载作用下钢楔式活络端的受力和变形机理，进一步开展关键参数对活络端的抗弯性能的影响研究；然后，建立适合于钢楔式活络端的弯矩-转角模型；最后，结合实际工程及常用活络端的相关设计参数，从机理出发给出钢楔式活络端偏心荷载作用下的使用建议。
1. 数值模拟与验证
1.1 有限元模型
目前在施工现场常见的钢楔式活络端的结构形式如图 2所示。
文献[2]对钢楔式活络端开展了试验研究，试验结果显示加载过程中试件焊缝未见明显开裂，于是在数值模型中将焊缝假定为刚性连接。模型各部件的几何尺寸均与试件相对应。模型网格划分采用C3D8I单元，材料关键参数采用Guo等[13]提出的Q235钢的实测屈服强度、抗拉强度和弹性模量。本构关系采用田芳等[14]给出的Q235钢材真实应力和真实应变定义的弹塑性本构关系，如表 1所示，材料泊松比取0.3。
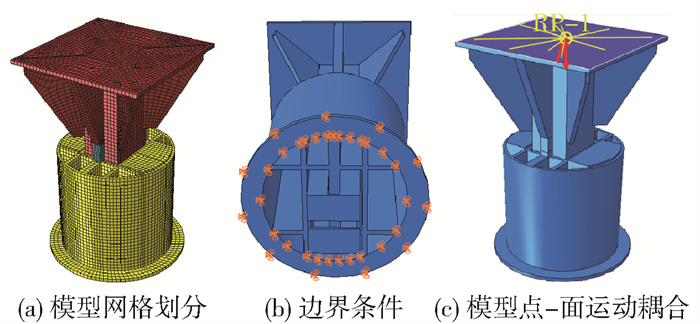
表 1 Q235钢材的应力-应变关系Table 1. Stress-strain relation of Q235 steel应力/MPa 0 215.7 250 325 372 402 应变/% 0 0.1 0.3 10.0 17.7 34.3 由于焊缝与母材具有相同强度，且焊缝在加载过程中没有开裂，因此将活动部分和固定部分分别合并为一个部件。钢楔式活络端的网格划分如图 3(a)所示。试件边界条件采用约束法兰板任意方向的位移，不设转角约束，边界条件如图 3(b)所示。有限元模型中接触模式均为Surface-to-surface，法向设置为硬接触，且允许接触后分离，切向定义为罚函数摩擦接触，各向同性，摩擦因数为0.2。为了准确模拟荷载与试件端板的关系，有限元模型将活动部分端板正中心定为参考点RP-1，并与端板外表面设置运动耦合，将集中荷载施加于RP-1上。集中力F从0加载到6 200 kN，共分100步逐级加载，每步加载增量为1%。试验选用含有球铰结构的压力机，因此定义F可随RP-1旋转，试件的点-面耦合如图 3(c)所示。
1.2 模型验证
1.2.1 破坏形态
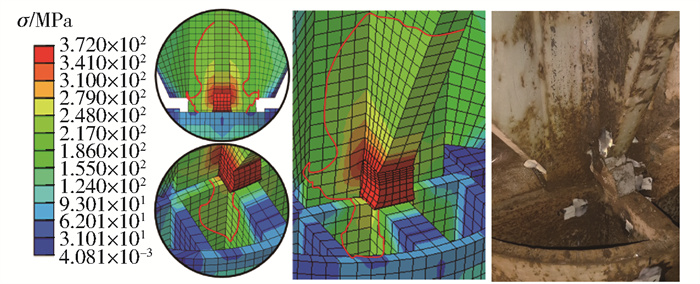
图 4对比了活络端关键损伤位置破坏形态的数值结果与试验结果，数值结果与试验结果吻合较好。试验结果中钢楔与中肋板下缘产生过度变形，根据Von-Mises应力云图，钢楔、中肋板和槽钢的接触区域存在明显的应力集中。接触区与中板上部的材料达到屈服状态，这与试件的破坏形态及应变分布情况是一致的。
1.2.2 荷载-位移曲线
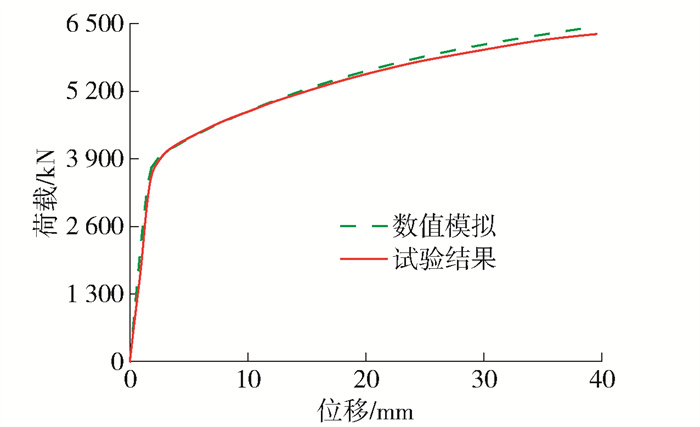
有限元模型的荷载-位移曲线取自参考点RP-1。数值结果与试验结果的荷载-位移曲线对比如图 5所示，二者吻合较好，数值结果在弹性及弹塑性阶段与试验结果非常接近。在加载后期，数值结果与试验结果有一定偏差。但在实际工程中，单个节点的变形不能过大，要满足支护体系的整体变形要求。
本文所建立的有限元模型能够准确地预测钢楔式活络端应力分布及变形情况，因此，该有限元模型可用于钢楔式活络端抗弯性能研究。
2. 偏心荷载作用下的变形和受力机理
为了进一步研究偏心荷载作用下钢楔式活络端的力学响应，笔者建立偏心荷载作用下的有限元模型，通过调节RP-1的位置来实现偏心荷载的作用。参考点与端板中心的距离为试件的偏心距e，如图 6所示。活络端的结构形式关于x轴和y轴对称，于是设置2个偏心方向，分别为x向和y向。
2.1 钢楔式活络端变形特征
2.1.1 沿x方向偏心
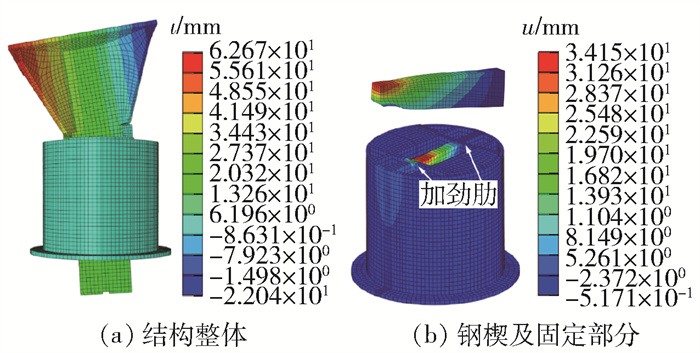
以偏心距为36.5 mm为例，在偏心荷载作用下，活动部分出现明显的偏转，活动部分绕y轴弯曲变形，这与某基坑事故中活络端在偏心荷载作用下的极端破坏形态吻合，如图 7所示，因此验证了本文所建立的有限元模型的合理性。在偏心荷载作用的一侧，槽钢向下变形较为明显，两侧槽钢变形不一致，相差约8.2 mm。活动部分整体向下变形，右侧槽钢向下变形约为43.3 mm，左侧槽钢向下变形为32.3 mm。钢楔在偏心荷载作用下呈弯曲变形，最大变形值为12 mm。固定部分的变形主要集中偏心荷载加载的一侧，中板的变形整体偏小，最大变形值仅为3.1 mm。
![]()
图 7 沿x方向偏心的竖向变形云图及破坏形态Figure 7. Failure mode and vertical deformation of eccentric point along the x direction2.1.2 沿y方向偏心加载
以偏心距为36.5 mm为例，模型的变形云图如图 8所示，活动部分绕x轴旋转明显，而固定部分则没有明显变形。当载荷达到5 000 kN时，活动部分端板绕x轴旋转变形约0.06 rad。偏心荷载侧端板最大垂直变形为62 mm。活动部位的相对变形主要来自钢楔，活动部位的绝对变形相对较小，这是由于槽钢对中肋板具有约束作用。钢楔的最大变形量为34 mm，发生在加载侧，而在另一侧没有变形。固定部分的最大垂直变形在中板处，同样也位于中板加载侧，如图 8所示。由于中板两侧加劲肋的作用，中板最大变形值仅为2.46 mm，为钢楔最大变形的7.2%。
![]()
图 8 沿y方向偏心的竖向变形云图Figure 8. Vertical deformation of eccentric point along the y direction2.2 钢楔式活络端应力分布特征
2.2.1 沿x方向偏心加载
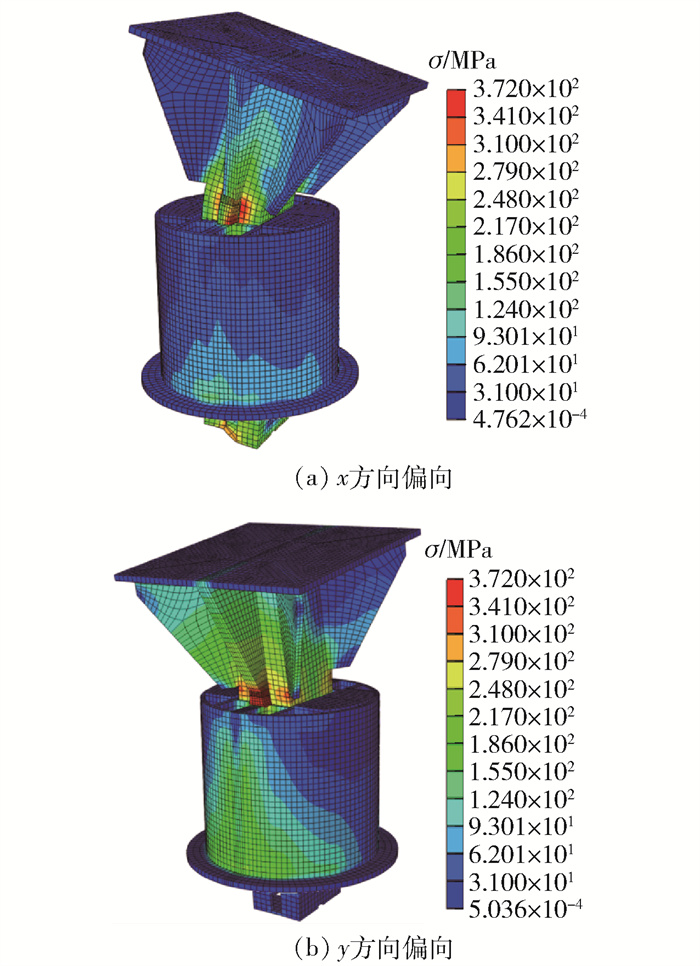
当荷载加载至3 341 kN时，由于变形增量过大而导致计算不收敛。图 9(a)给出加载结束时的应力分布情况，应力主要集中于偏心荷载作用的一侧，钢楔处的槽钢翼缘达到应力极限372 MPa，同时活动部分材料的屈服范围集中于钢楔处的槽钢翼缘。钢楔处的应力主要集中于偏心荷载作用的一侧，该侧与中板和中肋板接触的位置处的材料接近极限强度，几乎整个钢楔达到屈服状态。固定部分的应力值较小，中板应力较为集中，集中区域出现在偏心荷载作用一侧，最大应力值为262 MPa。
2.2.2 沿y方向偏心加载
模型的Von-Mises应力云图如图 9(b)所示。应力主要集中在偏心荷载作用的一侧。活动部分的应力主要集中在中肋板底部，即与钢楔的接触位置。当偏心荷载增加到3 360 kN时，中肋板受载侧材料开始屈服。当荷载增加到5 000 kN时，槽钢受压和受拉侧的材料接近极限强度。加载结束时，整个钢楔的材料几乎全部屈服。同时，超过一半的钢楔材料接近极限强度。因此，选用高强度钢加工钢楔可以显著提高活络端的承载性能。固定部分的应力主要集中在中板处，加载结束时，中间板的最大应力值为362 MPa，接近材料的极限强度。
3. 偏心荷载作用下的抗弯性能
为了深入研究关键部位的有限元模型参数对钢楔式活络端抗弯性能的影响，进行了一系列参数化研究。模型的偏心方向分别为x轴和y轴正方向，x方向偏心距为e1，y方向偏心距为e2。共建立33个模型，各模型的偏心距及关键位置的几何信息如表 2所示。
表 2 有限元模型参数Table 2. Parameters for finite element models编号 e1/mm e2/mm h①/mm l②/mm w③/mm t④/mm tc⑤/mm hm⑥/mm 1~4 36.50/73.00/
109.50/146.000 100 350 45 16 13 430 5~9 0 18.25/21.70/
36.50/54.75/
73.00100 350 45 16 13 430 10~13 73.0 0 100 250/300/
400/45045 16 13 430 14~17 73.0 0 100 350 25/30/35/40 16 13 430 18~21 73.0 0 50/150/
200/250350 45 16 13 430 22~26 73.0 0 100 350 45 10/12/14/
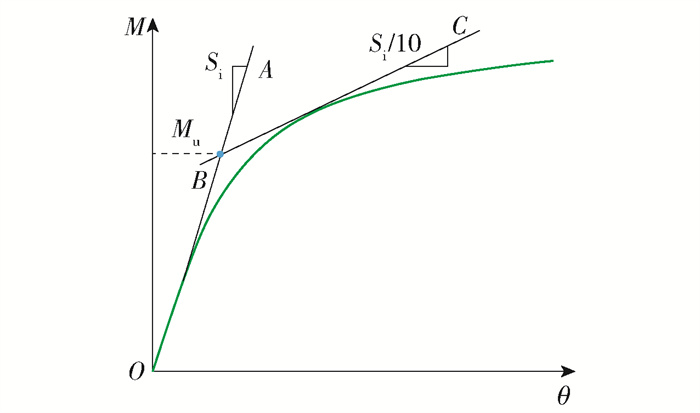
18/2013 430 27~30 73.0 0 100 350 45 16 7/10/16/19 430 31~33 73.0 0 100 350 45 16 13 330/380/480 ① h表示钢楔高度；② l表示钢楔长度；③ w表示钢楔宽度；④ t表示钢管壁厚；⑤ tc表示槽钢厚度；⑥ hm表示中肋板高度。 钢楔式活络端的抗弯性能通过初始抗弯刚度(Si)和塑性抗弯承载力(Mu)来评价。初始抗弯刚度为试件弯矩-转角曲线初始弹性段的斜率，塑性抗弯承载力为弯矩-转角曲线中直线段与曲线段交接点对应的弯矩值。由于各曲线是平滑的，没有明显的交接点，因此，取初始抗弯刚度的延伸线(OA)和斜率为Si/10的切线(BC)的交点对应的弯矩作为节点的塑性抗弯承载力[15]，具体选取方法如图 10所示。
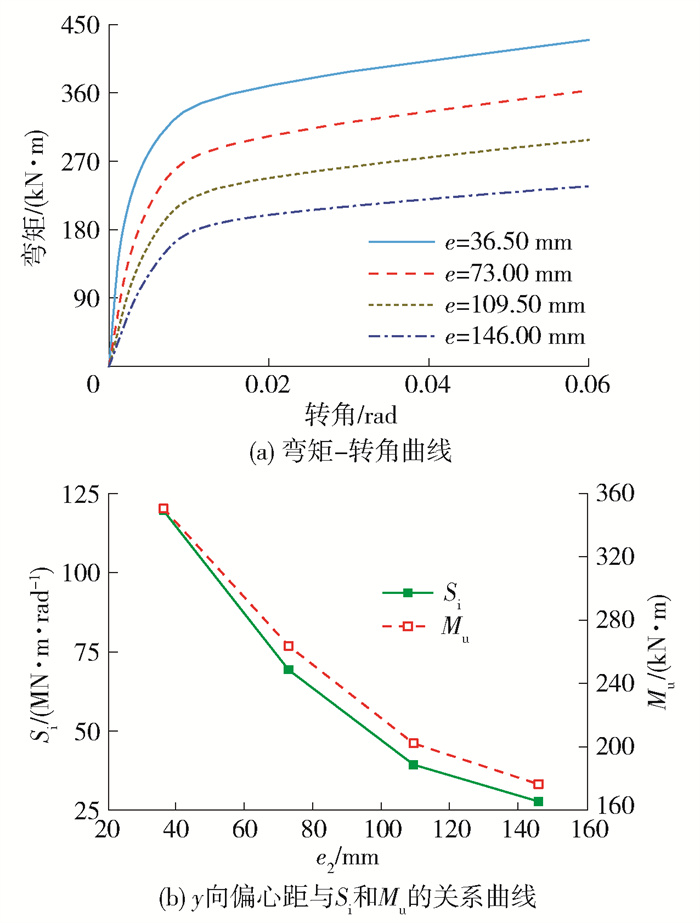
3.1 y方向偏心距的影响
图 11给出了y方向不同偏心距下活络端的弯矩-转角曲线，偏心距对活络端的抗弯性能影响显著，抗弯性能随偏心距的增加逐渐降低。当偏心距从36.50 mm增加至73.00 mm时，初始抗弯刚度和塑性抗弯承载力分别降低了50.3 MN ·m/rad和86.7 kN ·m；当偏心距从73.00 mm增加至109.50 mm时，初始抗弯刚度和塑性抗弯承载力分别降低了30.0 MN ·m/rad和61.6 kN ·m；而当偏心距从109.50 mm增加至146.00 mm时，初始抗弯刚度和塑性抗弯承载力仅分别降低了11.6 MN ·m/rad和25.8 kN ·m。
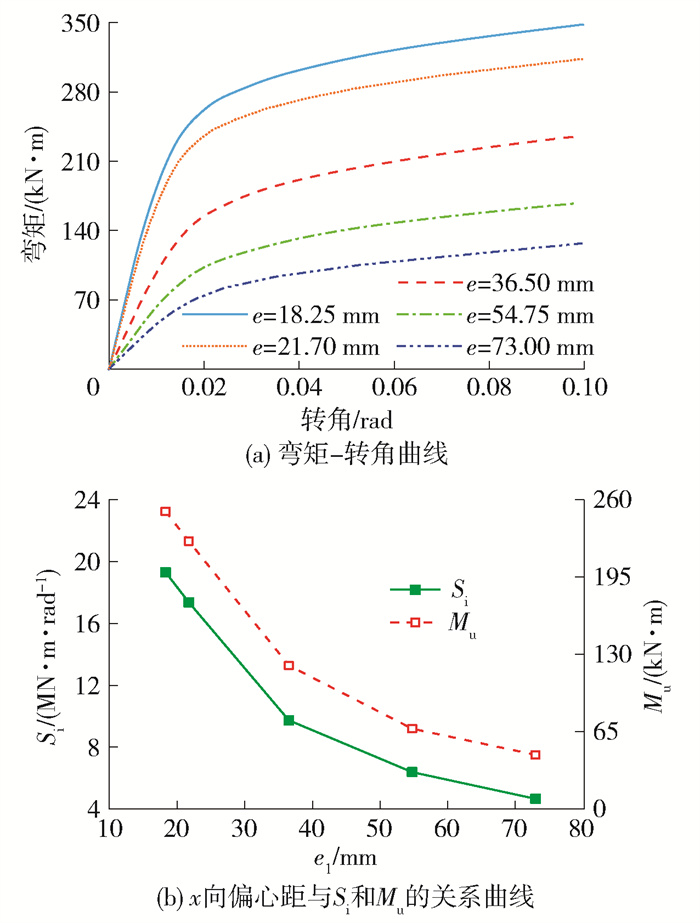
3.2 x方向偏心距的影响
随着x方向偏心距的增加，活络端的抗弯性能逐渐下降，并且下降速率逐渐减慢，如图 12(a)所示。相比于偏心荷载作用于y方向，作用于x方向可以使活络端的抗弯性能下降得更加迅速。根据图 12(b)，偏心距为73.00 mm时，初始抗弯刚度和塑性抗弯承载力分别为4.7 MN ·m/rad和45.5 kN ·m，仅分别相当于y方向偏心时的6.7%和1.7%。
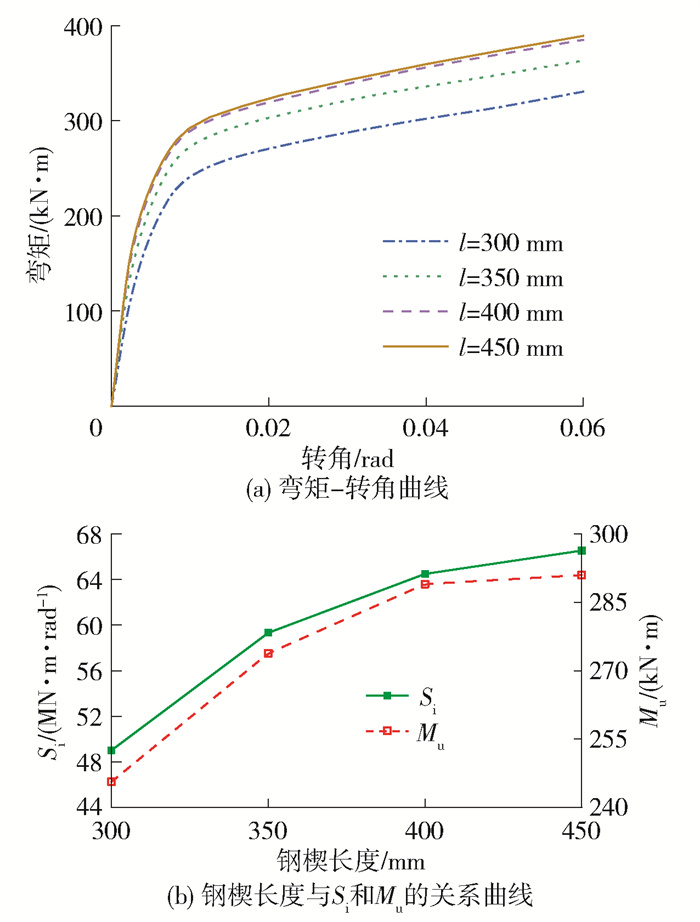
3.3 钢楔长度的影响
在一定范围内，增加钢楔长度能显著提升活络端的抗弯性能，如图 13所示。当钢楔长度小于350 mm时，钢楔长度与初始抗弯刚度和塑性抗弯承载力呈线性正相关，钢楔长度每增加50 mm，初始抗弯刚度和塑性抗弯承载力分别增加约9.5 MN ·m/rad和27.9 kN ·m，增加速率分别约为30.2%和12.9%。当钢楔长度超出350 mm后，超出了中肋板下边缘长度，钢楔长度不再是活络端抗弯性能的影响因素，当钢楔长度从350 mm增加至400 mm时，初始抗弯刚度和塑性抗弯承载力增加速率仅为8.7%和5.5%。
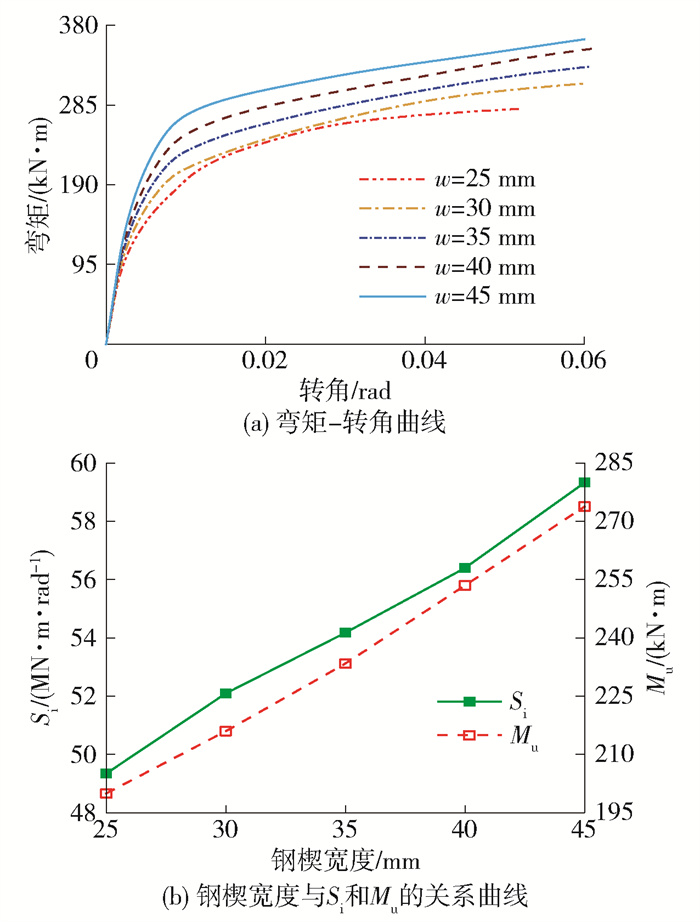
3.4 钢楔宽度的影响
如图 14(a)所示，钢楔宽度对活络端抗弯性能的影响较小，抗弯性能随钢楔宽度的增加而增加。钢楔宽度为25 mm时，在加载后期钢楔屈曲破坏，活络端抗弯性能不稳定。钢楔宽度与初始抗弯刚度和塑性抗弯承载力呈线性正相关，钢楔宽度每增加5 mm，初始抗弯刚度和塑性抗弯承载力约分别增加2.5 MN ·m/rad和18.5 kN ·m，增加率分别平均为4.7%和8.2%，如图 14(b)所示。
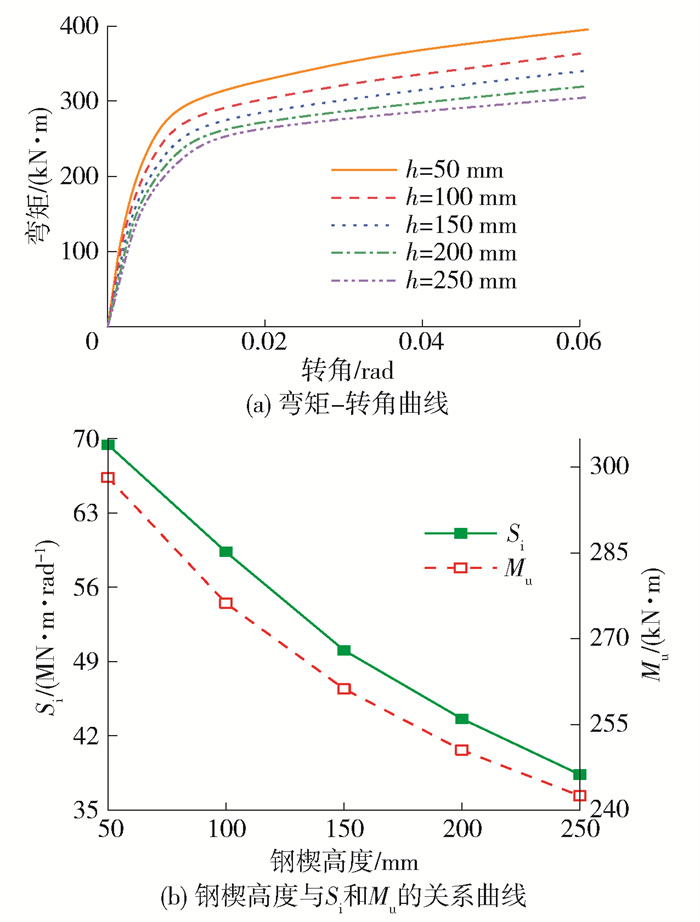
3.5 钢楔高度的影响
如图 15所示，钢楔高度与初始抗弯刚度和塑性抗弯承载力呈反相关，且相关性逐渐减弱。在钢楔高度从50 mm增加至100 mm时，初始抗弯刚度和塑性抗弯承载力分别减少10.1 MN ·m/rad和22 kN ·m，然而当钢楔高度从200 mm增加至250 mm时，初始抗弯刚度和塑性抗弯承载力分别仅减少5.3 MN ·m/rad和8 kN ·m。钢楔高度从50 mm增加至250 mm的各阶段内，初始抗弯刚度的减小速率分别为14.5%、13.3%、9.3%和7.6%，塑性抗弯承载力的减小速率分别为7.4%、5.0%、4.1%和3.2%。
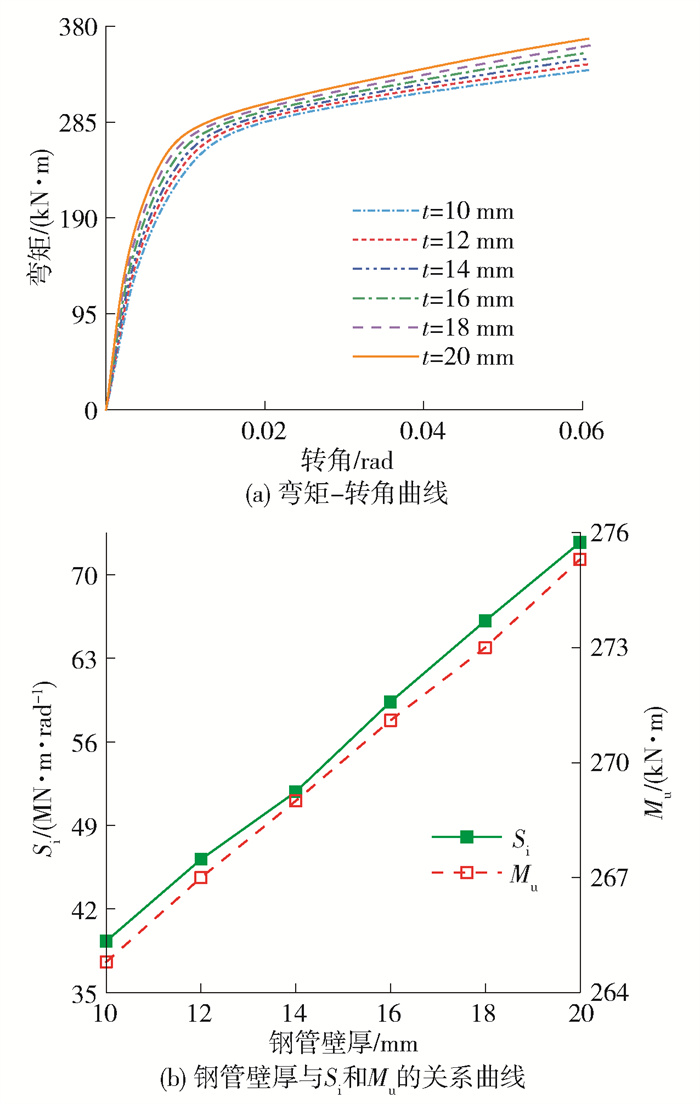
3.6 钢管壁厚的影响
根据图 16可知，钢管壁厚对活络端抗弯性能的影响较小。抗弯性能随钢管壁厚的增加而增加。初始抗弯刚度和塑性抗弯承载力随钢管壁厚的增加而线性增加，钢管壁厚每增加2 mm，初始抗弯刚度增加约6.7 MN ·m/rad，塑性抗弯承载力约增加2.1 kN ·m，二者的平均增加速率分别约为17.0%和0.8%。
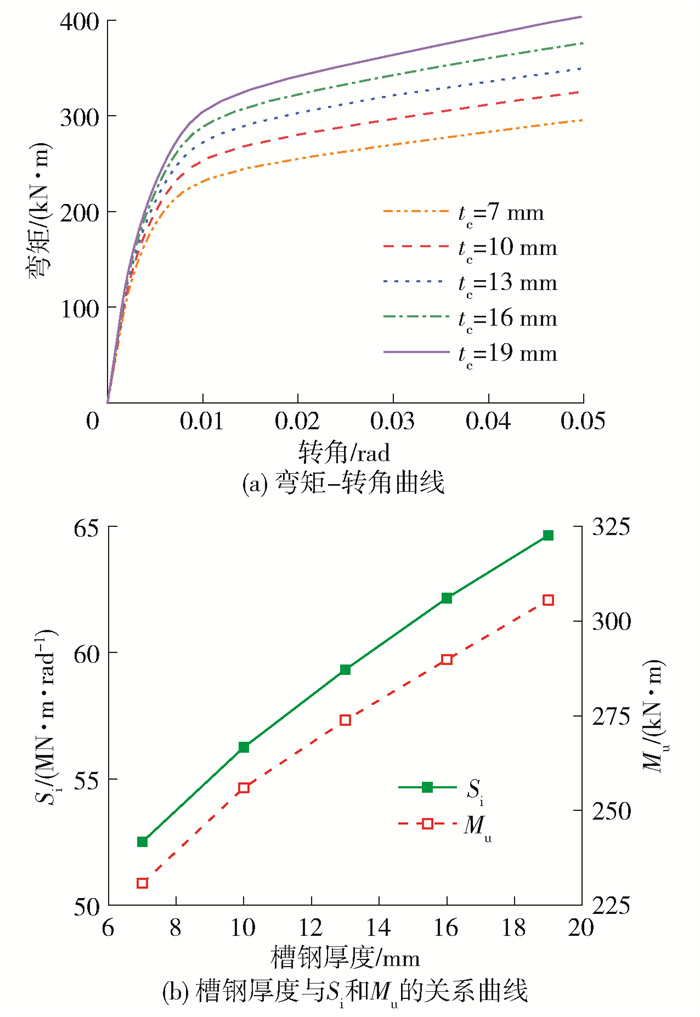
3.7 槽钢厚度的影响
图 17(a)给出不同槽钢厚度下活络端的弯矩-转角曲线。弯矩值小于150 kN ·m时，不同槽钢厚度对活络端抗弯性能影响较小。当弯矩值大于150 kN ·m时，槽钢厚度对活络端抗弯性能影响显著。如图 18(b)所示，初始抗弯刚度和塑性抗弯承载力随槽钢厚度的增加而增加，并且增加速率逐渐减弱。初始抗弯刚度的增加速率从最初的7.1%降至4.0%，塑性抗弯承载力的增加速率从最初的10.9%降至5.4%。
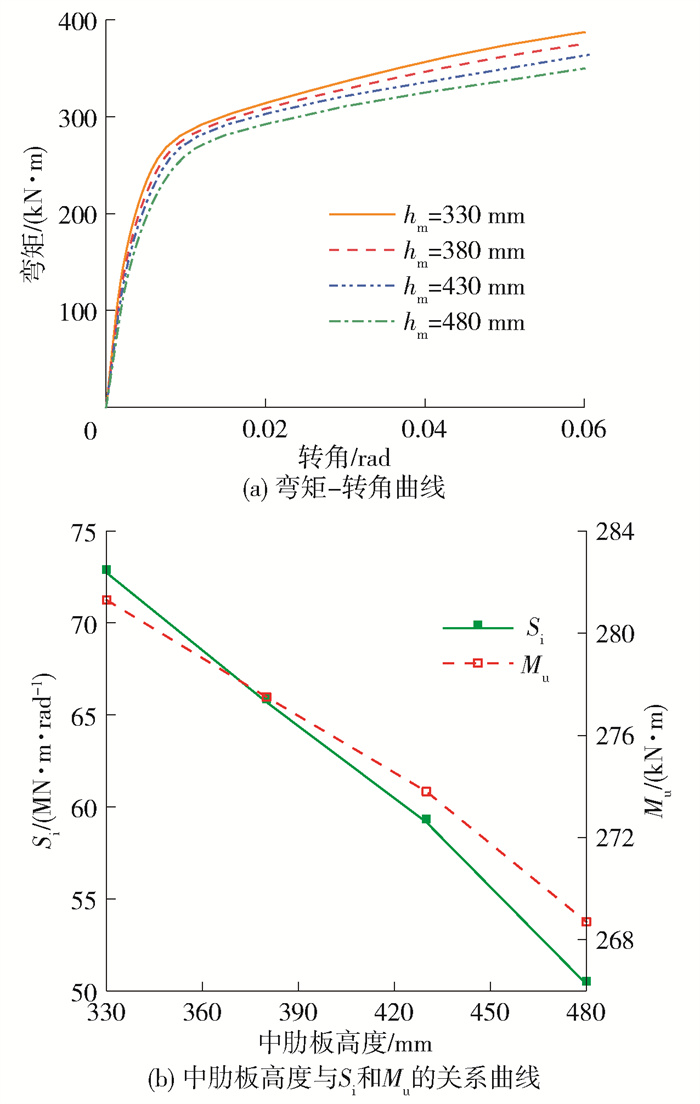
3.8 中肋板高度的影响
如图 18所示，活络端抗弯性能随中肋板高度的增加而减小，但由于中肋板两侧槽钢的约束作用，中肋板高度对抗弯性能的影响很小。初始抗弯刚度和塑性抗弯承载力随中肋板高度线性降低，当中肋板高度小于430 mm时，中肋板高度每增加50 mm，初始抗弯刚度和塑性抗弯承载力分别线性降低约7.8 MN ·m/rad和3.8 kN ·m，降低速率分别约9.3%和1.3%。当中肋板高度大于430 mm后，初始抗弯刚度和塑性抗弯承载力的降低速率略有增加，分别达到10.2%和1.5%。
4. 弯矩-转角模型
4.1 建立模型
在目前所提出的弯矩-转角模型中，Wu等[10]提出的半刚性节点模型能够很好地描述弯矩-转角曲线后期斜率仍不断增加的情况，这与钢楔式活络端的弯矩-转角曲线的变化趋势吻合。模型表达式为
$$ \frac{M}{M_{\mathrm{y}}}=n\left[\ln \left(1+\frac{\theta}{n \theta_0}\right)\right] $$ (1) 式中：M为结构所承受的弯矩；My为结构屈服时的抗弯承载力；θ为结构中心线的转角；θ0为参考塑性转角；n为结构的形状系数，需要通过拟合得到，是一个仅与θ0相关的参数。钢楔式活络端并非严格意义上的半刚性节点，因此，需要在此模型基础上加以修正，引入修正系数λ。修正后弯矩-转角模型表达式为
$$ M=\lambda \cdot M_y \cdot n\left[\ln \left(1+\frac{\theta}{n \theta_0}\right)\right] $$ (2) 钢楔式活络端在偏心荷载作用下结构的变形主要来自钢楔。中肋板由于槽钢的限制作用，下边缘处的变形仅相当于钢楔变形1%。中板变形仅为钢楔处的7%。因此，假定结构的转角由钢楔偏压变形和槽钢弯曲引起，忽略中板和中肋板下边缘的变形，所建立的弯矩-转角模型为偏心荷载作用于y方向时钢楔式活络端的弯矩-转角模型。
4.2 模型参数的确定
4.2.1 My的确定
钢楔式活络端在偏心荷载作用下为压弯构件，根据活络端的结构形式可以看出，槽钢的底部是自由的，槽钢仅受弯矩作用。因此活络端满足表达式
$$ M_y=\frac{A e W_{\mathrm{DH}} f_{\mathrm{y}}}{A e+W_{\mathrm{DH}}} $$ (3) 式中：fy为材料屈服强度；A为钢楔受压截面积；WDH为槽钢的抗弯截面系数。WDH计算公式为
$$ W_{\mathrm{DH}}=\frac{t_{\mathrm{c}} H^3+\left(t_{\mathrm{w}}-t_{\mathrm{c}}\right)\left[2 t_{\mathrm{c}}^3+6 t_{\mathrm{c}}\left(H-t_{\mathrm{c}}\right)^2\right]}{3 H}+\frac{w h^3}{12} $$ (4) 式中：H为槽钢腹板高度；tw为槽钢翼缘宽度。
4.2.2 θ0的确定
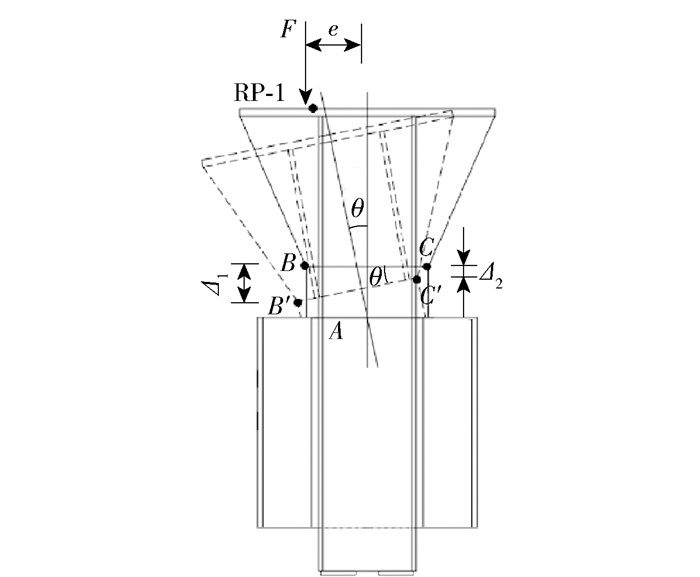
由于中间板的变形较小，A点可作为结构旋转中心。对于钢楔式活络端，θ为结构中心线绕A点的旋转角度，等于钢楔上表面变形前后的夹角，如图 19所示，Δ1为B点的竖向变形，Δ2为C点的竖向变形，则θ满足表达式
$$ \theta=\arctan \left(\frac{\varDelta_1-\varDelta_2}{l}\right) $$ (5) θ0为钢楔式活络端屈服时的旋转角。此时，活络端点竖向变形为Δ0, 1，C点竖向变形为Δ0, 2，满足$\theta_0=\arctan \left(\frac{\varDelta_{0, 1}-\varDelta_{0, 2}}{l}\right)$。当活络端达到θ0时，对应的荷载称为极限弯曲荷载。极限弯曲载荷Fy满足表达式
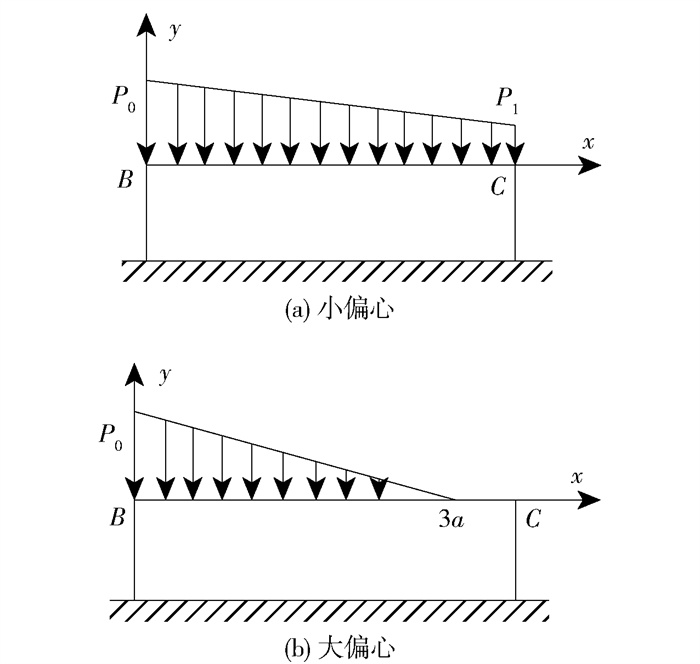
$$ F_{\rm y}=\frac{M_{\rm y}}{e_2} $$ (6) 当偏心距小于钢楔长度的1/6时，活络端为小偏心受压构件，否则为大偏心受压构件。不同偏心距下钢楔的受力形式如图 20所示，图中各参数满足表达式
$$ \begin{cases}P_0=\frac{F_y}{w \cdot l}\left(1+\frac{6 e_2}{l}\right) & \left(e_2 \leqslant \frac{l}{6}\right) \\ P_0=\frac{2 F_{\rm y}}{3 a w} & \left(e_2>\frac{l}{6}\right)\end{cases} $$ (7) $$ P_1=\frac{F_y}{w l}\left(1-\frac{6 e_2}{l}\right) $$ (8) $$ a=\frac{l}{2}-e_2 $$ (9) 1)Δ0, 1的计算
根据布辛奈斯克解可以求出弹性半空间表面上作用一个竖向集中力时，半空间内任意点处所引起的位移的弹性力学解计算公式为
$$ \omega(x, y)=\frac{1-\mu^2}{\pi E} \iint_A \frac{p(\xi, \eta)}{\sqrt{(x-\xi)^2+(y-\eta)^2}} \mathrm{~d} \xi \mathrm{~d} \eta $$ (10) 式中：x、y分别为弹性半空间表面上点的坐标；μ为活络端的泊松比；E为活络端的弹性模量。
将B点坐标为(0, 0)带入式(10)可以求出B点处钢楔变形，Δ0, 1满足表达式为
$$ \varDelta_{0, 1}=\omega(0, 0)=\frac{1-\mu^2}{\pi E} \int_0^w \int_0^b \frac{p(\xi, \eta)}{\sqrt{\xi^2+\eta^2}} \mathrm{~d} \xi \mathrm{~d} \eta $$ (11) 求解后，Δ1由两部分组成，可表示为
$$ \varDelta_{0, 1}=\varDelta_a+\varDelta_b $$ (12) 其中
$$ \begin{gathered} \varDelta_a=\frac{\left(1-\mu^2\right) P_0}{\pi E} \frac{w}{2}\left[\frac{5}{9} f\left(-\frac{\sqrt{15}}{5}\right)+\right. \\ \left.\frac{8}{9} f(0)+\frac{5}{9} f\left(\frac{\sqrt{15}}{5}\right)\right] \end{gathered} $$ (13) 式中
$$ \begin{aligned} f(x)= & \ln \left[\frac{b+\sqrt{b^2+\left(\frac{w x}{2}+\frac{w}{2}\right)^2}}{\frac{w x}{2}+\frac{w}{2}}\right] \\ \varDelta_b= & \frac{1-\mu^2}{\pi E} z\left[\frac{w^2}{2}-\frac{w}{2} \sqrt{b^2+w^2}-\right. \\ & \left.\frac{b^2}{2} \ln \left(\frac{w+\sqrt{b^2+w^2}}{b}\right)\right] \end{aligned} $$ (14) 式中
$$ z=\left\{\begin{array}{ll} \frac{P_0}{3 a}, & e_2>\frac{l}{6} \\ \frac{P_0-P_1}{l}, & e_2 \leqslant \frac{l}{6} \end{array} \quad b= \begin{cases}3 a, & e_2>\frac{l}{6} \\ l, & e_2 \leqslant \frac{l}{6}\end{cases}\right. $$ 2)Δ0, 2的计算
同理，将C点坐标为(l，0)带入式(10)即可求解C点处钢楔变形为Δ0, 2。
4.2.3 n的确定
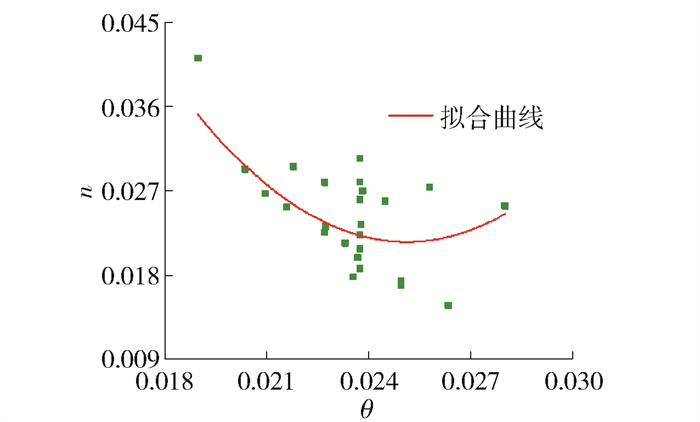
n不具备具体的物理含义，如图 21所示，通常n具有一定的离散性，同时不能推导出n的解析公式，因此有必要找到可以求解n的近似解或者拟合公式。将My和θ0的计算结果代入式(1)中，通过回归分析，初步确定n。之后根据n与θ0的相关性拟合n的计算公式。图 21中曲线为n的近似解。曲线方程为
$$ n=350.85 \theta_0^2-17.66 \theta_0+0.24 $$ (15) 4.2.4 λ的确定
为了减小由于形状系数及部分关键参数如钢楔高度等带来的误差影响，本文引入了修正系数λ，λ是与钢楔式活络端关键部位参数相关的系数。λ的计算公式为经验公式，根据回归分析结果拟合得到，无明确的推导过程。根据回归分析结果显示，λ是与l/h、hm/w、e2/(t+tc)相关的幂函数方程。通过曲线拟合得到λ的近似解为
$$ \lambda=37.923\left(\frac{l}{h}\right)^{0.237}\left(\frac{h_{\mathrm{m}}}{w}\right)^{-0.108}\left(\frac{e_2}{t+t_{\mathrm{c}}}\right)^{-1.097} $$ (16) 4.3 数值结果与解析结果的对比分析
4.3.1 全曲线对比分析
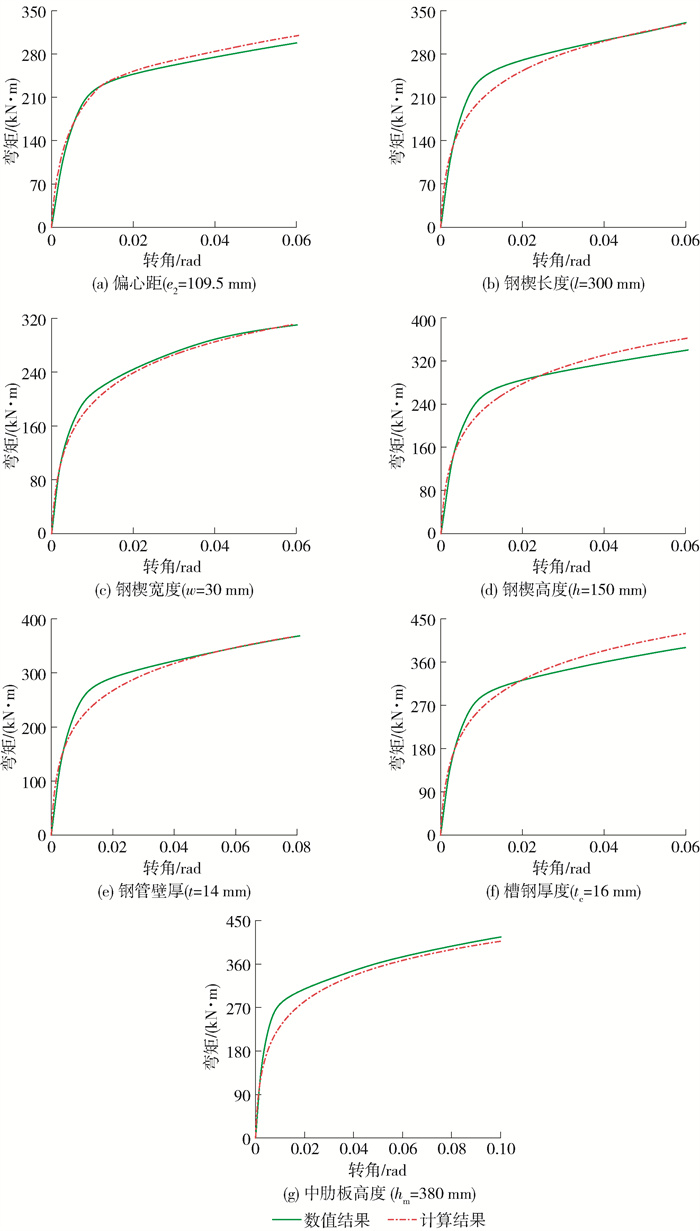
根据所建立的钢楔式活络端弯矩-转角模型，对表 2中的33组模型进行求解，得到各有限元模型弯矩-转角曲线的理论解。在各参数中各选取1条全曲线的计算结果与数值结果进行对比分析，如图 22所示。数值结果与计算结果的全曲线吻合较好，解析公式能够较准确、快速地确定钢楔式活络端的弯矩-转角曲线。对比各曲线中最大误差出现在图 22(g)中，为16%。最大误差出现在曲线的弹塑性阶段，但是通常保证活络端在弹性阶段工作，因此这种误差是可接受的。
4.3.2 抗弯性能力学指标对比分析
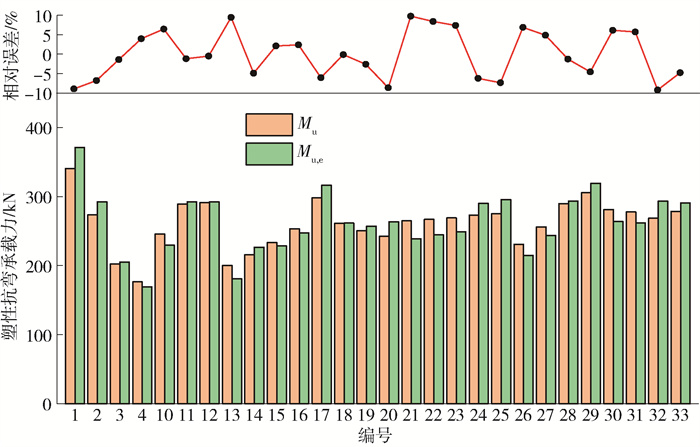
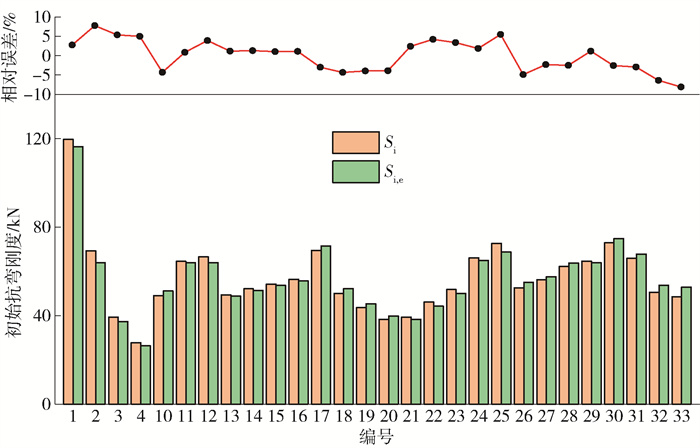
通过解析公式计算得到各个钢楔式活络端有限元模型的弯矩-转角曲线，并根据曲线确定各模型的初始抗弯刚度计算值(Si, e)和塑性抗弯承载力计算值(Mu, e)，将计算结果与数值结果对比分析。分析结果显示，初始抗弯刚度的解析结果与数值结果相差较小，相对误差均小于10%，超过46%的模型的相对误差小于5%，最大误差为9.7%，最小误差为-0.1%，平均误差为5.3%，如图 23所示。塑性抗弯承载力的对比分析及相对误差如图 24所示，超过85%的模型的相对误差小于5%，全部模型的相对误差小于10%，最大误差为7.7%，最小误差为0.8%，平均误差仅为3.3%。解析结果与数值结果离散性较小，二者吻合度较高，说明所推导的弯矩-转角模型能够较好地预测钢楔式活络端的抗弯性能，具有工程应用价值。
![]()
图 23 塑性抗弯承载力的计算结果与数值结果对比Figure 23. Comparison of flexural capacity between calculated and numerical results![]()
图 24 初始抗弯刚度的计算结果与数值结果对比Figure 24. Comparison of initial flexural stiffness between calculated and numerical results5. 结论
通过对钢楔式活络端在偏心荷载作用下的抗弯性能分析，可以获得下列结论：
1) 偏心荷载作用在x方向时，钢楔被压缩变形，槽钢弯曲变形显著；偏心荷载作用在y方向时，主要为钢楔的压缩变形。任何方向上施加偏心加载，钢楔式活络端应力都主要集中于钢楔及与其接触的槽钢、中肋板和中板处。
2) 钢楔式活络端的抗弯性能随偏心距、钢楔高度和中肋板高度的增加而降低，随钢楔长度、钢楔宽度、槽钢厚度和钢管壁厚的增加而增加。
3) 本文所建立的弯矩-转角模型能够较准确地预测钢楔式活络端的全过程曲线、初始抗弯刚度和塑性抗弯承载力。
4) x方向的偏心荷载比y方向对钢楔式活络端的抗弯性能影响更为显著，因此在架设钢楔式活络端时，应尽可能调整活络端使其y方向承受偏心荷载。
5) 槽钢对钢楔式活络端抗弯性能的影响显著，建议针对常用的钢楔式活络端适当增加槽钢厚度，能够有效提升钢楔式活络端的抗弯性能。
-
![]()
图 7 沿x方向偏心的竖向变形云图及破坏形态
Figure 7. Failure mode and vertical deformation of eccentric point along the x direction
![]()
图 8 沿y方向偏心的竖向变形云图
Figure 8. Vertical deformation of eccentric point along the y direction
![]()
图 23 塑性抗弯承载力的计算结果与数值结果对比
Figure 23. Comparison of flexural capacity between calculated and numerical results
![]()
图 24 初始抗弯刚度的计算结果与数值结果对比
Figure 24. Comparison of initial flexural stiffness between calculated and numerical results
表 1 Q235钢材的应力-应变关系
Table 1 Stress-strain relation of Q235 steel
应力/MPa 0 215.7 250 325 372 402 应变/% 0 0.1 0.3 10.0 17.7 34.3 
下载: 导出CSV
表 2 有限元模型参数
Table 2 Parameters for finite element models
编号 e1/mm e2/mm h①/mm l②/mm w③/mm t④/mm tc⑤/mm hm⑥/mm 1~4 36.50/73.00/
109.50/146.000 100 350 45 16 13 430 5~9 0 18.25/21.70/
36.50/54.75/
73.00100 350 45 16 13 430 10~13 73.0 0 100 250/300/
400/45045 16 13 430 14~17 73.0 0 100 350 25/30/35/40 16 13 430 18~21 73.0 0 50/150/
200/250350 45 16 13 430 22~26 73.0 0 100 350 45 10/12/14/
18/2013 430 27~30 73.0 0 100 350 45 16 7/10/16/19 430 31~33 73.0 0 100 350 45 16 13 330/380/480 ① h表示钢楔高度；② l表示钢楔长度；③ w表示钢楔宽度；④ t表示钢管壁厚；⑤ tc表示槽钢厚度；⑥ hm表示中肋板高度。
下载: 导出CSV
-
[1] ZHANG M J, XIE Z T, LI P F. Bearing capacity and failure behavior of disconnectable coupling joint with double row wedges (DCJD) used in the prestressed internal bracing[J]. Underground Space, 2022, 7(4): 498-513. doi: 10.1016/j.undsp.2021.11.003
[2] ZHANG M J, XIE Z T, LI P F. Experimental and numerical investigation on the bearing capacity of disconnectable coupling (DC) joints for prestressed internal bracing in subway excavations[J/OL]. Tunnelling and Underground Space Technology, 2020, 104: 103501[2020-6-12]. https://doi.org/10.1016/j.istruc.2024.106830 .
[3] 张明聚, 谢治天, 刘耀轩, 等. 基坑工程钢楔式活络端力学性能试验研究[J]. 北京工业大学学报, 2019, 45(12): 1223-1231. doi: 10.11936/bjutxb2018030010 ZHANG M J, XIE Z T, LIU Y X, et al. Experimental study on the mechanical properties of steel wedge active node in braced excavation engineering[J]. Journal of Beijing University of Technology, 2019, 45(12): 1223-1231. (in Chinese) doi: 10.11936/bjutxb2018030010
[4] 熊栋栋, 杨钊, 廖正根. 地铁深基坑钢支撑预加轴力分析[J]. 地下空间与工程学报, 2018, 14(4): 1049-1055. XIONG D D, YANG Z, LIAO Z G. Analysis on pre axial force of steel support in deep foundation pit of subway[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(4): 1049-1055. (in Chinese)
[5] 孙九春, 白廷辉. 地铁基坑钢支撑系统活络头承载力研究[J]. 施工技术, 2020, 49(2): 119-125. SUN J C, BAI T H. Research on the bearing capacity of the flexible head of the steel support system of the subway foundation excavation[J]. Construction Technology, 2020, 49(2): 119-125. (in Chinese)
[6] 张明聚, 谢治天, 李鹏飞, 等. 基于有限元分析的基坑工程钢支撑活络端偏心受压性能研究[J]. 土木工程学报, 2021, 54(10): 106-116. ZHANG M J, XIE Z T, LI P F, et al. Numerical studies on eccentric compression performance of disconnectable coupling joint in foundation pit project[J]. China Civil Engineering Journal, 2021, 54(10): 106-116. (in Chinese)
[7] 苑媛. 基坑工程钢支撑BFW活络端的力学性能和设计方法[D]. 北京: 北京工业大学, 2017: 16-29. YUAN Y. Mechanical properties and design method of BFW loose end of steel support in foundation pit engineering[D]. Beijing: Beijing University of Technology, 2017: 16-29. (in Chinese)
[8] 张明聚, 苑媛, 王锡军. 基坑工程钢支撑BFW活络端在偏心荷载作用下的力学性能[J]. 北京工业大学学报, 2018, 44(2): 251-258. doi: 10.11936/bjutxb2017050022 ZHANG M J, YUAN Y, WANG X J. Mechanical properties of BFW active node of steel strut under eccentric load in excavation engineering[J]. Journal of Beijing University of Technology, 2018, 44(2): 251-258. (in Chinese) doi: 10.11936/bjutxb2017050022
[9] LUI E M, CHEN W F. Analysis and behaviour of flexibly-jointed frames[J]. Engineering Structures, 1986, 8(2): 107-118.
[10] WU F H, CHEN W F. A design model for semi-rigid connections[J]. Engineering Structures, 1990, 12(2): 88-97.
[11] ANG K M, MORRIS G A. Analysis of three-dimensional frames with flexible beam-column connections[J]. Canadian Journal of Civil Engineering, 1984, 11(2): 245-254.
[12] 施刚, 石永久, 王元清. 钢结构梁柱半刚性端板连接弯矩-转角全曲线计算方法[J]. 工程力学, 2006, 23(5): 67-73, 55. SHI G, SHI Y J, WANG Y Q. Calculation method on moment-rotation curves of beam-to-column semirigid end-plate connections[J]. Engineering Mechanics, 2006, 23(5): 67-73, 55. (in Chinese)
[13] GUO X N, HUANG Z W, XIONG Z, et al. Numerical studies on behaviour of bolted ball-cylinder joint under axial force[J]. Steel and Composite Structures, 2016, 20(6): 1323-1343.
[14] 田芳, 刘财喜, 刘芳, 等. Q235钢真实应力-应变曲线研究[J]. 中南林业科技大学学报, 2011, 31(4): 182-186. TIAN F, LIU C X, LIU F, et al. Research on the true stress-strain curves of Q235 steel[J]. Journal of Central South University of Forestry & Technology, 2011, 31(4): 182-186. (in Chinese)
[15] European Convention for Constructional Steelwork. Recommended testing procedure for assessing the behaviour of structural steel elements under cyclic loads[S]. Brussels: ECCS, 1986.
计量
- 文章访问数: 64
- HTML全文浏览量: 12
- PDF下载量: 27
