Deep Clustering Network Based on Graph Relationship Selection
-
摘要:
针对在深度聚类中基于图卷积网络(graph convolutional network, GCN)编码图结构信息的方法存在过拟合的问题, 提出一种通过对比学习将图邻接关系融合到传统深度网络中对图结构进行编码的方法。首先, 该方法中使用自动编码器(auto-encoder, AE)来学习节点特征的深层次潜在表示; 然后, 通过对比学习从图关系中学习有区分性的节点表示, 同时设计了更细致的节点间影响力关系, 从而为对比学习提供有力的正负样本选择依据; 最后, 通过自监督的方式训练网络以实现聚类任务。在6个基准数据集上进行了大量实验, 结果表明, 提出的方法显著地提高了聚类精度。
-
关键词:
- 节点聚类 /
- 图卷积网络(graph convolutional network, GCN) /
- 自动编码器(auto-encoder, AE) /
- 图关系 /
- 对比学习 /
- 自监督
Abstract:To solve the problem of overfitting in the method of encoding graph structure information based on graph convolutional network (GCN) in depth clustering, a method is proposed to encode graph structure by fusing graph adjacency into traditional depth network through contrastive learning. First, in this method, an auto-encoder (AE) was used to learn the deep potential representation of node features. Then, through contrastive learning, discriminative node representations were learned from graph relationships, and more detailed inter node influence was designed to provide a strong basis for selecting positive and negative samples for contrastive learning. Finally, the network was trained by self-supervised learning to implement node clustering. A large number of experiments on six benchmark datasets show that the proposed method significantly improves the clustering accuracy.
-
聚类是模式识别和机器学习中的一个重要研究课题。在过去的几十年中,科研工作者在聚类领域进行了大量的研究,提出了许多经典的聚类方法。然而,过往的方法都是针对如图像和文本这类结构化的欧氏数据进行处理,在现实世界中存在很多如图结构这类非欧氏数据,用传统的聚类算法难以获得令人满意的性能。近年来,提出的图卷积网络(graph convolutional network, GCN)[1]在应用于图结构数据处理方面取得了很大的进展。为了利用图结构中存在的丰富信息,Kipf等[2]提出了图自动编码器(graph auto-encoder,GAE),以GCN作为编码图结构信息的编码器,可以充分发挥其从图结构数据中学习低维数据表示的能力。Wang等[3]在此基础上开发了一个带有注意力机制的自动编码器(auto-encoder,AE)DAEGC,一方面通过注意力机制更有效地集成结构和特征信息,用于潜在表示的学习,另一方面为图数据聚类提出了一个新的目标导向框架。该框架联合优化了表示学习和聚类任务,可以实现2个部分的协同优化。然而,图节点的聚类任务需要充分考虑图的结构信息和特征信息,基于GCN的AE在处理图形结构化数据时,不能全面地考虑节点特征信息。许多基于AE的聚类方法已被用来实现最先进的性能,在欧氏数据中,基于深度神经网络的AE通过学习原始数据特征的高维表示完成聚类任务,此类方法取得了令人满意的效果[4]。基于以上需求,Bo等[5]提出了结构化深度聚类网络(structural deep clustering network,SDCN),利用深度AE和GCN分别学习节点属性信息和图结构信息表示,并用自监督机制将它们集成到一个统一的框架中。该算法的提出为图节点聚类任务开拓了研究思路。为了更好地融合结构和特征信息,Peng等[6]提出了注意力驱动的图聚类网络(attention-driven graph clustering network,AGCN),将图结构信息和节点属性信息通过注意力机制进行融合以获得更利于聚类的节点表示。尽管这些模型取得了显著的改进,并且在聚类任务中表现优异,但都依赖于GCN从图结构中学习低维表示的能力。由于每一层GCN都只能聚合一阶邻域的信息,为了促进不直接相连的节点之间的交互,GCN通过堆叠层的方式来实现。随着网络层数的增加,每个节点的潜在表示趋于相近,使得学习出的节点表示失去了区分性,从而出现GCN的过平滑问题,同时,由于噪声节点的存在,依赖GCN学习图结构信息是有挑战性的。
为了避免这些问题,大多数基于GCN的方法都是浅层的,这样就无法从深度模型中受益,也有部分学者提出的GCN模型虽然实现了叠加更高的深度,但是仍需要预先确定合适的深度,这其中的操作涉及成本高昂的卷积计算[7-9]。尽管实验证明从输入图中随机移除边或节点的方法在深度增加时可以减轻网络的过平滑现象[10-11],但是移除图中的边或节点改变了节点间的邻接关系,删减不当会对网络学习造成致命的影响。因此,本文探索如何以更简单高效的方式解决这一问题。对比学习得益于能够通过关注抽象的语义信息学习样本区分性的能力,近年来广泛活跃于图像处理和图数据领域,对比损失函数分辨正负样本的能力对于学习高质量的节点表示是至关重要的。鉴于GCN存在的问题和对比学习的优势,Kulatilleke等[12]提出不使用GCN,而是在深度网络末端加入对比损失作为将图结构和深度网络结合并优化的手段。这一工作由于没有使用GCN,仅将邻接关系与深度网络相结合,从根本上避免了过平滑现象的产生。然而,该工作中在将邻接关系与深度网络相结合的部分设计有所欠缺,对节点之间的关系考虑不够全面。
针对将GCN和聚类任务相结合产生的模型过平滑、可扩展性差、参数敏感等问题,本文提出一种基于图关系选择的深度聚类网络(deep clustering network based on graph relationship selection,GRSDCN)。该方法主要设计了新的对比学习正负样本选择方案,并通过对比损失将图的邻接关系融合到深度网络中,使得深度网络在特征空间中学习节点潜在表示的时候携带了结构相关性,如此就可以利用深度网络的强大学习能力和图结构的节点依赖关系学习出高质量的节点表示,同时,又避免了深层GCN的过平滑现象。为了促进有效聚类,进一步使用了基于软标签的自监督方法共同指导聚类优化。该模型在6个公开的常用数据集上进行了实验,与8种方法对比,均取得了优于其他方法的效果。
1. 基于图关系选择的深度聚类网络模型
1.1 框架概述
首先介绍一些符号及概念,图可以表示为G=(V, E, X), 其中:V为节点矩阵;E为边矩阵;X∈PN×M,为节点的属性矩阵,N为节点数,M为特征的维度。图的邻接矩阵表示为A∈PN×N,如果节点vi和vj之间有边,则Aij=1,否则为0。给定一个图G和聚类数k,图节点聚类的目的是把图G中的节点划分到k个不相交的簇中,在该模型中依据拓扑信息和特征信息将它们分到不同的簇中。
1.2 框架概述
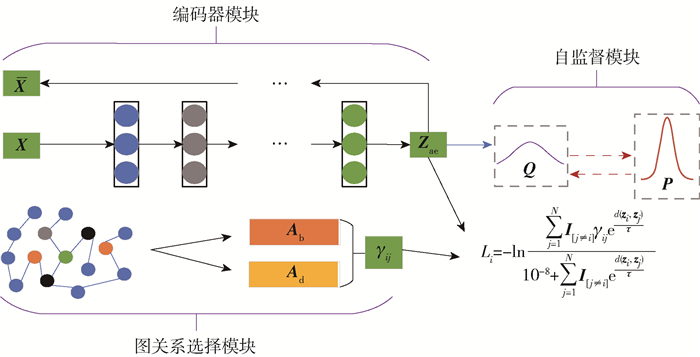
本文提出的GRSDCN模型框架如图 1所示,框架可分为编码器模块、图关系选择模块和自监督模块。整个网络结构主要使用AE[13]来提取特征,通过图关系选择模块为编码器加入节点间邻接关系信息作为约束,以自监督的方式训练整个网络。针对GCN叠加多层会由于过平滑使学习到的节点表示缺乏判别性,而叠加浅层学习能力又受到限制的问题,该方法提出了图关系选择模块,并与AE相结合,有效地缓解了该问题。
网络的输入部分包括节点特征X∈PN×M、节点间深度影响的邻接矩阵Ad(Ad∈$\mathbb{R}^{N \times N}$)和节点间广度影响的邻接矩阵Ab(Ab∈$\mathbb{R}^{N \times N}$);网络的输出部分是把N个节点划分到k个簇中的聚类结果,γij表示节点间的结构关系,Zae表示编码器模块计算得到的节点潜在特征,Li表示第i个节点的对比损失函数。
1.2.1 编码器模块
节点特征编码器的目的是从原始节点特征中学习出一个有判别性的节点表示用于后续的聚类任务。该模块采用经典的从节点特征层面进行特征提取的AE。AE的深层网络编码关注于数据本身的特征,可以学习到节点之间深层次的相互依赖关系,得到节点潜在特征Zae。该网络的输入是原始特征X,输出是Zae,其编码、解码和AE的重构损失分别表示为
$$ \boldsymbol{Z}^{(l)}=\sigma\left(\boldsymbol{W}_{\mathrm{e}}^{(l)} \boldsymbol{Z}^{(l-1)}+\boldsymbol{b}_{\mathrm{e}}^{(l)}\right) $$ (1) $$ \overline{\boldsymbol{Z}}^{(l)}=\sigma\left(\boldsymbol{W}_{\mathrm{d}}^{(l)} \boldsymbol{Z}^{(l-1)}+\boldsymbol{b}_{\mathrm{d}}^{(l)}\right) $$ (2) $$ L_{\mathrm{r}}=\frac{1}{2 N}\|\boldsymbol{X}-\overline{\boldsymbol{X}}\|_{\mathrm{F}}^{2} $$ (3) 式中:Z(l)、Z(l)分别表示编码器和解码器第l层的输出;在编码器的第1层中Z(0)表示原始特征X,编码器网络最后一层的Z(4)表示提取到的潜在特征(图 1中的Zae),解码器网络最后一层的Z(4)表示对原始数据重构后得到的特征X;We(l)和be(l)分别表示编码器网络第l层的权重和偏置;Wd(l)和bd(l)分别表示解码器网络第l层的权重和偏置;σ表示激活函数,如Sigmod、Relu等。
1.2.2 图关系选择模块
为了更好地区分正样本节点和负样本节点以获得更具判别性的潜在节点表示,通过在特征空间中使它们的距离更远或更近来实现这个目标。因此,本文使用了邻接关系引导的对比损失方法将图结构融合到节点表示中。具体而言,首先对节点间的关系进行细致的分析和建模,然后通过计算出更可靠的结构关系信息确定正样本和负样本,最后通过对比损失把这一结构关系与深度网络联合到一起。该对比损失描述为
$$ L_{i}=-\ln \frac{\sum\limits_{j=1}^{N} \boldsymbol{I}_{[j \neq i]} \gamma_{i j} \mathrm{e}^{d\left(\mathit{\boldsymbol{z}}_{i}, \mathit{\boldsymbol{z}}_{j}\right) / \tau}}{10^{-8}+\sum\limits_{j=1}^{N} \boldsymbol{I}_{[j \neq i]} \mathrm{e}^{d\left(\mathit{\boldsymbol{z}}_{i}, \mathit{\boldsymbol{z}}_{j}\right) / \tau}} $$ (4) 式中:zi和zj分别为由AE得到的节点i和j的节点潜在表示;I为一个值全为1的向量;τ为调整正负样本关注度的系数;d(·)为距离度量,在本文中使用余弦相似度计算2个节点vi和vj之间的距离。
在计算节点间影响力关系γij时,本文同时考虑了节点间的深度影响和广度影响。从深度方面来说,认为对于一个节点来自多个深度处的非相邻节点可以产生不同效果,随着深度的增加,影响逐渐减弱;从广度方面来说,认为对于一个节点来自一阶邻域的相邻节点也会产生不同的影响。该思想如图 2所示,图中红色节点为设定的锚节点,绿色节点的颜色越深表示对锚节点的影响越强,蓝色节点表示在该影响力计算中未涉及的节点。
1) 节点间深度影响
一个节点的K阶邻域对节点都有影响,只是随着阶数的增加,影响力越来越小。本文通过r阶邻域Aijr描述节点对r阶深度下的影响力,公式为
$$ \delta_{i j}=\sum\limits_{r=1}^{K} A_{i j}^{r} $$ (5) 2) 节点间广度影响
如图 2(b)所示,同为一阶邻域的节点具备不同的影响力,如果将影响力弱的节点剔除掉,仅保留影响力强的节点作为正样本,那么就更有利于编码器学习出判别性强的节点表示。因此,首先用节点特征的点积相似度衡量影响力,并计算出该节点邻域的影响力均值,再通过添加超参数构建影响力阈值的方法去除影响力弱的节点,其中点积相似度计算公式为
$$ \beta_{i j}=\boldsymbol{X}_{i} \cdot \boldsymbol{X}_{j}=\sum\limits_{l=1}^{M} x_{i}^{l} x_{j}^{l} $$ (6) 式中:βij为节点j对节点i的影响力;Xi和Xj分别为节点i和节点j的特征;xil、xjl分别为Xi、Xj的第l维分量。节点i的邻域影响力均值计算可以用公式描述为
$$ \beta_{i}^{\text {mean }}=\sum\limits_{j \neq i}^{n} \frac{\beta_{i j}}{n} $$ (7) 式中:βimean为节点i的邻域影响力均值;n为节点i的邻域节点个数。之后设定一个超参数θ以构造影响力阈值,使得当节点j对节点i的影响力大于阈值时才表示2个节点间存在影响关系,该阈值的设计用公式描述为
$$ \varepsilon=\theta \beta_{i}^{\text {mean }} $$ (8) 式中θ为一个超参数,根据不同的数据集动态调整,因此,最终节点间的广度影响力可以描述为
$$ \eta_{i j}= \begin{cases}1, & \beta_{i j} \geqslant \varepsilon\\ 0, & \beta_{i j}<\varepsilon\end{cases} $$ (9) 综上所述,γij表示为
$$ \gamma_{i j}=\delta_{i j}+\eta_{i j} $$ (10) 得到了γij之后,就可以根据这个影响力在特征空间中将正负样本分隔开来,为对比学习的应用创造了条件,之后通过对比损失的约束训练编码器学习到更高质量的节点表示用于后续的聚类任务,整个图上的对比损失公式为
$$ L_{\mathrm{C}}=\frac{1}{N} \sum\limits_{i=1}^{N} L_{i} $$ (11) 1.2.3 自监督模块
为了给聚类任务提供可靠的指导,本文采用了自监督的方案指导整个网络训练,其基本思想是从编码器学习的数据表示中生成聚类结果,然后计算聚类结果与聚类中心之间的相似度,不断优化样本和对应聚类中心间的距离。具体来说,在自监督模块中首先使用Student-t分布作为核来度量由AE学习到的节点表示中第i个样本和第j个聚类中心之间的相似性,得到聚类的软分配分布Q,其分量qij的计算公式为
$$ \begin{equation*} q_{i j}=\frac{\left(1+\left\|\boldsymbol{z}_{\mathrm{ae}, i}-\boldsymbol{\mu}_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum\limits_{j^{\prime}}\left(1+\left\|\boldsymbol{z}_{\mathrm{ae}, i}-\boldsymbol{\mu}_{j^{\prime}}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}} \end{equation*} $$ (12) 式中:zae, i表示AE学习到的节点表示Zae的第i个样本;μj表示对Zae进行K-means计算得到的第j个聚类中心;qij为Zae第i个样本zae, i分配到μj的概率;α为自由度,本文的实验中设置为1。
为了增加聚类的内聚力,使Q的数据表示更接近聚类中心,求得的Q的归一化目标分布P的分量为
$$ p_{i j}=\frac{q_{i j}^{2} / \sum\limits_{i} q_{i j}}{\sum\limits_{j^{\prime}} q_{i j^{\prime}}^{2} / \sum\limits_{i} q_{i j^{\prime}}} $$ (13) 最后,在Q和P的自监督下,训练AE学习到的潜在节点表示向目标分布对齐,实现数据聚类。本文以KL(Kullback-Leibler)散度衡量2个分布对齐的程度,公式为
$$ L_{\mathrm{KL}(\boldsymbol{P Q})}=\sum\limits_{i} \sum\limits_{j} p_{i j} \cdot \frac{p_{i j}}{q_{i j}} $$ (14) 式中LKL(PQ)为衡量P、Q间KL散度的自监督损失。
P是通过Q生成的,而P又反过来监督Q的更新,整个过程中没有人为进行引导,因此,称为自监督方式。在对网络进行训练后,通过Zae可以直接得到预测聚类结果,公式为
$$ y_{i}=\arg \max \boldsymbol{z}_{\mathrm{ae}, i} $$ (15) 式中:zae, i为Zae的第i个样本;yi为第i个样本预测的簇标签。
1.2.4 损失函数及模型优化
本文在模型的编码器模块、图关系选择模块和自监督模块分别定义了3个损失函数,为了使3个损失函数最大程度地发挥作用,通过3个超参数λ1、λ2和λ3平衡它们之间的关系,并使模型成为一个整体进行训练,最终本文提出的模型损失函数定义为
$$ L=\lambda_{1} L_{\mathrm{KL}(\mathit{\boldsymbol{PQ}})}+\lambda_{2} L_{\mathrm{C}}+\lambda_{3} L_{\mathrm{R}} $$ (16) 式中LR为AE的重构损失。
本文提出模型的算法步骤如下。
1. 输入:原始数据X、邻接矩阵A、聚类簇数k、最大迭代次数emax
2. 初始化AE的训练参数
3. 根据式(5)~(11)计算节点间影响力γij
4. while e < emax do
5. 根据式(1)(2)计算AE的编码器输出Zae和解码器输出X
6. 根据式(3)计算AE重构损失LR
7. 根据式(11)计算对比损失LC
8. 根据式(14)计算自监督损失LKL(PQ)
9. 根据式(16)计算模型全部损失L,并按照梯度反向传播更新参数
10. e←e+1
11. end while
12. 输出:聚类结果
2. 实验
2.1 数据集
本文在6个常用的基准数据集上进行了实验,包括1个图像数据集USPS、1个人类活动识别记录数据集HHAR、1个文本数据集Reuters和3个图数据集ACM、DBLP和CiteSeer,数据集的简要描述如表 1所示。
表 1 数据集描述Table 1. Description of datasets数据集 样本数 类别数 样本维度 ACM 3 025 3 1 870 DBLP 4 057 4 334 CiteSeer 3 327 6 3 703 Reuters 10 000 4 2 000 USPS 9 298 10 256 HHAR 10 299 6 561 本文在上述3个图数据集ACM、DBLP和CiteSeer上验证模型对图数据集的有效性,在3个非图数据集USPS、HHAR和Reuters上验证模型对非图数据集同样具有实用效果。其中为了满足本模型的输入需求,在非图数据集上节点的邻接关系由K近邻算法计算得出。
2.2 对比方法及实验设置
为了验证模型的有效性,本文将提出的方法与8种方法进行了对比,所有方法的预测性能都通过以下4个指标评价,分别是正确率ACC、调整兰德系数ARI、互信息NMI和综合评价指标F1值。
定义来自k个簇的N个样本数据为X={x1, x2, …, xN},它们对应的算法聚类结果为T={t1, t2, …, tK},真实标签为C={c1, c2, …, cK}。
ACC是指聚类正确的样本数占总样本数的比例,该指标越大表明聚类结果与真实情况越接近,其计算公式为
$$ A_{\mathrm{CC}}=\frac{\sum\limits_{i=1}^{N} \delta\left(c_{i}, \operatorname{map}\left(t_{i}\right)\right)}{N} $$ (17) 式中map(·)为映射函数,将模型得到的聚类标签与样本真实的标签进行映射,δ(·)定义为
$$ \delta(x, y)= \begin{cases}1, & x=y\\ 0, & \text { 其他 }\end{cases} $$ (18) ARI是对兰德系数RI的改进,RI从数值化的角度定义了聚类结果和真实标签的匹配程度。该指标越大表明聚类结果与真实情况越接近,其计算公式为
$$ A_{\mathrm{RI}}=\frac{R_{\mathrm{I}}-E\left(R_{\mathrm{I}}\right)}{\max \left(R_{\mathrm{I}}\right)-E\left(R_{\mathrm{I}}\right)} $$ (19) RI的计算公式为
$$ R_{\mathrm{I}}=\frac{T_{\mathrm{P}}+T_{\mathrm{N}}}{T_{\mathrm{P}}+F_{\mathrm{P}}+F_{\mathrm{N}}+T_{\mathrm{N}}} $$ (20) 式中:TP表示事实上是正样本且被预测为正样本的样本数;TN表示事实上是负样本且被预测为负样本的样本数;FP表示事实上是负样本且被预测为正样本的样本数;FN表示事实上是正样本且被预测为负样本的样本数。
NMI是用来衡量2个分布之间吻合程度的度量,在本文中比较聚类后的结果与真实标签的吻合程度,该指标越大表明聚类结果与真实情况越接近,其计算公式为
$$ N_{\mathrm{MI}}=\frac{I(T ; C)}{(H(T)+H(C)) / 2} $$ (21) 式中:T表示真实结果;C表示预测结果;H(·)表示熵的计算。
F1是准确率和召回率共同计算的结果,与RI注重TP与TN在全体情况下的占比相比,F1更注重TP在2种特定情况下的占比,该指标越大表明聚类结果与真实情况越接近,其计算公式为
$$ F_{1}=\frac{2 \times P \times R}{P+R} $$ (22) 式中:P表示准确率;R表示召回率。
本文中对比方法的结果均采用相应文献中的最优结果,该算法在训练时需要为网络设置一些参数,网络编码器模块中的AE网络权重使用均匀分布初始化,激活函数均采用Relu函数,为了在初始状态下尽可能由一个正确的目标分布指导编码器训练,先对AE进行30轮的预训练,学习率设置为0.001。在训练阶段编码器网络的3层维度统一设置为500-500-2000,解码器网络的3层维度统一设置为2000-500-500,迭代次数默认设置为100轮,根据各个数据集调整迭代次数、学习率和损失函数的超参数。为了加速训练和防止过拟合,使用了Dropout技术,该模型使用Pytorch深度学习框架编写,在单张Nvidia GeForce RTX 3090 GPU上运行,优化器选择Adam对模型进行优化,
2.3 实验结果及分析
与8种方法在6个数据集上的对比实验结果见表 2,其中粗体数字表示最佳的聚类性能,带下划线的数字表示次佳性能。实验结果表明,不论是在图数据集还是非图数据集中,该模型在大部分数据集上取得了最佳性能,充分证明了该算法的有效性。效果提升显著的原因有以下2个方面:首先,该方法通过使用深度网络学习潜在节点表示和将图结构信息联合到深度网络的方式避免了GCN存在的问题;其次,在将图结构的节点邻接关系信息通过对比损失加入到深度网络中时充分考虑了节点之间的深度影响和广度影响,相比直接使用图结构,提供了更可靠的拓扑信息。该模型的设计使对比学习区分正负样本的能力充分发挥,得到了更有判别性的节点表示,因此,取得了更高的性能。通过观察实验结果可以发现:与直接使用GCN学习节点表示的方法(SDCN和AGCN)对比,本文模型在精度上取得了1%~3%的提升;与将邻接关系和深度网络结合的SCGC方法对比,本文模型在精度上取得了1%~2%的提升,表明对节点间关系的深入考虑对提升聚类效果是有意义的。
表 2 聚类结果Table 2. Clustering results数据集 指标 VGAE[2] DAEGC[3] SDCN[5] AGCN[6] DCRN[14] SCGC[12] GC-SEE[15] DMDSC[16] GRSDCN ACM ACC 84.13±0.22 86.94±2.83 90.45±0.18 90.59±0.15 91.93±0.20 92.56±0.01 91.67±0.10 92.36±0.10 92.60±0.13 NMI 53.20±0.52 56.18±4.15 68.31±0.25 68.38±0.45 71.56±0.61 73.27±0.03 70.83±0.25 72.52±0.22 73.39±0.12 ARI 57.72±0.67 59.35±3.89 73.91±0.40 74.20±0.38 77.56±0.52 79.19±0.03 76.89±0.24 78.65±0.43 79.28±0.12 F1 84.17±0.23 87.07±2.79 90.42±0.19 90.58±0.17 91.94±0.20 92.54±0.01 91.66±0.09 92.36±0.11 92.61±0.13 DBLP ACC 58.59±0.06 62.05±0.48 68.05±1.81 73.26±0.37 79.66±0.25 77.67±0.14 79.23±0.96 75.33±0.33 80.23±0.38 NMI 26.92±0.06 32.49±0.45 39.50±1.34 39.68±0.42 48.95±0.44 47.05±0.16 48.04±1.46 44.30±0.50 51.05±0.26 ARI 17.92±0.07 21.03±0.52 39.15±2.01 42.49±0.31 53.60±0.46 51.07±0.22 53.51±1.82 46.17±0.21 55.76±0.19 F1 58.69±0.07 61.75±0.67 67.71±1.51 72.80±0.56 79.28±0.26 77.27±0.13 78.55±0.99 75.34±0.66 79.62±0.23 CiteSeer ACC 60.97±0.36 64.54±1.39 65.96±0.31 68.79±0.23 70.86±0.18 73.19±0.06 70.90±0.56 70.33±0.31 73.73±0.35 NMI 32.69±0.27 36.41±0.86 38.71±0.32 41.54±0.30 45.86±0.35 46.74±0.10 44.00±0.64 44.39±0.88 48.05±0.28 ARI 33.13±0.53 37.78±1.24 40.17±0.43 43.79±0.31 47.64±0.30 50.01±0.12 46.47±0.76 46.85±0.97 51.17±0.32 F1 57.70±0.49 62.20±1.32 63.62±0.24 62.37±0.21 65.83±0.21 63.34±0.04 63.12±0.66 65.43±0.63 63.81±0.34 USPS ACC 56.19±0.72 73.55±0.40 78.08±0.19 80.98±0.28 82.90±0.08 82.25±1.97 88.55±0.12 84.03±0.22 NMI 51.08±0.37 71.12±0.24 79.51±0.27 79.64±0.32 82.51±0.07 79.72±0.92 82.66±0.31 82.91±0.65 ARI 40.96±0.59 63.33±0.34 71.84±0.24 73.61±0.43 76.48±0.11 75.38±2.42 80.76±0.22 78.07±0.37 F1 53.63±1.05 72.45±0.49 76.98±0.18 77.61±0.38 80.06±0.05 76.83±1.26 87.59±0.97 80.28±0.26 HHAR ACC 71.30±0.36 76.51±2.19 84.26±0.17 88.11±0.43 89.49±0.22 89.63±0.22 90.42±0.31 NMI 62.95±0.36 69.10±2.28 79.90±0.09 82.44±0.62 84.24±0.29 83.47±0.64 87.39±0.47 ARI 51.47±0.73 60.38±2.15 72.84±0.09 77.07±0.66 79.28±0.28 79.30±0.25 81.14±0.43 F1 71.55±0.29 76.89±2.18 82.58±0.08 88.00±0.53 89.59±0.23 89.95±0.56 90.58±0.37 Reuters ACC 60.85±0.23 65.50±0.13 77.15±0.21 79.30±1.07 80.32±0.04 87.29±0.36 81.12±0.32 NMI 25.51±0.22 30.55±0.29 50.82±0.21 57.83±1.01 55.63±0.05 66.49±0.82 59.51±0.15 ARI 26.18±0.36 31.12±0.18 55.36±0.37 60.55±1.78 59.67±0.11 73.35±0.44 62.22±0.26 F1 57.14±0.17 61.82±0.13 65.48±0.08 66.16±0.64 63.66±0.03 77.46±0.42 66.92±0.47 2.4 模型收敛性验证
本文以SCGC方法作为基线,对比各模型在不同迭代次数下聚类准确率的变化情况,结果如图 3所示。可以看出,本文提出的模型在整个训练过程中基本上可以取得不低于对比方法的性能,能够随训练次数的增加稳定提升聚类效果。本文模型在各个数据集上的聚类结果随着训练次数的增加最终都趋向于一个稳定的值,证明该模型具有良好的收敛性。
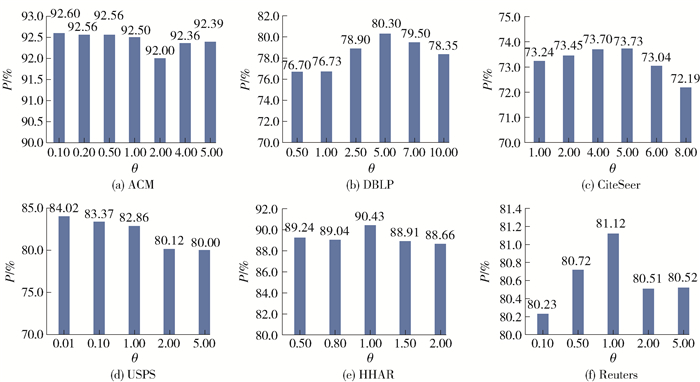
2.5 超参数对模型的影响
本文模型中有一个非常重要的超参数θ,主要用于节点间广度影响力阈值的计算,该值的合理设置对在不同数据集上使模型发挥出最佳性能具有重要的意义。因此,为了探究不同数据集上该值的变化对模型效果的影响,并找出最合理的值,在6个数据集上进行了实验分析,结果如图 4所示。通过实验发现,对于数据集ACM在θ=0.10时效果最好,DBLP和CiteSeer在θ=5.00时效果最好,USPS在θ=0.01时效果最好,HHAR和Reuters在θ=1.00时效果最好。这表明不同数据集的节点间广度影响是有很大差别的,因此,考虑该部分的影响力对模型效果是有意义的。
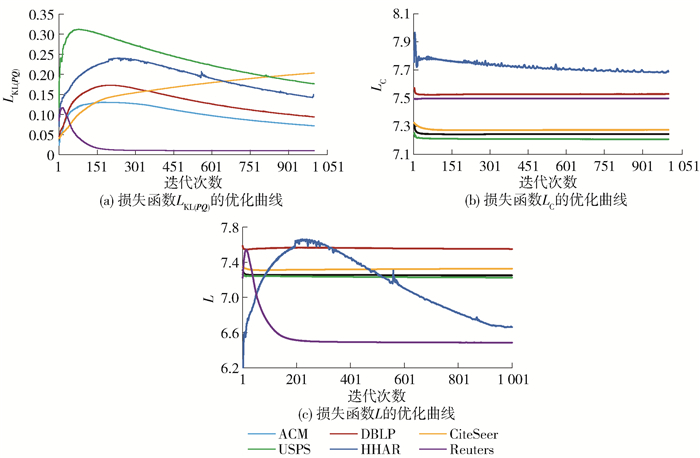
2.6 模型的优化
根据对模型的介绍可知,GRSDCN通过迭代更新的方式对变量进行优化。各个损失函数随迭代次数增加的优化过程曲线如图 5所示。通过该曲线可以看出,随着迭代次数增加,整个模型的损失函数逐渐降低到稳定状态,说明本文提出的算法具有收敛性。
3. 结论
1) 本文针对GCN叠加多层会出现过平滑导致学习出的节点表示没有区分度,而叠加浅层又会使网络学习能力受限的问题,提出了一个能够将图结构的邻接关系信息强加到深度网络中的模型GRSDCN。
2) 与现有的模型相比,该模型提出了主要使用AE在特征空间中提取特征,利用对比损失将图结构信息添加到深度网络中,使网络不仅可以发挥深度网络所具备的学习深层语义关系的能力,并且能够从特征空间中利用节点间的结构信息进行学习,从而得到更高质量的节点表示以用于聚类。为了使模型能够充分利用结构信息学习,该模型分别从节点的深度影响和广度影响方面进行了考虑,给模型提供了更清晰、有效的结构关系。
3) 在ACM、DBLP、CiteSeer、USPS、HHAR和Reuters这6个数据集上的大量实验表明,与当前最先进的方法相比,本文提出的将图结构有选择性地联合到深度网络中的方法具有一定的效果,能够在一定程度上提升聚类精度,实验结果的对比证明了该模型能够提升聚类性能,在进一步的模型收敛性实验中也证明了该模型具有良好的收敛性,最后在聚类结果的可视化实验中也显示出了该模型能够完成聚类任务。
-
表 1 数据集描述
Table 1 Description of datasets
数据集 样本数 类别数 样本维度 ACM 3 025 3 1 870 DBLP 4 057 4 334 CiteSeer 3 327 6 3 703 Reuters 10 000 4 2 000 USPS 9 298 10 256 HHAR 10 299 6 561 表 2 聚类结果
Table 2 Clustering results
数据集 指标 VGAE[2] DAEGC[3] SDCN[5] AGCN[6] DCRN[14] SCGC[12] GC-SEE[15] DMDSC[16] GRSDCN ACM ACC 84.13±0.22 86.94±2.83 90.45±0.18 90.59±0.15 91.93±0.20 92.56±0.01 91.67±0.10 92.36±0.10 92.60±0.13 NMI 53.20±0.52 56.18±4.15 68.31±0.25 68.38±0.45 71.56±0.61 73.27±0.03 70.83±0.25 72.52±0.22 73.39±0.12 ARI 57.72±0.67 59.35±3.89 73.91±0.40 74.20±0.38 77.56±0.52 79.19±0.03 76.89±0.24 78.65±0.43 79.28±0.12 F1 84.17±0.23 87.07±2.79 90.42±0.19 90.58±0.17 91.94±0.20 92.54±0.01 91.66±0.09 92.36±0.11 92.61±0.13 DBLP ACC 58.59±0.06 62.05±0.48 68.05±1.81 73.26±0.37 79.66±0.25 77.67±0.14 79.23±0.96 75.33±0.33 80.23±0.38 NMI 26.92±0.06 32.49±0.45 39.50±1.34 39.68±0.42 48.95±0.44 47.05±0.16 48.04±1.46 44.30±0.50 51.05±0.26 ARI 17.92±0.07 21.03±0.52 39.15±2.01 42.49±0.31 53.60±0.46 51.07±0.22 53.51±1.82 46.17±0.21 55.76±0.19 F1 58.69±0.07 61.75±0.67 67.71±1.51 72.80±0.56 79.28±0.26 77.27±0.13 78.55±0.99 75.34±0.66 79.62±0.23 CiteSeer ACC 60.97±0.36 64.54±1.39 65.96±0.31 68.79±0.23 70.86±0.18 73.19±0.06 70.90±0.56 70.33±0.31 73.73±0.35 NMI 32.69±0.27 36.41±0.86 38.71±0.32 41.54±0.30 45.86±0.35 46.74±0.10 44.00±0.64 44.39±0.88 48.05±0.28 ARI 33.13±0.53 37.78±1.24 40.17±0.43 43.79±0.31 47.64±0.30 50.01±0.12 46.47±0.76 46.85±0.97 51.17±0.32 F1 57.70±0.49 62.20±1.32 63.62±0.24 62.37±0.21 65.83±0.21 63.34±0.04 63.12±0.66 65.43±0.63 63.81±0.34 USPS ACC 56.19±0.72 73.55±0.40 78.08±0.19 80.98±0.28 82.90±0.08 82.25±1.97 88.55±0.12 84.03±0.22 NMI 51.08±0.37 71.12±0.24 79.51±0.27 79.64±0.32 82.51±0.07 79.72±0.92 82.66±0.31 82.91±0.65 ARI 40.96±0.59 63.33±0.34 71.84±0.24 73.61±0.43 76.48±0.11 75.38±2.42 80.76±0.22 78.07±0.37 F1 53.63±1.05 72.45±0.49 76.98±0.18 77.61±0.38 80.06±0.05 76.83±1.26 87.59±0.97 80.28±0.26 HHAR ACC 71.30±0.36 76.51±2.19 84.26±0.17 88.11±0.43 89.49±0.22 89.63±0.22 90.42±0.31 NMI 62.95±0.36 69.10±2.28 79.90±0.09 82.44±0.62 84.24±0.29 83.47±0.64 87.39±0.47 ARI 51.47±0.73 60.38±2.15 72.84±0.09 77.07±0.66 79.28±0.28 79.30±0.25 81.14±0.43 F1 71.55±0.29 76.89±2.18 82.58±0.08 88.00±0.53 89.59±0.23 89.95±0.56 90.58±0.37 Reuters ACC 60.85±0.23 65.50±0.13 77.15±0.21 79.30±1.07 80.32±0.04 87.29±0.36 81.12±0.32 NMI 25.51±0.22 30.55±0.29 50.82±0.21 57.83±1.01 55.63±0.05 66.49±0.82 59.51±0.15 ARI 26.18±0.36 31.12±0.18 55.36±0.37 60.55±1.78 59.67±0.11 73.35±0.44 62.22±0.26 F1 57.14±0.17 61.82±0.13 65.48±0.08 66.16±0.64 63.66±0.03 77.46±0.42 66.92±0.47 -
[1] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. [2020-11-09]. https://arxiv.org/abs/1609.02907.
[2] KIPF T N, WELLING M. Variational graph auto-encoders[EB/OL]. [2020-11-21]. https://arxiv.org/abs/1611.07308.
[3] WANG C, PAN S R, HU R Q, et al. Attributed graph clustering: a deep attentional embedding approach[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. [S.l.]: IJCAI, 2019: 3670-3676.
[4] LI X K, HU Y P, SUN Y Q, et al. A deep graph structured clustering network [J]. IEEE Access, 2020, 8: 161727-161738. doi: 10.1109/ACCESS.2020.3020192
[5] BO D Y, WANG X, SHI C, et al. Structural deep clustering network[C]//Proceedings of the Web Conference. New York: ACM, 2020: 1400-1410.
[6] PENG Z H, LIU H, JIA Y H, et al. Attention-driven graph clustering network[C]//Proceedings of the 29th ACM International Conference on Multimedia. New York: ACM, 2021: 935-943.
[7] KULATILLEKE G K, PORTMANN M, KO R, et al. FDGATⅡ: fast dynamic graph attention with initial residual and identity[C]//Australasian Joint Conference on Artificial Intelligence. Cham: Springer, 2022: 73-86.
[8] CHEN M, WEI Z W, HUANG Z F, et al. Simple and deep graph convolutional networks[C]//Proceedings of the 37th International Conference on Machine Learning. New York: ACM, 2020: 1725-1735.
[9] CHEN D L, LIN Y K, LI W, et al. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view [J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 3438-3445. doi: 10.1609/aaai.v34i04.5747
[10] RONG Y, HUANG W B, XU T Y, et al. DropEdge: towards deep graph convolutional networks on node classification[C]//International Conference on Learning Representations. Piscataway, NJ: IEEE, 2020: 1-13.
[11] CHENG K, ZHANG Y F, CAO C Q, et al. Decoupling GCN with DropGraph module for skeleton-based action recognition[C]//European Conference on Computer Vision. Cham: Springer, 2020: 536-553.
[12] KULATILLEKE G K, PORTMANN M, CHANDRA S S. SCGC: self-supervised contrastive graph clustering[EB/OL]. [2022-10-11]. https://arxiv.org/abs/2204.12656v1.
[13] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313: 504-507. doi: 10.1126/science.1127647
[14] LIU Y, TU W X, ZHOU S H, et al. Deep graph clustering via dual correlation reduction[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2022, 36(7): 7603-7611. doi: 10.1609/aaai.v36i7.20726
[15] DING S F, WU B Y, XU X, et al. Graph clustering network with structure embedding enhanced [J]. Pattern Recognition, 2023, 144: 109833. doi: 10.1016/j.patcog.2023.109833
[16] YANG Y C, SUN Y F, WANG S F, et al. A dual-masked deep structural clustering network with adaptive bidirectional information delivery[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(10): 14783-14796. doi: 10.1109/TNNLS.2023.3281570



 下载:
下载: