Axial Compression Mechanical Properties of ECC-Square Steel Tube-Recycled Aggregated Concrete Composite-Columns and Simplified Calculation Formula of Axial Compression Capacity
-
摘要:
为了解决方钢管-再生混凝土叠合柱(square steel pipe - recycled aggregated concrete composite-columns，SP-RAC-C)耐久性以及延性差等问题，提出一种工程水泥基复合材料(engineered cementitious composites，ECC)-方钢管-再生混凝土叠合柱(ECC-SP-RAC-C)，通过数值仿真分析探究宽厚比、材料强度和再生骨料取代率等参数对其轴压力学性能的影响规律，得到该型叠合柱的轴压承载力计算公式。结果表明：ECC-SP-RAC-C在延性、耗能和承载力等指标上均优于RAC-SP-RAC叠合柱；宽厚比越小(ECC壳越厚)则试件的延性越高，但承载力和耗能能力降低；随着钢管强度或厚度的增加，试件的承载力、耗能和延性均增加，但钢管强度越高ECC的作用越小，而钢管厚度影响反之；ECC、RAC强度的提高均增加了叠合柱的承载力和耗能能力，低强度的ECC、高强度的核心RAC展现了更好的组合效应和良好的延性；随着再生粗骨料取代率增加，叠合柱承载力下降、延性增加；叠合柱轴压承载力计算公式具有良好的适用性。
Abstract:To address the issues of durability and poor ductility of square steel pipe (SP)-recycled concrete composite column (RAC-SP-RAC-C), this paper introduces an ECC-square steel tube-recycled concrete composite column (ECC-SP-RAC-C), and investigates the influence of parameters such as width-to-thickness ratio, material strength and recycled aggregate replacement rate on its axial compression mechanical properties through numerical simulation analysis. The findings indicate that the axial compressive load capacity of ECC-SP-RAC-C is calculated by the formula. Results show that ECC-SP-RAC-C is better than RAC-SP-RAC composite columns in terms of ductility, energy dissipation and load carrying capacity. A smaller the width-to-thickness ratio (the thicker the ECC shell) the higher the ductility of the specimens, yet the load-bearing capacity and energy dissipation capacity are reduced. The increase of steel tube strength or thickness increases the bearing capacity, energy dissipation and ductility of the specimen, however the higher the steel tube strength the smaller the effect of ECC, and the opposite effect of steel tube thickness; the increase of ECC and RAC strength increases the bearing capacity and energy dissipation capacity of the composite column, and the low strength ECC and high strength core RAC exhibit a better combination effect and good ductility; with the increase of recycled coarse aggregate replacement rate, the load bearing capacity of the composite column decreases and ductility increases. The formula of axial compression load bearing capacity of composite columns exhibits good applicability.
-
方钢管- 再生混凝土柱(square steel pipe-recycled aggregated concrete-columns，SP-RAC-C)是一种利用钢管约束再生混凝土以达到有效利用再生混凝土的重要构件形式。SP-RAC-C具有承载能力高、构件形式简单、对再生混凝土利用率高等优点。国内外学者对SP-RAC-C的静力性能、抗震性能、冲击性能等进行了大量研究[1-9]，SP-RAC-C在高温、火灾、各类腐蚀[10-12]条件下的耐久性已成为限制其推广应用的关键。
有鉴于此，再生混凝土- 钢管- 再生混凝土叠合柱(RAC-SP-RAC-C)应运而生。Cai等[13]通过试验研究再生骨料替代率、箍筋间距、钢管直径等对RAC-SP-RAC-C轴压力学性能的影响，结果表明：RAC-SP-RAC-C表现出比钢筋再生混凝土柱更好的承载力和变形能力。牛海成等[14]，武骏宇[15]对RAC-SP-RAC-C的轴压力学性能进行试验研究，结果表明：RAC-SP-RAC-C与钢管普通混凝土叠合柱破坏模式相同，均经历了弹性阶段、弹塑性阶段和破坏阶段，RAC-SP-RAC-C承载力与钢管普通混凝土叠合柱承载力相当但延性较差。安钰丰[16]通过有限元仿真探究配筋RAC-SP-RAC-C的轴压受力全过程，指出配筋RAC-SP-RAC-C内部钢管再生混凝土与外部配筋再生混凝土的应变存在明显差异，内部钢管再生混凝土应力应变发展明显滞后。刘阳等[17]指出外部配筋再生混凝土的过早破坏会影响内部钢管再生混凝土承载能力的发挥。
工程水泥基复合材料(engineered cementitious composites，ECC)[18-20]具有高延性和多裂缝开裂等特点，可用于结构加固、构件力学性能提升、新型构造设计等领域，但弹性模量低、价格昂贵、现场施工难度大、现场施工质量难保证等问题限制了其在工程结构中的推广应用。在结构或构件中使用全ECC显然是不经济的。因此，在钢筋混凝土(reinforced concrete, RC)柱、RC梁、RC剪力墙的塑性铰区域使用ECC材料替代普通钢筋混凝土是必然选择。Cho等[21]指出在塑性铰区使用ECC不仅能够提高柱构件的侧向承载力、变形和耗能能力，同时能够大幅减少柱构件受弯临界区的弯剪斜裂缝。Pan等[22]通过试验和理论分析初步得到ECC-RC组合柱的正截面承载能力计算公式，以及ECC-RC组合柱中ECC截面的较优高度。Cai等[23]将普通混凝土(normal concrete, NC)叠合柱(NC-SP-NC-C)的外部配筋普通混凝土置换为配筋ECC，开展了EC C- 钢管- 普通混凝土叠合柱(ECC-SP-NC-C)轴压和偏压力学性能试验，结果表明：ECC-SP-NC-C的轴压和偏压力学性能均优于NC-SP-NC-C，ECC-SP-NC-C的内外侧协调变形能力优于NC-SP-NC-C。现有研究成果表明，利用ECC替代部分普通混凝土能够提高构件的承载能力和延性，改善NC-SP-NC-C内外侧变形和受力不协调的问题。
鉴于此，本文将ECC引入到RAC-SP-RAC-C中，提出ECC-SP-RAC-C构造形式，建立ECC-SP-RAC-C的三维仿真分析模型并基于既有试验结果验证，开展轴压荷载作用下ECC-SP-RAC-C的力学性能分析，重点探讨ECC壳厚度、钢管厚度、材料强度和再生粗骨料取代率等参数对其轴压力学性能的影响，进而提出其轴压承载力简化计算公式。
1. ECC-SP-RAC-C构造
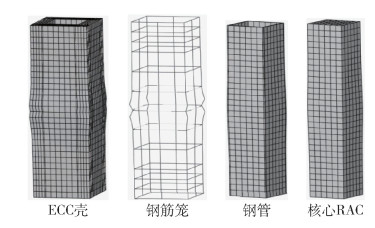
典型的ECC-SP-RAC-C构造如图 1所示。ECC-SP-RAC-C由两部分组成，一是外部钢筋增强ECC，二是内部的方钢管再生混凝土。本文主要关注于ECC与SP-RAC组合的可行性和有效性验证。实际应用时由于ECC壳施工难度较大，ECC-SP-RAC-C可在工厂进行预制加工或现场分段浇筑。为了发挥ECC的力学性能并提升该型墩柱的经济适用性，后期亦可通过仅在关键截面(力学性能需求较高、延性要求较大)设置该型组合构件，如ECC-RAC组合柱、仅柱端采用ECC-RAC组合截面RAC柱等。
2. 有限元模型建立及验证
2.1 材料本构关系
2.1.1 钢管
钢材采用ABAQUS中的弹塑性模型，应力- 应变关系选择Tao等[24]和Han等[25]提出的五线形本构模型。具体计算为
$$ \sigma_{\mathrm{s}}= \begin{cases}E_{\mathrm{s}} \varepsilon_{\mathrm{s}}, & \varepsilon_{\mathrm{s}} \leqslant \varepsilon_{\mathrm{e}} \\ -A \varepsilon_{\mathrm{s}}^2+B \varepsilon_{\mathrm{s}}+C, & \varepsilon_{\mathrm{e}}﹤\varepsilon_{\mathrm{s}} \leqslant \varepsilon_{\mathrm{el}} \\ f_{\mathrm{y}}, & \varepsilon_{\mathrm{e} 1}﹤\varepsilon_{\mathrm{s}} \leqslant \varepsilon_{\mathrm{e} 2} \\ f_{\mathrm{y}}\left(1+0.6 \frac{\varepsilon_{\mathrm{s}}-\varepsilon_{\mathrm{c} 2}}{\varepsilon_{\mathrm{e} 3}-\varepsilon_{\mathrm{e} 2}}\right), & \varepsilon_{\mathrm{e} 2}﹤\varepsilon_{\mathrm{s}} \leqslant \varepsilon_{\mathrm{e} 3} \\ 1.6 f_{\mathrm{y}}, 38 \varepsilon_{\mathrm{s}}>\varepsilon_{\mathrm{e} 3}\end{cases} $$ (1) 式中：fy为钢材的屈服应力；Es为钢材的弹性模量；εe为最大弹性应变。εe=0.8fy/Es；εe1=1.5εe；εe2=10εe1；εe3=100εe1；A=0.2fy/Es；B=2Aεe1；C=0.8fy+Aεe2－Bεe。
2.1.2 钢管再生混凝土
结合杨有福[2]和孟二从[26]再生混凝土约束系数和再生骨料替代率影响的研究成果，本文选取的核心再生混凝土本构关系为
$$ y= \begin{cases}2 x-x^2, & 0 \leqslant x﹤1 \\ \frac{x}{\beta(x-1)^\eta+x}, & x \geqslant 1\end{cases} $$ (2) 式中：
$$ \begin{gathered} x=\sigma / \sigma_0 \\ y=\varepsilon / \varepsilon_0 \\ \beta= \begin{cases}\frac{\left(f_{\mathrm{c}, \mathrm{r}}^{\prime}\right)^{0.1}}{1.35 \times \sqrt{1+\xi}}, & \xi \leqslant 3 \\ \frac{\left(f_{\mathrm{c}, \mathrm{r}}^{\prime}\right)^{0.1}}{1.35 \times \sqrt{1+\xi} \times(\xi-2)^2}, & \xi>3 \\ \eta=1.6+\frac{1.5}{x}\end{cases} \end{gathered} $$ 其中：
$$ \begin{gathered} \sigma_0=\left(1+A\left(24 / f_{\mathrm{c}, \mathrm{r}}^{\prime}\right)^{0.45}\right) \times f_{\mathrm{c}, \mathrm{r}}^{\prime} \\ \varepsilon_0=\left(\varepsilon_{\mathrm{cc}}+B \xi^{0.2}\right) \times\left(1+\frac{r}{\theta}\right) \times 10^{-6} \\ A=-0.0135 \xi^2+0.1 \xi \\ B=1330+760\left(\frac{f_{\mathrm{c}, \mathrm{r}}^{\prime}}{24}-1\right) \\ \varepsilon_{\mathrm{cc}}=\left(1300+12.5 \times f_{\mathrm{c}, \mathrm{r}}^{\prime}\right) \times 10^{-6} \\ \theta=65.715 r^2-109.43 r+48.989 \end{gathered} $$ $f_{\mathrm{c}, \mathrm{r}}^{\prime}$为再生混凝土圆柱体抗压强度；ξ为约束效应系数；r为再生混凝土粗骨料取代率。
2.1.3 ECC
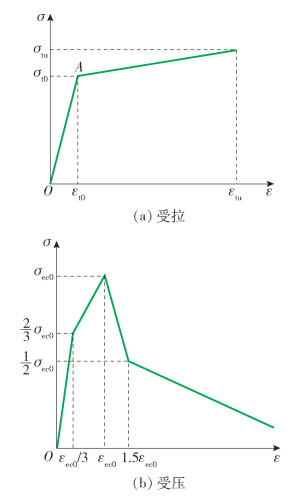
由于ECC具有显著的拉伸应变硬化性能，采用具有应变- 硬化阶段和软化阶段的三线性应力- 应变曲线单轴受拉本构，如图 2(a)所示。借鉴寇佳亮等[27]、程格格[28]提出单轴受压本构模型来考虑箍筋约束ECC，应力- 应变关系如式(3)所示。采用Yuan等[29]提出的单轴受压本构模型来模拟无箍筋约束ECC，如图 2(b)所示。
$$ y= \begin{cases}\frac{k x}{k-1+x^k}, & x \leqslant 1 \\ \frac{x}{\alpha(x-1)^2+x}, & x>1\end{cases} $$ (3) 式中：x=ε/εcc；y=σ/σcc；$\alpha = 1.98 - 2.32I_{\rm{e}}^{0.14}$；k=E0/Ec。其中：E0为ECC初始弹性模量；Ec为峰值点对应的割线模量；Ie代表有效约束指标；εcc为箍筋约束ECC的峰值应变；σcc为箍筋约束ECC的峰值应变。
2.2 单元选取与相互作用
再生混凝土、ECC壳、垫板及钢管均选用八节点实体单元(C3D8R)，钢筋选用两节点桁架单元(T3D2)。钢筋骨架被嵌入到ECC中，钢管与再生混凝土及配筋ECC之间的接触方式均设置为面与面接触，允许两两之间出现滑移，切向行为采用摩尔- 库伦摩擦模型，法向为硬接触。钢管与核心混凝土之间的黏结力计算公式为[30]
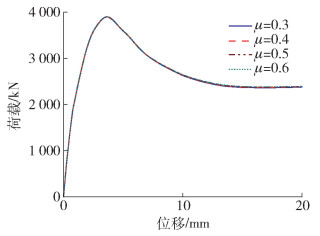
$$ \tau_{\mathrm{b}}=0.75 \times(2.314-0.0195 \times(D / t)) $$ (4) 式中：D是核心混凝土的边长；t为钢管厚度。钢管与ECC壳之间的黏结力也按式(4)计算。如图 3所示，不同的摩擦因数对轴压荷载- 位移曲线影响较小，故摩擦因数取0.6。为了模拟实际加载条件，将柱底垫板固结，柱顶除轴向自由度以外其余自由度均被约束，并采用位移加载。
2.3 模型合理性验证
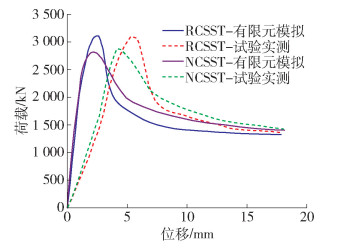
利用本文的建模参数和方法，对牛海成等[14]钢管再生混凝土叠合柱轴压试验进行模拟，如图 4所示。由图 4可知，数值计算曲线与试验曲线趋势相同，承载力与试验结果相差5%以内。需要指出的是数值模型的初始刚度比实测结果大很多，而造成这一差异的主要原因是试验中的边界条件、加载条件和试件参数均存在一定的不确定性。以本文研究的轴压试件为例，试验中的试件很难完全处于轴压状态，其中的影响因素就包括加载端的试件表面受力不均匀性(非均匀受力)、试件上下端边界差异(非完全刚接或铰接)、试件本身制作误差(非完全等截面或竖直)、试件材料性质不均匀性(各项非同性)、加载设备虚位移(加载空程)等。综上，本文参数选择和模拟方法可用于ECC-SP-RAC-C的轴压性能和参数影响分析。
2.4 分析工况设计
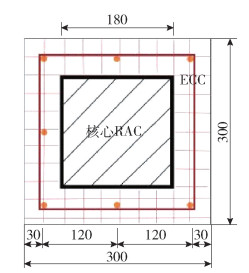
设计了22个轴压叠合柱模型(见表 1)，包括3个RAC-SP-RAC-C(简写为RR)，17个ECC-SP-RAC-C(简写为ER)。试件参数有钢管厚度(t)、箍筋间距(s)、纵筋直径(z)、ECC或RAC壳厚度(d)、RAC、ECC的抗压强度和钢管强度(σ)、再生骨料取代率(r)等。叠合柱均为方截面套方钢管叠合柱，柱高900 mm，高宽比均为3。典型的叠合柱横截面如图 5所示。
表 1 工况参数Table 1. Parameter analysis conditions编号 d/mm H/mm t/mm σ/MPa r s/mm z/mm 钢管 RAC ECC RRd-45 45 180 4 235 40 40 1.0 100 14 RRd-60 60 180 5 235 40 40 1.0 100 14 RRd-75 75 180 6 235 40 40 1.0 100 14 ERd-45 45 210 5 235 40 40 1.0 100 14 ERd-75 75 150 5 235 40 40 1.0 100 14 ERt-6 60 180 6 235 40 40 1.0 100 14 ERt-4 60 180 4 235 40 40 1.0 100 14 ER 60 180 5 235 40 40 1.0 100 14 ERσ-345 60 180 5 345 40 40 1.0 100 14 ERσ-420 60 180 5 420 40 40 1.0 100 14 ERσ-30-40 60 180 5 235 30 40 1.0 100 14 ERσ-50-40 60 180 5 235 50 40 1.0 100 14 ERσ-40-30 60 180 5 235 40 30 1.0 100 14 ERσ-40-50 60 180 5 235 40 50 1.0 100 14 ERr-0 60 180 5 235 40 40 0.3 100 14 ERr-0.3 60 180 5 235 40 40 0.3 100 14 ERr-0.5 60 180 5 235 40 40 0.5 100 14 ERr-0.7 60 180 5 235 40 40 0.7 100 14 ERs-150 60 180 5 235 40 40 1.0 150 14 ERs-200 60 180 5 235 40 40 1.0 200 14 ERz-10 60 180 5 235 40 40 1.0 100 10 ERz-12 60 180 5 235 40 40 1.0 100 12 注：试件编号依据试件参数确定，其中ER和RR分别代表ECC-RAC叠合柱和RAC-RAC叠合柱，随后的d、t、σ、r、s、z分别对应表头的物理量符号，“-”之后的数字为该物理量的取值。 3. 结果与分析
3.1 破坏模式
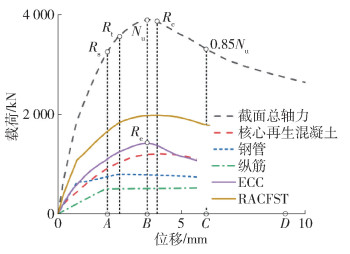
图 6给出ECC-SP-RAC-C典型破坏形式。叠合柱中间部分的ECC、钢管、核心再生混凝土有不同程度的外鼓、纵筋屈曲，ECC-SP-RAC-C与RAC-SP-RAC-C的破坏模式相同[14-15]。图 7给出试件加载过程的荷载- 位移全曲线。
![]()
图 7 典型叠合柱轴压荷载- 位移曲线Figure 7. Axial compression load-displacement curves of typical composite columns由图 7可知，试件位移- 荷载曲线可分为4个阶段。OA段为弹性阶段，在A点时纵筋屈服(Rs)，ECC和核心再生混凝土分别达到其峰值荷载的78%和76%。AB段为屈服阶段，包括钢管屈服阶段(Rt)和ECC峰值承载阶段(Re)。当ECC达到峰值强度时叠合柱承载力达到峰值(Nu)，核心再生混凝土也接近峰值强度。BC段为下降段，核心再生混凝土达到峰值强度(Rc)，在C点时叠合柱承载力已下降到峰值承载力的85%。CD段为破坏阶段，试件破坏。
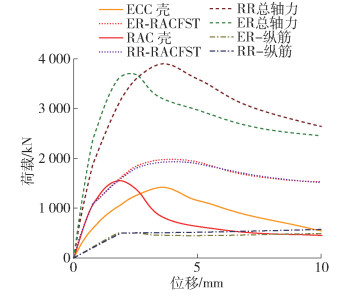
3.2 ECC-SP-RAC-C与RAC-SP-RAC-C对比分析
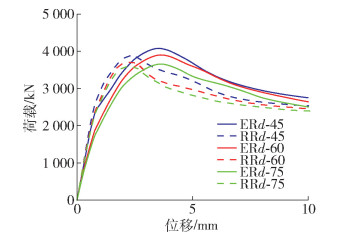
图 8为ER叠合柱和RR叠合柱轴心受压的位移- 荷载曲线。由图 8可知，RR柱为脆性破坏，而ER柱表现为延性破坏。RR柱下降段曲线呈“凹型”。这是因为RAC壳破坏时，钢管再生混凝土还未达到峰值。而ER柱达到峰值后，下降段曲线呈“凸型”，这主要得益于ECC的延性，ECC壳和钢管再生混凝土同时达到峰值，ER叠合柱各部件之间的协调变形能力较优。此外，ER柱的耗能能力也优于RR柱，但其初始刚度较小。
![]()
图 8 RR柱与ER柱荷载位移曲线对比Figure 8. Comparison of load displacement curves between RR columns and ER columns3.3 计算结果及参数分析
表 2给出各试件的主要性能参数统计。其中，强度系数定义为实际承载力与叠合柱各材料根据其抗压强度计算等效承载力代数相加值之比，计算式为
$$ \mathrm{SI}=\frac{N_{\mathrm{u}}}{A_{\mathrm{s}} f_{\mathrm{y}}+A_{\mathrm{t}} f_{\mathrm{y}, \mathrm{t}}+A_{\mathrm{u}} f_{\mathrm{c}}+A_{\mathrm{E}} f_{\mathrm{E}}} $$ 式中：Nu是试件的极限承载力；As、At、Ac、AE分别为纵筋、钢管、核心再生混凝土和ECC的截面积；fy、fy, t、fc、fE分别为对应的纵筋和钢管的屈服强度以及RAC和ECC轴心抗压强度标准值。依据强度系数的定义，强度系数越大表明各组成部分之间的组合约束效应越好。
延性系数定义为承载力下降到85%峰值承载力时所对应的位移与峰值点位移之比。累计耗能定义为位移荷载曲线在85%峰值承载力时累计耗能。
叠合柱塑性发展过程如图 8所示，ECC壳、核心RAC和钢管的塑性应变逐渐从两端向柱中发展，且ECC最先达到其最大塑性应变，核心RAC随后破坏。
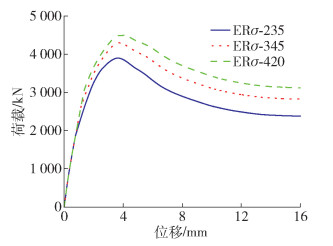
3.3.1 钢管强度
由图 9和表 2可知，钢管屈服刚度由235 MPa提升到420 MPa，试件的峰值荷载增加了15.4%。钢管强度越高，组合效应越差，延性略微提高，耗能提高43.7%。这是因为钢管强度的增加提升了钢管抵抗变形的能力，核心再生混凝土也受到更强的约束作用，但这也降低了各组成部分承载和变形的协调性。
![]()
图 9 不同钢管强度下的荷载- 位移曲线Figure 9. Load-displacement curves under different steel tube strength表 2 试件关键性能参数统计Table 2. Statistics of key performance parameters of specimens试件编号 峰值荷载/kN 强度系数 延性系数 累计耗能/J ERd-45 4 077.28 1.093 1.568 18 253 ERd-75 3 655.62 1.050 1.732 18 209 ER 3 899.03 1.081 1.663 18 611 ERt-4 3 737.41 1.081 1.611 17 426 ERt-6 4 042.23 1.079 1.751 20 791 ERσ-345 4 302.02 1.078 1.778 22 674 ERσ-420 4 500.85 1.058 1.871 26 737 ERσ-30-40 3 568.62 1.106 1.808 19 355 ERσ-50-40 4 181.24 1.050 1.582 18 753 ERσ-40-30 3 596.74 1.054 1.649 17 177 ERσ-40-50 4 101.15 1.080 1.641 19 825 ERr-0 4 101.17 1.079 1.488 17 364 ERr-0.3 4 011.17 1.079 1.534 17 110 ERr-0.5 3 961.48 1.076 1.558 17 266 ERr-0.7 3 920.01 1.077 1.641 18 255 RRd-45 3 775.28 1.040 1.956 14 596 RRd-60 3 652.02 1.026 1.651 11 260 RRd-75 3 589.32 1.031 1.519 10 621 ERs-150 3 824.33 1.038 1.623 17 572 ERs-200 3 745.13 1.060 1.602 16 855 ERz-10 3 700.92 1.082 1.662 16 558 ERz-12 3 798.32 1.080 1.663 17 225 3.3.2 钢管厚度
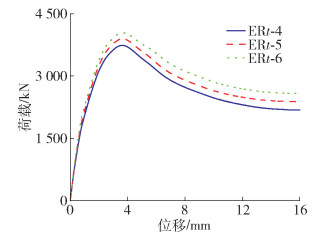
由图 10和表 2可知，钢管厚度增加并不会改变叠合柱的塑性发展，各试件同时达到峰值承载力但钢管厚度增加提高了试件的轴压性能，峰值承载能力和耗能分别提高8.2%和19.3%。钢管厚度的增加会提高其对核心再生混凝土约束作用，同时试件各材料协同变形良好。
![]()
图 10 不同钢管厚度下的荷载- 位移曲线Figure 10. Load-displacement curves under different steel tube thickness3.3.3 ECC、RAC壳宽厚
由图 11和表 2可知，ECC-SP-RAC-C的承载力和变形均大于RAC-SP-RAC-C。特别地，随着ECC、RAC壳厚度的增加，ER系列柱延性逐渐增加，而RR系列柱延性降低。这是因为ECC材料表现出良好的延性特征。此外，增加ECC壳的厚度，则叠合柱的初始刚度和峰值荷载降低。而强度系数变化规律表明，宽厚比越小组合效应则越好。设计时应综合考虑承载能力、延性和组合效应的影响确定较优的宽厚比。
![]()
图 11 不同ECC、RAC壳宽厚比下的荷载- 位移曲线Figure 11. Load-displacement curves under different width-thickness ratios of ECC and RAC3.3.4 ECC、RAC强度
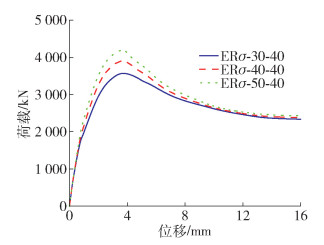
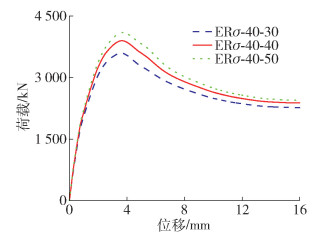
由图 12和表 2可知，ECC抗压强度标准值由30 MPa变为50 MPa，试件的承载力提高17.2%，但峰值后延性明显降低，组合效应降低。ECC抗压强度越高延性则越差，试件协调变形能力降低。由图 13和表 2可知，核心RAC抗压强度标准值由30 MPa变为50 MPa，试件承载力提高14%，但试件的延性下降并不明显。这是因为相同再生粗骨料替代率下的RAC强度提高，其变形能力也有提高。实际应用时可考虑适当增加核心再生混凝土的强度。
![]()
图 12 不同ECC强度下的荷载- 位移曲线Figure 12. Load-displacement curves under different ECC strengths![]()
图 13 不同RAC强度下的荷载- 位移曲线Figure 13. Load-displacement curves under different RAC strengths3.3.5 箍筋间距
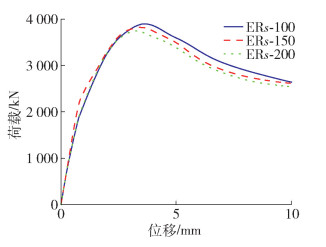
由图 14和表 2可知，箍筋间距从100 mm增加到200 mm，叠合柱的承载力降低4.1%，峰值位移也变小。箍筋约束ECC的强度和延性受到箍筋约束的影响较小，ECC能够发挥部分“箍筋”的作用。
![]()
图 14 不同箍筋间距下的荷载- 位移曲线Figure 14. Load-displacement curves under different stirrup spacings3.3.6 纵筋直径
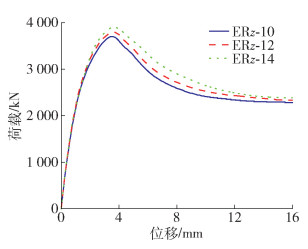
由图 15和表 2可知，纵筋直径从10 mm增加到14 mm，叠合柱初始刚度和峰值位移略微增大，峰值荷载显著增加。但叠合柱的延性和强度系数影响变化较小。这是因为增加纵筋直径相当于增加了叠合柱的抗压刚度，而ECC的受压延性仍保证了钢筋和ECC之间的协调变形。
![]()
图 15 不同纵筋直径下的荷载- 位移曲线Figure 15. Load-displacement curves under different longitudinal reinforcement diameters3.3.7 再生粗骨料取代率
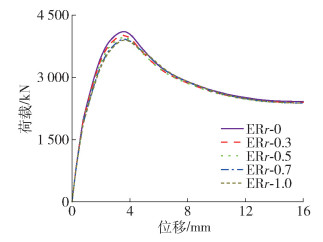
由图 16和表 2可知，再生粗骨料取代率对叠合注的峰值承载力、延性和强度系数影响均较小。这是因为再生骨料占比增加虽然会降低其抗压强度，但再生混凝土峰值应变变大会提高钢管再生混凝土的协调变形能力。
![]()
图 16 不同再生骨料取代率下的荷载- 位移曲线Figure 16. Load-displacement curves under different recycled aggregate replacement rates4. ECC-SP-RAC-C轴向承载机理和承载力计算公式
4.1 接触应力分析
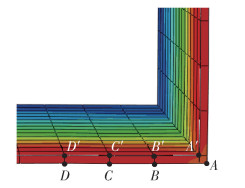
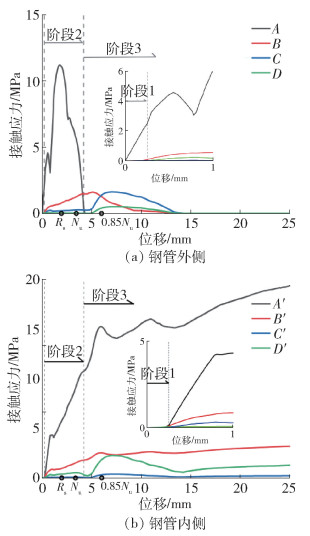
本节通过开展不同破坏模式下的接触应力分析对叠合柱的承载机理进行更深入的研究。选择A、B、C、D为钢管外侧与ECC接触的点，A′、B′、C′、D′为钢管内侧与RAC接触的点，如图 17所示。图 18给出各接触点在试件加载全过程中的应力变化曲线。由图 18可知，钢管与核心RAC和外部ECC的接触应力变化过程可大体分为3个阶段。
阶段1：钢管与ECC共同承载阶段。该阶段钢管与ECC挤压接触应力线性增加，而钢管与RAC接触应力基本为0。此阶段内，叠合柱各部分均处于弹性段(OA)。
阶段2：钢管、ECC、RAC共同承载阶段。钢管与RAC的接触应力呈增加趋势，而钢管与ECC接触应力呈先增大后减小趋势。试件进入屈服阶段(AB)后，ECC壳快速外鼓膨胀并逐渐脱离钢管，而核心RAC外鼓后其与钢管之间的接触应力不断增加，核心RAC受到越来越强的约束，核心RAC与钢管协调变形能力越来越强。在A点接触应力下降到5.5 MPa时，试件达到峰值，进入下降段(BC)，ECC的高延性保障了试件进入下降段之后的延性。
阶段3：钢管与RAC共同承载阶段。钢管与ECC之间的接触应力逐渐降低为0，而RAC的接触应力逐渐趋于稳定。
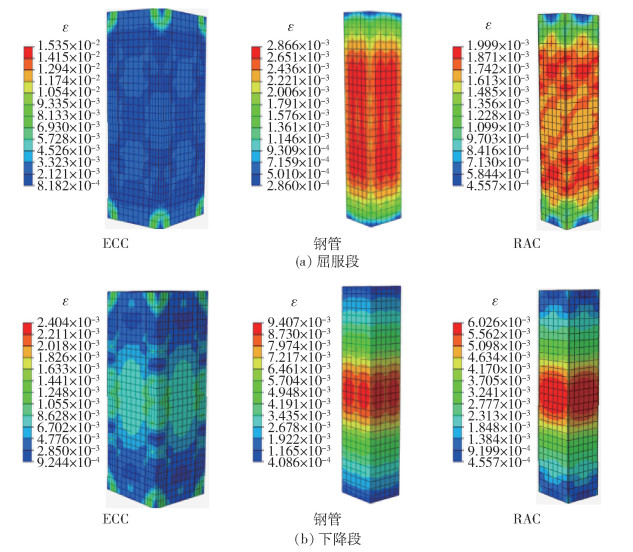
叠合柱的典型塑性损伤发展如图 19所示。ECC壳、核心RAC和钢管的塑性应变逐渐从两端向柱中发展，且ECC最先达到其最大塑性应变，核心RAC随后破坏。
4.2 叠合柱承载力
4.2.1 部件承载力贡献分析
ECC-SP-RAC-C叠合柱由两部分组成，即钢管外钢筋增强ECC壳和钢管再生混凝土。试件峰值承载力可看作此两部分抗力的组合。而钢管外钢筋增强ECC壳则又包含无箍筋约束ECC和箍筋约束ECC两部分。钢管再生混凝土与普通钢管混凝土类似，其承载力可借鉴钢管混凝土规范计算公式。为分析ECC-SP-RAC-C叠合柱在其达到峰值承载力时关键组成部分对其峰值承载力的贡献率，引入了部件承载力贡献系数，其定义为：构件达到峰值承载力时构件的关键组成部分所承担的荷载与关键组成部分在构件加载全过程中对应峰值荷载比值。构件关键组成部分的部件承载力贡献系数统计见表 3。
表 3 承载力贡献系数Table 3. Contribution coefficient of bearing capacity %试件编号 钢管再生混凝土 无箍筋约束ECC 箍筋约束ECC ERd-45 99.71 99.20 94.38 ERd-75 99.41 99.97 99.96 ER 99.83 99.69 95.14 ERt-4 99.94 99.45 96.50 ERt-6 99.86 99.51 97.24 ERσ-345 99.55 98.66 97.14 ERσ-420 97.34 95.38 98.30 ERσ-30-40 99.84 99.56 88.82 ERσ-50-40 99.83 99.72 98.36 ERσ-40-30 100.00 99.45 94.03 ERσ-40-50 99.62 98.98 96.65 ERs-150 99.81 99.16 98.27 ERs-200 98.73 99.31 99.84 ERz-10 99.63 99.39 90.93 ERz-12 99.74 98.73 91.56 从表 3中可知，钢管再生混凝土的部件承载力贡献系数均在97%以上，但构件达到峰值承载力时钢管再生混凝土仍未达到其极限承载力。无约束ECC部件承载力贡献系数均在95%以上，其在构件达到峰值承载力前已达到极限承载力。箍筋约束ECC部件承载力贡献系数在88%以上，与钢管再生混凝土部件类似，构件达到峰值承载力时箍筋约束ECC仍未达到其极限承载力。相关参数对部件承载力贡献系数的影响如下。
1) 钢管强度由235 MPa提高到420 MPa，无约束ECC承载力贡献系数从99.69%下降到95.38%，相反的箍筋约束ECC承载力贡献系数从95.14%增大至98.30%。这是因为钢管强度越高，试件峰值位移越大，使得箍筋约束ECC在加载过程中达到峰值荷载对应的位移与试件峰值位移更加接近，而试件峰值位移增加无约束ECC所能承载的荷载进一步降低。
2) 纵筋直径由10 mm增加到14 mm，无约束ECC承载力贡献系数均维持在98%以上，箍筋约束ECC承载力贡献系数由90.93%提升到95.00%以上。这是因为纵筋直径增加，纵筋分担了更多的荷载，导致ECC的峰值位移更接近于试件峰值位移。
3) ECC强度从30 MPa提高到50 MPa，无约束ECC承载力贡献系数维持在98%以上，箍筋约束ECC的承载力贡献系数从88.82%提升到98.00%以上。类似地，箍筋间距从100 mm增加到200 mm，无约束ECC承载力贡献系数维持在99%以上，箍筋约束ECC的承载力贡献系数从95.14%提高到99.00%以上。这是因为增加ECC强度或增加箍筋间距均会导致箍筋对ECC的约束作用变小，在试件的全过程加载中箍筋约束ECC更易达到其极限承载力。
4) ECC壳厚度从45 mm增加至75 mm，无约束ECC承载力贡献系数维持在99%以上，箍筋约束ECC的承载力贡献系数从94.38%提升到99.96%以上。这是因为ECC壳厚度增加后，钢管尺寸变小，钢管再生混凝土承担的荷载变小，试件的整体协同变形能力变好。
4.2.2 简化计算公式
依据刘阳等[17]相关研究成果，在计算叠合柱承载力时可引入承载力发挥系数和削弱系数来考虑钢筋ECC和钢管RAC两部分对峰值承载力的贡献，则钢筋增强ECC-方钢管再生混凝土柱的承载力计算公式可表示为
$$ N_{\mathrm{u}}=\alpha N_{\mathrm{RE}}+\beta N_{\mathrm{SP}-\mathrm{RAC}}+\gamma N_{\mathrm{s}} $$ (5) $$ N_{\mathrm{RE}}=\eta\left(N_{\mathrm{E}}+N_{\mathrm{SE}}\right) $$ (6) 其中：α、β和γ分别为ECC壳(含无约束ECC和箍筋约束ECC)、钢管再生混凝土和纵筋的承载力发挥系数。结合4.2.1的分析结果，当叠合柱达到峰值荷载时，无约束ECC、箍筋约束ECC、钢管再生混凝土等部件承载力贡献系数分别不低于95%，88%和97%，且纵筋已屈服，因此上述3个参数可分别取为0.90、0.95和1.00；η为考虑ECC承载力削弱系数，通过回归分析可取为0.95。NRE为配筋ECC强度叠加承载力，NE为无箍筋约束的ECC强度计算值，NSE为箍筋约束的ECC强度计算值，Ns为纵筋强度计算值。具体计算公式为
$$ N_{\mathrm{E}}=A_{\mathrm{E}} f_{\mathrm{ce}} $$ (7) $$ N_{\mathrm{SE}}=A_{\mathrm{SE}} f_{\mathrm{cce}} $$ (8) $$ N_{\mathrm{s}}=A_{\mathrm{s}} f_{\mathrm{vs}} $$ (9) 其中：AE、ASE、As分别为无箍筋约束ECC截面面积、箍筋约束ECC截面面积和纵筋截面面积；fce、fcce、fys分别为对应的抗压强度设计值。而方钢管混凝土柱的承载力NSP-RAC，可参考《钢管混凝土结构计算规范》[1]中计算公式，并考虑再生粗骨料替代率的影响，其计算公式为
$$ N_{\mathrm{SP}-\mathrm{RAC}}=A_{\mathrm{SC}} f_{\mathrm{SC}} $$ (10) 式中：ASC为钢管RAC几何截面面积；fSC为钢管RAC抗压统一强度值，计算公式为
$$ f_{\mathrm{sC}}=\left(1.212+B \theta+C \theta^2\right) f_{\mathrm{c}, \mathrm{r}} $$ (11) $$ {f_{{\rm{c, r}}}} = \left( {1 - 0.28r + 0.08{r^2}} \right){f_{{\rm{cc}}}} $$ (12) $$ \theta=\alpha_{\mathrm{SC}} \frac{f_{\mathrm{s}}}{f_{\mathrm{c}, \mathrm{r}}} $$ (13) $$ \alpha_{\mathrm{SC}}=\frac{A_{\mathrm{s}}}{A_{\mathrm{c}}} $$ (14) 式中：θ为钢管混凝土的套箍系数；fs、fc, r、fcc分别为钢管、核心再生混凝土和核心普通混凝土的抗压强度设计值；r为再生粗骨料替代率；αSC为钢管混凝土的含钢率；As、Ac分别为钢管及管内混凝土横截面面积；B、C为截面系数对套箍效应的影响系数，当截面为方形时，B、C的值计算公式分别为
$$ \begin{aligned} B & =\frac{0.131 f_{\mathrm{s}}}{213}+0.723 \\ C & =\frac{-0.070 f_{\mathrm{cc}}}{14.4+0.026} \end{aligned} $$ (15) 表 4给出利用上述简化计算公式求得的ECC-SP-RAC-C的轴压承载力与数值计算结果的对比。由表 4可知，简化公式计算值与有限元计算值的误差均小于5%，相关公式可用于估算ECC-SP-RAC-C的轴压承载力。
表 4 理论与数值计算结果对比Table 4. Comparison of theoretical and numerical calculation results试件编号 有限元计算值/kN 简化公式计算值/kN 误差/% ERd-45 4 077.28 4 009 1.7 ERd-75 3 655.00 3 582 2.0 ER 3 899.03 3 762 3.5 ERt-4 3 737.41 3 659 2.1 ERt-6 4 042.23 3 896 3.6 ERσ-345 4 302.02 4 205 2.3 ERσ-420 4 500.85 4 363 3.0 ERσ-30-40 3 568.62 3 422 4.1 ERσ-50-40 4 181.24 4 100 1.9 ERσ-40-30 3 596.74 3 463 3.7 ERσ-40-50 4 101.15 4 020 2.0 ERr-0 4 101.17 4 033 1.7 ERr-0.3 4 011.17 3 951 1.5 ERr-0.5 3 961.48 3 889 1.8 ERr-0.7 3 920.01 3 846 1.9 ERs-150 3 824.33 3 728 2.5 ERs-200 3 745.13 3 672 2.1 ERz-10 3 700.92 3 558 3.5 ERz-12 3 798.32 3 650 3.9 5. 结论
1) 钢筋增强ECC-方钢管再生混凝土叠合柱破坏模式与方钢管再生混凝土叠合柱一致，单向轴压荷载作用下试件的承载过程可分为弹性阶段、塑性发展阶段、塑性下降段和破坏阶段。
2) 钢筋增强ECC-方钢管再生混凝土叠合柱的峰值承载力、耗能、延性均优于相同参数的方钢管再生混凝土叠合柱。钢管厚度和强度增加可显著提高叠合柱的承载力和延性，钢管强度增加会降低试件各部分的组合性能，而增加钢管厚度则会提高组合性能。
3) 提高ECC和核心RAC强度，试件的承载能力均有显著提高。ECC强度越高叠合柱延性则越差，而核心RAC对试件的延性影响很小。实际应用时可考虑适当提高核心再生混凝土强度等级。再生骨料替代率增加，试件的承载力降低。
4) ECC-SP-RAC-C的轴压承载过程可分为弹性承载阶段，钢管、ECC、RAC共同承载阶段，以及钢管与RAC共同承载阶段，提出的简化计算公式能够较好地计算叠合柱轴压承载力。
-
![]()
图 7 典型叠合柱轴压荷载- 位移曲线
Figure 7. Axial compression load-displacement curves of typical composite columns
![]()
图 8 RR柱与ER柱荷载位移曲线对比
Figure 8. Comparison of load displacement curves between RR columns and ER columns
![]()
图 9 不同钢管强度下的荷载- 位移曲线
Figure 9. Load-displacement curves under different steel tube strength
![]()
图 10 不同钢管厚度下的荷载- 位移曲线
Figure 10. Load-displacement curves under different steel tube thickness
![]()
图 11 不同ECC、RAC壳宽厚比下的荷载- 位移曲线
Figure 11. Load-displacement curves under different width-thickness ratios of ECC and RAC
![]()
图 12 不同ECC强度下的荷载- 位移曲线
Figure 12. Load-displacement curves under different ECC strengths
![]()
图 13 不同RAC强度下的荷载- 位移曲线
Figure 13. Load-displacement curves under different RAC strengths
![]()
图 14 不同箍筋间距下的荷载- 位移曲线
Figure 14. Load-displacement curves under different stirrup spacings
![]()
图 15 不同纵筋直径下的荷载- 位移曲线
Figure 15. Load-displacement curves under different longitudinal reinforcement diameters
![]()
图 16 不同再生骨料取代率下的荷载- 位移曲线
Figure 16. Load-displacement curves under different recycled aggregate replacement rates
表 1 工况参数
Table 1 Parameter analysis conditions
编号 d/mm H/mm t/mm σ/MPa r s/mm z/mm 钢管 RAC ECC RRd-45 45 180 4 235 40 40 1.0 100 14 RRd-60 60 180 5 235 40 40 1.0 100 14 RRd-75 75 180 6 235 40 40 1.0 100 14 ERd-45 45 210 5 235 40 40 1.0 100 14 ERd-75 75 150 5 235 40 40 1.0 100 14 ERt-6 60 180 6 235 40 40 1.0 100 14 ERt-4 60 180 4 235 40 40 1.0 100 14 ER 60 180 5 235 40 40 1.0 100 14 ERσ-345 60 180 5 345 40 40 1.0 100 14 ERσ-420 60 180 5 420 40 40 1.0 100 14 ERσ-30-40 60 180 5 235 30 40 1.0 100 14 ERσ-50-40 60 180 5 235 50 40 1.0 100 14 ERσ-40-30 60 180 5 235 40 30 1.0 100 14 ERσ-40-50 60 180 5 235 40 50 1.0 100 14 ERr-0 60 180 5 235 40 40 0.3 100 14 ERr-0.3 60 180 5 235 40 40 0.3 100 14 ERr-0.5 60 180 5 235 40 40 0.5 100 14 ERr-0.7 60 180 5 235 40 40 0.7 100 14 ERs-150 60 180 5 235 40 40 1.0 150 14 ERs-200 60 180 5 235 40 40 1.0 200 14 ERz-10 60 180 5 235 40 40 1.0 100 10 ERz-12 60 180 5 235 40 40 1.0 100 12 注：试件编号依据试件参数确定，其中ER和RR分别代表ECC-RAC叠合柱和RAC-RAC叠合柱，随后的d、t、σ、r、s、z分别对应表头的物理量符号，“-”之后的数字为该物理量的取值。 
下载: 导出CSV
表 2 试件关键性能参数统计
Table 2 Statistics of key performance parameters of specimens
试件编号 峰值荷载/kN 强度系数 延性系数 累计耗能/J ERd-45 4 077.28 1.093 1.568 18 253 ERd-75 3 655.62 1.050 1.732 18 209 ER 3 899.03 1.081 1.663 18 611 ERt-4 3 737.41 1.081 1.611 17 426 ERt-6 4 042.23 1.079 1.751 20 791 ERσ-345 4 302.02 1.078 1.778 22 674 ERσ-420 4 500.85 1.058 1.871 26 737 ERσ-30-40 3 568.62 1.106 1.808 19 355 ERσ-50-40 4 181.24 1.050 1.582 18 753 ERσ-40-30 3 596.74 1.054 1.649 17 177 ERσ-40-50 4 101.15 1.080 1.641 19 825 ERr-0 4 101.17 1.079 1.488 17 364 ERr-0.3 4 011.17 1.079 1.534 17 110 ERr-0.5 3 961.48 1.076 1.558 17 266 ERr-0.7 3 920.01 1.077 1.641 18 255 RRd-45 3 775.28 1.040 1.956 14 596 RRd-60 3 652.02 1.026 1.651 11 260 RRd-75 3 589.32 1.031 1.519 10 621 ERs-150 3 824.33 1.038 1.623 17 572 ERs-200 3 745.13 1.060 1.602 16 855 ERz-10 3 700.92 1.082 1.662 16 558 ERz-12 3 798.32 1.080 1.663 17 225
下载: 导出CSV
表 3 承载力贡献系数
Table 3 Contribution coefficient of bearing capacity %
试件编号 钢管再生混凝土 无箍筋约束ECC 箍筋约束ECC ERd-45 99.71 99.20 94.38 ERd-75 99.41 99.97 99.96 ER 99.83 99.69 95.14 ERt-4 99.94 99.45 96.50 ERt-6 99.86 99.51 97.24 ERσ-345 99.55 98.66 97.14 ERσ-420 97.34 95.38 98.30 ERσ-30-40 99.84 99.56 88.82 ERσ-50-40 99.83 99.72 98.36 ERσ-40-30 100.00 99.45 94.03 ERσ-40-50 99.62 98.98 96.65 ERs-150 99.81 99.16 98.27 ERs-200 98.73 99.31 99.84 ERz-10 99.63 99.39 90.93 ERz-12 99.74 98.73 91.56
下载: 导出CSV
表 4 理论与数值计算结果对比
Table 4 Comparison of theoretical and numerical calculation results
试件编号 有限元计算值/kN 简化公式计算值/kN 误差/% ERd-45 4 077.28 4 009 1.7 ERd-75 3 655.00 3 582 2.0 ER 3 899.03 3 762 3.5 ERt-4 3 737.41 3 659 2.1 ERt-6 4 042.23 3 896 3.6 ERσ-345 4 302.02 4 205 2.3 ERσ-420 4 500.85 4 363 3.0 ERσ-30-40 3 568.62 3 422 4.1 ERσ-50-40 4 181.24 4 100 1.9 ERσ-40-30 3 596.74 3 463 3.7 ERσ-40-50 4 101.15 4 020 2.0 ERr-0 4 101.17 4 033 1.7 ERr-0.3 4 011.17 3 951 1.5 ERr-0.5 3 961.48 3 889 1.8 ERr-0.7 3 920.01 3 846 1.9 ERs-150 3 824.33 3 728 2.5 ERs-200 3 745.13 3 672 2.1 ERz-10 3 700.92 3 558 3.5 ERz-12 3 798.32 3 650 3.9
下载: 导出CSV
-
[1] 中国工程建设标准化协会. 钢管混凝土结构技术规范: GB50936-2014[S]. 北京: 中国建筑工业出版社, 2014. [2] 杨有福. 钢管再生混凝土构件荷载-变形关系的理论分析[J]. 工业建筑, 2007, 37(12): 1-6, 124. YANG Y F. Theoretical research on load-deformation relations of recycled aggregate concrete-filled steel tubular members[J]. Industrial Construction, 2007, 37(12): 1-6, 124. (in Chinese)
[3] 黄宏, 孙微, 陈梦成, 等. 方钢管再生混凝土轴压短柱力学性能试验研究[J]. 建筑结构学报, 2015, 36(增刊1): 215-221. HUANG H, SUN W, CHEN M C, et al. Experimental research on mechanical behavior of recycled concrete-filled square steel tubular stub columns subjected to axial compression[J]. Journal of Building Structures, 2015, 36(Suppl 1): 215-221. (in Chinese)
[4] 陈宗平, 张士前, 王妮, 等. 钢管再生混凝土轴压短柱受力性能的试验与理论分析[J]. 工程力学, 2013, 30(4): 107-114. CHEN Z P, ZHANG S Q, WANG N, et al. experimental study and theoretical analysis on axial compress capacity of recycled aggregate concrete-filled circle steel tube short column[J]. Engineering mechanics, 2013, 30(4): 107-114. (in Chinese)
[5] 牛海成, 曹万林, 周中一, 等. 足尺方钢管高强再生混凝土柱轴压试验[J]. 北京工业大学学报, 2015, 41(3): 395-402. doi: 10.11936/bjutxb2014070045 NIU H C, CAO W L, ZHOU Z Y, et al. Full-scale test on the performance of high-strength recycled concrete-filled square steel tube columns under axial compression[J]. Journal of Beijing University of Technology, 2015, 41(3): 395-402. (in Chinese) doi: 10.11936/bjutxb2014070045
[6] 黄一杰, 肖建庄. 钢管再生混凝土柱抗震性能与损伤评价[J]. 同济大学学报(自然科学版), 2013, 41(3): 330-335. HUANG Y J, XIAO J Z. Seismic behavior and damage assessment of recycled aggregate concrete-filled steel tube columns[J]. Journal of Tongji University (Natural Science), 2013, 41(3): 330-335. (in Chinese)
[7] YANG Y F, HAN L H, ZHU L T. Experimental performance of recycled aggregate concrete-filled circular steel tubular columns subjected to cyclic flexural loadings[J]. Advances in Structural Engineering, 2009, 12(2): 183-194. doi: 10.1260/136943309788251605
[8] YANG Y F, ZHU L T. Recycled aggregate concrete filled steel SHS beam-columns subjected to cyclic loading[J]. Steel & Composite Structures, 2009, 9(1): 19-38.
[9] 张智成. 钢管再生混凝土构件抗冲击性能研究[D]. 大连: 大连理工大学, 2014: 12-43. ZHANG Z C. Study on impact resistant behavior of recycled aggregate concrete filled steel tubular members[D]. Dalian: Dalian University of Technology, 2014: 12-43. (in Chinese)
[10] 赵磊. 高温后钢管再生混凝土组合柱基本力学性能研究[D]. 沈阳: 沈阳大学, 2013: 17-37. ZHAO L. Study on basic mechanical properties of recycled concrete filled steel tubular composite columns after high temperature[D]. Shenyang: Shenyang University, 2013: 17-37. (in Chinese)
[11] 杨有福, 张磊. 高温后钢管再生混凝土轴压短柱有限元分析[J]. 防灾减灾工程学报, 2015, 35(1): 17-22. YANG Y F, ZHANG L. Finite element analysis of axially loaded recycled aggregate concrete filled steel tube stub column after exposure to high temperature[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(1): 17-22. (in Chinese)
[12] 海然, 唐兵, 李永刚, 等. 氯盐弱腐蚀环境下圆形钢管再生混凝土短柱轴压试验研究[J]. 混凝土, 2022, 396(10): 11-15. HAI R, TANG B, LI Y G, et al. Axial compression test research of short recycled concrete filled circular steel tube column under weak corrosion of chloride salt[J]. Concrete, 2022, 396(10): 11-15. (in Chinese)
[13] CAI M, KE X, SU Y S. Axial compressive performance of RAC-encased RACFST composite columns[J/OL]. Engineering Structures, 2020, 210(5): 110393. [2023-03-24]. https://www.sciencedirect.com/science/article/pii/S0141029619346541.
[14] 牛海成, 高锦龙, 吉珈琨, 等. 钢管高强再生混凝土叠合柱轴压性能[J]. 复合材料学报, 2022, 39(8): 3994-4004. NIU H C, GAO J L, JI J K, et al. Axial compression behavior of high-strength recycled concrete filled steel tubular composite columns[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 3994-4004. (in Chinese)
[15] 武骏宇. 钢管再生混凝土组合柱轴压性能试验研究[D]. 南宁: 广西大学, 2016: 14-40. WU J Y. Experimental study on axial compression behavior of recycled concrete filled steel tubular composite columns[D]. Nanning: Guangxi University, 2016: 14-40. (in Chinese)
[16] 安钰丰. 方形钢管混凝土叠合压弯构件力学性能和设计方法研究[D]. 北京: 清华大学, 2015: 122-140. AN Y F. Study on mechanical properties and design method of concrete-filled square steel tube composite bending members[D]. Beijing: Tsinghua University, 2015: 122-140. (in Chinese)
[17] 刘阳, 郭子雄, 贾磊鹏, 等. 核心钢管混凝土叠合短柱轴压性能及设计方法研究[J]. 建筑结构学报, 2015, 36(12): 135-142. LIU Y, GUO Z X, JIA L P, et al. Experimental study on axial compression performance and design method of core steel tube reinforced concrete short columns[J]. Journal of Building Structures, 2015, 36(12): 135-142. (in Chinese)
[18] LI V C, WANG S, WU C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC)[J]. ACI Materials Journal, 2001, 98(6): 483-492.
[19] SAID S, RAZAK H. Structural behavior of RC engineered cementitious composite (ECC) exterior beam-column joints under reversed cyclic loading[J]. Construction and Building Materials, 2016, 107(15): 226-234.
[20] 陈全胜, 侯圣均, 蒋晨晨, 等. 钢-混凝土-ECC组合梁受弯性能试验研究与有限元分析[J]. 建筑结构学报, 2022, 43(增刊1): 136-142. CHEN Q S, HOU S J, JIANG C C, et al. Experimental research and FEA on bearing capacity under negative moment of steel-concrete-ECC composite beams[J]. Journal of Building Structures, 2022, 43(Suppl 1): 136-142. (in Chinese)
[21] CHO C G, KIM Y Y, FEO L, et al. Cyclic responses of reinforced concrete composite columns strengthened in the plastic hinge region by HPFRC mortar[J]. Composite Structures, 2012, 94(7): 2246-2253.
[22] PAN J L, LU B, GU D W, et al. Mechanical behavior of rectangular steel-reinforced ECC/concrete composite column under eccentric compression[J]. Transactions of Tianjin University, 2015, 21(3): 269-277.
[23] CAI J M, PAN J L, LI X P. Behavior of ECC-encased CFST columns under axial compression[J]. Engineering Structures, 2018, 171: 1-9.
[24] TAO Z, WANG Z B, YU Q. Finite element modelling of concrete-filled steel stub columns under axial compression[J]. Journal of Constructional Steel Research, 2013, 89: 121-131.
[25] HAN L H, YAO G H, TAO Z. Performance of concrete-filled thin-walled steel tubes under pure torsion[J]. Thin-Walled Structures, 2007, 45(1): 24-36.
[26] 孟二从. 方钢管再生混凝土柱-再生混凝土深受弯梁混合框架结构抗震性能研究[D]. 南宁: 广西大学, 2016: 153-158. MENG E C. Study on seismic behavior of recycled concrete column with square steel tube-recycled concrete deep bending beam hybrid frame structure[D]. Nanning: Guangxi University, 2016: 153-158. (in Chinese)
[27] 寇佳亮, 孙方辉, 梁兴文, 等. 箍筋约束纤维增强混凝土轴心受压性能试验研究[J]. 建筑结构学报, 2015, 36(7): 124-131. KOU J L, SUN F H, LIANG X W, et al. Experimental investigation on axial compression performance of fiber reinforced concrete confined with stirrups[J]. Journal of Building Structures, 2015, 36(7): 124-131. (in Chinese)
[28] 程格格. 箍筋约束ECC方形截面短柱力学性能试验研究[D]. 焦作: 河南理工大学, 2016: 61-73. CHENG G G. Experimental study on mechanical properties of ECC square section short columns confined by stirrups[D]. Jiaozuo: Henan Polytechnic University, 2016: 61-73. (in Chinese)
[29] YUAN F, PAN J L, WU Y F. Numerical study on flexural behaviors of steel reinforced engineered cementitious composite (ECC) and ECC/concrete composite beams[J]. Science China Technological Sciences, 2014, 57(3): 637-645.
[30] 刘威. 钢管混凝土局部受压时的工作机理研究[D]. 福州: 福州大学, 2005: 96-121. LIU W. Study on working mechanism of concrete filled steel tube under local compression[D]. Fuzhou: Fuzhou University, 2005: 96-121. (in Chinese)
计量
- 文章访问数: 53
- HTML全文浏览量: 5
- PDF下载量: 22
