Improved Propagator Method for DOA Estimation Based on Fourth-order Cumulant
-
摘要:
针对四阶累积量在多重信号分类(multiple signal classification, MUSIC)算法中计算复杂度高和在低信噪比情况下性能差的问题, 提出一种去冗余后平均的四阶累积量传播算子算法(modified fourth-order cumulant propagator method, MFOC-PM)。该算法通过引入传播算子算法线性地获得噪声子空间, 避免了特征值分解造成的计算量, 然后在保持四阶累积量阵列孔径扩展和抑制高斯噪声的优势下, 通过求平均后去除的方法将四阶累积量中冗余的部分去除, 降低了算法的复杂度。实验结果表明, 所提算法显著减少了算法的计算量, 可以实现角度的精确估计, 在低信噪比的情况下表现良好, 具有较好的实用价值。
Abstract:Aiming at the problem that the fourth-order cumulant has high computational complexity in multiple signal classification (MUSIC) and poor performance under low signal-to-noise ratio conditions, a modified fourth-order cumulant propagator method (MFOC-PM) was proposed. By introducing the propagation operator algorithm to obtain the noise subspace linearly, the algorithm avoided the computation caused by eigenvalue decomposition. To maintain the advantage of the aperture expansion of the fourth-order cumulant array and suppress Gaussian noise, the redundant part of the fourth-order cumulant was removed by the method of averaging and then removing. The experimental results demonstrate that the effectiveness and feasibility of the proposed MFOC-PM algorithm, which significantly reduces the computational complexity of the algorithm. Specifically, it achieves accurate angle estimation and performs well under low signal-to-noise ratio conditions. This indicates that the algorithm has significant practical value and can meet the requirements of DOA estimation in many practical application scenarios.
-
波达角估计(direction of arrival estimation, DOA)是信号处理领域的研究热点方向之一，在卫星通信、车载雷达、水下声呐定位等众多领域均有着广泛应用[1-3]。在DOA中基于子空间类的算法由于其具有超高的分辨率而被人们所熟知，主要有多重信号分类(multiple signal classification, MUSIC)算法、基于旋转不变性技术的信号参数估计(estimating signal parameter via rotational invariance techniques, ESPRIT)算法、传播算子算法等。其中MUSIC算法由于其通过特征值分解得到噪声子空间，算法计算量很高，而传播算子算法因其通过线性变换得到噪声子空间，降低了运算量，而且具有稳定性良好和角度估计准确的优势，成为波达角估计领域中关键的算法之一[4-6]。
近年来，许多学者对传播算子算法进行了研究改进。文献[7]提出一种将对称谱和传播算子算法结合的算法，该算法将空域角度划分为对称的两部分，可以使算法的计算量减半。文献[8]提出一种基于协方差扩展的传播算子算法，通过将协方差矩阵分块划分将其扩展，改善了在低信噪比下的角度估计精度。以上2种算法均需要进行谱峰搜索，适用于均匀线性阵列，但只能在高斯白噪声的环境背景下进行角度估计，如果是高斯色噪声估计效果就会大大降低。文献[9]提出一种基于最小冗余线阵的二维传播算子DOA估计算法，该算法也不需要进行谱峰搜索，利用三线阵之间的旋转关系可以估计出信号的方位角和俯仰角，最后通过快速配对算法进行配对。文献[10]提出一种基于双平行线阵的改进传播算子算法，该算法利用在2个阵列上的位移不变性得到噪声子空间，最后通过求根MUSIC算法计算得到角度。该算法虽然不需要谱峰搜索，但是只适用于双平行线阵。虽然上面介绍的算法在某些特定条件下可以实现DOA估计，但是如果是高斯色噪声或者在信噪比比较低的背景下，估计效果不够理想；因此, 需要研究一种能够适用高斯色噪声和等距均匀线阵的更有效的算法。
在信号处理领域中，用得比较多的分析方法是二阶统计量，其包含了功率谱和自相关函数，这种分析方法已经非常成熟。高阶统计量与二阶统计量相比，可以表示出更多的信息[11]。由于高阶统计量具有相位可检测性、盲高斯特性、阵列扩展特性等优势，在信号处理领域中广受关注[12]。将高阶累积量应用到DOA空间谱估计算法中不仅可以抑制高斯白噪声，而且可以抑制高斯色噪声，同时还具有扩展阵列孔径等优势。正是由于高阶累积量的空间谱估计具备如此多的优势，这类算法才受到了广大学者的关注，并对此进行了大量的研究[13-14]。
综上所述，四阶累积量具备许多优势，这使得一些基于四阶累积量的算法，能够在高斯噪声环境(包含高斯色噪声和高斯白噪声)下取得良好的估计效果[15-16]。虽然四阶累积量具有盲高斯特性、阵列扩展特性、相位可检测性等优势，但是也导致在快拍数较大的情况下计算量过高。
正如文献[16]所提的四阶累积量MUSIC算法，在高快拍数的情况下具有较高的复杂度，其原因就是四阶累积量中冗余的导向矢量和MUSIC算法需要特征值分解。当今所面临的技术难点是在保证算法估计性能不下降的情况下，解决高快拍数计算量过大的问题，从而降低算法的复杂度。文献[17]提出对于均匀线阵四阶累积量可以将阵元数目最多扩展为2M-1，即其他剩余的导向矢量都为冗余的，因此，将四阶累积量中冗余部分去除后，再进行后续处理。本文针对四阶累积量中复杂度过高的问题，提出了一种去冗余后平均的四阶累积量传播算子算法(modified fourth-order cumulant propagator method，MFOC-PM)，并通过实验证明了本文所提算法的有效性，尤其在低信噪比、低快拍数的情况下优势显著。
1. 阵列信号模型
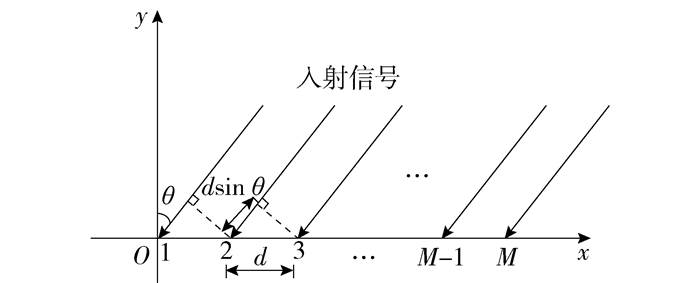
采取等距均匀线阵为天线阵列的结构，阵元的数目为M个，阵元之间具有相同的距离d，在t时刻，有K个远场窄带信号s1(t), s2(t), …, sK(t)入射到等距的均匀线性天线阵列中，每个信号的来波方向为θ1, θ2，…，θK，以均匀线阵中的首个阵元为参考，均匀线阵接收信号模型如图 1所示。
天线阵列中第i个阵元接收到的信号为
$$ s_i(t)=s\left(t-\tau_i\right)=u\left(t-\tau_i\right) \mathrm{e}^{\mathrm{j}\left(w_0\left(t-\tau_i\right)+\phi\left(t-\tau_i\right)\right)} $$ 式中：w0=2π(c/λ)，c为光速，λ为信号波长；τi表示信号到达第i个阵元的时延，信号的角度信息就包含在其中[18]。远场窄带信号可以近似认为
$$ u\left(t-\tau_i\right)=u(t), \phi\left(t-\tau_i\right)=\phi(t) $$ 因此，得出
$$ s_i(t)=s\left(t-\tau_i\right)=s(t) \mathrm{e}^{\mathrm{j} w_0 \tau_i} $$ 每个阵元信号可以表示为各个方向上信号的相加，计算公式为
$$ x_m(t)=\sum\limits_{k=1}^K s_k\left(t-\tau_{m, k}\right)+n_m(t) $$ (1) 式中：m=1, 2, …, M，表示阵元个数；nm(t)为第m个阵元上在t时刻接收到的高斯白噪声；τm, k表示第k个信号到达第m个阵元的延迟时间，在均匀线阵的条件下可表示为τm, k=2πd(m-1)sin θk/λ。因此，sk(t-τm, k)可以表示为sk(t)e-j2πd(m-1)sin θk/λ。
第k个信号到达各阵元的相位差，即各个信号的导向矢量，计算公式为
$$ \begin{aligned} \boldsymbol{a}\left(\theta_k\right)= & {\left[1, \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}} d \sin \theta_k / \lambda}, \cdots, \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}} d(M-1) \sin \theta_k / \lambda}\right]^{\mathrm{T}}=} \\ & {\left[a_1\left(\theta_k\right), a_2\left(\theta_k\right), \cdots, a_M\left(\theta_k\right)\right]^{\mathrm{T}} } \end{aligned} $$ (2) 则xm(t)可以写成
$$ x_m(t)=\sum\limits_{k=1}^K s_k(t) a_m\left(\theta_k\right)+n_m(t) $$ (3) 将K个信号的导向矢量代入式(3)，则整个阵列在某一时刻接收信号的矢量形式可以写为
$$ \boldsymbol{x}(t)=\boldsymbol{A} \boldsymbol{x}(t)+\boldsymbol{n}(t) $$ (4) 式中：x(t)=[x1(t), x2(t), …, xM(t)]T，为天线阵列的输出向量；s(t)=[s1(t), s2(t), …, sK(t)]T，为信源向量；n(t)=[n1(t), n2(t), …, nM(t)]T，表示噪声向量；A为阵列流型矩阵，具体形式为
$$ \boldsymbol{A}=\left[\begin{array}{ccc} 1 & \cdots & 1 \\ \mathrm{e}^{-\frac{\mathrm{j} 2 {\rm{ \mathsf{ π}}} d \sin \theta_1}{\lambda}} & \cdots & \mathrm{e}^{-\frac{\mathrm{j} 2 {\rm{ \mathsf{ π}}} d \sin \theta_K}{\lambda}} \\ \vdots & & \vdots \\ \mathrm{e}^{-\frac{\mathrm{j} 2 {\rm{ \mathsf{ π}}} d(M-1) \sin \theta_1}{\lambda}} & \cdots & \mathrm{e}^{-\frac{\mathrm{j} 2 {\rm{ \mathsf{ π}}} d(M-1) \sin \theta_K}{\lambda}} \end{array}\right] $$ (5) 矩阵A中第m行第k列的元素表示第k个目标信号到达第m个天线阵元的相位延迟信息。
2. 算法原理
2.1 传播算子算法原理
以图 1所示的均匀线性阵列为例，在入射信号相互独立的情况下，A是满秩的，因此，其一定存在K个线性独立行向量。假设矩阵A中前K行是线性不相关的，将矩阵A划分为2个子矩阵，那么具体的划分方式为
$$ \boldsymbol{A}=\left[\begin{array}{l} \boldsymbol{A}_1 \\ \boldsymbol{A}_2 \end{array}\right] $$ (6) 式中：A1为K×K维的子矩阵；A2为(M-K)×K维的子矩阵。
假设A1是非奇异矩阵，那么一定存在K×(M-K)维的传播算子P，使得
$$ \boldsymbol{P}^{\mathrm{H}} \boldsymbol{A}_1=\boldsymbol{A}_2 $$ (7) 定义伪传播算子QH=[PH-IM-K]，将其与矩阵A相乘并化简，可以得到
$$ \boldsymbol{Q}^{\mathrm{H}} \boldsymbol{A}=\left[\begin{array}{ll} \boldsymbol{P}^{\mathrm{H}} & -\boldsymbol{I}_{M-K} \end{array}\right]\left[\begin{array}{l} \boldsymbol{A}_1 \\ \boldsymbol{A}_2 \end{array}\right]={{\bf{0}}} $$ (8) 式中IM-K表示(M-K)×(M-K)维的单位矩阵。
由式(8)可知，矩阵A与定义的伪传播算子QH之间具有正交关系，根据前面的介绍可知，A中导向矢量和噪声子空间存在正交的关系，因此，传播算子Q与噪声子空间UN具有相同的张成空间，即
$$ \operatorname{span}\{\boldsymbol{Q}\}=\operatorname{span}\left\{\boldsymbol{U}_{\mathrm{N}}\right\} $$ (9) 由此可知，矩阵Q和导向矢量之间相互正交，即
$$ \boldsymbol{a}^{\mathrm{H}}(\theta) \boldsymbol{Q}={\mathbf{0}} $$ (10) 定义传播算子算法的空间谱函数为
$$ P(\theta)=\frac{1}{\boldsymbol{a}^{\mathrm{H}}(\theta) \boldsymbol{QQ} ^{\mathrm{H}} \boldsymbol{a}(\theta)} $$ (11) 则对式(11)进行谱峰搜索得到的K个谱峰对应的就是目标信号的方向角度。
2.2 四阶累积量理论基础
对于一个N维平稳随机过程x，假设其均值为0，则其四阶累积量的形式可以表示为
$$ \begin{gathered} \operatorname{cum}\left(k_1, k_2, k_3^*, k_4^*\right)= \\ \mathrm{E}\left[x_{k_1}(t) x_{k_2}(t) x_{k_3}^*(t) x_{k_4}^*(t)\right]- \\ \mathrm{E}\left[x_{k_1}(t) x_{k_3}^*(t)\right] \mathrm{E}\left[x_{k_2}(t) x_{k_4}^*(t)\right]- \\ \mathrm{E}\left[x_{k_1}(t) x_{k_4}^*(t)\right] \mathrm{E}\left[x_{k_2}(t) x_{k_3}^*(t)\right]- \\ \mathrm{E}\left[x_{k_1}(t) x_{k_2}^*(t)\right] \mathrm{E}\left[x_{k_3}(t) x_{k_4}^*(t)\right], \\ k_1, k_2, k_3, k_4 \in[1, 2, \cdots, N] \end{gathered} $$ (12) 式中cum(·)表示求累积量操作。
由文献[19]可知，四阶累积量具有如下性质。
1) 如果随机变量{xi}和{yi}相互独立，则
$$ \begin{gathered} \operatorname{cum}\left\{x_1+y_1, x_2+y_2, \cdots, x_n+y_n\right\}= \\ \operatorname{cum}\left\{x_1, x_2, \cdots, x_n\right\}+\operatorname{cum}\left\{y_1, y_2, \cdots, y_n\right\} \end{gathered} $$ (13) 成立。
2) 如果xi(i=1, 2, …, n)为随机变量，设αi(i= 1, 2, …, n)为常数，则
$$ \begin{gathered} \operatorname{cum}\left\{\alpha_1 x_1, \alpha_2 x_2, \cdots, \alpha_n x_n\right\}= \\ \prod\limits_{i=1}^n \alpha_i \operatorname{cum}\left\{x_1, x_2, \cdots, x_n\right\} \end{gathered} $$ (14) 3) 如果xi(i=1, 2, …, n)为随机变量，{xi}表示某一个子集，假设{xi}与集合中其他部分是不相关的，则有
$$ \operatorname{cum}\left\{x_1, x_2, \cdots, x_n\right\}=0 $$ (15) 4) 假设x服从高斯随机过程，那么其高阶矩可以描述为
$$ \begin{gathered} m_k=\mathrm{E}\left[x^k\right]= \\ \begin{cases}1 \times 3 \times \cdots \times(k-1) \sigma^2, & k \text { 为偶数 } \\ 0, & k \text { 为奇数 }\end{cases} \end{gathered} $$ (16) 由式(16)可以看出，如果随机过程服从高斯分布，那么其一阶累积量就相当于其均值，二阶累积量就相当于其方差，如果高斯随机变量的阶数大于2，那么其高阶矩就为零。因此，如果信号是非高斯信号，而背景噪声为高斯噪声，就可以通过四阶累积量滤除噪声，从而将信号和高斯噪声进行分离。
由上可知，均匀线阵阵列获得信号的数学模型为
$$ \begin{gathered} \boldsymbol{x}(t)=\boldsymbol{A} \boldsymbol{s}(t)+\boldsymbol{n}(t)= \\ \sum\limits_{i=1}^k \boldsymbol{a}_i s_i(t)+\boldsymbol{n}(t) \end{gathered} $$ (17) 将式(17)代入式(12)，化简可以得到
$$ \begin{gathered} \operatorname{cum}\left(k_1, k_2, k_3^*, k_4^*\right)= \\ \sum\limits_{i=1}^K \boldsymbol{a}_i\left(k_1\right) \boldsymbol{a}_i\left(k_2\right) \boldsymbol{a}_i\left(k_3^*\right) \boldsymbol{a}_i\left(k_4^*\right) \gamma_{4 s_i} \end{gathered} $$ (18) 式中：ai(k)表示第i个来波信号的导向矢量的第k个元素；γ4si表示第i个目标信号的四阶累积量。对于均匀线阵来说，如果阵元个数为M，那么式(18)中k1、k2、k3、k4的取值范围为1≤k1, k2, k3, k4≤M。显而易见，伴随着变量k1、k2、k3、k4的取值变化，四阶累积量cum(k1, k2, k3*, k4*)可以取的值共有M4个。为了使后续的操作简便，可以将这M4个值放到一个矩阵R4中，其维数为M2×M2，其表达式为
$$ \begin{array}{c} \boldsymbol{R}_4\left(\left(k_1-1\right) M+k_2, \left(k_3-1\right) M+k_4\right)=\\ \operatorname{cum}\left(k_1, k_2, k_3^*, k_4^*\right) \end{array} $$ (19) 即矩阵的第(k1-1)M+k2行及(k3-1)M+k4列的值为cum(k1, k2, k3*, k4*)。
依据式(18)(19)，可以推导出四阶累积量矩阵
$$ \boldsymbol{R}_4=\operatorname{cum}\left(k_1, k_2, k_3^*, k_4^*\right)=\boldsymbol{B} \boldsymbol{C}_{\mathrm{S}} \boldsymbol{B}^{\mathrm{H}} $$ (20) 式中: CS为目标信号的四阶累积量；B中每一列的具体形式表示为
$$ \boldsymbol{b}(\theta)=\boldsymbol{a}(\theta) \otimes \boldsymbol{a}(\theta) $$ (21) 因此，通过四阶累积量扩展的阵列导向矢量b(θ)的维度为M2×1。这表示比原来的阵列导向矢量的维数扩大了M倍，也就是说，四阶累积量扩展了天线阵列的阵元数目，对于均匀线阵，通过四阶累积量扩展后天线阵列的有效阵元数目为2M-1。为了更清晰地说明阵列扩展的过程，假设均匀线阵阵元个数为3个，那么式(20)可以表示为
$$ \begin{gathered} \boldsymbol{b}(\theta)=\boldsymbol{a}(\theta) \otimes \boldsymbol{a}(\theta)= \\ {\left[1, z, z^2\right]^{\mathrm{T}} \otimes\left[1, z, z^2\right]^{\mathrm{T}}=} \\ {\left[1, z, z^2, z, z^2, z^3, z^2, z^3, z^4\right]} \end{gathered} $$ (22) 式中：a(θ)=[1, z, z2]T；z=e-j2πdsin θ/λ。与阵列原始的导向矢量a(θ)相比，可以看出b(θ)中存在一些冗余项，而且其中有效的阵列扩展项为b(θ)中的第6项和第9项。
针对均匀线阵，去掉冗余数据的四阶累积量矩阵的维度是(2M-1)×(2M-1)，因此，可以从式(22)发现冗余的导向矢量在矩阵中的位置是有规律的。当阵元个数为M时，b(θ)中的第1项至第M项以及所有的kM(k=2, 3, …, M)项，共2M-1个有效项。除去这些有效项，其他的就是冗余的，将这些冗余的去除掉可以有效减少算法的计算量，从而降低算法的复杂度。
2.3 去冗余四阶累积量的传播算子DOA估计
对于均匀线阵四阶累积量中存在冗余的部分，为了有效利用各个导向矢量的信息，提高低信噪比下的估计性能，本文将原来的M2×M2维的四阶累积量矩阵降为(2M-1)×(2M-1)维，对于其中导向矢量相同的需要进行取平均后再去除。具体的构造方式为
$$ \left\{\begin{array}{l} \boldsymbol{R}_{4\left(2 M-1, M^2\right)}(i, :)=\frac{1}{i} \sum\limits_{j=1}^i \boldsymbol{R}_{4\left(M^2, M^2\right)}((j- \\ \;\;\;\;1)(M-1)+i, :), \quad i \leqslant M \\ \boldsymbol{R}_{4\left(2 M-1, M^2\right)}(2 M-i, :)=\frac{1}{i} \sum\limits_{j=1}^i \boldsymbol{R}_{4\left(M^2, M^2\right)}(M(M- \\ \;\;\;\;j+1)-i+j, :), \quad i<M \end{array}\right. $$ (23) $$ \left\{\begin{array}{l} \boldsymbol{R}_{4(2 M-1, 2 M-1)}(:, i)= \\ \quad \frac{1}{i} \sum\limits_{j=1}^i \boldsymbol{R}_{4\left(2 M-1, M^2\right)}(:, (j-1)(M-1)+i), \\ \quad i \leqslant M \\ \boldsymbol{R}_{4(2 M-1, 2 M-1)}(:, 2 M-i)= \\ \quad \frac{1}{i} \sum\limits_{j=1} \boldsymbol{R}_{4\left(2 M-1, M^2\right)}(:, M(M-j+1)-i+j), \\ \quad i<M \end{array}\right. $$ (24) 整个四阶累积量矩阵的构造过程可以简要表示为
$$ \boldsymbol{R}_{4\left(M^2, M^2\right)} \rightarrow \boldsymbol{R}_{4\left(2 M-1, M^2\right)} \rightarrow \boldsymbol{R}_{4(2 M-1, 2 M-1)} $$ (25) 通过式(23)~(25)降维后的四阶累积量矩阵R4(2M-1，2M-1)，将原来矩阵的所有信息保留了下来，不仅能够抑制高斯噪声，而且能够将阵列阵元的个数扩展为2M-1，并且使得算法的计算量降到最低。同时，针对文献[12]中四阶累积量MUSIC算法高复杂度的缺点，本文将传播算子算法引入到四阶累积量中，利用传播算子通过线性变换得到噪声子空间的优点降低文献[12]的复杂度。
与式(21)相似，降维后的R4可以表示为
$$ \boldsymbol{R}_4=\operatorname{cum}\left(k_1, k_2, k_3^*, k_4^*\right)=\boldsymbol{D} \boldsymbol{C}_{\mathrm{s}} \boldsymbol{D}^{\mathrm{H}} $$ (26) 式中D为阵列流型矩阵去掉冗余后的形式，维度是2M-1×K，其每一列的向量形式可以表示为d(θ)=[1, e-j2πdsin θ/λ, …, e-j2πd(2M-2)sin θ/λ]T。
由于D是范德蒙矩阵，当信号入射角度不同时，矩阵D必存在K个线性独立行，由线性代数的基础知识可以知道，矩阵D中剩余的行一定可以由这些线性独立行的线性组合表示。于是将D划分为2个子矩阵，表示为
$$ \boldsymbol{D}=\left[\begin{array}{l} \boldsymbol{D}_1 \\ \boldsymbol{D}_2 \end{array}\right] $$ (27) 式中：D1为K×K维；D2为(2M-1-K)×K维。
定义传播算子矩阵P，其可以表示为
$$ \boldsymbol{P}^{\mathrm{H}} \boldsymbol{D}_1=\boldsymbol{D}_2 $$ (28) 然后定义矩阵Q为
$$ \boldsymbol{Q}^{\mathrm{H}}=\left[\boldsymbol{P}^{\mathrm{H}}-\boldsymbol{I}_{2 M-1-K}\right] $$ (29) 结合式(27)~(29)，可以得出
$$ \boldsymbol{Q}^{\mathrm{H}} \boldsymbol{D}=\left[\boldsymbol{P}^{\mathrm{H}}-\boldsymbol{I}_{2 M-1-K}\right]\left[\begin{array}{l} \boldsymbol{D}_1 \\ \boldsymbol{D}_2 \end{array}\right]={\mathbf{0}} $$ (30) 由此可以证明，扩展后的矩阵D的列向量和矩阵Q的列向量之间是相互正交的。由此定义传播算子算法的空间谱的公式为
$$ P(\theta)=\frac{1}{\boldsymbol{d}^{\mathrm{H}}(\theta) \boldsymbol{Q} \boldsymbol{Q}^{\mathrm{H}} \boldsymbol{d}(\theta)} $$ (31) 因为在实际的环境中存在着各种各样的噪声，再加上信号采样快拍数的影响，不能得到理想中的四阶累积量矩阵R4，所以本文采用均匀线阵阵列接收到信号观测数据来获得$ \hat{\boldsymbol{R}}_4$。
通过式(23)(24)将$ \hat{\boldsymbol{R}}_4$降维，并将其划分为2个子矩阵，可以表示为
$$ \hat{\boldsymbol{R}}_4=\left[\begin{array}{l} \hat{\boldsymbol{R}}_{41} \\ \hat{\boldsymbol{R}}_{42} \end{array}\right] $$ (32) 式中$ \hat{\boldsymbol{R}}_{41}$和$ \hat{\boldsymbol{R}}_{42}$的维度分别为K×2(M-1)和(2M-1-K)×(2M-1)。
传播算子矩阵$ \hat{\boldsymbol{P}}$的估计值可以由最小代价函数ξ($ \hat{\boldsymbol{P}}$)得到，过程可以表示为
$$ \xi(\hat{\boldsymbol{P}})=\left\|\hat{\boldsymbol{R}}_{42}-\hat{\boldsymbol{R}}_{41} \hat{\boldsymbol{P}}^{\mathrm{H}}\right\|_{\mathrm{F}}^2 $$ (33) 式中‖·‖F代表F-范数，那么传播算子矩阵$ \hat{\boldsymbol{P}}$的最优解为
$$ \hat{\boldsymbol{P}}=\left(\hat{\boldsymbol{R}}_{41} \hat{\boldsymbol{R}}_{41}^{\mathrm{H}}\right)^{-1} \hat{\boldsymbol{R}}_{41}^{\mathrm{H}} \hat{\boldsymbol{R}}_{42} $$ (34) 与式(30)类似，定义
$$ \hat{\boldsymbol{Q}}^{\mathrm{H}}=\left[\hat{\boldsymbol{P}}^{\mathrm{H}}-\boldsymbol{I}_{2 M-1-K}\right] $$ (35) 由此得到传播算子算法中的噪声子空间，然后根据空间谱函数就可以估计出来波信号的角度。
综上所述，本文提出的去冗余平均的四阶累积量传播算子算法(modified fourth-order cumulant based propagator method, MFOC-PM)的具体步骤如下：
1) 根据式(19)得到$ \hat{\boldsymbol{R}}_{4}$。
2) 通过式(23)(24)将$ \hat{\boldsymbol{R}}_{4}$降维。
3) 通过式(34)(35)得到$ \hat{\boldsymbol{P}} $。
4) 根据空间谱函数可以估计出来波信号的角度。
3. 实验仿真
本文主要针对四阶累积量MUSIC算法在高复杂度和低快拍数、低信噪比情况下估计不准确的问题进行改进。文献[17]是针对复杂度过高进行改进的，因此，本文算法MFOC-PM与文献[17]的改进的四阶累积量多重分类(MFOC-MUSIC)算法和未去冗余的四阶累积量传播算子算法(four-order cumulant propagator method, FOC-PM)对比，更能体现本文算法的准确性。
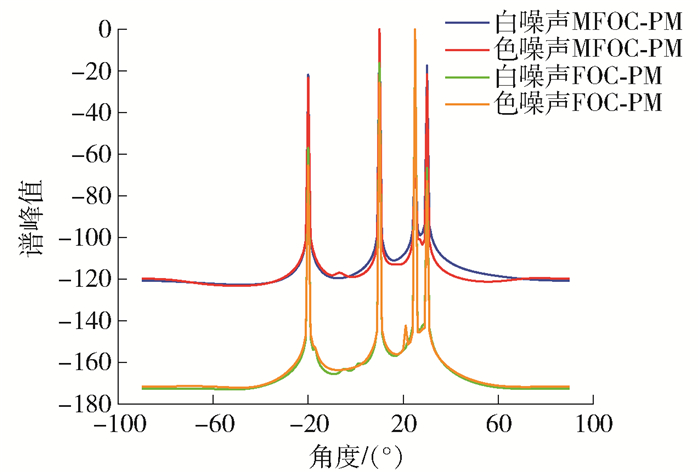
实验1 验证FOC-PM和MFOC-PM在高斯噪声和多信源背景下的有效性。
仿真参数设置如下: 均匀线阵阵元数为3，信源数为4，阵元间距d=0.5λ，采用2种环境背景噪声，即高斯白噪声和高斯色噪声，信源角度为(-20°，10°，25°，30°)，信噪比为20 dB，仿真结果如图 2所示。
由图 2的实验结果可以看出，即使在信源数比阵元数多的情况下，FOC-PM和MFOC-PM也能正确地估计出DOA角度，这是由于四阶累积量拥有阵列扩展的优势，能够将原有的M个阵元扩展为2M-1个阵元。除此之外，2种算法不仅适用于高斯白噪声，而且在高斯色噪声的背景下，估计性能也不错。从理论上分析，这是因为四阶累积量对高斯噪声具有滤除的效果。由图 2可知，本文算法的谱峰比原算法的更加尖锐，说明本文算法的性能更好。
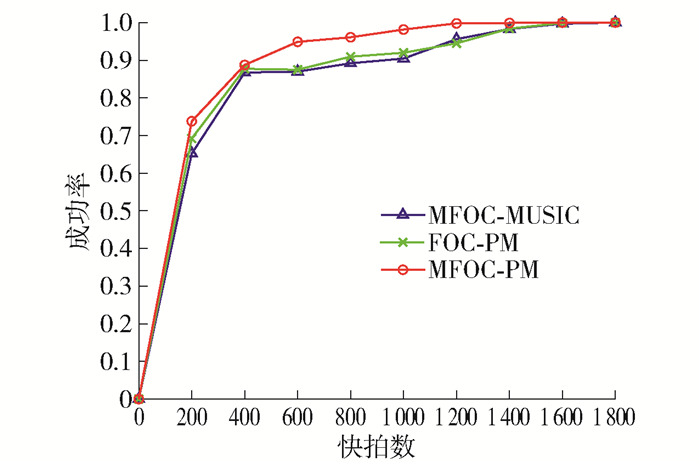
实验2 比较MFOC-MUSIC、FOC-PM、MFOC-PM的DOA估计成功率。
仿真参数设置如下: 均匀线阵阵元数为2，信源数为2，阵元间距d=0.5λ，信源角度为(-10°，20°)，信噪比为10 dB，噪声是加性高斯白噪声，采样快拍数为0~1 800，步进为200，每个快拍数做100次蒙特卡罗实验。3种算法的成功率随采样快拍数变化的情况如图 3所示。
![]()
图 3 各算法估计成功率随快拍数的变化曲线Figure 3. Variation curve of the success rate estimated by each algorithm with the number of fast beats由图 3可知，在采样快拍数从0变化到1 800的过程中，本文算法取得了比其他2种算法更好的估计性能，尤其是在低快拍数的情况下优势明显，其本质原因是本文算法对四阶累积量取平均后再去除，能够在低快拍数的情况下使性能更好。
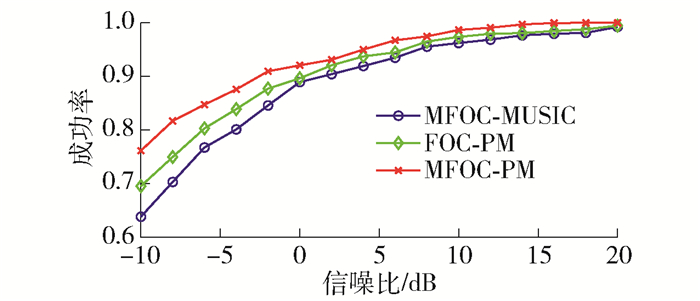
为了更好地比较不同算法在低信噪比下的估计性能，对不同算法在不同信噪比下的估计成功率进行了实验。将天线阵元数目设置为2个，信源数目为2个，入射角度为(-10°，20°)。采用高斯色噪声作为噪声，并从-10~20 dB逐渐增加信噪比，每个信噪比下进行了100次蒙特卡罗实验，并计算了对应的成功率，实验结果如图 4所示。
![]()
图 4 各算法估计成功率随信噪比变化的曲线Figure 4. Variation curve of the success rate estimated by each algorithm with the signal-to-noise ratio从图 4可以看出，在整个信噪比的变化区间，各算法的DOA估计成功率都随信噪比增加而逐渐增大。本文算法在低信噪比的情况下DOA估计成功率较高，在相同信噪比的条件下，本文算法的成功率优于其他算法，说明本文算法DOA估计准确度比其他算法更好，角度估计更加准确。
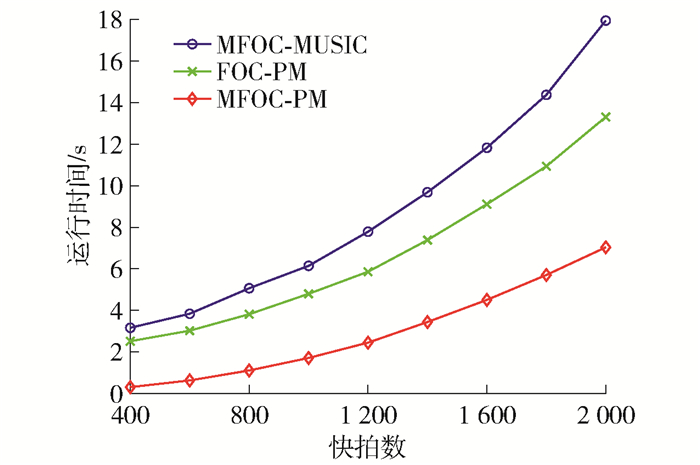
实验3 比较MFOC-MUSIC、FOC-PM、MFOC-PM随采样快拍数变化时的运行时间。
仿真参数设置如下: 均匀线阵阵元数为3，信源数为4，阵元间距d=0.5λ，入射角度为(-20°，10°，25°，30°)，信噪比为10 dB，噪声是加性高斯白噪声，快拍数从初始值400逐渐增加到2 000，增加间隔为200，每个快拍数做100次蒙特卡罗实验并记录平均值。各种算法的平均运行时间变化情况如图 5所示。
由图 5可以看出，MFOC-MUSIC的复杂度比其他算法都高，从理论上分析是因为其需要对R4进行特征值分解。本文所提算法的运行时间比FOC-PM短很多，表明本文算法复杂度比原算法小。这主要有两部分原因：一是MFOC-PM算法不需要特征值分解，直接通过线性变换得到噪声子空间；二是将四阶累积量中冗余的部分去除，计算量减小。
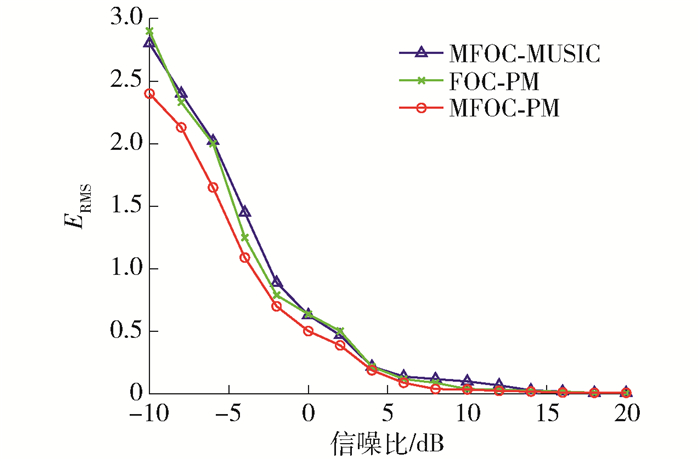
实验4 比较MFOC-MUSIC、FOC-PM、MFOC-PM的均方根误差(root mean square error, RMSE)ERMS。
为了比较算法改进前后的DOA精度，本文用RMSE来衡量算法性能的好坏。采用RMSE作为评估指标可以更加准确地反映算法的实际表现，并充分考虑到估计误差的整体特征，而不仅局限于某一个点或某一个角度。在实际应用中，准确的DOA估计精度是至关重要的，因此，采用RMSE进行评估具有重要的意义。DOA估计的RMSE定义为
$$ E_{\mathrm{RMS}}=\sqrt{\frac{1}{\text { num }} \sum\limits_{i=1}^{\text {num }}\left(\hat{\theta}_i-\theta_i\right)^2} $$ (36) 式中：θi为DOA估计的角度估计值；$ \hat{\theta}$为算法的角度估计值；num为蒙特卡罗仿真次数。实验选取5个信号源，以角度(-25°，-15°，10°，15°，25°)入射四元直线阵，信噪比的取值区间为[-10, 20]dB，步进为2 dB。在每个信噪比下做100次蒙特卡罗实验，并计算各个算法的RMSE，实验结果如图 6所示。
由图 6可知，在信噪比变化区间，本文算法的RMSE都小于其他算法，说明本文所提算法的性能优于原算法，更具有抗噪能力，尤其在低信噪比时，优势更加明显。从理论上分析，本文算法将四阶累积量中冗余的部分求平均后去除，因此，在计算复杂度降低的情况下，DOA估计精度得到了提高。
4. 结论
1) 将四阶累积量应用到传播算子算法中，并在此基础上将四阶累积量冗余的部分平均后去除，降低了原算法的复杂度。同时，在少快拍数和低信噪比的环境背景下，本文算法在稳定性和精度上都优于原算法。
2) 利用四阶累积量对高斯噪声滤除的特点，使得本文算法不仅适用高斯白噪声而且适用高斯色噪声，具有更好的抗噪能力。
3) 通过四阶累积量，扩展了阵元数目，从而在信源数比阵元数多的情况下，仍然能够完成DOA估计。
-
![]()
图 3 各算法估计成功率随快拍数的变化曲线
Figure 3. Variation curve of the success rate estimated by each algorithm with the number of fast beats
![]()
图 4 各算法估计成功率随信噪比变化的曲线
Figure 4. Variation curve of the success rate estimated by each algorithm with the signal-to-noise ratio
-
[1] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 253-273. [2] 张国光. 水声近场源目标的高分辨DOA估计方法改进研究[J]. 舰船电子工程, 2017, 37(2): 30-33, 46. ZHANG G G. Improvement of high resolution DOA estimation method for underwater acoustic near-field source[J]. Ship Electronic Engineering, 2017, 37(2): 30-33, 46. (in Chinese)
[3] 王平. 汽车毫米波雷达目标DOA估计研究[D]. 成都: 电子科技大学, 2021. WANG P. Research on target DOA estimation of automotive millimeter wave radar[D]. Chengdu: University of Electronic Science and Technology of China, 2021. (in Chinese)
[4] TANG W C, LIU L C, WANG Y D. A fast PM-based DOA estimation method with automatic pairing[C]//2018 10th International Conference on Communication Software and Networks. Piscataway, NJ: IEEE, 2018: 386-390.
[5] 张保锋. 几种DOA估计算法的性能分析[J]. 现代电子技术, 2003, 26(9): 35-37. ZHANG B F. Performance of several algorithim of DOA[J]. Modern Electronics Technique, 2003, 26(9): 35-37. (in Chinese)
[6] 窦慧晶, 孙璐, 谢金鑫. 基于阵列扩展的改进PM的二维DOA估计[J]. 北京工业大学学报, 2019, 45(9): 831-837. doi: 10.11936/bjutxb2018040021 DOU H J, SUN L, XIE J X. Improved PM in two-dimensional DOA estimation based on array expansion[J]. Journal of Beijing University of Technology, 2019, 45(9): 831-837. (in Chinese) doi: 10.11936/bjutxb2018040021
[7] 王传宇, 聂慧锋, 王林, 等. 快速DOA估计算法研究[J]. 舰船电子对抗, 2021, 44(5): 82-85. WANG C Y, NIE H F, WANG L, et al. Research into fast DOA estimation algorithm[J]. Shipboard Electronic Countermeasure, 2021, 44(5): 82-85. (in Chinese)
[8] 王绪虎, 田雨, 白浩东, 等. 基于协方差扩展PM算法的波达方向估计[J]. 声学技术, 2023, 42(1): 95-100. WANG X H, TIAN Y, BAI H D, et al. Direction of arrival estimation based on the covariance expanded PM algorithm[J]. Technical Acoustics, 2023, 42(1): 95-100. (in Chinese)
[9] 赵大勇, 陈超, 刁鸣. 基于最小冗余线阵的二维传播算子DOA估计[J]. 系统工程与电子技术, 2011, 33(4): 724-727. ZHAO D Y, CHEN C, DIAO M. Propagator method for two-dimensional DOA estimation based on minimum redundancy linear array[J]. Systems Engineering and Electronics, 2011, 33(4): 724-727. (in Chinese)
[10] 王志强. 基于传播算子的DOA估计算法研究[D]. 南昌: 南昌大学, 2020. WANG Z Q. Research on DOA estimation algorithm based on propagation operator[D]. Nanchang: Nanchang University, 2020. (in Chinese)
[11] 张家为. 高阶统计量的应用[J]. 中国科技信息, 2010(24): 49-50, 52. ZHANG J W. Application of higher-order statistics[J]. China Science and Technology Information, 2010(24): 49-50, 52. (in Chinese)
[12] 梁清泉. 基于高阶统计量的波达方向估计技术的研究[D]. 西安: 西北工业大学, 2002. LIANG Q Q. Research on DOA estimation technology based on higher-order statistics[D]. Xi'an: Northwestern Polytechnical University, 2002. (in Chinese)
[13] 段慧芳. 基于高阶统计量的互质阵DOA估计研究[D]. 昆明: 昆明理工大学, 2019. DUAN H F. Research on DOA estimation of coprime matrix based on higher-order statistics[D]. Kunming: Kunming University of Science and Technology, 2019. (in Chinese)
[14] CHEN Y H, LIN Y S. Fourth-order cumulant matrices for DOA estimation[J]. IEE Proceedings-Radar, Sonar and Navigation, 1994, 141(3): 144-148.
[15] ZHU Z H. The fourth order cumulants based modified MUSIC algorithm for DOA in colored noise[C]//2010 Asia-Pacific Conference on Wearable Computing Systems. Piscataway, NJ: IEEE, 2010: 345-347.
[16] 李丹宁, 石和平, 曹继华, 等. 基于四阶累积量的MUSIC算法性能仿真分析[J]. 天津职业技术师范大学学报, 2022, 32(3): 53-57. LI D N, SHI H P, CAO J H, et al. Performance simulation analysis of MUSIC algorithm based on fourth-order cumulants[J]. Journal of Tianjin University of Technology and Education, 2022, 32(3): 53-57. (in Chinese)
[17] 唐建红, 司锡才, 初萍. 改进的基于四阶累积量的MUSIC算法[J]. 系统工程与电子技术, 2010, 32(2): 256-259. TANG J H, SI X C, CHU P. Improved MUSIC algorithm based on fourth-order cumulants[J]. Systems Engineering and Electronics, 2010, 32(2): 256-259. (in Chinese)
[18] 窦慧晶, 肖子恒, 杨帆. 基于改进稀疏度自适应匹配追踪算法的压缩感知DOA估计[J]. 北京工业大学学报, 2021, 47(11): 1239-1246. doi: 10.11936/bjutxb2020060001 DOU H J, XIAO Z H, YANG F. Compressed sensing DOA estimation based on improved sparsity adaptive matching pursuit algorithm[J]. Journal of Beijing University of Technology, 2021, 47(11): 1239-1246. (in Chinese) doi: 10.11936/bjutxb2020060001
[19] 王猛. 基于高阶累积量的声矢量阵列信号DOA估计算法研究[D]. 长春: 吉林大学, 2017. WANG M. Research on acoustic vector sensor array DOA estimation algorithm based on high order cumulants[D]. Changchun: Jilin University, 2017. (in Chinese)
下载:
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
