Median Filtering of Quantum Signal Based on the Fractional Representation Model
-
摘要:
在过去10年里,基于量子力学的量子信号表示研究已经出现一些重要结果. 然而,关于量子信号处理方面的研究却相对滞后,其中就包括量子信号的滤波处理.首先,改进了现有的数字信号的量子表示模型(quantum representation of digital signals,QRDS),使其适用于任意长度的时间信号,同时还修改了QRDS模型中二补码的编码方法,使得新的编码更符合实际问题. 然后,基于改进的模型引入了中值滤波方案,该方案回避了量子计算不能直接实现卷积运算的缺陷. 为了实现该滤波方案的量子电路, 又给出了基本量子运算模块: 比较器模块、交换模块和中值计算模块. 最后,通过实例验证了文中所提滤波方案的有效性和合理性.
Abstract:In the past decade, quantum signal representation models based on quantum mechanics have produced some important results. However, researches on quantum signal processing is lagging behind, including the filtering of quantum signals. First, the fixed-point number quantum representation of digital signals (QRDS) proposed by Li Panchi et al. was improved, so that it is more suitable for time signals with any length. Then, a median filtering method was introduced based on the improved model, which avoids the drawback that quantum computing cannot directly implement convolution operations. To implement the quantum circuit of this filtering method, the basic quantum operation modules including comparator module, swap module and median calculation module were given in this paper. Finally, the effectiveness and rationality of the filtering method proposed in the paper were verified by examples.
-
在信息爆炸的时代,由于信息量级的快速增长,存储和处理数据的传统方法面临着严峻挑战, 因此,需要找到新的方法来处理这一问题. 量子计算的概念为计算科学带来了新的范式,它挑战了人们对复杂性理论的理解以及它与经典计算的关系. 作为一种新的计算方法,由于其具有叠加性和并行性等特性,使得基于量子算法的量子计算机的存储性能和运行速度都远远超过经典计算机,因此量子计算的出现为解决经典计算方法问题带来了曙光.
近年来,量子计算在科学界引起了众多学者们的兴趣. 首先,量子计算具有高度的跨学科性,涉及不同的研究主题. 例如在理论方面,涉及信息理论和量子力学的基础问题; 在实验方面,涉及量子、光学、原子和固态系统的物理学研究. 其次,该领域在不久的将来极有希望产生革命性的技术影响.
1982年,Feynman[1]首次提出量子计算机模型;之后,Shor提出的整数分解多项式时间算法[2]和Grover提出的数据库搜索算法[3]成为支持量子计算机运算能力的重要证据. 近年来,关于量子计算的研究已经出现在各个相关领域,例如密码学[4]、图像处理[5-8]、频域量子信息处理[9]、求根问题[10]和一些经典算法[11]等.
在过去10年中,针对滤波方面的研究主要围绕着量子图像进行,例如空间域的中值滤波[12]、空间域的加权平均滤波[13]和含噪图像的修复[14]等. 然而,对于另外一种重要的信息形式,即量子信号,还没有给予足够的研究. 由于量子信号的幅值不一定是整数,因此其表示模型也有别于量子图像,而其处理方法也比量子图像的处理方法更为复杂.
当前关于量子信号的表示模型有: 数字音频信号的量子表示(quantum representation of digital audio, QRDA)[15]、数字音频信号的灵活表示(flexible representation of digital audio, FRQA)[16]、数字信号的量子表示模型(quantum representation of digital signals,QRDS)[17]. 模型QRDA和FRQA把量子图像表示模型NEQR[18]的思想延拓到量子信号中,用计算基态表示时间信息,而用整数值近似代替振幅值,这是量子信号表示的一大进步,但是完全忽略小数部分会产生较大的误差.
QRDS模型首次采用(p+q+1)位(包括1个符号位、q个整数位和p个分数位)去存储信号中每个时刻对应的振幅值. QRDS的主要思想是将量子图像灰度值的整数表示法扩展为分数表示法. 对于量子信号来说,这是一个重要突破. 但是QRDS表示模型只适用于时间长度为2的整数幂的信号,并且编码结果与常用的编码结果也有所不同,这与实际问题中信号的时间长度是任意的这一事实并不相符,同时也给利用现有的编码运算器处理信号带来了困难.
所以,首先对量子信号QRDS模型进行了改进,使其适用于任意时间长度的量子信号,得到改进后的QRDS模型,这里记为NQRDS. 另外,前面3种表示模型仍然只关注信号的存储,所以量子信号处理仍然处于起步阶段. 量子信号处理包括诸如放大、滤波、积分等操作. 滤波是量子信号处理中一项基本的重要技术. 在经典信号中,通过采用信号与代表滤波信号掩码的卷积,可以很容易地实现滤波操作. 然而,量子计算却不能直接实现卷积操作. 其次,基于量子信号的NQRDS表示模型,提出了量子信号的中值滤波技术,成功地回避了上述问题. 文中最后在此基础上进行量子信号的中值滤波操作并给出实现该操作的量子电路. 由于设计中值滤波电路是一项复杂的任务,因此将设计过程分解成几个模块,包括比较器模块、交换模块、排序模块和基于NQRDS模型的中值计算模块.
本文的其余部分组织如下: 第1节给出了与研究内容相关的一些工作; 第2节给出了改进的QRDS模型(NQRDS); 第3节讨论并且给出了信号的中值滤波方法以及相关基本电路模块; 第4节给出了量子信号中值滤波的一个应用; 最后是结论部分.
1. 相关工作
2016年,Wang[15]首次提出QRDA. 设时间信号A=[a0, a1, …, aL-1],其中: L为信号的长度,at∈{0, 1, …, 2q-1}. QRDA使用q个比特序列Dt=Dt0Dt1…Dtq-2Dtq-1编码振幅值信息at,即at=Dt0Dt1…Dtq-2Dtq-1,Dti∈{0, 1},i=0, 1, …, q-1, 其中t=0, 1, …, L-1为时间信息. 因此,QRDA模型如下.
$$ \begin{gathered} |\boldsymbol{A}\rangle=\frac{1}{\sqrt{2^l}} \sum\limits_{t=0}^{L-1}\left|D_t\right\rangle \otimes|t\rangle \\ |t\rangle=\left|t_0, t_1, \cdots, t_{l-1}\right\rangle, t_i \in\{0, 1\} \\ \left|D_t\right\rangle=\left|D_t^0 D_t^1 \cdots D_t^{q-2} D_t^{q-1}\right\rangle, D_t^i \in\{0, 1\} \end{gathered} $$ 式中:
$$ l= \begin{cases}\left\lceil\log _2 L\right\rceil, & L>1 \\ 1, & L=1\end{cases} $$ QRDA在对振幅值的编码过程中,没有考虑到振幅值为负数的情况,也没有考虑到振幅值为分数的情况,这是它的重要缺陷.
2018年,Yan等[16]在分析QRDA模型缺陷的基础上,把振幅值在QRDA模型中由原码编码,修改成为二补码编码,从而成功地解决了QRDA模型不能编码负数振幅值的缺陷. 他们把这一量子信号的灵活表示模型简记为FRQA,定义为
$$ |\boldsymbol{A}\rangle=\frac{1}{\sqrt{2^l}} \sum\limits_{t=0}^{L-1}\left|D_t\right\rangle \otimes|t\rangle $$ 式中: |Dt〉=|Dt0Dt1…Dtq-2Dtq-1〉为振幅值的二补数编码;|t〉=|t0, t1, …, tl-1〉,ti∈{0, 1},为编码对应的时间信息. FRQA模型虽然解决了振幅值取负数的问题,但是对于分数的振幅值还是使用整数近似替代,因此信号处理的结果误差仍然较大.
同年,Li等[17]利用定点数的编码方法,把分数振幅值的整数部分和小数部分混合编码,并给出该类混合编码的二补码定义,从而把分数振幅值编码为上述二补码的形式,解决了前面2种模型只能处理整数振幅值的问题,文中称其为数字信号的量子表示模型,简记为QRDS.
令x为(p+q+1)比特的二进字符串,包括: 1个符号比特xq(0表示“+”,1表示“-”),q个整数比特,xq-1, xq-2, …, x0,以及p个分数比特,x-1, x-2, …, x-p. 当x=xq, xq-1xq-2…x0.x-1x-2…x-p时,其二补码[x]c定义为
$$ [x]_{\mathrm{c}}=\left\{\begin{array}{lll} 0, & x_{q-1} x_{q-2} \cdots x_0 \cdot x_{-1} x_{-2} \cdots x_{-p}, & x_q=0 \\ 1, & 2^q-x_{q-1} x_{q-2} \cdots x_0 \cdot x_{-1} x_{-2} \cdots x_{-p}, & x_q=1 \end{array}\right. $$ 利用上面定义的二补码,Li等给出的数字信号的量子表示如下.
设时间信号
$$\boldsymbol{x}=\left[x_0, x_1, \cdots, x_{2^k-1}\right] $$ 当t=0, 1, …, 2k-1时,
$$ x_t=x_t^q, x_t^{q-1} x_t^{q-2} \cdots x_t^0 \cdot x_t^{-1} x_t^{-2} \cdots x_t^{-p} $$ 此时的QRDS模型表示如下.
$$ \begin{aligned} |\boldsymbol{x}\rangle & =\frac{1}{\sqrt{2^k}} \sum\limits_{t=0}^{2^k-1}\left|\left[x_t\right]_c\right\rangle \otimes|t\rangle= \\ & \frac{1}{\sqrt{2^k}} \sum\limits_{t=0}^{2^k-1} \bigotimes_{i=-p}^q\left|x_t^i\right\rangle \otimes|t\rangle \end{aligned} $$ 从模型中可以看出,QRDS模型使用(k+p+q+1)个量子比特去存储时间长度为2k,同时振幅值处于
$$ \left(-2^q+\frac{1}{2^p}, 2^q-\frac{1}{2^p}\right) $$ 的时间信号,这是该模型的一大优点.
但是该模型的缺点也很明显: 其一在于该模型不能适用于任意长度的时间信号; 其二是该模型定义的二补码与经典的二补码定义有一些不同之处,从而不能直接运用现有的二补码运算器实现信号处理,如二补码的量子加法器和乘法器等运算器. 使用Li等给出的二补码定义,正数的二补码与经典二补码编码结果保持一致,但是对于负数来说,2种二补码的编码结果相差较大. 如设p=q=4,在新二补码编码下有
$$ [6.5]_{\mathrm{c}}^{\mathrm{new}}=0, 0110.1000, [-6.5]_{\mathrm{c}}^{\mathrm{new}}=1, 1001.1000 $$ 如果把6.5拆成6加上0.5,-6.5拆成-6加上-0.5,那么在经典二补码编码下有
$$ [6.5]_c^{\text {old }}=0, 0110.1000, [-6.5]_c^{\text {old }}=1, 1010.1000 $$ 通过比较可以看出,负数的2种编码方法编码结果相差较大.
2. 改进的QRDS模型
为了克服QRDS模型的2个缺点,给出了改进的QRDS模型(NQRDS). 与Li等的QRDS模型相比,NQRDS模型适用于任意时间长度的量子信号,同时振幅值的二补码表示也与经典的二补码定义相一致,使得模型的应用更具有灵活性和方便性. 新改进的模型为
$$|\boldsymbol{A}\rangle=\frac{1}{\sqrt{2^l}}\left(\sum\limits_{t=0}^L\left|I_t\right\rangle\left|D_t\right\rangle \otimes|t\rangle+\sum\limits_{t=L}^{2^l-1}|0\rangle^{\otimes(p+q)}|t\rangle\right) $$ (1) 式中:
$$l= \begin{cases}\left\lceil\log _2 L\right\rceil, & L>1 \\ 1, & L=1\end{cases} $$ L为正整数;|It〉=|It0It1…Itq-1〉, Iti∈{0, 1},为振幅值的整数部分,且It为二补码形式的二进制序列. 实际上,It∈{-2q-2, …, 2q-2-1},It0为符号位. 符号位0表示正的振幅值,而1则表示负的振幅值. |Dt〉=|Dt1Dt2…Dtp〉, Dti∈{0, 1},是振幅值的定点小数部分,也是二补码形式的二进制序列.
由于NQRDS模型的制备过程与QRDS模型的非常相似,这里不再详细推导,仅给出一般过程. 制备过程分为2步.
第1步 设初始态为
$$\left|\psi_0\right\rangle=|0\rangle^{\otimes(q+p+l)} $$ 定义算子
$$ U_1=I^{\otimes(q+p)} \otimes H^{\otimes l} $$ 式中: I为单位门;H为Hadamard门. 则有
$$ U_1\left|\psi_0\right\rangle=\frac{1}{\sqrt{2^l}} \sum\limits_{t=0}^{2^{l-1}}|0\rangle^{\otimes(q+p)} \otimes|t\rangle \triangleq\left|\psi_1\right\rangle $$ 第2步 对任意的t=0, 1, …, 2l-1,定义算子
$$ U_t=I^{\bigotimes(p+q)} \otimes \sum\limits_{i=0, i \neq t}^{2^l-1}|i\rangle\left\langle i\left|+\varOmega_t \otimes \varPsi_t \otimes\right| t\right\rangle\langle t| $$ 式中:
$$ \begin{aligned} & \varOmega_t=\bigotimes_{m=0}^{q-1} \varOmega_t^m, \varOmega_t^m:|0\rangle \rightarrow\left|0 \oplus I_t^m\right\rangle \\ & \varPsi_t=\bigotimes_{n=1}^p \varPsi_t^n, \varPsi_t^n:|0\rangle \rightarrow\left|0 \oplus D_t^n\right\rangle \end{aligned} $$ 其中$ \oplus $表示模2加法. 再定义算子
$$ U_2=\prod\limits_{t=0}^{2^l-1} U_t $$ 则有
$$ U_2\left|\psi_1\right\rangle=\frac{1}{\sqrt{2^l}} \sum\limits_{t=0}^{2^l-1}\left|I_t^0 I_t^1 \cdots I_t^{q-1}\right\rangle\left|D_t^1 D_t^2 \cdots D_t^p\right\rangle \otimes|t\rangle $$ 因此,复合酉变换U2U1把初始态演变为NQRDS态.
在制备过程的第1步,用到了(q+p)个单位门和l个Hadamard门. 在第2步中,U2由2l个子算子Ut复合而成,而每个Ut的复杂度为O(pl). 因此制备过程第2步的复杂度为O[(ql+pl)2l]. 综上可知,整个制备过程的复杂度为O[(ql+pl)2l].
下面针对振幅值的编码方法进行讨论.
编码规则如下: 正整数的编码为其整数部分的原码和小数部分(约定为0)的原码两部分; 正分数的编码为其正整数部分的原码和正分数部分的原码两部分; 负整数的编码为其负整数部分的二补码和负小数部分(约定为0)的原码两部分; 负分数的编码为其负整数部分的二补码和负小数部分的二补码两部分. 表 1给出了q=p=3时的编码实例.
表 1 NQRDS模型中二补码编码案例Table 1. Encoding examples of 2' complement in NQRDS真值 1.25 -0.75 -1.00 符号 0 1 1 整数的原码 1 0 1 分数的原码 10 110 0 整数的二补码 1 0 11 分数的二补码 10 10 0 新QRDS表示 0,01.010 1,00.010 1,11.000 从NQRDS模型可以看出,需要l个量子比特存储时间信息,q个量子比特存储振幅值的整数部分信息,p个量子比特存储振幅值的分数部分信息,因此该模型共需要(l+q+p)个量子比特存储长度为2l的时间信号. 新模型存储振幅值整数部分的范围为
$$ \left(-2^{q-2}, 2^{q-2}-1\right) $$ 相应地,分数部分的范围为
$$ \left(-2^{-1}-2^{-2}-\cdots-2^{-p}, 2^{-1}+2^{-2}+\cdots+2^{-p}\right) $$ 如果振幅的取值不在该范围内,则需要做近似处理. 仍以q=p=3为例,则有
$$\begin{aligned} & |0.53\rangle \approx|0, 00\rangle|100\rangle \\ & |0.70\rangle \approx|0, 00\rangle|110\rangle \\ & |-1.7\rangle \approx|1, 11\rangle|010\rangle \\ & |-0.251\rangle \approx|1, 00\rangle|110\rangle \end{aligned} $$ 3. 量子信号的中值滤波
量子信号表示模型为量子信号处理算法提供了研究基础,本节讨论如何使用改进的QRDS模型实现量子信号滤波,目的是去除原始量子信号中的噪声及其影响,同时将失真度控制在尽可能小的范围.
3.1 中值滤波方法
中值滤波是最常见的去除脉冲噪声的阶梯式滤波方法,中值滤波方法如下: 首先选择一个奇数大小的窗口; 其次将该窗口在信号的所有样本中移动; 再次将窗口中的振幅值按照升序或者降序排序; 最后从中选取中间值,即中值. 本文采用长度为3的窗口,结合使用左移算子Sx-和右移算子Sx+,一次得到3个相邻样本的中值.
3.2 基本量子模块
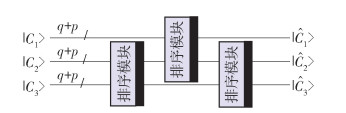
实现中值滤波的电路图分为3个部分: 循环移动模块(如Sx-和Sx+)、比较器模块、中值计算模块. 而中值计算模块由排序模块组成,排序模块包括比较器和交换运算器. 中值滤波器的整体框架如图 1所示. 为了适应新的定点小数,对运算符进行了修改.
1) 循环移动模块
为了利用相邻信息来计算相关样本的中值,需要使用循环移动变换,涉及算子Sx-和Sx+. 运用Sx-和Sx+于模型(1),则有
$$ \begin{aligned} & S_{t^{-}}:|\boldsymbol{A}\rangle \rightarrow\left|\boldsymbol{A}^{\prime}\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t=0}^{2^l-1}\left|I_t\right\rangle\left|D_t\right\rangle \otimes\left|(t-1) \bmod 2^l\right\rangle \\ & S_{t^{+}}:|\boldsymbol{A}\rangle \rightarrow\left|\boldsymbol{A}^{\prime}\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t=0}^{2^l-1}\left|I_t\right\rangle\left|D_t\right\rangle \otimes\left|(t+1) \bmod 2^l\right\rangle \end{aligned} $$ 图 2给出了Sx-和Sx+的量子电路. 从文献[19]可以看出,量子算子Sx-和Sx+可以通过使用不超过O(l2)个Toffoli门来实现,也就是说这个模块的复杂度不超过O(l2).
2) 比较器模块
当前常用的比较器是文献[18]设计的用于比较位置信息的比较器,本文把这种比较器表示为CMP.
考虑到振幅值具有正负的特殊性,本文通过对符号位和分数数值位的统一处理修改了CMP. 具体的量子电路如图 3所示.
利用比较器对机器数x和y进行比较,其中
$$ \begin{aligned} & |x\rangle=\left|I_t^0 I_t^1 \cdots I_t^{q-1}\right\rangle\left|D_t^1 D_t^2 \cdots D_t^p\right\rangle \\ & |y\rangle=\left|\hat{I}_t^0 \hat{I}_t^1 \cdots \hat{I}_t^{q-1}\right\rangle\left|\hat{D}_t^1 \hat{D}_t^2 \cdots \hat{D}_t^p\right\rangle \end{aligned} $$ 如果It0=0并且$ \hat{I}_t^0=1$,那么x>y,否则相反. 值得注意的是,当2个数值的符号相同时,x和y的绝对值将会用于参与比较过程. 所以,当2个数都是负数时,需要交换e1和e0,其中量子比特e1和e0是输出比特. 与文献[19]中的约定相同:e1e0=10表示x>y; e1e0=01表示x < y; e1e0=00表示x=y. 文献[17]指出: 一个l级控制的非门可以分解成2(l-1)个Toffoli门和一个非门,所以量子比较器的复杂度为(12l-11). 因此,该模块复杂度为O(q2+p2). 需要指出的是: 在比较器模块的实现电路中,输入信息为振幅值的原码,而文中模型给出的是振幅值的二补码. 因此,在输入环节需要把二补码转换为原码,而在输出环节又需要把原码转换为二补码. 这2个步骤都非常简单,仅仅用到了非门和加1模块,这里就不再累述.
3) 交换模块
如同它的名字所示,交换模块的功能是交换x和y这2个振幅值,其中
$$ \begin{aligned} & |x\rangle=\left|I_t^0 I_t^1 \cdots I_t^{q-1}\right\rangle\left|D_t^1 D_t^2 \cdots D_t^p\right\rangle \\ & |y\rangle=\left|\hat{I}_t^0 \hat{I}_t^1 \cdots \hat{I}_t^{q-1}\right\rangle\left|\hat{D}_t^1 \hat{D}_t^2 \cdots \hat{D}_t^p\right\rangle \end{aligned} $$ 在执行完交换模块后可以得到
$$\begin{gathered} |x\rangle|y\rangle \rightarrow\left|\hat{I}_t^0 \hat{I}_t^1 \cdots \hat{I}_t^{q-1}\right\rangle\left|\hat{D}_t^1 \cdots \hat{D}_t^p\right\rangle \\ \left|I_t^0 I_t^1 \cdots I_t^{q-1}\right\rangle\left|D_t^1 \cdots D_t^p\right\rangle \end{gathered} $$ 交换模块的量子电路如图 4所示. 从图 4中可以看到,交换模块中使用了(p+q)个交换门,每个交换门都根据文献[16]可以分解为3个受控非门,因此交换模块的复杂度为O(p+q).
4) 排序模块
该模块的功能是将2个数字按照升序排列. 首先,比较2个数字a和b,然后决定是否交换它们的顺序. 所以需要使用比较模块,如果e1e0=10(即a>b),那么需要交换a和b, 否则不需要交换. 图 5给出了排序模块的电路图. 很明显,排序模块是由比较模块和交换模块组成,所以复杂度不超过O(q2+p2).
5) 中值计算模块
中值位于排序后数字列表的“中间”. 为了方便起见,分别使用了n个左移运算算子和右移运算符算子,从而生成(2n+1)个信号,而中值位于排序列表中的第(n+1)个. 本节选取n=1,使用3个排序模块对3个数字C1、C2、C3进行排序,实现该模块的复杂度为O(q2+p2). 中值计算模块如图 6所示.
3.3 中值滤波实现电路
在中值滤波过程中,首先将原始量子信号分别向左和向右移动1个单位,生成3个量子信号. 然后中值滤波器依次对同一时间点3个量子信号中的3个振幅值进行分析.
事实上,来自3个信号相同时间点的3个振幅的中间数就是滤波后的信号相应时间点的振幅值. 信号滤波电路如图 7所示,具体的过程分为4个步骤.
步骤1 输入3个相同的信号A1、A、A2,也就是说如果ti=t,那么Iti=It,i=1, 2.
$$\left\{\begin{array}{l} \left|\boldsymbol{A}_1\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_1=0}^{2^{l-1}}\left|I_{t_1}\right\rangle\left|D_{t_1}\right\rangle\left|t_1\right\rangle \\ |\boldsymbol{A}\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t=0}^{2^l-1}\left|I_t\right\rangle\left|D_t\right\rangle|t\rangle \\ \left|\boldsymbol{A}_2\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_2=0}^{2^l-1}\left|I_{t_2}\right\rangle\left|D_{t_2}\right\rangle\left|t_2\right\rangle \end{array}\right. $$ (2) 步骤2 在|A〉不变的情况下,利用2个循环移动模块对A1和A2进行循环移动操作,得到3个信号,表示为
$$ \left\{ \begin{array}{l} \\ & S_{x^{-}}\left|\boldsymbol{A}_1\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_1=0}^{2^l-1}\left|I_{t_1}\right\rangle\left|D_{t_1}\right\rangle\left|\left(t_1-1\right) \bmod 2^l\right\rangle= \\ & \frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_1=0}^{2^l-1}\left|I_{t_1}\right\rangle\left|D_{t_1}\right\rangle\left|\hat{t}_1\right\rangle \\ & |\boldsymbol{A}\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t=0}^{2^l-1}\left|I_t\right\rangle\left|D_t\right\rangle|t\rangle \\ & S_{x^{+}}\left|\boldsymbol{A}_2\right\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_2=0}^{2^l-1}\left|I_{t_2}\right\rangle\left|D_{t_2}\right\rangle\left|\left(t_2+1\right) \bmod 2^l\right\rangle= \\ & \frac{1}{2^{\frac{l}{2}}} \sum\limits_{t_2=0}^{2^l-1}\left|I_{t_2}\right\rangle\left|D_{t_2}\right\rangle\left|\hat{t}_2\right\rangle \end{array} \right. $$ (3) 步骤3 使用2个比较器模块对时间点进行比较,找出3个信号中时间相同的振幅. 此时,如$ \hat{t}_1=t=\hat{t}_2$,那么有
$$ \left|I_{t_1}\right\rangle\left|D_{t_1}\right\rangle=\left|I_t\right\rangle\left|D_t\right\rangle=\left|I_{t_2}\right\rangle\left|D_{t_2}\right\rangle $$ 如果比较结果是e1e0=00,则x=y,此时使用2个空心点来控制整个电路.
步骤4 使用中值计算模块来获得3个时间相同的信号振幅值的中值,记为$\left|\hat{I}_t\right\rangle\left|\hat{D}_t\right\rangle $,从而得到中值滤波信号为
$$ |\hat{\boldsymbol{A}}\rangle=\frac{1}{2^{\frac{l}{2}}} \sum\limits_{t=0}^{2-1}\left|\hat{I}_t\right\rangle\left|\hat{D}_t\right\rangle|t\rangle $$ 接下来讨论滤波电路图 7的复杂度. 电路中一共使用了2个循环移动模块、2个比较器模块和1个中值计算模块. 如果不考虑量子信号的制备过程,那么完整的中值滤波电路的复杂度为O(4l2+3q2+3p2).
3.4 实例分析
由NQRDS模型可以看出:该模型表示的数据是等间隔采样的,采样长度为Δ,采样长度单位可以是时间单位(如时间信号数据),也可以空间单位(如二维图像降维后的一维数据); 样本值的单位可以为振幅值,也可以为图像的灰度值等. 因此为方便起见,下文中规定Δ=1,忽略长度单位和样本值单位. 下面通过实例说明中值滤波的具体处理过程. 给定数字信号
$$ \boldsymbol{S}=[0, -0.25, -1.70, -1.00, -0.25, 0.53, 0.70, 0.85] $$ 这里一共有8个样本点,即L=8,因此l=3. 根据改进的QRDS模型,取p=q=3,该量子信号可以近似表示为
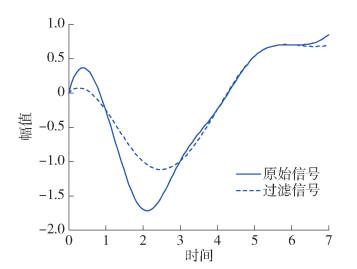
$$\begin{aligned} |\boldsymbol{A}\rangle= & \frac{1}{\sqrt{2^3}}(|000\rangle|000\rangle|000\rangle+|100\rangle|110\rangle|001\rangle+ \\ & |111\rangle|010\rangle|010\rangle+|100\rangle|000\rangle|011\rangle+ \\ & |100\rangle|110\rangle|100\rangle+|000\rangle|100\rangle|101\rangle+ \\ & |000\rangle|110\rangle|110\rangle+|000\rangle|111\rangle|111\rangle) \end{aligned} $$ 表 2给出了中值滤波的处理过程. 从图 8中可以直观地看出,中值滤波可以在去除脉冲峰值的同时保持信号的原始趋势.
表 2 中值滤波的过程Table 2. Process of median filtering原始信号 0.00 -0.25 -1.70 -1.00 -0.25 0.53 0.70 0.85 执行Sx-后的信号 0.85 0.00 -0.25 -1.70 -1.00 -0.25 0.53 0.70 执行Sx+后的信号 -0.25 -1.70 -1.00 -0.25 0.53 0.70 0.85 0.00 滤波后的振幅中值 0.00 -0.25 -1.00 -1.00 -0.25 0.53 0.70 0.70 4. 结论
1) 量子数据数理中的一个重要任务是数据的量子态表示,不同的表示方法对后期的处理结果有着十分显著的影响. 本文基于QRDS模型,提出了改进的NQRDS模型. 不但克服了现存其他相关模型只能表示数据整数部分的缺点,同时还解决了QRDS模型把数据整数和小数部分编码为二补码时与经典二补码编码的差异问题. 文中基于这种量子信号表示模型,引入了量子中值滤波方法,并给出了实现该类滤波方法的量子电路.
2) 在未来的研究工作中,可以向以下方向拓展: 其一,展开基于该类量子信号表示模型的一系列变换域研究,如量子傅里叶变换和小波变换;其二,由于量子信号处理还处于初期阶段,基于该模型可以进行最近邻插值、空间域滤波和自适应滤波等方面的研究.
-
表 1 NQRDS模型中二补码编码案例
Table 1 Encoding examples of 2' complement in NQRDS
真值 1.25 -0.75 -1.00 符号 0 1 1 整数的原码 1 0 1 分数的原码 10 110 0 整数的二补码 1 0 11 分数的二补码 10 10 0 新QRDS表示 0,01.010 1,00.010 1,11.000 表 2 中值滤波的过程
Table 2 Process of median filtering
原始信号 0.00 -0.25 -1.70 -1.00 -0.25 0.53 0.70 0.85 执行Sx-后的信号 0.85 0.00 -0.25 -1.70 -1.00 -0.25 0.53 0.70 执行Sx+后的信号 -0.25 -1.70 -1.00 -0.25 0.53 0.70 0.85 0.00 滤波后的振幅中值 0.00 -0.25 -1.00 -1.00 -0.25 0.53 0.70 0.70 -
[1] FEYNMAN R P. Simulating physics with computers[J]. International Journal of Theoretical Physics, 1982, 21(6/7): 467-488. doi: 10.5555/304763.305688
[2] SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring[C]//Proceedings 35th Annual Symposium on Foundations of Computer Science. Piscataway: IEEE, 1994: 124-134.
[3] GROVER L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the 28th Annual ACM Symposium on the Theory of Computing. Piscataway: IEEE, 1996: 212-219.
[4] LIU W Z, ZHANG Y Z, ZHEN Y Z, at al. Toward a photonic demonstration of device-independent quantum key distribution[J]. Physical Review Letters, 2022, 129: 5-29.
[5] DONG H, LU D Y, LI C. A novel qutrit representation of quantum image[J]. Quantum Information Processing, 2022, 21: 108. doi: 10.1007/s11128-022-03450-8
[6] LI C, LU D Y, DONG H. Quantum representations and scaling up algorithms of adaptive sampled-data in log-polar coordinates[J]. Entropy, 2021, 23: 1462. doi: 10.3390/e23111462
[7] JIANG N, JI Z X, LI H, at al. Quantum image interest point extraction[J]. Modern Physics Letters A, 2021, 36(9): 2150063. doi: 10.1142/S0217732321500632
[8] 王兵, 郝梦奇, 李盼池, 等. 量子索引图像的描述方法与隐写算法[J]. 计算机辅助设计与图形学学报, 2019, 31(11): 1995-2006. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201911014.htm WANG B, HAO M Q, LI P C, at al. Description method and steganography of quantum indexed images[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(11): 1995-2006. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201911014.htm
[9] YIN H T, LU D Y, ZHANG R. Quantum windowed Fourier transform and its application to quantum signal processing[J]. International Journal of Theoretical Physics, 2021, 60(10): 3896-3918. doi: 10.1007/s10773-021-04933-7
[10] 孙国栋, 苏盛辉, 徐茂智. 求根问题的量子计算算法[J]. 北京工业大学学报, 2015, 41(3): 366-371. doi: 10.11936/bjutxb2014040051 SUN G D, SU S H, XU M Z. Quantum mechanical algorithms for solving root finding problem[J]. Journal of Beijing University of Technology, 2015, 41(3): 366-371. (in Chinese) doi: 10.11936/bjutxb2014040051
[11] 冀俊忠, 程亮, 赵学武, 等. 量子蚁群算法求解多任务联盟问题[J]. 北京工业大学学报, 2013, 39(3): 412-419. https://journal.bjut.edu.cn/bjgydxxb/cn/article/id/7009c7b9-fb51-421c-977c-34428da7d3eb JI J Z, CHENG L, ZHAO X W, at al. Quantum ant colony algorithm for the multi-task coalition problem[J]. Journal of Beijing University of Technology, 2013, 39(3): 412-419. (in Chinese) https://journal.bjut.edu.cn/bjgydxxb/cn/article/id/7009c7b9-fb51-421c-977c-34428da7d3eb
[12] 赵娅, 郭嘉慧, 李盼池. 一种量子图像的中值滤波方案[J]. 电子与信息学报, 2021, 43(1): 204-211. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX202101026.htm ZHAO Y, GUO J H, LI P C. A median filtering scheme for quantum images[J]. Journal of Electronics & Information Technology, 2021, 43(1): 204-211. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX202101026.htm
[13] LI P C, LIU X D, XIAO H. Quantum image weighted average filtering in spatial domain[J]. International Journal of Theoretical Physics, 2017, 56(11): 1-27.
[14] LIU K, ZHANG Y, LU K, at al. Restoration for noise removal in quantum images[J]. International Journal of Theoretical Physics, 2017, 56(9): 2867-2886.
[15] WANG J. QRDA: quantum representation of digital audio[J]. International Journal of Theoretical Physics, 2016, 55: 1622-1641. doi: 10.1007%2Fs10773-015-2800-2.pdf
[16] YAN F, ILIYASU A M, GUO Y M, at al. Flexible representation and manipulation of audio signals on quantum computers[J]. Theoretical Computer Science, 2018, 752: 71-85. http://www.researchgate.net/profile/Abdullah_Iliyasu/publication/312091720_Flexible_Representation_and_Manipulation_of_Audio_Signals_on_Quantum_Computers/links/58a9798c4585150402fc058c/Flexible-Representation-and-Manipulation-of-Audio-Signals-on-Quantum-Computers.pdf
[17] LI P C, WANG B, XIAO H, at al. Quantum representation and basic operations of digital signals[J]. Theoretical Computer Science, 2018, 57(10): 3242-3270. http://www.onacademic.com/detail/journal_1000040417705410_ffd5.html
[18] ZHANG Y, LU K, GAO Y H, et al. NEQR: a novel enhanced quantum representation of digital images[J]. Quantum Information Process, 2013, 12(12): 2833-2860. doi: 10.1007%2Fs11128-013-0567-z.pdf
[19] NIELSEN M A, CHUANG I L. Quantum computation and quantum information[M]. New York: Cambridge University Press, 2000: 188-200.



 下载:
下载: