Predictive Control of Alumina Concentration Based on Recursive Subspace
-
摘要: 为实现氧化铝浓度精确控制,基于子空间辨识及模型预测控制技术,提出一种递推子空间氧化铝浓度自适应预测控制方法. 首先,采用带遗忘因子的递推子空间算法,建立氧化铝浓度的在线预测模型,自适应地根据铝电解过程工况变化准确预测氧化铝浓度;然后,应用预测控制实现氧化铝浓度的自适应控制;最后,基于某铝厂实际生产数据开展实验研究,验证所提控制方法在氧化铝浓度精确控制上的有效性和优越性.Abstract: To achieve accurate control of alumina concentration in aluminum electrolysis process, an adaptively predictive control method of recursive subspace for alumina concentration was proposed based on subspace identification and model predictive control technology. First, the recursive subspace algorithm with forgetting factor was used to establish an online prediction model of alumina concentration, which could adaptively predict the alumina concentration according to the change of working conditions. Then, the established model was applied to predictive control to achieve adaptive control of alumina concentration. Finally, based on the actual production data of an aluminum plant, experimental research was carried out to verify the effectiveness and superiority of the proposed control method for precise control of alumina concentration.
-
铝电解工业是具有战略意义的国民经济支撑性产业. 我国铝产量约占全球总产量的35%,但与国外铝工业强国相比,我国铝电解行业生产、过程控制水平相对落后,能源消耗过大,生态环境污染比较严重,急需向高效化、智能化、绿色化方向发展[1].
氧化铝浓度是铝电解过程核心参数,对工艺性能及生产安全至关重要. 大量实验发现,铝电解槽中氧化铝质量分数应控制在1.5%~3.5%的窄区间内,否则容易发生阳极效应、漏槽、电解液外溅、滚铝等常见事故[2]. 铝电解过程高温、强磁、强腐蚀、强耦合的复杂现场环境和槽内复杂的物理反应和化学反应,使得氧化铝浓度这一关键参数难以实现在线实时测量、建立其精确的机理模型和实现基于模型的控制[3-4]. 近年来,国内外学者针对基于数据驱动的氧化铝浓度建模与控制问题做了大量研究工作,如基于阳极电压、阳极电流的核极限学习机(kernel extreme learning machine,KELM)的氧化铝浓度在线软测量方法[5]、基于工业过程关键绩效指标(key performance indicator,KPI)的氧化铝浓度软传感器[6]、基于深度信念网络(deep belief network,DBN)的氧化铝浓度软测量模型[7]、基于最小二乘支持向量机(least squares support vector machines, LS-SVM)的氧化铝浓度预测模型[8]、基于粒子群优化(particle swarm optimization, PSO)的LS-SVM氧化铝浓度快速预测方法[9]. 除此之外,还有基于模糊控制[10-12]、神经网络控制[13]、模糊神经网络控制[14]及其各种改进方法的氧化铝浓度预测及控制方法[15-16]. 这些研究虽然实现了氧化铝浓度的自适应控制,但非常依赖专家知识和历史经验. 同时,基于智能算法的氧化铝浓度模型结构复杂,不利于控制器的设计,更难以在现行槽控机上实现.
模型预测控制是一种基于模型的计算机控制算法,广泛应用于规模大、约束多、耦合强的复杂大系统及过程工业,但模型和参数的不确定性影响预测控制器的性能. 子空间辨识方法(subspace identification method,SIM)是20世纪90年代初提出的一种辨识方法,直接基于输入输出数据,以多步预测误差的最小化为目标,得到预测输出形式的子空间预估器模型,不仅具备了预测控制对模型的要求,而且包含了用作预测模型的特点[17-19]. 近年来,子空间预测控制在复杂工业过程得到了越来越广泛的应用[20-23]. Cui等[23]将子空间预测控制应用于大型铝电解槽分布式多点下料控制,有效解决了铝电解槽稳定生产工况下氧化铝浓度均匀分布问题. 然而,由于铝电解运行过程中存在换极、出铝等周期性工况,离线确定的子空间预测模型无法满足铝电解过程工况时变的特性. 本文针对铝电解过程中工况时变情况下氧化铝浓度的精确建模和有效控制问题,基于递推最小二乘子空间辨识方法建立氧化铝浓度在线预测模型,利用铝电解过程的最新输入输出数据在线更新模型参数,保证工况变化时氧化铝浓度预测的准确性和稳定性,然后,将所建立的氧化铝浓度模型作为预测模型,应用于氧化铝浓度预测控制,实现氧化铝浓度自适应控制. 此方法对于提高铝电解生产效率、减少成本、节约能源等方面具有重大意义.
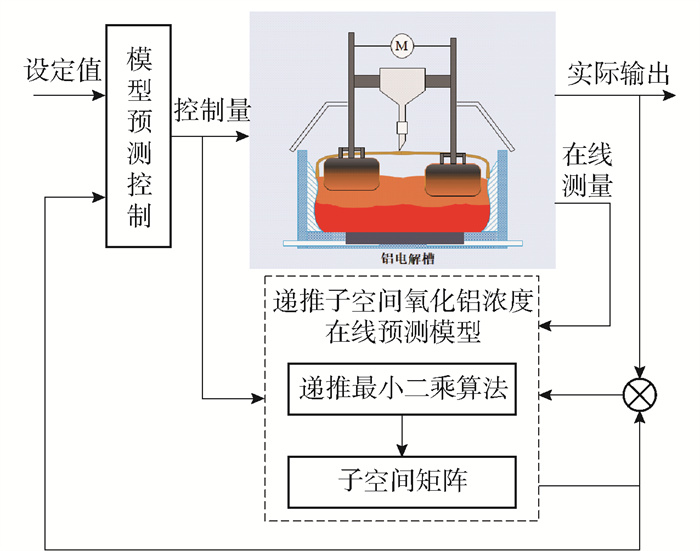
1. 铝电解过程工艺描述
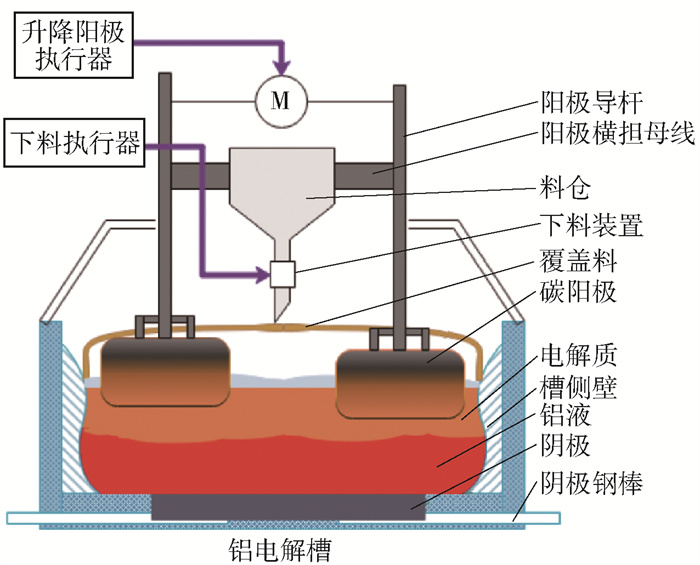
现阶段工业中普遍采用的制铝方法仍然是霍尔-埃鲁特法,即冰晶石-氧化铝熔盐电解法,预焙铝电解槽是目前铝电解生产的主流设备,单个铝电解槽的剖面简图如图 1所示.
氧化铝粉末等原料通过下料执行器添加到电解槽内的熔融电解质中,在950 ℃左右的高温环境下逐渐溶解. 在电解槽的阳极和阴极之间通入直流电,熔融的氧化铝在直流电的作用下发生电化学反应,化学方程式为
$$ \begin{array}{c} & 2 \mathrm{Al}_2 \mathrm{O}_3(\text { 熔融态 })+3 \mathrm{C}(\text { 固态 }) \stackrel{\text { 直流电 }}{=} \\ & 4 \mathrm{Al} \text { (液态 })+3 \mathrm{CO}_2 \text { (气态) } \uparrow \\ & \end{array} $$ (1) 在电解槽的阴极和阳极侧分别产生铝液和二氧化碳,铝液密度大于电解质,沉于槽底. 铝液存积到一定量时,执行出铝操作,通过真空抬包装置吸出,运送至铸造车间后进行进一步的加工处理. 电解产生的烟气通过集气送至干法净化器,分离其中的污染物,然后通过排烟风机将净化后的气体排入大气中[3].
铝电解过程物理化学反应十分复杂,是一个多相(气、液、固)-多场(电、磁、热、流、力)耦合的动态过程[1],难以建立其精确的机理模型. 基于智能算法的氧化铝浓度模型虽然具有较强的非线性拟合能力,但模型结构较为复杂,不利于控制器的设计. 铝电解过程涉及的工艺参数较多,与槽内氧化铝浓度相关的工艺参数包括电解温度、铝水平、电解质水平、电解质分子比、工作电压、氧化铝下料间隔、阳极电流等[1],这些参数之间存在较强的耦合关系,参数之间的解耦是一个难题. 另外,铝电解槽内现场环境异常复杂,受限于现有检测技术水平,铝电解过程氧化铝浓度这一关键参数难以实现在线实时测量[3-4],控制器无法及时获得氧化铝浓度反馈信息,不利于控制系统的实时调控,影响系统稳定性.
2. 氧化铝浓度自适应预测控制
基于递推子空间的氧化铝浓度建模与控制策略如图 2所示. 首先,对工业现场采集到的实际生产数据进行数据预处理;然后,采用递推子空间预估器在线建立氧化铝浓度模型;最后,将该模型应用于预测控制器设计,实现氧化铝浓度控制.
2.1 递推子空间预估器
子空间辨识算法基于系统的输入输出数据,借助简单的几何投影理论和线性代数工具,直接求解系统的状态空间模型[17]. 当子空间辨识算法与预测控制相结合时,可以推导出一种模型形式简单的输入输出模型,称之为子空间预估器.
线性时不变随机过程的状态空间表达式为
$$ \left\{\begin{array}{l} \boldsymbol{x}_{t+1}=\boldsymbol{A x}_t+\boldsymbol{B u}_t+\boldsymbol{w}_t \\ \boldsymbol{y}_t=\boldsymbol{C x}_t+\boldsymbol{D u}_t+\boldsymbol{v}_t \end{array}\right. $$ (2) 式中:ut∈Rl和yt∈Rm分别为t时刻系统的输入和输出,l、m分别为系统输入、输出的个数;xt∈Rn为t时刻系统的可测状态向量,n为系统的阶次;A∈Rn×n为系统矩阵;B∈Rn×m为输入矩阵;C∈Rl×n为输出矩阵;D∈Rl×m为直接作用矩阵;wt∈Rn和vt∈Rn分别为过程噪声和测量噪声,是不可测的高斯零均值白噪声,其协方差矩阵满足
$$ \mathrm{E}\left[\left(\begin{array}{l} \boldsymbol{w}_p \\ \boldsymbol{v}_p \end{array}\right)\left(\begin{array}{ll} \boldsymbol{w}_q^{\mathrm{T}} & \boldsymbol{v}_q^{\mathrm{T}} \end{array}\right)\right]=\left(\begin{array}{cc} \boldsymbol{Q} & \boldsymbol{S} \\ \boldsymbol{S}^{\mathrm{T}} & \boldsymbol{R} \end{array}\right) \delta_{p q} \geqslant 0 $$ (3) 式中:E为期望值算子;δpq为Kronecker算子,当p=q时,δpq=1,当p≠q时,δpq=0;Q、R分别为过程噪声和测量噪声的方差矩阵.
假设{A,B}能观测,{A,C}能控制,已经测量得到系统的输入输出数据序列为ut和yt(t∈{1, 2, …, j+M+N-1}),忽略过程噪声wt和测量噪声vt. 当输入输出数据序列足够大时,根据线性子空间预估器,系统未来输出和过去输入输出及未来输入之间的关系可表示为
$$ \boldsymbol{Y}_{\mathrm{f}}=\boldsymbol{L}_{\mathrm{w}} \boldsymbol{W}_{\mathrm{p}}+\boldsymbol{L}_{\mathrm{u}} \boldsymbol{U}_{\mathrm{f}} $$ (4) 式中:Wp=[YpT UpT]T为过去时刻输入输出矩阵;Lw和Lu为子空间模型参数矩阵,Up、Uf、Yp、Yf分别为过去时刻和未来时刻的输入、输出数据构成的Hankel矩阵. 假设预测时域为N,过去时域为M,则构建的Hankel矩阵[13]为
$$ \boldsymbol{U}_{\mathrm{p}}=\left(\begin{array}{cccc} \boldsymbol{u}_1 & \boldsymbol{u}_2 & \cdots & \boldsymbol{u}_j \\ \boldsymbol{u}_2 & \boldsymbol{u}_3 & \cdots & \boldsymbol{u}_{j+1} \\ \vdots & \vdots & & \vdots \\ \boldsymbol{u}_M & \boldsymbol{u}_{M+1} & \cdots & \boldsymbol{u}_{j+M-1} \end{array}\right) $$ (5) $$ \boldsymbol{U}_{\mathrm{f}}=\left(\begin{array}{cccc} \boldsymbol{u}_{M+1} & \boldsymbol{u}_{M+2} & \cdots & \boldsymbol{u}_{j+M} \\ \boldsymbol{u}_{M+2} & \boldsymbol{u}_{M+3} & \cdots & \boldsymbol{u}_{j+M+1} \\ \vdots & \vdots & & \vdots \\ \boldsymbol{u}_{M+N} & \boldsymbol{u}_{M+N+1} & \cdots & \boldsymbol{u}_{j+M+N-1} \end{array}\right) $$ (6) $$ \boldsymbol{Y}_{\mathrm{p}}=\left(\begin{array}{cccc} \boldsymbol{y}_1 & \boldsymbol{y}_2 & \cdots & \boldsymbol{y}_j \\ \boldsymbol{y}_2 & \boldsymbol{y}_3 & \cdots & \boldsymbol{y}_{j+1} \\ \vdots & \vdots & & \vdots \\ \boldsymbol{y}_M & \boldsymbol{y}_{M+1} & \cdots & \boldsymbol{y}_{j+M-1} \end{array}\right) $$ (7) $$ \boldsymbol{Y}_{\mathrm{f}}=\left(\begin{array}{cccc} \boldsymbol{y}_{M+1} & \boldsymbol{y}_{M+2} & \cdots & \boldsymbol{y}_{j+M} \\ \boldsymbol{y}_{M+2} & \boldsymbol{y}_{M+3} & \cdots & \boldsymbol{y}_{j+M+1} \\ \vdots & \vdots & & \vdots \\ \boldsymbol{y}_{M+N} & \boldsymbol{y}_{M+N+1} & \cdots & \boldsymbol{y}_{j+M+N-1} \end{array}\right) $$ (8) Hankel矩阵中的每一个元素均为一个列向量,参数N和M任意定义,为了降低对噪声的灵敏度,要求Hankel矩阵的列数j远远大于其行数(一般100倍),即M, N≥n, j»max (Nl, Nm, Ml, Mm).
系统未来输出Yf的最小方差预测值$\hat{\boldsymbol{Y}}_{\mathrm{f}}$可通过求解最小二乘问题
$$ \min\limits_{\boldsymbol{L}_{\mathrm{w}}, \boldsymbol{L}_{\mathrm{u}}}\left\|\boldsymbol{Y}_{\mathrm{f}}-\left(\begin{array}{ll} \boldsymbol{L}_{\mathrm{w}} & \boldsymbol{L}_{\mathrm{u}} \end{array}\right)\left(\begin{array}{l} \boldsymbol{W}_{\mathrm{p}} \\ \boldsymbol{U}_{\mathrm{f}} \end{array}\right)\right\|_{\mathrm{F}}^2 $$ (9) 得到. 式(9)的解可由Yf的行空间在Wp和Uf张成的行空间上的正交投影求得,即
$$ \hat{\boldsymbol{Y}}_{\mathrm{f}}=\boldsymbol{Y}_{\mathrm{f}} /\left(\begin{array}{l} \boldsymbol{W}_{\mathrm{p}} \\ \boldsymbol{U}_{\mathrm{f}} \end{array}\right) $$ (10) 通过正交分解可数值求解正交投影问题,公式为
$$ \left(\begin{array}{l} \boldsymbol{W}_{\mathrm{p}} \\ \boldsymbol{U}_{\mathrm{f}} \\ \boldsymbol{Y}_{\mathrm{f}} \end{array}\right)=\left(\begin{array}{ccc} \boldsymbol{R}_{11} & 0 & 0 \\ \boldsymbol{R}_{21} & \boldsymbol{R}_{22} & 0 \\ \boldsymbol{R}_{31} & \boldsymbol{R}_{32} & \boldsymbol{R}_{33} \end{array}\right)\left(\begin{array}{l} \boldsymbol{Q}_1^{\mathrm{T}} \\ \boldsymbol{Q}_2^{\mathrm{T}} \\ \boldsymbol{Q}_3^{\mathrm{T}} \end{array}\right) $$ (11) 为了简化描述,令
$$ \boldsymbol{L}=\left(\begin{array}{ll} \boldsymbol{L}_{\mathrm{w}} & \boldsymbol{L}_{\mathrm{u}} \end{array}\right)=\left(\begin{array}{ll} \boldsymbol{R}_{31} & \boldsymbol{R}_{32} \end{array}\right)\left(\begin{array}{ll} \boldsymbol{R}_{11} & 0 \\ \boldsymbol{R}_{21} & \boldsymbol{R}_{22} \end{array}\right)^{\dagger} $$ (12) 式中:†为矩阵的伪逆;L为系统输入输出子空间参数矩阵. 由分离矩阵L可得系统子空间模型参数矩阵Lw和Lu,公式分别为
$$ \begin{gathered} \boldsymbol{L}_{\mathrm{w}}=L(:, 1: M(l+m)) \\ \boldsymbol{L}_{\mathrm{u}}=L(:, M(l+m)+1: M(l+m)+N m) \end{gathered} $$ (13) 已知系统子空间模型参数矩阵Lw和Lu,以及系统k时刻之前M个输入输出数据序列和之后N个输入数据序列
$$ \left(\left(\begin{array}{c} \boldsymbol{u}_{k-M+1} \\ \boldsymbol{u}_{k-M+2} \\ \vdots \\ \boldsymbol{u}_k \end{array}\right), \left(\begin{array}{c} \boldsymbol{y}_{k-M+1} \\ \boldsymbol{y}_{k-M+2} \\ \vdots \\ \boldsymbol{y}_k \end{array}\right)\right) ;\left(\begin{array}{c} \boldsymbol{u}_{k+1} \\ \boldsymbol{u}_{k+2} \\ \vdots \\ \boldsymbol{u}_{k+N} \end{array}\right) $$ (14) 那么,由子空间预估器预测系统k时刻之后N个时域的输出可表示为
$$ \left(\begin{array}{c} \hat{\boldsymbol{y}}_{k+1} \\ \hat{\boldsymbol{y}}_{k+2} \\ \vdots \\ \hat{\boldsymbol{y}}_{k+N} \end{array}\right)=\boldsymbol{L}_{\mathrm{w}}\left(\begin{array}{c} \boldsymbol{y}_{k-M+1} \\ \vdots \\ \boldsymbol{y}_k \\ \boldsymbol{u}_{k-M+1} \\ \vdots \\ \boldsymbol{u}_k \end{array}\right)+\boldsymbol{L}_{\mathrm{u}}\left(\begin{array}{c} \boldsymbol{u}_{k+1} \\ \boldsymbol{u}_{k+2} \\ \vdots \\ \boldsymbol{u}_{k+N} \end{array}\right) $$ (15) 子空间预估器利用被控对象的一组输入输出数据序列离线求取系统的子空间模型参数Lw和Lu,无法满足铝电解过程工况时变的需求. 为了使子空间预估器适用于参数时变系统,在每个采样时刻更新输入输出向量,构造当前时刻Hankel矩阵,引入带有遗忘因子的递推最小二乘法求解子空间模型的时变参数矩阵Lw和Lu的估计值$\hat{L}_{\text {w }}$和$\hat{\boldsymbol{L}}_{\mathrm{u}}$,实现被控对象子空间模型参数在线更新. 具体求解过程为
$$ \hat{\boldsymbol{L}}_{k+1}=\hat{\boldsymbol{L}}_k+\boldsymbol{K}_{k+1}\left(\boldsymbol{y}_{k+1}^{\mathrm{T}}-\boldsymbol{x}_{k+1}^{\mathrm{T}} \hat{\boldsymbol{L}}_k\right) $$ (16) $$ \boldsymbol{K}_{k+1}=\boldsymbol{P}_k \boldsymbol{x}_{k+1}\left(\boldsymbol{\beta}+\boldsymbol{x}_{k+1}^{\mathrm{T}} \boldsymbol{P}_k \boldsymbol{x}_{k+1}\right)^{-1} $$ (17) $$ \boldsymbol{P}_{k+1}=\frac{1}{\boldsymbol{\beta}}\left(\boldsymbol{I}-\boldsymbol{K}_{k+1} \boldsymbol{x}_{k+1}^{\mathrm{T}}\right) \boldsymbol{P}_k $$ (18) 式中:$\hat{\boldsymbol{L}_k}=\left(\begin{array}{ll} \boldsymbol{L}_{\mathrm{w}} & \boldsymbol{L}_{\mathrm{u}} \end{array}\right)_k^{\mathrm{T}}$、$\hat{\boldsymbol{L}}_{k+1}=\left(\begin{array}{ll} \hat{\boldsymbol{L}}_{\mathrm{w}} & \hat{\boldsymbol{L}}_{\mathrm{u}} \end{array}\right)_{k+1}^{\mathrm{T}}$分别为k时刻和k+1时刻子空间模型参数矩阵;xk=(wpT ufT)k为k时刻的数据向量;yk+1为新的输出数据;Kk为增益矩阵;Pk为协方差矩阵;β为遗忘因子. 由此可得递推子空间预估器为
$$ \hat{\boldsymbol{y}}_{\mathrm{f}}=\hat{\boldsymbol{L}}_{\mathrm{w}} \boldsymbol{w}_{\mathrm{p}}+\hat{\boldsymbol{L}_{\mathrm{u}}} \boldsymbol{u}_{\mathrm{f}} $$ (19) 2.2 预测控制算法
模型预测控制主要解决工业过程中的输出约束以及最优问题. 模型预测控制算法主要包括预测模型、滚动优化和反馈校正三部分. 该算法基于系统的历史信息和未来输入,利用预测模型预测系统未来一定时域内的输出. 滚动优化环节反复在线进行,在每一采样时刻求解未来有限时域的开环最优控制问题,并将最优控制序列的第1个控制量作用于被控对象. 反馈校正环节检测系统的实际输出,利用这一反馈信息修正下一步的预测和优化,从而形成闭环控制.
子空间预测控制将子空间辨识和模型预测控制相结合,同时完成系统模型辨识与控制器参数设计. 模型预测控制器的目标函数为
$$ \begin{gathered} J=\sum\limits_{j=1}^{N_{\mathrm{p}}}\left(\boldsymbol{r}_{k+j}-\hat{\boldsymbol{y}}_{k+j \mid k}\right)^{\mathrm{T}} \boldsymbol{Q}\left(\boldsymbol{r}_{k+j}-\hat{\boldsymbol{y}}_{k+j \mid k}\right)+ \\ \sum\limits_{j=1}^{N_{\mathrm{e}}} \boldsymbol{u}_{k+j-1}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{u}_{k+j-1} \end{gathered} $$ (20) 式中:Np为预测时域;Nc为控制时域;rk为预测时域参考轨迹;$\hat{\boldsymbol{y}}_k$为系统的预测输出;uk为控制输入;Q∈RNpl×Npl、R∈RNcm×Ncm分别为误差权重矩阵和控制权重矩阵. 预测控制的目标就是寻找控制输入uk,使得该目标函数最小.
定义k时刻预测时域输入序列uNp、输出预测序列$\hat{\boldsymbol{y}}_{N_{\mathrm{p}}}$、跟踪轨迹rNp、控制时域输入序列uNc分别为
$$ \boldsymbol{u}_{N_{\mathrm{p}}}=\left(\begin{array}{c} \boldsymbol{u}_{k+1} \\ \boldsymbol{u}_{k+2} \\ \vdots \\ \boldsymbol{u}_{k+N_{\mathrm{p}}} \end{array}\right), \hat{\boldsymbol{y}}_{N_{\mathrm{p}}}=\left(\begin{array}{c} \hat{\boldsymbol{y}}_{k+1} \\ \hat{\boldsymbol{y}}_{k+2} \\ \vdots \\ \hat{\boldsymbol{y}}_{k+N_{\mathrm{p}}} \end{array}\right) $$ $$ \boldsymbol{r}_{N_{\mathrm{p}}}=\left(\begin{array}{c} \boldsymbol{r}_{k+1} \\ \boldsymbol{r}_{k+2} \\ \vdots \\ \boldsymbol{r}_{k+N_{\mathrm{p}}} \end{array}\right), \boldsymbol{u}_{N_{\mathrm{c}}}=\left(\begin{array}{c} \boldsymbol{u}_{k+1} \\ \boldsymbol{u}_{k+2} \\ \vdots \\ \boldsymbol{u}_{k+N_{\mathrm{c}}} \end{array}\right) $$ 由递推子空间预估器可知,$\hat{\boldsymbol{y}}_{N_{\mathrm{p}}}=\hat{\boldsymbol{L}}_{\mathrm{w}} \boldsymbol{w}_{\mathrm{p}}+\hat{\boldsymbol{L}}_{\mathrm{u}} \boldsymbol{u}_{N_{\mathrm{p}}}$,其中,$\boldsymbol{w}_{\mathrm{p}}=\left[\begin{array}{l} \boldsymbol{y}_{\mathrm{p}} \\ \boldsymbol{u}_{\mathrm{p}} \end{array}\right]$,yp、up为系统k时刻前M个输入输出数据,分别为
$$ \boldsymbol{y}_{\mathrm{p}}=\left(\begin{array}{c} \boldsymbol{y}_{k-M+1} \\ \vdots \\ \boldsymbol{y}_{k-1} \\ \boldsymbol{y}_k \end{array}\right), \boldsymbol{u}_{\mathrm{p}}=\left(\begin{array}{c} \boldsymbol{u}_{k-M+1} \\ \vdots \\ \boldsymbol{u}_{k-1} \\ \boldsymbol{u}_k \end{array}\right) $$ 代入式(20)可得
$$ \begin{gathered} J=\left(\boldsymbol{r}_{N_{\mathrm{p}}}-\hat{\boldsymbol{y}}_{N_{\mathrm{p}}}\right)^{\mathrm{T}} \boldsymbol{Q}\left(\boldsymbol{r}_{N_{\mathrm{p}}}-\hat{\boldsymbol{y}}_{N_{\mathrm{p}}}\right)+\boldsymbol{u}_{N_{\mathrm{c}}}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{u}_{N_{\mathrm{c}}}= \\ \left(\boldsymbol{r}_{N_{\mathrm{p}}}-\boldsymbol{L}_{\mathrm{w}} \boldsymbol{w}_{\mathrm{p}}-\boldsymbol{L}_{\mathrm{u}} \boldsymbol{u}_{N_{\mathrm{p}}}\right)^{\mathrm{T}} \boldsymbol{Q}\left(\boldsymbol{r}_{N_{\mathrm{p}}}-\boldsymbol{L}_{\mathrm{w}} \boldsymbol{w}_{\mathrm{p}}-\boldsymbol{L}_{\mathrm{u}} \boldsymbol{u}_{N_{\mathrm{p}}}\right)+ \\ \boldsymbol{u}_{N_{\mathrm{c}}}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{u}_{N_{\mathrm{c}}} \end{gathered} $$ (21) 最小化指标函数,可求得子空间预测控制的控制律为
$$ \boldsymbol{u}_{N_{\mathrm{c}}}=\left(\boldsymbol{R}+\boldsymbol{L}_{\mathrm{u}}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{L}_{\mathrm{u}}\right)^{-1} \boldsymbol{L}_{\mathrm{u}}^{\mathrm{T}} \boldsymbol{Q}\left(\boldsymbol{r}_{N_{\mathrm{p}}}-\boldsymbol{L}_{\mathrm{w}} \boldsymbol{w}_{\mathrm{p}}\right) $$ (22) uNc的第1项u1作为控制器的输出施加于系统.
综上所述,基于递推子空间预测控制器详细步骤如下:
1) 根据输入输出数据,按式(5)~(8)构建输入输出数据的Hankel矩阵Up、Uf、Yp、Yf.
2) 由式(11)得到子空间模型参数矩阵Lw和Lu.
3) 构建预测控制的输入向量wp,wp=(yk-M+1…yk uk-M+1…uk)T.
4) 求解控制律uNc,并将控制律uNc的第1项作用于系统;uNc=(R+LuTQLu)-1LuTQ(rNp-Lwwp).
5) 采集新的输入输出数据,根据式(16)~(18)递推更新子空间模型参数Lw和Lu.
6) 转至步骤3).
3. 实验验证
3.1 参数选取与数据采集
铝电解过程中影响氧化铝浓度变化的因素主要有下料和极距调整2个过程. 传统点式下料控制方式下料量固定,通过改变下料间隔实现下料控制,极距控制是基于槽电阻的区间控制[3]. 针对氧化铝浓度控制问题,综合分析下料和极距调整过程中参数的可控可测性,选取下料量和工作电压为子空间预估器的输入参数,氧化铝浓度为输出参数.
实验数据来源于国内某铝厂#2833铝电解槽(400 kA),工作电压、下料量通过生产现场日报数据获取,下料间隔通过现场记录获取,氧化铝浓度数据通过现场采集电解质样品并由实验室化验获取. 电解质样品具体采集流程如图 3所示.
氧化铝浓度数据基于人工采集和化验,存在部分跳变异常值,考虑采集的氧化铝浓度样本量较小且为时序数据,采用平均值修正方法对数据进行处理. 针对下料间隔与氧化铝浓度采集时间尺度不同的问题,根据氧化铝溶解机理获取氧化铝浓度溶解曲线,由溶解周期与下料间隔的关系,计算单个采样时间的氧化铝浓度,将下料间隔数据转化为连续时间内氧化铝的下料量.
实验共获得500组正常生产数据及500组更换阳极操作的数据.
3.2 子空间预估器实验分析
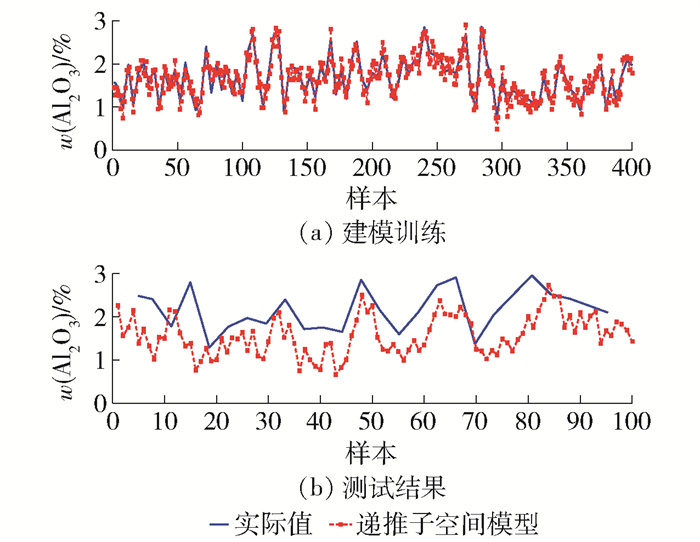
基于实验数据进行递推子空间建模实验,400组数据用于递推子空间建模训练,100组数据用于模型效果测试.
图 4描述了递推子空间预估器的建模训练和测试结果. 可以看出,建立的氧化铝浓度预测模型能有效预测氧化铝浓度的变化趋势.
通过分析递推子空间预估器训练及测试均方根误差(root mean square error,RMSE)及平均绝对误差(mean absolute error,MAE)(见表 1)可知:建立的模型在训练和测试数据上有一定的预测精度,有较小的估计误差;在氧化铝浓度预测过程中,递推子空间预估器算法具有更接近真实值的预测输出及数值更小的RMSE,因而能够更精确地描述氧化铝浓度的变化过程.
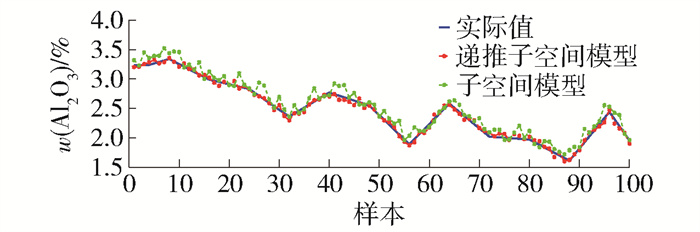
表 1 递推子空间模型预测效果分析Table 1. Prediction effect analysis of recursive subspace model数据 RMSE MAE 训练 0.014 8 0.025 4 测试 0.029 7 0.050 7 为了进一步分析递推子空间预估器的在线辨识能力,基于400组相同数据分别训练氧化铝浓度递推子空间和子空间预测模型. 然后,选用100组更换阳极操作数据进行测试,对比2种模型在工况变化下的预测精度. 实验结果如图 5和表 2所示,显然,递推子空间预估器的氧化铝质量分数预测值更接近实际值,预测精度明显优于子空间预估器. 因此,递推子空间预估器更适合工况时变的铝电解过程氧化铝浓度控制.
表 2 2种子空间模型算法的RMSE及MAE比较Table 2. Comparison of RMSE and MAE based on two algorithms of subspace models模型算法 RMSE MAE 子空间模型 0.123 7 0.100 4 递推子空间模型 0.047 1 0.041 4 3.3 控制效果实验分析
在氧化铝浓度预测控制实验中,某400 kA铝电解槽单次下料时间间隔为90 s左右,由于存在下料干扰等因素,考虑30 s的冗余,设置控制系统的预测时长为60 s,预测时域Np=12(步长为5 s). 综合考虑系统动态响应速度、稳态误差和计算复杂度,控制时域Nc=1,误差权重Q=1,控制权重R=0.2,铝电解过程是一个慢时变过程,遗忘因子β=0.95. 由于氧化铝浓度模型难以获得,实验中被控对象模型采用一组与训练数据不同的实际数据由子空间辨识建模得到.
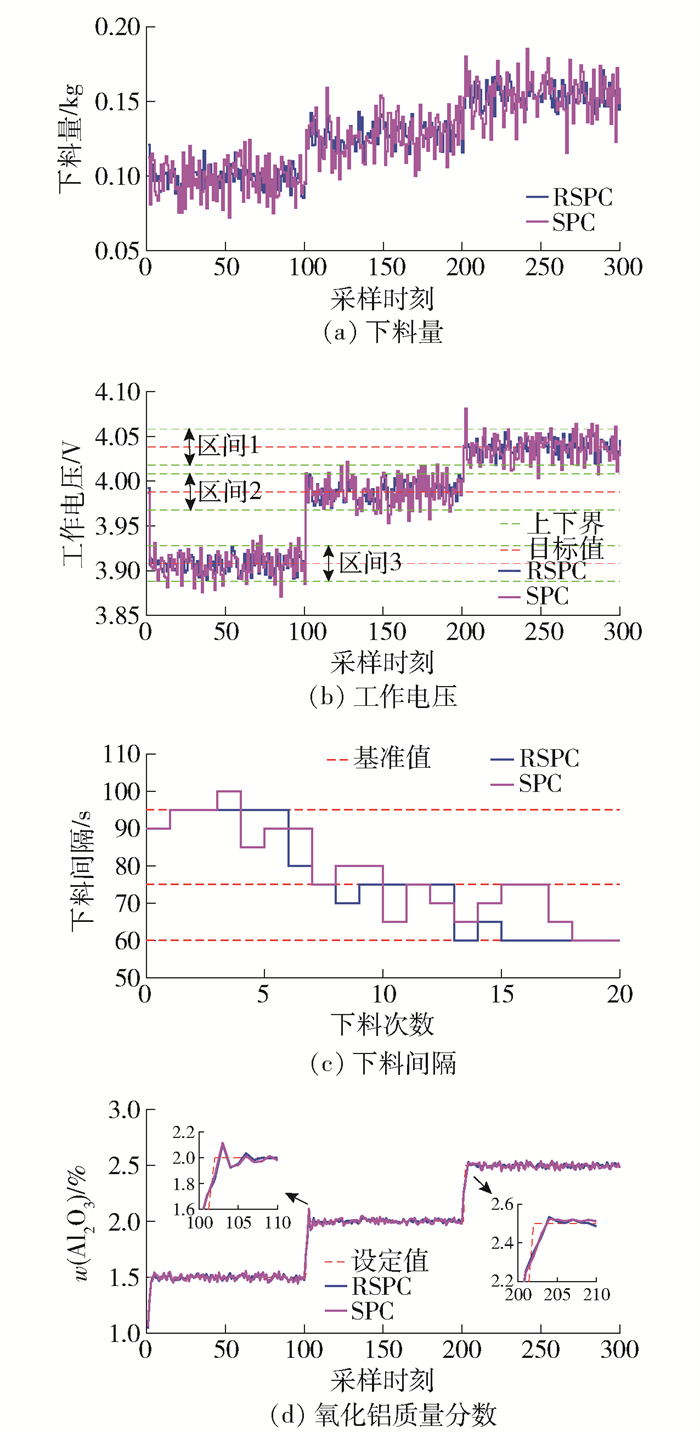
递推子空间预测控制(recursive subspace predictive control, RSPC)在每一个采样时刻,通过带有遗忘因子的递推子空间辨识算法在线更新预测模型参数,并结合预测控制实现自适应控制. 为了进一步分析递推子空间预测控制在氧化铝浓度控制的优越性,在相同工况及控制参数条件下,采用RSPC和子空间预测控制(subspace predictive control, SPC)分别进行设定值跟踪实验,并对控制效果进行对比分析,控制量和输出响应曲线如图 6所示,控制性能指标见表 3.
表 3 2种子空间模型控制效果对比Table 3. Comparison of control effects of two subspace models算法 调节时间/s 控制精度/% SPC 25 93.4 RSPC 20 96.5 图 6中(a)(b)(c)分别为下料量、工作电压及下料间隔的变化曲线,当下料量累积到单次下料量时,记为一次下料. 从图 6(a)(b)可以看出,RSPC比SPC的控制量波动更小,控制更稳定. 氧化铝质量分数跟踪效果曲线如图 6(d)所示. 从图 6(d)和表 3可以看出,在采样时刻100、200时氧化铝质量分数设定值发生阶跃变化,RSPC和SPC均能使氧化铝质量分数跟踪设定值的变化,但RSPC比SPC动态响应更快,控制精度更高. 另外,下料间隔和工作电压目标值及区间由子空间预测控制算法给出,不依赖于专家经验和知识,为实际铝电解生产中氧化铝浓度控制的下料量和极距调整提供一定的思路.
4. 结论
1) 针对铝电解过程氧化铝浓度难以进行机理建模和直接数据驱动控制问题,提出了一种基于递推子空间的氧化铝浓度预测控制方法. 实验结果表明,在铝电解过程中换极、出铝、阳极效应等工况变化时,递推子空间预测控制能够自适应地在线更新预测模型参数,提高了氧化铝浓度的精确控制,具有良好的控制性能和优良的鲁棒性.
2) 实际铝电解生产过程具有很强时变性、不确定性和复杂性,提出的递推子空间自适应预测控制方法虽然考虑了铝电解生产过程中工况变化对氧化铝浓度预测和控制的影响,但建立的模型是线性模型,如何建立便于控制器实现的氧化铝浓度非线性预测控制模型,进一步提高氧化铝浓度的控制精度,仍然是未来需要进一步研究的问题.
-
表 1 递推子空间模型预测效果分析
Table 1 Prediction effect analysis of recursive subspace model
数据 RMSE MAE 训练 0.014 8 0.025 4 测试 0.029 7 0.050 7 表 2 2种子空间模型算法的RMSE及MAE比较
Table 2 Comparison of RMSE and MAE based on two algorithms of subspace models
模型算法 RMSE MAE 子空间模型 0.123 7 0.100 4 递推子空间模型 0.047 1 0.041 4 表 3 2种子空间模型控制效果对比
Table 3 Comparison of control effects of two subspace models
算法 调节时间/s 控制精度/% SPC 25 93.4 RSPC 20 96.5 -
[1] 桂卫华, 岳伟超, 谢永芳, 等. 铝电解生产智能优化制造研究综述[J]. 自动化学报, 2018, 44(11):1957-1970. GUI W H, YUE W C, XIE Y F, et al. A review of intelligent optimal manufacturing for aluminum reduction production[J]. Acta Automatica Sinica, 2018, 44(11):1957-1970. (in Chinese) [2] 白文波. 复杂电解质体系下铝电解过程中氧化铝浓度的控制探讨[J]. 科学技术创新, 2018(36):53-54. BAI W B. Discussion on the control of alumina concentration during aluminum electrolysis under complex electrolyte system[J]. Scientific and Technological Innovation, 2018(36):53-54. (in Chinese) [3] 刘业翔, 李劼. 现代铝电解[M]. 北京:冶金工业出版社, 2020:301-453. [4] 崔家瑞, 李文浩, 苏成果, 等. 面向智能制造的大型铝电解槽分布式全要素模型研究进展[J]. 轻金属, 2021(11):30-38. CUI J R, LI W H, SU C G, et al. Research progress of distributed all-element model of large-amperage aluminum pots for intelligent manufacturing[J]. Light Metals, 2021(11):30-38. (in Chinese) [5] ZHANG S, ZHANG T, YIN Y, et al. Alumina concentration detection based on the kernel extreme learning machine[J]. Sensors, 2017, 17(9):2002.
[6] YANG X, ZHANG Y, SHARDT Y, et al. A KPI-based soft sensor development approach incorporating infrequent variable time delayed measurements[J]. IEEE Transactions on Control Systems Technology, 2020, 28(6):2523-2531.
[7] CUI J R, ZHANG N N, YANG X, et al. Soft sensing of alumina concentration in aluminum electrolysis industry based on deep belief network[C]//2020 Chinese Automation Congress. Piscataway:IEEE, 2020:1-5.
[8] 崔家瑞, 张政伟, 李擎, 等. 基于最小二乘支持向量机的氧化铝浓度预测[J]. 兵器装备工程学报, 2018, 39(12):249-253. CUI J R, ZHANG Z W, LI Q, et al. Prediction of alumina concentration based on LSSVM[J]. Journal of Ordnance Equipment Engineering, 2018, 39(12):249-253. (in Chinese) [9] 王明刚, 曹斌, 黄若愚, 等. 基于PSO优化的LS-SVM氧化铝浓度预测[J]. 轻金属, 2020(10):33-40. WANG M G, CAO B, HUANG R Y, et al. Prediction of alumina concentration based on LS-SVM with PSO optimization[J]. Light Metals, 2020(10):33-40. (in Chinese) [10] 李劼, 张文根, 丁凤其, 等. 基于在线智能辨识的模糊专家控制方法及其应用[J]. 中南大学学报(自然科学版), 2004, 35(6):911-914. LI J, ZHANG W G, DING F Q, et al. Fuzzy expert control method based on on-line intelligent identification and its application[J]. Journal of Central South University (Science and Technology), 2004, 35(6):911-914. (in Chinese) [11] 邹忠, 张红亮, 陆宏军. 铝电解过程中氧化铝浓度的控制[J]. 矿冶工程, 2004, 24(5):49-52. ZOU Z, ZHANG H L, LU H J. Control of alumina concentration in aluminum electrolysis[J]. Mining and Metallurgical Engineering, 2004, 24(5):49-52. (in Chinese) [12] 曾水平, 张秋萍, 赵国鑫. 铝电解槽氧化铝浓度的模糊控制[J]. 冶金自动化, 2001, 25(5):9-11. ZENG S P, ZHANG Q P, ZHAO G X. Fuzzy control for the alumina concentration in aluminium cells[J]. Metallurgical Industry Automation, 2001, 25(5):9-11. (in Chinese) [13] 李界家, 冯丹丹. 基于铝电解氧化铝浓度辨识的智能加料控制策略[J]. 轻金属, 2019(2):31-36. LI J J, FENG D D. Intelligent feeding control strategy based on aluminum concentration identification in aluminum electrolysis[J]. Light Metals, 2019(2):31-36. (in Chinese) [14] NAGEM N F, NETO J V D F, BRAGA C A. Pattern identification for feed control strategy using fuzzy neural algorithm[C]//2009 11th International Conference on Computer Modelling and Simulation. Piscataway:IEEE, 2009:380-385.
[15] 王佐邦, 李呈明, 贺文毅. 铝电解生产过程中氧化铝浓度的控制[J]. 有色金属设计, 2018, 45(2):101-103. WANG Z B, LI C M, HE W Y. Control of alumina concentration in aluminum electrolysis production[J]. Nonferrous Metals Design, 2018, 45(2):101-103. (in Chinese) [16] LAVOIE P, TAYLOR M P, METSON J B. A review of alumina feeding and dissolution factors in aluminum reduction cells[J]. Metallurgical and Materials Transactions B, 2016, 47(4):2690-2696.
[17] FAVOREEL W, MOOR B D, GEVERS M. SPC:subspace predictive control[C]//14th World Congress of IFAC. Amsterdam:Elsevier, 1999:4004-4009.
[18] YANG X, GAO J J, LI L L, et al. Data-driven design of fault-tolerant control systems based on recursive stable image representation[J]. Automatica, 2020, 122:109246.
[19] PATEL N, CORBETT B, MHASKAR P. Model predictive control using subspace model identification[J]. Computers and Chemical Engineering, 2021(149):107276.
[20] 李斌, 郭凤仪, 贾巍. 电炉温度的递推子空间自适应预测控制方法[J]. 中国电机工程学报, 2011, 31(增刊1):205-211. LI B, GUO F Y, JIA W. EAF temperature control method of recursive subspace adaptive predictive[J]. Proceedings of the CSEE, 2011, 31(Suppl 1):205-211. (in Chinese) [21] 宋贺达, 周平, 王宏, 等. 高炉炼铁过程多元铁水质量非线性子空间建模及应用[J]. 自动化学报, 2016, 42(11):1664-1679. SONG H D, ZHOU P, WANG H, et al. Nonlinear subspace modeling of multivariate molten iron quality in blast furnace ironmaking and its application[J]. Acta Automatica Sinica, 2016, 42(11):1664-1679. (in Chinese) [22] ZHOU P, DAI P, SONG H D. Data-driven recursive subspace identification based online modelling for prediction and control of molten iron quality in blast furnace ironmaking[J]. IET Control Theory and Applications, 2017, 11(14):2343-2351.
[23] CUI J R, WANG P N, LI X Q, et al. Multipoint feeding strategy of aluminum reduction cell based on distributed subspace predictive control[J]. Machines, 2022, 10(3):220.
-
期刊类型引用(0)
其他类型引用(5)



 下载:
下载: