Improved AES Based on Alternating Quantum Random Walk and Discrete Cosine Transform Image Encryption Algorithm
-
摘要:
随着科学技术手段飞速发展，图像加密算法被破解的风险也逐渐增加. AES(advanced encryption standard)算法虽然性能优越，但也存在着密钥固定等问题，未来量子计算机的问世将会对此造成重大威胁. 首先，该文采用离散余弦变换(discrete cosine transform, DCT)对明文图像进行DCT域的变换；其次，利用交替量子随机行走构造概率分布矩阵，对概率分布矩阵进行预处理，与DCT后的明文进行逐位异或的操作；最后，计算概率分布矩阵的奇异值，并给出对应的十六进制表达式作为AES的密钥，随机提取概率分布矩阵的一个元素，按照AES算法的编码规则构建轮常量Rcon，进而改进AES算法的加密迭代函数. 测试结果表明，该算法具有很好的加密效果和较高的鲁棒性，密文图像相邻像素在3个方向上的相关系数可以达到0.001 5的显著效果.
Abstract:With the rapid development of science and technology, the risk of image encryption algorithm being cracked is gradually increasing. Although AES (advanced encryption standard) algorithm has superior performance, it also has the problem of key fixation, which poses a major threat to the advent of quantum computers in the future. First, discrete cosine transform (DCT) was used to transform plaintext images in DCT domain. Second, the probability distribution matrix was constructed by alternating quantum random walk, and the probability distribution matrix was preprocessed to perform bit by bit XOR with the plaintext after DCT. Finally, the singular value of the probability distribution matrix was calculated, and the corresponding hexadecimal expression was given as the AES key. An element of the probability distribution matrix was randomly extracted, and the round constant Rcon was constructed according to the coding rules of the AES algorithm, thereby improving the encryption iteration function of the AES algorithm. The test results show that the algorithm has good encryption effect and high robustness, and the correlation coefficient of adjacent pixels in the ciphertext image in three directions can reach 0.001 5.
-
随着人工智能、大数据处理、量子计算等多种新兴技术手段飞速发展，在经典图像处理方面，传统图像加密研究成果丰硕[1-7]，同时也带来了一系列令人担忧的安全问题. 图像具有诸多重要信息，在网络传输过程中容易受到攻击和破坏，所以解决信息传输过程中的安全[8-9]问题尤为重要. 目前，量子信息技术成为重要发展方向，由于量子态拥有不可预测性和不可克隆性，对图像信息传输过程中的安全性、鲁棒性有进一步的加强.
随机行走的历史最早可以追溯到1828年初，植物学家罗伯特·布朗发现了液体中粒子的不规则运动. 1905年，爱因斯坦从理论上解释了这种随机运动(布朗运动)，并首次介绍了随机行走的物理过程. 从那时起，经典随机游走逐渐取得了很多重大进展. 量子随机行走(quantum walks)[10-11]作为一种新型量子计算模型近年来被提出并得到广泛应用，它具备的非线性及并行计算的双重特性使其相对于现有的混沌理论来说更具优势.
离散余弦变换(discrete cosine transform，DCT)[12-14]，是空域信号信息变换到频域信息的关键技术，避免在空域信号信息直接加密操作从而导致的加密后图像轮廓可见的非优化的状况，该变化具有良好的去相关性的优势. 此外，DCT变换将图像的原能量状态重新再调控，其分布结构发生变化. 其加密图像的像素值从图像上某个点的值，变化到某些点的能量聚集，因此具有很好的抗剪切攻击(对频域信息中某些像素点的部分能量进行剪切，提高加密方案的鲁棒性与测试速度)的能力.
1977年，美国国家标准技术局公布DES(data encryption standard)密码算法作为数据加密标准，这种对称密钥密码体制被广泛应用在政府、企业、金融等各个方面，其主要特点是发送方和接收方在加解密过程中使用的密钥必须完全相同. 由于密码学的不断优化和进步，DES的安全性和应用前景面临着非常大的挑战，为提高信息安全性，2001年，美国联邦政府又采用了AES(advanced encryption standard)，这是一种块加密标准[15-18]，AES相比DES拥有密钥长度和分组长度更为灵活、运算速度更快、对内存要求低等优点，所以AES逐渐取代了DES. 虽然AES算法具有多种优势，但存在种子密钥过于单一和密钥空间无变化等薄弱问题. 王兴刚[19]提出了一种双键算法. 在该算法中，使用的第一轮密钥与初始密钥无线性相关性，在此基础上进行密钥扩展. 该算法可以提高数据安全性，但增加了密钥管理的难度. 在文献[20]方法中，采用了2个相邻的圆键，它确保2个相邻的圆密钥不能由1个圆密钥推导，但数据安全并未得到改善. 文献[21]中提出了一种改进的算法，作为随机函数种子的一轮密钥用于生成下一轮密钥. 数据安全得到保证. 然而，这种方法效率低，难以在加密的两端同时实现.
本文提出了一种基于离散余弦变换、交替量子随机行走和改进的AES算法的图像隐私传输方案. 使用交替量子随机行走(alternate quantum walks，AQW)改进传统AES的密钥拓展函数，充分利用了AQW的混沌特性和不可预测性，结合DCT的去相关性和能量集中特性，增强了AES算法在图像加密过程中安全性和抵抗攻击的能力.
1. 相关基础
1.1 交替量子随机行走
交替量子随机行走系统使用漫步者的位置空间和硬币状态空间的直积形式来表示，$ \hat{H}_{\mathrm{w}} \otimes \hat{H}_{\mathrm{c}}$[22]. 漫步者的位置空间$ \hat{H}_{\mathrm{w}}$由位置向量$ |x, y\rangle(x, y \in \mathbb{Z})$组成. 硬币空间$ \hat{H}_{\mathrm{c}}$由硬币状态的向量|c〉(c=0, 1)线性组合组成，$ \hat{H}_{\mathrm{c}}=\cos \alpha|0\rangle+\sin \alpha|1\rangle, \alpha \in\left[0, \frac{{\rm{ \mathsf{ π}}}}{2}\right]$.
交替量子随机行走通过选择初始参数(N, T, α, θ)来控制漫步者的轨迹. 漫步者在二维直角坐标系上行走，N2为行走的总格点数，即漫步者的行走范围为D={(x, y)|－N≤x≤+N, －N≤y≤+N}(x, y∈$ \mathbb{Z}$)；T为行走的步数；α与硬币初始态有关；硬币操作符$ \hat{\boldsymbol{C}}$是关于θ的函数，硬币初始态为$ \hat{H}_{\mathrm{c}}=\cos \alpha |0>+\sin \alpha| 1>, \alpha \in\left[0, \frac{{\rm{ \mathsf{ π}}}}{2}\right]$.
$$ \hat{\boldsymbol{C}}=\left(\begin{array}{cc} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array}\right), \theta \in\left[0, \frac{{\rm{ \mathsf{ π}}}}{2}\right] $$ (1) 漫步者将在N×N个顶点上行走T步，每行走一步前，漫步者使用硬币操作符$ \hat{\boldsymbol{C}}$，作用到硬币态，根据作用后硬币的状态和位移算符$ \hat{{S}}$来执行位置操作，具体过程可由变换算子$ \hat{\boldsymbol{U}}$表示：
$$ \hat{\boldsymbol{U}}=\sum \hat{S}(\boldsymbol{I} \otimes \hat{\boldsymbol{C}}) $$ (2) 其中位移算符$ \hat{S}$表示为
$$ \begin{gathered} \hat{S}=|0\rangle\left\langle 0\left|\otimes \sum\right| x-1\right\rangle\langle x|+| 1\rangle\langle 1| \otimes \\ \sum|x+1\rangle\langle x| \end{gathered} $$ (3) 一般来说，硬币操作符$ \hat{\boldsymbol{C}}$写成$ \hat{\boldsymbol{H}}$，这时$ \theta=\frac{{\rm{ \mathsf{ π}}}}{4}$.
$$ \hat{\boldsymbol{H}}=\frac{1}{\sqrt{2}}\left(\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right) $$ (4) 整个系统经过T步后的状态|ψ〉T与系统初始状态|ψ〉0之间的演化关系为
$$ |\psi\rangle_T=(\hat{\boldsymbol{U}})^T|\psi\rangle_0 $$ (5) 变换算子$ \hat{\boldsymbol{U}}$作用到整个系统，经过T步后，测量漫步者在二维空间中位置的概率.
测量漫步者在点(x, y)处的概率计算式为
$$ \begin{gathered} P(x, y, T)=\left|\left\langle x, y, 0\left|(\hat{\boldsymbol{U}})^T\right| \psi\right\rangle_0\right|^2+ \\ \left|\left\langle x, y, 1\left|(\hat{\boldsymbol{U}})^T\right| \psi\right\rangle_0\right|^2 \end{gathered} $$ (6) 1.2 DCT
DCT是一种变换核为余弦函数的可分离的数学变换.
二维DCT正变换核为
$$ \begin{gathered} g(x, y, u, v)= \\ \frac{2}{\sqrt{M N}} C(u) C(v) \cos \frac{(2 x+1) u {\rm{ \mathsf{ π}}}}{2 M} \cos \frac{(2 y+1) v {\rm{ \mathsf{ π}}}}{2 N} \end{gathered} $$ (7) 式中：x, u=0, 1, 2, …, M－1；y, v=0, 1, 2, …, N－1.
二维DCT定义如下：
设f(x, y)为M×N的数字图像矩阵，则
$$ \begin{gathered} F(u, v)=\frac{2}{\sqrt{M N}} \sum\limits_{x=0}^{M-1} \sum\limits_{y=0}^{N-1} f(x, y) C(u) C(v) \cdot \\ \cos \frac{(2 x+1) u {\rm{ \mathsf{ π}}}}{2 M} \cos \frac{(2 y+1) v {\rm{ \mathsf{ π}}}}{2 N} \end{gathered} $$ (8) 1.3 改进AES算法
传统AES算法主要包括加密迭代过程和密钥扩展过程.
密钥长度以128位为例，通常执行10轮迭代对数据进行加密处理. 加密过程依次执行：字节替换(SubBytes)、行移位(ShiftRow)、列混合(MixColumns)、轮密钥加(AddRoundKey)，最后一轮加密处理不执行列混合变换.
AES算法的密钥扩展过程是通过扩展种子密钥来实现的，子密钥面向字节，在加密过程中对应轮密钥加操作. 通过密钥长度确定迭代步数，128位密钥需要10轮拓展过程，加上初始种子密钥，一个完整的加密过程需要11组密钥，每组密钥的长度均为128位，16个字节，密钥的总长度为176个字节. 轮常量Rcon的值如表 1所示.
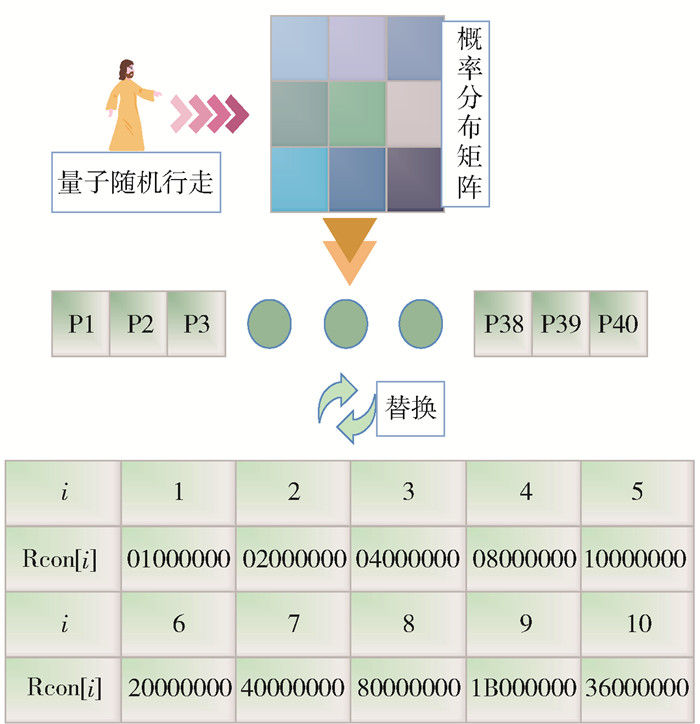
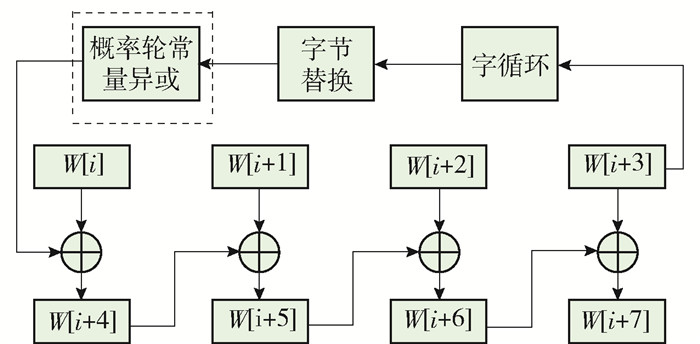
表 1 轮常量Rcon[i]值Table 1. Wheel constant Rcon[i] valuei 1 2 3 4 5 6 7 8 9 10 Rcon[i] 01 02 04 08 10 20 40 80 1B 36 该文算法对AES算法密钥拓展函数进行改进，由于轮常量Rcon固定不变，当攻击者破解出加密迭代流程时，攻击者使用定义好的轮常量Rcon，大大地增加了传统AES算法被破解的风险，该算法利用量子随机行走的混沌特性，提取预处理后概率密度分布矩阵的一个元素，将其转换为十六进制，按照RC[i]=x(RC[i－1])=x(i－1)生成新的轮常量Rcon的10个值替换原始的Rcon值. 在加密迭代过程中将会直接影响到每轮执行轮密钥加的结果. 经过改进后，使得算法的轮常量Rcon具有量子随机行走的混沌特性，加密方法更加灵活高效，如图 1所示. 在密钥拓展函数中，概率论常量异或的操作称为Pro-XOR操作，具体密钥扩展过程如图 2所示. W[i]~W[i+3]由W[i-4]~W[i-1]拓展生成，其中i∈[4, 40].
2. 加解密原理
2.1 加密算法
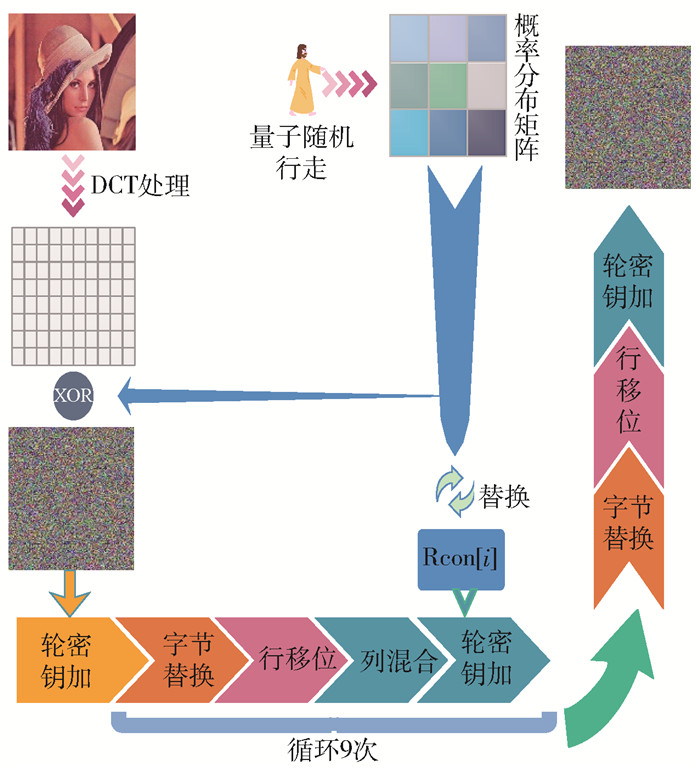
AES采用128位密钥. 具体加密算法步骤如下.
步骤1 对明文图像进行DCT变换，得到变换域(频域)的系数矩阵.
步骤2 选择初始参数(N, T, α, θ)执行交替量子随机行走，硬币的初始状态$ \hat{H}_{\mathrm{c}}=\cos \alpha|0\rangle+ \sin \alpha|1\rangle$，式中：硬币操作符$ \hat{\boldsymbol{C}}$为$ \hat{\boldsymbol{H}}$算子. 经过T步之后，通过测量得到一个具有混沌特性的概率分布矩阵P. 对矩阵进行预处理，确保提出的方法可以适应不同大小的明文图像. 该算法使用双三次插值缩放技术[23]将P转换为与明文(m×n)大小相同的P.
$$ \overline{\boldsymbol{P}}=\operatorname{cv} 2 . \operatorname{resize}(\boldsymbol{P}, (n, m)) $$ (9) 步骤3 利用等式(10)，将P里的每个元素变换为[0, 255]内的整数. 将DCT变换后的系数矩阵与概率矩阵P按位异或，完成图像的加密.
$$ \hat{\boldsymbol{P}}=\operatorname{fix}\left(P \times 10^{12}\right) \bmod 256 $$ (10) 步骤4 提取概率分布矩阵$ \hat{\boldsymbol{P}}$的奇异值，转换为相应的16进制，取其前16位作为改进AES算法的密钥部分，并提取概率分布矩阵$ \hat{\boldsymbol{P}}$的一个随机元素，按照RC[i]=x(RC[i－1])=x(i－1)将传统AES算法的轮常量Rcon替换更新.
步骤5 改进后的AES加密算法按字节替换、行变换、列混合、轮密钥加的顺序执行. 其中，列混合里矩阵元素的二元运算基于GF(28)的运算法则
$$ \begin{aligned} &\left(\begin{array}{llll} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{array}\right)\left(\begin{array}{llll} s_{0, 0} & s_{0, 1} & s_{0, 2} & s_{0, 3} \\ s_{1, 0} & s_{1, 1} & s_{1, 2} & s_{1, 3} \\ s_{2, 0} & s_{2, 1} & s_{2, 2} & s_{2, 3} \\ s_{3, 0} & s_{3, 1} & s_{3, 2} & s_{3, 3} \end{array}\right)= \\ & \;\;\;\;\;\;\;\;\;\;\;\;\left(\begin{array}{llll} s_{0, 0}^{\prime} & s_{0, 1}^{\prime} & s_{0, 2}^{\prime} & s_{0, 3}^{\prime} \\ s_{1, 0}^{\prime} & s_{1, 1}^{\prime} & s_{1, 2}^{\prime} & s_{1, 3}^{\prime} \\ s_{2, 0}^{\prime} & s_{2, 1}^{\prime} & s_{2, 2}^{\prime} & s_{2, 3}^{\prime} \\ s_{3, 0}^{\prime} & s_{3, 1}^{\prime} & s_{3, 2}^{\prime} & s_{3, 3}^{\prime} \end{array}\right) \end{aligned} $$ (11) 执行9轮迭代加密后，最后一轮加密过程按字节替换、行变换、轮密钥加的顺序进行，取消列混合.
步骤6 完成所有加密过程后，生成密文图像. 图 3为加密过程的具体流程图.
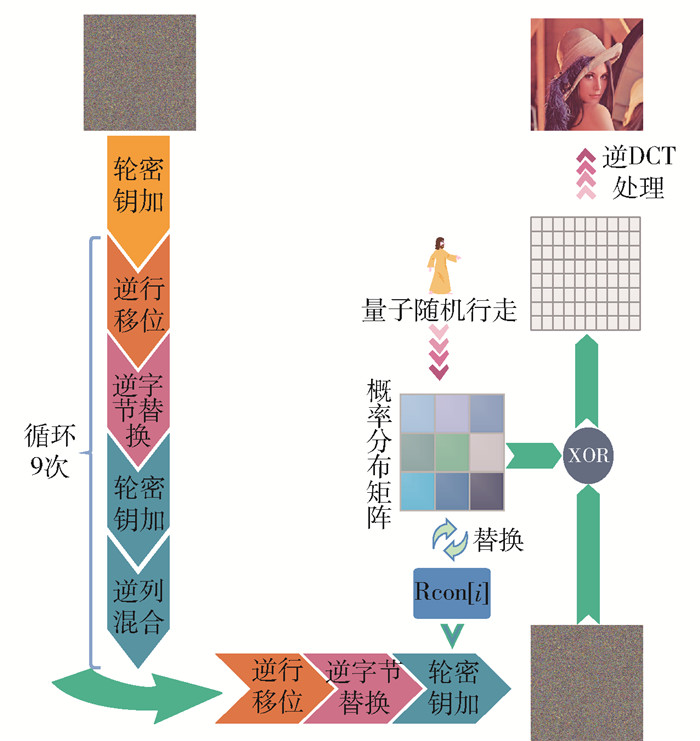
2.2 解密算法
解密算法是加密算法的逆过程. 图 4为解密过程的具体流程图.
3. 实验模拟与性能分析
该算法对(400, 400)大小的Lena、Peppers、Mandril进行安全性分析. 交替量子随机行走的初始关键参数设置为$ \left(N=400, T=500, \alpha=\frac{{\rm{ \mathsf{ π}}}}{3}, \theta=\right.\left.\frac{{\rm{ \mathsf{ π}}}}{4}\right)$. 基于分析不同像素直方图、相邻像素相关性、信息熵的数值、抵抗差分攻击、密钥空间的研究工作，从而评估提出的算法性能，并和传统AES算法性能进行比较.
3.1 加密效果
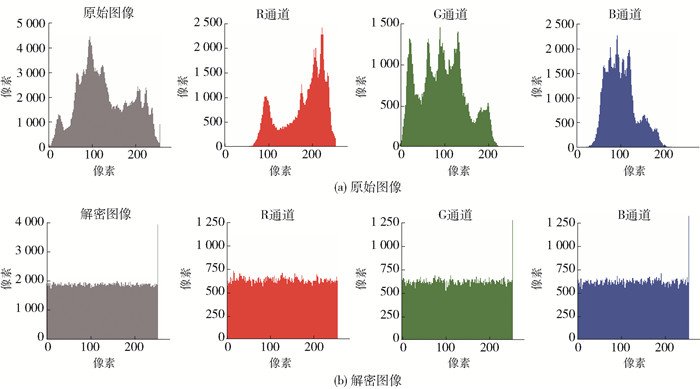
实验采用Windows系统，实验环境为Python 3.7. 使用Lena、Peppers和Mandril这3张图片来测试加密效果，并且经过图像解密后，解密图像与原始图像保持一致，如图 5所示.
3.2 直方图分析
通过对Lena密文图像进行测试，发现密文图像的直方图趋于均匀，每个像素值出现的次数大致相同，这表明本方案面对抵抗统计攻击具有良好的鲁棒性. Lena直方图分析如图 6所示.
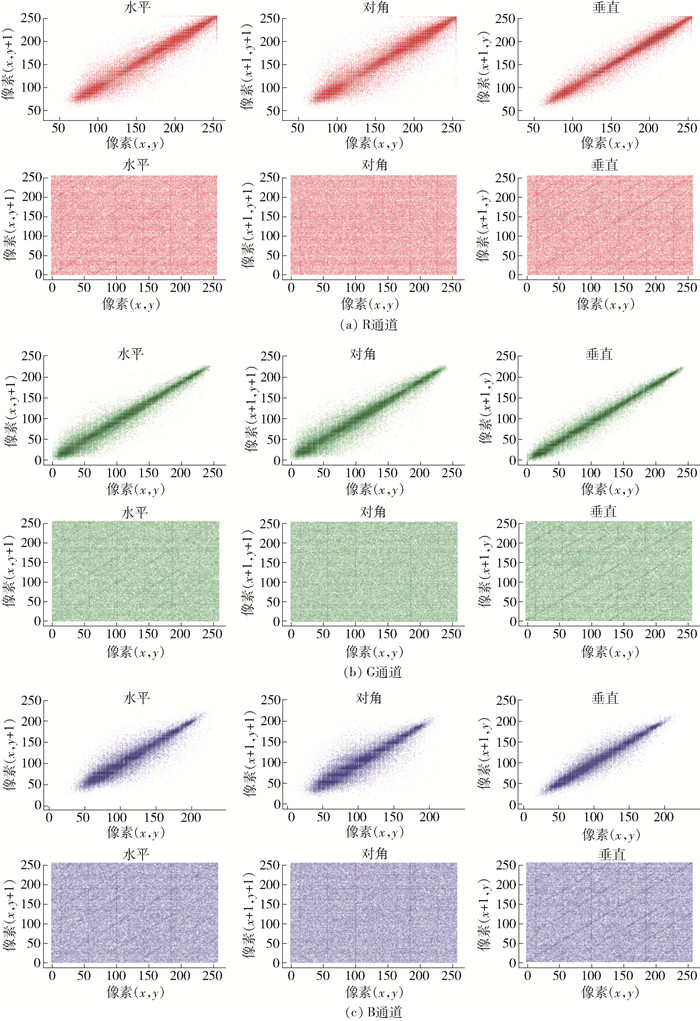
3.3 像素相关分析
在数值仿真中，对原始图像和加密图像中水平、垂直和对角线方向上相邻的像素分别计算分析，研究其相关性，统计每组数据的相关系数CAB，其对应公式为
$$ C_{A B}=\frac{\sum\limits_{n=1}^N\left(A_n-\bar{A}\right)\left(B_n-\bar{B}\right)}{\sqrt{\sum\limits_{n=1}^N\left(A_n-\bar{A}\right)^2\left(B_n-\bar{B}\right)^2}} $$ (12) 式中：An、Bn表示相邻像素的值；A、B表示平均值相邻像素的数量；N代表相邻像素对的总数.
Lena原始图像及Lena加密图像的相邻像素之间的相关性通过分析图 7可知，其在3个方向上的相关系数计算结果均接近于0，相邻像素相关性低，攻击者无法通过一个像素点推理预测相邻像素的灰度值. 具体相邻像素相关系数如表 2所示.
![]()
图 7 Lena的原始图像和加密图像相邻像素的相关分析Figure 7. Correlation analysis of adjacent pixels in original and encrypted images of Lena表 2 相邻像素相关系数Table 2. Adjacent pixel correlation coefficient图像 水平 垂直 对角 Lena-R 0.001 9 -0.001 5 0.000 1 Lena-G -0.000 6 -0.000 4 -0.000 1 Lena-B 0.002 5 -0.003 8 -0.002 3 Peppers-R -0.002 1 -0.001 40 0.000 090 Peppers-G 0.001 1 0.000 2 0.000 7 Peppers-B -0.000 04 -0.002 00 0.000 50 Mandril-R -0.001 2 0.001 7 -0.001 9 Mandril-G -0.003 1 0.000 6 0.001 2 Mandril-B 0.006 4 -0.000 2 -0.000 2 文献[16]-R 0.012 4 0.000 1 0.005 5 文献[16]-G 0.003 8 0.005 9 0.008 6 文献[16]-B 0.007 5 0.006 2 0.000 6 文献[17]-R 0.007 3 0.001 0 0.001 3 文献[17]-G 0.001 1 0.002 0 0.007 8 文献[17]-B 0.006 1 0.005 8 0.000 3 文献[18]-R 0.013 7 0.023 7 0.010 9 文献[18]-G 0.024 6 0.017 0 0.013 3 文献[18]-B 0.013 7 0.002 3 0.001 3 3.4 信息熵分析
在图像加密算法中，信息熵为加密算法的安全性提供评价标准. 实验结果表明，理想的随机图像信息熵为8[16]. 计算式为
$$ H=-\sum\limits_{i=0}^{255} p(i) \log _2 p(i) $$ (13) 像素值i的概率用p(i)表示，信息熵结果如表 3所示.
表 3 信息熵Table 3. Information entropy3.5 差分攻击分析
差分攻击是破解密文图像的一种常用方法，即攻击者对原始图像数据稍做改动，通过发现密文图像与数字图像之间的联系对密文图像进行破解. 提出的方法将Lena (0, 0)位置像素值改为0，使用一组固定的密钥对修改后的图像进行加密，比较2幅加密的密文图像. 像素数变化率(number of pixel change rate，NPCR)表达式和像素统一平均变化强度(uniform average change intensity，UACI)的表达式是像素变化灵敏度的2个重要参数，其对应的理想值分别为NPCR=99.609 4%和UACI=33.463 5%. 计算公式为
$$ \mathrm{NPCR}=\frac{\sum\limits_{(i, j)} D(i, j)}{M N} \times 100 $$ (14) 式中：M和N分别为随机图像的宽度和高度；D(i, j)的定义为
$$ D(i, j)=f(x)= \begin{cases}1, & C_1(i, j) \neq C_2(i, j) \\ 0, & C_1(i, j)=C_2(i, j)\end{cases} $$ (15) 相应地，UACI可用于测量颜色分量的对比度强度的平均值. 计算公式为
$$ \mathrm{UACI}=\frac{1}{M N} \frac{\sum\left(C_1(i, j)-C_2(i, j)\right)}{255} $$ (16) 提出算法的NPCR和UACI的计算结果接近理想值. 如表 4所示，该算法具有良好的抵抗差分攻击的能力.
表 4 NPCR和UACI的计算结果Table 4. Calculation results of NPCR and UACI图像 三通道 NPCR/% UACI/% Red 99.610 6 33.350 1 Lena Green 99.610 0 33.468 3 Blue 99.593 8 33.469 6 Red 99.607 8 33.504 2 Peppers Green 99.622 3 33.463 3 Blue 99.613 6 33.460 6 Red 99.628 8 33.435 0 Mandril Green 99.616 2 33.526 8 Blue 99.616 2 33.568 4 3.6 密钥空间分析
在蛮力攻击方面，暴力攻击是其中使用率最高的方式之一，攻击者将遍历所有可能的结果，直到找到正确的安全密钥. 一种优秀的加密算法的密钥空间必须足够大. 交替量子行走的参数(N, T, α, θ)和AES密钥构成该文算法的密钥，其中AES密钥由交替量子行走参数确定. 当计算精度为10－16时，密钥空间可以达到(1016)4=1064≈2210. 目前计算机的计算能力决定当密钥空间达到2128时，该算法可以抵抗任何形式的暴力攻击. 常规的AES算法的密钥长度为128位，可知其对应的密钥空间为2128. 与之相比，量子随机行走具有更大的优势，在无法得到初始密钥的情况下，密钥序列的随机性和不可预测性使得攻击者无法获得有效信息，可以有效抵抗暴力攻击.
4. 结论
1) 本文提出基于交替量子随机行走的改进AES算法和离散余弦变换对彩色图像进行加密. 明文图像通过DCT处理，可以得到频域上的加密. 量子随机行走为AES提供了密钥，改进了AES密钥拓展函数和迭代加密函数.
2) 实验表明，与传统AES算法相比，本文提出的算法不仅增加了密钥的随机性，而且使信息隐藏的效果更好. 密文图像相邻像素在3个方向上的相关系数可以达到0.001 5，信息熵可以达到7.998 9，保证了图像信息传输的安全性.
3) 本研究为以后的研究提供了可靠的事实依据，同时证明了量子技术在图像安全领域具有巨大的潜力，量子技术的优势将应用于其他图像处理的研究领域[24-28].
-
![]()
图 7 Lena的原始图像和加密图像相邻像素的相关分析
Figure 7. Correlation analysis of adjacent pixels in original and encrypted images of Lena
表 1 轮常量Rcon[i]值
Table 1 Wheel constant Rcon[i] value
i 1 2 3 4 5 6 7 8 9 10 Rcon[i] 01 02 04 08 10 20 40 80 1B 36 
下载: 导出CSV
表 2 相邻像素相关系数
Table 2 Adjacent pixel correlation coefficient
图像 水平 垂直 对角 Lena-R 0.001 9 -0.001 5 0.000 1 Lena-G -0.000 6 -0.000 4 -0.000 1 Lena-B 0.002 5 -0.003 8 -0.002 3 Peppers-R -0.002 1 -0.001 40 0.000 090 Peppers-G 0.001 1 0.000 2 0.000 7 Peppers-B -0.000 04 -0.002 00 0.000 50 Mandril-R -0.001 2 0.001 7 -0.001 9 Mandril-G -0.003 1 0.000 6 0.001 2 Mandril-B 0.006 4 -0.000 2 -0.000 2 文献[16]-R 0.012 4 0.000 1 0.005 5 文献[16]-G 0.003 8 0.005 9 0.008 6 文献[16]-B 0.007 5 0.006 2 0.000 6 文献[17]-R 0.007 3 0.001 0 0.001 3 文献[17]-G 0.001 1 0.002 0 0.007 8 文献[17]-B 0.006 1 0.005 8 0.000 3 文献[18]-R 0.013 7 0.023 7 0.010 9 文献[18]-G 0.024 6 0.017 0 0.013 3 文献[18]-B 0.013 7 0.002 3 0.001 3
下载: 导出CSV
表 3 信息熵
Table 3 Information entropy
下载: 导出CSV
表 4 NPCR和UACI的计算结果
Table 4 Calculation results of NPCR and UACI
图像 三通道 NPCR/% UACI/% Red 99.610 6 33.350 1 Lena Green 99.610 0 33.468 3 Blue 99.593 8 33.469 6 Red 99.607 8 33.504 2 Peppers Green 99.622 3 33.463 3 Blue 99.613 6 33.460 6 Red 99.628 8 33.435 0 Mandril Green 99.616 2 33.526 8 Blue 99.616 2 33.568 4
下载: 导出CSV
-
[1] AKHSHANI A, AKHAVAN A, LIM S C, et al. An image encryption scheme based on quantum logistic map[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 4653-4661. doi: 10.1016/j.cnsns.2012.05.033
[2] WANG X, ZHAO D. Simultaneous nonlinear encryption of grayscale and color images based on phase-truncated fractional Fourier transform and optical superposition principle[J]. Applied Optics, 2013, 52(25): 6170-6178. doi: 10.1364/AO.52.006170
[3] WANG X, LIU L. Cryptanalysis of a parallel sub-image encryption method with high-dimensional chaos[J]. Nonlinear Dynamics, 2013, 73(1): 795-800. http://www.researchgate.net/profile/Xingyuan_Wang/publication/257634161_Cryptanalysis_of_a_parallel_sub-image_encryption_method_with_high-dimensional_chaos/links/554978c10cf205bce7ac3155/Cryptanalysis-of-a-parallel-sub-image-encryption-method-with-high-dimensional-chaos.pdf
[4] CHNE L, ZHAO D, GE F. Image encryption based on singular value decomposition and Arnold transform in fractional domain[J]. Optics Communications, 2013, 291: 98-103. doi: 10.1016/j.optcom.2012.10.080
[5] WU X, WANG K, WANG X, et al. Lossless chaotic color image cryptosystem based on DNA encryption and entropy[J]. Nonlinear Dynamics, 2017, 90(2): 855-875. doi: 10.1007/s11071-017-3698-4
[6] EI-ASSAD S, FARAJALLAH M. A new chaos-based image encryption system[J]. Signal Processing: Image Communication, 2016, 41: 144-157. doi: 10.1016/j.image.2015.10.004
[7] REHMAN A U, LIAO X, ASHRAF R, et al. A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2[J]. Optik, 2018, 159: 348-367. doi: 10.1016/j.ijleo.2018.01.064
[8] KUMAR P, NISHCHAL N K. Enhanced exclusive-OR and quick response code-based image encryption through incoherent illumination[J]. Applied Optics, 2019, 58(6): 1408-1412. doi: 10.1364/AO.58.001408
[9] CHEN Q, SHEN X, CHENG Y, et al. Joint-transform correlator multiple-image encryption system based on quick-response code key[J]. Current Optics and Photonics, 2019, 3(4): 320-328.
[10] VENEGAS-ANDRACA S E. Quantum walks: a comprehensive review[J]. Quantum Information Processing, 2012, 11(5): 1015-1106. doi: 10.1007/s11128-012-0432-5
[11] CHILDS A M, GOSSET D, WEBB Z. Universal computation by multiparticle quantum walk[J]. Science, 2013, 339(6121): 791-794. doi: 10.1126/science.1229957
[12] AHMED N, NATARAJAN T, RAO K R. Discrete cosine transform[J]. IEEE Transactions on Computers, 1974, 100(1): 90-93.
[13] CHEN W H, SMITH C H, FRALICK S. A fast computational algorithm for the discrete cosine transform[J]. IEEE Transactions on Communications, 1977, 25(9): 1004-1009. doi: 10.1109/TCOM.1977.1093941
[14] LI X Z, CHEN W W, WANG Y Q. Quantum image compression-encryption scheme based on quantum discrete cosine transform[J]. International Journal of Theoretical Physics, 2018, 57(9): 2904-2919. doi: 10.1007/s10773-018-3810-7
[15] SUBRAMANYAN B, CHHABRIA V M, BABU T G S. Image encryption based on AES key expansion[C]//2011 Second International Conference on Emerging Applications of Information Technology. Piscataway: IEEE, 2011: 217-220.
[16] ZHANG Q, DING Q. Digital image encryption based on advanced encryption standard (AES)[C]//2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC). Piscataway: IEEE, 2015: 1218-1221.
[17] ZEGHID M, MACHHOUT M, KHRIJI L, et al. A modified AES based algorithm for image encryption[J]. International Journal of Computer Science and Engineering, 2007, 1(1): 70-75. http://www.researchgate.net/profile/Mohsen_Machhout/publication/242784814_A_Modified_AES_Based_Algorithm_for_Image_Encryption/links/0f31752f79f4571ed7000000?ev=pub_ext_doc_dl_meta
[18] YAHYA A, ABDALLA A M, ARABNIA H, et al. An AES-based encryption algorithm with shuffling[C]//Security and Management. Amman: Al-Zaytoonah University, 2009: 113-116.
[19] 王兴刚. 基于RSA和AES的混合算法的加密芯片设计[D]. 济南: 济南大学, 2011. WANG X G. Design of encryption chip based on RSA and AES hybrid algorithm[D]. Jinan: University of Jinan, 2011. (in Chinese)
[20] YAN J, CHEN F. An improved AES key expansion algorithm[C]//2016 International Conference on Electrical, Mechanical and Industrial Engineering. Amsterdam: Atlantis Press, 2016: 113-116.
[21] YANG X D, WANG Y. New methods of AES key expansion[J]. Microelectronics & Computer, 2012, 29: 102-104. http://en.cnki.com.cn/Article_en/CJFDTOTAL-WXYJ201201025.htm
[22] RONG Z, HAO Q, BAO T, et al. Disorder and decoherence in coined quantum walks[J]. Chinese Physics B, 2013, 22(11): 110312. doi: 10.1088/1674-1056/22/11/110312
[23] FADNAVIS S. Image interpolation techniques in digital image processing: an overview[J]. International Journal of Engineering Research and Applications, 2014, 4(10): 70-73.
[24] GAO Y, XIE H, ZHANG J, et al. A novel quantum image encryption technique based on improved controlled alternated quantum walks and hyperchaotic system[J]. Physica A: Statistical Mechanics and Its Applications, 2022, 598: 127334. doi: 10.1016/j.physa.2022.127334
[25] GAN W S. Quantum image processing[M]//Quantum Acoustical Imaging. Berlin: Springer, 2022: 83-86.
[26] SU Y, WANG X. A robust visual image encryption scheme based on controlled quantum walks[J]. Physica A: Statistical Mechanics and Its Applications, 2022, 587: 126529. doi: 10.1016/j.physa.2021.126529
[27] WANG M X, YANG H M, JIANG D H, et al. A novel quantum image watermarking scheme for tamper localization and self-recovery[J]. Quantum Information Processing, 2022, 21(8): 1-30. doi: 10.1007/s11128-022-03619-1
[28] ZHOU N R, ZHANG T F, XIE X W, et al. Hybrid quantum-classical generative adversarial networks for image generation via learning discrete distribution[J]. Signal Processing: Image Communication, 2022: 116891.
-
期刊类型引用(5)
1. 卢琼. 基于自适应编码的图像密文域可逆信息隐藏. 电子设计工程. 2025(06): 178-182 . 
百度学术
2. 许航志，唐庆伟. 基于信息动态加密方法的智慧后勤服务平台构建与应用. 自动化与仪器仪表. 2024(06): 146-150 . 百度学术
3. 欧阳志强，罗荣，张静. 基于ECC公钥加密体制的监控网络安全接入协议. 电子设计工程. 2024(18): 66-70 . 百度学术
4. 杨璐，李青云. 一种基于卷积神经网络压缩感知的图像加密算法. 智能制造. 2024(05): 99-103 . 百度学术
5. 施建，王帅. 混合云网络加密数据自动去重算法优化仿真. 计算机仿真. 2024(10): 351-354 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 473
- HTML全文浏览量: 6
- PDF下载量: 29
- 被引次数: 6
