Offloading Decision Optimization in the Cloud Edge Collaborative Computing Scenario of Smart City Early Warning System
-
摘要:
针对智慧城市预警系统存在的传感器设备(sensor device, SD)的计算与存储能力不足、预警数据处理实时性差等问题, 基于边缘计算技术, 提出了云边协同的城市预警系统任务卸载模型。该模型引入了云边协同缓存策略, 并依次设计了时延模型、能耗模型和负载失衡度模型; 将任务卸载问题转化为多目标优化问题, 给出了一种基于MOEA/D算法的卸载决策方案, 并通过对比实验进行了验证。实验结果表明: 该卸载方案能够在保证总时延与总能耗较小的情况下使负载达到均衡, 并且优于其他基准方案。
Abstract:To address the problems of insufficient computing and storage capacity of sensor devices (SD) and poor real-time processing of early warning data in smart city early warning system, a task offloading model of cloud-edge collaborative urban early-warning system was proposed based on edge computing technology. The cloud-edge collaborative cache strategy was introduced, and the delay model, energy consumption model and load imbalance model were designed in turn. The task offloading problem was transformed into a multi-objective optimization problem, and an offloading decision scheme based on MOEA/D was given, which was verified by comparative experiments. Results show that this offloading scheme can achieve load balancing with less total delay and total energy consumption, and is superior to other benchmark schemes.
-
城市物联网与通信技术飞速发展，促使城市现代化水平不断提高，城市规模扩大，流动人口增多，城市所面临灾害风险的复杂性与不确定性随之增加[1-2]，科学有效地提升城市灾害风险感知与响应能力十分重要[3]。
近年来，城市中部署的安全监测预警传感器设备(sensor device，SD)数量激增，此类设备会产生海量数据，并且数据处理时延敏感性强[4-5]，但SD数据处理能力有限，通常需要将采集数据上传到云服务器进行集中处理[6]。此外，SD与云服务器之间存在数据传输距离长、网络带宽受限等不足[7-8]，无法满足现有应急预警系统数据高效实时处理的要求。边缘计算场景中的边缘服务器(edge servers, ES)靠近SD边缘，具有较强的计算存储能力[9-10]，能满足时延敏感的预警数据处理需求。另外，城市中部署了需要数据处理框架(例如：AI视频处理框架)才能完成数据处理的SD[11]，利用边缘缓存技术[12]可缓存相关数据处理框架，使数据在边缘端得到及时有效的处理。
执行数据计算卸载任务时，数据处理时效性极大影响城市灾害预警效果，此外，能耗也是城市建设需要考虑的关键问题[13]，因此，应急预警数据计算卸载过程中须考虑时延和能耗[14]。另外，为实现城市全面精准的预警监测，SD放置数量激增，ES数据处理负担变重，可能会出现某些ES过载导致设备故障、某些ES欠载导致计算资源浪费的情况，应考虑SD的计算任务在多个ES间合理分配，实现ES间均衡负载[15]，使得城市预警系统更加合理高效地进行数据处理。
综上所述，本文把ES作为SD与云服务器间的“桥梁”，考虑ES任务处理框架缓存，构建城市预警系统模型，并创建任务计算卸载时延、能耗和负载失衡度模型，应用多目标优化算法得出解决方案，满足城市应急预警数据及时处理需求，减少系统能耗，实现ES间均衡负载。
1. 城市预警系统模型
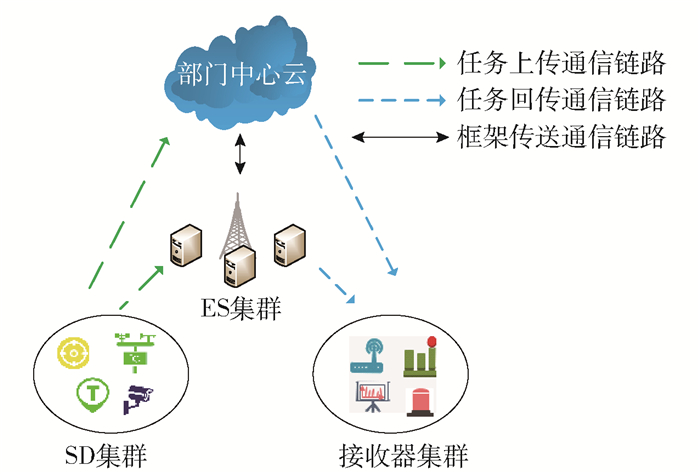
系统模型如图 1所示，共分为3层。第1层为终端设备层，包括采集、处理与上传预警数据的SD和接收来自ES层和部门云服务器层回传的预警信号的接收器设备，SD由U={u1, u2, …, ui, …, uN}表示，其中i∈{1, 2，…, N}。为了简化时延和能耗模型，本文假设SD同样充当接收器设备角色。第2层为ES层，ES由S={s1, s2, …, sj, …, sM}表示。其中：j∈{1, 2，…, M}；sj={Fjs, Cjs, Qjs}，Fjs表示sj的计算能力，Cjs表示sj的计算资源，Qjs表示sj的存储资源。在时隙Δt内，每一个SD都只产生一个待处理任务，任务表示为K={k1, k2, …, ki, …, kN}。其中：i∈{1, 2，…, N}；ki={diup, ωi, Ci, Qi}，diup表示ui上传或本地执行任务ki的数据量，ωi表示计算任务ki所需计算量，Ci表示执行任务ki所需的计算资源，Qi表示任务ki所需的存储资源。第3层为部门中心云层，云服务器由Cloud表示，可为SD提供计算卸载服务，为ES提供ki的任务处理框架。本文仅考虑Δt时刻的任务计算卸载状况。ES存储空间有限，不能缓存所有任务框架，并且ES缓存的任务处理框架需要经过较长时间才会释放，故本模型暂不考虑缓存释放。符号gij={0, 1}表示sj是否已缓存任务ki所需任务处理框架。gij=1表示sj已缓存任务ki所需任务处理框架；gij=0表示sj未缓存任务ki所需任务处理框架，需要从Cloud下载。
假设本系统仅考虑一个时隙Δt内任务计算卸载状况，在时隙Δt内每个ES和Cloud都会收到数量不等的计算任务。用xij={0, 1}表示任务ki是否卸载到sj或Cloud执行。xij=0表示任务ki在本地执行；xij=1, j∈{1, 2，…, M}，表示任务ki卸载到sj执行；xij=1, j=M+1，表示任务ki卸载到Cloud执行。
1.1 时延模型
本文主要考虑6种时延，即任务在本地的计算时延、任务卸载至ES的传输时延、任务在ES上的执行时延、Cloud下载任务处理框架至ES的任务处理框架的下载时延、任务卸载至Cloud的传输时延和Cloud回传计算结果至终端设备层的回传时延。考虑到终端设备层与ES之间的传输距离较短，并且回传至终端设备层的数据量较小，故本文不考虑ES层回传计算结果至终端设备层的回传时延。
任务ki在ui上的本地计算时延tilocal表示为
$$ t_i^{\text {local }}=\frac{\omega_i}{f_i^{\text {local }}} $$ (1) 式中filocal表示ui的计算能力。
任务ki卸载至sj的传输时延tijtran表示为
$$ t_{i j}^{\mathrm{tran}}=\frac{d_i^{\mathrm{up}}}{R_{i j}^{\mathrm{tran}}} \cdot x_{i j} $$ (2) 式中Rijtran为ui将任务ki卸载至sj的传输速率。
任务ki在sj上的计算执行时延tijs表示为
$$ t_{i j}^{\mathrm{s}}=\frac{x_{i j} g_{i j} \omega_i}{F_j^{\mathrm{s}}}+x_{i j} \cdot\left(1-g_{i j}\right) \cdot\left(\frac{\omega_i}{F_j^{\mathrm{s}}}+t_{\mathrm{Cloud}, s_j}^{\mathrm{app}}\right) $$ (3) 式中tCloud, sjapp为Cloud下载任务处理框架至sj的下载时延，表示为
$$ t_{\text {Cloud }, s_j}^{\text {app }}=\frac{d_{\text {Cloud }, s_j}^{\text {app }}}{R_{\text {Cloud }, s_j}^{\text {app }}} $$ (4) 式中：dCloud, sjapp为Cloud下载至sj的任务处理框架数据量大小; RCloud, sjapp为Cloud下载至sj的任务处理框架传输速率。本文不考虑sj向Cloud请求任务处理框架的传输时延。
任务ki卸载至Cloud的传输时延tijtran_Cloud表示为
$$ t_{i j}^{\text {tran_Cloud }}=\frac{x_{i j} d_i^{\text {up }}}{R_{i j}^{\text {tran_Cloud }}} $$ (5) 式中Rijtran_Cloud为ui将任务ki卸载至Cloud的传输速率。
Cloud将计算结果回传至ui的回传时延tjiback_Cloud表示为
$$ t_{j i}^{\text {back_Cloud }}=\frac{x_{i j} d_{j i}^{\text {back }}}{R_{j i}^{\text {back_Cloud }}} $$ (6) 式中：Rjiback_Cloud为Cloud将计算结果回传至ui的回传速率；djiback为回传数据量大小。
任务ki在Cloud上的处理时延tijCloud表示为
$$ t_{i j}^{\text {Cloud }}=\frac{x_{i j} \omega_i}{F^{\text {Cloud }}} $$ (7) 式中FCloud表示Cloud的计算能力。
最终所有任务的执行总时延Ttotal表示为
$$ \left\{\begin{array}{l} T^{\text {total }}=T^{\mathrm{ES}}+T^{\text {Cloud }}+T^{\text {local }} \\ T^{\mathrm{ES}}=\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left(t_{i j}^{\text {tran }}+t_{i j}^{\mathrm{s}}\right) \cdot x_{i j} \\ T^{\text {Cloud }}=\sum\limits_{i=1}^N \sum\limits_{j=M+1}\left(t_{i j}^{\text {tran_Cloud }}+t_{i j}^{\text {Cloud }}+t_{j i}^{\text {back_Cloud }}\right) \cdot x_{i j} \\ T^{\text {local }}=\sum\limits_{i=1}^N \sum\limits_{j=1}^{M+1} t_i^{\text {local }} \cdot\left(1-x_{i j}\right) \end{array}\right. $$ (8) 式中：TES为任务卸载到ES层的传输和计算总时延；TCloud为任务卸载到Cloud层的任务传输、计算和回传总时延。
1.2 能耗模型
任务ki在ui本地计算的能耗eilocal表示为
$$ e_i^{\text {local }}=t_i^{\text {local }} \cdot p_i^{\text {local }} $$ (9) 式中pilocal为任务ki在ui上的本地计算的能耗系数。
任务ki卸载至sj的传输能耗eijtran表示为
$$ e_{i j}^{\operatorname{tran}}=t_{i j}^{\operatorname{tran}} \cdot p_{i j}^{\operatorname{tran}} $$ (10) 式中pijtran为任务ki卸载至sj的传输能耗系数。
任务ki在sj上的执行能耗eijs表示为
$$ e_{i j}^{\mathrm{s}}=t_{i j}^{\mathrm{s}} \cdot p_{i j}^{\mathrm{s}} $$ (11) 式中pijs为任务ki在sj上的计算能耗系数。
任务ki卸载至Cloud的传输能耗eijtran_Cloud表示为
$$ e_{i j}^{\text {tran_Cloud }}=t_{i j}^{\text {tran_Cloud }} \cdot p_{i j}^{\text {tran_Cloud }} $$ (12) 式中pijtran_Cloud为任务ki卸载至Cloud的传输能耗系数。
任务ki在Cloud上的执行能耗eijCloud表示为
$$ e_{i j}^{\text {Cloud }}=t_{i j}^{\text {Cloud }} \cdot p_{i j}^{\text {Cloud }} $$ (13) 式中pijCloud为任务ki在Cloud上的计算能耗系数。
Cloud将任务计算结果回传至终端设备层的能耗ejiback_Cloud表示为
$$ e_{j i}^{\text {back_Cloud }}=t_{j i}^{\text {back_Cloud }} \cdot p_{j i}^{\text {back_Cloud }} $$ (14) 式中pjiback_Cloud为Cloud回传至终端设备层的回传能耗系数。
总能耗Etotal表示为
$$ \left\{\begin{array}{l} E^{\text {total }}=E^{\mathrm{ES}}+E^{\text {Cloud }}+E^{\text {local }} \\ E^{\mathrm{ES}}=\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left(e_{i j}^{\text {tran }}+e_{i j}^{\mathrm{s}}\right) \cdot x_{i j} \\ E^{\text {Cloud }}=\sum\limits_{i=1}^N \sum\limits_{j=M+1}\left(e_{i j}^{\text {tran_Cloud }}+e_{i j}^{\text {Cloud }}+e_{j i}^{\text {back_Cloud }}\right) \cdot x_{i j} \\ E^{\text {local }}=\sum\limits_{i=1}^N \sum\limits_{j=1}^{M+1} e_i^{\text {local }} \cdot\left(1-x_{i j}\right) \end{array}\right. $$ (15) 式中：EES为任务卸载到ES层的传输和计算总能耗；ECloud为任务卸载到Cloud层的传输、计算和回传总能耗；Elocal为任务本地计算的任务总能耗。
1.3 负载失衡度模型
本文应用负载均衡机制管理ES负载情况。sj接收到的卸载任务数量qj表示为
$$ q_j=\sum\limits_{i=1}^N x_{i j} $$ (16) 基于qj、sj的任务平均占用数量表示为
$$ A=\frac{\sum\limits_{j=1}^M q_j}{M} $$ (17) 负载失衡度可以表示为
$$ L^{\text {imblan }}=\frac{\sum\limits_{j=1}^M\left|q_j-A\right|}{M} $$ (18) 1.4 多目标优化模型
在智慧城市预警系统场景下，边缘计算卸载优化问题的优化目标是使系统总时延、总能耗、负载失衡度达到最小。该模型为三目标优化问题模型，属于多目标优化问题。建立计算卸载决策多目标优化模型，模型可表示为
$$ \begin{aligned} \min \;& T^{\text {total }}(X), \min E^{\text {total }}(X), \min L^{\text {imblan }}(X) \\ \text { s. t. }& \\ & 1 \leqslant i \leqslant N \\ & 1 \leqslant j \leqslant M+1 \\ & 0 \leqslant \sum\limits_{j=1}^{M+1} x_{i j} \leqslant 1 \\ & \sum\limits_{i=1}^N C_i \cdot x_{i j} \leqslant C_j^{\mathrm{s}} \\ & \sum\limits_{i=1}^N Q_i \cdot x_{i j} \leqslant Q_j^s \\ & \end{aligned} $$ (19) 对于约束条件的说明如下。
1) 1≤i≤N: 系统中有N个SD。
2) 1≤j≤M+1:系统中有M个ES和1个Cloud。
3) $0 \leqslant \sum\limits_{j=1}^{M+1} x_{i j} \leqslant 1 $：ui产生的任务ki最多卸载到1个ES或1个Cloud。
4) $ \sum\limits_{i=1}^N C_i \cdot x_{i j} \leqslant C_j^{\mathrm{s}}$：卸载到sj的卸载任务消耗的总计算资源小于或等于sj的计算资源上限。
5) $\sum\limits_{i=1}^N Q_i \cdot x_{i j} \leqslant Q_j^{\mathrm{s}} $：卸载到sj的卸载任务消耗的总存储资源小于或等于sj的存储资源上限。
在求解多目标组合优化问题的过程中，某一个目标函数值的优化可能伴随着其他目标函数值的劣化。这种多目标优化问题的目标之间存在相互制约关系，通常不存在一个解使得所有目标均达到最优，一般会得到一个解集，被称作Pareto最优解集。本文利用基于分解的MOEA/D算法求解多目标优化问题的优势对问题模型进行求解。
2. 利用MOEA/D算法求解卸载优化问题
MOEA/D算法将多目标问题分解为多个标量的单目标优化问题，应用均匀的权重向量和参考点能使算法所得解的多样性更佳，计算效率更高[16]。权重向量主要负责将目标空间进行划分, 种群的选择、进化、更新操作则在由多个权重向量构成的邻域中进行。权重向量确定后，多目标优化算法应用切比雪夫方法来比较进化解的优劣，指导种群进化方向。
2.1 问题编码
本文采用二进制编码和整数编码相结合方式对问题进行求解，对优化个体的约束检查和目标函数的计算均采用二进制编码方式，方便计算。对于个体进行进化操作时，采用整数编码方式。
采用二进制编码方案，个体X的编码表示为
$$ \boldsymbol{X}=\left(\begin{array}{ccc} x_{11} & \cdots & x_{1 j} \\ \vdots & & \vdots \\ x_{i 1} & \cdots & x_{i j} \end{array}\right) $$ (20) 式中xij∈X，i={1, 2, …, N}, j={1, 2, …, M+1}。xij=1分为2种情况：当j∈{1, 2，…, M}时，代表ui将任务ki卸载到sj上执行；当j=M+1时，代表ui将任务ki卸载到Cloud上执行。xij=0代表ui将任务ki在本地执行，j∈{1, 2，…, M+1}。
种群O的种群规模为H，其编码表示为
$$ O=\left\{\boldsymbol{X}^h \mid 1 \leqslant h \leqslant H\right\} $$ (21) 式中h代表种群O中第h个体X。
采用整数编码，同样种群规模为H的种群O的编码表示为
$$ O=\left\{y_i^h \mid 1 \leqslant i \leqslant N, 1 \leqslant h \leqslant H\right\} $$ (22) 式中：yih中的h表示种群中第h个个体，yih中的i表示第i个终端设备ui；yih=0表示任务ki在本地执行，当j∈{1, 2, …, M}时，yih=j，任务ki卸载到sj上执行，当j=M+1时，yih=j代表任务ki卸载到Cloud上执行。
2种编码方式的转换公式表示为
$$ y_i^h= \begin{cases}0, & \sum\limits_{j=1}^{M+1} x_{i j}=0 \\ j, & x_{i j}=1\end{cases} $$ (23) 采用二进制编码方案，编码方式表示为
$$ \boldsymbol{G}=\left(\begin{array}{ccc} g_{11} & \cdots & g_{1 j} \\ \vdots & & \vdots \\ g_{i 1} & \cdots & g_{i j} \end{array}\right) $$ (24) 式中G表示ES是否缓存任务ki的处理框架，gij∈G，i={1, 2, …, N}, j={1, 2, …, M}。如果gij=1，表示sj已缓存任务ki的处理框架；如果gij=0，表示sj未缓存任务ki的处理框架。具体分类情况如下。
1) (xij∈X, xij=0)∩(gij∈G, gij=0)表示sj未缓存任务ki的处理框架且任务ki在本地执行。
2) (xij∈X, xij=1)∩(gij∈G, gij=0)表示sj未缓存任务ki的处理框架且任务ki卸载至sj执行。
3) (xij∈X, xij=1)∩(gij∈G, gij=1)表示sj已缓存任务ki的处理框架且任务ki卸载至sj执行。
另外，以上3种情况中j∈{1, 2，…, M}，因为只讨论ES是否缓存任务处理框架。
2.2 算法流程
MOEA/D算法的流程见算法1。
算法1 MOEA/D 输入: 多目标优化问题(见式(19))；最大迭代次数gmax；子问题数量H；权重向量λ1, λ2, …, λH; 每个权重向量邻域内权重向量个数T 输出: 外部存档EP 初始化 1 外部存档EP=Ø。 2 计算2个权重向量之间的欧氏距离，然后算出每个权重向量邻域内最近的T个向量，对于每一个h=1, 2, …, H，设置B(h)=h1, h2, …, hT，λh1, λh1, …, λhT表示权重向量λh邻域内最近的T个向量。 3 随机生成初始种群O，并对种群中的每个个体Xh计算适应度。 4 初始化参考点z=(z1, z2, z3)T。 更新 5 for h=1, 2, …, H do 6 从B(h)中随机选择2个序号α、β，然后利用遗传算子对个体Xα、Xβ进行操作，产生一个新的个体Y。 7 根据约束修正个体Y，产生新个体Y′。 8 更新参考点z。 9 对于每一个j∈B(h)，应用切比雪夫法更新其邻域解。 10 更新外部存档EP。 11 终止判定。若满足终止条件则输出外部存档EP，否则转向步骤5。 3. 实验与分析
为了评价基于MOEA/D卸载决策方案的有效性，本文把系统的响应时延(总时延)、能量消耗(总能耗)和负载失衡度作为执行任务卸载的综合代价，在相同的条件下，将MOEA/D方案与基于NSGA-Ⅱ的方案、基于NSGA-Ⅲ的方案、随机卸载方案、全部本地执行方案分别从SD数量变化、ES数量变化、系统是否已部署边ES、ES有无缓存任务处理框架等方面进行对比实验。
3.1 实验参数设置
本文在内存为8 GB、CPU为2.1 GHz、安装Win10操作系统的笔记本电脑上应用Matlab2021软件进行仿真实验。
终端设备ui的计算能力filocal服从高斯分布filocal~CN(μ1, δ12)，其中均值μ1=6，方差δ12=0.5，单位GHz；任务ki卸载至sj的传输速率Rijtran服从高斯分布Rijtran~CN(μ2, δ22)，其中均值μ2=10，方差δ22=1，单位Mbit/ms；任务ki上传或本地执行的数据量diup服从高斯分布diup~CN(μ3, δ32)，其中均值μ3=10，方差δ32=3，单位Mbit；任务ki的计算量ωi服从高斯分布ωi~CN(μ4, δ42)，其中均值μ4=20，方差δ42=3；任务ki所需计算资源Ci随机分布在[100, 200]；任务ki所需存储资源Qi随机分布在[100, 300]；sj的计算能力Fjs随机分布在[40, 50]，单位GHz；Cloud下载任务处理框架至sj的任务处理框架数据量dCloudsjapp设为300，单位Mbit；Cloud下载任务处理框架至sj的框架传输速率RCloudsjapp值设为100，单位Mbit/ms；sj的计算资源Cjs服从高斯分布Cjs~CN(μ5, δ52)，均值μ5=1 500，方差δ52=115；sj的存储资源Qjs服从高斯分布Qjs~CN(μ6, δ62)，均值μ6=950，方差δ62=300；Cloud的计算能力FCloud随机分布在[200, 500]，单位GHz；任务ki卸载至Cloud的传输速率Rijtran_Cloud服从高斯分布Rijtran_Cloud~CN(μ7, δ72)，其中均值μ7=2.5，方差δ72=0.2，单位Mbit/ms；Cloud回传计算结果至ui的数据量djiback服从高斯分布djiback~CN(μ8, δ82)，其中均值μ8=5，方差δ82=1，单位Mbit；Cloud回传计算结果至ui的回传速率Rjiback_Cloud服从高斯分布Rjiback_Cloud~CN(μ9, δ92)，其中均值μ9=4，方差δ92=0.2，单位Mbit/ms。
为了公平起见，3种算法设置参数相同，其中种群规模H=105，交叉概率pc=0.9，变异概率pm=1/D，D为变量维数。
3.2 实验结果及讨论
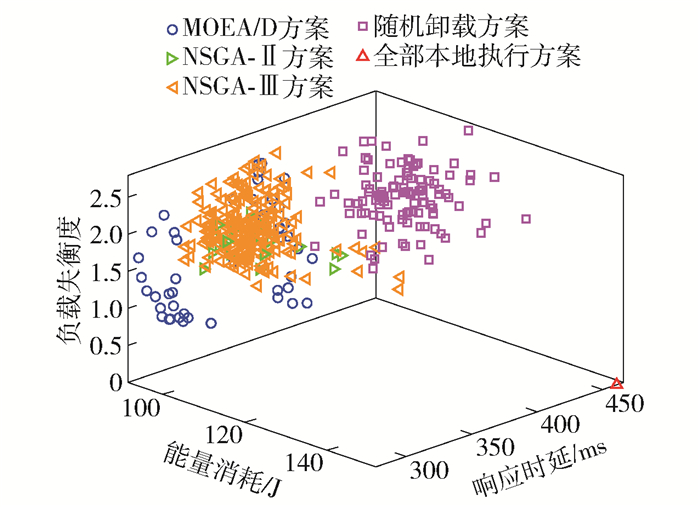
本文对各个实验进行25次独立运行，取平均效果，并且本文假设SD卸载的计算任务均需任务处理框架才能完成任务计算，云服务已缓存全部任务处理框架，SD拥有计算本设备产生的部分任务处理框架。本实验的SD数量为140个，ES数量为20个。5种方案的Pareto解集在3个约束目标上的分布情况如图 2所示。
![]()
图 2 Pareto解集在3个约束目标上的分布Figure 2. Distribution of Pareto solution set on three constrained targets从图 2可以看出：MOEA/D方案得到的解在多数情况下优于其他4种方案；NSGA-Ⅱ方案和NSGA-Ⅲ方案的效果相当；MOEA/D方案、NSGA-Ⅱ方案和NSGA-Ⅲ方案均优于随机卸载方案；MOEA/D方案、NSGA-Ⅱ方案和NSGA-Ⅲ方案在时延和能耗方面均优于全部本地执行方案。
3.3 SD数量变化对3个约束目标的影响
为研究SD数量变化对3个约束目标的影响，本实验将SD数量分别设置为100、120、140、160、180、200、220、240、260、280个，ES数量设置为20个。
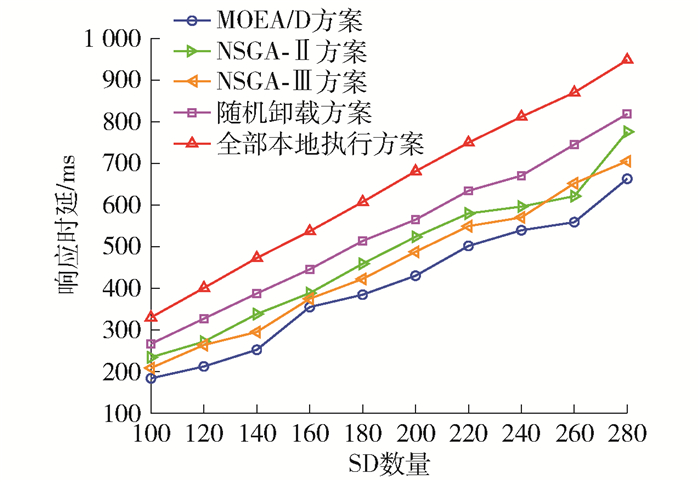
5种方案随SD数量变化对响应时延的影响如图 3所示。可以看出，随着SD数量增加，5种方案所得系统的响应时延均呈上升趋势。这是因为在ES数量不变的情况下，SD数量增加导致系统总任务量增加，需要消耗更长时间处理SD产生的计算任务，造成系统总的响应时延增大。通过对比5种卸载方案可以看出，随着SD数量增加，MOEA/D方案的响应时延均明显小于NSGA-Ⅱ方案、NSGA-Ⅲ方案、随机卸载方案、全部本地执行方案的总的响应时延。
![]()
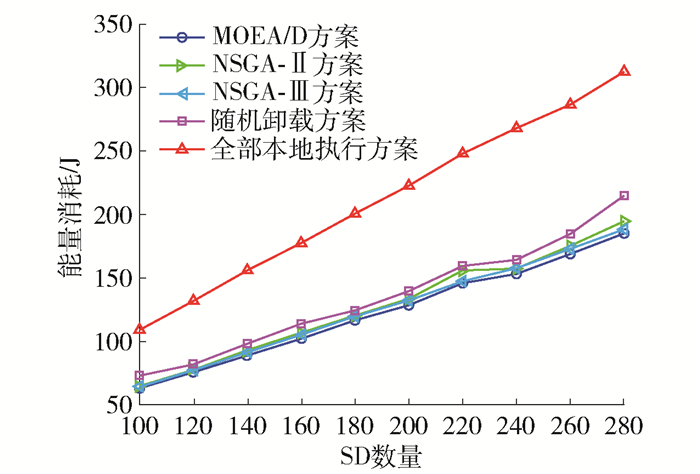
图 3 5种方案随SD数量变化对响应时延的影响Figure 3. Effect of five schemes on response delay with the number of SD5种方案随SD数量变化对能量消耗的影响如图 4所示。可以看出，随着SD数量增加，5种方案所得系统总的能量消耗呈上升趋势。这是因为在ES数量不变的情况下，SD数量增加导致了系统总任务量增加，需要消耗更多能量处理SD产生的计算任务，造成系统总的能量消耗增大。通过对比5种卸载方案可以看出，随着SD数量增加，MOEA/D方案的能量均优于NSGA-Ⅱ方案、NSGA-Ⅲ方案、随机卸载方案、全部本地执行方案的总的能量消耗。
![]()
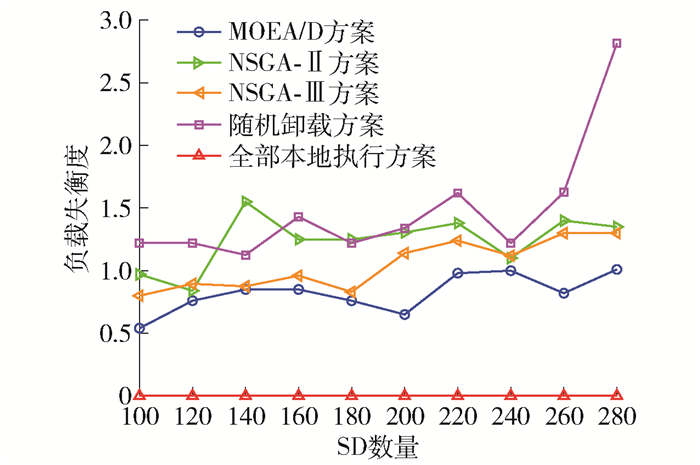
图 4 5种方案随SD数量变化对能量消耗的影响Figure 4. Effect of five schemes on energy consumption with the number of SD5种方案随SD数量变化对负载失衡度的影响如图 5所示。可以看出，随着SD数量增加，虽然5种方案的负载失衡度均无明显趋势，但MOEA/D方案的负载失衡度均优于NSGA-Ⅱ方案、NSGA-Ⅲ方案和随机卸载方案，因为全部本地执行方案不需要计算负载失衡度，所以值均为0，并且不作为对比方案。
![]()
图 5 5种方案随SD数量变化对负载失衡度的影响Figure 5. Effect of five schemes on load imbalance with the number of SD综上所述，随着SD数量的增加，MOEA/D方案均能在3个约束目标上表现最优。
3.4 ES数量变化对3个约束目标的影响
为研究ES数量变化对3个约束目标的影响，本实验将ES数量分别设置为10、12、14、16、18、20、22、24、26、28个，SD数量设置为140个。
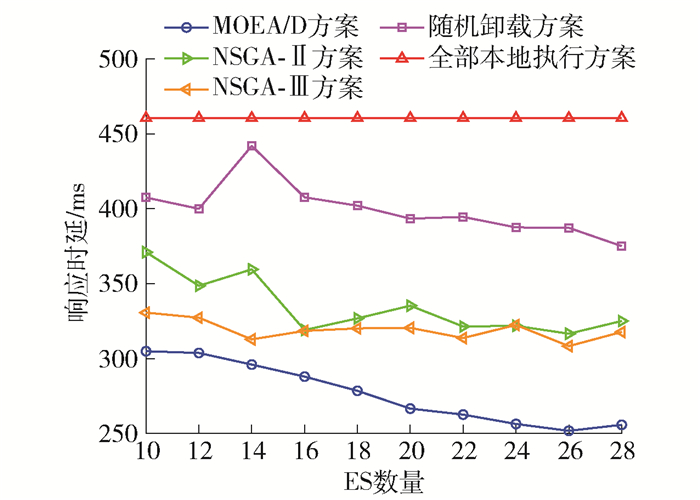
5种方案随ES数量变化对响应时延的影响如图 6所示。可以看出，随着ES数量增加，MOEA/D、NSGA-Ⅱ、NSGA-Ⅲ和随机卸载这4种方案所得系统总的响应时延总体呈下降趋势，并且MOEA/D方案的响应时延均优于其他4种方案。另外，由于SD数量固定，系统产生的总的任务计算量固定，随着ES数量变化，全部本地执行方案的响应时延保持不变。
![]()
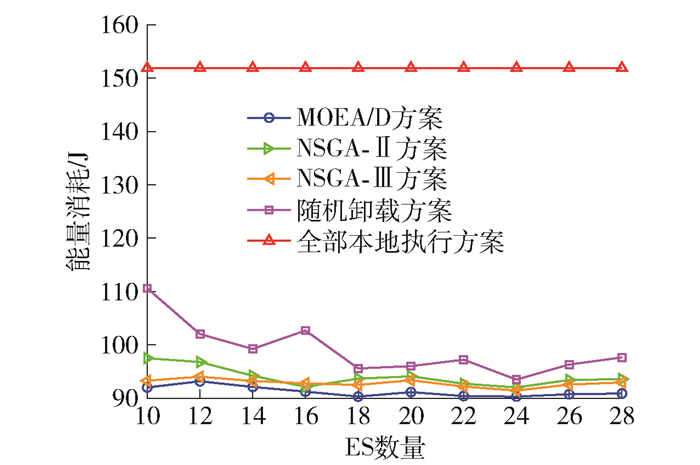
图 6 5种方案随ES数量变化对响应时延的影响Figure 6. Effect of five schemes on response delay with the number of ES5种方案随ES数量变化对能量消耗的影响如图 7所示。可以看出，随着ES数量增加，MOEA/D、NSGA-Ⅱ、NSGA-Ⅲ和全部本地卸载这4种方案所得系统总的能量消耗总体波动较小且呈现平稳趋势。随机卸载方案的能量消耗波动较大，MOEA/D方案的能量消耗均优于其他4种方案。
![]()
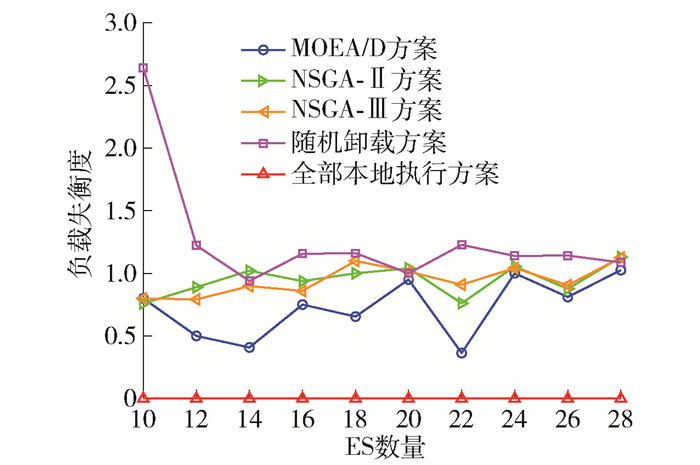
图 7 5种方案随ES数量变化对能量消耗的影响Figure 7. Effect of five schemes on energy consumption with the number of ES5种方案随ES数量变化对负载均衡度的影响如图 8所示。可以看出，随着ES数量增加，虽然5种方案的负载失衡度均无明显趋势，但MOEA/D方案的负载失衡度均优于NSGA-Ⅱ方案、NSGA-Ⅲ方案和随机卸载方案。因为全部本地执行方案不需要计算负载失衡度，所以值均为0且不作为对比方案。
![]()
图 8 5种方案随ES数量变化对负载失衡度的影响Figure 8. Effect of five schemes on load imbalance with the number of ES综上所述，随着ES数量的增加，MOEA/D方案均能在3个约束目标上表现最优。
3.5 ES有无缓存框架对响应时延的影响
为研究ES有无缓存任务处理框架对响应时延的影响，将SD数量设定为140个，ES数量设定为20个。
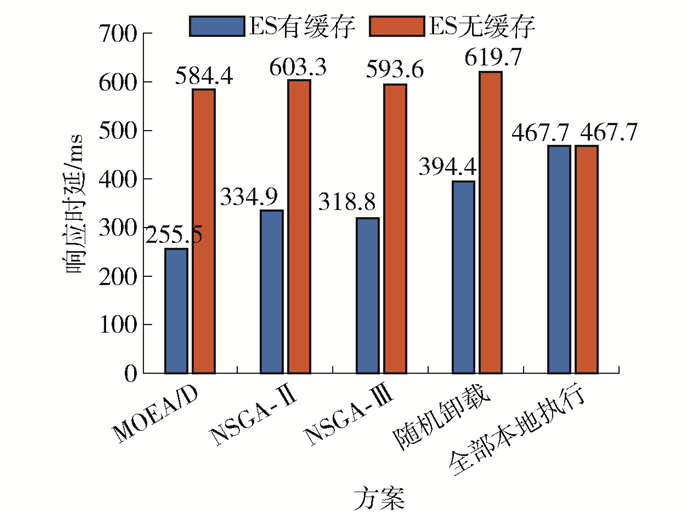
5种方案在ES有缓存任务处理框架和ES无缓存任务处理框架2种情况下，响应时延的变化如图 9所示。可以看出，除全部本地执行方案外，ES有缓存任务处理框架与无缓存任务处理框架相比，均可降低其他4种方案的响应时延。此外，MOEA/D方案在ES有缓存任务处理框架情况下得到的响应时延均优于其他4种方案。MOEA/D方案在ES无缓存任务处理框架情况下得到的响应时延均优于NSGA-Ⅱ、NSGA-Ⅲ、随机卸载这3种方案，这是因为在无边缘缓存情况下，ES计算传感器卸载的任务时，需要从Cloud下载任务处理框架，使得响应时延增加，导致MOEA/D方案劣于全部本地执行方案。
![]()
图 9 ES有无缓存框架对响应时延的影响Figure 9. Effect of ES with or without caching framework on response delay3.6 系统是否部署ES对响应时延和能量消耗的影响
为研究系统中是否部署ES对系统响应时延和能量消耗的影响，本文考虑系统中部署ES和系统中未部署ES这2种情况。2种情况的SD数量均设定为140个。已部署ES时，将其数量设定为20个；未部署ES时，将其数量设定为0个。
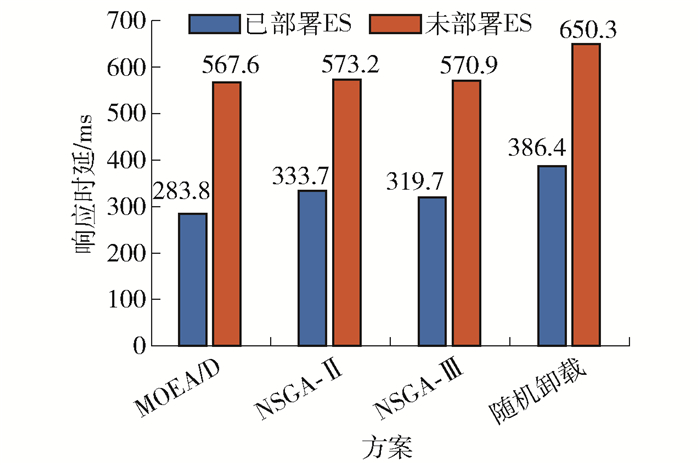
4种方案在系统中是否部署ES场景下响应时延变化如图 10所示。可以看出，系统中部署ES场景下4种方案的响应时延均比系统未部署ES场景下4种方案的响应时延低。此外，MOEA/D方案在系统中部署ES和未部署ES这2种场景下的响应时延均优于其他3种方案。
![]()
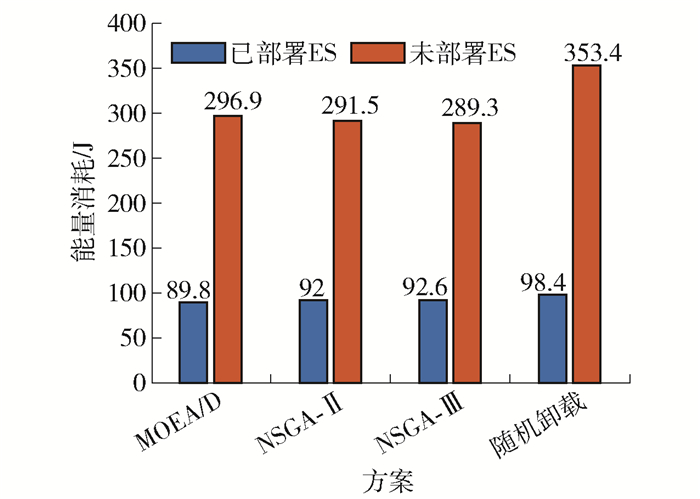
图 10 4种方案在系统中是否部署ES场景下响应时延变化Figure 10. Response delay change in the scenario of whether ES are deployed in the system for the four schemes4种方案在系统中是否部署ES场景下能量消耗变化如图 11所示。可以看出，系统中部署ES场景下4种方案的能量消耗均比系统未部署ES场景下4种方案的能量消耗低。此外，MOEA/D方案在系统中部署ES和未部署ES这2种场景下的能量消耗均优于其他3种方案。
![]()
图 11 4种方案在系统中是否部署ES场景下能量消耗变化Figure 11. Energy consumption change in the scenario of whether ES are deployed in the system for the four schemes4. 结论
1) 本文建立了智慧城市预警系统边缘计算场景下的任务卸载多目标优化问题模型，考虑了响应时延、能量消耗和负载失衡度这3个优化目标。
2) 应用MOEA/D算法对所构造的多目标优化问题模型进行求解，仿真结果表明，本文给出的MOEA/D卸载方案较优。
3) 下一步工作，将研究智慧城市预警系统中数据安全和隐私保护问题。
-
![]()
图 2 Pareto解集在3个约束目标上的分布
Figure 2. Distribution of Pareto solution set on three constrained targets
![]()
图 3 5种方案随SD数量变化对响应时延的影响
Figure 3. Effect of five schemes on response delay with the number of SD
![]()
图 4 5种方案随SD数量变化对能量消耗的影响
Figure 4. Effect of five schemes on energy consumption with the number of SD
![]()
图 5 5种方案随SD数量变化对负载失衡度的影响
Figure 5. Effect of five schemes on load imbalance with the number of SD
![]()
图 6 5种方案随ES数量变化对响应时延的影响
Figure 6. Effect of five schemes on response delay with the number of ES
![]()
图 7 5种方案随ES数量变化对能量消耗的影响
Figure 7. Effect of five schemes on energy consumption with the number of ES
![]()
图 8 5种方案随ES数量变化对负载失衡度的影响
Figure 8. Effect of five schemes on load imbalance with the number of ES
![]()
图 9 ES有无缓存框架对响应时延的影响
Figure 9. Effect of ES with or without caching framework on response delay
![]()
图 10 4种方案在系统中是否部署ES场景下响应时延变化
Figure 10. Response delay change in the scenario of whether ES are deployed in the system for the four schemes
![]()
图 11 4种方案在系统中是否部署ES场景下能量消耗变化
Figure 11. Energy consumption change in the scenario of whether ES are deployed in the system for the four schemes
算法1 MOEA/D 输入: 多目标优化问题(见式(19))；最大迭代次数gmax；子问题数量H；权重向量λ1, λ2, …, λH; 每个权重向量邻域内权重向量个数T 输出: 外部存档EP 初始化 1 外部存档EP=Ø。 2 计算2个权重向量之间的欧氏距离，然后算出每个权重向量邻域内最近的T个向量，对于每一个h=1, 2, …, H，设置B(h)=h1, h2, …, hT，λh1, λh1, …, λhT表示权重向量λh邻域内最近的T个向量。 3 随机生成初始种群O，并对种群中的每个个体Xh计算适应度。 4 初始化参考点z=(z1, z2, z3)T。 更新 5 for h=1, 2, …, H do 6 从B(h)中随机选择2个序号α、β，然后利用遗传算子对个体Xα、Xβ进行操作，产生一个新的个体Y。 7 根据约束修正个体Y，产生新个体Y′。 8 更新参考点z。 9 对于每一个j∈B(h)，应用切比雪夫法更新其邻域解。 10 更新外部存档EP。 11 终止判定。若满足终止条件则输出外部存档EP，否则转向步骤5。 
下载: 导出CSV
-
[1] 鲁钰雯, 翟国方. 人工智能技术在城市灾害风险管理中的应用与探索[J]. 国际城市规划, 2021, 36(2): 22-31, 39. https://www.cnki.com.cn/Article/CJFDTOTAL-GWCG202102004.htm LU Y W, ZHAI G F. Applications and exploration of artificial intelligence technology in urban disaster risk management[J]. Urban Planning International, 2021, 36(2): 22-31, 39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWCG202102004.htm
[2] 石娟, 郑鹏, 常丁懿. 大数据环境下的城市公共安全治理: 区块链技术赋能[J]. 中国安全科学学报, 2021, 31(2): 24-32. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK202102004.htm SHI J, ZHENG P, CHANG D Y. Governance of urban public safety in context of big data: block chain technology enablement[J]. China Safety Science Journal, 2021, 31(2): 24-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK202102004.htm
[3] 郑宇. 城市治理一网统管[J]. 武汉大学学报(信息科学版), 2022, 47(1): 19-25. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH202201001.htm ZHENG Y. Unified urban governance models[J]. Geomatics and Information Science of Wuhan University, 2022, 47(1): 19-25. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH202201001.htm
[4] 张伟东, 高智杰, 王超贤. 应急管理体系数字化转型的技术框架和政策路径[J]. 中国工程科学, 2021, 23(4): 107-116. https://www.cnki.com.cn/Article/CJFDTOTAL-GCKX202104014.htm ZHANG W D, GAO Z J, WANG C X. Digital transformation of emergency management system: technical framework and policy path[J]. Strategic Study of CAE, 2021, 23(4): 107-116. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCKX202104014.htm
[5] EVANGELOS M, LAZAROS K, ARIS D, et al. Public safety in smart cities under the edge computing concept[C]//IEEE International Mediterranean Conference on Communications and Networking. Piscataway: IEEE, 2021: 88-93.
[6] PERNA G, ROSMANINHO R, HUGO S, et al. On the performance of 5G for cloud-and edge-based emergency services in smart cities[C]//2021 12th International Conference on Network of the Future. Piscataway: IEEE, 2021: 1-5.
[7] JIANG X T, YU F R, SONG T, et al. A survey on multi-access edge computing applied to video streaming: some research issues and challenges[J]. IEEE Communications Surveys & Tutorials, 2021, 23(2): 871-903.
[8] WU H M, ZHANG Z R, GUAN C, et al. Collaborate edge and cloud computing with distributed deep learning for smart city Internet of things[J]. IEEE Internet of Things Journal, 2020, 7(9): 8099-8110. doi: 10.1109/JIOT.2020.2996784
[9] ZHAO X B, ZENG Y, DING H W, et al. Optimize the placement of edge server between workload balancing and system delay in smart city[J]. Peer-to-Peer Networking and Applications, 2021, 14(6): 3778-3792. doi: 10.1007/s12083-021-01208-0
[10] 张依琳, 梁玉珠, 尹沐君, 等. 移动边缘计算中计算卸载方案研究综述[J]. 计算机学报, 2021, 44(12): 2406-2430. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202112004.htm ZHANG Y L, LIANG Y Z, YIN M J, et al. Survey on the methods of computation offloading in mobile edge computing[J]. Chinese Journal of Computers, 2021, 44(12): 2406-2430. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202112004.htm
[11] 栾清华, 秦志宇, 王东, 等. 城市暴雨道路积水监测技术及其应用进展[J]. 水资源保护, 2022, 38(1): 106-116, 140. https://www.cnki.com.cn/Article/CJFDTOTAL-SZYB202201014.htm LUAN Q H, QIN Z Y, WANG D, et al. Review on monitoring technology of urban road waterlogging after rainstorm and its application[J]. Water Resources Protection, 2022, 38(1): 106-116, 140. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SZYB202201014.htm
[12] 黄永明, 郑冲, 张征明, 等. 大规模无线通信网络移动边缘计算和缓存研究[J]. 通信学报, 2021, 42(4): 44-61. https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB202104003.htm HUANG Y M, ZHENG C, ZHANG Z M, et al. Research on mobile edge computing and caching in massive wireless communication network[J]. Journal on Communications, 2021, 42(4): 44-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB202104003.htm
[13] LEE K, SILVA B N, HAN K J. Algorithmic implementation of deep learning layer assignment in edge computing based smart city environment[J]. Computers & Electrical Engineering, 2021, 89: 106909.
[14] XU X L, GU R H, DAI F, et al. Multi-objective computation offloading for Internet of vehicles in cloud-edge computing[J]. Wireless Networks, 2020, 26(11): 1611-1629.
[15] XU X L, HUANG Q H, YIN X C, et al. Intelligent offloading for collaborative smart city services in edge computing[J]. IEEE Internet of Things Journal, 2020, 7(9): 7919-7927.
[16] 李林林, 刘东梅, 王显鹏. 基于改进MOEA/D的多目标置换流水车间调度问题[J]. 计算机集成制造系统, 2021, 27(7): 1929-1940. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ202107008.htm LI L L, LIU D M, WANG X P. Multi-objective permutation flowshop scheduling problem based on improved MOEA/D[J]. Computer Integrated Manufacturing Systems, 2021, 27(7): 1929-1940. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ202107008.htm
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
