Feasibility of Dynamic Backcalculation on Pavement Performance Reduction Analysis
-
摘要:
为对沥青路面结构性能衰减演化分析提供参考，以不同基层类型的沥青路面结构作为研究对象，分析动态反演方法在路面结构性能衰减研究中的可行性. 首先，收集了实验路段2010年和2015年的实测弯沉数据，采用动态和静态方法进行路面力学参数反演，分析反演结果在服役期的变化趋势. 其中，动态方法采用谱单元法进行沥青路面动态黏弹分析，以弯沉时程曲线构造力学参数优化目标函数，得到沥青层的复数模量和其他结构层的弹性模量. 静态方法以层状弹性理论作为正分析方法，以弯沉盆进行反演得到各结构层的弹性模量. 继而采用动态反演力学参数进行移动荷载作用下的路面分析，计算了基层层底和沥青层层中的应力、应变等力学响应，分析了力学响应随服役时间的变化. 结果表明：静态反演结果表现出较大的波动性，2015年的静态反演结果甚至大于2010年的结果; 动态反演结果比静态反演结果更加稳定，参数变化趋势可以客观描述路面结构性能的衰减，而且与基于动态反演参数的路面力学响应变化趋势具有合理的一致性. 动态反演方法可以充分利用实测弯沉信息，有效避免模量窜层引起的静态反演结果误差，为路面结构性能衰减演化分析提供了便利和途径.
Abstract:To provide a reference for the reduction analysis of pavement performance, an asphalt pavement with different base types was taken as research object in this study to evaluate the feasibility of the dynamic backcalculation in pavement performance reduction. The field deflection measured at 2010 and 2015 was backcalculated by using dynamic and static approaches to study the various tendencies of the layer property during the service life. The spectral element method was adopted in the dynamic approach to conduct dynamic viscoelastic analysis and the deflection time-history was used to construct the optimization objective function. The complex modulus of asphalt layer and the elastic modulus for other layers were obtained. The layered elastic theory was adopted as forward analysis engine in the static method, and the deflection basin as constrain in the optimization process, and the elastic moduli for all layers were obtained. The dynamic backcalculated layer property was employed for pavement analysis under moving vehicles. The strainress at the bottom of the layer and the vertical strain at the mid depth of the asphalt layer were calculated to study the various tendencies of response within service life. Result shows that the layer property from static approach is fluctuant, and the result of 2015 is even greater than that of 2010. The dynamic backcalculated layer property is more stable, and its tendency can objectively characterize the pavement performance reduction. The analyzed response based on dynamic backcalculated layer property shows reasonable variation and it is consistent with the layer property. The deflection time-history can provide more constrains in optimization process, which can be efficient to avoid the error of static approach due to the modulus compensating phenomenon. The research provides an efficient and convenient routine for pavement performance reduction analysis.
-
精准预测在役路面结构性能的衰变行为对通过维养提升路面使用性能以及延长路面寿命具有重要指导性作用[1-2]. 室内测试手段无法真实模拟路面材料的实际受力状态，测试结果无法客观地反映筑路材料在实际服役环境下的性能[3]. 落锤式弯沉仪(falling weight deflectometer, FWD) 能够模拟行车冲击荷载，并得到不同位置处的弯沉时程曲线，为路面质量评定和养护决策制定提供了基础数据[4]. Gedafa等[5]基于现场FWD测试结果，利用Sigmoid函数建立了荷载中心处的弯沉峰值和剩余寿命的关联模型. 然而，该模型仅采用路面结构整体强度作为分析指标，无法解释结构内部各层位力学参数的衰减和剩余寿命的关系. 采用FWD实测弯沉，通过反演手段确定筑路材料的力学参数，能够更加客观反映材料的实际性能，而且可以和路面力学分析有效衔接.
目前，成熟的路面力学参数反演软件中，大部分采用层状弹性理论计算路面弯沉或形成数据库[6-7]，反演得到各结构层的弹性模量. 沥青混合料力学性能具有明显的荷载频率和温度依赖性，而且FWD的荷载作用时间极短，接近于冲击荷载，荷载和筑路材料的特性导致动、静态方法分析得到的路面弯沉误差可达40%以上[8]. Lee等[9]收集了不同时期内的现场弯沉测试结果，采用动态方法反演得到沥青层的动态模量主曲线和其他层的弹性模量，结果表明筑路材料的力学参数随着路面服役时间的延长会逐渐减小，然而在分析中忽略了路面力学响应的变化.
本文以山西大新高速公路典型的半刚性基层和柔性基层沥青路面结构作为研究对象，收集了不同服役时长的路面弯沉实测数据. 分别采用动、静态方法反演得到各结构层的力学参数，分析反演参数随结构服役时间的变化趋势. 然后，采用动态反演力学参数计算了移动荷载作用下的路面力学响应，并分析了其在服役期间的变化，验证了动态反演方法在路面结构性能衰减分析中的可行性.
1. 力学参数反演
路面力学参数反演过程由正分析过程和优化过程两部分构成. 首先，利用正分析方法得到弯沉理论计算结果; 然后，在优化过程中以弯沉计算值和实测值的误差建立目标优化函数，通过不断修正路面力学参数以保证弯沉误差满足计算精度要求[10]. 本文在沥青路面动态黏弹分析中采用谱单元法，因此，下面对谱单元法进行简单介绍.
1.1 正分析方法
$$ [\lambda(t)+\mu(t)] \nabla \nabla \cdot \boldsymbol{U}+\mu(t) \nabla^{2} \boldsymbol{U}=\rho \ddot{\boldsymbol{U}} $$ (1) 式中：U为位移向量; $ \ddot{\boldsymbol{U}}$为位移对时间的二阶导数; $\nabla \cdot $和$ \nabla^{2} $分别为散度和拉普拉斯算子; ρ为材料的密度; λ(t)和μ(t)为材料的拉梅常数.
谱单元法在分析过程中，利用傅里叶变换对响应控制方程进行时间和空间变换，在频率-波数域内对控制方程进行求解，不需要对路面结构层进行划分，大大地提高了正分析的计算效率，并采用双节点谱单元描述有限厚度的结构层，采用单节点谱单元描述半空间无限厚度土基. 在频率-波数域内，根据亥姆霍兹定理，将荷载应力波分解为径向的膨胀波和竖向的剪切波，对分项波动方程进行推导得到谱单元节点的位移解析表达式. 根据路面结构荷载和边界条件，建立谱单元的刚度矩阵以及结构总体刚度矩阵，求解得到该域内的位移结果. 将不同频率-波数域内的结果相加，利用傅里叶逆变换可以得到时域内的力学响应. 具体的计算方法见文献[11-14].
谱单元方法中将沥青层作为黏弹性材料，其他结构层作为弹性材料. 本文采用修正的Havriliak-Negami(modified Havriliak-Negami，MHN)模型[15]描述沥青混合料的黏弹性力学行为，公式为
$$ E^{*}(\omega)=E_{0}^{*}+\frac{E_{\infty}^{*}-E_{0}^{*}}{\left[1+\left(\frac{\omega_{0}}{{\rm{i}}\omega}\right)^{\alpha}\right]^{\beta}} $$ (2) 式中：$\mathrm{i}=\sqrt{-1} $; ω为角频率; E∞*和E0*分别表示ω趋于无穷大和零时的复数模量; α、β和ω0为模型系数，其中α、β和材料的松弛特性有关，ω0与主曲线的水平位置有关.MHN模型是复数模量模型，通过线黏弹性理论可以计算得到动态模量和相位角主曲线，两者结合可以全面描述材料的黏弹特性. 常用的Prony系列需要至少13个系数才能精确描述材料的黏弹特性，而MHN模型仅需要5个参数，大大减少了优化过程中的参数数量. 采用谱单元法进行路面分析时不需要对路面结构进行单元划分，因此，计算效率优于有限元法，精度验证见文献[13, 16]，此处不再赘述.
1.2 参数优化过程
路面力学参数优化过程关键在于建立目标优化函数，在传统的静态反演方法中，通过采用各传感器测量弯沉峰值构成的弯沉盆建立目标优化函数，忽略了时程曲线中包含的大量信息，如不同位置处弯沉峰值时间和响应黏滞信息等[9, 16-17]. 在动态反演方法中，利用不同位置处弯沉时程曲线的实测值和计算值的均方误差建立目标优化方程
$$ F=\sqrt{\frac{1}{K N} \sum\limits_{i=1}^{K} \sum\limits_{j=1}^{N}\left(\frac{d_{\mathrm{cal}, i, j}-d_{\mathrm{mea}, i, j}}{d_{\mathrm{mea}, i, j}}\right)^{2}} $$ (3) 式中：F为目标优化函数; K为传感器个数; N为各传感器收集的弯沉数据长度; dcal, i, j和dmea, i, j分别表示第i个传感器、第j个弯沉的计算值和实测值. 动态反演方法能够更全面采用时程曲线中的有效信息，在参数优化过程中提供更多的约束条件，保证反演力学参数趋于真实值.
2. 弯沉测试及典型反演结果
2.1 测试路段信息
现场弯沉测试在山西大新高速公路不同基层类型的路段上进行，本文选取了2段路面结构，分别为半刚性基层路面结构A和柔性基层路面结构B. 路面结构A各层的级配及材料类型为：4 cmAC-16+5 cmAC-20+6 cmAC-20+16 cm水稳碎石+14 cm三灰碎石+20 cm水稳砂砾+土基; 路面结构B各层的级配及材料类型为：4 cmAC-16+5 cmAC-20+6 cmAC-20+15 cmATB-30+35 cm级配碎石+土基. 在路面分析和参数反演中，为了便于分析和提高计算效率，根据各结构层材料的特性，将路面结构简化为4层路面结构，各结构层厚度及物理参数如表 1所示[18-19].
表 1 路面结构信息Table 1. Pavement information结构层 厚度/cm 泊松比 阻尼因数 密度/(kg·m-3) 面层 15 0.30 2 400 基层 30 (A) 0.20 0.02 2 250 15 (B) 0.30 2 400 底基层 20 (A) 0.25 0.03 2 200 35 (B) 0.35 0.03 2 150 土基 ∞ 0.40 0.05 1 600 2.2 力学参数典型反演结果分析
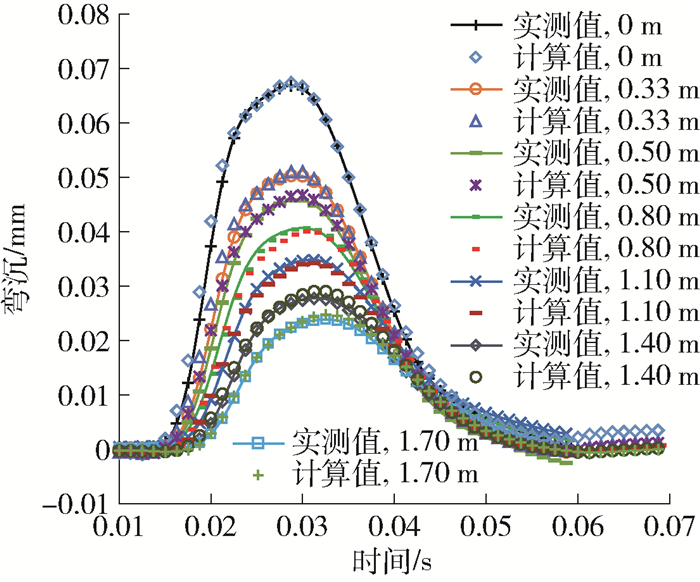
现场弯沉测试在不同时间进行，测试荷载峰值均设定为0.7 MPa，荷载作用半径为0.15 m，弯沉传感器距荷载中心的距离分别为0、0.33、0.50、0.80、1.10、1.40、1.70 m. 本文收集了2007年、2010年和2015年的实测弯沉数据. 经调研，大新高速于2010年统一进行了罩面养护，2017年由于各路段病害类型不同，采用了不同的养护措施，为保证分析弯沉测试环境及路面状况的一致性，本文选取2010年和2015年的弯沉数据进行力学参数反演，2010年罩面厚度为2.5 cm，并在后文分析中对面层厚度进行修正.
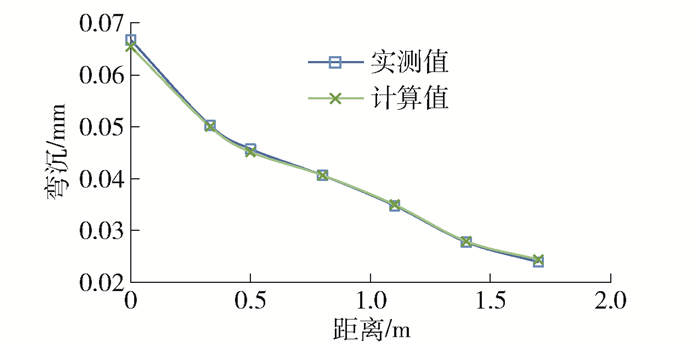
本文动态反演方法如前文所述，静态方法采用软件EVERCALC进行[6]. 为分析动、静态反演结果的差异性，选取了2010年典型测试结果分别进行动、静态反演，反演结果如图 1、2所示.
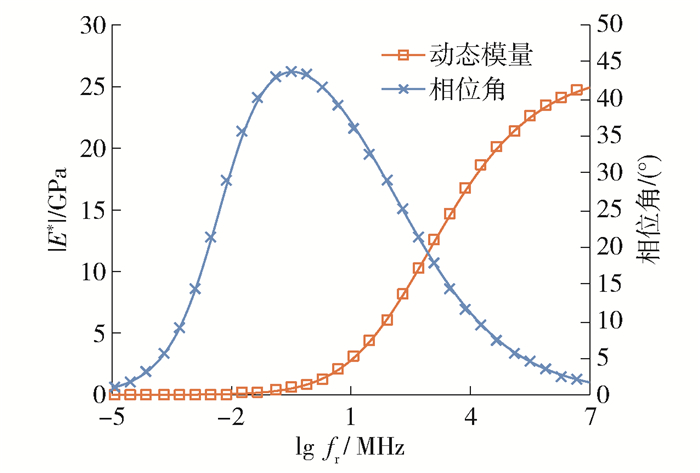
由图可知，动、静态方法反演得到的弯沉均能很好地吻合实测弯沉曲线，这表明反演得到的路面动、静态力学参数均能表征路面结构在荷载下的力学行为. 2种方法的反演结果如表 2所示，可见动态方法得到了沥青层的MHN模型参数，以及其他结构层的弹性模量. 有了MHN模型参数，就可以得到沥青层的动态模量|E*|和相位角主曲线，如图 3所示. 图中主曲线的参考温度为测试现场实际温度(28 ℃)，fr为缩减频率. 静态反演方法仅仅得到筑路材料单一弹性模量值，与动态反演方法存在一定差异，基层和土基的静态反演结果比动态反演结果分别大70%和40%以上，而底基层的静态反演结果比动态反演结果小30%左右. 由图 3可见，动态模量和相位角主曲线可以描述沥青混合料力学特性随荷载频率的变化趋势，比单一的弹性模量能更全面地描述沥青混合料的温度、荷载频率的依赖性[15, 20].
表 2 典型结构层反演模量Table 2. Typical backcalculated modulus of structural layerMPa 方法 面层 基层 底基层 土基 动态 — 7 748.6 1 620.3 264.4 静态 10 942.0 13 777.0 1 131.5 372.5 3. 反演结果分析
本文以2010年和2015年实测弯沉作为力学参数反演的基础数据，在反演过程中，对2010年数据采用人工调试的方法，获得反演结果的初始值. 然后，以2010年反演结果的平均值作为2015年力学参数反演的初始值，对比分析2010年和2015年的反演力学参数的衰减演变规律. 在分析中，根据测试点的桩号位置，选取同一桩号的测试结果作为对比对象，而且分析测试点位置处路表没有明显的病害. 其中半刚性基层路面结构A共有11个测点，柔性基层路面结构B共有6个测点. 为避免测试温度对反演结果的影响，在对比分析中，将沥青层的反演结果统一转化为20 ℃下的模量进行分析[21-22].
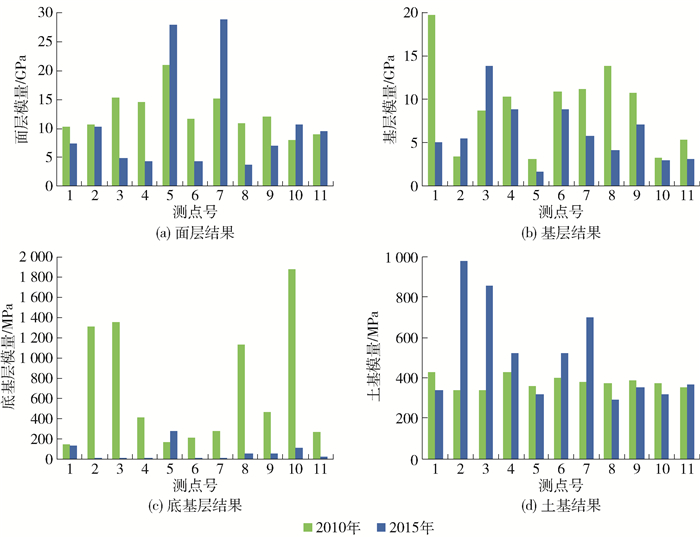
3.1 半刚性基层路面结构
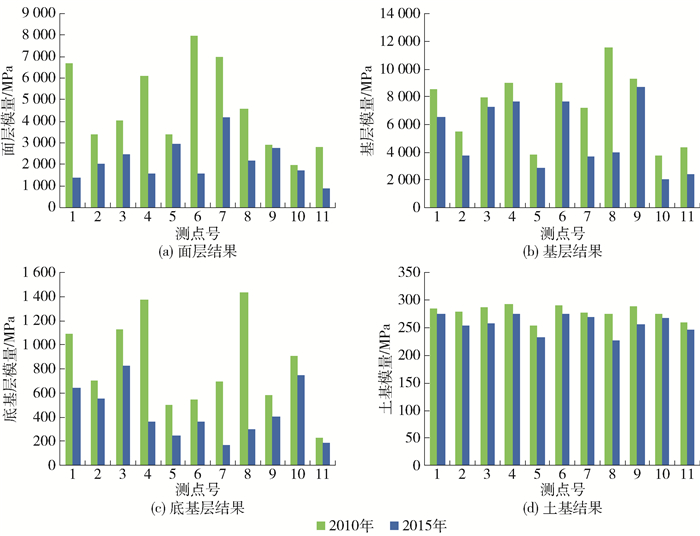
由上述内容可知，通过动态反演得到沥青层的复数模量. 为便于定量分析，计算了沥青层在温度为20 ℃、荷载作用频率为10 Hz时的动态模量. 图 4给出了动态反演参数随测点桩号的分布结果.
![]()
图 4 半刚性基层路面结构动态反演结果Figure 4. Dynamic backcalculated results for pavement with semi-rigid base由图可知，通过动态方法反演得到的不同测点的结构层模量虽然表现出一定的波动性，但是反演得到的2015年各结构层的模量值均小于2010年结果，表明相对于2010年，2015年各结构层强度均有一定的衰减. 土基层反演结果的变化程度明显小于其他结构层，表明面层、基层和底基层的强度衰减程度明显大于土基，尤其是8号测点的反演结果，面层、基层和底基层的模量减少了50%以上.
图 5给出了静态反演方法结果. 可见静态反演得到的各测点处模量波动程度明显大于动态反演结果. 模量窜层现象[8, 16, 23]导致部分结构层模量被传递到相邻结构层，如2015年，2号和3号测点反演得到的土基模量结果大于800 MPa，而底基层(水稳砂砾)的反演模量小于100 MPa，反演结果不能客观描述土基和底基层的材料特性. 部分测点处2015年的反演结果反而大于2010年的反演结果，服役期间车辆荷载会造成路面材料进一步压实，然而7号测点处的面层模量增长了70%以上，反演结果不能正确地描述筑路材料在服役期间的性能变化.
![]()
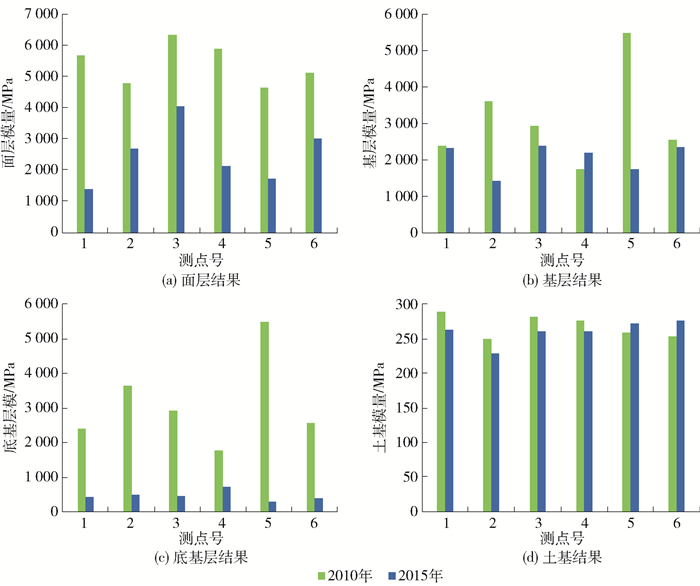
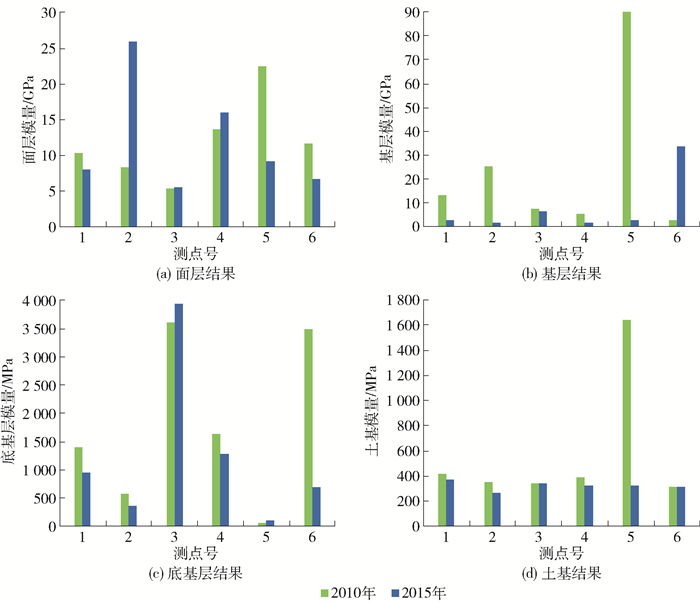
图 5 半刚性基层路面结构静态反演结果Figure 5. Static backcalculated results for pavement with semi-rigid base3.2 柔性基层路面结构
对于柔性基层沥青路面结构，动态反演方法将沥青面层和沥青处治基层均作为黏弹性材料，其余结构层作为弹性材料，同理计算沥青层的当量回弹模量，取面层的荷载频率为10 Hz，基层的荷载频率为5 Hz，分析温度均为20 ℃. 图 6中绘出了柔性基层路面结构的动态反演结果.
![]()
图 6 柔性基层路面结构动态反演结果Figure 6. Dynamic backcalculated results for pavement with flexible base由图可知，各结构层力学参数的动态反演结果均在筑路材料的合理范围内. 5号和6号测点处的土基模量反而有一定的增长，增长幅度小于10%，而底基层的模量衰减程度较大，这一现象是由于底基层强度的衰减，土基承受更多的荷载压力导致的.
图 7给出了通过静态反演得到的结构层模量随测点的分布结果，可见部分测点处基层和土基的静态反演结果超出了材料力学参数的合理范围. 2号测点处面层和6号测点处基层的2015年的反演结果远大于2010年的结果，结果显示筑路材料的强度没有减小，反而有了大幅度的增长，静态反演结果无法解释路面结构服役性能的降低.
![]()
图 7 柔性基层路面结构静态反演结果Figure 7. Static backcalculated results for pavement with flexible base为更清晰分析各结构层的模量衰减情况，计算了2个路面结构不同测点的反演结果的平均衰减比，计算公式为
$$ R=\frac{1}{N} \sum\limits_{i=1}^{N} \frac{E_{2010, i}-E_{2015, i}}{E_{2010, i}} \times 100 \% $$ (4) 式中：R为模量衰减比; N为同一路段结构的测点数; E2010, i和E2015, i分别表示第i个测点的2010年和2015年的反演结果. 其中：正值表示2015年反演结果小于2010年反演结果; 负值表示2015年反演结果大于2010年反演结果. 计算结果列于表 3中.
表 3 反演结果衰减比Table 3. Decrease percentage of backcalculated results% 结构 面层 基层 底基层 土基 动态结果 静态结果 动态结果 静态结果 动态结果 静态结果 动态结果 静态结果 A 44.7 18.4 30.7 20.1 41.5 67.6 7.3 -37.4 B 45.5 -18.4 44.9 -121.2 76.1 6.9 2.8 22.5 可见，各结构层模量的动态反演结果表现出不同程度的衰减，而静态反演结果中，部分结构层的模量反而有所提升，尤其是柔性基层的反演结果增大了1.2倍以上，这一现象不能客观地描述路面结构承载能力的衰变. 针对半刚性基层路面结构，面层、基层和底基层的模量衰减比相近，表明各结构层强度衰减程度较一致. 对于柔性基层沥青路面，底基层的模量衰减比达到了76.1，明显大于面层和基层的反演结果，底基层模量的衰减将导致沥青基层产生更大的荷载应力，这将进一步导致沥青层疲劳裂缝的发生. 2个路面结构中，土基模量衰减比均小于其他结构层，表明土基在服役期间的强度衰减程度较小. 由上可知，动态方法在路面力学参数反演和结构性能衰减分析方面明显优于静态反演方法.
4. 基于动态反演结果的路面力学分析
为进一步验证动态反演结果的合理性，采用2010年和2015年动态反演力学参数进行路面分析，研究路面结构力学响应的变化. 通过动态反演得到沥青层的黏弹力学参数，因此，分析方法采用层状黏弹性理论，荷载采用移动荷载，移动速度选取我国高速公路设计速度的下限值，即80 km/h，具体计算流程可见文献[24]. 在分析过程中，采用整个路段的反演结果平均值作为沥青层的黏弹性参数以及其余结构层的弹性模量. 分析荷载采用单轴单轮荷载，荷载半径为0.15 m，荷载幅值为0.7 MPa. 对于半刚性基层路面结构，计算了沥青层层中竖向应变和底基层层底水平应力; 对于柔性基层路面结构，计算了沥青层层中竖向应变和沥青层层底水平应变.
4.1 半刚性基层沥青路面结构
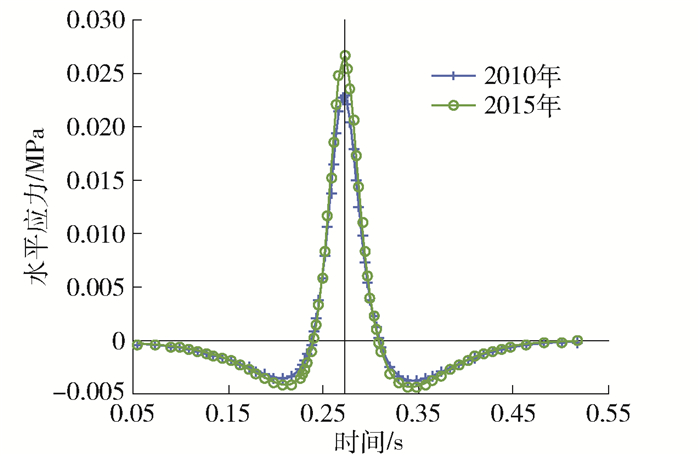
图 8绘出了半刚性底基层层底的水平纵向应力结果. 其中：正值表示受拉; 负值表示受压; 竖线表示荷载作用于分析点正上方时刻. 可见荷载移动过程中，分析点处于受压—受拉—受压的交变状态. 采用反演力学参数计算得到的2015年层底水平应变峰值比2010年结果增加了15%左右，表明随着结构层模量的降低，路面结构内部产生了更大的应力结果，这将导致路面结构服役能力的进一步衰减.
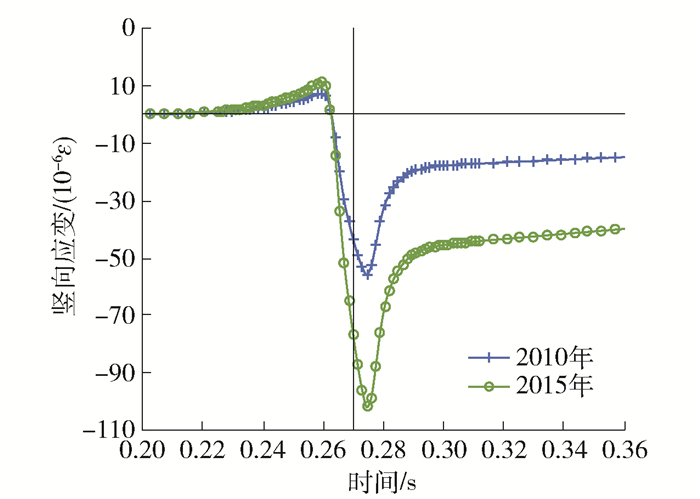
图 9绘出了沥青层层中竖向应变的分析结果. 可见，沥青层层中竖向应变峰值增加了80%左右，而且在荷载驶离分析点之后，2015年分析结果的尾部大于2010年的结果，表明2015年产生了较大的永久变形，需要更长的时间恢复变形，分析结果能够描述路面车辙的发展变化[25-26].
4.2 柔性基层沥青路面结构
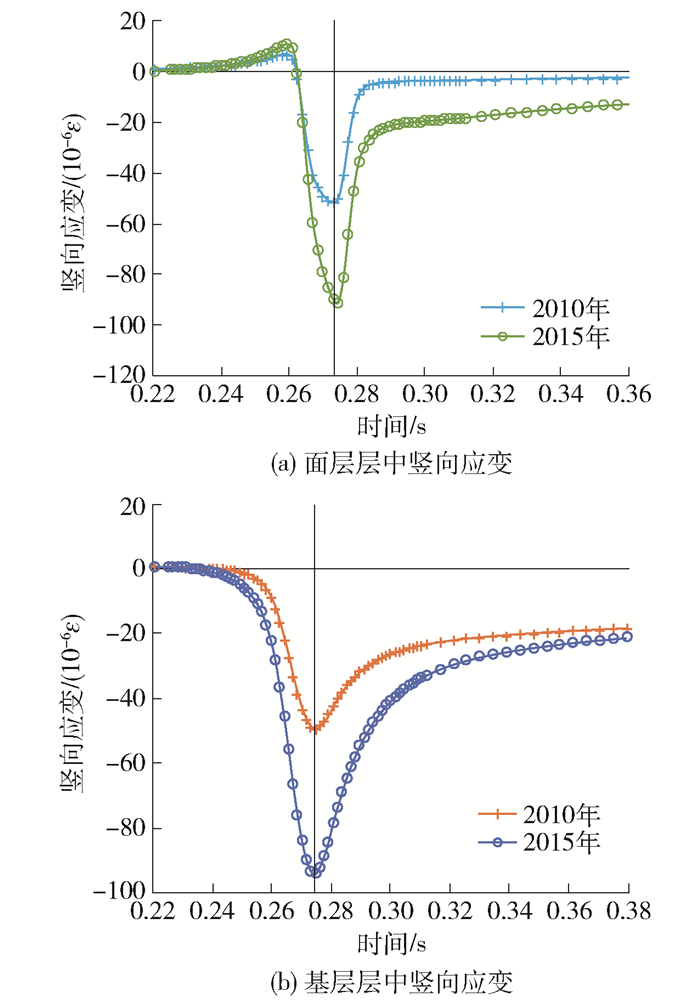
图 10中绘出了柔性基层路面面层和基层层中竖向应变分析结果. 与半刚性基层路面结构相似，计算得到的2015年竖向应变峰值均有所增加，而且产生的永久变形大于2010年的分析结果. 基层和面层层中竖向应变的峰值均增大了70%以上，而且基层分析结果尾部的永久变形大于面层分析结果，表明底基层模量的衰减导致基层和面层产生更大的应力响应，而且基层将产生更大的永久变形.
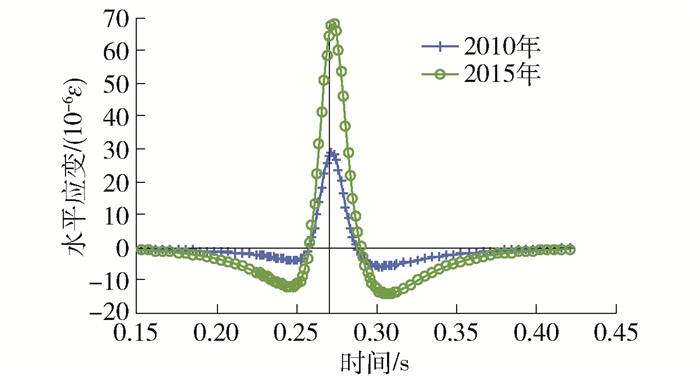
图 11中绘出了沥青层层底水平应变的分析结果. 可见2015年的分析结果明显大于2010年分析结果，峰值的增加程度大于竖向应变结果，表明结构层强度衰减程度不同，将导致结构内部力学响应重分布.
为进一步分析不同结构层模量衰减对路面结构内部力学响应的影响，计算了分析得到的2015年和2010年力学响应峰值的比值(见表 4)，可见不同位置处的力学响应峰值有不同程度的增加，表明结构层强度的衰减程度不同，导致路面结构内部产生的荷载应力空间分布特性发生改变. 对于半刚性基层路面结构，沥青层竖向应变的比值大于基层层底水平应力结果. 由表 3可知，在分析服役时间内，基层的力学参数衰减程度较低，则在路面结构承载能力中，基层将会承担更多的荷载应力，以保护底基层不至于产生较大的响应. 对于柔性基层路面结构，沥青层层底水平应变峰值比值为2.36，明显大于沥青层层中分析结果，而且基层应变比值大于面层分析结果，可见随着底基层模量的衰减，将导致面层和基层承受较大的荷载应力，尤其是基层层底的水平应变. 采用动态反演结果分析得到路面力学响应结果的变化，与路面力学参数的衰减变化具有高度的一致性，进一步验证了采用动态方法反演路面力学参数，进行路面结构性能衰减分析的可行性.
表 4 2010年和2015年力学响应峰值比值Table 4. Ratio of response peaks of 2015 to that of 2010基层类型 响应类型 比值 半刚性 底基层层底水平应力 1.15 沥青层层中竖向应变 1.82 柔性 面层层中竖向应变 1.75 基层层中竖向应变 1.88 沥青层层底水平应变 2.36 5. 结论
1) 采用动态反演方法可以得到沥青层的复数模量主曲线，可以在较宽的频率内描述材料性能，比单一的弹性模量值能更全面描述沥青混合料的温度、荷载频率依赖性.
2) 动态反演得到同一路段不同测点处的结果稳定性高于静态反演结果，动态反演结果可以较好地描述路面力学参数在服役期间的衰减.
3) 分析结果表明，土基层的强度衰减程度明显小于其他结构层结果. 柔性基层路面结构底基层的弹性模量衰减可达70%以上，底基层的衰减导致沥青层承担更大的荷载应力，将会导致路面病害的进一步发展.
4) 利用动态反演力学参数分析得到的路面力学响应的增长趋势和反演力学参数的衰减具有高度的一致性，验证了采用动态反演方法进行路面性能衰减分析的可行性. 研究结论有待于在更多的路面结构类型中进行论证，并考虑不同维养措施的影响，进一步提升路面结构性能衰减的分析精度.
-
![]()
图 4 半刚性基层路面结构动态反演结果
Figure 4. Dynamic backcalculated results for pavement with semi-rigid base
![]()
图 5 半刚性基层路面结构静态反演结果
Figure 5. Static backcalculated results for pavement with semi-rigid base
![]()
图 6 柔性基层路面结构动态反演结果
Figure 6. Dynamic backcalculated results for pavement with flexible base
![]()
图 7 柔性基层路面结构静态反演结果
Figure 7. Static backcalculated results for pavement with flexible base
表 1 路面结构信息
Table 1 Pavement information
结构层 厚度/cm 泊松比 阻尼因数 密度/(kg·m-3) 面层 15 0.30 2 400 基层 30 (A) 0.20 0.02 2 250 15 (B) 0.30 2 400 底基层 20 (A) 0.25 0.03 2 200 35 (B) 0.35 0.03 2 150 土基 ∞ 0.40 0.05 1 600 
下载: 导出CSV
表 2 典型结构层反演模量
Table 2 Typical backcalculated modulus of structural layer
MPa 方法 面层 基层 底基层 土基 动态 — 7 748.6 1 620.3 264.4 静态 10 942.0 13 777.0 1 131.5 372.5
下载: 导出CSV
表 3 反演结果衰减比
Table 3 Decrease percentage of backcalculated results
% 结构 面层 基层 底基层 土基 动态结果 静态结果 动态结果 静态结果 动态结果 静态结果 动态结果 静态结果 A 44.7 18.4 30.7 20.1 41.5 67.6 7.3 -37.4 B 45.5 -18.4 44.9 -121.2 76.1 6.9 2.8 22.5
下载: 导出CSV
表 4 2010年和2015年力学响应峰值比值
Table 4 Ratio of response peaks of 2015 to that of 2010
基层类型 响应类型 比值 半刚性 底基层层底水平应力 1.15 沥青层层中竖向应变 1.82 柔性 面层层中竖向应变 1.75 基层层中竖向应变 1.88 沥青层层底水平应变 2.36
下载: 导出CSV
-
[1] 曹明明, 乔世哲, 岳建洪, 等. 基于沥青路面性能衰变特征的养护效果后评估[J]. 交通科技, 2021, 308(5): 17-22. doi: 10.3963/j.issn.1671-7570.2021.05.004 CAO M M, QIAO S Z, YUE J H, et al. Post-evaluation of maintenance effect based on asphalt pavement performance degradation characteristics[J]. Transportation Scienceand Technology, 2021, 308(5): 17-22. (in Chinese) doi: 10.3963/j.issn.1671-7570.2021.05.004
[2] 宋波, 张金喜, 薛忠军, 等. 既有半刚性基层沥青路面大修处治策略[J]. 北京工业大学学报, 2017, 43(8): 1212-1219. SONG B, ZHANG J X, XUE Z J, et al. Treatment strategy of existing asphalt pavement with semi-rigid base course[J]. Journal of Beijing University of Technology, 2017, 43(8): 1212-1219. (in Chinese)
[3] MA W, TRAN N H, TAYLOR A J, et al. Comparison of laboratory cracking test results and field performance[J]. Asphalt Paving Technology, 2015(84): 243-268.
[4] 交通运输部. 公路技术状况评定标准: JTG 5210—2018[S]. 北京: 人民交通出版社, 2018: 71-85. [5] GEDAFA D S, HOSSAIN M, MILLER R, et al. Estimation of remaining service life of flexible pavements from surface deflections[J]. Journal of Transportation Engineering, 2010, 136(4): 342-352. doi: 10.1061/(ASCE)TE.1943-5436.0000094
[6] LEE S W, MAHONEY J P, JACKSON N C. Verification of backcalculation of pavement moduli[J]. Transportation Research Record, 1988(1196): 85-95.
[7] SCULLION T, UZAN J, PAREDES M. MODULUS: microcomputer based backcalculation system[J]. Transportation Research Record, 1990(1260): 180-191.
[8] 曹丹丹, 赵延庆, 孔繁盛, 等. 刚性基层沥青路面参数动态反演[J]. 中国公路学报, 2018, 31(8): 66-73. doi: 10.3969/j.issn.1001-7372.2018.08.007 CAO D D, ZHAO Y Q, KONG F S, et al. Dynamic backcalculation for parameters of asphalt pavement with rigid base[J]. China Journal of Highway Transportation, 2018, 31(8): 66-73. (in Chinese) doi: 10.3969/j.issn.1001-7372.2018.08.007
[9] LEE H, AYYALA D, VON Q H. Dynamic backcalculation of viscoelastic asphalt properties and master curve construction[J]. Transportation Research Record: Journal of the Transportation Research Board, 2017(2641): 29-38.
[10] CHATTI K, KUTAY M E, LAJNEF N, et al. Enhanced analysis of falling weight deflectometer data for use with mechanistic-empirical flexible pavement design and analysis and recommendations for improvements to falling weight deflectometers[R]. Washington, D.C. : Federal Highway Administration, 2017: 43-158.
[11] BORTFELD R. Viscoelastic waves in layered media[M]. Cambridge: Cambridge University Press, 2009: 70-278.
[12] AL-KHOURY R, SCARPAS A, KASBERGEN C, et al. Spectral element technique for efficient parameter identification of layered media, Part I. forward calculation[J]. International Journal of Solids and Structures, 2000, 38(9): 1605-1623.
[13] ZHAO Y Q, CAO D D, CHEN P S. Dynamic backcalculation of asphalt pavement layer properties using spectral element method[J]. Road Materialsand Pavement Design, 2015(164): 870-888.
[14] 曹丹丹. 沥青路面力学参数动态反演及性能分析研究[D]. 大连: 大连理工大学, 2018: 25-67. CAO D D. Dynamic backcalculation of layer property and performance evaluation for asphalt pavement[D]. Dalian: Dalian University of Technology, 2018: 25-67. (in Chinese)
[15] ZHAO Y Q, LIU H, BAI L, et al. Characterization of linear viscoelastic behavior of asphalt concrete using a complex modulus model[J]. Journal of Materials in Civil Engineering, 2013, 25(10): 1543-1548. doi: 10.1061/(ASCE)MT.1943-5533.0000688
[16] 曹丹丹, 赵延庆, 田泽峰, 等. 沥青路面动态黏弹反演研究[J]. 土木工程学报, 2017, 50(9): 104-109. CAO D D, ZHAO Y Q, TIAN Z F, et al. Back-calculation study on asphalt pavement using dynamic viscoelastic method[J]. China Civil Engineering Journal, 2017, 50(9): 104-109. (in Chinese)
[17] CAO D D, ZHOU C J, ZHAO Y Q, et al. Effectiveness of static and dynamic backcalculation approaches for asphalt pavement[J]. Canadian Journal of Civil Engineering, 2020(47): 846-855.
[18] JIANG X, ZENG C, GAO X F, et al. 3D FEM analysis of flexible base asphalt pavement structure under non-uniform tyre contact pressure[J]. International Journal of Pavement Engineering, 2019, 20(9): 999-1011. doi: 10.1080/10298436.2017.1380803
[19] LI P, LIU J Y, ZHAO S, et al. Implementation of stress-dependent resilient modulus of asphalt-treated base for flexible pavement design[J]. International Journal of Pavement Engineering, 2018, 19(5): 439-446. doi: 10.1080/10298436.2017.1402600
[20] TSCHOEGL N W. The phenomenological theory of linear viscoelastic behavior[M]. 2nd ed. Berlin: Springer, 2003: 75-249.
[21] 石志勇, 李倩倩, 周兴业, 等. 沥青路面弯沉的温度修正研究[J]. 中外公路, 2021, 41(1): 36-42. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL202101009.htm SHI Z Y, LI Q Q, ZHOU X Y, et al. Study on temperature correction of asphalt pavement deflection[J]. Journal of China and Foreign Highway, 2021, 41(1): 36-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL202101009.htm
[22] 宋小金, 樊亮. 基于FWD的沥青路面动态弯沉温度修正系数[J]. 土木工程学报, 2018, 51(3): 123-128. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201803015.htm SONG X J, FAN L. Temperature correction coefficient for dynamic deflection of asphalt pavement based on FWD[J]. China Civil Engineering Journal, 2018, 51(3): 123-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201803015.htm
[23] CAO D D, ZHAO Y Q, ZHANG J X, et al. Investigation of the interface condition influence on backcalculated layer properties[J]. Journal of Transportation Engineering, Part B: Pavements, 2021, 147(3): 04021026. doi: 10.1061/JPEODX.0000281
[24] ZHAO Y Q, NI Y B, WANG L, et al. Viscoelastic response solutions of multilayered asphalt pavements[J]. Journal of Engineering Mechanics, 2014, 140(10): 2729-2737.
[25] VISHNU R, RAJASHEKAR R D, ANUPAM M, et al. Evaluation of rutting potential of asphalts using resilient modulus test parameters[J]. Road Materials and Pavement Design, 2019(20): 1-16.
[26] LEE J H, BAEK S B, LEE K H, et al. Long-term performance of fiber-grid-reinforced asphalt overlay pavements: a case study of Korean national highways[J]. Journal of Traffic and Transportation Engineering: English Edition, 2019, 6(4): 366-382. doi: 10.1016/j.jtte.2018.01.008
-
期刊类型引用(2)
1. 王圣棋. 基于结构层模量衰减的半刚性沥青路面力学分析. 交通科技与管理. 2024(06): 140-142 . 
百度学术
2. 陈然. 市政道路动态弯沉检测技术的应用分析. 江西建材. 2024(06): 81-82+99 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 796
- HTML全文浏览量: 8
- PDF下载量: 65
- 被引次数: 4
