Mobile Robot Exploration Strategy Based on Multiple Information Gain
-
摘要:
针对移动机器人在未知环境中自主探索及建图存在盲目性的问题, 提出了一种基于贝叶斯优化评估多重信息增益的探索策略。在候选点提取方法上采用融合前沿点聚类与可通行区域的方式综合衡量提取, 相较于传统的前沿点检测方法有效解决了候选点集合过大及环境信息缺失等问题; 在候选点评估方法上利用贝叶斯优化计算多重信息增益, 综合考虑地图熵值与距离成本, 相较于仅考虑地图熵值选取最佳候选点的方法, 有效改进了机器人在环境中的冗余路径。该算法在机器人操作系统(robot operating system, ROS)中采用Gazebo进行仿真实验验证, 构建环境地图。结果表明, 该方法可以使移动机器人快速有效地探索未知环境, 高质量完成建图任务。
Abstract:Aiming at solving the problem of blindness in autonomous exploration and mapping by mobile robots in unknown environments, an exploration strategy based on Bayesian optimization to evaluate multiple information gains was proposed. In the candidate point extraction method, the method of integrating frontier point clustering and passable area to comprehensively measure and extract was adopted. Compared with the traditional frontier point detection method, it effectively solved the problems of excessive candidate point sets and missing environmental information. The Bayesian optimization was used to calculate multiple information gains considering both map entropy and distance costs. Compared with the method of selecting the best candidate point based solely on map entropy, this method effectively improved the redundancy path of the robot in the environment. Gazebo was used to verify the algorithm in robot operating system (ROS) and build environment map. Results show that the proposed method can enable the mobile robot to explore the unknown environment quickly and efficiently and complete the mapping task with high quality.
-
在机器人领域高速发展的今天，移动机器人在各个领域都得到了广泛的应用[1]，其中，来自室内场景下的全自主移动机器人应用需求日益增多[2]。如何在先验未知的环境中自主探索并构建地图是机器人研究领域的一个关键问题[3]，在不同的任务场景下对建图的要求也不尽相同。例如：在受灾环境下进行救援的机器人对建图的快速性有较高的要求[4]，而对于一些人类尚未涉足，但是又具有一定研究价值的环境，此时，对机器人的建图精度就更为看重[5]。一个典型的探索过程描述如下：首先，通过安装在机器人上的激光扫描仪或其他检测传感器观察其周围环境，并将传感器数据转化为机器人的局部地图；其次，通过将新获取的局部地图与定位信息结合，更新环境的全局地图；最后，根据某种探索策略确定下一个最佳观察位置，机器人将在那里自主导航[6]。
1997年，Yamauchi[7]首次提出基于边界的探索策略，这是最著名的探索策略之一。其仅按距离进行选择，并没有考虑各个边界之间预期信息增益的差异。探索策略的另一个分支是随机搜索算法，通过在空间中随机采样来获取环境信息，其中最具代表性的算法之一为快速搜索随机树(rapidly-exploring random tree, RRT)算法[8]。RRT算法具有扩展速度快、搜索效率高等优点，但是传统RRT算法具有盲目性。针对上述算法的不足，Bircher等[9]提出一种策略来寻找具有最大信息增益的节点，以此来快速降低地图的熵。实际上，自主探索最关键的问题是根据当前的地图和机器人的位置确定下一个探索目的地，从而有效获得准确的环境地图[10]。
最早的信息理论探索策略由Whaite等[11]提出，他们提出探索先验未知环境的目标就是最大程度地降低地图熵。由于在3D环境中得到了大量的前沿点，直接使用会造成计算量过大[12]，因此，需要对前沿点进行筛选。Belavadi等[13]采用K-means聚类技术将前沿点划分为分区，将前沿集群的质心集合作为候选点集合，由成本函数进行评估。预测每一个候选点对地图熵值影响的成本巨大，当评估成本过大时，贝叶斯优化具有较大优势[14]。Bai等[15]提出将贝叶斯优化应用于预测互信息问题，其目的是预测候选点处的信息增益，快速降低地图的熵，探索未知环境并建图，但该方法存在过多冗余路径问题。
综合已有的研究成果，本文提出了一种基于多重信息增益的移动机器人探索算法。首先，提出一种将采用K-means聚类算法[16]对前沿点进行聚类与基于可通行区域提取候选点相结合的方法对候选点进行提取，该策略在降低候选点规模的同时也保证了对环境的完全探索；然后，采用贝叶斯优化构建环境高斯模型，对多重信息增益进行评估，使移动机器人使用较少的步数便可获得较大的收益。在考虑候选点信息增益的同时，不仅考虑对地图熵值的贡献，同时考虑距离成本，以此减少机器人的冗余路径，并确保环境信息的完整性。
1. 复合候选点提取策略
常见的一种提取候选点策略是在二维栅格地图上提取前沿点，在此基础上利用不同的几何规则选取候选点集合[17]，然后，对候选点集合进行评估以筛选出机器人下一个行进目标点，但是这种提取策略存在一些问题[18]，比如：机器人会更加倾向于探索前沿点，可能会造成环境信息的缺失和探索不完全。
本文采用一种候选点复合提取策略，即：机器人通过自身携带RGB-D相机感知当前位置的周围环境，使用占用栅格模型[19]将机器人所处连续环境离散化，作为机器人的环境模型。具体提取策略步骤如下：
1) 机器人通过RGB-D相机检测到边界点，即未知环境与已知环境的交界，并将其作为本次探索的初始前沿点集合。
2) 对初始前沿点集合采用K-means聚类算法进行聚类，保留聚类的中心，作为关键前沿点。
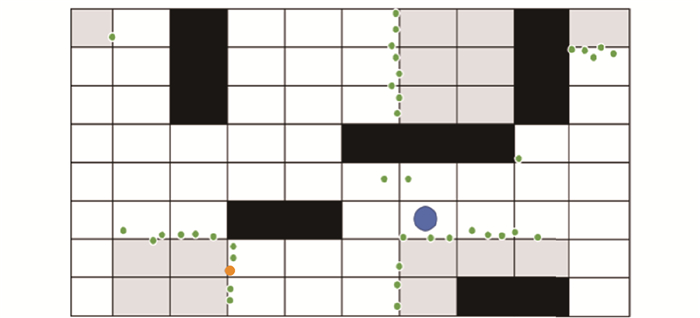
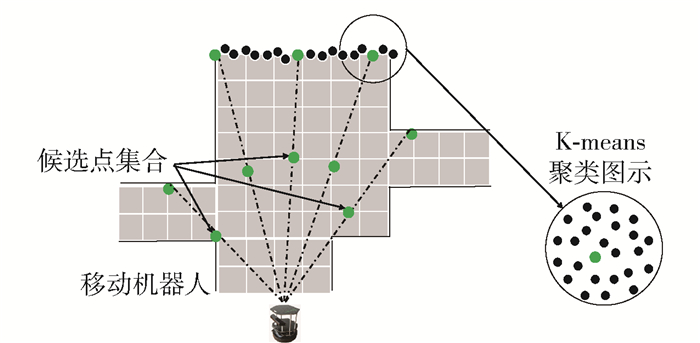
3) 从机器人当前位置向周围做不同角度的多条线段，延伸至关键前沿点处，将其作为第1个候选点，间隔距离d生成第2个候选点，直至机器人当前位置，剔除其中不在可通行区域中的点，至此完成一轮候选点集合提取，如图 1所示。
2. 多重信息增益评估策略
2.1 贝叶斯优化
2.1.1 基本贝叶斯优化算法
近年来，贝叶斯优化作为一种全局优化算法在科学研究与工业领域得到了广泛的应用[20]，通过设计合理的概率代理模型与采集函数，贝叶斯优化框架只需要经过数次迭代便可以得到理想解[21-22]，有效解决了序贯决策理论中经典的机器智能问题[23]，即：根据未知目标函数获取的信息，找到下一个评估位置，从而最快地达到最优解[24]，公式为
$$ x^*=\arg \max\limits _{x_i \in \chi } f\left(x_i\right) $$ (1) 式中：x*表示最佳位置；χ表示决策空间；xi表示决策变量；f(·)表示目标函数。贝叶斯优化的目标就是找到式(1)的最优解。
贝叶斯优化框架主要包括2个核心部分[25]：概率代理模型和采集函数。其中，概率代理模型用于代理未知目标函数，采集函数则是根据后验概率分布构造的。通过最大化采集函数选择下一个最优潜力的评估点，同时，有效的采集函数可以保证选择的评估点使得总损失最小。贝叶斯优化框架伪代码如算法1所示。
算法1 贝叶斯优化框架 1: 设xt为迭代t时选择的采样点 2: 设S为采集函数 3: for t=1, 2, … do 4: 通过采样域评估S(x) 5: 计算$ x_t=\arg \max\limits _{x_i \in \chi } f\left(x_i\right)$ 6: 在未知空间中随机采样 7: 利用新采样点更新高斯过程(Gaussian process，GP)模型 8: end for 2.1.2 高斯模型与采集函数
高斯过程是贝叶斯优化中常用的一种非参数统计模型，它将x∈χ中的每一个点建模为高斯随机变量[26]。在本文中，将机器人每一步所做的决策看作自变量x，x′为机器人即将到达的下一个位置，χ为机器人的动作空间，预测到达选定最佳候选点之后互信息的大小为f(x)，它完全由一个均值函数m(x)和协方差函数k(x，x′)来表示，公式为
$$ f(\boldsymbol{x}) \sim \mathrm{GP}\left(m(\boldsymbol{x}), k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\right) $$ (2) 式中：GP(·)为高斯过程函数；均值函数m(x)=E(f(x))；协方差函数k(x，x′)=E[(f(x)-m(x))· (f(x′)-m(x′))]。为了简单起见，通常设置均值函数m(x)=0。
当成功构建机器人环境模型之后，接下来的关键问题就是如何确定下一个迭代点。贝叶斯优化的最佳候选点是由采集函数计算而来，如式(1)所示，但是想要达到这种效果却并不简单。
一般情况下，将机器人所做决策分为2个部分[27]：一部分是探索，找到不同的方案，改进构建的高斯环境模型，若探索不足，将极易陷入局部最优，但过多探索又会消耗较多成本；另一部分是利用，在搜索过程中利用局部信息生成更好的解。过多的探索会减慢算法的收敛速度，过多的利用又会使机器人容易陷入局部最优，这就使得平衡探索和利用显得尤为重要。目前，比较常见的采集函数为改进期望(expected improvement, EI)、改进概率(probability of improvement, PI)、熵搜索(entropy search, ES)、高斯过程置信上界(Gaussian process-upper confidence bound, GP-UCB)等，本文采用GP-UCB完成采集功能，它是最直观的采集函数之一[28]，通过超参数来平衡探索和利用，公式为
$$ g(x)=\mu_t(x)+\sqrt{\beta_t} \sigma_t(x) $$ (3) 式中：μt(x)和σt(x)分别为从高斯回归过程中得到的预测均值和方差；βt为探索和利用之间的平衡参数。增加βt会使采集函数偏向方差高的点，引起更多的探索，而降低βt会使采集函数偏向均值较高的点，引起更多的利用，本文中βt=5.76。Thrun[29]证明了使用βt可以很好限制累计误差，保证整体的收敛速度。
2.2 多重信息增益算法
机器人自主探索环境问题可以描述为在移动机器人对环境没有先验知识的情况下，它必须对下一步的行进方向做出顺序决策[30]。对此，提出了一种基于贝叶斯优化预测信息增益与距离成本相结合的方法，选择机器人当前视野范围内信息最合适的位置作为候选点来探索环境。该算法的长期目标是减少机器人环境地图的熵，短期目标就是机器人在每一步决策时找到信息最大且距离合适的点。
2.2.1 单一信息增益算法
将机器人传感器可以测量到的空间定义为配置空间l∈ $\mathbb{R}^d $，其属于欧几里得空间的子集。假设机器人配备了RGB-D深度相机，机器人的环境模型为其占用栅格地图(单元格之间相互独立)，并且将占用栅格地图离散化以表示配置空间。在没有障碍物的情况下，机器人被认为能够从地图上的任一单元格到达任何其他的单元格。在占用栅格地图上定义香农熵[31]，公式为
$$ H(m)=-\sum\limits_i \sum\limits_j p\left(m_{i, j}\right) \log \left(m_{i j}\right) $$ (4) 式中：m为单元格；索引i表示地图中的单个单元；索引j表示每个网格单元的伯努利随机变量的可能结果，该网格是空闲的或者是已知占用的；p为单元格被占用或空闲的概率。若该单元格还未被观察到，则p(mij)=0.5，熵仅由未知的单元格决定，内容完全已知的单元格对地图熵值没有贡献。因此，仅通过地图熵值作为互信息I(m, xi)计算依据来评估关于特定位置单元格xi的期望信息增益，公式为
$$ I\left(m, x_i\right)=H(m)-H\left(m \mid x_i\right) $$ (5) 式中：H(m)是当前地图的信息熵；H(m|xi)是在xi处给定的一个新的传感器测量出来的地图的期望信息熵。目标就是选择最佳位置x*，使预期中传感器在此处探测的信息增益最大化，公式为
$$ x^*=\arg \max\limits _{x_i \in l_{\text {action }}} I\left(m, x_i\right) $$ (6) 式中laction表示机器人配置空间的子集，机器人下一个要行进的目标点将从中选取。探索过程如图 2所示。图中：蓝色的点为机器人当前位置；绿色的点为当前候选点集合；橙色的点为经过贝叶斯优化评估后机器人选定的最佳候选点。
2.2.2 多重信息增益算法
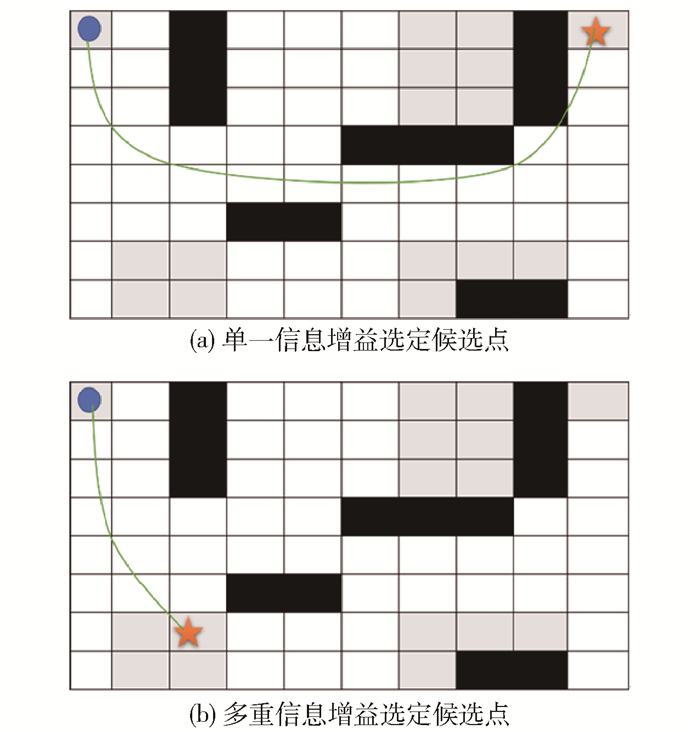
在地图探索过程中，发现仅凭熵值一种判定条件来计算互信息时会出现过多的冗余路径，尤其在地图面积较大、探索接近完备时，这种情况尤为严重。图 3(a)展示了仅凭熵值判断下一个最佳候选点会出现的情况，白色栅格为已知区域，黑色为障碍物，灰色为未知区域，蓝色的点为机器人当前位置，五角星为机器人选定的最佳候选点，绿色实线为机器人自动规划的路径。在不考虑路径成本的情况下，机器人选择距离自己较远的右侧目标点进行探索，但是距离自己较近的区域还未完成探索，故机器人势必还要返回左侧，由此就产生了冗余路径，希望机器人探索过程如图 3(b)所示，因此，在熵值差异不是特别大时，优先选择距离自己较近的点，以此来减少机器人的重复路径，提高探索的效率。图 3(b)展示了加入距离成本之后对最佳候选点的选取过程。由此，本文提出了一种地图熵值与距离成本相结合的多重信息增益算法，公式为
$$ \begin{gathered} I\left(m, x_i\right)= \\ \alpha\left(H(m)-H\left(m \mid x_i\right)\right)+(1-\alpha) \operatorname{DC}\left(x, x_i\right) \end{gathered} $$ (7) ![]()
图 3 2种算法选定最佳候选点的轨迹对比Figure 3. Comparison of trajectories of the best candidate points selected by the two algorithms式中：α为信息-距离因子，取值范围为0~1；DC(x, xi)为x到xi的距离函数，DC(x, xi)=1/d, 其中d为x到xi的曼哈顿距离，即
$$ d=\left|a_1-a_2\right|+\left|b_1-b_2\right| $$ (8) 式中：(a1，b1)为x的二维坐标；(a2，b2)为xi的二维坐标。在本文所搭建的仿真环境中共进行了60次探索。将这60次探索分成6组，保持其他因素不变，仅将α的取值作为变量，分别为0.1、0.2、0.3、0.5、0.7、0.8，每个取值分别进行10次实验。经过实验参数调整和探索验证，当取值为0.2时，对最佳候选点的选取最为合理，此时探索情况最佳。当α取值为0时，对候选点的选取则退化为最近边界搜索；当α取值为1.0时，则仅考虑地图熵值，变为单一信息增益探索，故此时α的取值需要同时顾及熵值与距离的影响，以地图熵值为主、距离成本为辅，选取最优参数使机器人探索效率达到最佳。
2.2.3 整体探索算法
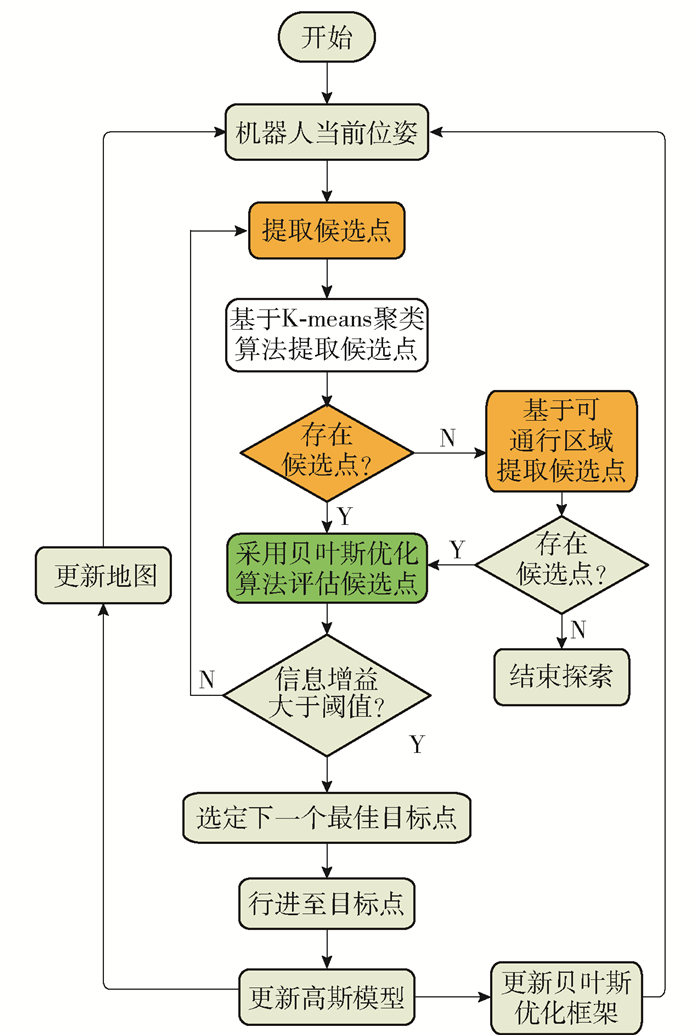
整体探索流程如图 4所示。其中，针对候选点提取部分，本文首先采用基于K-means聚类算法对前沿点进行聚类，在此基础上基于可通行区域来提取候选点，完成候选点提取部分工作，接着采用贝叶斯优化对候选点集合中的多重信息增益进行评估，选取最佳候选点，迭代此过程直至完成环境探索。具体实现步骤如下：
1) 初始化环境为栅格地图，初始化机器人位置信息与候选点集合。
2) 从机器人当前位置利用K-means聚类算法与基于可通行区域相结合的方式提取候选点集合。
3) 采用贝叶斯优化算法评估当前候选点集合，选取信息增益最大的候选点作为下一个目标点，利用A*算法进行路径规划。
4) 将当前动作加入历史动作集合，更新环境模型，更新贝叶斯优化框架并更新地图。
5) 判断是否存在候选点，存在则返回步骤2)继续探索，否则算法结束。
3. 实验结果
3.1 实验框架设计
为了验证本文提出算法的优越性，在Ubuntu 16.04中利用机器人操作系统(robot operating system，ROS)设计了多组仿真实验，将本文算法与传统的利用单一信息熵探索策略进行对比。
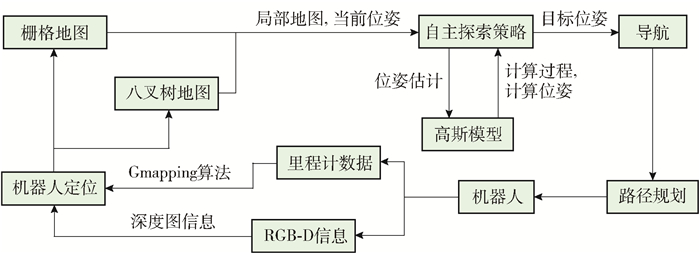
整体系统框架如图 5所示，机器人自身携带了里程计与RGB-D相机等传感器，通过底层depthimage_to_laserscan包与Gmapping算法等完成机器人定位，构建二维栅格地图，与此同时，利用机器人传入的RGB-D信息中的彩色图与深度图构建八叉树地图，之后将当前地图信息与机器人当前位姿作为本文提出的自主探索算法输入，计算下一个最佳候选点并更新环境的高斯模型，最后，在地图上进行路径规划到达目标点，迭代此过程直至环境探索完成。
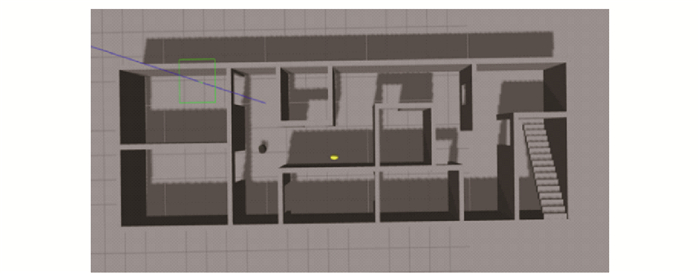
在Gazebo中搭建10 m×30 m的室内环境，如图 6所示。使用Turtlebot机器人搭载了RGB-D相机作为视觉传感器，让机器人在上述环境中自主探索，同时构建地图。
3.2 传统RRT随机采样探索策略
采用传统的随机搜索边界点算法探索环境，以其中具有代表性的RRT为例，不考虑地图熵值等，在空间中随机扩展节点，由于RRT具有偏向未知环境的特性，随着树的不断生长，边界点也会被一一检测。在同时检测到多个边界点时，直接选取最近的边界点作为机器人下一个行进目标，实际上自主探索最关键的问题就是如何快速有效地遍历整个环境。该算法仅将边界点作为机器人候选点且仅选取最近边界点作为下一个目标点。在探索初期，因为环境大部分是未知的，RRT的生长空间很大，所以探索较为快速。但是随着树的生长，空间被分为越来越小的Voronoi区域，此时探索速率开始下降，另外，由于该算法仅将边界点作为候选点，并不能完整遍历环境，会丢失部分环境信息。
图 7为采用传统RRT算法探索环境的过程，可以看到环境的一些小角落并没有被探索到，环境信息存在缺失，最终并没有构建出完整的二维栅格地图，故此不采用其构建八叉树地图。
3.3 单一信息增益探索策略
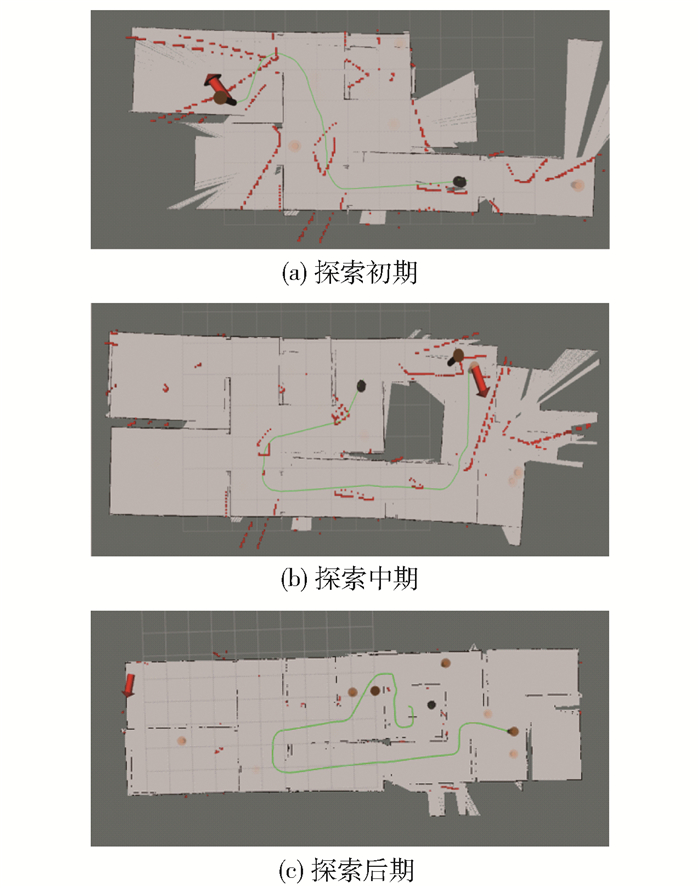
基于传统RRT算法存在的不足，足以证明有目的地选取候选点集合以及考虑地图熵值是十分有必要的，因此，采用基于传统贝叶斯优化的单一信息增益探索策略对环境进行探索，探索过程如图 8所示。图中：红色的箭头为机器人选定的最佳候选点；绿色的实线为机器人规划的路径；红色的小方点为构建八叉树地图的过程展示。虽然传统的探索策略可以基本保证探索完成，但是在探索的过程中存在过多的冗余路径，不仅浪费了时间，也消耗了较多的能量，在危险环境中仅仅依靠机器人探索环境的话，显然是不可取的。
![]()
图 8 使用单一信息增益机器人的探索轨迹Figure 8. Trajectory exploration using a single information gain robot3.4 多重信息增益探索策略
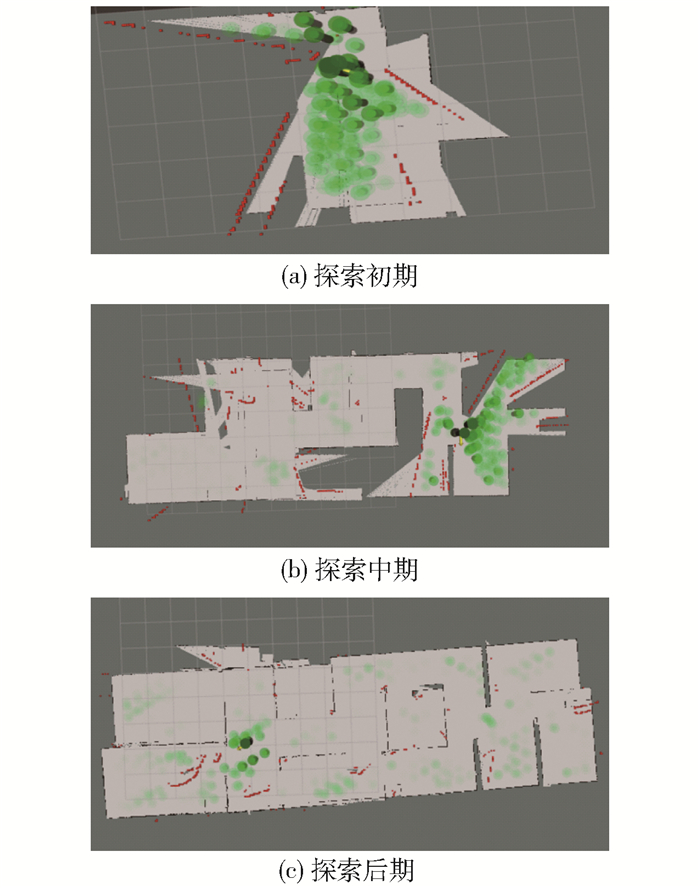
使用本文提出的贝叶斯优化多重信息探索策略对环境进行探索，探索过程如图 9所示。图中绿色的点为机器人的候选点集合，深绿色的点为机器人选定的最佳候选点，候选点是基本可以覆盖全局的，但是最佳候选点往往是距离机器人较近的点。本文算法在选取最佳候选点时考虑了距离成本，因此，最终评估选定的候选点距离机器人更近，更加合理，这样可以保证在较大的未知环境中探索时，机器人尽量将自身周围区域地图构建完成后再向较远的区域探索，避免较多的冗余路径产生。在传统的单一信息增益探索策略基本完成探索的基础之上，本文算法不仅可以很好地完成探索，并且去除了大量的冗余路径。最终2种算法构建的八叉树地图如图 10所示。使用单一信息增益和多重信息增益构建的八叉树地图在精度上基本保持一致。
![]()
图 9 使用多重信息增益机器人的探索轨迹Figure 9. Trajectory exploration using multiple information gain robots3.5 实验结果与分析
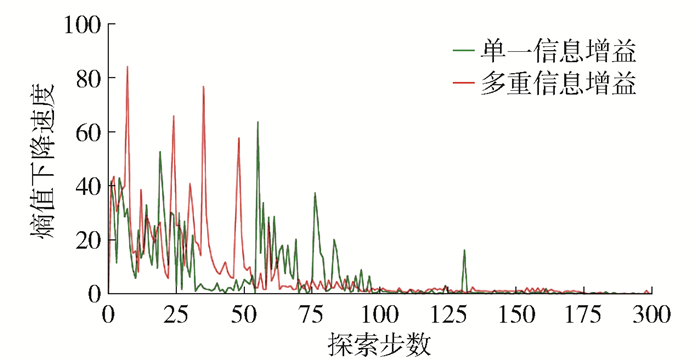
在地图熵下降速度与探索步数上的对比结果如图 11所示。
![]()
图 11 2种算法地图熵值下降速度曲线对比Figure 11. Comparison of map entropy decreasing speed curves between the two algorithms图 11中显示的是地图熵下降速度，值越高，表明地图熵值下降越快。由于传统RRT算法并未考虑地图熵值这一重要因素，此处仅为基于信息增益算法的对比，纵坐标为熵值下降速度，波动较大时说明地图还未探索完成且取值越大表明机器人到达该位置时地图熵值下降越快，红色曲线为多重信息增益探索策略，绿色曲线为单一信息增益探索策略，大部分时候都是本文算法选取的互信息值比较大且在100步左右就已经接近平稳了，仅凭单一信息的探索策略在第130步的时候还出现了较大波动，说明地图此时还没有探索完成，由此可见，在选取候选点时将距离成本考虑进去可以使机器人用更少的步数完成探索。
分别重复上述实验30次，并对步数进行统计。该步数为机器人探索完成环境所需步数，虽然采用传统RRT算法会丢失部分环境信息，本文依然统计了传统RRT算法完成构建大部分环境所用步数，步数为216步，没有合理地选取候选点集合且对下一步行进目标点选取较为简略，造成了探索不完全且冗余路径较多的情况。使用单一信息增益探索环境平均所需步数为145步，采用多重信息增益探索环境平均所需步数为112步。
结果显示，本文提出的算法在冗余路径上有较大改进，主要原因是在提取目标时采用基于K-means聚类算法对前沿点进行聚类，有效减少了前沿点的个数，但是仅从前沿点处筛选候选点可能会使机器人丢失部分环境信息，因此，本文将采用K-means聚类算法对前沿点进行聚类与基于可通行区域提取候选点策略相结合，保证了探索环境的完整性，并且在评估最佳候选点的同时还考虑了距离成本，相较于仅考虑地图熵这一单一信息增益来说，在贝叶斯优化评估过程中增加了一步对于距离函数的计算，由于本文采用基础的曼哈顿距离公式计算距离，较为简单，并不会过多增加整个贝叶斯优化流程的计算成本。实验结果表明，本文提出的算法考虑距离因素可以有效减少机器人的冗余步数，节省探索成本。
4. 结论
1) 在提取候选点时，本文采用K-means聚类算法对前沿点进行聚类，使用基于可通行区域提取候选点策略扩展候选点集合，将二者结合相对于传统的采用前沿点检测算法来说，保证了计算量不会过大的同时，也保证了探索过程中不会丢失环境信息，机器人可以完整地遍历整个环境。
2) 与基于传统的贝叶斯优化单一信息增益探索策略相比，本文所提出的算法将地图熵值与距离成本共同作为信息增益来评估最佳候选点，在探索过程中，冗余路径会大大降低，有效提高了机器人探索效率。
-
![]()
图 3 2种算法选定最佳候选点的轨迹对比
Figure 3. Comparison of trajectories of the best candidate points selected by the two algorithms
![]()
图 8 使用单一信息增益机器人的探索轨迹
Figure 8. Trajectory exploration using a single information gain robot
![]()
图 9 使用多重信息增益机器人的探索轨迹
Figure 9. Trajectory exploration using multiple information gain robots
![]()
图 11 2种算法地图熵值下降速度曲线对比
Figure 11. Comparison of map entropy decreasing speed curves between the two algorithms
算法1 贝叶斯优化框架 1: 设xt为迭代t时选择的采样点 2: 设S为采集函数 3: for t=1, 2, … do 4: 通过采样域评估S(x) 5: 计算$ x_t=\arg \max\limits _{x_i \in \chi } f\left(x_i\right)$ 6: 在未知空间中随机采样 7: 利用新采样点更新高斯过程(Gaussian process，GP)模型 8: end for 
下载: 导出CSV
-
[1] 曹风魁, 庄严, 闫飞, 等. 移动机器人长期自主环境适应研究进展和展望[J]. 自动化学报, 2020, 46(2): 205-221. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202002001.htm CAO F K, ZHUANG Y, YAN F, et al. Research progress and prospect of long-term autonomous environment adaptation for mobile robots[J]. Acta Automatica Sinica, 2020, 46(2): 205-221. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202002001.htm
[2] CASTELLANOS J A, MONTIEL J, NEIRA J, et al. The SPmap: a probabilistic framework for simultaneous localization and map building[J]. IEEE Transactions on Robotics and Automation, 1999, 15(5): 948-952. doi: 10.1109/70.795798
[3] 罗元, 傅有力, 程铁凤. 基于改进Rao-Blackwellized粒子滤波器的同时定位与地图构建[J]. 控制理论与应用, 2015(2): 267-272. https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201502019.htm LUO Y, FU Y L, CHENG T F. Simultaneous localization and map construction based on improved Rao-Blackwellized particle filter[J]. Control Theory and Applications, 2015(2): 267-272. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201502019.htm
[4] 贾建华, 张静. 基于GIS的矿井救援机器人定位导航研究[J]. 煤炭科学技术, 2010(5): 76-79. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201005024.htm JIA J H, ZHANG J. Research on localization and navigation of mine rescue robot based on GIS[J]. Coal Science and Technology, 2010(5): 76-79. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201005024.htm
[5] PIMENTEL J M, ALVIM M S, CAMPOS M F M, et al. Information-driven rapidly-exploring random tree for efficient environment exploration[J]. Journal of Intelligent & Robotic Systems, 2018, 91(2): 313-331.
[6] AMIGONI F, CAGLIOTI V. An information-based exploration strategy for environment mapping with mobile robots[J]. Robotics & Autonomous Systems, 2010, 58(5): 684-699.
[7] YAMAUCHI B. A frontier-based approach for autonomous exploration[C]//Proceedings of 1997 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Piscataway: IEEE, 1997: 146-151.
[8] UMARI H, MUKHOPADHYAY S. Autonomous robotic exploration based on multiple rapidly-exploring randomized trees[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway: IEEE, 2017: 1396-1402.
[9] BIRCHER A, KAMEL M, ALEXIS K, et al. Receding horizon "next-best-view" planner for 3D exploration[C]//IEEE International Conference on Robotics and Automation. Piscataway: IEEE, 2016: 1462-1468.
[10] 李秀智, 龚月, 张祥银, 等. 一种室内移动机器人自主探索方法[J]. 控制与决策, 2019, 34(6): 1227-1233. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201906013.htm LI X Z, GONG Y, ZHANG X Y, et al. An autonomous exploration method for an indoor mobile robot[J]. Control and Decision, 2019, 34(6): 1227-1233. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201906013.htm
[11] WHAITE P, FERRIE F P. Autonomous exploration: driven by uncertainty[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(3): 193-205. doi: 10.1109/34.584097
[12] GOLDMAN R E, BAJO A, SIMAAN N. Algorithms for autonomous exploration and estimation in compliant environments[J]. Robotica, 2013, 31(PT. 1): 1146-1150.
[13] BELAVADI S S, BEIR R, MALIK V. Frontier exploration technique for 3D autonomous SLAM using K-means based divisive clustering[C]//2017 Asia Modelling Symposium. Piscataway: IEEE, 2017: 95-100.
[14] FONTANELLI D, SHAMSFAKHR F, MACII D, et al. An uncertainty-driven and observability-based state estimator for nonholonomic robots[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-12.
[15] BAI S, WANG J, CHEN F, et al. Information-theoretic exploration with Bayesian optimization[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway: IEEE, 2016: 1816-1822.
[16] KANUNGO T, MOUNT D M, NETANYAHU N S, et al. A local search approximation algorithm for k-means clustering[J]. Computational Geometry, 2004, 28(2/3): 89-112.
[17] 李秀智, 邱欢, 贾松敏, 等. 基于动态精简式混合地图的移动机器人自主探索[J]. 控制与决策, 2017, 32(5): 817-822. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201705007.htm LI X Z, QIU H, JIA S M, et al. Autonomous exploration of mobile robot based on dynamic compact hybrid map[J]. Control and Decision, 2017, 32(5): 817-822. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201705007.htm
[18] 阮晓钢, 周静, 张晶晶, 等. 基于子目标搜索的机器人目标导向RRT路径规划算法[J]. 控制与决策, 2020, 35(10): 2543-2548. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202010028.htm RUAN X G, ZHOU J, ZHANG J J, et al. Robot goal-directed RRT path planning algorithm based on sub-target search[J]. Control and Decision, 2020, 35(10): 2543-2548. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202010028.htm
[19] MORAVEC H, ELFES A. High resolution maps from wide angle sonar[C]//Proceedings of 1985 IEEE International Conference on Robotics and Automation. Piscataway: IEEE, 1985, 2: 116-121.
[20] PELIKAN M. Bayesian optimization algorithm[M]//Hierarchical Bayesian Optimization Algorithm. Berlin: Springer, 2005: 31-48.
[21] SHAHRIARI B, SWERSKY K, WANG Z, et al. Taking the human out of the loop: a review of Bayesian optimization[J]. Proceedings of the IEEE, 2015, 104(1): 148-175.
[22] FRAZIER P I. Bayesian optimization[M]//Recent Advances in Optimization and Modeling of Contemporary Problems. Cambridge: Cambridge University Press, 2018: 255-278.
[23] LIU D, XUE S, ZHAO B, et al. Adaptive dynamic programming for control: a survey and recent advances[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 51(1): 142-160.
[24] VEERAVALLI V V. Sequential decision fusion: theory and applications[J]. Journal of the Franklin Institute, 1999, 336(2): 301-322.
[25] 崔佳旭, 杨博. 贝叶斯优化方法和应用综述[J]. 软件学报, 2018, 29(10): 3068-3090. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201810011.htm CUI J X, YANG B. A review of Bayesian optimization methods and applications[J]. Journal of Software, 2018, 29(10): 3068-3090. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201810011.htm
[26] CONTAL E PERCHET V, VAYATIS N. Gaussian process optimization with mutual information[C]//International Conference on Machine Learning. New York: PMLR, 2014: 253-261.
[27] 张明状. 移动机器人室内环境自主探索与认知[D]. 大连: 大连理工大学, 2009. ZHNANG M Z. Autonomous exploration and cognition of indoor environment for mobile robots[D]. Dalian: Dalian University of Technology, 2009. (in Chinese)
[28] WANG Z, ZHOU B, JEGALKA S. Optimization as estimation with Gaussian processes in bandit settings[C]//Artificial Intelligence and Statistics. New York: PMLR, 2016: 1022-1031.
[29] THRUN S. Probabilistic robotics[J]. Communications of the ACM, 2002, 45(3): 52-57.
[30] PELIKAN M. Bayesian optimization algorithm[M]//Hierarchical Bayesian Optimization Algorithm. Berlin: Springer, 2005: 31-48.
[31] 程昌秀, 陆峰, 牛方曲. 栅格地图信息量计算方法的验证分析[J]. 地球信息科学, 2006, 8(1): 127-130. https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX200601026.htm CHENG C X, LU F, NIU F Q. Verification of raster-based map information measurement[J]. Journal of Geo-Information Science, 2006, 8(1): 127-130. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX200601026.htm
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 133
- HTML全文浏览量: 21
- PDF下载量: 44
- 被引次数: 1
