Method of Feature Weight Optimization Based on Grey Wolf and Bird Swarm Algorithm
-
摘要:
针对特征权重难以准确量化的问题, 提出一种基于灰狼优化(grey wolf optimizer, GWO)算法和鸟群算法(bird swarm algorithm, BSA)的混合算法, 用于特征权重的寻优。首先, 将Chebyshev映射、反向学习与精英策略用于混合算法的初始种群生成; 其次, 将改进后的GWO算法位置更新策略融入BSA的觅食行为中, 得到一种新的局部搜索策略; 然后, 将BSA的警觉行为与飞行行为用作混合算法的全局搜索平衡策略, 从而得到一种收敛的灰狼-鸟群算法(grey wolf and bird swarm algorithm, GWBSA), 通过GWBSA的迭代寻优可获得各特征的权重值。利用标准测试函数和标准分类数据集进行了对比实验, 与遗传算法、蚁狮算法等方法相比, GWBSA具有较快的收敛速度且不易陷入局部最优, 可以提高模式分类问题的求解质量。
-
关键词:
- 特征权重 /
- 灰狼优化(grey wolf optimizer, GWO)算法 /
- 鸟群算法(bird swarm algorithm, BSA) /
- 混合算法 /
- 问题求解 /
- 模式分类
Abstract:To solve the problem that the feature weights are difficult to quantify accurately, a hybrid algorithm based on grey wolf optimizer (GWO) algorithm and bird swarm algorithm (BSA) was proposed to optimize the feature weights. First, Chebyshev map, opposition-based learning and elitism strategy were used to initialize the population of the hybrid algorithm. Second, the location updating formula of GWO algorithm and the foraging behavior of BSA were combined as the improved location updating strategy of the algorithm for local search. Then, the vigilance behavior and flight behavior of BSA were integrated into the hybrid algorithm to obtain a balance strategy for global search. A convergent grey wolf and bird swarm algorithm (GWBSA) was obtained, and the feature weights were optimized through the iteration of GWBSA. Experiments were carried out by using benchmark functions and standard classification data sets, respectively. Compared with the genetic algorithm, the ant lion algorithm and other algorithms, the GWBSA has fast convergence speed and is hard to fall into local optimum, which can improve the solution quality of pattern classification problems.
-
在模式识别[1]、数值预测[2]或多属性决策[3]等领域经常涉及特征权重的评估与赋值。特征权重是指某一特征在整个特征集中的相对重要程度,权重值的分配情况会直接影响问题求解的质量。权重分配方法的收敛性、计算效率等对分类、预测、决策的科学性、正确性等性能具有重要作用。因此,特征权重的分配方法是研究人员广泛关注的热点问题。
国内外研究表明,权重分配方法主要包括主观赋权法、客观赋权法及主客观组合赋权法。主观赋权法包括专家评估法[4]、德尔菲法[5]、层次分析法[6]等。其中:专家评估法和德尔菲法是由专家根据已有的经验或知识对权重进行评估;层次分析法将定性分析与定量分析相结合,由多个专家进行群体决策来分配权重。主观赋权方法往往缺乏客观可信的依据,从而导致赋权结果存在主观性、不确定性等。为了避免这些缺陷,一些客观赋权法被相继提出,比如遗传算法(genetic algorithm, GA)[7]、神经网络法[8]、熵权法[9]等。GA通过对权重不断迭代寻优找到最优权重来模拟生物进化的规律,具有灵活、运行方便等优点,但其收敛速度慢且易陷入局部最优。神经网络通过训练样本得到计算特征权重的模型,但它依赖于样本的分布和数量情况,在应用时具有一定局限性。熵权法利用信息熵计算出各特征的熵权,再通过熵权对各特征的权重进行修正,如果样本不断更新变化则会使得权重值产生较大的波动。除上述主客观赋权法外,也有将它们结合起来形成主客观组合赋权法[10],这类方法虽然结合了主观法与客观法各自的特点,但其计算过程可能会很复杂,所得结果具有一定随机性。综上,虽然不同的权重分配方法均取得了一定的应用成效,但在方法的收敛性、计算效率等性能方面还存在提高的空间,特征权重的分配方法仍需进一步研究。
群体智能优化算法起源于各种自然现象,比如兽群、鸟群、鱼群的群体觅食行为,这些方法的显著特点是不需要先验知识,通过生成一组或多组解决方案,并让这些解决方案在迭代过程中不断完善,可以应用于包括特征权重分配等许多领域的优化求解问题。目前,已经提出许多群体智能算法,比如:粒子群算法[11]、人工蜂群算法[12]、人工蚁群算法[13]、萤火虫算法[14]、蚁狮优化(ant lion optimizer, ALO)算法[15]等。灰狼优化(grey wolf optimizer, GWO)算法由Mirjalili等[16]提出,该算法模拟了灰狼的狩猎行为。在GWO算法中,由α、β、γ狼搜索猎物的位置信息,ω狼在α、β、γ狼的指导下逐步向猎物包围,在不断迭代探索的过程中逐步找到猎物所在位置,即近似最优解。GWO算法对最优解有较好的收敛能力,在局部搜索方面也有一定的优势,但GWO算法缺乏全局搜索策略,随着迭代过程的不断进行,GWO算法中的灰狼可能经历数代而位置都不再发生变化,进而会脱离全局搜索区域,陷入局部最优[17],导致GWO算法无法找到全局最优解。鸟群算法(bird swarm algorithm, BSA)由Meng等[18]提出,该算法分析鸟类的群体行为,通过模拟鸟群的觅食行为、警觉行为和飞行行为构建模型,并根据上述行为策略获得最优解。BSA的警觉行为与飞行行为使得它具有较好的全局搜索能力,不易陷入局部最优,但BSA在局部搜索时个体仅参照单一方向[19],效率欠佳。
综合上述分析,针对GWO算法和BSA初始种群随机生成后在解空间中分布不均匀、多样性较差的问题[20-21],首先,使用Chebyshev映射[22]生成的混沌序列与反向学习生成的解作为初始种群,并采用精英策略保留初始种群中适应度较高的个体;然后,将改进的GWO算法的位置更新策略融入BSA中,形成一种混合的灰狼-鸟群算法(grey wolf and bird swarm algorithm, GWBSA),并对函数最小值问题进行优化求解,结果表明该算法的收敛性能与寻优能力得以提升;最后,将GWBSA应用于特征权重的迭代寻优,并通过实验验证了GWBSA优化分配权重方法的有效性。
1. 基于GWBSA的权重分配
1.1 GWBSA的实现
1.1.1 种群初始化策略
随机分布函数生成的初始种群分布不均匀、多样性较差,而混沌映射生成的种群具有分布均匀、多样性丰富的特点[23],因此,为提高GWBSA的收敛速度、避免算法陷入局部最优,使用混沌映射来生成初始种群。Chebyshev映射是一种常见的混沌映射,具体表达式为
$$ \theta(k+1)=\cos (\mu \cdot \arccos (\theta(k))) $$ (1) 式中:θ为迭代时生成的随机数,-1≤θ≤1;k为迭代次数,由1逐渐迭代到N(N为种群数目);μ为控制参数,μ≥2。根据式(1),首先生成混沌种群Xc={Xi, i=1, 2, …, N},其中个体Xi={Xid, d=1, 2, …, D},D为个体Xi的维度,Xid的公式为
$$ X_{i d}=L+|\theta(k)| \cdot(U-L) $$ (2) 式中U和L分别为有约束优化问题的上边界和下边界。在此基础上,为了使算法探索到更广泛的可行解空间,提高优化算法的收敛速度,通过反向学习[24]生成混沌种群Xc的反向种群Xo={Xj, j=1, 2, …, N},其中个体Xj={Xjd, d=1, 2, …, D},Xjd的公式为
$$ X_{j d}=L+U-X_{i d} $$ (3) 最后,将混沌种群Xc与反向种群Xo合并,并采取精英策略[25]保留种群中适应度较高的个体。以选定N个初始种群为例,生成的初始种群Xm为
$$ \boldsymbol{X}_{\mathrm{m}}=\text { best } N \text { of }\left(\boldsymbol{X}_{\mathrm{c}} \cup \boldsymbol{X}_{\mathrm{o}}\right) $$ (4) 1.1.2 局部搜索策略
在GWO算法迭代过程中,所有的ω狼都必须依照α、β、γ狼的位置进行更新,这种更新机制会导致算法过早收敛,在迭代后期局部搜索能力欠佳[26],原因是对α、β、γ狼的位置信息求均值的方式未能突出这3只狼的各自作用,使得ω狼不能更为有效地探索搜索空间。因此,采用文献[27]中的自适应系数替代ω狼位置更新公式中的平均配比,以平衡算法在迭代前后期的搜索能力。同时,文献[26]指出,GWO算法中γ狼冗余,影响算法的局部搜索能力,因此,在GWBSA中仅保留α、β狼,并采用该文献中的非线性自适应平衡概率动态地向α、β狼的方向或α狼的方向更新ω狼的位置,进一步加快算法的收敛速度。改进后的ω狼的合成位置公式为
$$ \boldsymbol{X}_{\mathrm{g}}(t+1)= \begin{cases}\delta_1 \cdot \boldsymbol{X}_1(t)+\delta_2 \cdot \boldsymbol{X}_2(t), & r \leqslant p \\ \boldsymbol{X}_1(t), & r>p\end{cases} $$ (5) 式中:t为当前迭代次数;Xg(t+1)为第t+1次迭代时ω狼的合成位置;X1(t)、X2(t)分别为ω狼第t次迭代时向α、β狼方向更新后的位置[16];r为(0, 1)中的随机数;δ1和δ2为自适应系数,均为正数且δ1+δ2=1;p为非线性自适应平衡概率,0 < p < 1。公式分别为
$$ \left\{\begin{array}{l} \boldsymbol{X}_1(t)=\boldsymbol{X}_\alpha(t)-\boldsymbol{A}_1 \cdot D_\alpha(t) \\ \boldsymbol{X}_2(t)=\boldsymbol{X}_\beta(t)-\boldsymbol{A}_2 \cdot D_\beta(t) \end{array}\right. $$ (6) $$ \left\{\begin{array}{l} \delta_1=\frac{\left|\boldsymbol{X}_1(t)\right|}{\left|\boldsymbol{X}_1(t)\right|+\left|\boldsymbol{X}_2(t)\right|} \\ \delta_2=\frac{\left|\boldsymbol{X}_2(t)\right|}{\left|\boldsymbol{X}_1(t)\right|+\left|\boldsymbol{X}_2(t)\right|} \end{array}\right. $$ (7) $$ p=1-1.01\left(\frac{t}{t_{\mathrm{m}}}\right)^3 $$ (8) 式中:t为当前迭代次数;tm为最大迭代次数;Xα(t)、Xβ(t)分别为第t次迭代时α、β狼的位置;A1、A2为系数向量[16];Dα(t)、Dβ(t)分别为第t次迭代时ω狼与α、β狼的距离[16]。公式分别为
$$ \left\{\begin{array}{l} \boldsymbol{A}_1=2 a \cdot \boldsymbol{r}_1-a \cdot \boldsymbol{e} \\ \boldsymbol{A}_2=2 a \cdot \boldsymbol{r}_2-a \cdot \boldsymbol{e} \end{array}\right. $$ (9) $$ \left\{\begin{array}{l} D_\alpha(t)=\left|C_1 \cdot \boldsymbol{X}_\alpha(t)-\boldsymbol{X}_{\mathrm{g}}(t)\right| \\ D_\beta(t)=\left|C_2 \cdot \boldsymbol{X}_\beta(t)-\boldsymbol{X}_{\mathrm{g}}(t)\right| \end{array}\right. $$ (10) 式中:a为线性收敛参数[16],随着迭代次数的增加逐渐由2线性衰减到0;e为单位向量;r1、r2为每一维均在[0, 1]中的随机向量;Xg(t)为第t次迭代时ω狼的位置;C1、C2为系数参数[16]。公式分别为
$$ a=2\left(1-\frac{t}{t_{\mathrm{m}}}\right) $$ (11) $$ \left\{\begin{array}{l} C_1=2 r_3 \\ C_2=2 r_4 \end{array}\right. $$ (12) 式中r3、r4为[0, 1]中的随机数。
BSA中的觅食公式[18]利用了鸟类个体的历史最佳位置和当前的最佳位置,不仅可以完成鸟类个体的位置更新,而且具有较好的寻优能力,但觅食公式在迭代时仅参照当前最佳个体的位置,忽略了对其他个体位置信息的利用,因此,将觅食公式与式(5)相结合作为GWBSA的位置更新公式用于GWBSA的局部搜索。在改进的公式中,既保留了个体的历史最佳位置,同时融入了α、β狼位置信息,改善了觅食公式在局部搜索时仅参照单一方向的缺陷,公式为
$$ \begin{gathered} \boldsymbol{X}(t+1)=\boldsymbol{X}(t)+C \cdot r_5 \cdot[\boldsymbol{P}(t)-\boldsymbol{X}(t)]+ \\ S \cdot r_6 \cdot\left[\boldsymbol{X}_{\mathrm{g}}(t+1)-\boldsymbol{X}(t)\right] \end{gathered} $$ (13) 式中:X(t)、X(t+1)分别为第t、t+1次迭代时个体的位置;C和S为2个正实数,分别为认知加速因子和社会加速因子[18];P(t)为个体的历史最佳位置;r5、r6为(0, 1)中的2个随机数。
1.1.3 全局搜索平衡策略
文献[17]指出,GWO算法缺乏全局平衡策略,在迭代的后期,GWO算法中灰狼的位置可能收敛到一个局部空间而不再发生变化,从而导致GWO算法无法找到全局最优解。BSA中鸟类个体通过警觉行为与飞行行为展开全局搜索[18],可以避免算法陷入局部最优。因此,将BSA中个体的警觉行为与飞行行为作为GWBSA的全局搜索平衡策略。
1) 警觉行为
个体有一定的概率会跳出当前局部搜索位置并试图移动到群体的中心,它们不可避免地会相互竞争。因此,单个个体都不会直接向群体的中心移动,而会受到其他个体的干扰。这些动作可表述为
$$ \begin{gathered} \boldsymbol{X}_{\mathrm{v}}(t+1)=\boldsymbol{X}_{\mathrm{v}}(t)+B_1 \cdot r_7 \cdot\left(\boldsymbol{M}(t)-\boldsymbol{X}_{\mathrm{v}}(t)\right)+ \\ B_2 \cdot r_8 \cdot\left(\boldsymbol{X}_i(t)-\boldsymbol{X}_{\mathrm{v}}(t)\right), r_{\mathrm{v}}>p_{\mathrm{v}} \end{gathered} $$ (14) 式中:Xv(t)为警觉行为发生前个体的位置;Xv(t+1)为警觉行为发生后个体的位置;Xi(t)为第t次迭代过程中第i个个体的位置,i为[1, N]的随机正整数,Xi(t)≠Xv(t);r7、rv为(0, 1)的随机数;M(t)为当前所有个体的平均位置,即种群中心;r8为(-1, 1)的随机数;pv为警觉行为发生的概率,0.8≤pv≤1.0;B1和B2为某个个体试图移动到种群中心时,其他个体对该个体的影响因子,计算公式为
$$ \left\{\begin{array}{l} B_1=b_1 \cdot \exp \left(-\frac{f}{s+\varepsilon} \cdot N\right) \\ B_2=b_2 \cdot \exp \left(\frac{f-f_i}{\left|f-f_i\right|+\varepsilon} \cdot \frac{N \cdot f_i}{s+\varepsilon}\right) \end{array}\right. $$ (15) 式中:b1、b2为(0, 2)的2个正常数;f为Xv(t)的历史最佳适应度;fi为Xi(t)的历史最佳适应度;s为种群中所有个体的历史最佳适应度之和;ε为计算机中最小的常数(2.225 1×10-308),用来避免发生除零错误。
2) 飞行行为
种群全体会以一定的频率跳出当前局部搜索位置并在新的位置展开搜索,当到达一个新的位置时,种群中的个体会分为两部分:一部分为生产者,另一部分为乞食者。生产者和乞食者的行为可以分别用数学方法描述,公式为
$$ \left\{\begin{array}{l} \boldsymbol{X}_{\mathrm{p}}(t+1)=\boldsymbol{X}_{\mathrm{p}}(t)+r_9 \cdot \boldsymbol{X}_{\mathrm{p}}(t), \\ \boldsymbol{X}_{\mathrm{s}}(t+1)=\boldsymbol{X}_{\mathrm{s}}(t)+R \cdot r_{10} \cdot\left(\boldsymbol{X}_j(t)-\boldsymbol{X}_{\mathrm{s}}(t)\right), \\ t \% Q=0 \end{array}\right. $$ (16) 式中:Xp(t)、Xs(t)分别为飞行行为发生前生产者与乞食者的位置;Xp(t+1)、Xs(t+1)分别表示飞行行为发生后生产者与乞食者的位置;Xj(t)为乞食者中第j个个体的位置,j为[1, N]的随机正整数,Xj(t)≠Xs(t);r9为服从均值为0、标准差为1的高斯分布的随机数;r10为(0, 1)的随机数;R为(0, 2)的随机数,表示乞食者跟随生产者寻找食物的频率;%为求余运算符;Q为正整数,表示飞行行为发生的频率。
综上,通过种群初始化、局部搜索和全局搜索平衡3个策略,实现了GWBSA,见算法1。
算法1 GWBSA 输入:种群个体数目N, 特征维度D,上边界U,下边界L,最大迭代次数tm,认知加速因子C,社会加速因子S,警觉行为影响因子b1、b2,警觉行为发生概率pv,飞行行为频率Q,乞食者寻找食物频率R。 输出:最优个体Xα(t)。 1. 根据式(2)使用Chebyshev映射生成混沌种群Xc 2. 根据式(3)通过反向学习方法生成Xc的反向种群Xo 3. 根据式(4)合并混沌种群与反向种群,采取精英策略保留适应度排在前N的个体,生成初始种群Xm 4. 令当前迭代次数t=1 5. 根据式(8)(9)(11)(12)分别初始化p、A1、A2、a、C1、C2 7. while t < tm 8. 令Xα(t)表示当前适应度最高个体的位置, Xβ(t) 表示当前适应度次高个体的位置 9. if t mod Q=0 10. for每个ω狼个体 11. if rand≤pv 12. if rand≤p 13. 根据式(5)向α、β狼的方向更新ω狼的合成位置 14. else 15. 根据式(5)向α狼的方向更新ω狼的合成位置 16. end if 17. 根据式(13)更新个体的位置 18. else 19. 个体发生警觉行为,根据式(14)更新个体位置 20. end if 21. 通过式(11)更新参数a 22. 通过式(8)更新非线性自适应平衡概率p 23. 通过式(9) (12)更新A1、A2和C1、C2 24. end for 25. else 26. 将种群中的个体分为生产者与乞食者,并根据式(16)更新个体位置 27. end if 28.重新计算所有个体的适应度值 29.t=t+1 30.end while 31.返回最优个体Xα(t) 1.2 收敛性分析
根据文献[28]可知优化算法全局收敛需要满足的条件如下。
假设1 f(E(X, ξ))≤f(X)且如果ξ∈S, 有f(E(X, ξ))≤f(ξ)。式中:f为适应度函数;E为优化算法;ξ为E在迭代中曾经搜索到的解;S为可行解空间;X为S中的一个解。
满足假设1保证了E的适应度f(X)在迭代过程中是非递增的。
假设2 对于S的任意Borel子集A,如果其Lebesgue测度v(A)>0,则有
$$ \prod\limits_{t=0}^{\infty}\left[1-\mu_t(A)\right]=0 $$ (17) 式中μt(A)为算法第t次迭代搜索解在集合A上的概率测度。
满足假设2保证了E在连续无穷次迭代后搜索不到全局最优解的概率为0。
定理1 若E同时满足假设1与假设2,则有
$$ \lim _{t \rightarrow \infty} P\left(\boldsymbol{X}(t) \in R_{\varepsilon}\right)=1 $$ (18) 式中:X(t)为E在第t次迭代时的解;Rε为最优解集空间;P(X(t)∈Rε)为E在第t次迭代时X(t)在Rε中的概率。
定理1为E全局收敛的充要条件,即经历无穷多次迭代后,E能搜索到最优解的概率为1。
下面,根据上述条件证明GWBSA的全局收敛性。
引理1 GWBSA满足假设1。
证明 GWBSA每次迭代都要对最优解进行选择,即
$$ \boldsymbol{Z}(t)=\left\{\begin{array}{l} \boldsymbol{Z}(t), f[\boldsymbol{Z}(t)] \leqslant f[\boldsymbol{X}(t)] \\ \boldsymbol{X}(t), f[\boldsymbol{X}(t)] \leqslant f[\boldsymbol{Z}(t)] \end{array}\right. $$ (19) 式中Z(t)为第t次迭代时的全局最优解。
所以,GWBSA每次都保存最优解,保证了适应度是非递增的,满足假设1。
引理2 GWBSA满足假设2。
证明 在GWBSA中增加全局搜索策略,经历无穷多次迭代后有$v\left(\bigcup\limits_{t=0}^{\infty} B_t\right)=v(S)$(Bt为每次迭代时搜索的子空间),从而在0~∞中存在t,使得μt(A)=1,从而满足假设2。
引理3 GWBSA全局收敛。
证明 由引理1和引理2可知GWBSA满足定理1,从而可得GWBSA全局收敛。
1.3 GWBSA权重寻优
在模式分类领域,数据样本往往有若干个特征,这些特征对分类结果的影响不一,特别是以特征加权方式进行分类的机器学习方法对特征权重的分配较为敏感,如K近邻、案例推理方法等。为考察GWBSA对特征权重进行优化分配的效果,下面以案例推理分类器为例,给出GWBSA权重寻优的步骤。
步骤1 初始化参数:种群数目N,最大迭代次数tm,权重的上界U、下界L,认知加速因子C,社会加速因子S,警觉行为影响因子b1、b2,警觉行为发生概率pv,飞行行为发生频率Q,乞食者寻找食物频率R。
步骤2 记权重的符号为Ω (对应算法1中的X),根据算法1中1~3步生成初始权重种群。
步骤3 计算每组权重的适应度(即案例推理分类器的准确率),记种群中适应度最高的权重为Ωα,其次为Ωβ,剩余个体记为Ωω。
步骤4 根据算法1中9~27步对权重种群进行迭代寻优。
步骤5 若未达到最大迭代次数,转至步骤3,否则转至步骤6。
步骤6 返回最优权重解Ωα,GWBSA权重寻优结束。
2. 实验及结果
在1.1节中,通过改进种群初始化策略、局部搜索策略和全局搜索平衡策略,得到了GWBSA的整套算法,目标是实现局部与全局搜索的策略平衡,并对特征权重进行优化分配。为此,设计了2个实验:一是通过函数全局最小值迭代实验测试GWBSA的性能,二是通过权重寻优实验测试GWBSA的有效性。实验在MATLAB R2018b环境下通过编程实现,所用计算机CPU为Intel(R) Core(TM) i5-9300H CPU@ 2.40 GHz, 内存为8 GB,系统为WIN10 64位。
2.1 GWBSA性能测试
将仅包含1.1.1节改进初始种群生成策略的算法记为A1,仅包含1.1.2节改进局部搜索策略的算法记为A2。为了评估GWBSA的性能,选取了8个标准测试函数来测试算法求取函数最小值的性能,并与GA、ALO、GWO、BSA、A1和A2等算法进行对比。这8个标准测试函数如表 1所示。其中:f1(x)-f4(x)为单峰函数,f5(x)-f8(x)为多峰函数。文献[18]中的实验证实了令C=S=1.5时,算法具有较好的局部搜索能力;当令b1=b2=1、pv在[0.8, 1.0]中随机变化、R在[0.5, 0.9]中随机变化和Q=3时,算法具有良好的全局搜索平衡能力,同时,个体警觉行为发生的概率与飞行行为发生的频次也不至于过高,不会影响算法的局部搜索速度。为了保证实验的公平性,将BSA、A1、A2和GWBSA的参数均设为一致,避免参数不同对实验结果造成的影响,表 2给出了上述几种算法参数的详细设置情况。
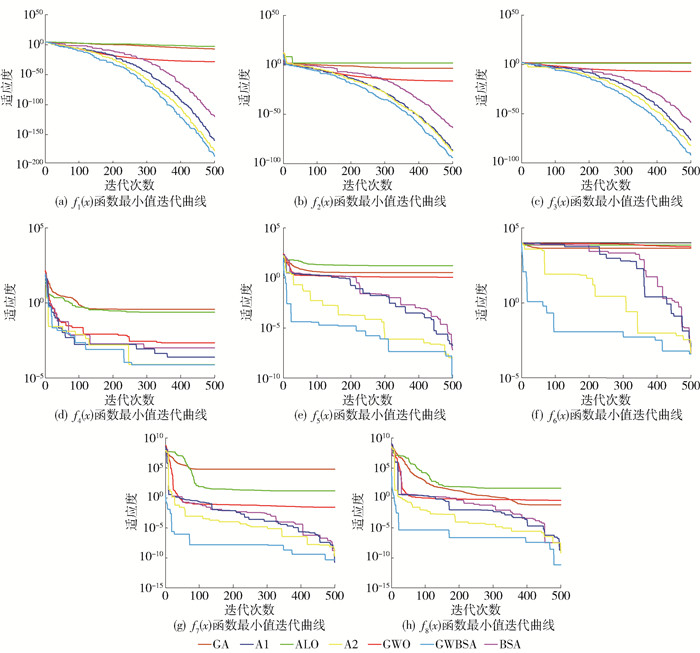
表 1 标准测试函数Table 1. Benchmark functions函数 维度n 定义域 最小值 $f_1(x)=\sum\limits_{i=1}^n x_i^2$ 30 [-100, 100] 0 $f_2(x)=\sum\limits_{i=1}^n\left|x_i\right|+\prod\limits_{i=1}^n\left|x_i\right|$ 30 [-10, 10] 0 $f_3(x)=\max_i\left\{\left|x_i\right|, 1 \leqslant x_i \leqslant n\right\}$ 30 [-100, 100] 0 $f_4(x)=\sum\limits_{i=1}^n i x_i^4+\operatorname{random}[0, 1)$ 30 [-1.28, 1.28] 0 $\begin{gathered} f_5(x)=\sin ^2\left({\rm{ \mathsf{ π} }} \omega_1\right)+\sum\limits_{i=1}^{n-1}\left(\omega_i-1\right)^2\left[1+10 \sin ^2\left({\rm{ \mathsf{ π} }} \omega_i+1\right)\right]+ \\ \left(\omega_n-1\right)^2\left[1+\sin ^2\left(2 {\rm{ \mathsf{ π} }} \omega_n\right)\right], \omega_i=1+\frac{x_i-1}{4} \end{gathered}$ 30 [-10, 10] 0 $f_6(x)=418.9829 n-\sum\limits_{i=1}^n x_i \sin \left(\sqrt{\left|x_i\right|}\right)$ 30 [-500, 500] 0 $\begin{array}{l} f_7(x)= \frac{{\rm{ \mathsf{ π} }}}{n}\left\{10 \sin \left({\rm{ \mathsf{ π} }} \omega_1\right)+\sum\limits_{i=1}^{n-1}\left(\omega_1-1\right)^2\left[1+10 \sin ^2\left({\rm{ \mathsf{ π} }} \omega_i+1\right)\right]+\left(\omega_i-1\right)^2\right\}+ \\ \sum\limits_{i=1}^n u\left(x_i, 10, 100, 4\right), \omega_i=1+\frac{x_i+1}{4}, \\ u\left(x_i, a, k, m\right)= \begin{cases}k\left(x_i-a\right)^m, & x_i>a \\ 0-a, & x_i <a \\ k\left(-x_i-a\right)^m, & x_i <-a\end{cases} \end{array}$ 30 [-50, 50] 0 $\begin{aligned} f_8(x)= & 0.1\left\{\sin ^2\left(3 {\rm{ \mathsf{ π} }} x_i\right) \sum\limits_{i=1}^n\left(x_i-1\right)^2\left[1+\sin ^2\left(3 {\rm{ \mathsf{ π} }} x_i+1\right)\right]+\right. \\ & \left.\left(x_n-1\right)^2\left[1+10 \sin ^2\left(2 {\rm{ \mathsf{ π} }} x_n\right)\right]\right\}+\sum\limits_{i=1}^n u\left(x_i, 5, 100, 4\right) \end{aligned}$ 30 [-50, 50] 0 为了保证实验的合理性,将所有的算法种群规模设置为30,将最大迭代次数设置为500,上述每种算法均独立运行30次,记录所求最小值的平均值与标准差,如表 3所示。表中黑体字为最佳结果。可以看出,在8个标准测试函数迭代实验过程中,GWBSA得到的函数最小值的平均值与标准差均为最佳,说明GWBSA的寻优精度远远高于其他算法且优化结果较为稳定。通过比较发现:GA、ALO算法和GWO算法缺乏全局搜索策略,在迭代后期易陷入局部停滞,因而寻优结果较差;BSA虽能跳出局部最优,但局部搜索能力欠佳,难以获得更优的结果;A1与A2相对于其他算法效果更佳,说明改进的种群初始化与局部搜索策略均能增强算法的寻优能力;A2的寻优精度高于A1,说明改进的局部搜索策略对算法性能的提升更为明显,而GWBSA优化效果又优于A1和A2,可以搜索到更好的全局最优解,说明上述改进策略结合后表现更好。
表 3 函数最小值的平均值与标准差Table 3. Mean and standard deviation of minimum value of functions函数 指标 GA ALO GWO BSA A1 A2 GWBSA f1(x) 平均值 1.41×10-1 1.31×10-3 1.42×10-27 1.63×10-123 2.67×10-159 5.08×10-171 3.36×10-186 标准差 2.15×10-1 1.18×10-3 1.83×10-27 3.58×10-123 0 0 0 f2(x) 平均值 9.17×100 4.55×101 1.07×10-16 5.81×10-60 1.82×10-81 7.23×10-86 5.12×10-95 标准差 6.67×10-0 5.40×101 8.49×10-17 1.70×10-59 3.08×10-81 1.93×10-85 7.68×10-95 f3(x) 平均值 2.40×101 1.62×101 8.58×10-7 1.52×10-57 1.37×10-70 8.71×10-79 3.30×10-90 标准差 4.79×100 3.86×100 8.00×10-7 1.90×10-57 4.33×10-70 2.75×10-78 8.38×10-90 f4(x) 平均值 7.76×10-1 2.66×10-1 2.07×10-3 6.69×10-4 3.51×10-4 1.47×10-4 3.66×10-5 标准差 1.26×10-1 6.86×10-2 9.28×10-4 4.37×10-4 2.32×10-4 1.04×10-4 2.18×10-5 f5(x) 平均值 3.00×101 1.09×101 1.14×100 7.79×10-8 8.59×10-9 2.18×10-9 2.58×10-10 标准差 1.19×101 3.81×100 2.20×10-1 7.25×10-8 8.31×10-9 4.11×10-9 2.82×10-10 f6(x) 平均值 5.05×103 7.08×103 6.23×103 1.87×10-3 8.16×10-4 4.78×10-4 4.04×10-4 标准差 1.17×103 6.53×101 5.60×102 2.10×10-3 3.75×10-4 7.66×10-5 4.99×10-4 f7(x) 平均值 6.99×102 1.18×101 4.67×10-2 2.67×10-9 1.33×10-9 3.50×10-10 4.43×10-11 标准差 1.22×102 4.40×100 2.15×10-2 1.78×10-9 1.27×10-9 3.25×10-10 4.27×10-11 f8(x) 平均值 3.91×102 2.63×101 6.20×10-1 2.27×10-8 1.29×10-8 4.82×10-9 4.24×10-10 标准差 4.61×102 1.94×101 2.70×10-1 2.25×10-8 1.27×10-8 7.37×10-9 5.14×10-10 各类算法在8个标准测试函数测试实验中的对比收敛见图 1。可以看出,在迭代过程中,GA、ALO算法和GWO算法过早收敛,陷入局部停滞,而全局搜索策略使得GWBSA可以快速跳出局部最优,具有较好的全局搜索能力。相较于BSA,GWBSA的收敛速度更快,说明使用混沌映射、反向学习与精英策略对种群初始化方式改进后,GWBSA的收敛性能显著提升且使用改进的位置更新公式后,GWBSA的局部搜索速度明显加快,具有较强的寻优能力与稳定性。
2.2 权重寻优实验
2.2.1 分类准确率测试
为了验证所提算法优化特征权重的有效性,选取5个UCI数据集对各特征的权重进行了寻优实验,数据集的具体信息如表 4所示。以文献[29]中的案例推理算法为例,考察了GWBSA与均权法(记为MA)、GA、ALO算法、GWO算法、BSA的实验结果。案例推理算法中的近邻数为1,权重寻优的所有算法种群规模设置为20,最大迭代次数设置为20。为了使结果数据具有统计学意义且验证算法中随机性对实验结果的影响,对各个方法分别进行30次重复实验并采取5折交叉实验,结果参见表 5,最佳结果以黑体标注。
表 4 数据集信息Table 4. Information of datasets编号 数据集名称 案例数 特征数 类别数 D1 Breast Cancer Wisconsin (Prognostic) 198 33 2 D2 Connectionist Bench (Sonar Mines vs Rocks) 208 60 2 D3 Glass Identification 214 9 6 D4 Statlog (Vehicle Silhouettes) 846 18 4 D5 Wine 178 13 3 表 5 分类准确率的实验结果对比Table 5. Comparison of experiment results of classification accuracy% 编号 MA GA ALO GWO BSA GWBSA D1 69.27 68.13 67.66 67.06 67.25 74.33 D2 77.83 78.80 78.31 78.47 78.56 81.01 D3 67.26 70.08 71.05 71.90 71.50 73.57 D4 68.92 70.57 70.69 70.71 70.93 71.26 D5 94.90 95.49 95.46 95.63 95.63 96.47 平均 75.64 76.61 76.63 76.75 76.77 79.33 以上实验结果显示,GWBSA所获得的分类准确率最高且优于GWO算法与BSA,说明混合后的GWBSA充分融合了二者的优势,实现了局部搜索与全局搜索的动态平衡,可以获得更好的全局最优权重,从而提高了分类准确率。
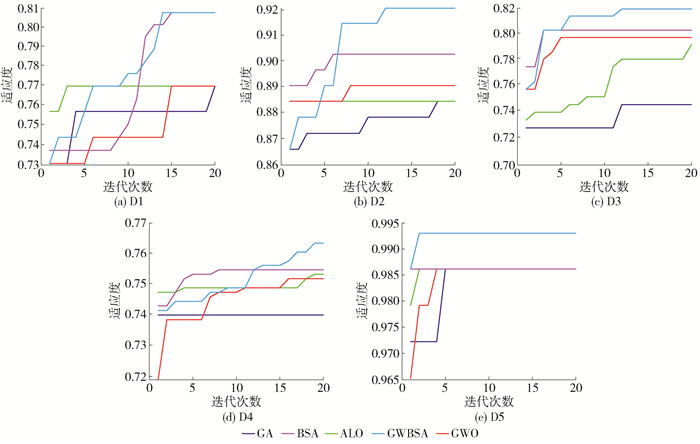
为进一步分析上述方法对特征权重的寻优性能,对权重寻优的迭代曲线进行了比较,如图 2所示。可以看出,GWBSA对特征权重的收敛速度与寻优精度明显高于其他算法,说明改进的种群初始化与局部搜索策略使得GWBSA相较于其他方法对特征权重优化问题的求解具有更好的收敛性能与收敛速度。
2.2.2 显著性检验
考虑到统计学中概率的影响,对分类实验结果进行了显著性检验,因样本量不大于30,故进行t检验。对GWBSA与MA采取单样本均值检验,GWBSA与其他方法之间采取两独立样本均值检验。假设显著性检测结果H={0, 1},当H=0时,表示分类结果无明显差异;当H=1时,表示GWBSA分类性能优于其他方法。设置显著水平α=0.01,当检验概率P大于α时,H=0;当P小于α时,H=1。具体检验结果如表 6所示,H=1时用黑体标记。
表 6 显著性检验Table 6. Significance test编号 指标 GWBSA-MA GWBSA-GA GWBSA-ALO GWBSA-GWO GWBSA-BSA D1 H 1 1 1 1 1 P 1.30×10-15 6.14×10-20 8.95×10-14 1.98×10-22 3.10×10-20 D2 H 1 1 1 1 1 P 5.92×10-17 5.08×10-8 9.56×10-15 3.17×10-9 6.48×10-10 D3 H 1 1 1 1 1 P 2.83×10-21 4.51×10-11 7.38×10-28 1.06×10-4 4.09×10-8 D4 H 1 1 1 1 1 P 1.65×10-16 3.81×10-5 2.26×10-27 1.53×10-3 7.27×10-8 D5 H 1 1 1 1 1 P 1.44×10-15 6.36×10-2 3.09×10-8 6.01×10-3 1.18×10-5 在5个分类数据集的对比结果中,GWBSA相对于其他分类器的H均为1,表明GWBSA可以显著提升分类器的准确率。可以看出,基于GWBSA的权重优化分配方法可以明显提升分类器的性能,相较于GA、ALO算法、GWO算法和BSA等优化方法,GWBSA对特征权重的优化效果更为显著。
综上所述,函数迭代的实验结果验证了GWBSA具有较高的收敛性能与收敛速度;分类实验的结果表明GWBSA相较于其他权重分配方法可有效挖掘出特征中潜在的重要信息,获得更合理的权重值,进而提高了模式分类问题的求解质量。
3. 结论
1) 混沌映射、反向学习与精英策略的引入使得初始种群更具多样性,进而增强了算法的收敛性能。
2) 改进了GWO算法的位置更新公式并融入BSA的觅食公式中得到了新的局部搜索策略,提升了算法的局部搜索能力。
3) 对比实验表明,混合后的GWBSA在收敛速度与收敛精度上均优于其他算法,实现了局部搜索与全局搜索的动态平衡,不易陷入局部最优,在获取全局最优权重、提高分类准确率方面具有较大优势。
4) 虽然本算法在解决特征权重的优化分配领域有一定的应用价值,但在处理高维多分类的特征权重优化问题方面仍有一些不足,如何获得性能更加完善、适用范围更广的权重优化方法将是下一阶段的研究重点。
-
算法1 GWBSA 输入:种群个体数目N, 特征维度D,上边界U,下边界L,最大迭代次数tm,认知加速因子C,社会加速因子S,警觉行为影响因子b1、b2,警觉行为发生概率pv,飞行行为频率Q,乞食者寻找食物频率R。 输出:最优个体Xα(t)。 1. 根据式(2)使用Chebyshev映射生成混沌种群Xc 2. 根据式(3)通过反向学习方法生成Xc的反向种群Xo 3. 根据式(4)合并混沌种群与反向种群,采取精英策略保留适应度排在前N的个体,生成初始种群Xm 4. 令当前迭代次数t=1 5. 根据式(8)(9)(11)(12)分别初始化p、A1、A2、a、C1、C2 7. while t < tm 8. 令Xα(t)表示当前适应度最高个体的位置, Xβ(t) 表示当前适应度次高个体的位置 9. if t mod Q=0 10. for每个ω狼个体 11. if rand≤pv 12. if rand≤p 13. 根据式(5)向α、β狼的方向更新ω狼的合成位置 14. else 15. 根据式(5)向α狼的方向更新ω狼的合成位置 16. end if 17. 根据式(13)更新个体的位置 18. else 19. 个体发生警觉行为,根据式(14)更新个体位置 20. end if 21. 通过式(11)更新参数a 22. 通过式(8)更新非线性自适应平衡概率p 23. 通过式(9) (12)更新A1、A2和C1、C2 24. end for 25. else 26. 将种群中的个体分为生产者与乞食者,并根据式(16)更新个体位置 27. end if 28.重新计算所有个体的适应度值 29.t=t+1 30.end while 31.返回最优个体Xα(t) 表 1 标准测试函数
Table 1 Benchmark functions
函数 维度n 定义域 最小值 $f_1(x)=\sum\limits_{i=1}^n x_i^2$ 30 [-100, 100] 0 $f_2(x)=\sum\limits_{i=1}^n\left|x_i\right|+\prod\limits_{i=1}^n\left|x_i\right|$ 30 [-10, 10] 0 $f_3(x)=\max_i\left\{\left|x_i\right|, 1 \leqslant x_i \leqslant n\right\}$ 30 [-100, 100] 0 $f_4(x)=\sum\limits_{i=1}^n i x_i^4+\operatorname{random}[0, 1)$ 30 [-1.28, 1.28] 0 $\begin{gathered} f_5(x)=\sin ^2\left({\rm{ \mathsf{ π} }} \omega_1\right)+\sum\limits_{i=1}^{n-1}\left(\omega_i-1\right)^2\left[1+10 \sin ^2\left({\rm{ \mathsf{ π} }} \omega_i+1\right)\right]+ \\ \left(\omega_n-1\right)^2\left[1+\sin ^2\left(2 {\rm{ \mathsf{ π} }} \omega_n\right)\right], \omega_i=1+\frac{x_i-1}{4} \end{gathered}$ 30 [-10, 10] 0 $f_6(x)=418.9829 n-\sum\limits_{i=1}^n x_i \sin \left(\sqrt{\left|x_i\right|}\right)$ 30 [-500, 500] 0 $\begin{array}{l} f_7(x)= \frac{{\rm{ \mathsf{ π} }}}{n}\left\{10 \sin \left({\rm{ \mathsf{ π} }} \omega_1\right)+\sum\limits_{i=1}^{n-1}\left(\omega_1-1\right)^2\left[1+10 \sin ^2\left({\rm{ \mathsf{ π} }} \omega_i+1\right)\right]+\left(\omega_i-1\right)^2\right\}+ \\ \sum\limits_{i=1}^n u\left(x_i, 10, 100, 4\right), \omega_i=1+\frac{x_i+1}{4}, \\ u\left(x_i, a, k, m\right)= \begin{cases}k\left(x_i-a\right)^m, & x_i>a \\ 0-a, & x_i <a \\ k\left(-x_i-a\right)^m, & x_i <-a\end{cases} \end{array}$ 30 [-50, 50] 0 $\begin{aligned} f_8(x)= & 0.1\left\{\sin ^2\left(3 {\rm{ \mathsf{ π} }} x_i\right) \sum\limits_{i=1}^n\left(x_i-1\right)^2\left[1+\sin ^2\left(3 {\rm{ \mathsf{ π} }} x_i+1\right)\right]+\right. \\ & \left.\left(x_n-1\right)^2\left[1+10 \sin ^2\left(2 {\rm{ \mathsf{ π} }} x_n\right)\right]\right\}+\sum\limits_{i=1}^n u\left(x_i, 5, 100, 4\right) \end{aligned}$ 30 [-50, 50] 0 表 2 算法参数设置
Table 2 Setting of algorithm parameters
表 3 函数最小值的平均值与标准差
Table 3 Mean and standard deviation of minimum value of functions
函数 指标 GA ALO GWO BSA A1 A2 GWBSA f1(x) 平均值 1.41×10-1 1.31×10-3 1.42×10-27 1.63×10-123 2.67×10-159 5.08×10-171 3.36×10-186 标准差 2.15×10-1 1.18×10-3 1.83×10-27 3.58×10-123 0 0 0 f2(x) 平均值 9.17×100 4.55×101 1.07×10-16 5.81×10-60 1.82×10-81 7.23×10-86 5.12×10-95 标准差 6.67×10-0 5.40×101 8.49×10-17 1.70×10-59 3.08×10-81 1.93×10-85 7.68×10-95 f3(x) 平均值 2.40×101 1.62×101 8.58×10-7 1.52×10-57 1.37×10-70 8.71×10-79 3.30×10-90 标准差 4.79×100 3.86×100 8.00×10-7 1.90×10-57 4.33×10-70 2.75×10-78 8.38×10-90 f4(x) 平均值 7.76×10-1 2.66×10-1 2.07×10-3 6.69×10-4 3.51×10-4 1.47×10-4 3.66×10-5 标准差 1.26×10-1 6.86×10-2 9.28×10-4 4.37×10-4 2.32×10-4 1.04×10-4 2.18×10-5 f5(x) 平均值 3.00×101 1.09×101 1.14×100 7.79×10-8 8.59×10-9 2.18×10-9 2.58×10-10 标准差 1.19×101 3.81×100 2.20×10-1 7.25×10-8 8.31×10-9 4.11×10-9 2.82×10-10 f6(x) 平均值 5.05×103 7.08×103 6.23×103 1.87×10-3 8.16×10-4 4.78×10-4 4.04×10-4 标准差 1.17×103 6.53×101 5.60×102 2.10×10-3 3.75×10-4 7.66×10-5 4.99×10-4 f7(x) 平均值 6.99×102 1.18×101 4.67×10-2 2.67×10-9 1.33×10-9 3.50×10-10 4.43×10-11 标准差 1.22×102 4.40×100 2.15×10-2 1.78×10-9 1.27×10-9 3.25×10-10 4.27×10-11 f8(x) 平均值 3.91×102 2.63×101 6.20×10-1 2.27×10-8 1.29×10-8 4.82×10-9 4.24×10-10 标准差 4.61×102 1.94×101 2.70×10-1 2.25×10-8 1.27×10-8 7.37×10-9 5.14×10-10 表 4 数据集信息
Table 4 Information of datasets
编号 数据集名称 案例数 特征数 类别数 D1 Breast Cancer Wisconsin (Prognostic) 198 33 2 D2 Connectionist Bench (Sonar Mines vs Rocks) 208 60 2 D3 Glass Identification 214 9 6 D4 Statlog (Vehicle Silhouettes) 846 18 4 D5 Wine 178 13 3 表 5 分类准确率的实验结果对比
Table 5 Comparison of experiment results of classification accuracy
% 编号 MA GA ALO GWO BSA GWBSA D1 69.27 68.13 67.66 67.06 67.25 74.33 D2 77.83 78.80 78.31 78.47 78.56 81.01 D3 67.26 70.08 71.05 71.90 71.50 73.57 D4 68.92 70.57 70.69 70.71 70.93 71.26 D5 94.90 95.49 95.46 95.63 95.63 96.47 平均 75.64 76.61 76.63 76.75 76.77 79.33 表 6 显著性检验
Table 6 Significance test
编号 指标 GWBSA-MA GWBSA-GA GWBSA-ALO GWBSA-GWO GWBSA-BSA D1 H 1 1 1 1 1 P 1.30×10-15 6.14×10-20 8.95×10-14 1.98×10-22 3.10×10-20 D2 H 1 1 1 1 1 P 5.92×10-17 5.08×10-8 9.56×10-15 3.17×10-9 6.48×10-10 D3 H 1 1 1 1 1 P 2.83×10-21 4.51×10-11 7.38×10-28 1.06×10-4 4.09×10-8 D4 H 1 1 1 1 1 P 1.65×10-16 3.81×10-5 2.26×10-27 1.53×10-3 7.27×10-8 D5 H 1 1 1 1 1 P 1.44×10-15 6.36×10-2 3.09×10-8 6.01×10-3 1.18×10-5 -
[1] WAN Q Z, YU Y. Power load pattern recognition algorithm based on characteristic index dimension reduction and improved entropy weight method[J]. Energy Reports, 2020, 6(Suppl 9): 797-806.
[2] THAKKAR A, CHAUDHARI K. Predicting stock trend using an integrated term frequency-inverse document frequency-based feature weight matrix with neural networks[J]. Applied Soft Computing, 2020, 96: 106684. doi: 10.1016/j.asoc.2020.106684
[3] ZHOU M, LIU X B, CHEN Y W, et al. Assignment of attribute weights with belief distributions for MADM under uncertainties[J]. Knowledge-Based Systems, 2020, 189(2): 105-110.
[4] MACH K J, MASTRANDREA M D, FREEMAN P T, et al. Unleashing expert judgment in assessment[J]. Global Environmental Change, 2017, 44(2): 1-14.
[5] LIN C. Application of fuzzy Delphi method (FDM) and fuzzy analytic hierarchy process (FAHP) to criteria weights for fashion design scheme evaluation[J]. International Journal of Clothing Science and Technology, 2013, 25(3): 171-183. doi: 10.1108/09556221311300192
[6] CHEN Y T, CHEN C H, WU S, et al. A two-step approach for classifying music genre on the strength of AHP weighted musical features[J]. Mathematics, 2019, 7(1): 1-17.
[7] PHAN A V, NGUYEN M L, BUI L T. Feature weighting and SVM parameters optimization based on genetic algorithms for classification problems[J]. Applied Intelligence, 2017, 46(2): 455-469. doi: 10.1007/s10489-016-0843-6
[8] BISWAS S K, CHAKRABORTY M, SINGH H R, et al. Hybrid case-based reasoning system by cost-sensitive neural network for classification[J]. Soft Computing, 2017, 21(24): 7579-7596. doi: 10.1007/s00500-016-2312-x
[9] ZHOU M, LIU X B, YANG J B, et al. Evidential reasoning approach with multiple kinds of attributes and entropy-based weight assignment[J]. Knowledge-Based Systems, 2019, 163(1): 358-375.
[10] 程启月. 评测指标权重确定的结构熵权法[J]. 系统工程理论与实践, 2010, 30(7): 1225-1228. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201007012.htm CHENG Q Y. Structure entropy weight method to confirm the weight of evaluating index[J]. Systems Engineering-Theory & Practice, 2010, 30(7): 1225-1228. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201007012.htm
[11] SENGUPTA S, BASAK S, PETERS II R A. Particle swarm optimization: a survey of historical and recent developments with hybridization perspectives[J]. Machine Learning and Knowledge Extraction, 2019, 1(1): 157-191.
[12] ARRIF T, BENCHABANE A, GERMOUI M, et al. Optimisation of heliostat field layout for solar power tower systems using iterative artificial bee colony algorithm: a review and case study[J]. International Journal of Ambient Energy, 2021, 42(1): 65-80. doi: 10.1080/01430750.2018.1525581
[13] SHANG J L, WANG X, WU X Y, et al. A review of ant colony optimization based methods for detecting epistatic interactions[J]. IEEE Access, 2019, 7(2): 13497-13509.
[14] YANG X S, HE X. Firefly algorithm: recent advances and applications[J]. International Journal of Swarm Intelligence, 2013, 1(1): 36-50. doi: 10.1504/IJSI.2013.055801
[15] MIRJALILI S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83(5): 80-98.
[16] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61.
[17] SINGH N, SINGH S B. A novel hybrid GWO-SCA approach for optimization problems[J]. Engineering Science and Technology-An International Journal, 2017, 20(6): 1586-1601. doi: 10.1016/j.jestch.2017.11.001
[18] MENG X B, GAO X Z, LU L H, et al. A new bio-inspired optimisation algorithm: bird swarm algorithm[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2016, 28(4): 673-687.
[19] YANG H, CHEN T, HUANG N J. An adaptive bird swarm algorithm with irregular random flight and its application[J]. Journal of Computational Science, 2019, 35(6): 57-65.
[20] 龙文, 蔡绍洪, 焦建军, 等. 求解高维优化问题的混合灰狼优化算法[J]. 控制与决策, 2016, 31(11): 1991-1997. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201611010.htm LONG W, CAI S H, JIAO J J, et al. Hybrid grey wolf optimization algorithm for high-dimensional optimization[J]. Control and Decision, 2016, 31(11): 1991-1997. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201611010.htm
[21] VAROL A E, BILAL A. Bird swarm algorithms with chaotic mapping[J]. Artificial Intelligence Review, 2020, 53(2): 1373-1414. doi: 10.1007/s10462-019-09704-9
[22] LIAO X, LI X, PEN J, et al. A digital secure image communication scheme based on the chaotic Chebyshev map[J]. International Journal of Communication Systems, 2004, 17(5): 437-445. doi: 10.1002/dac.655
[23] GANDOMI A H, YANG X S. Chaotic bat algorithm[J]. Journal of Computational Science, 2014, 5(2): 224-232.
[24] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition versus randomness in soft computing techniques[J]. Applied Soft Computing, 2008, 8(2): 906-918. doi: 10.1016/j.asoc.2007.07.010
[25] GAIDHANE P J, NIGAM M J. A hybrid grey wolf optimizer and artificial bee colony algorithm for enhancing the performance of complex systems[J]. Journal of Computational Science, 2018, 27(6): 284-302.
[26] ARORA S, SINGH H, SHARMA M, et al. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection[J]. IEEE Access, 2019, 7(1): 26343-26361.
[27] TENG Z J, LV J L, GUO L W. An improved hybrid grey wolf optimization algorithm[J]. Soft Computing, 2019, 23(15): 6617-6631.
[28] SOLIS F J, WETS R J B. Minimization by random search techniques[J]. Mathematics of Operations Research, 1981, 6(1): 19-30.
[29] 严爱军, 余凌云, 倪鹏飞. 反渗透膜故障的案例推理诊断方法[J]. 北京工业大学学报, 2018, 44(11): 1396-1400. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201811005.htm YAN A J, YU L Y, NI P F. Fault diagnosis method by case-based reasoning for reverse osmosis membrane[J]. Journal of Beijing University of Technology, 2018, 44(11): 1396-1400. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201811005.htm
-
期刊类型引用(1)
1. 杨世忠,宫钰程,王伟. 基于改进灰狼算法的空调送风温度自抗扰控制. 科学技术与工程. 2025(13): 5491-5500 .  百度学术
百度学术
其他类型引用(4)



 下载:
下载: