Characteristic Variable Selection Method and Predictive Modeling for Municipal Solid Waste Heat Value
-
摘要:
在垃圾焚烧的过程中，垃圾热值的波动会影响垃圾焚烧的稳定性.为了实现城市生活垃圾热值的实时在线预测以及变化趋势预测，采用模糊神经网络软测量方法，利用焚烧发电厂在线运行数据作为输入，实现垃圾热值的实时预测功能.首先采用互信息方法从若干特征变量中剔除部分无关变量；然后将模糊神经网络和粒子群优化算法结合起来从上述选择出的特征变量中进一步剔除冗余变量，从而确定预测垃圾热值的输入变量，并从中训练出垃圾热值的模糊神经网络预测模型；最后通过采集的样本数据进行性能测试.结果表明该方法有较好的预测准确率和实时性，适用于垃圾热值的在线预测.
Abstract:In the process of municipal solid waste incineration, the fluctuation of waste heat value affects the stability of waste incineration. To make the real-time online prediction and change the trend of the waste heat value, the fuzzy neural network soft sensing method was adopted, and the on-line operation data of the incineration power plant was used as the input to accomplish the real-time prediction function of the waste heat value. First, the mutual information method was used to eliminate irrelevant variables from characteristic variables. Then, the fuzzy neural network and particle swarm optimization algorithm were combined to further eliminate redundant variables from the selected characteristic variables, so as to determine the input variables for predicting the waste heat value, and the fuzzy neural network prediction model for waste heat value was trained. Finally, the performance test was carried out through the collected sample data. Results show that this method has good prediction accuracy and real-time performance, and is suitable for online prediction of waste heat value.
-
城市生活垃圾(municipal solid waste, MSW)焚烧发电在垃圾的资源化、无害化、减量化等方面具有显著优势并成为垃圾处理技术的首选[1]. 城市生活垃圾由几种不均匀物质组成，这些物质大多数可通过热化学过程回收其所包含的能量. 当将垃圾进行热化学处理时，用于测量收集的垃圾在进行热化学处理时可用的能量参数称为垃圾热值[2]. 垃圾热值是决定焚烧炉内是否需要加入辅助燃料的重要条件，而且它的变化会对焚烧过程的稳定性产生很大的影响. 因此，对垃圾热值进行精准的预测具有重要的意义. 采取技术先进、科学合理的预测模型对垃圾热值进行准确而快速的预测是实现垃圾焚烧经济性和垃圾焚烧系统稳定运行的保障. 目前，城市生活垃圾热值的测定方法有2种，一种是直接测定法[3-4]，另一种是经验公式计算法[5-10]. 直接测定法一般采取氧弹式量热计进行测定. 因为垃圾的组分非常复杂，并且大小尺度不一，在通过氧弹式量热计对垃圾热值进行测定时，存在许多问题. 比如，在对垃圾进行取样、分拣以及比例的测定时，如果不是具有丰富经验的专业人员进行操作，非常容易导致所选取的样本不具有代表性且不均匀，从而对后续垃圾的烘干、破碎产生较大影响. 计算法按照采取组成数据的不同种类，可以分为工业分析法、元素分析法和物理成分组成法，最广泛采用的是物理成分组成法. 由于城市生活垃圾的组成成分非常复杂、多变，并且水分、灰土亦会对其产生影响，从而造成经验公式计算法的估算结果具有一定偏差.
人工神经网络作为人工智能领域的一种方法，具有自学习能力和泛化能力，可以解决采用传统方法不可解决的难题，因而被广泛应用. 神经网络方法可以有效克服城市生活垃圾复杂多变所带来的影响，从而得到满意的预测精度. 文献[11]中采用多元回归及BP神经网络对城市生活垃圾热值进行预测，其预测结果精度要高于多元回归的预测结果. 文献[12]构建了基于BP神经网络的低位垃圾热值预测模型，其中输入参数为垃圾的成分比例含量，输出参数为低位热值大小. 实验结果表明，其预测精度高于经验公式计算法. 文献[13]构建了基于L-M反向传播算法的神经网络模型，完成了城市生活垃圾热值的预测，其中输入参数为垃圾组分的元素含量，输出为垃圾热值的大小. 实验结果表明，该模型能够较为准确地预测城市生活垃圾热值，具有一定的实用性. 文献[14]提出利用神经网络对垃圾热值进行软测量，解决了垃圾热值无法直接测量的问题. 但采用此方法进行测量所获取的是正在燃烧生活垃圾的平均热值，不能实现实时在线预测及其变化趋势. 文献[15]将垃圾的成分比例含量作为输入变量，可燃成分的低位热值作为输出变量，分别采用BP、RBF和ANFIS对生活垃圾可燃成分的热值进行预测. 实验结果表明，RBF模型的预测准确率相对较高.
虽然人工神经网络建模方法相比经验计算方法的预测精度有所提高，但其主要是将垃圾的主要组成成分作为输入，垃圾热值的大小作为输出，通过神经网络建模方法进行预测. 由于垃圾组分通常由人为选定，不可避免地引起偏差；除此之外，在线获得垃圾热值的主要成分也是不现实的，因此上述方法主要是针对离线的统计和分析，难以用于垃圾热值的在线预测. 因而，探索一种能够快速分析垃圾热值的方法显得尤为迫切.
随着传感器技术的不断推进与发展，能够获取许多过程工业数据，使得数据驱动预测方法具有了保障[16]. 因此，可以通过将垃圾焚烧厂的在线测量数据作为输入参数，实现垃圾热值整体水平的在线预测，从而避免了对垃圾成分等参数进行离线测定.
为了实现垃圾热值的实时预测，本文构建了基于模糊神经网络(fuzzy neural network, FNN)的垃圾热值预测模型. 首先采用互信息(mutual information, MI)方法从若干特征变量中剔除部分无关变量；然后将模糊神经网络和粒子群优化算法(particle swarm optimization, PSO)结合起来从上述选择出的特征变量中进一步剔除冗余变量，从而得到预测垃圾热值的输入变量，同时，获得了垃圾热值的模糊神经网络预测模型，通过实验检验了方法的有效性.
1. 城市生活垃圾焚烧过程
本节首先介绍城市生活垃圾焚烧过程的工艺流程，然后分析垃圾热值对焚烧过程的影响，并从中总结出反映垃圾热值变化的过程参数.
1.1 过程描述
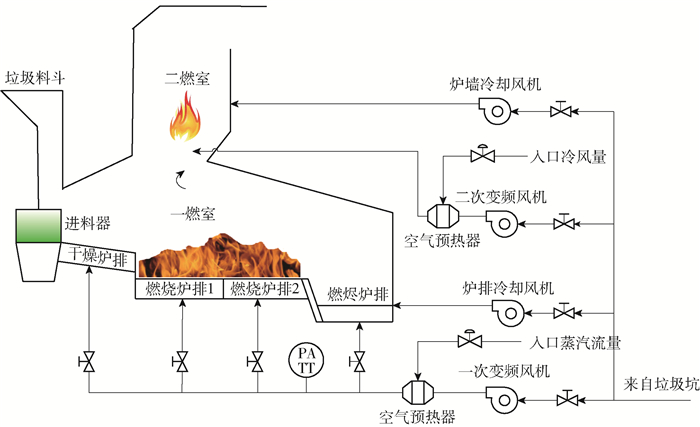
以北京市某垃圾焚烧公司的焚烧过程为例，其工艺流程如图 1所示. 整个垃圾焚烧过程主要分为炉膛燃烧、炉排速度调节、炉排温度控制和空气流量调节4个子过程.
具体处理流程描述如下：首先，通过进料器将垃圾送入焚烧炉内；然后，在干燥炉排上通过一次风和炉膛内的高温进行水分干燥处理；接着，将完成干燥处理之后的垃圾在两段燃烧炉排上焚烧并析出挥发份；最后，在燃烬炉排上将垃圾中的固定碳燃烧生成碳化物，同时将燃烧段析出的挥发份通过一次风和一燃室中的氧气进行燃烧，未能完全燃烧的部分在二燃室通过二次风的作用进行完全燃烧.
1.2 垃圾热值的影响
垃圾热值的变化会对焚烧过程产生很大的影响，当垃圾焚烧系统在垃圾热值较高的情况下长期稳定运行时，蒸发量与进料量成正比，产出的蒸汽品质良好，反映蒸汽品质的相关变量主要有主蒸汽量、主蒸汽压力、主蒸汽温度. 当垃圾热值变化较大时，焚烧炉内的温度会有较大的波动. 当垃圾热值较低时，蒸发量随之减少，炉内温度降低，并且会造成垃圾的不完全焚烧，从而增加污染气体的排放量.
针对炉排式垃圾焚烧炉，可能反映出垃圾热值大小及其变化趋势的特征变量有炉膛燃烧子过程(包括主蒸汽量、主蒸汽压力和主蒸汽温度、炉膛烟气温度等)共16个变量，炉排速度调节子过程(包括干燥段、燃烧一段、燃烧二段、燃烬段炉排速度等)共18个变量，炉排温度控制子过程(包括干燥段、燃烧一段、燃烧二段、燃烬段炉排温度等)共24个变量，空气流量调节子过程(与风机和空气预热器相关的温度、风量和风压等)共18个变量，总计76个可能反映垃圾热值大小及变化趋势的变量. 由于相关的特征变量较多，可能存在冗余或无关的变量，若采取所有变量构建垃圾热值的预测模型，则会造成模型的复杂度高，从而导致拟合的误差大. 因此需要先进行特征选择，然后再构建垃圾热值预测模型.
2. 相关知识
本节介绍本文所采用的特征选择方法以及模糊神经网络的相关知识.
2.1 特征选择方法
本文所处理的问题是城市生活垃圾热值的相关特征变量选择及在线预测建模，由于各相关特征变量之间以及这些变量与垃圾热值之间呈现强非线性关系，因而传统的线性特征提取方法如PCA、LDA、ICA无法处理. 从广义来讲，特征选择分为过滤式特征选择方法[17]、封装式特征选择方法[18]和混合式特征选择方法[19-21]. 过滤式特征选择方法主要是采用某种评价准则对特征变量进行约减. MI[22]能够衡量2个变量之间的依赖程度，并且其度量不局限于线性关系，亦能评估非线性关系. 它主要是利用信息熵[23]等量化变量之间共同拥有信息的含量，从而得到变量之间互相依赖的程度并完成特征的选择. 定义为
$$ I(X ; Y)=\sum\limits_{x \in X} \sum\limits_{y \in Y} p(x, y) \log \frac{p(x, y)}{p_{X}(x) p_{Y}(y)} $$ (1) 式中：X和Y为给定的2个随机变量；pX(x)和pY(y)为边缘概率分布；p(x, y)为联合概率分布. 当变量X和Y相互独立或完全无关时，互信息最小，为0，表明2个变量不相关；相反，2个变量的依赖程度越高，I(X；Y)的值越大，相关度越高. 依据式(1)的计算结果，设置一个互信息阈值用于选择所需相关的特征变量.
封装式特征选择方法是将预测器或分类器作为黑箱，以预测器或分类器的准确率或精确度评估特征选择是否有效，在完成特征选择的同时训练出预测器或分类器的模型. 封装式特征选择分为搜索特征子集和评估特征子集2个步骤. 特征子集的搜索方式分为启发式搜索、随机搜索和完全搜索. 常见的完全搜索方法有分支限界搜索、广度优先搜索等，此种方法的时间复杂度会随着特征变量的增加呈指数型增长，所以不适用于多变量的情况. 启发式搜索和随机搜索则舍弃了全局最优，提升了算法的效率. 典型的方法有序列特征选择算法(sequential selection, SF)[24]、遗传算法GAs[25]、粒子群算法PSO[26]等.
混合式特征选择方法采用顺序法，第1阶段采用某种评价准则约减特征变量，第2阶段在第1阶段特征选择的基础上建立封装式模型以获取期望的特征变量.
过滤式特征选择方法与后续的训练模型无关，效率高，但评价与后续训练模型的性能偏差大；而封装式特征选择方法采用后续训练模型的准确率评价特征子集，虽然能够有效地去掉冗余变量和无关变量，但其计算量大，效率低. 为了弥补各自的不足之处，并且考虑到垃圾热值是由若干个模糊等级划分而成，本文拟将基于MI的过滤式特征选择方法与基于PSO-FNN的封装式特征选择方法相结合，采用过滤-封装的混合式特征选择方法实现垃圾热值的特征变量选择.
2.2 模糊神经网络
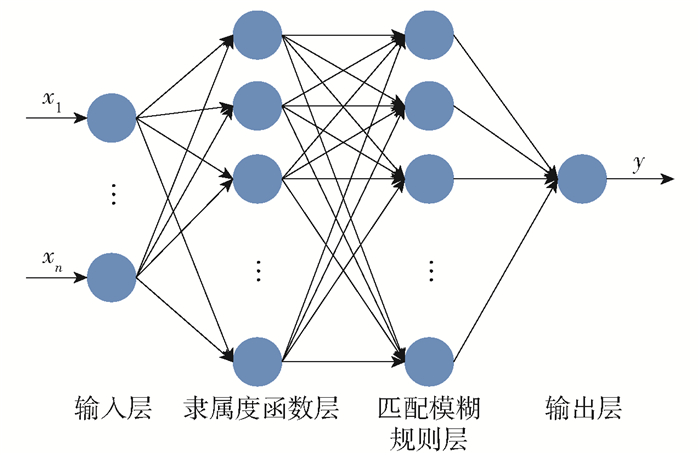
FNN结合了神经网络和模糊理论的优点，在处理非线性、模糊性等问题上有很大的优越性，在许多领域得到广泛的应用[27-30]. 为了实现垃圾热值的实时在线预测，本文构建了基于FNN的预测模型，其结构如图 2所示[31]. 采用模糊语言表示形式的原因是垃圾热值不能完成实时测量，因而垃圾热值是由操作人员根据经验和实际运行工况统计而得到的一种垃圾热值的模糊集形式. 除此之外，将神经网络与模糊推理和模糊控制相结合，增加了模糊推理和模糊控制的学习功能，使其应用在垃圾焚烧模糊控制过程中更加有效.
各层的数学描述如下所示.
第1层为输入层，将输入值x=(x1, x2, …, xn)传送到下一层，该层的节点数为n，代表影响垃圾热值的特征变量个数.
第2层为隶属度函数层，具有M个节点，每个节点是由n个模糊规则组成的RBF形式. 在此层中通过隶属函数计算各输入分量模糊集合的隶属度. 模糊隶属度函数通常有梯形、高斯函数、三角形、钟形4种形式. 本文取高斯函数作为隶属度函数，即
$$ \mu_{j}^{i}=\mathrm{e}^{-\frac{\left(x_{i}-m_{j}^{i}\right)^{2}}{2\left(b_{j}^{i}\right)^{2}}} $$ (2) 式中：i=1, 2, …, n，n为输入量的维数；j=1, 2, …, m，m为模糊类的分割数(RBF神经网络的隐含层节点个数)；mji和bji分别为第j个节点中第i个隶属度的中心和宽度. 第j个节点的输出值μj为
$$ \mu_{j}=\mu_{j}^{1} \mu_{j}^{2} \cdots \mu_{j}^{i} \cdots \mu_{j}^{m} $$ (3) 第3层为匹配模糊规则层，该层的节点数为M，第j个节点的输出值vj为
$$ v_{j}=\frac{\mu_{j}}{\sum\limits_{j=1}^{M} \mu_{j}} $$ (4) 第4层为输出层，由于垃圾热值是工作人员根据经验所得到的模糊等级，因此推理输出不需要加反模糊化过程. 输出为
$$ y=\sum\limits_{j=1}^{M} \mu_{j} \omega_{j} $$ (5) 式中：y为垃圾热值预测模型的输出；ωj为垃圾热值预测模型匹配模糊规则层与输出层之间的权值.
3. 基于模糊神经网络垃圾热值预测模型
本节建立一种基于FNN的垃圾热值预测模型. 采用MI、PSO和FNN获取一种混合式特征变量选择方法，完成对城市生活垃圾热值特征变量的选择，并训练出基于FNN的垃圾热值预测模型. 下面分别介绍垃圾热值混合式特征变量选择方法、基于FNN预测模型的建立以及算法步骤.
3.1 混合式特征变量选择
3.1.1 基于MI的第1阶段特征选择
以炉膛子过程为例：首先，采用文献[32]中的MI计算公式，计算第i个特征变量x1i与垃圾热值y的互信息I11sti(x1i; y)，计算公式为
$$ \begin{aligned} I_{1}^{1 \mathrm{st}i}\left(x_{1}^{i} ; y\right)=& \iint p\left(x_{1}^{i} y\right) \log \frac{p\left(x_{1}^{i}, y\right)}{p\left(x_{1}^{i}\right) p(y)} \mathrm{d} x_{1}^{i} \mathrm{~d} y=\\ & H\left(x_{1}^{i}\right)-H\left(x_{1}^{i} \mid y\right) \end{aligned} $$ (6) 式中：p(x1i)为x1i的边缘概率密度；p(y)为y的边缘概率密度；p(x1i, y)为x1i与y的联合概率密度；H(x1i)为x1i的信息熵；H(x1i|y)为条件熵.
当完成炉膛子过程内全部特征变量与y的互信息计算之后，根据MI大小降序排列并设置阈值θ1. 当I11sti(x1i; y)≥θ1时，保留该特征变量，反之剔除. 阈值θ1根据
$$ \theta_{1}=\alpha_{1} \frac{\sum\limits_{i=1}^{n_{1}} I_{1}^{1 \mathrm{st}i}\left(x_{1}^{i} ; y\right)}{n_{1}} $$ (7) 进行设置. 式中：α1为炉膛子过程对垃圾热值的影响因子，依据每个特征对垃圾热值MI的均值大小进行定义；n1为炉膛子过程初始特征变量的个数.
最后，将每个子过程选择出来的特征变量进行合并，表示为
$$ X^{1 \mathrm{st}}=X_{1}^{1 \mathrm{st}} \cup X_{2}^{1 \mathrm{st}} \cup X_{3}^{1 \mathrm{st}} \cup X_{4}^{1 \mathrm{st}} $$ (8) 3.1.2 基于PSO-FNN第2阶段特征选择
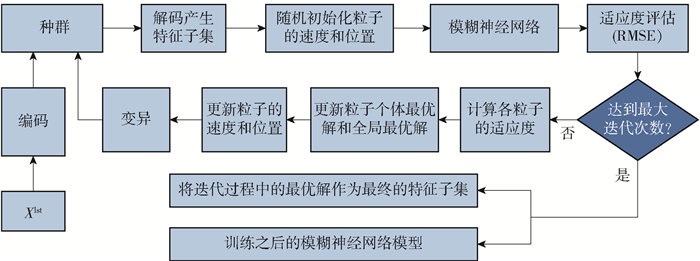
由于基于MI的第1阶段特征选择只是评估了单个特征变量与输出y的相关性，而未考虑各个变量间的关系. 因此，本文在基于MI第1阶段特征选择的基础上，将PSO和FNN相结合，构成PSO-FNN封装式第2阶段特征选择方法. 通过将基于MI的过滤式特征选择方法与基于PSO-FNN封装式特征选择方法融合，使其集中了过滤式的高效率和封装式的高准确率，PSO-FNN特征选择方法流程图如图 3所示.
1) 编码和解码
粒子群算法是一种模仿鸟类寻食的集群智能寻优算法. 粒子的每一维对应一个特征. 为了便于后续算法步骤的实现，对第一次特征选择选出的特征子集进行编码. 编码后的特征子集以粒子位置向量的形式操作，编码规则为
$$ \boldsymbol{X}_{i}^{k}=\left[x_{i 1}^{k}, \cdots, x_{i j}^{k}, \cdots, x_{i n}^{k}\right] $$ (9) 式中：Xik为第k代粒子群中的第i个粒子的位置，当粒子的第j维数值为1时，对应的特征被选择，为0则不被选择；n为完成第一阶段特征选择之后的特征数量. 对位置向量Xik中的元素进行排序，可得到一个次序s. 在迭代计算过程中，随着粒子位置向量的更新，s不断发生变化.
根据上述的编码排序，随机产生第一代种群. 其中，粒子的数量为P，粒子的每一维数值从0或1中随机产生.
解码是将每个粒子位置向量对应的值映射至特征子集的过程，对应关系表示为
$$ \boldsymbol{Y}_{i}^{k}=\left[x_{i 1}^{k} y_{i 1}^{k}, \cdots, x_{i j}^{k} y_{i j}^{k}, \cdots, x_{i n}^{k} y_{i n}^{k}\right] $$ (10) 式中：Yik为第k代粒子群中第i个粒子的位置对应的特征子集.
2) 随机初始化粒子的速度和位置
首先，设置最大迭代次数T、变异次数q、目标函数的自变量个数n、粒子的最大速度vmax，位置信息为整个搜索空间，在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模为P，每个粒子随机初始化一个飞翔速度vi.
3) 适应度评估
适应度函数的选择是粒子群算法的一个重要步骤. 本文选择FNN预测模型所获取的垃圾热值的均方根误差定义适应度函数，表示为
$$ \text { fitness }_{i}^{k}=\frac{1}{\text { RMSE }} $$ (11) 式中：RMSE为基于FNN预测模型的训练结果与实际值的均方根误差(root mean square error)，计算公式为
$$ \operatorname{RMSE}_{i}^{k}=\sqrt{\frac{\sum\limits_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}}{m}} $$ (12) 式中：m为训练样本的数量；$\hat{y}_{i}$为FNN垃圾热值预测模型的输出；yi为垃圾热值的实际模糊等级.
4) 更新粒子的速度和位置
第i个粒子的速度和位置更新公式分别为
$$ v_{i j}^{k+1}=\omega v_{i j}^{i}+c_{1} r_{1}^{k}\left(\text { pbest }_{i j}^{k}-x_{i j}^{k}\right)+c_{2} r_{2}^{k}\left(\text { gbest }_{i j}^{k}-x_{i j}^{k}\right) $$ (13) $$ \begin{cases}x_{i j}^{k}=1, & \rho<\frac{1}{1+\exp \left(-v_{i j}^{k}\right)} \\ x_{i j}^{k}=0, & \text { 其他 }\end{cases} $$ (14) 式中：c1、c2为加速因子，前者为每个粒子的个体学习因子，后者为每个粒子的群体学习因子; pbest为粒子的个体最优解；gbest为粒子的全局最优解；k为迭代次数；r1、r2为随机数，取值范围是0~1；ρ取值为0.5；ω为惯性因子，其值为非负，通过调整其大小，可以对全局寻优性能和局部寻优性能进行调整. ω较大时，全局寻优能力强，局部寻优能力弱；ω较小时，全局寻优能力弱，局部寻优能力强.
5) 变异
在更新的过程中，若某个粒子找到当前的最优位置，则其他的粒子将会快速移动到此位置. 若此位置是局部最优点，粒子群不能在解空间内进行重新搜索，算法将会陷入局部最优，出现过早收敛. 为了解决该问题，本文PSO算法在陷入局部极值时对群体最优解gbest进行自适应t分布变异，从而跳出局部极值. 对gbest进行t分布变异的条件是停滞进化周期大于变异触发阈值T′，计算公式为
$$ \text { gbest }^{\prime}=\text { gbest }+\rho_{j} t_{n} $$ (15) 式中：$\rho_{j}(k)=\left[\beta^{k} \frac{f_{\max }(k)-f_{\min }(k)}{f_{\max }(k)}+\left(1-\beta^{k}\right)\right] \beta^{k}$(gbestmax-gbestmin)；fmax(k)为第k代中最优粒子的适应度值f(gbest)；fmin(k)为第k代中最差粒子的适应度值；gbestmax为群体极值gbest的最大值；gbestmin为群体极值gbest的最小值；β是略小于1的常数，本文取值为β=0.97.
3.2 算法步骤
综上所述，混合式的特征选择方法和FNN预测建模算法的步骤如下.
步骤1 将第1阶段特征选择各子过程对垃圾热值的影响因子α、粒子数量P、粒子的速度和位置、粒子群的迭代次数T、变异次数q以及PSO-FNN算法的执行次数J进行参数的初始化处理，并对数据进行标准化处理.
步骤2 通过式(6)计算每个特征变量xi与垃圾热值y的互信息I1sti(xi; y)，并通过式(7)计算各子过程的阈值θ，若I1sti(xi; y)≥θ，则该特征变量被选择，反之被剔除. 通过式(8)将各子过程选出的特征变量合并为X1st. 基于MI的第1阶段特征选择完成.
步骤3 判断J是否等于0，若等于0，转到步骤9，否则继续按顺序执行.
步骤4 对第1阶段特征选择选出的特征进行编码，随机产生第1代种群.
步骤5 将每个粒子进行解码，采用梯度下降法训练FNN，并将每个粒子按式(10)转化成特征向量，计算每个粒子的适应度值，并按照适应度值排序.
步骤6 如果满足PSO-FNN算法收敛条件(即达到最大迭代次数)，则将迭代过程中的最优解作为特征子集输出并训练出相应的FNN垃圾热值预测模型，令J=J-1，并执行步骤3，否则继续按顺序执行.
步骤7 计算特征子集的适应度函数值，如果粒子的个体极值和群体极值优于历史位置，则更新pbest和gbest，并更新粒子位置和速度.
步骤8 如果粒子的进化停留周期大于变异触发阈值T′，则利用式(15)对gbest进行q次变异操作，从中选择出适应度最好的gbest′. 如果f(gbest′)>f(gbest)，则gbest=gbest′. 按照粒子的变异构建新一代种群，返回步骤5.
步骤9 对执行J次PSO-FNN算法之后输出的特征子集进行统计分析，输出特征子集，并训练出相应的FNN垃圾热值模型.
4. 模型的应用实验
为了便于查看，对缩写词进行如下规定：互信息特征选择方法记为MI；粒子群优化方法记为PSO；采用MI特征选择的结果对模糊神经网络模型进行训练的方法记为MI-FNN；采用PSO-FNN特征选择的结果对模糊神经网络模型进行训练的方法记为PSO-FNN；采用MI和PSO-FNN混合式特征选择的结果对模糊神经网络模型进行训练的方法记为MI-PSO-FNN.
4.1 实验参数
实验在MATLAB R2016a 9.0.0环境下编程实现，所用的计算机CPU为Intel(R) Core(TM) i5-5200U CPU @ 2.20 GHz，内存为4 GB. 各种方法中的参数设置如下：炉膛、炉排速度、炉排温度、空气流量这4个子过程对垃圾热值的影响因子分别是0.9、0.8、0.8、0.9；粒子数量P=50，种群最大迭代次数为T=200，变异次数q=100，变异触发阈值T′=5，惯性因子ω=0.8. 个体学习因子c1=1.5，群体学习因子c2=1.5；采用梯度下降法对模糊神经网络模型的参数进行调整，学习率为0.02，最大训练次数为2 000，模糊隶属度函数选取高斯函数.
本文实验过程的数据来自北京市某垃圾焚烧发电厂2019年7月不同时段的1 500条历史数据，选取其中200组数据进行实验，其中一半作为训练集，另一半作为测试集，并通过Z-SCORE标准化方法对这些数据进行标准化处理. 采用本文构建的模型对北京市某垃圾焚烧厂的入炉垃圾热值进行实时在线预测，模型的输出是以模糊集的形式，垃圾热值样本数据的模糊等级均由现场的操作人员根据经验和实际运行工况进行判断，垃圾热值分为-3.0、-2.5、-2.0、-1.5、-1.0、-0.5、0、0.5、1.0、1.5、2.0、2.5、3.0共13个等级，其模糊子集记为[-3.0，-2.5，-2.0，-1.5，-1.0，-0.5，0，0.5，1.0，1.5，2.0，2.5，3.0].
4.2 应用实验与结果分析
4.2.1 基于MI的特征选择结果
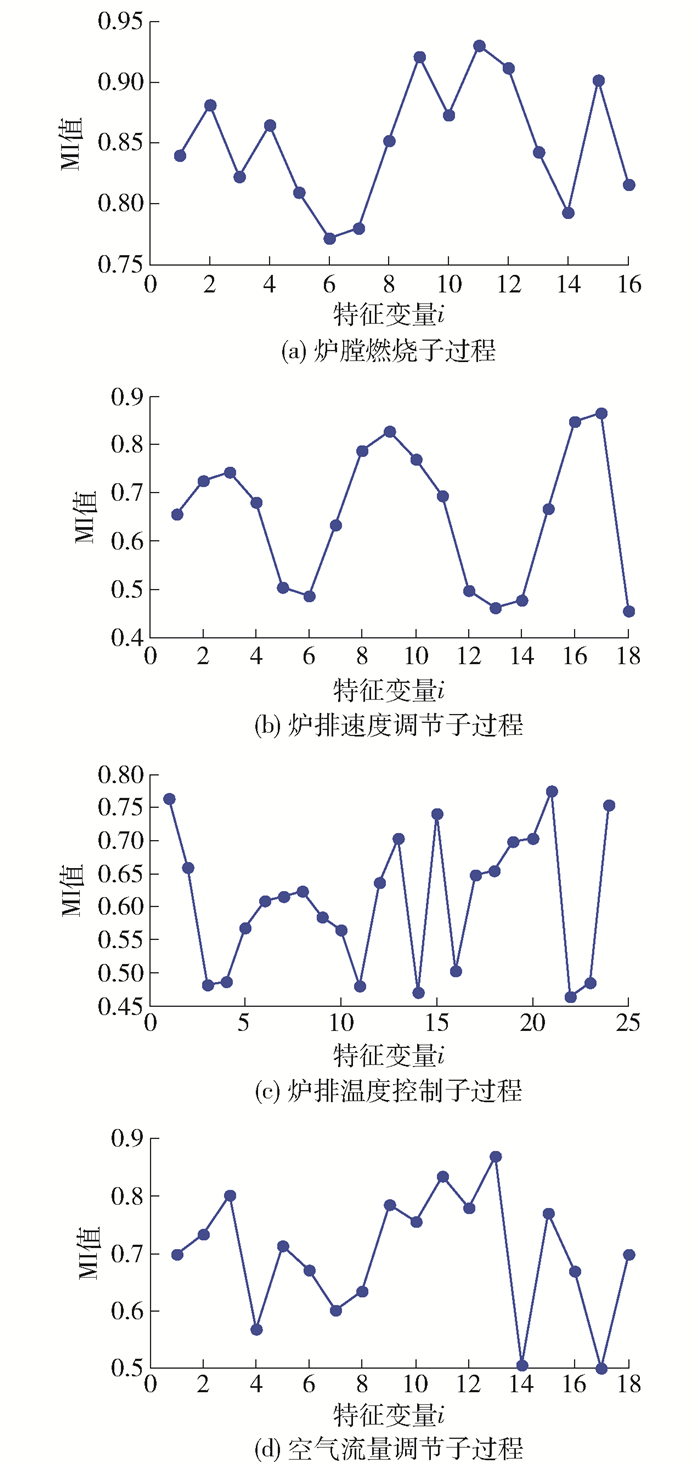
针对垃圾焚烧过程，炉膛燃烧子过程、炉排速度调节子过程、炉排温度控制子过程以及空气流量调节子过程对垃圾热值的影响因子分别为0.9、0.8、0.8、0.9.4个子过程中的特征变量与垃圾热值的MI值如图 4所示.
![]()
图 4 各个子过程特征变量与垃圾热值的MI值Figure 4. MI value between characteristic variables and waste heat value of each sub process由图 4可以看出，各个子过程特征变量与垃圾热值的MI值存在差别，将垃圾焚烧的4个子过程的特征变量与垃圾热值之间MI的最大值、最小值和平均值的结果进行统计如表 1所示.
表 1 各个子过程特征变量的互信息度量结果Table 1. MI measurement results of characteristic variables in each sub process垃圾焚烧过程 最大值 最小值 平均值 炉膛燃烧子过程 0.935 1 0.771 5 0.850 7 炉排速度调节子过程 0.864 3 0.453 8 0.653 8 炉排温度控制子过程 0.775 3 0.463 5 0.611 3 空气流量调节子过程 0.870 2 0.501 4 0.699 8 由表 1可看出，子过程中MI均值的最大值来自炉膛燃烧子过程，其值为0.850 7. 炉膛燃烧子过程包括主蒸汽量、主蒸汽压力和主蒸汽温度、炉膛烟气温度这些特征变量. 这与有经验操作人员根据实际运行工况统计所得到的垃圾热值变化和焚烧工况之间的规律一致，即当垃圾焚烧系统在垃圾热值较高的情况下长期稳定运行时，蒸发量与进料量成正比，产出的蒸汽品质良好，反映蒸汽品质的相关变量主要有主蒸汽量、主蒸汽压力、主蒸汽温度，而炉膛烟气温度是最直接表明垃圾热值变化趋势的一个参数. 若焚烧过程中炉膛烟气温度始终保持较高值，则表明垃圾热值较高且波动较小；若炉膛烟气温度变化较大，则说明垃圾热值发生了较大的变化. 由于风量的大小亦会影响炉膛烟气温度，需综合考虑风量和炉膛烟气温度的波动. 空气预热器风压的大小可以说明焚烧炉里垃圾料层的厚度，当其值较低时，则表明料层较薄；反之，表明料层较厚. 即空气预热器风压能够间接说明垃圾焚烧速度和垃圾可燃成分的含量.
进而，将基于MI的第1阶段特征选择的计算结果进行统计，如表 2所示.
表 2 基于MI方法所选择特征变量的数量Table 2. Number of characteristic variables selected by MI method垃圾焚烧过程 原始特征数量 MI方法 炉膛燃烧子过程 16 16 炉排速度调节子过程 18 12 炉排温度控制子过程 24 18 空气流量调节子过程 18 14 4.2.2 不同特征选择的对比实验
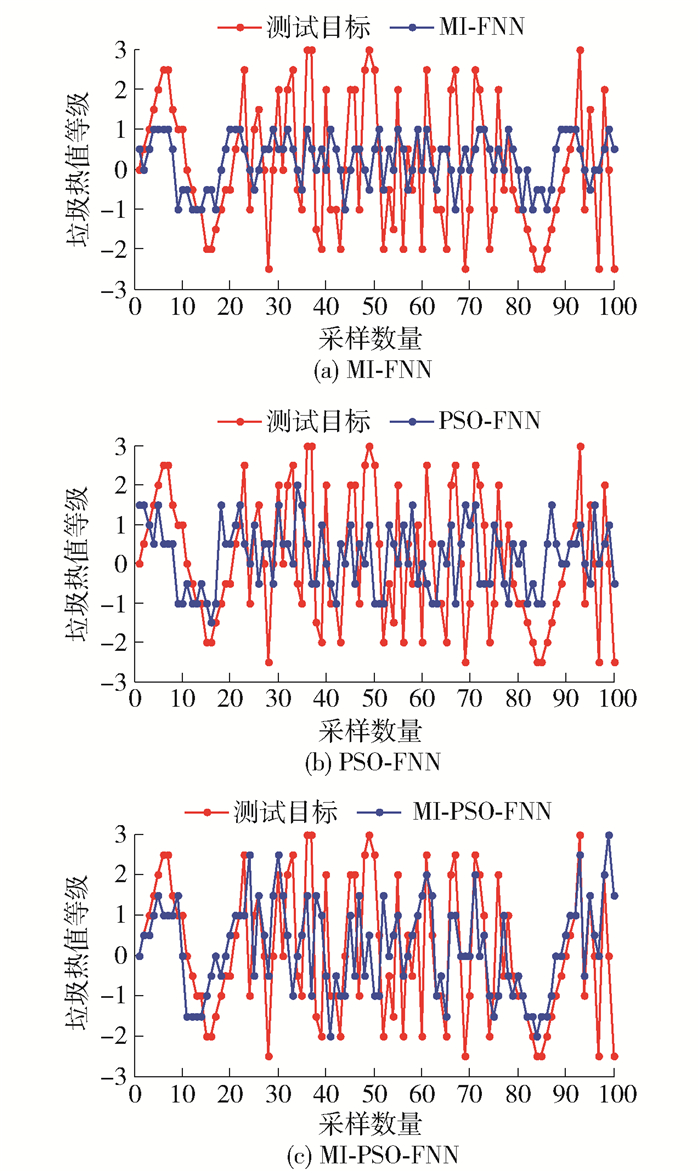
为了验证本文采用混合式特征选择的有效性，将本文方法MI-PSO-FNN与MI-FNN、PSO-FNN方法的模型预测精度、运行时间和特征数量通过测试数据集进行对比，实验结果如图 5所示，数据统计如表 3所示. 由图 5可以看出，本文提出的MI-PSO-FNN模型的预测精度更高，能够更好地预测垃圾热值及其变化趋势. 由表 3看出，MI-FNN的运行速度远快于其他2个模型，但其预测精度低；PSO-FNN模型的预测精度较高，但其运行速度很慢；本文提出的特征选择方法不仅能够有效地约简模型的特征数量，提高了运行速度，而且其模型的预测精度也高于其他2个模型.
![]()
图 5 不同特征选择方法训练出FNN预测模型的拟合效果对比Figure 5. Fitting effect of fuzzy neural network prediction model trained by different characteristic selection methods表 3 不同方法的实验结果对比Table 3. Experimental results comparison of different methods方法 运行时间 特征数量 RMSE MI-FNN 22.35 60 7.781 4 PSO-FNN 298.34 41 4.954 0 MI-PSO-FNN 235.65 26 2.256 4 根据上述实验，在MI阶段特征选择的基础上，采用基于PSO-FNN的第2阶段特征选择方法筛选出来的特征变量分别为：炉膛燃烧子过程(包括主蒸汽量、主蒸汽压力和主蒸汽温度、炉膛烟气温度等)共16个变量，干燥段炉排速度、燃烧一段炉排速度，燃烧二段炉排速度、干燥段炉排温度、燃烧一段炉排温度、燃烧二段炉温度、总风量、空气预热器风压、一次风压、二次风压，总计26个与垃圾热值相关度较高的变量.
4.2.3 基于MO-PSO-FNN模型的评估实验
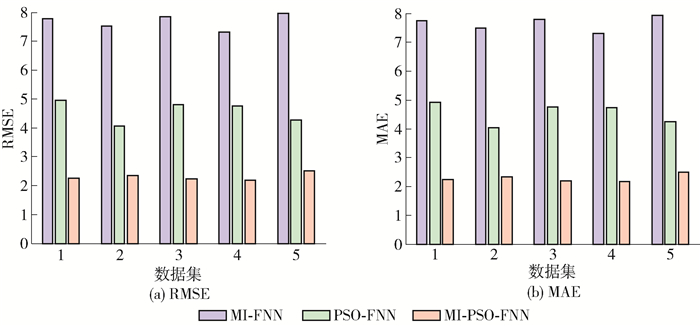
为了对基于MI-PSO-FNN垃圾热值预测模型的预测精度进行评估，本文分别采用RMSE和平均绝对误差(mean absolute error, MAE)作为评估指标，将筛选出来的26个特征变量作为FNN预测模型的输入，通过垃圾焚烧现场采集到的样本数据构建出5个数据集进行实验，实验结果统计如表 4所示. 不同方法的RMSE、MAE对比如图 6所示. 由图可看出，本文方法的RMSE、MAE在5个数据集的实验中均低于其他2种方法，表明本文方法的预测精度最高，这同时也验证了本文特征选择方法的有效性.
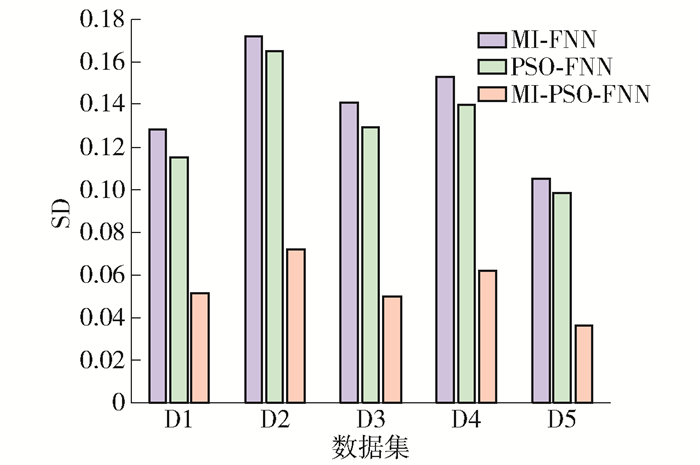
表 4 不同方法在5个数据集实验下的RMSE、MAE统计结果Table 4. RMSE and MAE statistical results of different methods in five data sets评价指标 方法 D1 D2 D3 D4 D5 平均值 MI-FNN 7.781 4 7.529 8 7.847 6 7.321 4 7.954 0 7.686 9 RMSE PSO-FNN 4.754 0 4.364 7 4.705 1 4.748 9 4.465 4 4.567 6 MI-PSO-FNN 2.256 4 2.354 0 2.225 8 2.287 6 2.421 7 2.309 1 MI-FNN 7.749 2 7.502 6 7.809 1 7.298 3 7.932 4 7.658 3 MAE PSO-FNN 4.923 5 4.029 8 4.768 9 4.726 3 4.240 6 4.537 8 MI-PSO-FNN 2.224 1 2.321 4 2.192 3 2.163 5 2.501 8 2.280 6 为了验证本文基于MI-PSO-SCN垃圾热值预测建模方法的稳定性，分别计算上述所构建出5个数据集中10组RMSE的标准差(standard deviation, SD)，并将其结果进行统计，如表 5所示. 为了更直观地看出本文方法与其他方法的对比效果，绘制了如图 7所示的柱状图. 由图 7可以看出，本文基于MI-PSO-SCN垃圾热值预测建模方法的SD在5个数据集的实验中均低于其他2种方法，说明本文基于MI-PSO-SCN垃圾热值预测建模方法的稳定性更好.
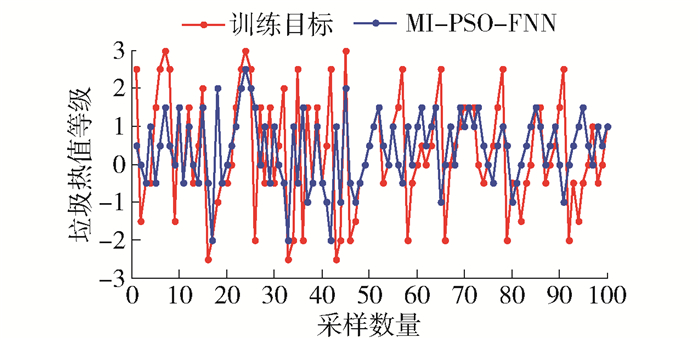
表 5 不同方法的SD统计结果Table 5. SD statistical results of different methods数据集 MI-FNN PSO-FNN MI-PSO-FNN D1 0.128 0.115 0.051 4 D2 0.172 0.165 0.070 2 D3 0.141 0.129 0.049 7 D4 0.153 0.140 0.062 1 D5 0.105 0.098 0.035 8 平均值 0.150 0.129 0.053 8 为了验证本文方法用于垃圾热值在线预测的有效性和合理性，将经过2个阶段特征选择之后的26个特征变量作为模型的输入，采用FNN建立预测模型，并对其预测精度进行分析. 通过训练数据集对模型进行训练得到如图 8所示的结果，由图可以看出，基于FNN模型的拟合效果较好，能够较好地预测垃圾热值的整体变化趋势.
![]()
图 8 FNN垃圾热值预测模型的训练结果Figure 8. Training results of fuzzy neural network waste heat value prediction model综上所述，将MI-FNN、PSO-FNN以及本文MI-PSO-FNN方法的RMSE、MAE、SD、运行时间、特征数量等实验结果统计如表 6所示. 通过实验结果表明，本文方法不仅能够有效地剔除无关变量和冗余变量，提高预测精度并降低计算成本，而且稳定性较好. 因此，本文方法可以满足垃圾热值的在线预测及其变化趋势，具有一定的应用价值.
表 6 不同方法的结果对比Table 6. Comparison results of different methods参数 MI-FNN PSO-FNN MI-PSO-FNN RMSE 7.686 9 4.567 6 2.309 1 MAE 7.658 3 4.537 8 2.280 6 SD 0.150 0.129 0.053 8 运行时间/s 22.35 298.34 235.65 特征数量 60 41 26 在垃圾焚烧的实际运行过程中，其工况会不断地发生变化. 随着焚烧过程的推进，其数据量不断增加，从而导致模型的计算负荷大大增加. 为了解决该问题，本文采用混合式特征选择方法对相关的特征变量进行约简，能够提高后续训练模型的效率，减少计算负荷；除此之外，利用FNN能够进行自学习的功能逐渐地更替模型预测所需的数据库，即当数据量增大时，用最新工况的样本替换掉原来的样本并离线训练模型，从而使计算负荷不会发生明显的增加，同时能够更好地跟踪焚烧过程中的当前工况，确保预测模型的精确度.
在无法实现对垃圾热值准确值的在线测量情况下，实际垃圾焚烧过程中需要掌握的是垃圾热值的整体水平以及变化趋势，上述实验均验证了本文方法的有效性. 将本文基于MI-PSO-FNN模型预测的垃圾热值结果作为现场操作人员对运行参数进行实时调整的依据，或者视为前端信号用于垃圾焚烧过程的自动控制系统中，以保证垃圾的稳定焚烧.
5. 结论
1) 针对垃圾热值相关特征变量众多，并且各相关特征变量之间以及这些变量与垃圾热值之间呈现强非线性关系，使得传统的线性特征提取方法如PCA、LDA、ICA无法处理的问题，本文提出了基于MI和PSO-FNN的混合式特征变量选择方法. 首先采用基于MI的方法从特征变量中去掉无关变量，完成第1阶段的特征变量选择，提升模型的效率. 然后将PSO算法和FNN结合起来，从第1阶段选择出的特征变量中进一步去除冗余变量，完成第2阶段的特征变量选择.
2) 针对垃圾焚烧过程中垃圾热值无法实现在线预测的问题，本文利用FNN在处理非线性、模糊性等问题上的优越性，构建出基于FNN的垃圾热值预测模型，将操作人员根据经验得到的垃圾热值等级作为样本数据，实现对垃圾热值在线变化趋势的预测.
3) 通过垃圾焚烧现场的实际数据以及操作人员根据经验得到的垃圾热值等级进行应用实验. 实验结果表明，本文采用的混合式特征变量方法能够有效地去除无关变量和冗余变量，提高预测模型的精度；基于FNN的预测模型能够实现垃圾热值的在线预测以及变化趋势预测，并且具有较好的预测精度和稳定性.
-
![]()
图 4 各个子过程特征变量与垃圾热值的MI值
Figure 4. MI value between characteristic variables and waste heat value of each sub process
![]()
图 5 不同特征选择方法训练出FNN预测模型的拟合效果对比
Figure 5. Fitting effect of fuzzy neural network prediction model trained by different characteristic selection methods
![]()
图 8 FNN垃圾热值预测模型的训练结果
Figure 8. Training results of fuzzy neural network waste heat value prediction model
表 1 各个子过程特征变量的互信息度量结果
Table 1 MI measurement results of characteristic variables in each sub process
垃圾焚烧过程 最大值 最小值 平均值 炉膛燃烧子过程 0.935 1 0.771 5 0.850 7 炉排速度调节子过程 0.864 3 0.453 8 0.653 8 炉排温度控制子过程 0.775 3 0.463 5 0.611 3 空气流量调节子过程 0.870 2 0.501 4 0.699 8 
下载: 导出CSV
表 2 基于MI方法所选择特征变量的数量
Table 2 Number of characteristic variables selected by MI method
垃圾焚烧过程 原始特征数量 MI方法 炉膛燃烧子过程 16 16 炉排速度调节子过程 18 12 炉排温度控制子过程 24 18 空气流量调节子过程 18 14
下载: 导出CSV
表 3 不同方法的实验结果对比
Table 3 Experimental results comparison of different methods
方法 运行时间 特征数量 RMSE MI-FNN 22.35 60 7.781 4 PSO-FNN 298.34 41 4.954 0 MI-PSO-FNN 235.65 26 2.256 4
下载: 导出CSV
表 4 不同方法在5个数据集实验下的RMSE、MAE统计结果
Table 4 RMSE and MAE statistical results of different methods in five data sets
评价指标 方法 D1 D2 D3 D4 D5 平均值 MI-FNN 7.781 4 7.529 8 7.847 6 7.321 4 7.954 0 7.686 9 RMSE PSO-FNN 4.754 0 4.364 7 4.705 1 4.748 9 4.465 4 4.567 6 MI-PSO-FNN 2.256 4 2.354 0 2.225 8 2.287 6 2.421 7 2.309 1 MI-FNN 7.749 2 7.502 6 7.809 1 7.298 3 7.932 4 7.658 3 MAE PSO-FNN 4.923 5 4.029 8 4.768 9 4.726 3 4.240 6 4.537 8 MI-PSO-FNN 2.224 1 2.321 4 2.192 3 2.163 5 2.501 8 2.280 6
下载: 导出CSV
表 5 不同方法的SD统计结果
Table 5 SD statistical results of different methods
数据集 MI-FNN PSO-FNN MI-PSO-FNN D1 0.128 0.115 0.051 4 D2 0.172 0.165 0.070 2 D3 0.141 0.129 0.049 7 D4 0.153 0.140 0.062 1 D5 0.105 0.098 0.035 8 平均值 0.150 0.129 0.053 8
下载: 导出CSV
表 6 不同方法的结果对比
Table 6 Comparison results of different methods
参数 MI-FNN PSO-FNN MI-PSO-FNN RMSE 7.686 9 4.567 6 2.309 1 MAE 7.658 3 4.537 8 2.280 6 SD 0.150 0.129 0.053 8 运行时间/s 22.35 298.34 235.65 特征数量 60 41 26
下载: 导出CSV
-
[1] TOZLU A, ÖZAHI E, ABUSOGLU A. Waste to energy technologies for municipal solid waste management in Gaziantep[J]. Renewable & Sustainable Energy Reviews, 2016, 54: 809-815. http://www.sciencedirect.com/science/article/pii/S1364032115011764
[2] DRUDI K, DRUDI R, MARTINS G, et al. Statistical model for heating value of municipal solid waste in Brazil based on gravimetric composition[J]. Waste Management, 2019, 87(3): 782-790.
[3] DOMALSKI E S, CHURNEY K L. MSW calorimetry[J]. Mechanical Engineering, 1986, 108(8): 32-35. http://www.researchgate.net/publication/293621881_MSW_CALORIMETRY
[4] 江娟, 孙蔚旻. 全自动热量计在固体废物热值测定中的应用[J]. 分析仪器, 2004(4): 46-47. doi: 10.3969/j.issn.1001-232X.2004.04.014 JIANG J, SUN W M. Application of automatic calorimeter in measurement of heat values of solid wastes[J]. Analytical Instrumentation, 2004(4): 46-47. (in Chinese) doi: 10.3969/j.issn.1001-232X.2004.04.014
[5] THIPSE S S, SHENG C, BOOTY M R, et al. Chemical makeup and physical characterization of a synthetic fuel and methods of heat content evaluation for studies on MSW incineration[J]. Fuel, 2002, 81(2): 211-217. doi: 10.1016/S0016-2361(01)00133-8
[6] DAVID C C, BRAIN K, JOHN M. Estimating the lower heating values of hazardous and solid wastes[J]. Air & Waste Management Association, 1999, 49(4): 471-476. doi: 10.1080/10473289.1999.10463816?needAccess=true
[7] 刘慧君, 王明杰, 高敏, 等. 城市生活垃圾热值估算方法研究[J]. 环境卫生工程, 1999, 7(3): 100-106. https://www.cnki.com.cn/Article/CJFDTOTAL-HJWS199903004.htm LIU H J, WANG M J, GAO M, et. al. Study on approaches for estimation heat value of municipal solid waste[J]. Environmental Sanitation Engineering, 1999, 7(3): 100-106. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJWS199903004.htm
[8] TIAN W D, WEI X L, WU D Y, et al. Analysis of ingredient and heating value of municipal solid waste[J]. Journal of Environmental Sciences, 2001, 13(1): 87-91. http://europepmc.org/abstract/MED/11590726
[9] MASTRO F L, MISTRETTA M. Cogeneration from thermal treatment of selected municipal solid wastes. A stoichiometric model building for the case study on Palermo[J]. Waste Management, 2004, 24(3): 309-317. doi: 10.1016/j.wasman.2003.10.007
[10] LIN X B, WANG F, CHI Y, et al. A simple method for predicting the lower heating value of municipal solid waste in China based on wet physical composition[J]. Waste Management, 2015, 36(12): 24-32. http://www.ncbi.nlm.nih.gov/pubmed/25536862
[11] 董长青, 金保升. 神经网络法用于预测城市生活垃圾热值[J]. 热能动力工程, 2002, 17(3): 275-278. doi: 10.3969/j.issn.1001-2060.2002.03.016 DONG C Q, JIN B S. Prediction of the heating value of municipal solid waste with the use of a neural network method[J]. Journal of Engineering for Thermal Energy & Power, 2002, 17(3): 275-278. (in Chinese) doi: 10.3969/j.issn.1001-2060.2002.03.016
[12] 张瑛华, 张友富, 王洪. 基于神经网络的生活垃圾低位热值计算模型的研究与应用[J]. 电力建设, 2010, 31(9): 94-97. doi: 10.3969/j.issn.1000-7229.2010.09.024 ZHANG Y H, ZHANG Y F, WANG H. Research and application of the LHV of MSW calculation model based on neural network[J]. Electric Power Construction, 2010, 31(9): 94-97. (in Chinese) doi: 10.3969/j.issn.1000-7229.2010.09.024
[13] AKKAYA E, DEMIR A. Predicting the heating value of municipal solid waste-based materials: an artificial neural network model[J]. Energy Sources Part A: Recovery, Utilization & Environmental Effects, 2010, 32(19): 1777-1783. doi: 10.1080/15567030902882950
[14] 马晓茜, 谢泽琼. 基于BP神经网络的垃圾热值预测模型[J]. 科技导报, 2012, 30(23): 46-50. doi: 10.3981/j.issn.1000-7857.2012.23.006 MA X Q, XIE Z Q. Prediction models for the heating values of municipal refuse based on BP neural network[J]. Science & Technology Review, 2012, 30(23): 46-50. (in Chinese) doi: 10.3981/j.issn.1000-7857.2012.23.006
[15] 丁兰, 张文阳, 张良均, 等. 基于人工神经网络的居民生活垃圾可燃成分热值预测[J]. 环境工程学报, 2016, 10(2): 899-905. https://www.cnki.com.cn/Article/CJFDTOTAL-HJJZ201602061.htm DING L, ZHANG W Y, ZHANG L J, et al. Prediction of household waste combustible component calorific value based on artificial neural network[J]. Chinese Journal of Environmental Engineering, 2016, 10(2): 899-905. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJJZ201602061.htm
[16] QIN S J. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220-234. doi: 10.1016/j.arcontrol.2012.09.004
[17] LIU Y, NIE F P, WU J G, et al. Efficient semi-supervised feature selection with noise insensitive trace ratio criterion[J]. Neurocomputing, 2013, 105(10): 12-18.
[18] KOHAVI R, JOHN G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1): 273-324. http://doi.ieeecomputersociety.org/resolve?ref_id=doi:10.1016/S0004-3702(97)00043-X&rfr_id=trans/tp/2004/09/ttp2004091154.htm
[19] HU Z Y, BAO Y K, XIONG T, et al. Hybrid filter-wrapper feature selection for short-term load forecasting[J]. Engineering Applications of Artificial Intelligence, 2015, 40(4): 17-27. doi: 10.1016/j.engappai.2014.12.014
[20] YAN X A, JIA M P. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection[J]. Knowledge-Based Systems, 2019, 163(1): 450-471. http://www.sciencedirect.com/science/article/pii/S0950705118304556
[21] TANG J, CHAI T Y, YU W, et al. Feature extraction and selection based on vibration spectrum with application to estimating the load parameters of ball mill in grinding process[J]. Control Engineering Practice, 2012, 20(8): 911-1004. http://www.sciencedirect.com/science/article/pii/S0967066112000846
[22] GAO W F, HU L, ZHANG P. Class-specific mutual information variation for feature selection[J]. Pattern Recognition, 2018, 79(1): 328-339. http://www.sciencedirect.com/science/article/pii/S0031320318300736
[23] LIMONGELLI M P, GIORDANO P F. Vibration-based damage indicators: a comparison based on information entropy[J]. Journal of Civil Structural Health Monitoring, 2020, 10(2): 251-266. doi: 10.1007/s13349-020-00381-9
[24] YAN K, MA L L, DAI Y T, et al. Cost-sensitive and sequential feature selection for chiller fault detection and diagnosis[J]. International Journal of Refrigeration, 2018, 86(2): 401-409. http://www.sciencedirect.com/science/article/pii/S0140700717304449
[25] SAYED S, NASSEF M, BADR A, et al. A nested genetic algorithm for feature selection in high-dimensional cancer microarray datasets[J]. Expert Systems with Applications, 2019, 121(5): 233-243. http://www.researchgate.net/publication/329670215_A_Nested_Genetic_Algorithm_for_Feature_Selection_in_High-dimensional_Cancer_Microarray_Datasets
[26] AMOOZEGAR M, MINAEI-BIDGOLI B. Optimizing multi-objective PSO based feature selection method using a feature elitism mechanism[J]. Expert Systems with Applications, 2018, 113(15): 499-514. http://www.sciencedirect.com/science/article/pii/S0957417418304287
[27] 杨伟, 章慧芸, 仲海波. 基于模糊神经网络的VSC-HVDC系统控制器的研究[J]. 电力系统保护与控制, 2014, 42(8): 115-120. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201408019.htm YANG W, ZHANG H Y, ZHONG H B. Research on controller of VSC-HVDC system based on fuzzy neural network[J]. Power System Protection & Control, 2014, 42(8): 115-120. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201408019.htm
[28] CHEN S G, LIN F J, LIANG C H. Intelligent maximum power factor searching control using recurrent chebyshev fuzzy neural network current angle controller for SynRM drive system[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3496-3511. doi: 10.1109/TPEL.2020.3016709
[29] 张璐, 张嘉成, 韩红桂, 等. 基于模糊神经网络的污水处理生化除磷过程控制[J]. 化工学报, 2020, 71(3): 1217-1225. https://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ202003033.htm ZHANG L, ZHANG J C, HAN H G, et al. FNN-based process control for biochemical phosphorus in WWTP[J]. Journal of Chemical Industry & Engineering, 2020, 71(3): 1217-1225. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ202003033.htm
[30] 俞建成, 张艾群, 王晓辉, 等. 基于模糊神经网络水下机器人直接自适应控制[J]. 自动化学报, 2007, 33(8): 840-846. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO200708012.htm YU J C, ZHANG A Q, WANG X H, et al. Direct adaptive control of underwater vehicles based on fuzzy neural network[J]. Acta Automatica Sinica, 2007, 33(8): 840-846. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO200708012.htm
[31] 韩红桂, 郐晓丹, 张璐, 等. 基于模糊神经网络的废旧手机价值评估方法[J]. 北京工业大学学报, 2019, 45(11): 1033-1040. doi: 10.11936/bjutxb2019070010 HAN H G, KUAI X D, ZHANG L, et al. Value assessment method of waste mobile phones based on fuzzy neural network[J]. Journal of Beijing University of Technology, 2019, 45(11): 1033-1040. (in Chinese) doi: 10.11936/bjutxb2019070010
[32] PENG H C, LONG F H, DING C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27(8): 1126-1138. http://www.tandfonline.com/servlet/linkout?suffix=CIT0015&dbid=8&doi=10.1080%2F01431161.2012.663111&key=16119262
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
