Sputtering Parameters Optimization of Mo Thin Films Based on Orthogonal Experiment
-
摘要:
Mo薄膜是CIGS薄膜太阳电池背电极的首选材料，对薄膜与基底间的结合力提出很大要求.为提高Mo薄膜与基底结合力，借助L9（33）正交表研究基底温度、溅射气压和溅射功率3种影响因素对Mo薄膜结合力的影响，针对每种因素各选取3个水平值.采用压入法衡量薄膜与基底的结合力，结合力的评价指标为压入引起的裂纹的面积，利用改进版龟裂评级法得出裂纹面积.通过极差分析得到基底温度、溅射气压、溅射功率所对应的R值分别为6.51、18.29、5.96；最优水平组合为A1B2C3，此时裂纹面积最小，为2.41 μm2.结果表明：影响Mo薄膜与基底结合力的因素由主到次为溅射气压、基底温度、溅射功率，综合考虑3种影响因素下Mo薄膜的最优制备工艺参数为溅射功率150 W，溅射气压0.5 Pa，基底温度100℃.
Abstract:Mo thin films are the preferred material for the back electrode of CIGS solar cells, which puts forward great demands on the adhesion strength between the thin films and the substrate. To improve the adhesion strength, the effect of three factors (depositing temperature, vacuum degree, and sputtering power) on adhesion strength with the help of L9(33) orthogonal table was studied and three levels were selected for each factor. The indentation method was used to measure the adhesion strength between films and substrates. The evaluation criterion of the adhesion strength was the area of indentation-induced cracks, which could be obtained by the improved Uddeholm method. Through range analysis, the R values of depositing temperature, vacuum degree, and sputtering power were 6.51, 18.29, and 5.96, respectively. The optimal combination was A1B2C3, and the area of cracks was the smallest at that time, which was 2.41. Results show that the effect of vacuum degree on adhesion strength is the largest, then depositing temperature, while the effect of sputtering power is the least. Considering the three factors, the optimal sputtering parameter combination is: power 150 W, pressure 0.5 Pa, and temperature 100 ℃.
-
Mo元素广泛应用于多个工业领域[1]，如用于集成电路栅极材料[2]、真空电子管灯丝材料[3]、CIGS太阳能电池背电极材料等[4]. Mo薄膜由于具备低的电阻率、良好的热稳定性以及与CIGS层可形成很好的欧姆接触，同时与CIGS层相近的热膨胀系数等特点，是CIGS薄膜太阳电池背电极的首选材料[5]. Mo薄膜作为CIGS太阳能电池的背电极材料，是电池中最重要的一层，对薄膜与基底间的结合力提出很大要求[6]. 胶带测试法(tape test method)是国际上常用于测试Mo背电极结合力的方法[7-8]，是用标准面积的胶带以恒定的速度和一定的角度从实验材料上剥离，若薄膜被剥离下来则不通过测试(fail)，若薄膜仍在衬底上表示通过测试(pass)[9].
目前常用制备Mo薄膜的方法有化学气相沉积(chemical vapor deposition，CVD)[10-11]和物理气相沉积(physical vapor deposition，PVD)[12]两大类. 其中，磁控溅射由于制备工艺简单，便于大面积成膜的特点被广泛应用，并且磁控溅射制备的薄膜结构致密，可以通过调控制备参数得到不同性质的薄膜. Mobtakeri等[13]研究表明在相同基底温度下，溅射气压和功率会影响薄膜的晶体结构和表面形貌，且溅射功率越大，Mo薄膜的晶粒尺寸越大[14]，Derby等[15]研究表明溅射时的基底温度对薄膜形貌和性能有直接的影响. 可以看出，基底温度、溅射气压和溅射功率是对薄膜质量和性能影响最大的3个因素. 为了得到与基底结合良好的钼膜，本文基于正交试验研究了基底温度、溅射气压和溅射功率对结合力的影响，并优化制备结合良好的Mo薄膜的工艺参数.
1. 材料与试验方法
1.1 Mo薄膜的制备
本次试验采用JPG-450B型三靶磁控溅射. 沉积的基底为轧制Mo块，线切割成规格为20 mm×20 mm×2 mm的方片. 试验前先用不同型号的砂纸对Mo块基底单面打磨，并机械抛光至光学显微镜下观察无划痕，再依次用丙酮、无水乙醇、去离子水各超声清洗15 min，最后用N2吹干放入溅射真空室. 溅射所用的Mo靶纯度为99.95%，靶基距为45 mm. 溅射镀膜的背底真空度为6.5×10-4 Pa，工作气体为99.99%的高纯Ar气. 在正式镀膜之前需对Mo靶材进行5 min预溅射以除掉表面的氧化物等杂质.
1.2 正交试验设计
磁控溅射法制备薄膜的影响因素有：溅射功率、溅射气压、基底温度、气体流量. 在实际溅射过程中，气体流量与溅射气压对薄膜成形质量的影响具有相似性[16]，故主要影响因素实际为3个. 本次试验选用L9(33)正交表进行系列试验. 3个试验水平根据实际经验选取，正交试验的因素和水平如表 1所示. Mo膜与基底有足够的结合强度是CIGS太阳能电池一切优良性能的前提，本次试验选取结合强度为正交试验的评价指标. 因素A、B、C分别表示基底温度、溅射气压，测射功率.
表 1 正交试验因素水平表Table 1. Factors and levels of orthogonal experiment水平 因素A/℃ 因素B/Pa 因素C/W 水平1 100 0.5 100 水平2 300 1.0 150 水平3 500 2.0 200 1.3 测试方法
由于胶带测试法的结果太过于笼统，只表示为通过和不通过2种结果. 因此，本次试验在胶带测试法的基础上，引入压入法来对结合力进行具体的量化. Buijnsters等[17]采用压入法和划痕法对金刚石薄膜与基底的结合力进行研究，表明2种方法均可表征薄膜与基底的结合力，且相比于其他方法，Ollendorf等[18]认为压入法操作方便、结果直观.
在本次试验中，用HXD-1000型数字式显微硬度计在Mo膜样品中心连续打点3次，并且要保持后一个选取点与前一个选取点的距离均保持相等. 每次施加10 g载荷、加载时间10 s，以压出裂纹，并用Olympus BX51型光学显微镜观察裂纹，通过对裂纹的分析得出薄膜结合力的评价. 本课题组曾提出一种改进版龟裂评级法(improved uddeholm method)[19]用于定量分析热疲劳裂纹. 首先利用图像处理软件对裂纹进行标定；再用像素统计功能统计各条裂纹的像素数；最后将像素数转化为裂纹的评定参量，要确保所有图片都具有相同的放大倍数及分辨率. 本试验在此基础上进行改进，采用的裂纹评定参量为裂纹面积，先标定出每个像素格子对应的实际面积，再结合像素数就可以得到实际的裂纹面积. 标尺是连接像素数与实际尺寸之间关系的唯一参量，先确定像素数与实际尺寸之间的转化率，即
$$ Z = \frac{{{L_{\rm{R}}}}}{R} $$ (1) 式中：Z为像素数与实际尺寸之间的转换率，μm/px；LR为标尺的实际长度，μm；R表示标尺像素数，px.
由此可得图片上任一线段的长度L，且
$$ L = Z \times M $$ (2) 式中M为任一线段的像素数. 对于一个像素格子，其像素数为1，所以可得该像素格子的边长对应的实际尺寸LP为
$$ {L_{\rm{P}}} = Z \times 1 $$ (3) 该像素格子的面积SP为
$$ {S_{\rm{P}}} = L_{\rm{P}}^2 $$ (4) 调整图片的对比度、亮度和色彩，利用软件工具选中裂纹区域并填充颜色，再用像素统计功能得出裂纹区的像素数N，就可以得到实际裂纹面积
$$ {S_{\rm{R}}} = {S_{\rm{P}}} \times N $$ (5) 2. 结果与讨论
2.1 正交试验结果分析
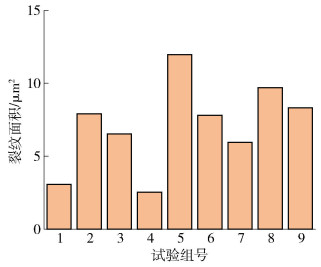
本次正交试验选取的评价指标为薄膜表面裂纹面积. 三因素三水平的正交试验一共需要9组实验，在每次实验完成后需要计算同一样品表面连续3个压痕的裂纹面积的平均值并填入表中，试验结果如表 2所示. 图 1更为直观地表现出9组正交试验的结果. 从表 2与图 1中可以看出，钼薄膜与基底的结合力明显受到磁控溅射工艺参数的影响. 其中，基底温度为300 ℃、溅射气压为0.5 Pa、溅射功率为150 W时，压痕平均裂纹面积最小；基底温度为300 ℃、溅射气压为1.0 Pa、溅射功率为100 W时，压痕平均裂纹面积最大.
表 2 正交试验方案结果Table 2. Results of orthogonal experiment试验组号 磁控溅射工艺参数 裂纹面积平均值/μm2 因素A/℃ 因素B/Pa 因素C/W 1 100(1) 0.5(1) 200(3) 3.05 2 100(1) 1.0(2) 150(2) 7.89 3 100(1) 2.0(3) 100(1) 6.51 4 300(2) 0.5(1) 150(2) 2.52 5 300(2) 1.0(2) 100(1) 11.95 6 300(2) 2.0(3) 200(3) 7.80 7 500(3) 0.5(1) 100(1) 5.95 8 500(3) 1.0(2) 200(3) 9.70 9 500(3) 2.0(3) 150(2) 8.31 通过计算可以得到每个因素对试验结果的影响程度次序，且
$$ {K_{xm}} = \frac{{{y_{m1}} + {y_{m2}} + \cdots + {y_{mn}}}}{n} $$ (6) $$ {R_{0x}} = \max \left\{ {{K_{x1}},{K_{x2}},{K_{x3}}, \cdots } \right\} $$ (7) $$ {R_{1x}} = \min \left\{ {{K_{x1}},{K_{x2}},{K_{x3}}, \cdots } \right\} $$ (8) $$ {R_x} = {R_{0x}} - {R_{1x}} $$ (9) 式中：Kxm代表在水平m下，因素x的指标平均值，每个指标记为ymn；R0x和R1x表示在同一因素所有水平下的Kxm对应的最大值与最小值；Rx即为每个因素对应的极差值.
计算结果如表 3所示，极差R的大小代表了相应因素的重要程度，即R越大表明该因素对评价指标的影响越大. 可以看出基底温度、溅射气压、溅射功率3个因素所对应的R值分别为6.51、18.29、5.96. 可以得到：对于薄膜表面裂纹面积而言，溅射气压(因素B)为主要影响因素，其次为基底温度(因素A)，影响程度最小的是溅射功率(因素C). 第4组的压痕平均裂纹面积最小，即从9组试验中直观地得出较优水平组合为A2B1C2，但从极差分析结果得到的最优组合为A1B1C2，故采用补充试验对第4组工艺条件进行验证，优化方案记为第10组，3个压痕的裂纹如图 2所示，经计算其平均裂纹面积为2.41 μm2. 可以看出，通过极差分析得到的最优组合(第10组)，其表面平均裂纹面积相比于正交试验的最好组合(第4组)减少了4%，对应地也说明第10组的结合力要稍好于第4组. 对第10组进行胶带测试，测试结果为通过. 所以第10组已满足国际上对Mo薄膜背电极材料结合力的要求，且用裂纹面积具体量化了结合力，比只用胶带测试法得出的结果更具说服力.
表 3 正交试验极差分析Table 3. Calculation results of range analysis水平 因素 A B C 1 17.45(KA1) 11.52(KB1) 24.41(KC1) 2 22.27(KA2) 29.54(KB2) 18.72(KC2) 3 23.96(KA3) 22.62(KB3) 20.55(KC3) R 6.51(KA) 18.02(KB) 5.69(KC) ![]()
图 2 补充试验(第10组)3次压痕裂纹Figure 2. Three indentation-induced cracks of supplementary experiment (group 10)2.2 各工艺参数对Mo薄膜结合力的影响
参考正交试验设计理论，正交试验可以在B、C两个因素变动的情况下比较A因素的水平对试验指标的影响. 因为B、C两个因素的水平变动是有规律且均衡分散的，所以试验指标的变化主要是由A因素的单个水平不同引起的[20]. 在本试验中，有A、B、C三个因素，以基底温度A为例，该因素的3个温度值A1、A2、A3条件下各有溅射压强B、溅射功率C的3个不同水平，如表 4所示. 把表 4的9个试验组合分为3个组合，每个组合只有A1、A2、A3参加试验，而在3组之间其余因素B、C的各个水平参加的次数完全相同，亦即在3组试验中其余因素对裂纹面积之和的贡献完全相等，可视为一种随机干扰. 这种对比排除了其他因素的影响，只反映因素A的水平改变对裂纹面积之和所起的作用[21]，所以可以用来分析因素A不同水平值的改变对裂纹面积之和的影响，分析因素B、C时也同理.
表 4 基底温度(A)与溅射气压(B)、测射功率(C) 的搭配组合Table 4. Combination of depositing temperature (A) with vacuum degree (B) and sputtering power (C)第1组 第2组 第3组 A1 B1C3 A2 B1C2 A3 B1C1 B2C2 B2C1 B2C3 B3C1 B3C3 B3C2 2.2.1 基底温度
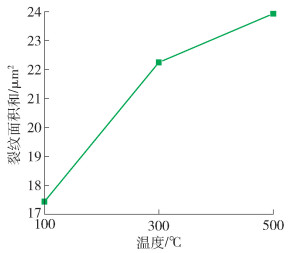
图 3为同一基底温度下各组试验裂纹面积之和. 借助正交试验的数据综合可比性，可以排除溅射功率和溅射气压的影响，只反映基底温度对裂纹面积之和的影响，又因为裂纹面积之和与结合力负相关，所以可以通过裂纹面积之和反映基底温度对结合力的影响. 从图 3可以看出基底温度对Mo薄膜结合力有较为明显的影响，在100~500 ℃内，随温度的增加薄膜裂纹也增大，表明结合力也逐渐变差. 其中100 ℃时裂纹面积和最小，500 ℃时裂纹面积和最大. 这是因为Mo原子到达100 ℃的基底上时没有被迅速冷却，仍有多余的能量进行迁移扩散至稳定位置，形成缺陷数量较少的均匀薄膜，具有较强的结合力. 并且基底温度较低时，容易形成大量细小的晶粒，增加Mo薄膜与基底的结合力，所以裂纹面积和较小. 而温度升高时，尽管高温能够促进Mo原子在基底上迁移扩散到稳定位置减少界面处缺陷的数量提高结合力，但高温也会促进晶界迁移和晶粒长大，得到相对粗大的组织降低结合力，薄膜与基底的结合受到这2种相互制约的因素协同影响. 300 ℃和500 ℃下裂纹面积和较大表明：在此温度下，晶界迁移和晶粒长大对结合力的影响要大于迁移扩散的影响.
![]()
图 3 裂纹面积之和与基底温度关系Figure 3. Relationship between cracks area and depositing temperature2.2.2 溅射气压
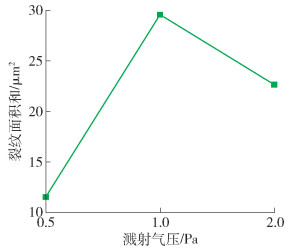
图 4为同一溅射气压下各组试验裂纹面积之和，在0.5~2.0 Pa内，0.5 Pa时裂纹面积和远小于1 Pa和2 Pa时的裂纹面积之和. 0.5 Pa时裂纹面积之和最小，即结合力最好的原因可能与靶材原子的平均自由程有关. 被溅射Mo原子的平均自由程λ与溅射气压的关系有[22]
$$ \mathit{\lambda } = \frac{{{K_{\rm{b}}}T}}{{\sqrt 2 {\rm{ \mathit{ π} }}{{\left( {{r_{\rm{g}}} + {r_{\rm{m}}}} \right)}^2}p}} $$ (10) 式中：Kb为玻尔兹曼常数；T为气体温度，一般为室温；rg、rm分别代表工作气体的半径和被溅射原子的半径；p为溅射气压. 可知，溅射气压为0.5 Pa时，Mo原子的平均自由程要比1 Pa和2 Pa时大，与腔体中的Ar原子碰撞次数少，到达基底时仍具有较高的能量进行迁移，迁移到稳定沉积位置可以减少界面处缺陷的产生，从而提高薄膜的均匀性得到结合力较好的Mo薄膜；而溅射气压增大到1 Pa时，Mo原子的平均自由程减小，到达基底时能量降低，没有足够的能量进行迁移扩散，界面处缺陷数量增多，导致薄膜与基底结合力降低. 本试验中，溅射气压为2 Pa时薄膜裂纹面积和比1 Pa时有所减小，这可能是因为受到其他工艺参数的影响，但总体来说还是低溅射气压时裂纹面积和最小.
2.2.3 溅射功率
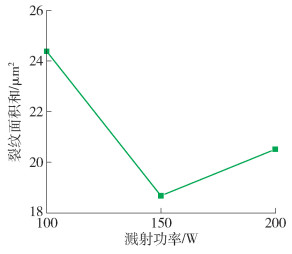
图 5为同一溅射功率下各组试验裂纹面积之和，在100~200 W内，150 W时裂纹面积之和最小，表明此功率下制备的Mo薄膜的结合力最好. 而当溅射功率为100 W和200 W时裂纹面积之和较大，表明这2种功率下制备的薄膜结合力不如150 W时制备的薄膜. 溅射功率从150 W增加到200 W时，Ar+入射能量也增大，靶材中被溅射出来的Mo原子数量增加. 溅射出来的Mo原子数量增加则会导致沉积Mo薄膜的速率加快，速率过快时Mo原子易于形成团簇形貌，甚至在表面出现大颗粒，会严重影响薄膜的均匀性[16]，从而对结合力产生不良影响，所以200 W时的结合力不如100 W时的结合力；当功率变为100 W时，被溅射出来的Mo原子的平均动能太小，不利于Mo原子与基底的结合，并且原子到达基底时没有足够的能量进行迁移扩散，迁移扩散不充分会导致薄膜与基底结合面缺陷的产生，使得薄膜疏松粗糙，影响与基底的结合力. 在实际制备Mo薄膜过程中需要合理选择溅射功率，才能得到与基底结合良好的致密Mo薄膜.
3. 结论
1) 影响Mo薄膜与基底结合力的因素由主到次分别为溅射气压、基底温度、溅射功率.
2) 磁控溅射制备Mo薄膜的优化工艺为溅射功率150 W，溅射气压0.5 Pa，基底温度100 ℃.
3) 溅射功率过大或过小都不利于获得结合良好的Mo薄膜，要合理选择合适的溅射功率.
-
![]()
图 2 补充试验(第10组)3次压痕裂纹
Figure 2. Three indentation-induced cracks of supplementary experiment (group 10)
![]()
图 3 裂纹面积之和与基底温度关系
Figure 3. Relationship between cracks area and depositing temperature
表 1 正交试验因素水平表
Table 1 Factors and levels of orthogonal experiment
水平 因素A/℃ 因素B/Pa 因素C/W 水平1 100 0.5 100 水平2 300 1.0 150 水平3 500 2.0 200 
下载: 导出CSV
表 2 正交试验方案结果
Table 2 Results of orthogonal experiment
试验组号 磁控溅射工艺参数 裂纹面积平均值/μm2 因素A/℃ 因素B/Pa 因素C/W 1 100(1) 0.5(1) 200(3) 3.05 2 100(1) 1.0(2) 150(2) 7.89 3 100(1) 2.0(3) 100(1) 6.51 4 300(2) 0.5(1) 150(2) 2.52 5 300(2) 1.0(2) 100(1) 11.95 6 300(2) 2.0(3) 200(3) 7.80 7 500(3) 0.5(1) 100(1) 5.95 8 500(3) 1.0(2) 200(3) 9.70 9 500(3) 2.0(3) 150(2) 8.31
下载: 导出CSV
表 3 正交试验极差分析
Table 3 Calculation results of range analysis
水平 因素 A B C 1 17.45(KA1) 11.52(KB1) 24.41(KC1) 2 22.27(KA2) 29.54(KB2) 18.72(KC2) 3 23.96(KA3) 22.62(KB3) 20.55(KC3) R 6.51(KA) 18.02(KB) 5.69(KC)
下载: 导出CSV
表 4 基底温度(A)与溅射气压(B)、测射功率(C) 的搭配组合
Table 4 Combination of depositing temperature (A) with vacuum degree (B) and sputtering power (C)
第1组 第2组 第3组 A1 B1C3 A2 B1C2 A3 B1C1 B2C2 B2C1 B2C3 B3C1 B3C3 B3C2
下载: 导出CSV
-
[1] ZHANG Z, QIAN Q, LI B. Interface engineering of monolayer MoS2/GaN hybrid heterostructure: modified band alignment for photocatalytic water splitting application by nitridation treatment[J]. ACS Applied Materials & Interfaces, 2018, 10(20): 17419-17422.
[2] JUANG M H, LIN T Y, JANG S L. Formation of Mo gate electrode with adjustable work function on thin Ta2O5 high-k dielectric films[J]. Solid-State Electronics, 2006, 50(2): 114-118. doi: 10.1016/j.sse.2005.10.029
[3] CAOGEN Y, HONGJUN L, ZHIPING H, et al. A study on carburized La-Mo cathode material[J]. International Journal of Refractory Metals and Hard Materials, 2000, 18(6): 261-265. doi: 10.1016/S0263-4368(00)00022-6
[4] ASSMANN L, BERNōDE J C, DRICI A, et al. Study of the Mo thin films and Mo/CIGS interface properties[J]. Applied Surface Science, 2005, 246(1): 159-166.
[5] 沈晓月. 磁控溅射法制备CIGS薄膜光伏电池Mo背电极的研究[D]. 大连: 大连工业大学, 2013. SHEN X Y. Performance of the Mo thin film back electrode by magnetron sputtering for CIGS solar cells[D]. Dalian: Dalian Polytechnic University, 2013. (in Chinese)
[6] YANG C, SONG K, XU X, et al. Strain dependent effect on power degradation of CIGS thin film solar cell[J]. Solar Energy, 2020, 195: 121-128. doi: 10.1016/j.solener.2019.11.012
[7] PETHE S A, TAKAHASHI E, KAUL A, et al. Effect of sputtering process parameters on film properties of molybdenum back contact[J]. Solar Energy Materials and Solar Cells, 2012, 100: 1-5. doi: 10.1016/j.solmat.2011.11.038
[8] BADGUJAR A C, DHAGE S R, JOSHI S V. Process parameter impact on properties of sputtered large-area Mo bilayers for CIGS thin film solar cell applications[J]. Thin Solid Films, 2015, 589: 79-84. doi: 10.1016/j.tsf.2015.04.046
[9] LI Z-H, CHO E-S, KWON S J. Molybdenum thin film deposited by in-line DC magnetron sputtering as a back contact for Cu(In, Ga)Se2 solar cells[J]. Applied Surface Science, 2011, 257(22): 9682-9688. doi: 10.1016/j.apsusc.2011.06.101
[10] GESHEVA K A, KRISOV T A, SIMKOV U I, et al. Deposition and study of CVD—tungsten and molybdenum thin films and their impact on microelectronics technology[J]. Applied Surface Science, 1993, 73: 86-89. doi: 10.1016/0169-4332(93)90150-A
[11] GESHEVA K, CZIRAKI A, IVANOVA T, et al. Structure and composition of thermally annealed Mo- and W-based CVD metal oxide thin films[J]. Thin Solid Films, 2005, 492(1): 322-326.
[12] ZAOUALI M, LEBRUN J L, GERGAUD P. X-ray diffraction determination of texture and internal stresses in magnetron PVD molybdenum thin films[J]. Surface and Coatings Technology, 1991, 50(1): 5-10. doi: 10.1016/0257-8972(91)90185-Y
[13] MOBTAKERI S, AKALTUN Y, ÖZER A, et al. Gallium oxide films deposition by RF magnetron sputtering: a detailed analysis on the effects of deposition pressure and sputtering power and annealing[J]. Ceramics International, 2021, 47(2): 1721-1727. doi: 10.1016/j.ceramint.2020.08.289
[14] LIU Y J, OU C Y, LU C H. Effects of Mo films prepared via different sputtering conditions on the formation of MoSe2 during selenization[J]. Journal of Alloys and Compounds, 2018, 747: 621-628. doi: 10.1016/j.jallcom.2018.02.236
[15] DERBY B, CUI Y, BALDWIN J K, et al. Effects of substrate temperature and deposition rate on the phase separated morphology of co-sputtered, Cu-Mo thin films[J]. Thin Solid Films, 2018, 647: 50-56. doi: 10.1016/j.tsf.2017.12.013
[16] 马国政, 徐滨士, 王海斗等. 磁控溅射制备Mo薄膜的优化工艺和组织及性能研究[J]. 稀有金属材料与工程, 2014, 4(9): 2221-2226. https://www.cnki.com.cn/Article/CJFDTOTAL-COSE201409034.htm MA G Z, XU B S, WANG H D, et al. Optimal process, microstructure and properties of Mo films deposited by magnetron sputtering[J]. Rare Metal Materials and Engineering, 2014, 4(9): 2221-2226. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-COSE201409034.htm
[17] BUIJNSTERS J G, SHANKAR P, VAN ENCKEVORT W J P, et al. Adhesion analysis of polycrystalline diamond films on molybdenum by means of scratch, indentation and sand abrasion testing[J]. Thin Solid Films, 2005, 474(1): 186-196.
[18] OLLENDORF H, SCHNEIDER D. A comparative study of adhesion test methods for hard coatings[J]. Surface and Coatings Technology, 1999, 113(1): 86-102.
[19] QI Y, WANG B, LI S, et al. Improved quantitative analysis method for evaluating fatigue cracks in thermal fatigue testing[J]. Materials Letters, 2019, 242: 115-118. doi: 10.1016/j.matlet.2019.01.113
[20] 刘选民. 试验设计方法[M]. 北京: 科学出版社, 2006: 70-71. [21] 沈邦兴, 文昌俊. 实验设计及工程应用[M]. 北京: 中国计量出版社, 2005: 120-121. [22] VVLLERS F T N, SPOLENAK R. Alpha- vs. beta-W nanocrystalline thin films: a comprehensive study of sputter parameters and resulting materials' properties[J]. Thin Solid Films, 2015, 577: 26-34. doi: 10.1016/j.tsf.2015.01.030
-
期刊类型引用(1)
1. 张开策，时晓光，周艳文，粟志伟，徐帅，王鼎. 基于正交试验的磁控溅射铝涂层对孪晶诱发塑性钢耐蚀性的影响. 表面技术. 2023(04): 223-232 . 
百度学术
其他类型引用(5)
计量
- 文章访问数: 231
- HTML全文浏览量: 7
- PDF下载量: 54
- 被引次数: 6
