Comparison of Design Methods for Tensile Capacity of Screw Connections in Cold-formed Steel Structures
-
摘要:
基于国内外学者相关研究文献及已有的342组自攻螺钉拉拔和拉脱试验结果,对冷弯型钢结构中自攻螺钉连接抗拔性能、抗拉脱性能的研究现状进行总结,并对《冷弯薄壁型钢结构技术规范》(GB 50018—2002)、《冷弯型钢结构技术规范(征求意见稿)》(GB50018—2017)、美国规范(AISI S136-16)、澳大利亚/新西兰规范(AS/NZS 4600:2018)、英国规范(BS5950-5-1998)和欧洲规范(BS EN 1993-1-3:2006)中自攻螺钉设计方法的计算精度和适用性进行比较分析.比较结果表明,《冷弯型钢结构技术规范(征求意见稿)》(GB 50018—2017)的自攻螺钉抗拉设计方法计算精度较高、适用性最好.对于厚度不超过0.75 mm的550级高强超薄板受拉承载力,《冷弯型钢结构技术规范(征求意见稿)》(GB 50018—2017)的安全度略低,需要乘以0.8的折减系数;对于板厚超过2 mm的中低强度薄板受拉承载力,冷弯型钢结构技术规范(征求意见稿)偏于不经济.此外,建议自攻螺钉名义直径与压型钢板板厚之比(d/t)不超过8,以保证螺钉节点在达到最大抗拔承载力时可以较好地发挥自攻螺钉和板件的连接性能.
Abstract:Based on the relevant research literature and the existing 342 sets of self-drilling screw tensile test results, the research status of the pull-out behavior and pull-over behavior of self-drilling screw connection in cold-formed steel structure were summarized. The calculation accuracy and applicability of self-drilling screw design methods in Technical Code of Cold-formed Thin-walled Steel Structures(GB 50018-2002), Technical Code of Cold-formed Steel Structures (Draft for Comments), American code (AISI S136-16), Australian code (AS/NZS 4600:2018), British code (BS 5950-5-1998) and European code (BS EN 1993-1-3:2006) were compared and analyzed in this paper. Results show that design method in Technical Code of Cold-formed Steel Structures (Draft for Comments) has highest accuracy and applicability. For 550 grade steel plate with thickness lower, a reduction factor of 0.8 on the tensile capacity is needed. For medium and low strength steel plate with thickness more than 2 mm, design value by Technical Code of Cold-formed Steel Structures (Draft for Comments) is uneconomical. In addition, it is suggested that the ratio of nominal diameter of screw to plate thickness should not exceed 8 to ensure that the connection performance of self-drilling screw and steel plate can be better exerted when the maximum pull-out capacity of screw joint is reached.
-
风灾对轻钢结构造成的损伤主要为围护系统的破坏. 2004年台风“云娜”登陆浙江省温岭市,造成大规模屋面板被掀飞. 2008年台风“黑格比”登陆广东省茂名市,部分轻钢结构完全倒塌. 2015年台风“苏迪罗”登陆福建沿海地区,轻钢屋面和屋架破坏严重. 2016年台风“莫兰蒂”登陆厦门地区,大面积轻钢屋面板在风吸力的作用下被刮飞. 众多学者对我国轻钢结构在风灾下的破坏进行调查与分析[1-6],围护结构风致破坏原因可归纳为3类,一是围护构件与主体结构的连接强度不足,二是压型钢板的强度不足,三是薄弱部位没有进行抗风处理,其中以连接强度不足导致的破坏为主. 轻钢房屋的金属屋面系统、墙面系统中厚度较薄的压型钢板多通过自攻螺钉连接[7-8]. 风荷载作用下,自攻螺钉作为屋面系统的重要连接件,在风吸力作用下发生拉拔或拉脱破坏.
近年来,随着我国装配式钢结构的快速发展,冷弯型钢结构相关的理论体系与设计方法日趋完善. 我国《冷弯型钢结构技术规范》(征求意见稿):GB50018—2017[9]对钢材选用范围和自攻螺钉抗拉承载力计算方法进行了修订. 本文就冷弯型钢结构中自攻螺钉抗拉性能的研究现状进行总结,根据已有204组实测自攻螺钉拉拔破坏荷载和138组实测自攻螺钉拉脱破坏荷载,对《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[10](以下简称中国规范)、《冷弯型钢结构技术规范(征求意见稿)》[9](以下简称中国规范意见稿)、美国规范(AISI S100-16)[11]、澳大利亚/新西兰规范(AS/NZS 4600: 2018)[12]、英国规范(BS 5950-5-1998)[13]和欧洲规范(EN 1993-1-3: 2006)[14]自攻螺钉抗拉设计方法的计算精度以及适用情况进行比较分析,在此基础上对中国规范意见稿[9]的抗拉承载力设计方法提出几点建议.
1. 单颗自攻螺钉抗拉连接破坏模式
连接压型钢板与冷弯型钢构件的自攻螺钉在拉力作用下出现3种破坏模式:1)拉拔破坏. 螺钉从基材中拔出而发生破坏. 2)拉脱破坏. 钉孔周围出现应力集中,靠近钉头一侧的板从钉头拉脱而发生破坏. 3)拉断破坏. 螺钉质量较差,钉杆自身被拉断而发生脆性破坏. 前2种破坏模式较为常见[15].
通常当连接压型钢板的檩条、墙架、屋架等基材的强度低且翼缘较薄时,在拉力作用下会发生自攻螺钉被拔出的现象. 拉拔破坏模式可分为2种[16-17]. 板厚与螺纹间距比值小于1时,钉孔处的钢板受到钉杆传递的拉力在最终拉拔破坏前发生明显的弯曲变形,见图 1(a);钢板厚度与螺纹间距比值大于1时,螺纹剪切钉孔处的钢板发生无明显弯曲变形的拉拔破坏,见图 1(b).
拉脱破坏也有2种模式,即拉脱破坏和凹陷破坏[18-19],见图 2. 拉脱破坏是一种脆性破坏,当钉孔周围压型钢板向下凹陷时,由于纵向应变增长速度过快,钉孔周围钢板发生横向开裂,压型钢板强度高、延性差时容易发生此种破坏,螺钉紧固过紧或施工质量差也会加快初始开裂的发生[20]. 压型钢板延性较好时则容易发生凹陷破坏,凹陷破坏是一种塑性破坏,这种破坏在静力荷载作用下不会发生拉脱,但在循环荷载作用下开裂会加速开展,很快形成拉脱破坏.
2. 自攻螺钉抗拔性能研究进展
2.1 自攻螺钉抗拔性能研究现状
Mahendran等[16]完成592组缩尺模型试验以探究金属屋面系统中自攻螺钉的抗拔强度. 在比较试验值与计算值后,发现美国、欧洲规范设计方法对G550级薄钢板适用性低. 在进行参数研究后提出计算公式
$$ {F_{{\rm{ou}}}} = kd{p^{0.2}}{t^{1.3}}{f_{\rm{u}}} $$ (1) 式中: Fou为单个螺钉抗拔承载力;d为螺钉名义直径; p为螺纹间距; t为板厚; fu为抗拉强度; k为常数,对厚度小于3 mm的G250、G450、G500、G550钢材取0.75. 通常认为板厚范围内的螺纹数量越多,螺钉节点的抗拔性能越强,即抗拔承载力与t/p成正比,与式(1)给出的设计方法不符. Sivapathasundaram等[17]在文献[16]的基础上完成187组缩尺模型试验,考察更多种类自攻螺钉与不同板厚组合下螺钉节点的抗拔性能. 考虑螺纹内径和钻尖直径的影响后提出计算公式
$$ {P_{\rm{u}}} = 1.62k{t^{1.3}}{d^{0.7}}{f_{\rm{u}}}{\left( {\frac{{d - {d^*}}}{p}} \right)^{0.3}} $$ (2) 式中: Pu为单螺钉抗拔承载力;d*为螺纹内径和钻头直径的较大值; k对厚度小于1.21 mm的G550、G500钢材取0.91, 对厚度为1.21~2.93 mm的G450钢材取1.07, 对G250钢材取1.14. Mahendran等[21]在文献[16]的静力研究结果上进一步分析175组常幅循环加载作用下螺钉节点的失效模式.
李元齐等[22]完成105个冷弯薄壁型钢螺钉连接试件的抗拔性能试验,研究并比较抗拔性能的影响因素和各国规范设计方法对LQ550级钢材、S350级钢材的适用性. 发现抗拔承载力与板厚成正比,但比例系数与板厚和螺纹间距之比有关;美国和澳大利亚/新西兰规范公式计算值最接近试验值. 参考欧洲规范公式,考虑板厚和螺纹间距之比的影响后,建议对中国规范意见稿中LQ550级钢材的抗拔承载力计算公式乘以0.8的折减系数.
周元等[23]、吴银飞等[24]证实有限元对自攻螺钉抗拔性能分析的可行性. 周元等[23]发现当螺钉名义直径与板厚之比为0.9~1.2时,抗拔连接模型在达到最大承载力时可以充分发挥自攻螺钉与钢板的材料性能. 该比值区间所对应的板厚范围为3~7 mm,但常用薄钢板的厚度一般在3 mm以内. 刘翔[25]进行类似研究,发现螺钉破坏恰好先于铝板破坏时螺钉直径与铝板厚度的比值为1.05~1.20.
不同于单颗螺钉连接的轴心受力模式,多颗螺钉连接下节点受到偏心力,失效模式更复杂. 段圣杰[26]研究筑巢轻钢结构中自攻螺钉的抗拔性能发现:在螺钉总数相同时,螺钉单排钻设的抗拉承载力明显高于双排钻设;等效单颗自攻螺钉抗拉刚度随螺钉数量增多而降低. 于敬海等[27]对直立锁边金属屋面系统中多颗自攻螺钉连接固定支座与檩条的节点进行研究,并将试验结果与国内外规范的计算值进行对比,发现各国规范计算结果均偏于保守. Sivapathasundaram等[28]研究多颗自攻螺钉连接帽形衬檩的拉拔破坏,自攻螺钉穿过帽形衬檩的2个下翼缘与檩条相接. 在式(2)的基础上引入折减系数以考虑多颗自攻螺钉的影响. 结果表明当使用2颗和4颗自攻螺钉连接帽形衬檩时,节点的抗拔强度分别只比单颗螺钉连接时分别提高40%和29%.
除了上述自攻螺钉用于薄壁冷弯型钢构件的连接外,自攻螺钉也被用于铝合金构件的连接. 曾滨等[29]、曹曦等[30]研究幕墙系统中自攻螺钉连接铝合金构件的受力性能,发现自攻螺钉抗拔承载力受入槽深度、螺钉类型、螺杆直径的影响.
综上所述,国内外均有一些学者对自攻螺钉连接冷弯薄壁型钢构件的抗拔性能进行了研究. 相比之下,国内研究还不够完善,总结为两方面:
1) 国外学者发现钢材的材料性能差异对抗拔承载力影响较大,而国内试验数据较少导致难以对我国设计方法的安全性和经济性进行全面的评价.
2) 部分学者发现除钢材等级、钢板厚度、螺钉名义直径等影响因素外,螺钉名义直径与板厚的比值、板厚与螺纹间距的比值同样会对抗拔承载力产生影响,但具体关系还有待探究.
2.2 自攻螺钉抗拉脱性能研究现状
Mahendran[31-32]、Xu等[33-34]通过试验与数值模拟对澳大利亚3种常用压型钢板的静力拉脱性能进行研究. 试验从加载到破坏经历了4个阶段,分别是弹性阶段、弹塑性过渡阶段、局部塑性破坏阶段和强化阶段. 金属屋面板系统最终破坏是由中心位置钉孔周围存在大量纵向应力造成的局部破坏. 压型钢板的板型尺寸和螺钉的连接形式都对自攻螺钉的拉脱性能有明显影响,弧线形波纹板和梯形波纹板承载力较低,发生凹陷破坏;宽肋波纹板承载力较高,破坏没有经历塑性变形阶段,最终破坏模式为拉脱破坏. 相比自攻螺钉隔波峰连接的形式,自攻螺钉相邻波峰连接钢板可改善横截面扭曲;自攻螺钉波谷连接钢板的破坏没有经历塑性变形阶段;加设垫片可在一定程度内抵制初始横截面扭曲出现,减少局部塑性变形,提高承载力. Majid等[35]建立足尺双跨梯形屋面板的有限元模型,研究屋面板不同位置的螺钉节点破坏荷载大小. 结果表明中心螺钉节点处最为薄弱,这与文献[31, 33]结论一致;而压型钢板两侧波峰1/4位置处的螺钉节点破坏荷载稍大于中心螺钉节点处,同样容易发生拉脱破坏.
Mahendran等[18]完成103组自攻螺钉拉脱破坏试验,比较美国、欧洲规范设计方法的适用性. 结果表明美国、欧洲规范设计方法不适用于自攻螺钉波峰连接G550级薄钢板的拉脱承载力计算,因此提出修正的设计方法
$$ {F_{{\rm{ov }}}} = c{d^\mathit{\alpha }}{t^\mathit{\beta }}f_{{\rm{u }}}^\mathit{\chi } $$ (3) 式中: Fov为单个螺钉抗拉脱承载力;c、α、β、χ为考虑压型钢板板型影响的常数. 式(3)提供了自攻螺钉波峰连接压型钢板的拉脱承载力计算方法,但是式(3)只对澳大利亚常用压型钢板的拟合效果较好,当板件几何参数差异较大时可能不适用.
李元齐等[22]通过111组矩形平钢板钉头拉脱试验,比较各国规范设计方法对LQ550级钢材和S350级钢材拉脱承载力的计算精度和适用性. 结果表明中国规范、中国规范意见稿的设计方法分别对S350级钢材、LQ550级钢材的计算精度最高. 但中国规范意见稿对LQ550级钢材的设计安全度稍低,建议对中国规范意见稿的抗拉脱承载力设计方法乘以0.8的折减系数,以提高安全储备. 黄宏等[36]对HXY-98型屋面板进行足尺试验以探究螺钉固定位置和钢材强度不同对抗拉承载力的影响.
文献[31-34]在有限元分析时假定材料具有无限延性,是一种理想弹塑性材料,只能用于凹陷破坏的研究,对于拉脱破坏则要建立合适的破坏准则. Mahaarachchi等[19, 37-40]完成一系列足尺双跨板试验和缩尺试验,根据试验结果确定的破坏准则为当屋面板膜应变大于钉孔周围最大表面拉应变的60%,或当钉孔周围最大表面拉应变等于材料单轴拉伸试验开裂应变时,中心位置钉孔边缘会发生横向开裂. 这一破坏准则在数值模拟中被证实有较好的适用性,但研究对象限于澳大利亚常用的强度高、厚度薄的压型钢板. 文献[31-34]中选用的单波距模型虽然建模简单,但模型假设屋面由一个无限大的连续板组成,忽略了板件纵向搭接缝造成的刚度变化. 文献[39-40]中选择的半宽试验模型通过合理施加对称条件,计算出的结果更接近试验值. 进行参数分析后给出自攻螺钉波峰连接压型钢板的拉脱承载力设计方法
$$ \begin{array}{c} {F_{{\rm{ov}}}} = \mathit{\alpha }{\left( {\mathit{\mu } + \phi \frac{{Et}}{{{f_{\rm{y}}}d}}} \right)^\mathit{\delta }}{\left( {\vartheta \frac{{{h_{\rm{c}}}}}{p}} \right)^\mathit{\varepsilon }}{\left( {\mathit{\omega }\frac{{{w_{\rm{t}}}}}{{{w_{\rm{c}}}}}} \right)^\mathit{\lambda }}.\\ {\left( {\mathit{\kappa } + \mathit{\varphi }\frac{{{t^2}}}{{Ld}}} \right)^\mathit{\rho }}dt{f_{\rm{y}}} \end{array} $$ (4) 式中: E为弹性模量; fy为屈服强度; wc、wt、p、hc、ph为图 3所示的几何参数; α、μ、ϕ、δ、ϑ、ε、ω、λ、κ、φ、ρ为常数,文献[38, 40-41]中分别根据钢材强度和板型进行赋值. 式(4)充分考虑板型几何的影响,但计算过程比较烦琐.
Sivapathasundaram等[41-44]研究自攻螺钉连接帽型衬檩节点的拉脱性能. 通过与足尺试验结果比较,发现缩尺试验结果保守,可代替足尺试验. 参数研究结果表明衬檩厚度对拉脱承载力影响较大;钉头直径对低强度钢材的承载力影响大,对高强度钢材的承载力影响不明显. 将平均等效塑性应变达到材料模型中定义的恒定破坏应变作为拉脱破坏准则. 结合试验和数值模拟研究结果,给出自攻螺钉在帽形衬檩-檩条连接处的抗拉脱设计方法
$$ {P_{{\rm{nov}}}} = \left\{ {\begin{array}{*{20}{l}} {8.68{t^2}{f_{\rm{u}}}}&{({\rm{G}}550\& {\rm{G}}500)}\\ {3.07{t^{1.4}}{d^{0.6}}{f_{\rm{u}}}}&{({\rm{G}}250)} \end{array}} \right. $$ (5) 式(5)被澳大利亚/新西兰规范所采纳. 此外提出一种用于加强螺钉节点抗拉脱性能的构造措施.
综上所述,国外学者对自攻螺钉波峰连接屋面板的抗拉脱性能研究较多,国内对自攻螺钉抗拉脱性能的研究还在起步阶段,后续研究应在以下3方面开展:
1) 不同于澳大利亚,我国通常采用自攻螺钉波谷连接压型钢板,这种连接方式的拉脱承载力明显高于波峰连接的情况[45]. 因此需开展此类连接形式下螺钉节点拉脱性能的研究从而为我国设计规范提供参考.
2) 数值模拟中螺钉节点处拉脱破坏准则的适用性、有限元模型分析中所做假设的合理性、对初始缺陷考虑的准确度等都还有待探究.
3) 我国学者未考虑不同压型钢板板型以及板跨、波高、波距等几何参数对拉脱承载力的影响.
3. 各国规范设计方法比较分析
3.1 各国规范自攻螺钉抗拉承载力计算方法介绍
中国规范[10]、中国规范意见稿[9]、美国规范[11]、澳大利亚/新西兰规范[12]、英国规范[13]、欧洲规范[14]均提出钢板-钢板连接单颗自攻螺钉抗拉承载力的计算方法. 对于抗拔承载力,各国规范设计方法主要考虑板厚、钢材强度、螺钉名义直径的影响;对于抗拉脱承载力,中国、美国、澳大利亚/新西兰和英国规范设计方法主要考虑板厚、钢材强度、钉头直径的影响,欧洲规范还考虑了螺纹间距对抗拉脱承载力的影响.
Pekoz[46]和Toma等[47]最早通过大量试验研究总结单颗自攻螺钉抗拉承载力计算公式,分别为美国规范和欧洲规范提供基础. 中国规范采用欧洲建议(recommendations for steel construction ECCS-TC7, the design and testing of constructions in steel sheeting and section)给出的设计方法.
中国规范意见稿补充厚度为0.6~2.0 mm的S280、S350及LQ550MPa级钢材的强度设计指标,增加了压型钢板波峰采用自攻螺钉连接的试验方法,考虑了钉头和垫圈直径对抗拉脱承载力的影响,且放宽了钉头直径不小于14 mm的要求等.
3.2 自攻螺钉抗拔承载力计算方法比较
选用文献[16-17, 21-22]中实测拉拔破坏荷载,共计204组数据,包括名义屈服强度为550、500、450、350、250 MP的钢材,钢板厚度实测为0.38~2.98 mm,螺钉实测名义直径为2.84~6.39 mm. 对中国规范、美国规范、澳大利亚/新西兰规范、英国规范、欧洲规范中自攻螺钉抗拔承载力公式计算精度进行比较,结果见表 1.
表 1 抗拔承载力计算公式精度比较Table 1. Accuracy comparison of calculation formulas for pull-out capacity文献号 数量 t/mm d/mm Pt/N Pt/PCN Pt/PUS(PAU) Pt/PBS Pt/PEU [16] 116 0.38~2.93 4.67~6.39 412~12 140 0.59~2.15 0.52~1.50 0.81~2.48 0.98~2.84 [17] 54 0.55~1.52 4.73~6.38 834~4 526 0.46~1.49 0.41~1.24 0.64~1.93 0.76~2.34 [21] 16 0.38~0.95 4.67~6.39 554~3 558 0.67~1.54 0.58~1.15 0.91~1.80 1.10~2.18 [22] 18 0.55~2.98 2.84~6.19 855~6 974 0.86~1.48 0.74~1.13 1.06~1.75 0.97~2.13 平均值 1.12 0.90 1.42 1.59 标准差 0.36 0.23 0.38 0.40 注:美国规范和澳大利亚/新西兰规范的拉拔承载力计算公式相同,表中已合并. 表 1中以Pt代表抗拔承载力试验值,PCN代表中国规范计算值,PUS代表美国规范计算值,PAU代表澳大利亚/新西兰规范计算值,PBS代表英国规范计算值,PEU代表欧洲规范计算值. 由表 1可见,中国规范设计方法的计算值具有合适的安全储备且离散程度仅次于美国、澳大利亚/新西兰规范,适用性最高. 美国和澳大利亚/新西兰规范的计算值最接近试验值且离散程度最小,但安全度较低. 英国规范和欧洲规范的计算值过于保守且离散程度较大.
3.3 自攻螺钉抗拉脱承载力计算方法比较
共选取实测拉脱破坏荷载138组数据,其中选用文献[18-20, 32, 38, 45, 48]中自攻螺钉波峰连接压型钢板的63组数据,选用文献[45]中自攻螺钉波谷连接压型钢板的11组数据,选用文献[41-42, 49]中自攻螺钉连接帽形衬檩的47组数据,选用文献[22]中矩形平钢板从钉头拉脱的17组数据. 对不同连接形式下各国规范自攻螺钉抗拉脱设计方法的计算精度进行比较,结果见表 2. 表 2中以PCN1代表中国规范计算值,PCN2代表中国规范意见稿计算值,dw代表钉头或垫圈直径.
表 2 抗拉脱承载力计算公式精度比较Table 2. Accuracy comparison of calculation formulas for pull-over capacity连接形式 t/mm dw/mm Pt/PCN1 Pt/PCN2 Pt/PUS Pt/PAU Pt/PBS Pt/PEU 波峰连接压型钢板 0.35~0.48 14.50~22.00 0.12~0.37 0.11~0.37 0.09~0.29 0.09~0.29 0.15~0.48 0.13~0.44 平均值 0.27 0.25 0.20 0.20 0.32 0.30 标准差 0.06 0.06 0.04 0.04 0.07 0.07 波谷连接压型钢板 0.42 14.50 0.79~1.06 0.78~1.03 0.62~0.83 0.62~0.83 1.01~1.34 0.93~1.24 平均值 0.93 0.91 0.73 0.73 1.18 1.09 标准差 0.08 0.08 0.07 0.07 0.11 0.10 连接帽形衬檩 0.55~1.15 11.00~14.50 0.24~1.00 0.24~0.98 0.19~0.70 0.86~1.12 0.31~1.13 0.29~1.04 平均值 0.57 0.65 0.50 0.98 0.81 0.74 标准差 0.22 0.25 0.17 0.06 0.28 0.26 连接矩形平钢板 0.55~2.98 5.49~16.27 0.29~1.46 0.74~1.52 0.56~1.04 0.56~1.04 0.92~1.67 0.85~1.56 平均值 0.85 1.16 0.83 0.83 1.35 1.24 标准差 0.33 0.21 0.12 0.12 0.20 0.18 从表 2可见,各国规范公式均不适用于自攻螺钉波峰连接压型钢板的拉脱承载力计算,该连接形式的承载力需要按照规范的试验方法进行测试. 对于自攻螺钉连接帽形衬檩的情况,澳大利亚/新西兰规范给出专用于该种连接形式的设计方法,见式(5),除澳大利亚/新西兰规范外,其他国家规范公式均不适用于这种连接形式.
与波峰连接压型钢板和连接帽形衬檩2种连接形式相比,各国规范公式对波谷连接压型钢板和连接矩形平钢板的自攻螺钉拉脱承载力计算精度较高. 英国规范和欧洲规范公式对自攻螺钉波谷连接压型钢板的拉脱承载力计算有较好的适用性,中国规范和中国规范意见稿的安全度略低. 但由于该种连接形式的实测数据均为厚度小于0.5 mm的G550级压型钢板,因此还要进行更全面的参数研究.
对于自攻螺钉连接矩形平钢板的情况,结果表明中国规范意见稿具有合适的安全储备,但离散性较高. 英国规范、欧洲规范过于保守. 美国、澳大利亚/新西兰规范虽然离散性最低,但是计算结果不安全.
4. 螺钉节点抗拉设计方法的几点建议
4.1 自攻螺钉抗拔承载力计算方法的修正系数
通过分析表 1,发现板厚对承载力的计算方法影响最大,钢材强度有一定影响,螺钉名义直径的影响不明显.
表 3、4分别给出不同钢材强度和板厚范围下中国规范自攻螺钉抗拔承载力的计算精度(Pt/PCN),其中对于钢材名义屈服强度为550 MPa和板厚小于0.8 mm的情况计算精度较低,Pt/PCN的均值和标准差分别为0.865和0.198,以及0.878和0.215;对于板厚大于2 mm的情况,中国规范公式计算过于保守,Pt/PCN的均值和标准差分别为1.757和0.265. 此外,从表 3中可以看出450级钢材计算结果最为保守,但离散程度最大,这是由于数据中450 MPa的钢板相对较厚(1.52~2.93 mm),表现出较好的塑性性能,延缓了拉拔破坏的发生.
表 3 不同钢材强度下中国规范抗拔承载力计算精度Table 3. Calculation accuracy of pull-out capacity of Chinese code under different steel strength钢材名义屈服强度/MPa Pt/PCN 平均值 标准差 550 0.865
(0.999)0.198
(0.188)500 1.027 0.188 450 1.526 0.322 350 1.231 0.216 250 1.168 0.227 注:“()”中的值为按本文建议系数修正后的平均值和标准差. 表 4 不同板厚下中国规范抗拔承载力计算精度Table 4. Calculation accuracy of pull-out capacity of Chinese code under different plate thickness板厚/mm Pt/ PCN 平均值 标准差 0.380~0.784 0.878
(1.010)0.215
(0.198)0.950~1.210 1.126 0.228 1.491~1.965 1.276 0.210 2.300~2.980 1.757 0.265 注:“()”中的值为按本文建议系数修正后的平均值和标准差. 因此,综合考虑钢材强度和板厚的影响后,建议中国规范对板厚不超过0.75 mm且名义屈服强度为550 MPa级的钢材乘以0.8的折减系数;中国规范低估了板厚超过2 mm且名义屈服强度不超过450 MPa钢材的抗拔承载力,可适当考虑放宽以保证结构的经济性,但是需要通过更加广泛的试验研究和有限元分析加以验证. 考虑修正系数后,规范设计方法对550级钢材的Pt/PCN平均值和标准差分别为0.999和0.188,计算值更加接近实测值且离散性降低,建议的系数具有一定的适用性.
4.2 自攻螺钉抗拔承载力随d/t的变化关系
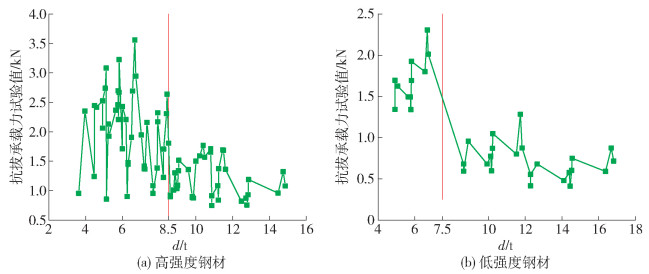
探讨了自攻螺钉名义直径和板厚之比(d/t)合适的取值范围,以便在工程应用中充分发挥自攻螺钉与钢板连接的抗拔性能. 实测数据中550级钢材和250级钢材的d/t范围较广,因此以这2种强度钢材分别代表高强度钢材(名义屈服强度为550 MPa的钢材)和低强度钢材(名义屈服强度为250 MPa的钢材).
抗拔承载力试验值随d/t变化的关系,见图 4. 由图 4可见,不论是低强度钢材还是高强度钢材,当d/t超过某一界限值时,承载力将维持在某一较低水平. 该界限值对高强度钢材取8.5,对低强度钢材取7.5.
表 5给出高、低强度钢材界限值前后规范公式计算精度的变化情况. 由此可见,当d/t超过界限值时,不论是高强度钢材还是低强度钢材,计算精度都有较大幅度下滑,2个界限值的选取具有一定适用性.
表 5 界限值前后各国规范计算精度变化Table 5. Change of calculation accuracy of national codes before and after the limit value项目 Pt/PCN Pt/PUS(PAU) Pt/PBS Pt/PEU 550级钢材 d/t < 8.5 平均值 0.956 0.832 1.295 1.571 标准差 0.198 0.168 0.261 0.317 d/t≥8.5 平均值 0.759 0.667 1.038 1.259 标准差 0.137 0.120 0.187 0.227 250级钢材 d/t < 7.5 平均值 1.336 1.003 1.562 1.895 标准差 0.159 0.119 0.186 0.225 d/t≥7.5 平均值 1.071 0.830 1.291 1.567 标准差 0.202 0.156 0.243 0.295 综合考虑将界限值定为8,即建议进行构件设计时d/t不超过8,从而保证螺钉节点在达到最大抗拔承载力时可以较好地发挥自攻螺钉和板件的连接性能.
4.3 自攻螺钉抗拉脱承载力计算方法的修正系数
自攻螺钉波峰连接压型钢板的拉脱承载力应按中国规范意见稿中给出的试验方法进行测试. 自攻螺钉连接帽形衬檩的拉脱承载力可参考澳大利亚/新西兰规范计算公式(5)进行设计. 对于自攻螺钉波谷连接压型钢板和连接矩形平钢板的拉脱承载力可以按照中国规范意见稿给出的公式进行计算. 对于名义屈服强度为550 MPa级高强钢材,中国规范和中国规范意见稿的计算精度平均值和标准差分别为0.766和0.244,以及0.922和0.116,2个规范计算结果的差别在于中国规范严重高估了钉头直径小于14 mm时螺钉节点的抗拉脱承载力. 鉴于中国规范意见稿的安全度稍低,综合考虑钢材强度和板厚的影响后建议对板厚不超过0.75 mm且名义屈服强度为550 MPa级的钢材乘以0.9的折减系数. 按本文建议的系数改进后,对名义屈服强度为550 MPa级高强钢材的计算精度平均值和标准差分别为0.997和0.104,计算值的准确度和离散度都得到了优化.
5. 结论
1) 中国规范抗拔承载力设计方法的计算值有较高的安全度且离散度较低,与美国规范、澳大利亚/新西兰规范、英国规范和欧洲规范相比适用性最高;中国规范意见稿对螺钉波谷连接高强压型钢板的抗拉脱承载力计算安全度略低,对螺钉连接矩形平钢板的情况有合适的安全储备. 自攻螺钉波峰连接压型钢板的拉脱承载力应按照中国规范意见稿中给出的试验方法进行测试.
2) 对于抗拔承载力计算,建议中国规范意见稿对板厚不超过0.75 mm且名义屈服强度为550 MPa的钢材乘以折减系数0.8;中国规范意见稿低估了板厚超过2 mm且名义屈服强度不超过450 MPa钢材的抗拔承载力,可适当考虑放宽以保证结构的经济性.
3) 建议设计时d/t不超过8,从而保证螺钉节点在达到最大抗拔承载力时可以较好发挥自攻螺钉和板件的连接性能.
4) 对于抗拉脱承载力的计算,建议中国规范意见稿对板厚不超过0.75 mm且名义屈服强度为550 MPa级钢材的情况应乘以0.9的折减系数.
-
表 1 抗拔承载力计算公式精度比较
Table 1 Accuracy comparison of calculation formulas for pull-out capacity
文献号 数量 t/mm d/mm Pt/N Pt/PCN Pt/PUS(PAU) Pt/PBS Pt/PEU [16] 116 0.38~2.93 4.67~6.39 412~12 140 0.59~2.15 0.52~1.50 0.81~2.48 0.98~2.84 [17] 54 0.55~1.52 4.73~6.38 834~4 526 0.46~1.49 0.41~1.24 0.64~1.93 0.76~2.34 [21] 16 0.38~0.95 4.67~6.39 554~3 558 0.67~1.54 0.58~1.15 0.91~1.80 1.10~2.18 [22] 18 0.55~2.98 2.84~6.19 855~6 974 0.86~1.48 0.74~1.13 1.06~1.75 0.97~2.13 平均值 1.12 0.90 1.42 1.59 标准差 0.36 0.23 0.38 0.40 注:美国规范和澳大利亚/新西兰规范的拉拔承载力计算公式相同,表中已合并. 表 2 抗拉脱承载力计算公式精度比较
Table 2 Accuracy comparison of calculation formulas for pull-over capacity
连接形式 t/mm dw/mm Pt/PCN1 Pt/PCN2 Pt/PUS Pt/PAU Pt/PBS Pt/PEU 波峰连接压型钢板 0.35~0.48 14.50~22.00 0.12~0.37 0.11~0.37 0.09~0.29 0.09~0.29 0.15~0.48 0.13~0.44 平均值 0.27 0.25 0.20 0.20 0.32 0.30 标准差 0.06 0.06 0.04 0.04 0.07 0.07 波谷连接压型钢板 0.42 14.50 0.79~1.06 0.78~1.03 0.62~0.83 0.62~0.83 1.01~1.34 0.93~1.24 平均值 0.93 0.91 0.73 0.73 1.18 1.09 标准差 0.08 0.08 0.07 0.07 0.11 0.10 连接帽形衬檩 0.55~1.15 11.00~14.50 0.24~1.00 0.24~0.98 0.19~0.70 0.86~1.12 0.31~1.13 0.29~1.04 平均值 0.57 0.65 0.50 0.98 0.81 0.74 标准差 0.22 0.25 0.17 0.06 0.28 0.26 连接矩形平钢板 0.55~2.98 5.49~16.27 0.29~1.46 0.74~1.52 0.56~1.04 0.56~1.04 0.92~1.67 0.85~1.56 平均值 0.85 1.16 0.83 0.83 1.35 1.24 标准差 0.33 0.21 0.12 0.12 0.20 0.18 表 3 不同钢材强度下中国规范抗拔承载力计算精度
Table 3 Calculation accuracy of pull-out capacity of Chinese code under different steel strength
钢材名义屈服强度/MPa Pt/PCN 平均值 标准差 550 0.865
(0.999)0.198
(0.188)500 1.027 0.188 450 1.526 0.322 350 1.231 0.216 250 1.168 0.227 注:“()”中的值为按本文建议系数修正后的平均值和标准差. 表 4 不同板厚下中国规范抗拔承载力计算精度
Table 4 Calculation accuracy of pull-out capacity of Chinese code under different plate thickness
板厚/mm Pt/ PCN 平均值 标准差 0.380~0.784 0.878
(1.010)0.215
(0.198)0.950~1.210 1.126 0.228 1.491~1.965 1.276 0.210 2.300~2.980 1.757 0.265 注:“()”中的值为按本文建议系数修正后的平均值和标准差. 表 5 界限值前后各国规范计算精度变化
Table 5 Change of calculation accuracy of national codes before and after the limit value
项目 Pt/PCN Pt/PUS(PAU) Pt/PBS Pt/PEU 550级钢材 d/t < 8.5 平均值 0.956 0.832 1.295 1.571 标准差 0.198 0.168 0.261 0.317 d/t≥8.5 平均值 0.759 0.667 1.038 1.259 标准差 0.137 0.120 0.187 0.227 250级钢材 d/t < 7.5 平均值 1.336 1.003 1.562 1.895 标准差 0.159 0.119 0.186 0.225 d/t≥7.5 平均值 1.071 0.830 1.291 1.567 标准差 0.202 0.156 0.243 0.295 -
[1] 宋芳芳, 欧进萍. 轻钢结构工业厂房风灾损伤估计与预测[J]. 土木建筑与环境工程, 2009, 31(6): 71-80. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200906011.htm SONG F F, OU J P. Wind damage estimation and prediction of light steel industrial buildings[J]. Journal of Civil Architectural & Environmental Engineering, 2009, 31(6): 71-80. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200906011.htm
[2] 金玉芬, 杨庆山, 李启. 轻钢房屋围护结构的台风灾害调查与分析[J]. 建筑结构学报, 2010(增刊2): 197-201. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB2010S2036.htm JIN Y F, YANG Q S, LI Q. Typhoon damage investigation of claddings of light steel buildings[J]. Journal of Building Structures, 2010(Suppl 2): 197-201. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB2010S2036.htm
[3] 王赛宁, 李文波. 从风荷载对轻钢结构房屋的破坏看抗风设计[J]. 中国建筑防水, 2010(7): 14-20. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJF201007005.htm WANG S N, LI W B. Design of wind resistance for lightweight steel building[J]. China Building Waterproofing, 2010(7): 14-20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJF201007005.htm
[4] 邱发强. 轻钢结构在台风破坏下的灾害调查与分析[J]. 工程质量, 2017, 35(11): 26-29. doi: 10.3969/j.issn.1671-3702.2017.11.007 QIU F Q. Disaster investigation and analysis of lightweight steel constructions damaged by typhoon[J]. Construction Security, 2017, 35(11): 26-29. (in Chinese) doi: 10.3969/j.issn.1671-3702.2017.11.007
[5] 宋芳芳, 欧进萍. 台风"黑格比"对城市建筑物破坏调查与成因分析[J]. 自然灾害学报, 2010, 19(4): 8-16. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201004002.htm SONG F F, OU J P. Investigation and analysis of structures damage caused by typhoon "Hagubit"[J]. Journal of Natural Disasters, 2010, 19(4): 8-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201004002.htm
[6] 霍林生, 王银坤, 李永鑫, 等. 台风"苏迪罗"对福建沿海村镇房屋破坏情况的调研[J]. 防灾减灾工程学报, 2016, 36(2): 315-322. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201602024.htm HUO L S, WANG Y K, LI Y X, et al. Investigation of building damage conditions of coastal towns and villages in Fujian province by typhoon "Soudelor"[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(2): 315-322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201602024.htm
[7] 李元齐, 潘斯勇. 自攻螺钉连接承载力研究现状[J]. 结构工程师, 2008, 24(6): 154-158. doi: 10.3969/j.issn.1005-0159.2008.06.030 LI Y Q, PAN S Y. Research progress on self-drilling screw connection capacity[J]. Structural Engineers, 2008, 24(6): 154-158. (in Chinese) doi: 10.3969/j.issn.1005-0159.2008.06.030
[8] 侯兆欣, 吕健, 王宇红, 等. 自攻螺钉连接在建筑上的应用[J]. 工业建筑, 1999, 29(9): 52-54. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ199909011.htm HOU Z X, LÜ J, WANG Y H, et al. Application of self-drilling screws for metal roofing & cladding[J]. Industrial Construction, 1999, 29(9): 52-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ199909011.htm
[9] 中南建筑设计院股份有限公司. 冷弯型钢结构技术规范(征求意见稿)[S/OL]. [2020-12-15]. http://www.doc88.com/p-6817670977425.html. [10] 中华人民共和国建设部, 中华人民共和国国家质量监督检验检疫总局. 冷弯薄壁型钢结构技术规范: GB 50018—2002[S]. 北京: 中国计划出版社, 2002: 36-37. [11] AISI. North american specification for the design of cold-formed steel structural members AISI S100-16[S]. Washington, D.C. : American Iron and Steel Institute, 2016.
[12] Council of Standards Australia, New Zealand Standards Approval Board. Cold-formed steel structures AS/NZS 4600: 2018[S]. Sydney: Standards Australia Limited, 2018.
[13] BSI. Structural use of steelwork in building-part 5: code of practice for design of cold formed thin gauge sections BS 5950-5-1998[S]. London: British Standard Institution, 1998.
[14] CEN. Eurocode3-design of steel structures-part 1-3: general rules-supplementary rules for cold-formed members and sheeting EN 1993-1-3: 2006[S]. Brussels: The European Committee for Standardization, 2006.
[15] 雷宏刚, 邱斌, 姬艳玲. 装配式轻钢结构住宅中自攻螺丝连接受力性能研究评述[J]. 太原理工大学学报, 2017, 48(3): 265-274. https://www.cnki.com.cn/Article/CJFDTOTAL-TYGY201703001.htm LEI H G, QIU B, JI Y L. An overview study on bearing capacity properties of self-tapping screw connection in prefabricated light-gauge steel structure residence[J]. Journal of Taiyuan University of Technology, 2017, 48(3): 265-274. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TYGY201703001.htm
[16] MAHENDRAN M, TANG R B. Pull-out strength of steel roof and wall cladding systems[J]. Journal of Structural Engineering, 1998, 124(10): 1192-1201. doi: 10.1061/(ASCE)0733-9445(1998)124:10(1192)
[17] SIVAPATHASUNDARAM M, MAHENDRAN M. New pull-out capacity equations for the design of screw fastener connections in steel cladding systems[J]. Thin-Walled Structures, 2018, 122: 439-451. doi: 10.1016/j.tws.2017.08.019
[18] MAHENDRAN M, TANG R B. Pull-through strength of high tensile steel cladding systems[J]. Australian Journal of Structural Engineering, 1999, 2(1): 37-50.
[19] MAHAARACHCHI D, MAHENDRAN M. A strain criterion for pull-through failures in crest-fixed steel claddings[J]. Engineering Structures, 2009, 31(2): 498-506. doi: 10.1016/j.engstruct.2008.09.013
[20] MAHENDRAN M, MAHAARACHCHI D. Splitting failures in trapezoidal steel roof cladding[J]. Journal of Performance of Constructed Facilities, 2004, 18(1): 4-11. doi: 10.1061/(ASCE)0887-3828(2004)18:1(4)
[21] MAHENDRAN M, MAHAARACHCHI D. Cyclic pull-out strength of screwed connections in steel roof and wall cladding systems using thin steel battens[J]. Journal of Structural Engineering, 2002, 128(6): 771-778. doi: 10.1061/(ASCE)0733-9445(2002)128:6(771)
[22] 李元齐, 帅逸群, 沈祖炎, 等. 冷弯薄壁型钢自攻螺钉连接抗拉性能试验研究[J]. 建筑结构学报, 2015, 36(12): 143-152. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201512018.htm LI Y Q, SHUAI Y Q, SHEN Z Y, et al. Experimental study on tension behavior of self-drilling screw connections for cold-formed thin-walled steel structures[J]. Journal of Building Structures, 2015, 36(12): 143-152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201512018.htm
[23] 周元, 朱召泉. 自攻螺钉抗拔连接承载力的有限元分析[J]. 四川建筑科学研究, 2015, 41(2): 61-63. doi: 10.3969/j.issn.1008-1933.2015.02.015 ZHOU Y, ZHU Z Q. Finite element analysis of anti-tension capacity of self-tapping screw connection[J]. Sichuan Building Science, 2015, 41(2): 61-63. (in Chinese) doi: 10.3969/j.issn.1008-1933.2015.02.015
[24] 吴银飞, 朱召泉. 自攻螺钉拉剪耦合作用数值分析[J]. 钢结构, 2017, 32(2): 50-53. https://www.cnki.com.cn/Article/CJFDTOTAL-GJIG201702011.htm WU Y F, ZHU Z Q. Numerical analysis of tension-shear coupling effect of self-tapping screws[J]. Steel Construction, 2017, 32(2): 50-53. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GJIG201702011.htm
[25] 刘翔. 集成式铝合金结构房屋标准编制及足尺试验研究[D]. 广州: 华南理工大学, 2018. LIU X. Standard preparation and full-scale model test study of integrated aluminum alloy housing[D]. Guangzhou: South China University of Technology, 2018. (in Chinese)
[26] 段圣杰. 筑巢轻钢结构体系节点自攻螺钉抗拉性能及节点模型化研究[D]. 重庆: 重庆大学, 2014. DUAN S J. Study on tensile properties of self-tapping screws and a modeling approach of joints in nested light-gauge steel system[D]. Chongqing: Chongqing University, 2014. (in Chinese)
[27] 于敬海, 赵彧洋, 蒋智宇, 等. 直立锁边金属屋面系统关键连接节点抗拉承载力试验[J]. 建筑科学与工程学报, 2019, 36(1): 112-119. doi: 10.3969/j.issn.1673-2049.2019.01.013 YU J H, ZHAO Y Y, JIANG Z Y, et al. Tension bearing capacity of key connections of standing seam metal system[J]. Journal of architecture and civil engineering, 2019, 36(1): 112-119. (in Chinese) doi: 10.3969/j.issn.1673-2049.2019.01.013
[28] SIVAPATHASUNDARAM M, MAHENDRAN M. Pull-out capacity of multiple screw fastener connections in cold-formed steel roof battens[J]. Journal of Constructional Steel Research, 2018, 144: 40-52. doi: 10.1016/j.jcsr.2018.01.013
[29] 曾滨, 惠存, 韩维池, 等. S60框架幕墙系统自攻螺钉抗拉拔性能试验研究和计算方法分析[J]. 工业建筑, 2015, 45(11): 176-180. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201511036.htm ZENG B, HUI C, HAN W C, et al. Experimental study and calculation method analysis of pull-out resistance performance for self-tapping screws in S60 frame curtain wall system[J]. Industrial Construction, 2015, 45(11): 176-180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201511036.htm
[30] 曹曦, 王志宇, 陈杨, 等. 玻璃幕墙中铝合金立柱螺钉连接节点抗拉性能试验[J]. 科学技术与工程, 2019, 19(20): 293-304. doi: 10.3969/j.issn.1671-1815.2019.20.044 CAO X, WANG Z Y, CHEN Y, et al. Experiment on tension behavior of aluminum alloy column with screw connections for glass curtain wall[J]. Science Technology and Engineering, 2019, 19(20): 293-304. (in Chinese) doi: 10.3969/j.issn.1671-1815.2019.20.044
[31] MAHENDRAN M. Static behavior of corrugated roofing under simulated wind loading[J]. Civil Engineering Transaction, 1990, 32(4): 211-218.
[32] MAHENDRAN M. Behavior and design of crest-fixed profiled steel roof claddings under wind uplift[J]. Engineering Structures, 1994, 16(5): 368-376. doi: 10.1016/0141-0296(94)90030-2
[33] XU Y L, REARDON G F. Test of screw fastened profiled roofing sheets subject to simulated wind uplift[J]. Engineering Structures, 1993, 15(6): 423-430. doi: 10.1016/0141-0296(93)90060-H
[34] XU Y L, TENG J G. Local plastic failure of light gauge steel roofing sheets: finite element analysis versus experiment[J]. Journal of Constructional Steel Research, 1994, 30(2): 125-150. doi: 10.1016/0143-974X(94)90047-7
[35] MAJID T A, MUHAMMAD M K, RAMLI N I, et al. Behavior of trapezoidal roof cladding under different location of point load[J]. Journal of Civil Engineering Research, 2014, 4(3A): 149-153.
[36] 黄宏, 陈杰, 陈友泉, 等. 自攻螺钉式金属屋面板抗风揭试验研究[J]. 华东交通大学学报, 2019, 36(5): 97-101. https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201905013.htm HUANG H, CHEN J, CHEN Y Q, et al. Experimental study on wind stripping resistance of self-tapping screw roof slab[J]. Journal of East China Jiaotong University, 2019, 36(5): 97-101. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201905013.htm
[37] MAHAARACHCHI D, MAHENDRAN M. Finite element analysis and design of crest-fixed trapezoidal steel claddings with wide pans subject to pull-through failures[J]. Engineering Structures, 2004, 26(11): 1547-1559. doi: 10.1016/j.engstruct.2004.05.007
[38] MAHAARACHCHI D, MAHENDRAN M. Pull-through failures of crest-fixed steel claddings initiated by transverse splitting[C]//15th International Specialty Conference on Cold-Formed Steel Structures. St. Louis, Missouri: Missouri University of Science and Technology, 2000: 19-20.
[39] MAHAARACHCHI D, MAHENDRAN M. Wind uplift strength of trapezoidal steel cladding with closely spaced ribs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(3): 140-150.
[40] MAHAARACHCHI D, MAHENDRAN M. Strength of screwed connections in crest-fixed trapezoidal steel claddings[J]. Australian Journal of Structural Engineering, 2005, 6(1): 11-23. doi: 10.1080/13287982.2005.11464941
[41] SIVAPATHASUNDARAM M, MAHENDRAN M. Development of suitable test methods for the screw connections in cold-formed steel roof battens [J/OL]. Journal of Structural Engineering, 2016, 142(6): 04016025. [2016-02-04]. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001476.
[42] SIVAPATHASUNDARAM M, MAHENDRAN M. Experimental studies of thin-walled steel roof battens subject to pull-through failures[J/OL]. Engineering Structures, 2016, 113: 388-406.
[43] SIVAPATHASUNDARAM M, MAHENDRAN M. Numerical modeling of thin-walled steel roof battens subject to pull-through failures[J/OL]. Journal of Structural Engineering, 2017, 143(6): 04017014. [2017-02-01]. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001740.
[44] SIVAPATHASUNDARAM M, MAHENDRAN M. Numerical studies and design of thin steel roof battens subject to pull-through failures[J]. Engineering Structures, 2017, 146: 54-74. doi: 10.1016/j.engstruct.2017.05.038
[45] MAHENDRAN M. Test methods for the determination of pull-through strength of screwed connections in profiled steel claddings[J]. Science & Engineering Faculty, 1995, 37(3): 219-227.
[46] PEKOZ T. Design of cold-formed steel screw connections[C]//Tenth International Specialty Conference on Cold-Formed Steel Structures. St. Louis, Missouri: Missouri University of Science and Technology, 1990: 575-587.
[47] TOMA A, SEDLACEK G, WEYNAND K. Connections in cold-formed steel[J]. Thin Walled Structures, 1993, 16: 219-237. doi: 10.1016/0263-8231(93)90046-D
[48] MAHENDRAN M. Profiled steel roof claddings under high wind forces[J]. Journal of Singapore Structural Steel Society, 1994, 5(1): 95-106.
[49] MYURAN K, MAHENDRAN M. Unified static-fatigue pull-through capacity equations for cold-formed steel roof battens[J]. Journal of Constructional Steel Research, 2017, 139: 135-148. doi: 10.1016/j.jcsr.2017.09.027
-
期刊类型引用(1)
1. 周婷,孙克肇,陈志华,肖潇. 冷弯薄壁型钢自攻螺钉厚钢板连接的抗剪及抗拔性能试验研究. 建筑钢结构进展. 2023(07): 32-40 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: