An Approach to Improve the Mechanical Performance of Existing High-speed Railway Through Arch Bridge
-
摘要:
大跨度高速铁路桥常采用刚度和动力性能良好的拱桥结构，但是随着拱桥服役期增长，列车运营速度不断提高，结构性能退化严重，难以满足正常运营的要求.为了解决现役铁路拱桥存在力学性能不足的问题，基于三角形稳定性和桁架结构变形小的原理，提出一种结构改进方法，具体做法为在拱肋与主梁之间增设若干个V型结构，使其与拱和梁段构成若干个连续的三角形结构，从而对主梁与拱肋进行有效约束.V型结构布置的位置需综合考虑对拱肋与主梁的均匀约束及其结构的薄弱位置，其个数尽可能使结构的刚度与温度响应之间达到较为合理的平衡状态.有限元分析结果表明，该方法能有效改善原结构的刚度、动力特性、抗疲劳性和稳定性；通过合理设置V型结构个数及截面特性参数能使拱桥的各项力学性能指标达到最优的设计效果.改造后的拱桥结构合理、施工便捷，具有较大的推广应用价值.
Abstract:Long-span high-speed railway bridges usually adopt arch bridge structures with good stiffness and dynamic performance. However, as the service life of the arch bridge increases and the train operating speed increases continuously, the structural performance degrades seriously and is difficult to meet the requirements of normal operation. To improve mechanical performance of railway arch bridge in service, a structural improvement method was proposed based on the principle of triangular stability and small deformation of the truss structure in this paper. Several V-shaped components between the arch rib and the main beam were added, so that it formed several continuous triangles consisting of the arch and beam sections. Triangle structures effectively restrained the main beam and arch rib. The location of the V-shaped components needs to be comprehensively considered for the uniform constraints on the arch ribs and the main beam and the weak position of the structure. The number of V-shaped components should be as reasonable as possible to achieve a reasonable balance between the stiffness of the structure and the temperature response. The results of finite element analysis show that the proposed method effectively improves the rigidity, dynamic characteristics, fatigue resistance and stability of the original structure by reasonably setting the number of V-shaped components and cross-sectional characteristic parameters, the mechanical performance indexes of the arch bridge can reach the most excellent design effect. The reconstructed arch bridge has reasonable structure and convenient construction, which has great value in popularization and application.
-
近30年以来，我国高速铁路拱桥发展迅速，跨径和数量不断刷新纪录[1-3]. 主要是因为拱桥承载力高、刚度大、经济并且施工工艺成熟，是大跨度铁路用桥的首选桥型[4-7]. 现在我国拱桥设计发生质的飞跃，已处于世界桥梁的领先地位，著名的大跨径铁路拱桥有南广铁路西江特大桥[8-9]，主跨为450 m中承式钢箱系杆拱桥，以及沪昆高铁北盘江特大桥[10]，为上承式劲性骨架钢筋混凝土拱桥，主跨达445 m.
高铁具有运营速度高、安全平稳性好、行车舒适、高密度连续运营等特点，因而对高铁桥梁的质量[11-12]提出更高的要求，包括足够的强度、刚度、抗扭能力、减振降噪能力等. 目前，随着高铁的不断提速，我国现役高铁拱桥病害问题[13]集中表现为悬吊桥面刚度和整体性较差、振害明显、高强吊杆疲劳问题严重、支座变形与位移超限等，直接威胁到桥梁的耐久性和高铁列车的行驶安全. 因此要想提高现役高铁拱桥的列车运行速度，改善其动力性能，必须进行高速铁路拱桥的改造[14]，一般常用的改造方法[15]有加大截面法、体外索法、体系加固法等，但是这些方法存在一定的局限性，如改造效果差、效率低和造成承载力下降等.
为了从结构形式[16]上解决以上问题，首先提出一种提高现役高速铁路拱桥力学性能的有效方法，主要介绍改造方法及其力学原理，并通过有限元对改造前后拱桥的刚度、承载力、稳定性、动力特性及疲劳幅值等进行对比，最后还对V型结构特性对本文拱桥的力学性能影响进行了分析.
1. 改造方法及力学原理
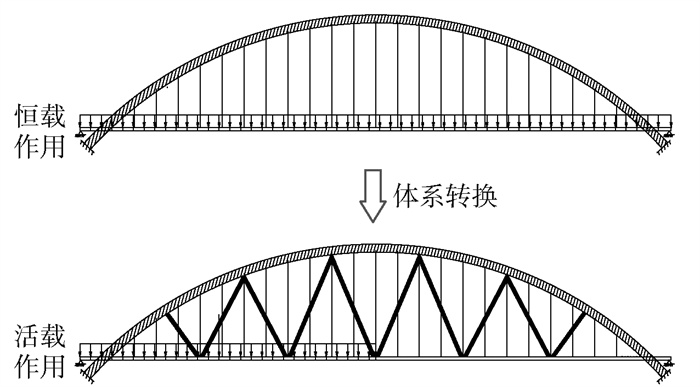
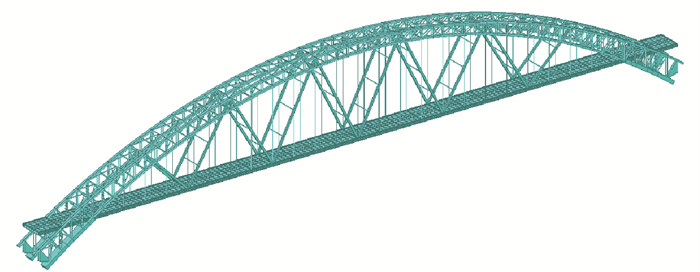
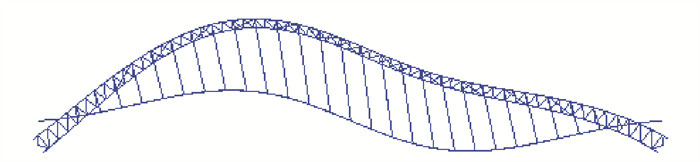
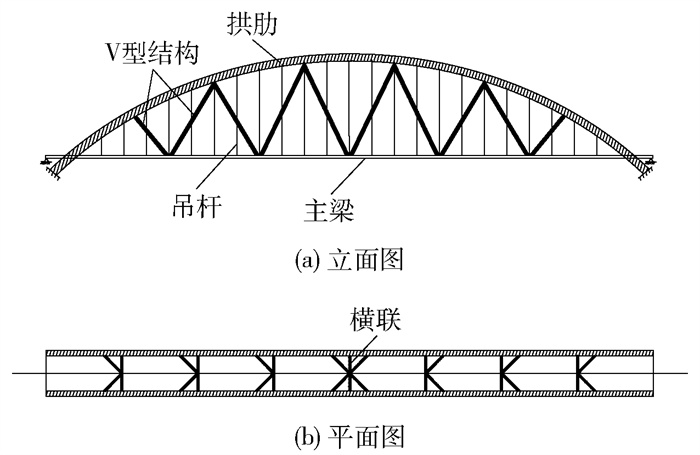
给出的改造方法为在原有下承式结构的拱肋与主梁间增设若干对V型结构，因此，改造后的拱桥主要由拱肋、主梁、V型结构、吊杆、横联等组成，吊杆垂直布置，主梁两端简支于桥台上，拱肋与拱座基础固结，在竖平面内共设置若干对V型结构，为了避免与吊杆在同一竖直平面内发生碰撞冲突，一般将其结构形式设置为双肢格构式，让吊杆可以在肢间穿过. 本文拱桥的总体布置如图 1所示，其力学原理分析如下.
1.1 转换结构受力体系
改造前拱桥的主要承重结构为拱肋，主梁和吊杆基本上起收集和传递荷载的作用，为拱式简单体系受力. 改造后拱桥在原拱桥基础上增设了V型构件，结构受力体系发生变化：恒载仍由拱肋承担，因此保留了拱桥在恒载下受力的优越性，活载则大部分由拱肋、主梁和V型结构形成的变高桁架结构承担，发挥了桁架结构刚度大的优势，为组合拱梁体系结构整体协同受力状态，其体系转换示意图如图 2所示.
1.2 引入三角形理念对拱肋及主梁进行有效约束
三角形稳定性是基于三角形受节点力作用，使其处于轴向变形状态. 然而，与其他结构不同的是，桥梁主要受移动荷载作用，这样就会使以上所形成的三角形受非节点力作用，从而在一定程度上降低三角形的稳定性，为此，需对主梁设置足够密的柔性吊杆，增加对主梁的弹性约束，提高其线刚度以减少弯曲变形，使多个连续三角形均能保证有良好的稳定性. 基于以上分析，本文拱桥在主梁与每条拱肋间增设若干个V型结构，使其与拱和梁段构成若干个连续的三角形结构，从而对主梁与拱肋进行有效约束，提高结构的整体刚度.
1.3 结合位移包络图合理布置三角形角点
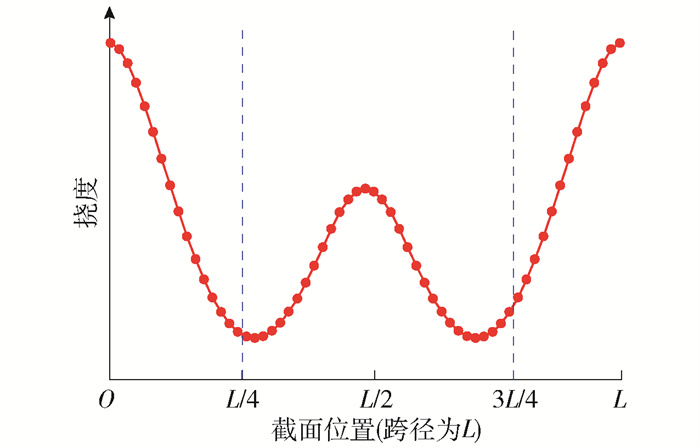
位移包络图反映出各个截面在移动荷载作用下位移的极限值，从而得知结构的薄弱之处，拱肋和主梁的位移包络图形态如图 3所示，其极值出现在L/4、L/2和3L/4截面位置附近. 结合位移包络图，三角形角点布置的方式是：首先，尽可能通过角点分别对拱肋和主梁进行均匀约束，从而达到既提高它们的线刚度又使其受力均匀的目的；其次，保证有约束点落在拱肋和主梁位移包络图的极值点处，使主梁或拱肋的薄弱处得到加强，改善结构的力学性能.
1.4 控制V型结构个数以达到刚度与温度响应之间的平衡
由于增加V型结构会增加体系的超静定次数，因此当增加的V型结构过多时，其温度应力显著增大；而当增加的V型结构较少时，又会对拱肋和主梁的约束不足，造成结构刚度不理想. 因此，控制好V型结构个数可以让两者达到较为合理的状态.
1.5 V型结构连接及杆件自身加强设计
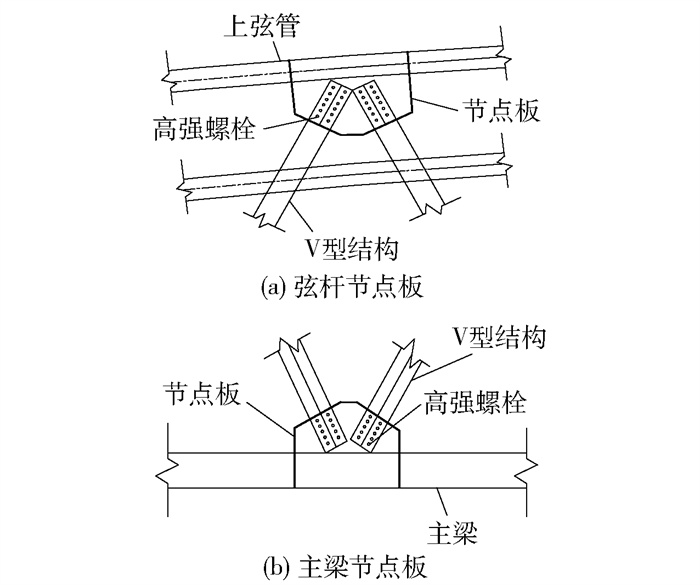
在活载作用下，本文拱桥在V型结构与拱肋或主梁连接处往往承受较大的应力集中和动荷载往复冲击作用，容易发生局部屈曲和节点疲劳问题，需进行强节点设计及拱肋、主梁局部加劲处理. 参考TB 10091—2017第4.3.1节规定和文献[17]，结合本文拱桥实际情况，将节点板部分与拱肋弦杆、主梁焊接，外露部分采用高强螺栓和V型结构连接，见图 4. 同时，为规避V型结构与吊杆在同一平面问题，V型结构可采用双肢格构形式.
此外，当V型结构计算长度过长时，容易发生屈曲. 因此可采用带有加劲肋的箱型截面杆件，同时在横桥向方向设置横向连接.
1.6 连续布置三角形以提高体系的抗变形能力
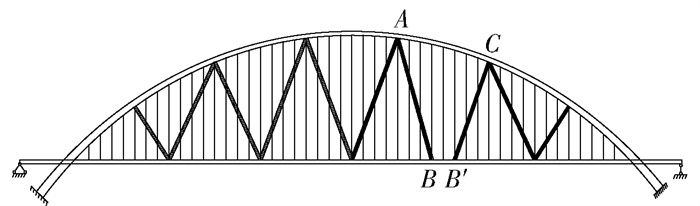
改造后拱桥所增设的连续三角形可使结构的抗变形能力大幅提高，这是因为此时三角形边所受的力以轴力为主，主要产生轴向变形. 当三角形的布置不连续时，会出现梁段在剪力作用下发生较大的弯曲变形. 分析如下：任选一个△ABC分离出梁段BB′, 如图 5所示, 由节点B平衡可知，在BB′段产生了剪力，于是在BB′梁段就会产生弯曲变形，因此，所布置的三角形必须保证连续以减少结构的变形.
![]()
图 5 三角形结构不连续布置示意图Figure 5. Schematic diagram of discontinuous arrangement of triangular structures2. 算例对比分析
为了研究本文改造方法的有效性，以钢管混凝土双线高速铁路拱桥为例，通过有限元建模分析其刚度、强度、稳定性、动力特性、温度响应及构件疲劳等问题.
2.1 计算参数
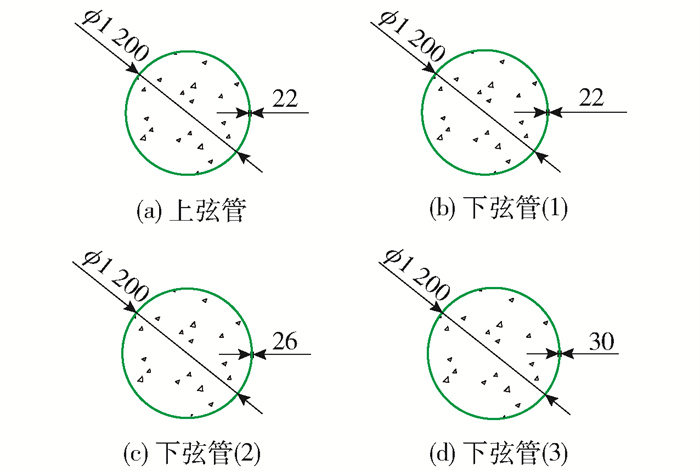
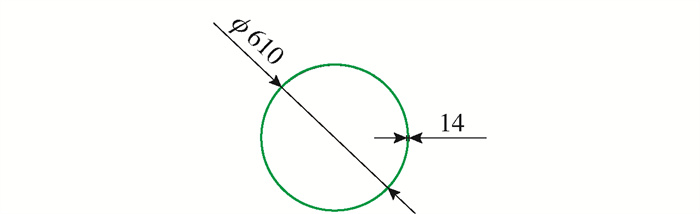
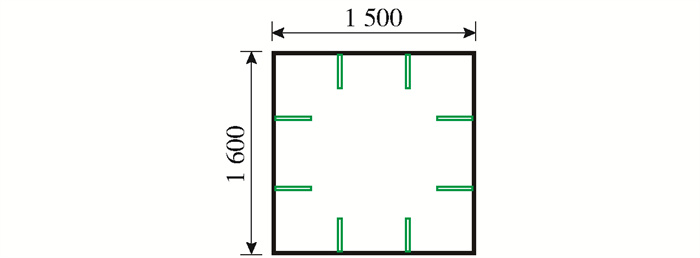
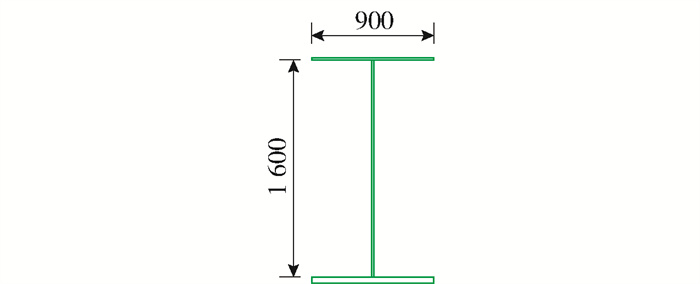
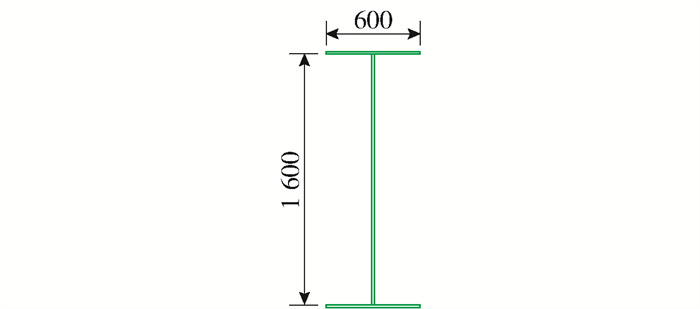
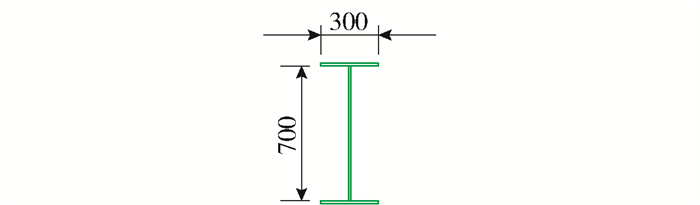
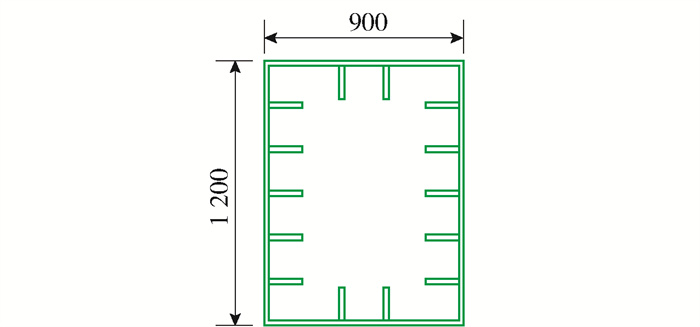
本算例主桥采用中承式钢管混凝土拱桥，计算跨径L=451.38 m，矢跨比为1/6，有限元模型如图 6、7所示. 主拱采用钢管混凝土桁式结构[18]，上下2根ϕ1 200 mm钢管混凝土弦管，管内混凝土强度等级为C70，通过腹杆连接主管构成矩形截面，主跨横撑采用K型钢管斜撑；吊杆采用整束挤压钢绞线吊索，吊杆间距为15 m，增设的V型结构采用双肢格构形式，桥面以下设置立柱，加劲梁通过吊杆或立柱支撑于拱肋之上；铁路桥面系采用纵横梁体系的正交异性桥面板结构，铁路桥面顶板厚16 mm，在10 m宽的道砟范围内铁路桥面顶板厚19 mm. 具体构件的几何参数和材料属性见表 1和图 8~15.
表 1 拱桥构件参数Table 1. Component parameters of arch bridge构件 截面形式 材料属性 截面面积/m2 截面惯性矩/m4 质量/t 上弦管 实腹圆型 Q390+C70 0.270 0 0.029 90 6 484.5 下弦管(1) 实腹圆型 Q390+C70 0.270 0 0.029 90 2 011.8 下弦管(2) 实腹圆型 Q390+C70 0.282 0 0.031 90 2 164.2 下弦管(3) 实腹圆型 Q390+C70 0.294 0 0.033 80 2 310.7 腹杆 空腹圆型 Q345 0.026 2 0.001 16 935.0 吊杆 圆型 高强钢丝1 860 MPa 0.070 7 0.000 40 1 269.4 主纵梁 带肋矩型 Q345 0.222 0 0.075 40 1 572.1 主横梁 工字型 Q345 0.078 6 0.006 65 270.1 次纵梁 工字型 Q345 0.044 3 0.000 58 470.7 次横梁 工字型 Q345 0.017 6 0.000 07 252.7 V型结构 带肋矩形 Q345 0.011 6 0.008 58 868.0 边界条件处理为：拱脚处固结，主梁端部和立柱上端设置弹性支承.
2.2 改造前后刚度对比分析
为了研究改造后拱桥的刚度，在原拱桥上增设V型结构，对比分析3种活载组合下结构的最大挠度和结构的刚度变化，并研究拱桥在L/4和L/2处的挠度影响线.
组合1：列车活载.
组合2：列车活载+0.5倍温度荷载.
组合3：0.63倍列车活载+温度荷载.
根据规范TB 10091—2017第4.3.2节条文规定[19]，组合1~3列车活载采用ZK活载，按双线最不利位置承受100%的ZK活载计算；温度荷载考虑为整体升温20 ℃或者整体降温25 ℃中最不利效应进行组合计算.
2.2.1 增设V型结构前后结构的刚度变化
为了研究在原拱桥基础上增设V型结构时结构的刚度变化，在原拱桥拱肋与主梁间增加5对V型结构，其截面积为0.086 m2，用钢量共为853.6 t，大约为全桥总用钢量的10.02%.
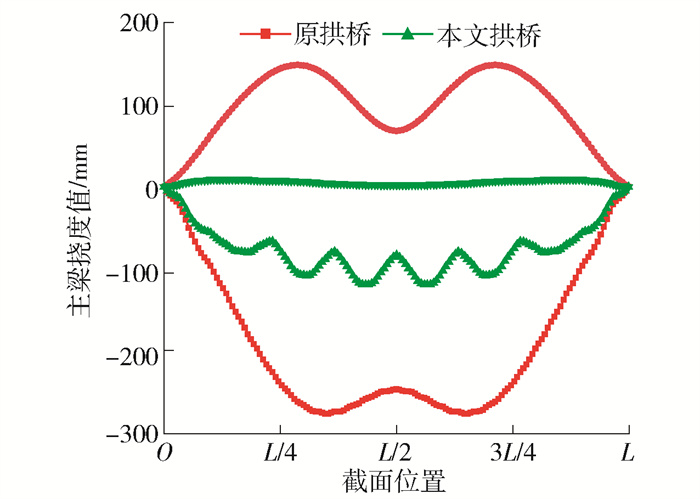
组合1作用下改造前后拱桥主梁的位移包络图如图 16所示，组合1~3下主梁的最大挠度值如表 2所示. 由主梁包络图可知，本文拱桥的包络面积和峰值均显著小于原拱桥，且本文拱桥的上挠包络值基本为0. 在列车活载(组合1)下，本文拱桥与原拱桥主梁最大下挠值分别为119、276 mm，相比后者下挠值减小了56.9%. 当考虑温度的影响时，本文拱桥在组合2和组合3下的主梁下挠值分别为192、221 mm，原拱桥分别为360、357 mm，相比后者分别减小了46.7%和38.1%. 在列车静活载下L/4处原拱桥主梁上下挠度(绝对值)之和为386 mm，而本文拱桥主梁上挠值基本为0，故此项无须进行验算.
表 2 主梁最大下挠值Table 2. Maximum displacement of main beam组合 主梁最大下挠值/mm 变化率/% 容许值 原拱桥 本文拱桥 1 276 119 56.9 L/1 000 2 360 192 46.7 L/1 000 3 357 221 38.1 L/1 000 考虑所有不利组合下，原拱桥和本文拱桥的最大挠度分别为386、221 mm，与原拱桥相比，挠度减小了74.66%，由此可见原拱桥在改造后刚度得到大幅度提高，在一定程度上保证了行车安全平稳性、乘车舒适性和高稳定性.
2.2.2 挠度影响线分析
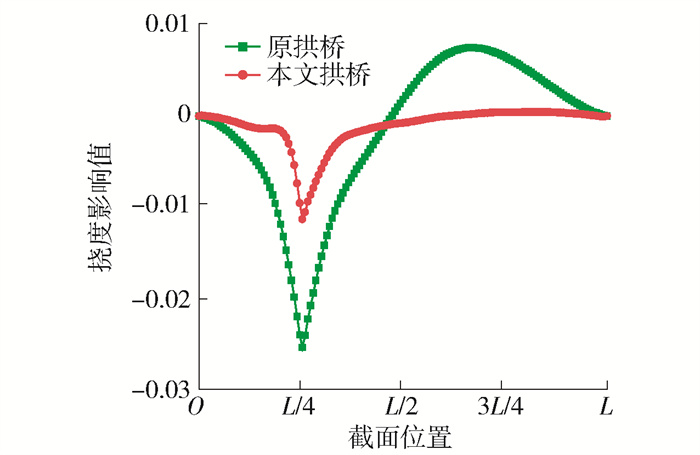
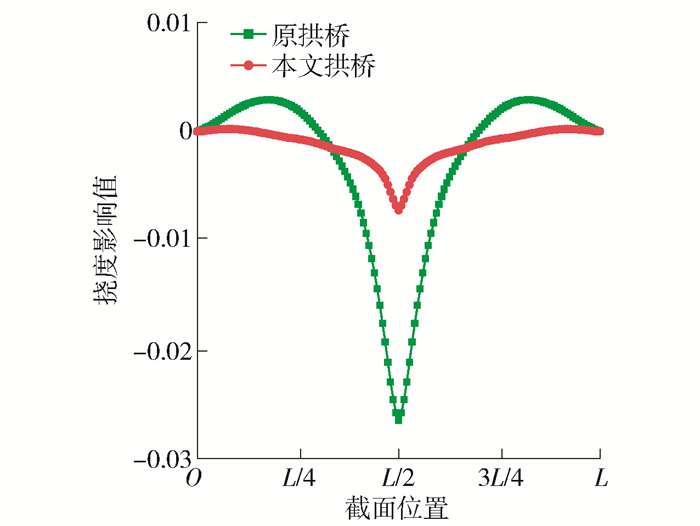
为了研究在移动荷载下结构挠度的变化规律及特征，图 17、18分别为本文拱桥与原拱桥主梁在L/4和L/2处的挠度影响线，结果表明：本文拱桥的挠度值显著小于原拱桥，且前者的挠度值基本上是同向的，而后者存在反向挠度影响线面积，说明改造后拱桥已经基本消除了拱桥的跷跷板效应，具有桁式结构变形的特征. 且前者的峰值明显小于后者，主要是由于拱肋、主梁和V型结构形成的变高桁架结构大大减小了拱肋的剪切变形，因此在活载下结构变形很小，有利于行车，特别适用于高铁桥的建设.
2.3 改造前后应力对比分析
为了进一步研究本文改造方法对各种荷载及其组合下结构应力的影响，通过有限元进行应力对比分析，主要考虑4个荷载工况对结构进行强度及温度响应分析.
工况Ⅰ：恒载(自重+二期).
工况Ⅱ：ZK活载.
工况Ⅲ：整体升温20 ℃或整体降温-25 ℃.
工况Ⅳ：恒载+ZK活载+整体升温20 ℃或降温-25 ℃.
工况Ⅰ~Ⅳ下本文拱桥与原拱桥拱肋上下弦管的最大应力对比见表 3. 计算结果表明，本文拱桥与原拱桥相比承载力有所提高. 在工况Ⅰ下，本文拱桥与原拱桥相比上下弦管应力基本相等(差值在5%以内)；在工况Ⅱ下，本文拱桥上下弦管应力分别降低54.49%和26.72%，主要是由于新增V型结构使拱肋在活载下变形大大减小；在工况Ⅲ下，本文拱桥上下弦管应力分别提高21.95%和3.02%，其主要是由于新增V型结构增加了结构的超静定次数，因此产生的温度应力略有提高；在工况Ⅳ下，本文拱桥上下弦管应力分别降低14.08%和4.23%. 综合以上可知，本文拱桥在活载下拱肋的应力值大幅减小，虽然温度应力略有提高，但是组合后结构应力水平下降，表明本文拱桥与原拱桥相比承载力略有提高.
表 3 拱肋弦管最大应力计算结果Table 3. Maximum stress of arch rib chord工况 原拱桥/MPa 本文拱桥/MPa 变化率/% 上弦管 下弦管 上弦管 下弦管 上弦管 下弦管 Ⅰ 26.39 31.32 27.31 32.80 -3.49 -4.73 Ⅱ 15.60 13.06 7.10 9.57 -54.49 -26.72 Ⅲ 13.62 4.31 16.61 4.18 21.95 3.02 Ⅳ 36.43 47.81 31.30 45.79 -14.08 -4.23 注：工况Ⅲ和Ⅳ计算效应时根据最大应力取升温或降温进行组合. 2.4 改造前后动力特性及稳定性对比分析
为了进一步研究本文方法对稳定性、动力特性的影响，对本文拱桥与原拱桥的自振特性与稳定性进行分析.
2.4.1 动力特性分析
本文拱桥与原拱桥的前6阶自振频率计算结果如表 4所示，1阶面内和面外振型图如图 19~22所示，结果表明，原拱桥基频为0.173 2，为面外振动；本文拱桥基频为0.188 1，为面外振动，相比原拱桥基频提高了8.6%，由此可见，V型结构的增设减弱了原桥的横向振动，由振动模态图可知，本文拱桥拱肋与主梁的振动相对位移值小于原拱桥，其主要是由于V型结构的增设强化了拱肋与桥面系的连接，使拱肋与桥面系的振动滞后性减弱，同步性得到加强. 原拱桥的面内振动频率为0.448 9，而本文拱桥的面内振动频率为1.029 4，相比原拱桥提高了129.3%，主要是由于本文拱桥的面内刚度大幅度提高，从而面内基频也大幅提高，表明本文改造方法大大提高了拱桥的面内振动频率，有利于改善高速铁路拱桥的动力特性.
表 4 动力特性计算结果Table 4. Result of dynamic characteristics阶数 原拱桥 本文拱桥 振型 振频 振型 振频 1 面外正对称 0.173 2 面外正对称 0.188 1 2 面外正对称 0.235 0 面外正对称 0.271 8 3 面内反对称 0.448 9 面外反对称 0.478 0 4 面外反对称 0.464 0 面外反对称 0.607 2 5 面外反对称 0.575 5 面外正对称 0.806 9 6 面内正对称 0.632 7 面内非对称 1.029 4 ![]()
图 19 原拱桥第1阶面外振型Figure 19. First-order out-of-plane mode shape of original arch bridge![]()
图 21 本文拱桥第1阶面外振型Figure 21. First-order out-of-plane mode shape of present arch bridge2.4.2 稳定性分析
随着跨径增大，拱肋稳定问题也越来越突出[20]，为此，进行本文拱桥与原拱桥的弹性屈曲分析，其弹性稳定计算结果如表 5所示，结果表明，原拱桥和本文拱桥的第1阶失稳模态均为面外失稳，稳定系数分别为5.87和5.84，基本保持相等；原拱桥面内稳定系数为9.56，而本文拱桥的面内稳定系数达到26.37，表明本文拱桥的面内稳定性得到大幅度提高.
表 5 弹性稳定计算结果Table 5. Analysis of branch point instability阶数 原拱桥 本文拱桥 失稳模态 稳定系数 失稳模态 稳定系数 1 面外正对称 5.87 面外正对称 5.84 2 面外反对称 6.00 面外反对称 6.21 3 面外正对称 7.85 面外正对称 8.05 4 面外反对称 7.88 面外反对称 8.07 5 面外正对称 8.19 面外正对称 8.73 6 面外正对称 8.63 面外正对称 8.83 2.5 改造前后吊杆疲劳幅值对比分析
2.5.1 吊杆疲劳对比分析
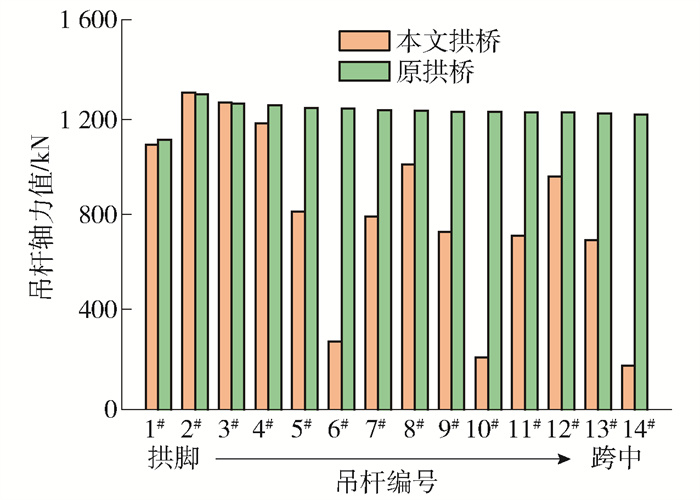
拱桥的拉索是易损的关键构件，在日常活载作用下，疲劳问题较突出[21]. 因此有必要对改造前后吊杆的疲劳问题进行分析. 图 23为列车活载下本文拱桥和原拱桥吊杆轴力幅值对比，其中1#~14#吊杆按从拱脚到跨中编号. 由图可知，在列车活载下，本文拱桥靠近拱脚处的1#~4#短吊杆轴力幅值基本与原拱桥保持相等，而5#~14#吊杆轴力幅值则得到有效减小，总的来说，本文拱桥吊杆的轴力幅值总体上小于原拱桥，表明增设V型结构后本文拱桥吊杆的疲劳效应有效得到改善，主要是由于本文拱桥增设的刚度较大的V型结构，能与拱肋、主梁共同抵抗铁路活载的作用，因此吊杆受力减小.
![]()
图 23 活载下吊杆轴力幅值对比Figure 23. Comparison of axial force amplitude of suspenders under live load2.5.2 本文拱桥V型结构疲劳分析
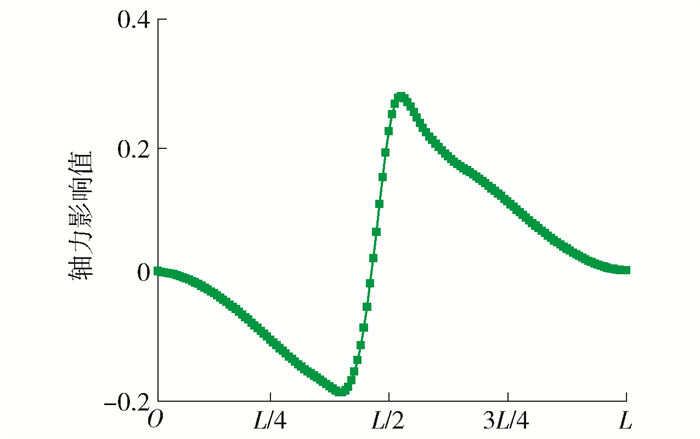
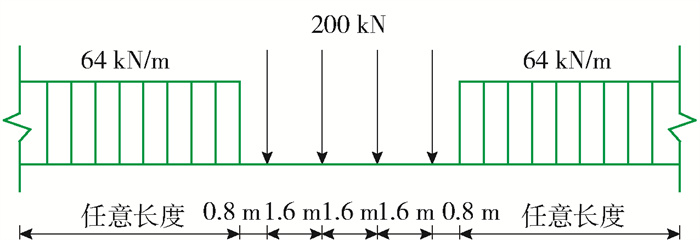
为研究V型结构疲劳问题，绘制跨中1#V型结构轴力影响线，如图 24所示，由图可知，1#V型结构轴力影响线有正有负，且正的峰值大于负的峰值，说明在活载作用下杆件会同时出现受拉和受压2种受力状态，且受拉值大于受压值，需要对V型构件进行疲劳应力幅分析. 进一步模拟ZK列车活载(如图 25所示)通过全桥过程中各构件出现的最大应力，应力包络图如图 26所示，由图可知，V型结构的最大拉、压应力分别为59.71、40.62 MPa，杆件最大疲劳应力幅值为100.33 MPa，出现在V型结构与拱肋或主梁连接处. 依据TB 10091—2017表 3.2.7-1规定，当V型结构与拱肋、主梁之间的连接方式采用双面拼接，第一排螺栓无滑移的连接类型(即V型结构节点处，沿横桥向设置节点板与主梁连接，见图 4)，此条件下的疲劳容许应力为109.6 MPa，应力幅值满足规范规定的疲劳容许应力幅，符合疲劳验算的要求.
3. V型结构特性对本文拱桥力学性能的影响
3.1 V型结构个数对改造后拱肋温度效应的影响
温度荷载是桥梁设计不可忽略的可变荷载，会对结构特别是热膨胀系数较大的钢结构产生较大的效应. 增设V型结构后，结构超静定次数增加，结构刚度提高，温度变化对结构的影响更加不容忽视. 基于第2节算例，改变V型结构的数量，分别设置3对、4对、5对、6对、7对V型构件，研究在工况Ⅴ(整体升温20 ℃)和工况Ⅵ(整体降温25 ℃)作用下拱肋温度应力的变化，计算结果见表 6.
表 6 拱肋最大温度应力Table 6. Maximum temperature stress of arch rib and chordMPa 构件类型 工况 V型结构数量 3对 4对 5对 6对 7对 弦管 工况Ⅴ 10.1 9.8 9.8 10.7 11.7 工况Ⅵ -17.1 -16.6 -16.6 -18.2 -18.5 腹杆 工况Ⅴ 63.9 61.2 67.6 67.0 98.0 工况Ⅵ -79.9 -76.5 -84.5 -83.7 -122.5 注：“-”号表示受压. 由表 6可知，随着V型结构个数的增加，拱肋的温度应力整体呈现增大趋势. 当V型结构数量从3对增加到7对时，弦管在工况Ⅴ作用下，温度应力提高了15.8%，在工况Ⅵ作用下，温度应力提高了8.2%；腹杆在工况Ⅴ作用下，温度应力提高了53.4%，在工况Ⅵ作用下，温度应力提高了53.3%. 主要原因是，增设V型结构增加了拱桥整体结构的超静定次数，导致拱肋结构温度响应增大. 因此，需要控制V型结构个数以考虑V型结构带来的不利温度影响.
3.2 V型结构截面积对改造后拱桥力学性能的影响
V型结构的设计是改造原拱桥力学性能的重要环节，直接影响其刚度、动力特性与稳定性的改善效果. 通过研究V型结构面积对结构主要性能指标的影响，选择出最适合的取值，为设计提供参考. 本节计算在第2节的模型基础上改变V型结构面积，其变化范围为0.02~0.22 m2.
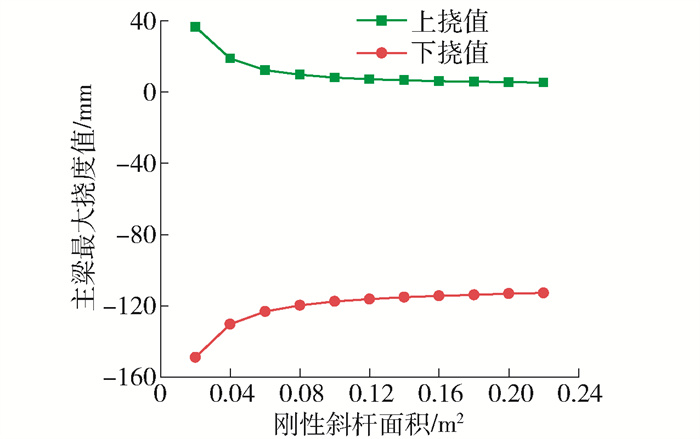
在变V型结构面积下本文拱桥主梁挠度变化曲线如图 27所示，结果表明，随着V型结构面积的增大，主梁上、下挠值均不断减小，但变化趋势不断减缓；在0.02~0.16 m2范围内上、下挠值绝对值下降速度较快，在0.16~0.22 m2范围内上、下挠值绝对值减小速度放慢；随着V型结构面积的不断增大，上、下挠度绝对值的比值从1∶4.1下降到1∶21.3，表明拱桥上挠现象越来越不明显，拱桥的跷跷板负效应不断减弱.
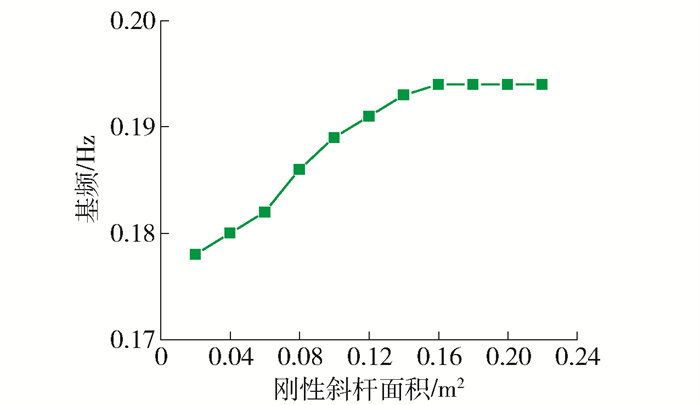
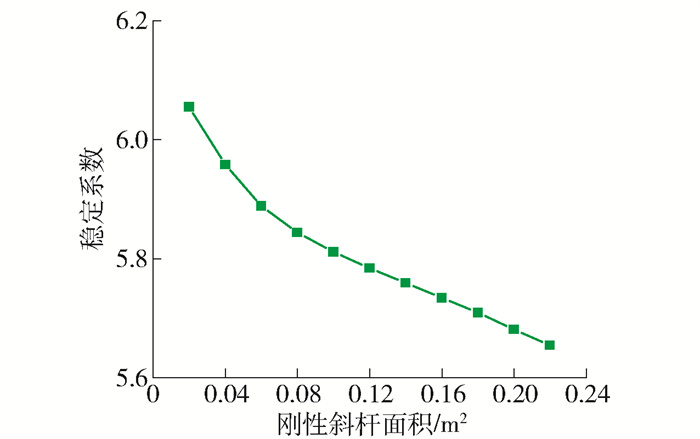
在变V型结构面积下本文，拱桥基频与稳定系数的变化曲线如图 28、29所示，结果表明，结构基频随V型结构面积增大不断提高，在0.02~0.16 m2范围内提高明显，其后变化趋势趋于平缓；稳定系数则随着V型结构面积增大而降低.
![]()
图 28 本文拱桥基频变化Figure 28. Variation of the fundamental frequency of present arch bridge![]()
图 29 本文拱桥稳定系数变化Figure 29. Variation of the stability coefficient of present arch bridge4. 结论
本文提出了一种提高现役高速铁路拱桥力学性能的有效方法，即在拱肋和主梁之间增设若干对V型结构与拱肋及主梁节段形成多个连续三角形，使拱肋和主梁薄弱处得到加强，并提高拱肋和主梁的线刚度. 本文算例通过在原拱桥上增设V型结构(约增加总用钢量的10%)，对改造前后的拱桥进行有限元分析，得出以下结论：
1) 结构的整体刚度提升. 在活载组合1~3下，原拱桥和本文拱桥的最大挠度分别为386、221 mm，与原拱桥相比，挠度减小了74.66%，可见，本文方法显著提高了原桥的竖向刚度.
2) 强度承载力有所提高. 在列车活载作用下，由V型结构与拱肋及主梁节段所形成的三角形参与抵抗其变形，从而拱肋变形大幅减小，应力水平有所下降. 计算表明，在活载下，本文拱桥拱肋的上、下弦杆的最大应力分别减少54.49%和26.72%，在恒载+活载+温度荷载组合后，其上、下弦杆最大应力较原拱桥分别减小14.08%和4.23%.
3) 动力特性有效改善，稳定性有所提高. 动力特性分析表明，两者的第1阶振型均为面外振动，本文拱桥的基频为0.188 1，原拱桥的基频为0.173 2，较后者提高8.6%，且前者行车面内1阶振动的频率为1.029 4，而后者仅为0.448 9，较后者提高了129.3%. 弹性稳定分析结果表明，两者的面外稳定系数基本相同，但本文拱桥的面内稳定系数为26.37，明显高于面内稳定系数为9.56的原拱桥.
4) 吊杆疲劳幅值减小，V型结构的疲劳幅值满足规范要求. 计算表明，本文拱桥的吊杆轴力幅值总体得到有效的减小，V型结构疲劳应力幅为100.33 MPa，满足规范规定的疲劳容许应力幅.
5) V型结构个数和截面特性敏感性分析表明，通过合理选择V型结构个数、适当调整V型结构面积，能使本文拱桥的各项力学性能指标达到最优的设计效果.
综上所述，本文的改造方法使原拱桥整体刚度得到大幅度提高，且其强度、动力特性及稳定性等力学特性均得到一定的改善，疲劳验算也满足规范要求. 改造后的拱桥结构合理、适用性强、具有一定的推广应用价值，该方法可供设计研究人员参考.
-
![]()
图 5 三角形结构不连续布置示意图
Figure 5. Schematic diagram of discontinuous arrangement of triangular structures
![]()
图 19 原拱桥第1阶面外振型
Figure 19. First-order out-of-plane mode shape of original arch bridge
![]()
图 21 本文拱桥第1阶面外振型
Figure 21. First-order out-of-plane mode shape of present arch bridge
![]()
图 23 活载下吊杆轴力幅值对比
Figure 23. Comparison of axial force amplitude of suspenders under live load
![]()
图 28 本文拱桥基频变化
Figure 28. Variation of the fundamental frequency of present arch bridge
![]()
图 29 本文拱桥稳定系数变化
Figure 29. Variation of the stability coefficient of present arch bridge
表 1 拱桥构件参数
Table 1 Component parameters of arch bridge
构件 截面形式 材料属性 截面面积/m2 截面惯性矩/m4 质量/t 上弦管 实腹圆型 Q390+C70 0.270 0 0.029 90 6 484.5 下弦管(1) 实腹圆型 Q390+C70 0.270 0 0.029 90 2 011.8 下弦管(2) 实腹圆型 Q390+C70 0.282 0 0.031 90 2 164.2 下弦管(3) 实腹圆型 Q390+C70 0.294 0 0.033 80 2 310.7 腹杆 空腹圆型 Q345 0.026 2 0.001 16 935.0 吊杆 圆型 高强钢丝1 860 MPa 0.070 7 0.000 40 1 269.4 主纵梁 带肋矩型 Q345 0.222 0 0.075 40 1 572.1 主横梁 工字型 Q345 0.078 6 0.006 65 270.1 次纵梁 工字型 Q345 0.044 3 0.000 58 470.7 次横梁 工字型 Q345 0.017 6 0.000 07 252.7 V型结构 带肋矩形 Q345 0.011 6 0.008 58 868.0 
下载: 导出CSV
表 2 主梁最大下挠值
Table 2 Maximum displacement of main beam
组合 主梁最大下挠值/mm 变化率/% 容许值 原拱桥 本文拱桥 1 276 119 56.9 L/1 000 2 360 192 46.7 L/1 000 3 357 221 38.1 L/1 000
下载: 导出CSV
表 3 拱肋弦管最大应力计算结果
Table 3 Maximum stress of arch rib chord
工况 原拱桥/MPa 本文拱桥/MPa 变化率/% 上弦管 下弦管 上弦管 下弦管 上弦管 下弦管 Ⅰ 26.39 31.32 27.31 32.80 -3.49 -4.73 Ⅱ 15.60 13.06 7.10 9.57 -54.49 -26.72 Ⅲ 13.62 4.31 16.61 4.18 21.95 3.02 Ⅳ 36.43 47.81 31.30 45.79 -14.08 -4.23 注：工况Ⅲ和Ⅳ计算效应时根据最大应力取升温或降温进行组合.
下载: 导出CSV
表 4 动力特性计算结果
Table 4 Result of dynamic characteristics
阶数 原拱桥 本文拱桥 振型 振频 振型 振频 1 面外正对称 0.173 2 面外正对称 0.188 1 2 面外正对称 0.235 0 面外正对称 0.271 8 3 面内反对称 0.448 9 面外反对称 0.478 0 4 面外反对称 0.464 0 面外反对称 0.607 2 5 面外反对称 0.575 5 面外正对称 0.806 9 6 面内正对称 0.632 7 面内非对称 1.029 4
下载: 导出CSV
表 5 弹性稳定计算结果
Table 5 Analysis of branch point instability
阶数 原拱桥 本文拱桥 失稳模态 稳定系数 失稳模态 稳定系数 1 面外正对称 5.87 面外正对称 5.84 2 面外反对称 6.00 面外反对称 6.21 3 面外正对称 7.85 面外正对称 8.05 4 面外反对称 7.88 面外反对称 8.07 5 面外正对称 8.19 面外正对称 8.73 6 面外正对称 8.63 面外正对称 8.83
下载: 导出CSV
表 6 拱肋最大温度应力
Table 6 Maximum temperature stress of arch rib and chord
MPa 构件类型 工况 V型结构数量 3对 4对 5对 6对 7对 弦管 工况Ⅴ 10.1 9.8 9.8 10.7 11.7 工况Ⅵ -17.1 -16.6 -16.6 -18.2 -18.5 腹杆 工况Ⅴ 63.9 61.2 67.6 67.0 98.0 工况Ⅵ -79.9 -76.5 -84.5 -83.7 -122.5 注：“-”号表示受压.
下载: 导出CSV
-
[1] 姚玲森. 桥梁工程[M]. 2版. 北京: 人民交通出版社, 2016: 4-5. [2] HU N, DAI G L, YAN B, et al. Recent development of design and construction of medium and long span high-speed railway bridges in China[J]. Engineering Structures, 2014, 74: 233-241. doi: 10.1016/j.engstruct.2014.05.052
[3] ZHENG J, WANG J. Concrete-filled steel tube arch bridges in China[J]. Engineering, 2018, 4(1): 143-155. doi: 10.1016/j.eng.2017.12.003
[4] 陈宝春, 韦建刚, 周俊, 等. 我国钢管混凝土拱桥应用现状与展望[J]. 土木工程学报, 2017, 50(6): 50-61. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201706006.htm CHEN B C, WEI J G, ZHOU J, et al. Application status and prospects of concrete-filled steel tubular arch bridges in China[J]. China Civil Engineering Journal, 2017, 50(6): 50-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201706006.htm
[5] 吴庆雄, 黄宛昆, 陈宝春. 中、下承式钢管混凝土拱桥车振调查与动力分析[J]. 工程力学, 2013, 30(1): 147-155. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201301024.htm WU Q X, HUANG W K, CHEN B C. Investigation and dynamic analysis of vehicle vibration of middle and lower concrete filled steel tubular arch bridges[J]. Engineering Mechanics, 2013, 30(1): 147-155. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201301024.htm
[6] 徐艳, 胡世德. 钢管混凝土拱桥的动力稳定极限承载力研究[J]. 土木工程学报, 2006, 37(9): 68-73. doi: 10.3321/j.issn:1000-131X.2006.09.011 XU Y, HU S D. Study on dynamic stability ultimate bearing capacity of concrete-filled steel tubular arch bridge[J]. China Civil Engineering Journal, 2006, 37(9): 68-73. (in Chinese) doi: 10.3321/j.issn:1000-131X.2006.09.011
[7] ANG C, SCHNEIDER S, WENNER M. Development of design and construction of high-speed railway bridges in Germany[J]. Engineering Structures, 2018, 163: 184-196. doi: 10.1016/j.engstruct.2018.02.059
[8] 翟建平. 肇庆西江特大桥动力特性分析[J]. 铁道科学与工程学报, 2011, 8(3): 13-17. doi: 10.3969/j.issn.1672-7029.2011.03.003 ZHAI J P. Analysis of dynamic characteristics of Xijiang bridge in Zhaoqing[J]. Journal of Railway Science and Engineering, 2011, 8(3): 13-17. (in Chinese) doi: 10.3969/j.issn.1672-7029.2011.03.003
[9] 徐升桥, 彭岚平, 张华. 南广铁路西江特大桥的技术创新[J]. 铁道标准设计, 2013(2): 50-57. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201302015.htm XU S Q, PENG L P, ZHANG H. Technology innovation of Xijiang bridge of Nanguang railway[J]. Railway Standard Design, 2013(2): 50-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201302015.htm
[10] 张正阳, 赵人达. 基于贝叶斯理论的钢管混凝土劲性骨架拱桥收缩徐变效应分析[J]. 铁道标准设计, 2017, 61(5): 86-90, 95. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201705019.htm ZHANG Z Y, ZHAO R D. Analysis of shrinkage and creep effect of concrete filled steel tubular arch bridge based on Bayesian theory[J]. Railway Standard Design, 2017, 61(5): 86-90, 95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201705019.htm
[11] ZHAO H W, DING Y L, NAGARAJAIAH S, et al. Behavior analysis and early warning of girder deflections of a steel-truss arch railway bridge under the effects of temperature and trains: case study[J]. Journal of Bridge Engineering, 2018, 24(1): 05018013.
[12] 赵瀚玮, 丁幼亮, 李爱群. 高速列车作用下南京大胜关大桥动位移响应分析[J]. 铁道科学与工程学报, 2018, 15(9): 2187-2195. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201809001.htm ZHAO H W, DING Y L, LI A Q. Analysis of dynamic displacement response of Nanjing Dashengguan bridge under the action of high speed train[J]. Journal of Railway Science and Engineering, 2018, 15(9): 2187-2195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201809001.htm
[13] 桑德才. 高速铁路桥梁病害与加固改造分析[J]. 交通世界, 2017(29): 135-136. https://www.cnki.com.cn/Article/CJFDTOTAL-JTSJ201729060.htm SANG D C. Analysis of diseases and reinforcement transformation of high-speed railway bridges[J]. Transpoworld, 2017(29): 135-136. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTSJ201729060.htm
[14] WALLIN J, LEANDER J, KAROUMI R. Strengthening of a steel railway bridge and its impact on the dynamic response to passing trains[J]. Engineering Structures, 2011, 33(2): 635-646. doi: 10.1016/j.engstruct.2010.11.022
[15] 王宗林, 王潮海. 大跨径钢管混凝土拱桥的动力性能改造[J]. 公路交通科技, 2006(11): 73-77, 94. doi: 10.3969/j.issn.1002-0268.2006.11.018 WANG Z L, WANG C H. Reconstruction of dynamic performance of long span CFST arch bridge[J]. Journal of Highway and Transportation, 2006(11): 73-77, 94. (in Chinese) doi: 10.3969/j.issn.1002-0268.2006.11.018
[16] 乔健. 漫谈中国铁路桥梁发展的历程[J]. 铁道标准设计, 2012(3): 27-30. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201203011.htm QIAO J. Talking about the development of China's railway bridges[J]. Railway Standard Design, 2012(3): 27-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201203011.htm
[17] 周凌宇, 贺桂超. 大跨度钢-混凝土组合桁架铁路桥端节点模型试验研究[J]. 土木工程学报, 2012, 45(1): 92-99. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201201015.htm ZHOU L Y, HE G C. Model test research on the end joint of long-span steel-concrete composite truss railway bridge[J]. Journal of Civil Engineering, 2012, 45(1): 92-99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201201015.htm
[18] 杨勇. 重载铁路大跨度上承式钢管混凝土拱桥设计研究[J]. 铁道标准设计, 2018, 62(4): 107-111, 186. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201804022.htm YANG Y. Design of large-span steel-concrete arch bridge with heavy-duty railways[J]. Railway Standard Design, 2018, 62(4): 107-111, 186. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201804022.htm
[19] 国家铁路局. 铁路桥涵设计规范: TB10002—2017[S]. 北京: 中国铁道出版社, 2017: 19-20. [20] 司万胜. 高速铁路(110+208+110)m连续梁-钢管混凝土拱屈曲分析[J]. 铁道标准设计, 2019, 63(3): 95-99. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201903020.htm SI W S. Buckling analysis of high-speed railway (110+208+110)m continuous beam-steel tube concrete arch[J]. Railway Standard Design, 2019, 63(3): 95-99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201903020.htm
[21] PELLEGRINO C, CUPANI G, MODENA C. The effect of fatigue on the arrangement of hangers in tied arch bridges[J]. Engineering Structures, 2010, 32(4): 1140-1147. http://www.researchgate.net/profile/Carlo_Pellegrino/publication/239347875_The_effect_of_fatigue_on_the_arrangement_of_hangers_in_tied_arch_bridges/links/5565eac208aeab77721cb40c.pdf
-
期刊类型引用(1)
1. 王海桥. 未铺装桥面的钢箱拱桥架桥机携梁过桥受力分析. 铁道建筑技术. 2023(02): 148-151+194 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 237
- HTML全文浏览量: 5
- PDF下载量: 54
- 被引次数: 1
