Optimal Control for Municipal Wastewater Treatment Process Based on Dynamic Decomposed Multiobjective Particle Swarm Optimization
-
摘要:
为了实现城市污水处理过程各性能指标的优化运行，提出了一种动态分解多目标粒子群优化控制（optimal control based on dynamic decomposed multiobjective particle swarm optimization，OC-DDMOPSO）策略.首先，构建了基于自适应核函数的运行性能指标模型，确定了优化运行目标.其次，设计了基于档案库动态分解的多目标粒子群优化算法，实时获取操作变量的优化设定值.最后，利用预测控制策略跟踪优化设定值，完成了城市污水处理过程优化控制.将提出的OC-DDMOPSO应用于基准仿真平台BSM1，实验结果显示，OC-DDMOPSO能够实现城市污水处理过程稳定运行，保证出水水质达标排放和降低运行成本.
Abstract:To realize the optimal operation of the performance indices in municipal wastewater treatment process (MWWTP), an optimal control based on dynamic decomposed multiobjective particle swarm optimization (OC-DDMOPSO) was proposed in this paper. First, the dynamic performance models were formulated by using the adaptive kernel functions, and the optimization objectives could be then obtained. Second, multiobjective particle swarm optimization algorithm based on the dynamic decomposed archive was developed, and the optimal set-points could be then derived. Third, a predictive control strategy was designed to trace the obtained optimal set-points, and the optimal control of MWWTP could be then realized. Finally, the proposed OC-DDMOPSO strategy was tested on the benchmark simulation model No.1. Results show that OC-DDMOPSO can not only facilitate the stable operation of MWWTP, but also guarantee the effluent qualities, as well as reduce the operation cost.
-
城市污水处理过程主要通过持续曝气促进微生物分解来去除污水中可溶性有机物及部分不溶性无机物[1]. 该过程同时包含生物反应、化学反应等，各反应过程运行机理异常复杂[2]. 此外，城市污水处理过程同时包含多种运行性能指标，各指标之间相互影响、相互耦合[3]. 由于复杂的运行机理和耦合的性能指标，城市污水处理过程难以实现优化运行[4]. 究其根本原因，主要难点在于性能指标模型的构建和优化方法的设计.
为了构建城市污水处理过程性能指标模型，van Staden等[5]设计了一种基于动力学特性的泵送能耗模型，该模型能够描述泵送能耗指标与硝态氮等过程变量的关系，实验结果表明所提出的泵送能耗模型能够完成对城市污水处理过程泵送指标动态特性的表达. 为了同时考虑城市污水处理过程的曝气和泵送能耗，Ashrafi等[6]提出了一种基于硝化和反硝化机理模型的曝气和泵送能耗模型，该模型能够描述能耗与溶解氧、硝态氮等过程变量的关系，实验结果表明该模型能够实现对能耗动态特性的获取. 此外，随着城市污水处理过程出水水质的排放要求越来越严格，出水水质也成为城市污水处理过程的重要性能指标[7]. 为了实现对城市污水处理过程曝气能耗、泵送能耗和出水水质指标动态特性的获取，Alsina等[8]提出了一种基于机理模型的城市污水处理过程性能指标综合评价模型，用于描述曝气能耗、泵送能耗、出水水质与溶解氧等过程变量之间的关系，结果显示所提出的性能指标综合评价模型能够实时获取城市污水处理过程的动态特性. 但是，由于城市污水处理是典型的复杂非线性过程，上述基于机理模型的性能指标模型参数较多，难以根据动态的运行过程进行自适应调整，无法保证性能指标模型的精度[9].
为了解决基于机理模型的污水处理过程性能指标模型的不足，数据驱动的性能指标模型得到了广泛的关注[10]. Zeng等[11]提出了一种数据驱动的泵送能耗模型，通过非线性规划模型建立泵送能耗与溶解氧、硝态氮等过程变量的关系，利用贪婪算法对模型参数进行调整，提高泵送能耗模型的自适应能力，实验结果表明所提出的数据驱动的泵送能耗模型能实现对泵送过程动态特性的描述. Huang等[12]提出了一种基于扩展Elman神经网络的城市污水处理过程性能评价模型，该性能评价模型能够描述城市污水处理过程能耗和出水水质之间的关系，利用梯度下降算法对模型参数进行自适应调整，保证性能评价模型的有效性. 此外，为了实现对能耗和出水水质动态特性的准确描述，Durrenmatt[13]提出了一种基于自组织映射的污水处理过程能耗和出水水质评价模型，实验结果表明所提出的能耗和出水水质评价模型能实现对城市污水处理过程运行状态的准确描述. 然而，由于城市污水处理过程复杂，各性能指标具有强非线性等特点，如何根据运行特点建立准确的性能指标模型仍是一个亟待解决的难题[14].
有效的优化方法也是保证城市污水处理稳定优化运行的关键[15]. Duzinkiewicz等[16]设计了一种基于遗传算法的优化控制策略，利用遗传算法对能耗模型进行优化，获得溶解氧质量浓度的优化设定值，并通过预测控制策略实现溶解氧质量浓度的跟踪控制，降低城市污水处理过程的操作能耗. 此外，Guerrero等[17]提出了一种基于模式搜索算法的优化控制策略，实现城市污水处理过程氨氮和硝态氮质量浓度优化设定值的实时获取和跟踪控制. 该策略通过模式搜索算法最小化能耗模型获得控制变量优化设定值，利用比例-积分-微分(proportional-integral-derivative, PID)控制策略实现对氨氮和硝态氮质量浓度优化设定值的跟踪控制，结果表明所提出的方法能够保证城市污水处理过程稳定运行. 考虑到城市污水处理过程的动态特性，Sweetapple等[18]设计了一种基于动态遗传算法的优化控制策略，用于同时优化运行成本、污泥排放质量浓度等指标模型，获取总氮和氨氮质量浓度的优化设定值. 实验结果表明，所提出的方法不仅能够降低运行成本，而且可以保证出水水质达标排放. 然而，由于城市污水处理是一个动态的复杂非线性过程，如何设计一种有效的动态优化方法来获取有效的控制变量优化设定值仍然是一个挑战性问题[19].
为了实现城市污水处理过程的优化运行，文中提出了一种动态分解多目标粒子群优化控制(optimal control based on dynamic decomposed multiobjective particle swarm optimization, OC-DDMOPSO)策略. 相比其他的优化控制策略，所提出的OC-DDMOPSO具有以下优势：
1) 构建了一种基于自适应核函数的性能指标模型，实现对城市污水处理过程动态特性的描述，完成OC-DDMOPSO目标函数的构建.
2) 设计了一种基于档案库动态分解的多目标粒子群优化算法，完成对OC-DDMOPSO目标函数的优化，获得优化设定值.
3) 利用预测控制策略实现对优化设定值的跟踪控制，保证城市污水处理过程稳定优化运行.
1. 城市污水处理过程特性分析
城市污水处理过程常采用厌氧-缺氧-好氧(A2/O)处理工艺实现污水的净化处理. 污水通过粗格栅和细格栅去除大的悬浮物及漂浮物后，利用生化反应池进行硝化和反硝化处理去除污水中的有机污染物，生化反应池出水进入到生化沉淀池完成泥水分离，污水上清液达到排放标准后直接排放，部分污泥通过污泥回流泵回流到生化反应池前端，其他污泥则排入污泥贮存池. 因此，城市污水处理是一个复杂的动态非线性过程，其运行特点可总结如下：
1) 非线性特性 城市污水处理过程是一个典型的非线性过程，生物反应、化学反应等同时发生，各反应过程运行机理复杂，具有强非线性特点.
2) 多指标特性 城市污水处理过程同时包含多种性能操作指标，如曝气能耗、泵送能耗、出水水质等，各性能指标之间相互影响、相互耦合，难以获取多指标之间的平衡关系.
3) 时变特性 城市污水处理过程是一个时变的操作系统，其入水水质、水量等被动接受，其微生物活性随着曝气过程、生物反应、化学反应等的影响进行动态变化. 固定的控制变量优化设定值难以保证污水处理效果.
因此，基于城市污水处理过程的运行特性，设计OC-DDMOPSO策略，保证城市污水处理过程的稳定优化运行.
2. OC-DDMOPSO策略设计
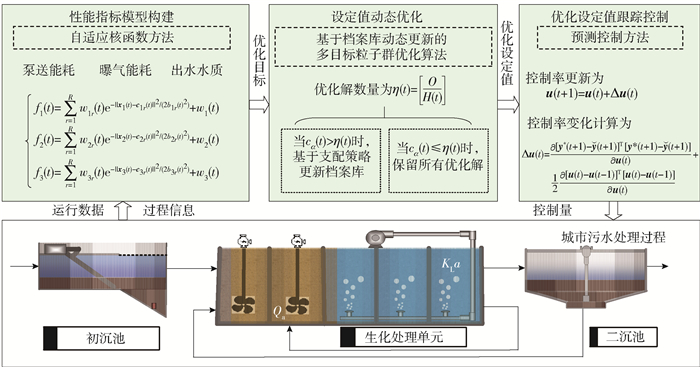
OC-DDMOPSO策略通过优化构建的性能指标模型获取控制变量优化设定值，实现城市污水处理过程的优化运行. OC-DDMOPSO策略主要包含3个部分：动态性能指标模型构建、控制变量设定值动态优化和控制变量优化设定值跟踪控制.
2.1 动态性能指标模型构建
城市污水处理过程的主要操作目标是保证出水水质达到排放标准的同时尽最大可能降低操作成本. 为了实现城市污水处理过程操作目标的动态优化，首先要准确获取操作过程相关性能指标动态特性. 城市污水处理过程关键性能指标包括泵送能耗(pumping energy, PE)EPE、曝气能耗(aeration energy, AE)EAE和出水水质(effluent quality, EQ)ρEQ. EPE主要指由内回流量、外回流量等引起的能耗；EAE主要是由不同分区氧传递系数引起的能耗；ρEQ主要指向受纳水体中排放的污染物的质量浓度之和. 通过机理特性获取影响性能指标的变量，影响EPE的变量主要有入水流量(influent quality, IQ) Qin、硝态氮(nitrate nitrogen, NN)质量浓度ρNN、混合悬浮物固体(mixed liquor suspended solids, MLSS)质量浓度ρMLSS；影响EAE的变量主要有Qin、溶解氧(dissolved oxygen, DO)质量浓度ρDO、ρNN；影响ρEQ的变量主要有Qin、ρDO、ρNN、氨氮(ammonia nitrogen, AN) 质量浓度ρAN和ρMLSS. 基于自适应核函数建立出水水质指标与主要变量之间的关系模型，其表达式为
$$ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{PE}}}}(t) = {f_1}\left( {{Q_{{\rm{in}}}}(t),{\rho _{{\rm{NN}}}}(t),{\rho _{{\rm{MLSS}}}}(t)} \right)}\\ {{E_{{\rm{AE}}}}(t) = {f_2}\left( {{Q_{{\rm{in}}}}(t),{\rho _{{\rm{DO}}}}(t),{\rho _{{\rm{NN}}}}(t)} \right)}\\ {{\rho _{{\rm{EQ}}}}(t) = {f_3}\left( {{Q_{{\rm{in}}}}(t),{\rho _{{\rm{DO}}}}(t),{\rho _{{\rm{NN}}}}(t),{\rho _{{\rm{AN}}}}(t),{\rho _{{\rm{MISS}}}}(t)} \right)} \end{array}} \right. $$ (1) 式中：f1(·)为t时刻PE模型表达式；f2(·)为t时刻AE模型表达式；f3(·)为t时刻EQ模型表达式. 具体可表示为
$$ \left\{ {\begin{array}{*{20}{l}} {{f_1}(t) = \sum\limits_{r = 1}^R {{w_{1r}}} (t) \times {{\rm{e}}^{ - {{\left\| {{x_1}(t) - {c_{1r}}(t)} \right\|}^2}/\left( {2{b_{1r}}{{(t)}^2}} \right)}} + {w_1}(t)}\\ {{f_2}(t) = \sum\limits_{r = 1}^R {{w_{2r}}} (t) \times {{\rm{e}}^{ - \left\| {{x_2}(t) - {c_{2r}}(t)} \right\|2/\left( {2{b_{2r}}{{(t)}^2}} \right)}} + {w_2}(t)}\\ {{f_3}(t) = \sum\limits_{r = 1}^R {{w_{3r}}} (t) \times {{\rm{e}}^{ - {{\left\| {{x_3}(t) - {c_{3r}}(t)} \right\|}^{2/\left( {2{b_{3r}}{{(t)}^2}} \right)}}}} + {w_3}(t)} \end{array}} \right. $$ (2) 式中：x1(t)为PE模型输入，x1(t)=[Qin(t), ρNN(t), ρMLSS(t)]；x2(t)为AE模型输入，x2(t)=[Qin(t), ρNN(t), ρDO(t)]；x3(t)为EQ模型输入，x3(t)=[Qin(t), ρDO(t), ρNN(t), ρAN(t), ρMLSS(t)]；c1r(t)、c2r(t)和c3r(t)分别为PE、AE和EQ模型在t时刻第r个核函数的中心；b1r(t)、b2r(t)和b3r(t)分别为PE、AE和EQ模型在t时刻第r个核函数的宽度；w1r(t)、w2r(t)和w3r(t)分别为PE、AE和EQ模型在t时刻第r个核函数的连接权值；r=1，2，…，R，R为核函数的个数.
基于自适应核函数的PE、AE和EQ模型能够建立性能指标与过程变量的关系，完成对城市污水处理过程动态特性的准确描述. 此外，为了进一步提高性能指标模型的有效性，计算模型实际输出与预测输出之间的误差，采用自适应二阶L-M算法对性能指标模型参数进行实时校正，其更新过程可描述为
$$ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(t + 1) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(t) + {(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}(t) + \lambda (t) \times \mathit{\boldsymbol{I}})^{ - 1}} \times \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}(t) $$ (3) 式中：Φ(t)为包含所有核函数模型的参数；Ψ(t)为拟海瑟矩阵；Ω(t)为梯度向量；I为单位矩阵；λ(t)为自适应学习率，其更新过程为
$$ {\lambda (t) = \mu (t)\lambda (t - 1)} $$ (4) $$ {\mu (t) = \frac{{{\tau ^{\min }}(t) + \lambda (t - 1)}}{{{\tau ^{\max }}(t) + 1}}} $$ (5) 式中：τmax(t)和τmin(t)分别为Ψ1(t)的最大和最小特征值；0 < τmin(t) < τmax(t)，0 < λ(t) < 1.
2.2 控制变量设定值动态优化
有效地控制变量优化设定值能够保证城市污水处理过程的稳定运行，改善系统性能. 为了获取控制变量优化设定值，文中设计了基于档案库动态分解的多目标粒子群优化算法.
基于已建立的出水水质性能指标模型设计优化目标，其优化目标函数可表示为
$$ {F(t) = \min {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{l_1}(t),{l_2}(t),{l_3}(t)} \right\}} $$ (6) 式中
$$ {\left\{ {\begin{array}{*{20}{l}} {{l_1}(t) = {E_{{\rm{PE}}}}\left( {{\rho _{{\rm{NN}}}}(t)} \right)}\\ {{l_2}(t) = {E_{{\rm{AE}}}}\left( {{\rho _{{\rm{DO}}}}(t),{\rho _{{\rm{NN}}}}(t)} \right)}\\ {{l_3}(t) = {\rho _{{\rm{EQ}}}}\left( {{\rho _{{\rm{DO}}}}(t),{\rho _{{\rm{NN}}}}(t)} \right)} \end{array}} \right.} $$ (7) 利用基于档案库动态分解的多目标粒子群优化算法对优化目标进行优化. 为了保证更新过程中优化解信息的有效性，设计了一种动态分解的档案库更新策略. 在更新过程中，计算新产生的优化解与参考方向向量的夹角，将夹角最小的方向向量所对应的子空间作为归属空间，对所有的优化解进行归属分配，对任意一个子空间α，其包含的优化解集可表示为
$$ \begin{array}{c} {c_\alpha }(t) = \left\{ {{s_i}(t)\mid \left\langle {\lambda \left( {{s_i}(t)} \right),{\mathit{\boldsymbol{v}}_\alpha }} \right\rangle \le \left\langle {\lambda \left( {{s_i}(t)} \right),{\mathit{\boldsymbol{v}}_j}} \right\rangle } \right.,\\ \left. {{s_i}(t) \in S(t),i = 1,2, \cdots ,|S(t)|} \right\} \end{array} $$ (8) 式中：cα(t)为优化解集；si(t)为优化解；vα为子空间α的方向向量；vj为任意方向向量，j=1, 2, …, J. 其中，j≠α，S(t)为更新之前外部档案中的优化解集.
为了减少档案库中由于优化解聚集程度不同导致的搜索能力差的问题，设计一种空间优化解筛选策略，定义每个子空间优化解的数量上限
$$ \eta (t) = \left\lfloor {\frac{O}{{H(t)}}} \right\rfloor $$ (9) 式中：O为档案库优化解数量的设定值；H(t)为第t次迭代时包含优化解的子空间数量. 当H(t)较小时，应保留足够多的优化解以保证粒子在目标空间上的探索能力；当H(t)逐渐变大时，应保留收敛性较好的优化解来加速算法的收敛. 因此，子空间内优化解选择策略可设计为：
1) 当cα(t)>η(t)时，通过Pareto支配策略判断子空间中解的支配能力，获取非支配解，更新后的子空间优化解集为c′α(t). 若c′α(t)>η(t)，则比较c′α(t)中优化解的位置向量与给定方向向量的夹角大小，保留具有最小夹角的非支配解；若c′α(t)≤η(t)，则保留子空间解集中所有的优化解.
2) 当cα(t)≤η(t)时，保留子空间中所有的优化解，增强算法在子空间中的搜索能力.
最后，合并所有子空间中的优化解集，保存到档案库中. 基于上述子空间分配策略和优化解选择策略以及出水水质中能耗最小准则(ρNH和ρSS达标时能耗最小)选择一组最优解gBest
$$ {g_{{\rm{Best }}}} = \left[ {\rho _{{\rm{DO}}}^*,\rho _{{\rm{NN}}}^*} \right] $$ 实现性能指标PE、AE和EQ间的平衡.
2.3 控制变量设定值跟踪控制
为了实现对控制变量优化设定值ρDO*和ρNN*的快速准确跟踪控制，设计一种模型预测控制方法，实现对优化设定值的准确跟踪. 在模型预测控制方法中，其控制率更新方式可表示为
$$ \mathit{\boldsymbol{u}}(t + 1) = \mathit{\boldsymbol{u}}(t) + \Delta \mathit{\boldsymbol{u}}(t) $$ (10) 式中：u(t+1)为t+1时刻控制率；Δu(t)为控制率变化量，Δu(t)=[Δu1(t), Δu2(t)]T，Δu1(t)为氧传递系数KLa的变化量，Δu2(t)为内回流Qa的变化量，Δu1(t)=[Δu1(t), Δu1(t+1), …, Δu1(t+Hu-1)]，Hu为控制时域，其计算过程为
$$ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{u}}(t) = }\\ {\frac{{\partial {{\left[ {{\mathit{\boldsymbol{y}}^*}(t + 1) - \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}(t + 1)} \right]}^{\rm{T}}}\left[ {{\mathit{\boldsymbol{y}}^*}(t + 1) - \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}(t + 1)} \right]}}{{\partial \mathit{\boldsymbol{u}}(t)}} + }\\ {\frac{1}{2}\frac{{\partial {{[\mathit{\boldsymbol{u}}(t) - \mathit{\boldsymbol{u}}(t - 1)]}^{\rm{T}}}[\mathit{\boldsymbol{u}}(t) - \mathit{\boldsymbol{u}}(t - 1)]}}{{\partial \mathit{\boldsymbol{u}}(t)}}} \end{array} $$ (11) 式中：y*(t+1)=[y1*(t+1), y2*(t+1)]T=[ρDO*(t+1), ρNN*(t+1)]T；$ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}(t + 1) = [{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}}_1}(t + 1),{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}}_2}(t + 1)]$，$ {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}}_1}(t + 1) = [{y_1}(t),{y_1}(t + 1), \cdots ,{y_1}(t + {H_p})]$，Hp为预测时域，${{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}}_1}(t + 1) $为预测的(t+1)时刻的控制变量ρDO，$ {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over y} }}}_2}(t + 1)$为预测的(t+1)时刻的控制变量ρNN，其预测结果是通过模糊神经网络实现的. 根据式(10)(11)，可实现对ρDO*和ρNN*的跟踪控制.
城市污水处理过程优化控制架构见图 1.
![]()
图 1 城市污水处理过程优化控制架构Figure 1. Scheme of the optimal control for municipal wastewater treatment process3. 实验结果及分析
为了验证所提出的OC-DDMOPSO方法的有效性，将该方法应用于基准仿真平台BSM1进行测试应用. 通过平均泵送能耗EPE、平均曝气能耗EAE和平均出水水质值ρEQ及控制指标绝对误差积分(integral of absolute error，IAE)IAE验证所提出的模型预测控制方法的性能.
$$ {I_{{\rm{AE}}}} = \sum\limits_{b = 1}^2 {\int_{{t_0}}^{{t_{\rm{f}}}} {\left| {y_b^\prime (t) - {y_b}(t)} \right|} } {\rm{d}}t $$ (12) 式中：y′1(t)和y′2(t)分别为t时刻ρDO和ρNN的优化设定值；y1(t)和y2(t)分别为t时刻ρDO和ρNN的控制输出值；t0为积分下限，t0=0；tf为积分上限，tf=14.
3.1 实验参数设置
将设计的OC-DDMOPSO方法应用于基准仿真平台BSM1晴天天气下进行验证，总体优化时间为14d，性能指标优化周期为2h. 核函数的个数R为10，核函数的初始中心、宽度、权值随机给定；档案库中S(t)的最大容量设置为100，方向向量个数为100. 预测控制策略预测时域Hp=5，控制时域Hu=1. 为了验证方法的有效性，将所提出的OC-DDMOPSO方法与动态多目标优化控制策略DMOOC[4]、实时优化控制策略RTOC[18]和基于自适应多目标差分进化的优化控制策略AMODE-OC[20]进行对比，证明所提出的方法能够改善城市污水处理过程性能.
3.2 实验结果及分析
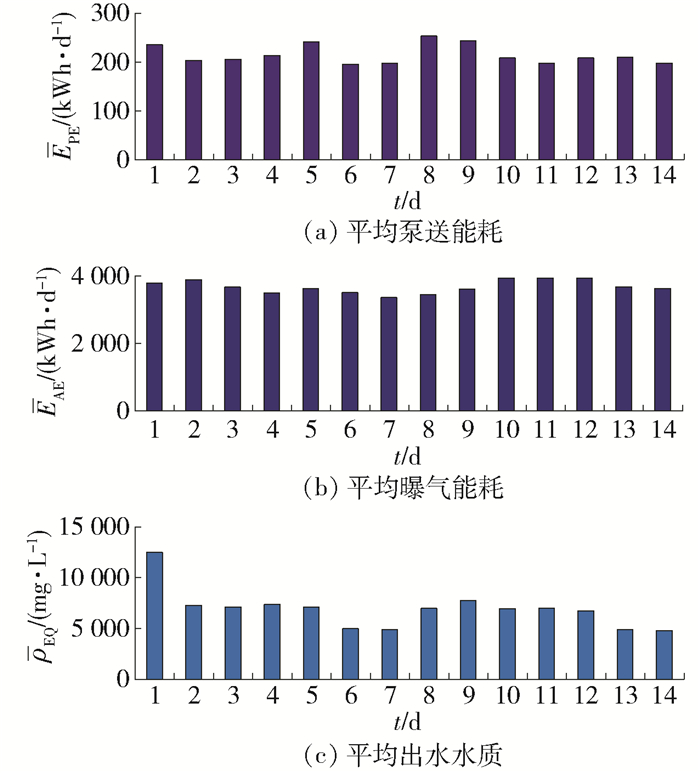
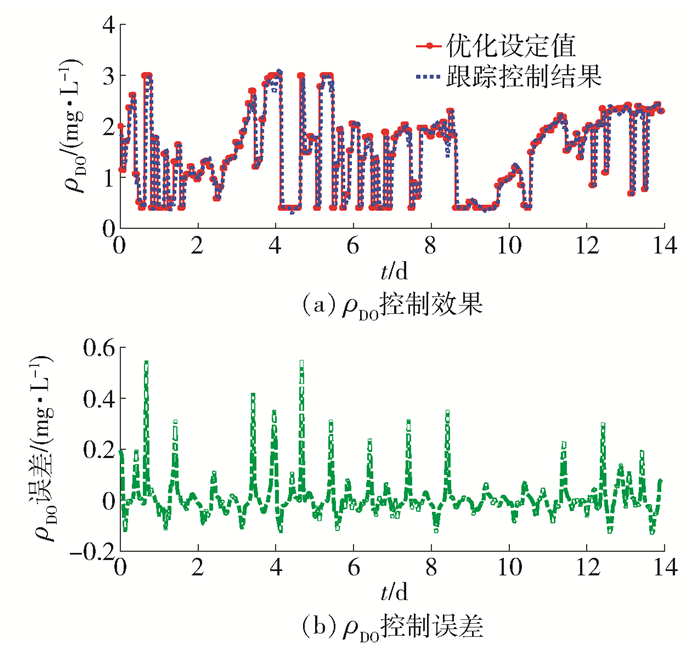
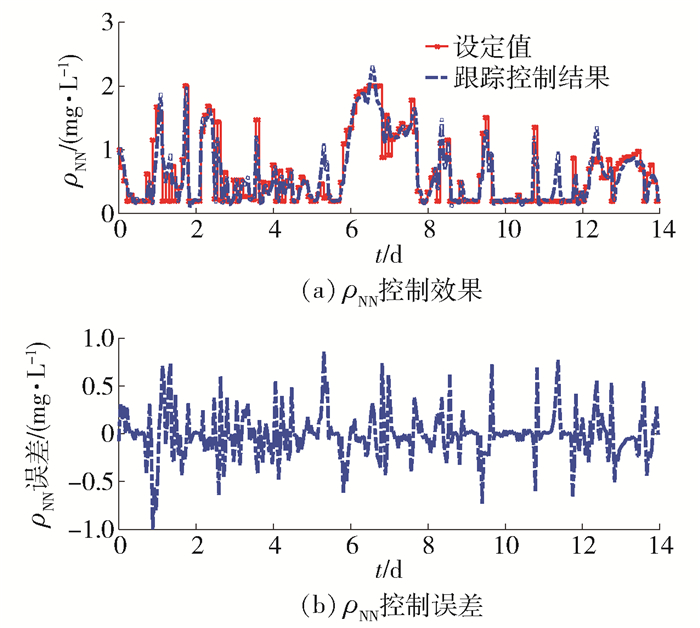
基于OC-DDMOPSO所获得的优化控制结果如图 2~4所示. 图 2给出了平均性能指标值EPE、EAE和ρEQ，图 3、4分别给出了控制变量ρDO和ρNN的优化设定值、优化设定值跟踪效果以及跟踪控制误差.
图 2给出了基于OC-DDMOPSO策略获得的EPE、EAE和ρEQ. 从图中可以看出，EPE、EAE和ρEQ值会根据反应过程进行动态调整. 为了突出所设计的基于OC-DDMOPSO算法的优势，将其与其他优化控制算法进行对比，对比结果如表 1所示. 从表中可以看出，所设计的OC-DDMOPSO算法能够获得最小的EPE和ρEQ值，有效平衡多个指标间的关系，具有较好的优化效果.
表 1 不同优化控制方法性能指标对比Table 1. Comparison of the performance indices with different optimal control strategies图 3、4分别给出了ρDO和ρNN的跟踪控制效果. 从图中可以看出，所设计的OC-DDMOPSO策略能够实现对动态优化设定值的准确跟踪控制，ρDO控制误差可以保持在[-0.2, 0.6]mg/L，同时，ρNN控制误差可以维持在[-1.0, 1.0]mg/L，其结果再次验证了所设计的OC-DDMOPSO策略能够实现对动态控制变量的高精度跟踪控制. 具体的跟踪控制对比结果如表 2所示，其中，OC-DDMOPSO策略的IAE为0.084，低于其他对比的优化控制方法，其出水平均氨氮ρAN和出水平均总氮ρTN分别为3.12、12.49mg/L，均小于其他优化控制算法. 表 2中的结果再次验证了所提出的优化控制算法的性能.
表 2 不同优化控制方法控制性能比较Table 2. Comparison of control performance of different optimal control methods4. 结论与展望
1) 针对城市污水处理过程动态优化设定值难以实时获取的问题，本文提出了一种基于动态分解多目标粒子群优化算法的优化控制策略. 在该策略中，通过自适应核函数建立城市污水处理过程性能指标优化模型，利用基于档案库动态分解的多目标粒子群优化算法获取优化设定值. 结果表明，所提出的OC-DDMOPSO策略能够提高污水处理过程运行性能，降低操作能耗，改善出水水质.
2) 提出的OC-DDMOPSO策略能够取得较好的运行效果，但是由于城市污水处理过程是一个具有多时间尺度操作特点的过程，其性能指标模型具有多时间尺度特点，如何根据不同操作时间的性能指标模型设计多时间尺度优化控制策略仍然是未来需要解决的难题.
-
![]()
图 1 城市污水处理过程优化控制架构
Figure 1. Scheme of the optimal control for municipal wastewater treatment process
表 1 不同优化控制方法性能指标对比
Table 1 Comparison of the performance indices with different optimal control strategies
下载: 导出CSV
-
[1] HAN H G, QIAO J F. Nonlinear model-predictive control for industrial processes: an application to wastewater treatment process[J]. IEEE Transactions on Industrial Electronics, 2013, 61(4): 1970-1982.
[2] 乔俊飞, 鞠岩, 韩红桂. 基于自组织随机权神经网络的BOD软测量[J]. 北京工业大学学报, 2016, 42(10): 1451-1460. doi: 10.11936/bjutxb2016040021 QIAO J F, JU Y, HAN H G. BOD Soft-sensing based on SONNRW[J]. Journal of Beijing University of Technology, 2016, 42(10): 1451-1460. (in Chinese) doi: 10.11936/bjutxb2016040021
[3] 韩红桂, 伍小龙, 张璐, 等. 城市污水处理过程异常工况识别和抑制研究[J]. 自动化学报, 2018, 44(11): 1971-1984. HAN H G, WU X L, ZHANG L, et al. Identification and suppression of abnormal conditions in municipal wastewater treatment process[J]. Acta Automatica Sinica, 2018, 44(11): 1971-1984. (in Chinese)
[4] QIAO J F, ZHANG W. Dynamic multi-objective optimization control for wastewater treatment process[J]. Neural Computing and Applications, 2018, 29(11): 1261-1271. doi: 10.1007/s00521-016-2642-8
[5] VAN STADEN A J, ZHANG J F, XIA X H. A model predictive control strategy for load shifting in a water pumping scheme with maximum demand charges[J]. Applied Energy, 2011, 88(12): 4785-4794. doi: 10.1016/j.apenergy.2011.06.054
[6] ASHRAFI O, YERUSHALMI L, HAGHIGHAT F. Greenhouse gas emission and energy consumption in wastewater treatment plants: impact of operating parameters[J]. Clean-Soil, Air, Water, 2014, 42(3): 207-220. doi: 10.1002/clen.201200158
[7] ZHAO L J, CHAI T Y, YUAN D C. Selective ensemble extreme learning machine modeling of effluent quality in wastewater treatment plants[J]. International Journal of Automation and Computing, 2012, 9(6): 627-633. doi: 10.1007/s11633-012-0688-3
[8] FLORES-ALSINA X, ARNELL M, AMERLINCK Y, et al. Balancing effluent quality, economic cost and greenhouse gas emissions during the evaluation of (plant-wide) control/operational strategies in WWTPs[J]. Science of the Total Environment, 2014, 466/467: 616-624. doi: 10.1016/j.scitotenv.2013.07.046
[9] AMAND L, CARLSSON B. Optimal aeration control in a nitrifying activated sludge process[J]. Water Research, 2012, 46(7): 2101-2110. doi: 10.1016/j.watres.2012.01.023
[10] ZHAN J X, IKEHATA M, MAYUZUMI M, et al. An aeration control strategy for oxidation ditch processes based on online oxygen requirement estimation[J]. Water Science and Technology: a Journal of the International Association on Water Pollution Research, 2013, 68(1): 76-82. doi: 10.2166/wst.2013.226
[11] ZENG Y H, ZHANG Z J, KUSIAK A, et al. Optimizing wastewater pumping system with data-driven models and a greedy electromagnetism-like algorithm[J]. Stochastic Environmental Research and Risk Assessment, 2016, 30(4): 1263-1275. doi: 10.1007/s00477-015-1115-4
[12] HUANG X Q, HAN H G, QIAO J F. Energy consumption model for wastewater treatment process control[J]. Water Science and Technology, 2013, 67(3): 667-674. doi: 10.2166/wst.2012.563
[13] DURRENMATT D J. Data mining and data-driven modeling approaches to support wastewater treatment plant operation[J]. Environmental Modelling & Software, 2011, 30(5): 47-56.
[14] YANG Y, YANG J, ZUO J, et al. Study on two operating conditions of a full-scale oxidation ditch for optimization of energy consumption and effluent quality by using CFD model[J]. Water Research, 2011, 45(11): 3439-3452. doi: 10.1016/j.watres.2011.04.007
[15] 乔俊飞, 王亚清, 柴伟. 基于迭代ADP算法的污水处理过程最优控制[J]. 北京工业大学学报, 2018, 44(2): 200-206. doi: 10.11936/bjutxb2017030032 QIAO J F, WANG Y Q, CHAI W. Optimal control based on iterative ADP for wastewater treatment process[J]. Journal of Beijing University of Technology, 2018, 44(2): 200-206. (in Chinese) doi: 10.11936/bjutxb2017030032
[16] DUZINKIEWICZ K, BRDYS M A, KUREK W, et al. Genetic hybrid predictive controller for optimized dissolved-oxygen tracking at lower control level[J]. IEEE Transactions on Control Systems Technology, 2009, 17(5): 1183-1192. doi: 10.1109/TCST.2008.2004499
[17] GUERRERO J, GUISASOLA A, VILANOVA R, et al. Improving the performance of a WWTP control system by model-based setpoint optimisation[J]. Environmental Modelling & Software, 2011, 26(4): 492-497.
[18] SWEETAPPLE C, FU G, BUTLER D. Multi-objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions[J]. Water Research, 2014, 55: 52-62. doi: 10.1016/j.watres.2014.02.018
[19] ARAUJO C B, GALLANI S, MULAS M, et al. Sensitivity analysis of optimal operation of an activated sludge process model for economic controlled variable selection[J]. Industrial & Engineering Chemistry Research, 2013, 52(29): 9908-9921.
[20] QIAO J F, HOU Y, HAN H G. Optimal control for wastewater treatment process based on an adaptive multi-objective differential evolution algorithm[J]. Neural Computing and Applications, 2019, 31(7): 2537-2550. doi: 10.1007/s00521-017-3212-4
-
期刊类型引用(9)
1. 李志峰，熊伟丽. 基于多目标麻雀算法的污水处理过程优化控制. 控制工程. 2025(01): 76-85 . 
百度学术
2. 王鼎，李鑫. 迁移增量启发式动态规划及污水处理应用. 北京工业大学学报. 2025(03): 277-283 . 本站查看
3. 邢萍，郭晶. 集成式全分布工业污水处理自动控制模型构建研究. 环境科学与管理. 2025(04): 115-119 . 百度学术
4. 李华. 基于多粒子群协同的环境污染传感监测点布置优化研究. 环境科学与管理. 2024(01): 104-109 . 百度学术
5. 韩红桂，赵雅倩，杨宏燕，伍小龙. 数据驱动的污水处理曝气过程低碳优化控制方法. 北京工业大学学报. 2024(02): 131-139 . 本站查看
6. 王勇，苏晓亮，刘佳，焦峰，季子禾. 基于AI的污水处理监控与自动调节技术. 中国新技术新产品. 2024(13): 115-117+127 . 百度学术
7. 吴桐，于广平，袁德成，刘坚，李健，孙宏存. 基于案例推理的曝气过程智能控制方法. 控制工程. 2023(11): 2041-2047 . 百度学术
8. 杨军，闫德鑫. 基于Copt-aiNet的污水处理过程控制优化研究. 现代工业经济和信息化. 2022(04): 94-96 . 百度学术
9. 崔心惠，李文萱，朱山川，张祝威. 多目标海洋捕食者算法的污水处理优化控制. 宜宾学院学报. 2022(06): 13-21+66 . 百度学术
其他类型引用(11)
计量
- 文章访问数: 162
- HTML全文浏览量: 5
- PDF下载量: 41
- 被引次数: 20
