Flexible Bus Route Optimal Scheduling Model in Response to Dynamic Demand
-
摘要:
为解决灵活公交乘客需求差异性大、实时变化性大的问题,提出一种考虑乘客动态需求的灵活公交路径优化调度模型.在已知乘客预约需求量、车辆载客容量、车队规模等条件下,根据乘客需求动态变化特征对接驳行程时间进行实时迭代更新,将车辆的运营成本(车辆行驶时间)和乘客的时间成本(乘客上车前等待车辆的时间、实际到达时间与期望到达时间之间的差值)最小化作为目标,构建了考虑乘客动态需求的灵活型公交路径优化调度模型,并采用基于引力模型的启发式算法进行求解.最后,通过实例分析验证了模型和算法的可行性.结果表明:对随机产生的15个需求点的102个出行需求,全部服务完成所需车辆为17~21辆,平均每辆车的旅行时间为24.59 min,100组数据的求解时间均在25.00 s以内,计算耗时平均为12.04 s.可见该优化模型能够在实时调整接驳规划时间的前提下,更大程度满足乘客动态需求,有效减小规划路径的误差,缩短行车距离和乘客出行时间,相比忽略接驳行程时间变化的灵活公交调度模型结果更优.
Abstract:To solve the problem that the demand of flexible bus passengers varies significantly and the demand of flexible bus passengers varies significantly in real time, a flexible bus route optimization scheduling model considering the dynamic demand of passengers was proposed. Under the conditions of known passenger reservation demand, vehicle passenger capacity and the team known condition such as size, according to the dynamic changes of passenger demand for real-time iterative update shuttle travel time, the operating costs of the vehicle (vehicle) and time cost for passengers before (the passengers waiting time of the vehicle, the actual time of arrival and the difference in value between expected time of arrival) minimization as the target, was established considering the passenger dynamic demand type flexible bus route optimization scheduling model, and USES the heuristic algorithm based on gravity model. Finally, the feasibility of the model and algorithm was verified by an example. The analysis results show that for the 102 travel demands of 15 randomly generated demand points, the number of vehicles needed to complete all the services is 17-21, the average travel time of each vehicle is 24.59 minutes, the solution time of 100 sets of data is all within 25.00 seconds, and the average calculation time is 12.04 seconds. It can be seen that under the premise of real-time adjustment of connection planning time, this optimization model can satisfy the dynamic demand of passengers to a greater extent, effectively reduce the error of the planning path, shorten the driving distance and passenger travel time, and achieve better results than the flexible bus scheduling model that ignores the change of connection travel time.
-
Keywords:
- traffic engineering /
- urban traffic /
- route optimization /
- heuristic algorithms /
- flexible bus /
- dynamic demand
-
城市公交线路优化调度是提高公交运行效率、降低乘客出行和公交运营成本的主要手段. 一个好的公交调度系统能够根据乘客的出行需求,快速优化调整线路运营方案,提高线路服务率,减少运行时间,降低乘客出行时间成本[1-3]. 传统公交路径优化方法主要是通过长期的经验观察或IC卡数据统计分析,对部分线路进行延长、缩短、增删、调整走向等优化,优先满足大客流站点的乘客需求,这类方法主要适用于固定线路的公交路径优化,线路调整周期较长[4-7]. 灵活型公交的出现,为线路的动态优化调整提供了可能[7-10],目前国内外学者均开展了相关研究. 其中,Quadrifoglio等[11-12]通过对灵活公交系统关键参数的分析,建立了公交系统运行效率参数优化调整模型,并针对其前期建立的系统线路设计和调度问题,进行了仿真验证分析,对模型进行了参数修正. 付晓等[13]利用超级网络同时模拟用户的活动与出行行为,并根据用户出行行为特征建立了公交路径选择模型. Koffman[14]提出了基于多目标需求的城市公交智能调度算法;Tsubouchi[15]提出了利用最小生成树寻优公交路径最优算法;熊杰[16]通过对区域内潜在公交用户需求的分析,建立了接驳轨道交通的公交线路优化模型;Li等[17]、Chen等[18]通过对乘客预期等待时间和线路上客概率的推导,建立了超路径的公交运输路径调整模型;潘述亮[19]重点考虑了长时预约对灵活公交线路调整的影响,并提出了优化调度方法;郭晓俊[20]重点考虑了短时预约对灵活公交线路调整的影响,并提出了优化调度方法. 这些研究虽然都是根据乘客的预约需求建立的灵活型公交路径优化算法,但其前提条件均是乘客需提前发出预约或假设乘客需求已知,相对即时预约来说均属于“静态需求”. 然而,在乘客出行过程中,往往会根据出行需要发出短时预约或即时预约,灵活型公交需要根据乘客的“动态需求”,计算因动态需求变化导致的车辆接驳行程时间变化,即时调整线路实现路径的动态优化.
鉴于此,考虑到乘客需求的动态变化以及由于需求变化导致的车辆接驳行程时间变化,本文提出了一种基于乘客动态需求的灵活公交路径优化调度方法. 在已知车辆载客容量、车队规模等条件下,根据乘客需求动态变化特征对接驳行程时间实时迭代更新,将车辆运营成本和乘客出行成本最小化作为主要目标,建立了考虑乘客动态需求的灵活型公交路径优化调度模型.
1. 问题描述与建模
1.1 问题描述
在传统的固定型接驳公交运营中,公交线路规划设计与车辆运营调度是2个独立的过程,一般在线路规划设计完成之后制定车辆运营调度方案,调度方案在相当长一段时间内不发生变化. 这就造成了线路设计和车辆调度之间脱节,两者不能有效衔接的问题,且线路设计和车辆调度无法根据乘客需求进行及时调整. 但高效的接驳公交系统,应能够根据乘客的实际需求及时调整运营线路,并根据线路和乘客需求实时动态调整车辆调度方案.
灵活型公交是一种以需求为基础的交通系统,它能根据乘客发出的需求,以最短路线服务最多乘客为目标,动态调整运营线路,并在线路调整同时,融合分析沿线乘客需求数量、车辆载客容量等因素,实时调整车辆调度方案,最大程度地满足更多乘客需求,解决传统固定型接驳公交的乘客需求与线路规划、车辆调度脱节的问题.
本文提出的响应动态需求的灵活公交路径优化调度模型,将乘客即时需求作为公交路径动态优化调整的依据之一,根据乘客出行需求点位、需求量和需求时间,对公交路径和行车方案进行实时优化和调度. 为使得本文所建立的模型更合理、得当,本文综合考虑乘客需求、运营成本等各方面的因素,进行如下灵活型公交路径优化模型假设、参数选取和建模.
1.2 模型假设
对灵活型公交路径优化模型的建立提出如下假设,其中1)、2)为动态假设,3)~6)为静态假设.
1) 每个站点的乘客预约需求量动态变化.
2) 车辆站点之间的行程时间动态变化.
3) 每个站点的位置均已知.
4) 预约后,每个乘客拟到达目标站点的时间已知.
5) 乘客到站上车的服务时间为常数.
6) 接驳车辆的载客容量已知.
1.3 模型参数
按照上述模型假设,对各模型变量进行定义,如表 1所示.
表 1 模型参数Table 1. Medol parameter变量 定义及说明 参数类型 Z 优化路径的总时间成本 因变量 H 乘客需求站点集合 常量 D 目标站点集合 常量 K 接驳运营车辆集合 常量 R 乘客需求集合 常量 dr 乘客需求r的目标站点d 决策变量 Tt 目标站的第t个发车时刻 决策变量 N 乘客需求总量 决策变量 pr 乘客需求r的上车站点p 决策变量 Tr 乘客需求r的期望发车时刻 决策变量 cij 站点i和j之间的旅行时间 决策变量 V 接驳车队规模 决策变量 Qk 接驳车辆k的载客容量 决策变量 M 足够大的一个常数 常量 Xrkt t时刻时车辆k将需求r接驳至乘客期望的站点,Xrkt为1;否则为0 决策变量 Yijk 车辆k选择(i, j)路段作为途经路径时,Yijk为1;否则为0 决策变量 ar 车辆行驶至需求r所在公交站点的时间 决策变量 er 乘客需求r到达目标站的时间 决策变量 as 车辆行驶至需求s所在站点的时间 决策变量 Uik 决定车辆k的运行线路不出现闭环的变量. 如果接驳车辆离开站点i,则Uik=0;如果接驳车辆到达站点i,则Uik=1 辅助变量 Ujk 决定车辆k的运行线路不出现闭环的变量. 如果接驳车辆离开站点j,则Ujk=0;如果接驳车辆到达站点j,则Ujk=1 辅助变量 1.4 模型表述
按照上述模型假设和变量设置情况,采用非线性规划形式对灵活型公交路径优化模型进行表述,即
$$ \begin{array}{*{20}{c}} {Z = \min \left[ {\sum\limits_{i \in H \cup D} {\sum\limits_{H \cup D} {\sum\limits_{k \in K} {{c_{ij}}} } } {Y_{ijk}} + \sum\limits_{r \in R} {{a_r}} + } \right.}\\ {\left. {\sum\limits_{r \in R} {\sum\limits_{k \in K} {\sum\limits_t {\left( {{X_{rkt}}{T_t} - {e_r}} \right)} } } } \right]} \end{array} $$ (1) 式(1)为灵活型公交路径优化模型表述的目标方程,由3个部分之和组成,取其最小化值:1)所有车辆的行驶时间,以降低运营成本;2) 每个乘客在需求点等候车辆抵达的时间之和,以减少乘客的总出行时间;3) 每个乘客等待车辆的实际到达时间与期望到达时间的差值之和,以减少乘客的总出行时间.
$$ {\sum\limits_{j \in H \cup D} {\sum\limits_{k \in K} {{Y_{ijk}}} } \ge 1,\forall i \in H} $$ (2) $$ {\sum\limits_{j \in H \cup D} {\sum\limits_{k \in K} {{Y_{ijk}}} } \le V,\forall i \in H} $$ (3) 约束式(2)(3)表示在任意一个乘客需求点,保证车辆进行服务,且车辆数在1与V之间.
$$ \sum\limits_{i \in H} {\sum\limits_{k \in K} {{Y_{ijk}}} } \le V,\forall j \in D $$ (4) 约束式(4)表示参与服务的车辆总数不超过V辆.
$$ \sum\limits_{j \in H \cup D} {{Y_{ijk}}} - \sum\limits_{p \in H} {{Y_{pik}}} \ge 0,\forall i \in H,k \in K $$ (5) 约束式(5)表示对任意一个需求点,任一参与服务的车辆均有到达和离开的过程.
$$ {U_{ik}} - {U_{jk}} + |H| \times {Y_{ijk}} \le |H| - 1,\forall i,j \in H \cup D,k \in K $$ (6) 约束式(6)保证了系统规划路径的单向性,即不能产生往返回路.
$$ \sum\limits_{i \in H} {\sum\limits_{j \in D} {{Y_{ijk}}} } \ge 1,\forall k \in K $$ (7) $$ \sum\limits_{i \in H} {\sum\limits_{j \in D} {{Y_{ijk}}} } \le 0,\forall k \in K $$ (8) 约束式(7)(8)表示参与服务的任意一辆车必须将乘客运送至目标站点.
$$ \sum\limits_{r \in R} {\sum\limits_{t \in T} {{X_{rkt}}} } \le {Q_k},\forall k \in K $$ (9) 约束式(9)保证车辆不能超载运输.
$$ \sum\limits_{k \in K} {\sum\limits_{t \in T} {{X_{rkt}}} } = 1,\forall r \in R $$ (10) 约束式(10)表示乘客发出需求后,只能被一辆车服务,不能同时被多辆车服务.
$$ \begin{array}{*{20}{c}} {\sum\limits_{m \in T/\{ t\} } {{X_{skm}}} - \left( {1 - {X_{rkt}}} \right)M \le 0,\forall r,s \in R,}\\ {\forall k \in K,\forall t \in T} \end{array} $$ (11) 约束式(11)表示一辆接驳车辆在单程接驳运送中,只能服务于一个目标站点的一个发车时刻.
$$ \sum\limits_{r \in R} {\sum\limits_{k \in K} {\sum\limits_{t \in T} {{X_{rkt}}} } } = N $$ (12) 约束式(12)表示所有接驳车辆实际服务的需求数量与预约的需求量相等.
$$ {a_r} + {c_{{p_r}{p_s}}} - {a_s} + {Y_{{p_r}{p_s}k}}M \le M,\forall r,s \in R,\forall k \in K $$ (13) $$ {a_s} - {a_r} - {c_{{p_r}{p_s}}} + {Y_{{p_r}{p_s}k}}M \le M,\forall r,s \in R,\forall k \in K $$ (14) 约束式(13)(14)表示当同一接驳车辆为相邻2个站点提供接驳服务时,后一个站点接受服务的时间应等于前一个站点接受服务的时间与两站点间行程时间之和.
$$ {{a_r} + {c_{{p_r}j}} - {a_s} + {Y_{{p_r}{p_s}k}}M \le M,\forall r \in R,\forall k \in K,\forall j \in D} $$ (15) $$ {{a_s} - {a_r} - {c_{{p_r}j}} + {Y_{{p_r}{p_s}k}}M \le M,\forall r \in R,\forall k \in K,\forall j \in D} $$ (16) 约束式(15)(16)表示接驳车辆到达目标站点的时间等于为最后一个需求点提供服务的时间与需求点与目标站点之间的行程时间之和.
$$ {e_r} \le \sum\limits_{k \in K} {\sum\limits_{t \in T} {{X_{rkt}}} } {T_t},\forall r \in R $$ (17) 约束式(17)表示接驳车辆应在目标站点车辆发车之前抵达目标站点.
2. 模型求解
本文提出的面向多目标站的灵活性公交路径优化调度问题,是一类典型的非确定性多项式问题都能在多项式时间复杂度内归约到的问题(non-deterministic polynomial hard,NP-hard). 在问题规模较大时计算量和复杂程度会急速增加. 因此,为了应对复杂问题的快速高效计算问题,通常采用可同时保证计算速度和计算精度的启发式算法进行求解. 当在一定区域范围内,多个点位同时发出出行需求时,可看作同时存在的多个引力点. 受点位间距离影响,不同点位之间引力大小各有不同,可对应理解为车辆在2个需求点间接驳运送的时间成本各不相同. 因此,为使车辆能够快速在需求最多、距离最小的点位间进行接驳服务,受四阶段出行分布预测的引力模型启发,本文提出一种基于引力模型的启发式算法. 总体思路是:首先基于引力模型生成较优的初始解,再利用路线间和路线内的优化算法分别改进路线,从而得到最终路线. 详细步骤介绍如下.
2.1 乘客出行预约与需求分配
首先,将乘客发出出行预约和进行需求服务分配分为以下4个步骤:
步骤1 乘客按其出行需求,进行预约出行. 每个乘客将其出发站、目标站、期望到达目标站的时间等信息传输到出行预约平台. 考虑到乘客需求和接驳车辆站点之间的行程时间的动态变化特征,预约平台的乘客需求和接驳车辆站点之间的行程时间每5 min进行一次更新.
步骤2 出行预约平台根据每个乘客的目标站和期望到达目标站的时间,按照实际到达时间不晚于乘客期望值的原则,对所有乘客进行聚类.
步骤3 根据2.2、2.3节中路径生成结果,结合接驳车辆到达时间、平均行驶速度、乘客需求点的位置、各需求点乘客数量等因素,初步估算车辆到达的时间.
步骤4 将初步估计的接驳车辆到达各需求点的时间,发送给对应需求点的乘客,乘客根据接驳车辆到达时间的合理性,选择是否确定乘车.
2.2 基于引力模型的生成初始车辆路径解
基于引力模型的计算方法,以起始需求点为已知站点,根据引力模型的原理遍历所有剩余需求点,查找与已知点之间引力最大的点,并将最新搜索到的站点作为新的已知点,继续遍历剩余需求点确定下一个与已知点之间引力最大的点,按此步骤逐步迭代,直到所有需求点均被查找到,从而可以生成可行的初始车辆路径解. 定义两站点间的引力
$$ F_{i j}=\frac{N_{i} N_{j}}{c_{i j}^{2}} $$ (18) 式中:Ni为站点i的上车人数;cij为站点i和站点j之间的车辆行驶时间. Fij的值越大,说明这2个站点的乘客数越多且旅行花费越小,需要优先服务,应该将站点j设为站点i的下一个站点.
在已知车辆载客限定辆Q时,按如下步骤生成初始路径的解:
步骤1 确定车辆出发站点. 初始k=1,从有乘客上车需求的站点中,随机抽取一个作为车辆k的出发点.
步骤2 判断是否还有同类乘客未服务. 若有,则跳至步骤3;否则,跳至步骤5.
步骤3 搜索下一站点. 在包含同类乘客的上车站点中,找出与当前站点之间吸引力最大的站点X,尝试将站点X加入路径选择链,计算车辆在加入该需求点后车上总人数,以及加入该需求点X后直接行驶至目标站点所需的时长.
步骤4 判断加入站点X后,车辆路线是否合理. 若当前车辆服务的乘客数量未超过车载容量Qk,且到达目标站点的时间未超过乘客需求的时间,则以站点X为新的起点,跳至步骤3;否则,跳至步骤5.
步骤5 判断是否所有类别的乘客均被安排服务. 若还有乘客未被安排服务,则调度下一辆车,k=k+1,跳至步骤1;否则,输出当前全部初始解,结束基于引力模型的初始解计算步骤.
2.3 基于站点均衡与交换的车辆路径优化
介绍路线间和路线内的路径优化算法,使得路径质量和乘客服务水平进一步提升. 需要注意的是,算法的步骤1和步骤2均属于车辆路径间的优化,在步骤1和步骤2的路径优化算法执行过程中,可能会搜索出多组可行的路线解. 若在搜索时仅保存当前最优的一组解,再执行步骤3,可能搜索到的最终路线结果并不是最优. 所以,本算法会保存步骤1和步骤2寻找到的所有可行解组,并对每一组可行解执行步骤3,综合评价所有的路线解组的目标函数,以找到最终的最优解.
步骤1 首先对服务于目标站点和到达目标站点时间需求相同的车辆之间进行站点数量均衡. 检查各接驳车辆是否存在服务需求点过多或过少的现象. 如果有,则在确保车辆不超载的条件下,将需经过站点数量较多的车辆路线中的部分站点,转移给经过站点数量较少的车辆路线,并安排合理的站点顺序.
步骤2 尝试对服务于目标站点和到达目标站点时间需求相同的车辆之间进行路径优化. 主要应用两路线间,交换两站点的方式,搜索更优的路线. 在交换优化的过程中,保证车辆不超载和按时到达目标站点的需求.
步骤3 对每一辆车的路线进行内部优化. 主要在同一车辆路线内,尝试交换两站点的顺序,评估目标函数值是否减少. 若减少,则交换站点顺序;否则舍弃本次交换. 在尝试一定次数之后,结束计算流程,生成最终路线结果.
步骤4 考虑到乘客需求的动态变化特征和站点之间旅行时间的变化特征,每5 min进行一次各站点需求的采集和重新计算,重复以上步骤1至步骤3.
经过如上4个步骤,可在保证乘客按照预期时间到达目标站点的前提下,使得路径调度模型的目标函数最优,全部服务时间缩短,每一辆车的路线更加合理,车辆的运行成本降低,乘客的等待时间减少,提升服务质量和效率.
3. 案例分析
3.1 案例假设
北京市回龙观地区是通勤人群居住密集区,高峰时段出行需求量大,不同工作性质和通勤距离的出行者出行时间差异较大,因此适合作为需求响应型灵活公交模型验算的案例. 为了便于模型分析,本文对回龙观区域公交网络进行了抽象化提取,保留网络拓扑结构.
根据实际情况下乘客的出行需求,假设一个乘客出行案例,采用上述模型对案例进行求解,验证本文所提模型的可用性. 小型网络常变量的输入参数如表 2所示,初始时刻每个站点的乘客需求如表 3所示,初始时刻站与站之间的旅行耗时矩阵如表 4所示,其中H为需求点,D为目标站.
表 2 案例中的常变量Table 2. Constant variables in the case变量名称 变量值 需求点数量/个 15 目标站点数量/个 3 车辆额定载客量/人 7 车队规模/辆 18 期望到达站点时间/min 30/40/50 乘客到站上车服务时间/min 0.5 表 3 初始时刻各站点乘客需求(初始5 min)Table 3. Quantity demanded at the demand point (the first 5 minutes)乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 1 1 1 30 31 1 2 30 61 1 3 30 2 1 1 50 32 1 2 50 62 1 3 50 3 1 1 50 33 2 2 30 63 1 3 50 4 2 1 30 34 2 2 50 64 2 3 30 5 2 1 50 35 3 2 30 65 2 3 50 6 3 1 30 36 3 2 40 66 3 3 30 7 3 1 40 37 3 2 50 67 3 3 40 8 4 1 30 38 4 2 30 68 4 3 30 9 5 1 30 39 5 2 30 69 5 3 30 10 5 1 40 40 5 2 40 70 5 3 40 11 5 1 50 41 5 2 50 71 5 3 50 12 5 1 50 42 6 2 30 72 5 3 50 13 6 1 30 43 6 2 40 73 6 3 30 14 6 1 40 44 6 2 50 74 6 3 40 15 7 1 30 45 7 2 30 75 7 3 30 16 7 1 50 46 7 2 50 76 7 3 50 17 7 1 50 47 8 2 30 77 8 3 30 18 8 1 30 48 8 2 40 78 8 3 40 19 8 1 40 49 8 2 50 79 8 3 50 20 9 1 40 50 9 2 40 80 9 3 40 21 10 1 40 51 10 2 40 81 10 3 40 22 10 1 50 52 10 2 50 82 10 3 50 23 11 1 40 53 11 2 40 83 11 3 40 24 11 1 50 54 12 2 30 84 12 3 30 25 12 1 30 55 12 2 50 85 12 3 50 26 12 1 50 56 12 2 50 86 12 3 50 27 13 1 30 57 13 2 30 87 13 3 30 28 14 1 40 58 14 2 40 88 14 3 40 29 14 1 40 59 15 2 40 89 15 3 40 30 15 1 40 60 15 2 40 90 15 3 40 表 4 初始时的乘客行程时间矩阵(初始5 min)Table 4. Case network travel time matrix (the first 5 minutes)H1 H2 H3 H4 H5 H6 H7 H8 H9 H10 H11 H12 H13 H14 H15 D1 D2 D3 H1 0 3 6 5 4 5 8 6 9 9 6 3 3 4 8 3 9 9 H2 7 0 6 9 8 3 5 5 4 7 9 3 3 3 6 3 8 7 H3 9 6 0 6 5 8 8 8 3 7 9 4 5 5 5 9 7 9 H4 4 7 6 0 9 7 8 5 5 7 7 4 5 6 8 9 5 6 H5 5 3 8 8 0 5 7 9 5 6 3 8 6 5 8 9 6 5 H6 8 3 5 9 5 0 5 4 5 9 9 8 7 8 6 9 8 3 H7 9 8 4 5 6 8 0 3 4 8 6 8 8 8 5 6 7 6 H8 5 5 5 7 5 6 6 0 6 4 4 9 5 8 5 8 5 6 H9 3 5 8 5 4 5 5 6 0 7 3 6 8 3 3 6 8 3 H10 5 9 9 5 9 4 5 5 5 0 9 9 4 3 5 6 8 7 H11 5 3 7 6 6 7 8 3 3 4 0 7 4 9 6 3 7 9 H12 5 3 9 9 6 6 7 7 9 5 9 0 7 3 5 5 5 4 H13 7 5 7 9 7 8 7 5 3 7 5 7 0 5 5 6 5 5 H14 9 5 6 5 6 4 8 5 8 9 5 9 9 0 6 8 8 9 H15 6 9 6 4 8 8 3 4 5 3 4 5 9 4 0 7 9 6 3.2 案例计算
根据本文提出的计算模型和方法,对上述假设案例进行计算,获取各接驳车辆的行驶路线、接驳乘客的数量、每条路线对应的目标函数如表 5所示.
表 5 初始时刻车辆的服务路径结果(初始5 min)Table 5. Service path results of vehicles at initial time (the first 5 minutes)车辆编号 车辆路径 服务的乘客数量/个 期望到站时间/min 路径对应的目标函数值 1 5-2-3-12-4-D1 1-1-1-1-1 30 83 2 13-1-7-8-6-D1 1-1-1-1-1 30 92 3 14-3-11-15-10-D1 2-1-1-1-1 40 123 4 8-5-6-9-D1 1-1-1-1 40 109 5 1-2-10-D1 2-1-1 50 156 6 7-11-12-5-D1 2-1-1-2 50 216 7 5-13-6-3-12-7-D2 1-1-1-1-1-1 30 102 8 4-1-8-2-D2 1-1-1-1 30 72 9 6-15-3-9-11-D2 1-2-1-1-1 40 130 10 8-14-10-5-D2 1-1-1-1 40 111 11 7-2-6-1-3-D2 1-1-1-1-1 50 163 12 12-8-10-5-D2 2-1-1-1 50 180 13 5-2-12-7-3-D3 1-1-1-1-1 30 85 14 4-8-6-1-13-D3 1-1-1-1-1 30 86 15 15-10-6-9-14-D3 2-1-1-1-1 40 135 16 3-8-11-5-D3 1-1-1-1 40 113 17 8-10-2-D3 1-1-1 50 125 18 12-5-7-1-D3 2-2-1-2 50 235 之后,随着乘客需求和站点之间旅行时间的动态变化,上述路径规划结果无法满足当前乘客需求和真实状况,需进行新的路径规划. 此时,预约平台将汇总的第一个5 min后新的乘客需求和接驳车辆站点之间的行程时间并进行更新,如表 6所示,再次利用2.2节中所述的方法进行求解.
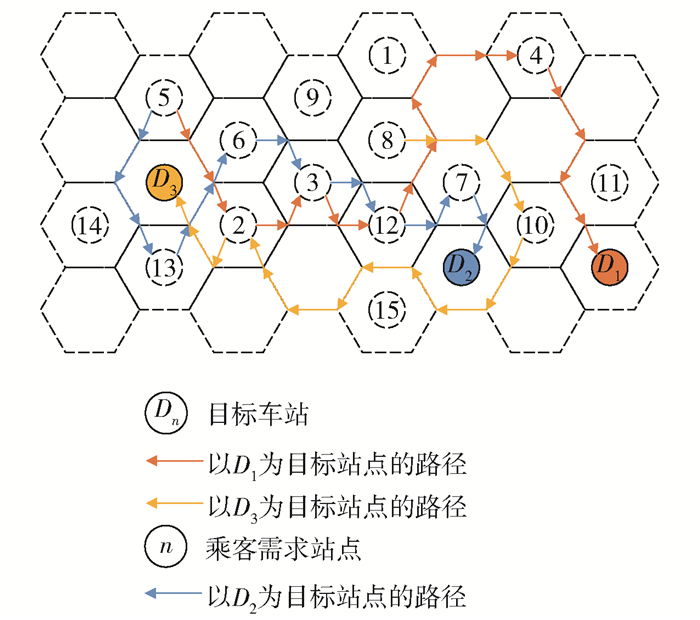
表 6 5 min后各站点乘客需求Table 6. Passenger demand of each station in 5 minutes乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 1 1 1 30 35 1 2 30 69 1 3 50 2 1 1 50 36 1 2 50 70 1 3 50 3 1 1 50 37 2 2 30 71 2 3 30 4 2 1 30 38 2 2 50 72 2 3 40 5 2 1 50 39 2 2 50 73 2 3 50 6 3 1 30 40 3 2 30 74 3 3 30 7 3 1 40 41 3 2 40 75 3 3 40 8 4 1 30 42 3 2 50 76 3 3 50 9 5 1 30 43 4 2 30 77 4 3 30 10 5 1 30 44 5 2 30 78 5 3 30 11 5 1 30 45 5 2 40 79 5 3 40 12 5 1 30 46 5 2 50 80 5 3 50 13 5 1 40 47 6 2 30 81 5 3 50 14 5 1 50 48 6 2 40 82 6 3 30 15 5 1 50 49 6 2 50 83 6 3 40 16 6 1 30 50 7 2 30 84 7 3 30 17 6 1 40 51 7 2 50 85 7 3 50 18 7 1 30 52 8 2 30 86 8 3 30 19 7 1 50 53 8 2 40 87 8 3 40 20 7 1 50 54 8 2 50 88 8 3 50 21 8 1 30 55 9 2 40 89 9 3 40 22 8 1 40 56 10 2 40 90 10 3 40 23 9 1 40 57 10 2 40 91 10 3 50 24 10 1 40 58 10 2 50 92 11 3 40 25 10 1 50 59 11 2 40 93 12 3 30 26 11 1 40 60 12 2 30 94 12 3 50 27 11 1 50 61 12 2 50 95 12 3 50 28 12 1 30 62 12 2 50 96 13 3 30 29 12 1 50 63 13 2 30 97 13 3 30 30 13 1 30 64 14 2 40 98 14 3 40 31 14 1 40 65 15 2 40 99 15 3 40 32 14 1 40 66 15 2 40 100 15 3 40 33 15 1 40 67 1 3 30 101 15 3 40 34 15 1 50 68 1 3 30 102 15 3 40 之后,根据乘客需求和站点之间旅行时间的动态变化信息,预约平台汇总第2个5 min后新的乘客需求,并更新接驳车辆站点之间的行程时间,如表 7所示,再次利用2.2节中所述的方法进行求解. 以此类推,预约平台继续汇总之后每个5 min的乘客需求和更新接驳车辆站点之间的行程时间,并利用2.2节中所述的方法进行求解,直至能满足所有需求站点的所有乘客需求,如表 8所示. 当前假设下,车辆行驶最终路径结果如图 1所示,此时,15个需求站点发出的102个预约需求全部得以满足(为便于识别,分别以D1、D2、D3作为目标站点,给出了5-2-3-12-4-D1、5-13-6-3-12-7-D2、8-10-2-D3三条路径作为示意,并未列举所有路径).
表 7 5 min后案例网络的旅行时间矩阵Table 7. Travel time matrix of case network after 5 minutesH1 H2 H3 H4 H5 H6 H7 H8 H9 H10 H11 H12 H13 H14 H15 D1 D2 D3 H1 0 7 8 9 5 7 7 4 9 6 4 3 7 6 5 5 3 3 H2 6 0 3 5 4 9 7 9 3 4 4 3 8 3 7 9 7 9 H3 6 8 0 7 5 4 3 5 8 5 4 8 3 7 8 6 5 3 H4 9 5 7 0 9 3 6 5 5 6 3 8 8 5 5 8 9 4 H5 8 5 8 8 0 6 9 8 9 7 3 3 7 4 6 6 4 3 H6 5 3 4 9 5 0 5 6 6 4 9 5 7 8 9 8 4 7 H7 7 8 4 5 7 8 0 9 5 7 7 8 7 4 5 8 8 3 H8 7 5 6 5 5 5 8 0 3 6 5 4 6 6 5 4 5 8 H9 9 6 5 7 8 8 3 4 0 7 3 4 7 4 5 3 3 3 H10 9 3 9 5 8 6 5 3 6 0 7 4 6 9 8 6 8 6 H11 9 8 4 3 9 9 6 5 7 5 0 3 3 7 3 9 5 7 H12 7 3 3 4 9 4 9 9 7 6 3 0 3 9 9 3 9 9 H13 7 3 5 6 7 4 7 8 3 8 7 8 0 3 7 6 3 5 H14 4 8 6 5 7 7 6 8 5 9 7 8 9 0 4 6 5 8 H15 6 3 9 4 8 4 9 6 7 6 3 3 9 6 0 7 6 5 表 8 5 min后车辆的服务路径结果Table 8. Service path results of vehicles after 5 minutes车辆编号 车辆路径 服务的乘客数量/个 期望到站时间/min 路径对应的目标函数值 1 5-2-3-12-4-D1 2-1-1-1-1 30 84 2 13-1-7-8-6-5-D1 1-1-1-1-1-2 30 132 3 14-3-11-15-10-D1 2-1-1-1-1 40 123 4 8-5-6-9-D1 1-1-1-1 40 109 5 1-2-10-D1 2-1-1 50 156 6 7-11-15-12-5-D1 2-1-1-1-2 50 259 7 5-13-6-3-12-7-D2 1-1-1-1-1-1 30 102 8 4-1-8-2-D2 1-1-1-1 30 72 9 6-15-3-9-11-D2 1-2-1-1-1 40 130 10 8-14-10-5-10-D2 1-1-1-1-1 40 131 11 7-2-6-1-3-D2 1-1-1-1-1 50 163 12 12-8-10-5-2-D2 2-1-1-1-1 50 191 13 5-2-12-7-3-D3 1-1-1-1-1 30 85 14 4-8-6-1-13-1-D3 1-1-1-1-1-1 30 95 15 15-10-6-9-14-D3 2-1-1-1-1 40 135 16 3-8-15-11-5-13-2-D3 1-1-2-1-1-1-1 40 175 17 8-10-2-D3 1-1-1 50 125 18 12-5-7-1-3-D3 2-2-1-2-1 50 288 3.3 结果验证
为确保计算模型的准确性,保持现有常变量不变,保持假设案例中任意接驳车辆的行程时间不变,对100组由系统随机给出的15个需求点发出的102个预约需求进行算法验算,测试结果如下:
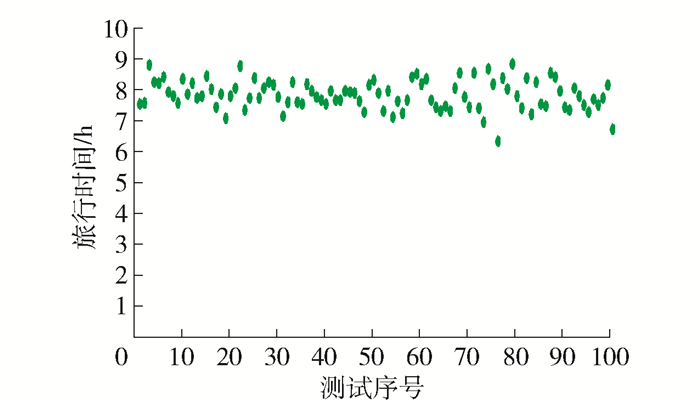
1) 在当前假定情况下,满足15个需求点的102个出行预约,需要的接驳车辆为17~21辆,84%的接驳车辆行程时长为6.67~8.33 h,如图 2所示. 每辆接驳车辆的行驶时长约为24.59 min,这说明所建立的模型随机波动性较小,计算结果相对稳定可靠.
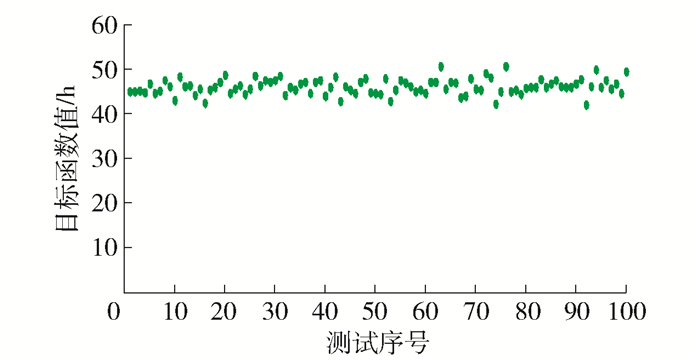
2) 模型计算结果显示:100组随机案例数据情况下,模型总目标函数值均在43.33~48.33 h,如图 3所示. 也就是说在乘客预约需求变化较为频繁的情况下,目标函数受需求变化的影响较小,所建立的模型具有较高的鲁棒性.
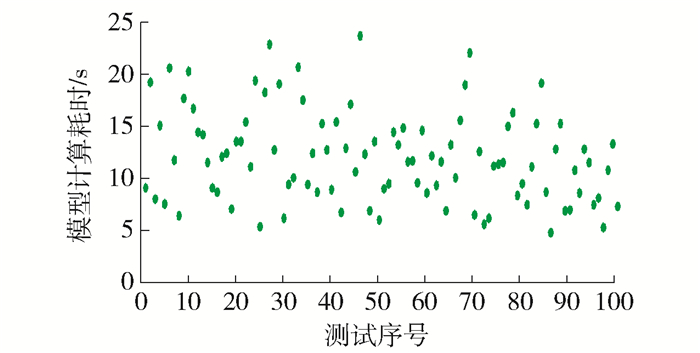
3) 计算结果表明:100组随机案例的模型计算时长均小于25.00 s,如图 4所示,案例平均计算耗时约为12.04 s,因此可以证明本文所提出的模型能够满足大批量运算的要求,可为出行者和车辆运营企业节约等待时间,提升用户体验效果.
4. 结论
1) 以最大化乘客服务量、最小化所有乘客出行时间、最小化所有车辆运营时间为优化目标的灵活公交路径优化调度模型,能够更大程度满足乘客动态需求,有效减小规划路径的误差,缩短行车距离和乘客出行时间.
2) 乘客预约需求变化较为频繁的情况下,规划路径的总时间成本波动较小,说明所建立的模型具有较高的鲁棒性.
3) 基于引力模型的启发式算法能够较为精确且快速求得线路规划的模型的最优解. 随机产生的15个需求点的102个出行需求,全部服务完成所需车辆为17~21辆,平均每辆车的旅行时间为24.59 min,100组数据的求解时间均在25.00 s以内,计算耗时平均为12.04 s.
-
表 1 模型参数
Table 1 Medol parameter
变量 定义及说明 参数类型 Z 优化路径的总时间成本 因变量 H 乘客需求站点集合 常量 D 目标站点集合 常量 K 接驳运营车辆集合 常量 R 乘客需求集合 常量 dr 乘客需求r的目标站点d 决策变量 Tt 目标站的第t个发车时刻 决策变量 N 乘客需求总量 决策变量 pr 乘客需求r的上车站点p 决策变量 Tr 乘客需求r的期望发车时刻 决策变量 cij 站点i和j之间的旅行时间 决策变量 V 接驳车队规模 决策变量 Qk 接驳车辆k的载客容量 决策变量 M 足够大的一个常数 常量 Xrkt t时刻时车辆k将需求r接驳至乘客期望的站点,Xrkt为1;否则为0 决策变量 Yijk 车辆k选择(i, j)路段作为途经路径时,Yijk为1;否则为0 决策变量 ar 车辆行驶至需求r所在公交站点的时间 决策变量 er 乘客需求r到达目标站的时间 决策变量 as 车辆行驶至需求s所在站点的时间 决策变量 Uik 决定车辆k的运行线路不出现闭环的变量. 如果接驳车辆离开站点i,则Uik=0;如果接驳车辆到达站点i,则Uik=1 辅助变量 Ujk 决定车辆k的运行线路不出现闭环的变量. 如果接驳车辆离开站点j,则Ujk=0;如果接驳车辆到达站点j,则Ujk=1 辅助变量 表 2 案例中的常变量
Table 2 Constant variables in the case
变量名称 变量值 需求点数量/个 15 目标站点数量/个 3 车辆额定载客量/人 7 车队规模/辆 18 期望到达站点时间/min 30/40/50 乘客到站上车服务时间/min 0.5 表 3 初始时刻各站点乘客需求(初始5 min)
Table 3 Quantity demanded at the demand point (the first 5 minutes)
乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 1 1 1 30 31 1 2 30 61 1 3 30 2 1 1 50 32 1 2 50 62 1 3 50 3 1 1 50 33 2 2 30 63 1 3 50 4 2 1 30 34 2 2 50 64 2 3 30 5 2 1 50 35 3 2 30 65 2 3 50 6 3 1 30 36 3 2 40 66 3 3 30 7 3 1 40 37 3 2 50 67 3 3 40 8 4 1 30 38 4 2 30 68 4 3 30 9 5 1 30 39 5 2 30 69 5 3 30 10 5 1 40 40 5 2 40 70 5 3 40 11 5 1 50 41 5 2 50 71 5 3 50 12 5 1 50 42 6 2 30 72 5 3 50 13 6 1 30 43 6 2 40 73 6 3 30 14 6 1 40 44 6 2 50 74 6 3 40 15 7 1 30 45 7 2 30 75 7 3 30 16 7 1 50 46 7 2 50 76 7 3 50 17 7 1 50 47 8 2 30 77 8 3 30 18 8 1 30 48 8 2 40 78 8 3 40 19 8 1 40 49 8 2 50 79 8 3 50 20 9 1 40 50 9 2 40 80 9 3 40 21 10 1 40 51 10 2 40 81 10 3 40 22 10 1 50 52 10 2 50 82 10 3 50 23 11 1 40 53 11 2 40 83 11 3 40 24 11 1 50 54 12 2 30 84 12 3 30 25 12 1 30 55 12 2 50 85 12 3 50 26 12 1 50 56 12 2 50 86 12 3 50 27 13 1 30 57 13 2 30 87 13 3 30 28 14 1 40 58 14 2 40 88 14 3 40 29 14 1 40 59 15 2 40 89 15 3 40 30 15 1 40 60 15 2 40 90 15 3 40 表 4 初始时的乘客行程时间矩阵(初始5 min)
Table 4 Case network travel time matrix (the first 5 minutes)
H1 H2 H3 H4 H5 H6 H7 H8 H9 H10 H11 H12 H13 H14 H15 D1 D2 D3 H1 0 3 6 5 4 5 8 6 9 9 6 3 3 4 8 3 9 9 H2 7 0 6 9 8 3 5 5 4 7 9 3 3 3 6 3 8 7 H3 9 6 0 6 5 8 8 8 3 7 9 4 5 5 5 9 7 9 H4 4 7 6 0 9 7 8 5 5 7 7 4 5 6 8 9 5 6 H5 5 3 8 8 0 5 7 9 5 6 3 8 6 5 8 9 6 5 H6 8 3 5 9 5 0 5 4 5 9 9 8 7 8 6 9 8 3 H7 9 8 4 5 6 8 0 3 4 8 6 8 8 8 5 6 7 6 H8 5 5 5 7 5 6 6 0 6 4 4 9 5 8 5 8 5 6 H9 3 5 8 5 4 5 5 6 0 7 3 6 8 3 3 6 8 3 H10 5 9 9 5 9 4 5 5 5 0 9 9 4 3 5 6 8 7 H11 5 3 7 6 6 7 8 3 3 4 0 7 4 9 6 3 7 9 H12 5 3 9 9 6 6 7 7 9 5 9 0 7 3 5 5 5 4 H13 7 5 7 9 7 8 7 5 3 7 5 7 0 5 5 6 5 5 H14 9 5 6 5 6 4 8 5 8 9 5 9 9 0 6 8 8 9 H15 6 9 6 4 8 8 3 4 5 3 4 5 9 4 0 7 9 6 表 5 初始时刻车辆的服务路径结果(初始5 min)
Table 5 Service path results of vehicles at initial time (the first 5 minutes)
车辆编号 车辆路径 服务的乘客数量/个 期望到站时间/min 路径对应的目标函数值 1 5-2-3-12-4-D1 1-1-1-1-1 30 83 2 13-1-7-8-6-D1 1-1-1-1-1 30 92 3 14-3-11-15-10-D1 2-1-1-1-1 40 123 4 8-5-6-9-D1 1-1-1-1 40 109 5 1-2-10-D1 2-1-1 50 156 6 7-11-12-5-D1 2-1-1-2 50 216 7 5-13-6-3-12-7-D2 1-1-1-1-1-1 30 102 8 4-1-8-2-D2 1-1-1-1 30 72 9 6-15-3-9-11-D2 1-2-1-1-1 40 130 10 8-14-10-5-D2 1-1-1-1 40 111 11 7-2-6-1-3-D2 1-1-1-1-1 50 163 12 12-8-10-5-D2 2-1-1-1 50 180 13 5-2-12-7-3-D3 1-1-1-1-1 30 85 14 4-8-6-1-13-D3 1-1-1-1-1 30 86 15 15-10-6-9-14-D3 2-1-1-1-1 40 135 16 3-8-11-5-D3 1-1-1-1 40 113 17 8-10-2-D3 1-1-1 50 125 18 12-5-7-1-D3 2-2-1-2 50 235 表 6 5 min后各站点乘客需求
Table 6 Passenger demand of each station in 5 minutes
乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 乘客编号 出发站 目标站 期望到站时间/min 1 1 1 30 35 1 2 30 69 1 3 50 2 1 1 50 36 1 2 50 70 1 3 50 3 1 1 50 37 2 2 30 71 2 3 30 4 2 1 30 38 2 2 50 72 2 3 40 5 2 1 50 39 2 2 50 73 2 3 50 6 3 1 30 40 3 2 30 74 3 3 30 7 3 1 40 41 3 2 40 75 3 3 40 8 4 1 30 42 3 2 50 76 3 3 50 9 5 1 30 43 4 2 30 77 4 3 30 10 5 1 30 44 5 2 30 78 5 3 30 11 5 1 30 45 5 2 40 79 5 3 40 12 5 1 30 46 5 2 50 80 5 3 50 13 5 1 40 47 6 2 30 81 5 3 50 14 5 1 50 48 6 2 40 82 6 3 30 15 5 1 50 49 6 2 50 83 6 3 40 16 6 1 30 50 7 2 30 84 7 3 30 17 6 1 40 51 7 2 50 85 7 3 50 18 7 1 30 52 8 2 30 86 8 3 30 19 7 1 50 53 8 2 40 87 8 3 40 20 7 1 50 54 8 2 50 88 8 3 50 21 8 1 30 55 9 2 40 89 9 3 40 22 8 1 40 56 10 2 40 90 10 3 40 23 9 1 40 57 10 2 40 91 10 3 50 24 10 1 40 58 10 2 50 92 11 3 40 25 10 1 50 59 11 2 40 93 12 3 30 26 11 1 40 60 12 2 30 94 12 3 50 27 11 1 50 61 12 2 50 95 12 3 50 28 12 1 30 62 12 2 50 96 13 3 30 29 12 1 50 63 13 2 30 97 13 3 30 30 13 1 30 64 14 2 40 98 14 3 40 31 14 1 40 65 15 2 40 99 15 3 40 32 14 1 40 66 15 2 40 100 15 3 40 33 15 1 40 67 1 3 30 101 15 3 40 34 15 1 50 68 1 3 30 102 15 3 40 表 7 5 min后案例网络的旅行时间矩阵
Table 7 Travel time matrix of case network after 5 minutes
H1 H2 H3 H4 H5 H6 H7 H8 H9 H10 H11 H12 H13 H14 H15 D1 D2 D3 H1 0 7 8 9 5 7 7 4 9 6 4 3 7 6 5 5 3 3 H2 6 0 3 5 4 9 7 9 3 4 4 3 8 3 7 9 7 9 H3 6 8 0 7 5 4 3 5 8 5 4 8 3 7 8 6 5 3 H4 9 5 7 0 9 3 6 5 5 6 3 8 8 5 5 8 9 4 H5 8 5 8 8 0 6 9 8 9 7 3 3 7 4 6 6 4 3 H6 5 3 4 9 5 0 5 6 6 4 9 5 7 8 9 8 4 7 H7 7 8 4 5 7 8 0 9 5 7 7 8 7 4 5 8 8 3 H8 7 5 6 5 5 5 8 0 3 6 5 4 6 6 5 4 5 8 H9 9 6 5 7 8 8 3 4 0 7 3 4 7 4 5 3 3 3 H10 9 3 9 5 8 6 5 3 6 0 7 4 6 9 8 6 8 6 H11 9 8 4 3 9 9 6 5 7 5 0 3 3 7 3 9 5 7 H12 7 3 3 4 9 4 9 9 7 6 3 0 3 9 9 3 9 9 H13 7 3 5 6 7 4 7 8 3 8 7 8 0 3 7 6 3 5 H14 4 8 6 5 7 7 6 8 5 9 7 8 9 0 4 6 5 8 H15 6 3 9 4 8 4 9 6 7 6 3 3 9 6 0 7 6 5 表 8 5 min后车辆的服务路径结果
Table 8 Service path results of vehicles after 5 minutes
车辆编号 车辆路径 服务的乘客数量/个 期望到站时间/min 路径对应的目标函数值 1 5-2-3-12-4-D1 2-1-1-1-1 30 84 2 13-1-7-8-6-5-D1 1-1-1-1-1-2 30 132 3 14-3-11-15-10-D1 2-1-1-1-1 40 123 4 8-5-6-9-D1 1-1-1-1 40 109 5 1-2-10-D1 2-1-1 50 156 6 7-11-15-12-5-D1 2-1-1-1-2 50 259 7 5-13-6-3-12-7-D2 1-1-1-1-1-1 30 102 8 4-1-8-2-D2 1-1-1-1 30 72 9 6-15-3-9-11-D2 1-2-1-1-1 40 130 10 8-14-10-5-10-D2 1-1-1-1-1 40 131 11 7-2-6-1-3-D2 1-1-1-1-1 50 163 12 12-8-10-5-2-D2 2-1-1-1-1 50 191 13 5-2-12-7-3-D3 1-1-1-1-1 30 85 14 4-8-6-1-13-1-D3 1-1-1-1-1-1 30 95 15 15-10-6-9-14-D3 2-1-1-1-1 40 135 16 3-8-15-11-5-13-2-D3 1-1-2-1-1-1-1 40 175 17 8-10-2-D3 1-1-1 50 125 18 12-5-7-1-3-D3 2-2-1-2-1 50 288 -
[1] FLUSBERG M. An innovative public transportation system for a small city: the merrill, wisconsin, case study[J]. Transportation Research Record, 1976(606): 54-59. http://www.mendeley.com/catalog/innovative-public-transportation-system-small-city-merrill-wisconsin-case-study/
[2] 雷永巍, 林培群, 姚凯斌. 互联网定制公交的网络调度模型及其求解算法[J]. 交通运输系统工程与信息, 2017, 17(1): 157-163. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201701024.htm LEI Y W, LIN P Q, YAO K B. The network scheduling model and its solution algorithm of Internet customized shuttle bus[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 157-163. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201701024.htm
[3] 云亮, 蒋阳升, 宋雪梅. 机动式辅助客运系统(MAST)及其研究进展综述[J]. 交通运输工程与信息学报, 2009, 7(4): 79-83, 123. https://www.cnki.com.cn/Article/CJFDTOTAL-JTGC200904017.htm YUN L, JIANG Y S, SONG X M. Introduction of mobility allowance shuttle transit system (MAST) and the summary of its research progress[J]. Journal of Transportation Engineering and Information, 2009, 7(4): 79-83, 123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTGC200904017.htm
[4] 沈昱, 关函非. 响应需求公交系统分析与实施要点研究[J]. 交通与运输(学术版), 2010(H12): 75-78. https://www.cnki.com.cn/Article/CJFDTOTAL-JTYH201002025.htm SHEN Y, GUAN H F. Study on demand responsive transport system and implementation issues[J]. Traffic & Transportation, 2010(H12): 75-78. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTYH201002025.htm
[5] CHEN P, NIE Y. Optimal design of demand adaptive paired-line hybrid transit: case of radial route structure[J]. Transportation Research Part E: Logistics & Transportation Review, 2018(110): 71-89. http://smartsearch.nstl.gov.cn/paper_detail.html?id=1f521fbe27d3bd25f9dd9d132e7a2bda
[6] 郭晨. 面向轨道交通的灵活型接驳公交站点选址研究[D]. 济南: 山东大学, 2015. GUO C. Locating flexible feeder bus stations to connect urban railway systems[D]. Jinan: Shandong University, 2015. (in Chinese)
[7] CEDER A. Integrated smart feeder/shuttle transit service: simulation of new routing strategies[J]. Journal of Advanced Transportation, 2013, 47(6): 595-618. doi: 10.1002/atr.185
[8] 潘述亮, 俞洁, 卢小林, 等. 灵活型公交服务系统及其研究进展综述[J]. 城市交通, 2014, 12(2): 62-68. https://www.cnki.com.cn/Article/CJFDTOTAL-CSJT201402012.htm PAN S L, YU J, LU X L, et al. Review of flexible transit service[J]. Urban Transport of China, 2014, 12(2): 62-68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSJT201402012.htm
[9] PRATELLI A, SCHOEN F. A mathematical programming model for the bus deviation route problem[J]. Journal of the Operational Research Society, 2001, 52(5): 494-502. doi: 10.1057/palgrave.jors.2601109
[10] KIM M E, SCHONFELD P. Integration of conventional and flexible bus services with timed transfers[J]. Transportation Research Part B: Methodological, 2014, 68: 76-97. doi: 10.1016/j.trb.2014.05.017
[11] QUADRIFOGLIO L, DESSOUKY M. Insertion heuristic for scheduling mobility allowance shuttle transit (MAST) services: sensitivity to service area[J]. Computer-Aided Systems in Public Transport, Springer Series: Lecture Notes in Economics and Mathematical Systems, 2007, 600: 419-437. http://dl.acm.org/citation.cfm?id=1188200
[12] QUADRIFOGLIO L, DESSOUKY M M. Sensitivity analyses over the service area for mobility allowance shuttle transit (MAST) services[J]. Computer-aided Systems in Public Transport, 2008, 600: 419-432. http://www.springerlink.com/index/l304416064897442.pdf
[13] 付晓, 顾宇, 刘志远. 多模式公交网络中考虑定制公交的活动与出行建模[J]. 交通运输系统工程与信息, 2019, 19(4): 20-27. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201904004.htm FU X, GU Y, LIU Z Y. Scheduling activity and travel patterns in multi-modal transit networks with customized bus services[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(4): 20-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201904004.htm
[14] KOFFMAN D. Operational experiences with flexible transit services: a synthesis of transit practice[R]. Washington, D C.: Transportation Research Board, 2015.
[15] TSUBOUCHI K, YAMATO H. Adapted scheduling algorithm for on-demand bus system[J]. International Journal of Intelligent Transportation Systems Research, 2012, 10(2): 82-92. doi: 10.1007/s13177-012-0044-6
[16] 熊杰. 接驳地铁的社区公交微循环系统优化研究[D]. 北京: 北京交通大学, 2015. XIONG J. Research on optimal microcirculation system of community shuttle linked with metro service[D]. Beijing: Beijing Jiaotong University, 2015. (in Chinese)
[17] LI Q F, CHEN P, NIE Y. Finding optimal hyperpaths in large transit networks with realistic headway distributions[J]. European Journal of Operational Research, 2015, 240(1): 98-108. doi: 10.1016/j.ejor.2014.06.046
[18] CHEN P, NIE Y. Optimal transit routing with partial online information[J]. Transportation Research Part B: Methodological, 2015, 72: 40-58. doi: 10.1016/j.trb.2014.11.007
[19] 潘述亮. 面向换乘站点的灵活型公交微循环系统设计理论与方法研究[D]. 济南: 山东大学, 2015. PAN S L. The design theory and methodology of flexible microcirculation transit system oriented on the transfer station[D]. Jinan: Shandong University, 2015. (in Chinese)
[20] 郭晓俊. 基于需求响应的实时定制公交系统研究[D]. 北京: 北京交通大学, 2016. GUO X J. Research of demand response based real-time custom bus system[D]. Beijing: Beijing Jiaotong University, 2016. (in Chinese)
-
期刊类型引用(7)
1. 史淼,陈艳艳,张妍,高月喆,孙昊. 高铁站接驳需求响应公交线路布设研究. 交通运输研究. 2025(01): 79-89 .  百度学术
百度学术
2. 李欣,滕章华,许航,袁昀. 需求响应公交和共享单车联合出行系统与优化. 交通运输工程与信息学报. 2024(02): 21-33 .  百度学术
百度学术
3. 易奎,张雨乐,庄夏,付文,王泽潭. 民航车辆调度现状分析及发展趋势综述. 科学技术与工程. 2024(36): 15321-15333 .  百度学术
百度学术
4. 李利华,曹慧琪,邓亚军,邢璐,靳竹喧. 基于站点群体聚集性客流的公交串车调度优化. 中国公路学报. 2023(02): 203-215 .  百度学术
百度学术
5. 宋翠颖,王鹤玲,田泽尚,牛学勤. 需求响应式公交车辆调度模型和算法研究综述. 北京交通大学学报. 2023(04): 31-44 .  百度学术
百度学术
6. 张泽瑞,李昊,陶学强,鹿国伟,陈恩. 基于改进蚁群算法的血液保障车辆动态路径优化研究. 中国急救复苏与灾害医学杂志. 2022(07): 957-962+972 .  百度学术
百度学术
7. 陈可嘉,方云飞,骆佳艺. 灵活多车场多类型的叫车接送问题的规划模型. 交通信息与安全. 2021(03): 103-110 .  百度学术
百度学术
其他类型引用(19)



 下载:
下载: