Set-valued and Interval-valued Multivariate Time Series
-
摘要:
研究集值多元时间序列的一些初步的理论,这为拓广经典的多元时间序列模型提供了理论基础.首先,基于集值理论,进一步提出集值向量、集值随机向量的定义,并给出集值随机向量的期望向量、交叉协方差阵与交叉相关阵的定义与性质.然后,在此基础上,给出集值多元时间序列的定义,并研究关于集值多元时间序列的平稳性,期望向量、交叉协方差阵和交叉相关阵的定义及性质,讨论平稳的集值多元时间序列的最优线性预测问题.最后,在集值多元时间序列的基础之上,讨论区间值多元时间序列,并建立区间值多元自回归模型.模拟研究与实证分析验证了该模型与所提出方法的合理性.
Abstract:Some preliminaries for set-valued multivariate time series were studied, which provides a theoretical basis for extending the classical multivariate time series models. First, this paper introduced the definitions of set-valued vectors and set-valued random vectors based on the set-valued random variable theory. The definitions of expectation vectors, cross covariance matrixes and cross correlation matrixes were also given in this paper. Then, the set-valued multivariate time series was defined and the stationary property, expectation vectors, cross covariance matrixes and cross correlation matrixes of set-valued multivariate time series were discussed. Furthermore, the optimal linear forecast of stationary set-valued multivariate time series was studied. Finally, the interval-valued multivariate time series were discussed based on set-valued multivariate time series, and the interval-valued vector autoregressive model was built. Simulation study and real data analysis show the efficiency of the proposed model and approach.
-
时间序列分析的研究有着悠久的历史以及大量的学术成果, 并在很多领域中都有着广泛的应用, 例如Box等[1]、Tsay[2]、Brockwell等[3]的专著及其所引用的参考文献.经典时间序列模型研究的对象通常是随着时间推移而形成的随机变量或随机向量序列, 通过建立时间序列模型来分析这些序列的动态规律.
然而, 随着技术的发展, 人们收集到的数据变得更加复杂, 经典的时间序列模型不再适用于一些较为复杂的数据.例如, 在分析股票数据时通常选取每个交易日的收盘价作为研究对象.然而,当今的技术使得股票数据刷新频率很高, 收盘价并不足以反映当天股票价格的变化.比如说, 某一个交易日里某一支股票价格所有的观测值为x1, x2, …, xn, 这里n的值很大, 而收盘价只是集合{x1, x2, …, xn}中的一个元素.为能更准确地研究股票数据, 有一种方法是取每个交易日里股票价格的最高价和最低价, 将其作为一个区间的2个端点, 即研究对象是
$$ {X_t} = \left[ {\min \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\},\max \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}} \right] $$ 将区间Xt视为一个数据单元来研究问题.可以看出, 区间Xt不仅包含了收盘价的信息, 而且还有当天股价变动的情况, 这无疑是一个好的处理方法.通过区间值或集值数据来描述一类复杂数据, 是一种分析复杂数据的手段.另一方面, 由于系统的复杂性, 使得到的数据是某个范围而不是一个确定的实数值.比如让专家估计明年中国的经济增长率,专家们往往会给出3%~6%, 3.5%~5.7%这样的数据, 显然用区间来刻画这类数据更加贴切.引入区间值和集值数据, 不仅是对观测数据的一种处理方式, 而且还是对收集到的数据一种客观并且准确的体现.
事实上, 区间是集合的一个特例, 区间值随机变量的相关性质都可以从集值随机变量的性质中推导.自从20世纪中叶, 以经济学诺贝尔奖获得者Aumann和Debreu为代表的一批研究者在研究市场均衡等经济问题时引入了集值映射的概念及方法, 集值随机理论有了较为完善的发展. Aumann[4]通过集值随机变量的选择集给出了集值随机变量期望的定义, 这里集值随机变量的期望是选择集中元素的期望构成的集合. Hiai等[5]定义了集值随机变量的条件期望. Lyashenko[6]讨论了欧式空间中集值随机变量的性质, 提出了集值随机变量方差的定义, 并给出了集值高斯随机变量的定义及表达定理. Vitale[7]研究了集合的Lp距离的性质.需注意的是, 相较于集合的Hausdorff距离, Lp距离具有非常好的数学性质, 这使得集值和区间值的统计模型大多数都建立在Lp距离之上. Diamond[8]讨论了区间值仿射函数的最小二乘估计方法. Li等[9-10]研究了集值鞅的收敛性问题. Li等[11]的书中系统地总结了集值随机变量的空间、期望与条件期望, 强大数定律与中心极限定理等理论. Gil等[12]推广了Lp距离. Yang等[13]通过Lp距离定义了集值随机变量的协方差和相关系数, 并讨论了方差、协方差和相关系数的性质.张文修等[14]的书中阐述了集值随机过程的一系列理论.
作为集合最简单的特例, 区间值时间序列被广泛地讨论.有一类文献是将区间的2个端点或中心半径看作2个实值随机变量, 然后通过区间的2个端点或中心半径来给出区间值时间序列模型, 例如Wang等[15]、González-Rivera等[16]、唐娜娜[17]等.而另一类文献则是将区间值数据看成一个整体, 使用集值随机理论来分析区间值数据, 并建立区间值时间序列模型, 例如王洵[18]、Wang等[19]、章磊[20]等.
区间值时间序列可以看作集值时间序列的一个特例, 区间值时间序列的相关理论可以通过集值时间序列推出, 而对集值时间序列的讨论建立在集值随机过程理论的框架下.张文修等[14]的专著中, 系统地介绍了集值随机过程的一系列理论. Wang等[21]定义了严平稳的集值随机过程并讨论了它的一系列性质.然而, 虽然在严平稳性的条件下, 集值随机过程有许多好的性质, 但在实际应用中难以使用.因此Wang等[19]通过集值随机变量的期望[4]和协方差[13]定义了集值时间序列的弱平稳性, 并进一步讨论了弱平稳条件下集值时间序列统计量的估计及其渐近性质.
本文在Wang等[19]、章磊[20]研究的基础之上, 进一步讨论了集值随机向量和集值多元时间序列的相关定义及性质.首先,给出集值向量与集值随机向量的相关理论;然后,讨论集值多元时间序列;第三,给出集值多元时间序列在区间值情形下的应用;第四,给出区间值多元自回归模型的一个实证分析;最后,简要地给出结论.
1. 集值向量与集值随机向量
1.1 集合与集值向量
记${{\mathbb{R}}^{d}}$为d-维欧式空间, ${{\mathbb{R}}^{d}}$中所有非空紧凸集为K(${{\mathbb{R}}^{d}}$).任意2个集合A、B的加法与数乘运算定义为
$$ A + B = \left\{ {a + b:a \in A,b \in B} \right\} $$ $$ \mathit{\Lambda }A = \left\{ {\lambda a;a \in A} \right\},\forall \lambda \in \mathbb{R} $$ Vitale[7]通过支撑函数定义了K(${{\mathbb{R}}^{d}}$)中2个元素间的Lp距离,1≤p<∞.集合A∈K(${{\mathbb{R}}^{d}}$)的支撑函数定义为
$$ s\left( {\mathit{\boldsymbol{x}},A} \right) = \mathop {\sup }\limits_{\mathit{\boldsymbol{a}} \in A} \left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{a}}} \right\rangle ,\mathit{\boldsymbol{x}} \in S $$ 式中:〈·, ·〉为${{\mathbb{R}}^{d}}$中2个向量的内积; S为${{\mathbb{R}}^{d}}$中的单位球面.集合A和B间的Lp距离定义为
$$ {L_p}\left( {A,B} \right) = {\left[ {\int_S {{{\left| {s\left( {\mathit{\boldsymbol{x}},A} \right) - s\left( {\mathit{\boldsymbol{x}},B} \right)} \right|}^p}{\text{d}}\mu } } \right]^{\frac{1}{p}}} $$ 不失一般性, 本文接下来取p=2.进一步地, 由Yang等[13]可知空间(K(${{\mathbb{R}}^{d}}$), L2)是完备可分的.
称由k个K(${{\mathbb{R}}^{d}}$)中的集合A1, A2, …, Ak构成的集值向量A=(A1, A2, …, Ak)T为k维集值向量.记k维集值向量族为Kk(${{\mathbb{R}}^{d}}$).需注意的是, 集值向量A是${{\mathbb{R}}^{kd}}$中一个k维的超立方体.由于假定了集值向量中每个元素都是Kk(${{\mathbb{R}}^{d}}$)中的集合,因此,可以推出关系式Kk(${{\mathbb{R}}^{d}}$)⊆K(${{\mathbb{R}}^{kd}}$)成立.
假定k≤m, 任意的k维集值向量和m维集值向量A=(A1, A2, …, Ak)T, B=(B1, B2, …, Bm)T间的加法运算定义为
$$ \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}} = {\left( {{A_1} + {B_1}, \cdots ,{A_k} + {B_k},{B_{k + 1}}, \cdots ,{B_m}} \right)^{\text{T}}} $$ 进一步地,k维集值向量A与p×k的实值矩阵Λ=(λi, j)i=1, 2, …, p, j=1, 2, …, k间的矩阵乘法运算定义为
$$ \mathit{\boldsymbol{ \boldsymbol{\varLambda} A}} = {\left( {\sum\limits_{j = 1}^k {{\lambda _{1,j}}{A_j}} , \cdots ,\sum\limits_{j = 1}^k {{\lambda _{p,j}}{A_j}} } \right)^{\text{T}}} $$ 式中:ΛA是一个p维集值向量.特别地, 当p=1时, Λ=(λ1, λ2, …, λk)是一个1×k的实值行向量, 乘积$\boldsymbol{\mathit{\Lambda}} \boldsymbol{A}=\sum\limits_{j=1}^{k} \lambda_{j} A_{j}$是一个K(${{\mathbb{R}}^{d}}$)中的集合.
1.2 集值随机变量
令(Ω, $\mathscr{A}$, P)是一个完备的概率空间.称集值映射X(ω):Ω→K(${{\mathbb{R}}^{d}}$)为一个集值随机变量, 如果对于任意开集C, 都有X-1(C)∈$\mathscr{A}$, 式中X-1(C)={ω∈Ω:X(ω)∩C≠Ø}.
记u[Ω, K(${{\mathbb{R}}^{d}}$)]为K(${{\mathbb{R}}^{d}}$)中的集值随机变量族. 2个集值随机变量X1、X2间的D2距离定义为
$$ {D_2}\left( {{X_1},{X_2}} \right) = {\left[ {{\text{E}}L_2^2\left( {{X_1},{X_2}} \right)} \right]^{\frac{1}{2}}} $$ 接下来可以通过Aumann[4]积分, 给出集值随机变量X期望的定义
$$ {\text{E}}\left[ X \right] = \int_\mathit{\Omega } {X{\text{d}}P} = \left\{ {\int_\mathit{\Omega } {f{\text{d}}P} :f \in S_X^1} \right\} $$ 式中SX1是集值随机变量X的选择集, 即
$$ S_X^1 = \left\{ {f \in {L^1}\left[ {\mathit{\Omega },\mathbb{R}} \right];f\left( \omega \right) \in X\left( \omega \right)a.\;e.\;\left( P \right)} \right\} $$ 式中L1[Ω, ${{\mathbb{R}}^{d}}$]为一阶矩存在的实值随机向量族.
注意到u[Ω, K(${{\mathbb{R}}^{d}}$)]并非是一个线性空间, 这使得许多通过线性空间的特性讨论的统计问题无法平行地推广至集值的情形, 例如并不能直接定义集值随机变量的方差和协方差, 然而,可以通过D2距离来刻画集值随机变量的离散程度. Yang等[15]讨论了通过D2距离定义的集值随机变量方差的性质, 并给出了集值随机变量协方差和相关系数的定义.
对于u[Ω, K(${{\mathbb{R}}^{d}}$)]中的元素, 进一步地记
$$ {\mathscr{L}^2}\left[ {{\mathit{\Omega}} ,K\left( {{\mathbb{R}^d}} \right)} \right] = \left\{ {X:D_2^2\left( {X,\left\{ 0 \right\}} \right) < \infty } \right\} $$ 为所有D2距离存在的集值随机变量族.集值随机变量X1, X2∈$\mathscr{L}$2[Ω, K(${{\mathbb{R}}^{d}}$)]的方差、协方差和相关系数分别定义为
$$ \begin{array}{*{20}{c}} {{\rm{Var}}\left( {{X_1}} \right) = D_2^2\left( {{X_1},{\rm{E}}\left[ {{X_1}} \right]} \right) = }\\ {{\rm{E}}\left( {\int_S {{{\left[ {\mathit{{s}}\left( {x,{X_1}} \right) - s\left( {x,{\rm{E}}\left[ {{X_1}} \right]} \right)} \right]}^2}} {\rm{d}}\mu } \right)} \end{array} $$ $$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{X_1},{X_2}} \right) = {\rm{E}}\left( {\int_S {\left( {\mathit{{s}}\left( {x,{X_1}} \right)} \right.} - } \right.}\\ {\left. {\left. {s\left( {x,{\rm{E}}\left[ {{X_1}} \right]} \right)} \right)\left( {s\left( {x,{X_2}} \right) - s\left( {x,{\rm{E}}\left[ {{X_2}} \right]} \right)} \right){\rm{d}}\mu } \right)} \end{array} $$ $$ Cor\left( {{X_1},{X_2}} \right) = \frac{{{\rm{Cov}}\left( {{X_1},{X_2}} \right)}}{{\sqrt {{\rm{Var}}\left( {{X_1}} \right){\rm{Var}}\left( {{X_2}} \right)} }} $$ 式中Var(X1)Var(X2)≠0.
为便于接下来的讨论, 下面给出集值随机变量协方差的一些性质.
命题1 集值随机变量X1、X2、X3的协方差具有下面几个性质:
1) Cov(C, X1)=0, 式中C是一个常集合.
2) Cov(λX1, X2)=λCov(X1, X2), 式中λ≥0是一个常数.
3) Cov(X1+X2, X3)=Cov(X1, X3)+Cov(X2, X3).
命题1的证明以及关于集值随机变量方差、协方差的更多性质见Yang等[13]、Wang等[19].
1.3 集值随机向量
考虑完备的概率乘积空间
$$ \left( {{\mathit{\Omega }_1},{\mathscr{A}_1},{P_1}} \right) \times \cdots \times \left( {{\mathit{\Omega }_k},{\mathscr{A}_k},{P_k}} \right) $$ 称向量X=(X1, X2, …, Xk)T为k维集值随机向量, 如果X1, X2, …, Xk是K(${{\mathbb{R}}^{d}}$)中的集值随机变量.记u[Ω1×Ω2×…×Ωk, Kk(${{\mathbb{R}}^{d}}$)]为k维集值随机向量族.
k维集值随机向量X的期望E[X]定义为
$$ {\rm{E}}\left[ \mathit{\boldsymbol{X}} \right] = {\left( {{\rm{E}}\left[ {{X_1}} \right],{\rm{E}}\left[ {{X_2}} \right], \cdots ,{\rm{E}}\left[ {{X_k}} \right]} \right)^{\rm{T}}} $$ 式中E[X1], E[X2], …, E[Xk]为X的不同分量在不同的概率测度P1, P2, …, Pk下的期望.然而为了简化记号, 并不对不同概率测度下的期望加以记号区分, 下面的协方差阵和交叉协方差阵等记号也同样.
如果k维集值随机向量X1=(X1, 1, X2, 1, …, Xk, 1)T, 和X2=(X1, 2, X2, 2, …, Xk, 2)T的每一个分量都有Xi, j∈$\mathscr{L}$2[Ωi, j, K(${{\mathbb{R}}^{d}}$)], i=1, 2, j=1, 2, …, k, 那么X1的协方差阵为
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} {{\rm{Var}}\left( {{X_{1,1}}} \right)}&{{\rm{Cov}}\left( {{X_{1,1}},{X_{2,1}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{1,1}},{X_{k,1}}} \right)}\\ {{\rm{Cov}}\left( {{X_{2,1}},{X_{1,1}}} \right)}&{{\rm{Var}}\left( {{X_{2,1}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{2,1}},{X_{k,1}}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{\rm{Cov}}\left( {{X_{k,1}},{X_{1,1}}} \right)}&{{\rm{Cov}}\left( {{X_{k,1}},{X_{2,1}}} \right)}& \cdots &{{\rm{Var}}\left( {{X_{k,1}}} \right)} \end{array}} \right)} \end{array} $$ X1和X2的交叉协方差阵为
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{X_{1,1}},{X_{1,2}}} \right)}&{{\rm{Cov}}\left( {{X_{1,1}},{X_{2,2}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{1,1}},{X_{k,2}}} \right)}\\ {{\rm{Cov}}\left( {{X_{2,1}},{X_{1,2}}} \right)}&{{\rm{Cov}}\left( {{X_{2,1}},{X_{2,2}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{2,1}},{X_{k,2}}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{\rm{Cov}}\left( {{X_{k,1}},{X_{1,2}}} \right)}&{{\rm{Cov}}\left( {{X_{k,1}},{X_{2,2}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{k,1}},{X_{k,2}}} \right)} \end{array}} \right)} \end{array} $$ X1和X2的交叉相关阵为
$$ Cor\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}} \right) = \mathit{\boldsymbol{D}}_1^{ - 1}{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}} \right)\mathit{\boldsymbol{D}}_2^{ - 1} $$ 式中矩阵$\boldsymbol{D}_{1}=\operatorname{diag}(\sqrt{\operatorname{Var}\left(X_{1, 1}\right)}, \cdots, \sqrt{\operatorname{Var}\left(X_{k, 1}\right)})$和$\boldsymbol{D}_{2}=\operatorname{diag}(\sqrt{\operatorname{Var}\left(X_{1, 2}\right)}, \cdots, \sqrt{\operatorname{Var}\left(X_{k, 2}\right)})$分别为由X1和X2的每个分量的标准差组成的对角矩阵.
命题2 k维集值随机向量X1、X2、X3的交叉协方差阵具有下面几个性质:
1) Cov(X1, X2)=Cov(X2, X1)T.
2) Cov(C, X1)=0k×k, 式中C=(c1, c2, …, ck)T是一个常集值向量, 0k×k是k×k的零矩阵.
3) 下面关系式成立
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_3}} \right) = }\\ {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_3}} \right) + {\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_3}} \right)} \end{array} $$ 4) Cov(PX1, QX2)=PCov(X1, X2)QT, 式中P=(pi, j)i=1, …, p, j=1, …, k, Q=(qi, j)i=1, …, p, j=1, …, k是2个所有元素都非负的实值矩阵.
证明:
1) 由下面的表达式
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_1}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{X_{1,2}},{X_{1,1}}} \right)}&{{\rm{Cov}}\left( {{X_{1,2}},{X_{2,1}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{1,2}},{X_{k,1}}} \right)}\\ {{\rm{Cov}}\left( {{X_{2,2}},{X_{1,1}}} \right)}&{{\rm{Cov}}\left( {{X_{2,2}},{X_{2,1}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{2,2}},{X_{k,1}}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{\rm{Cov}}\left( {{X_{k,2}},{X_{1,1}}} \right)}&{{\rm{Cov}}\left( {{X_{k,2}},{X_{2,1}}} \right)}& \cdots &{{\rm{Cov}}\left( {{X_{k,2}},{X_{k,1}}} \right)} \end{array}} \right)} \end{array} $$ 可证得1).
2) 由命题1, 可以推出
$$ {\rm{Cov}}\left( {\mathit{\boldsymbol{C,}}{\mathit{\boldsymbol{X}}_1}} \right) = {\left( {{\rm{Cov}}\left( {{c_i},{X_{j,1}}} \right)} \right)_{i,j = 1, \cdots ,k}} = {\left( 0 \right)_{i,j = 1, \cdots ,k}} $$ 即为2).
3) 由命题1, 可以推出
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_3}} \right) = }\\ {{{\left( {{\rm{Cov}}\left( {{X_{i,1}} + {X_{i,2}},{X_{j,3}}} \right)} \right)}_{i,j = 1, \cdots ,k}} = }\\ {{{\left( {{\rm{Cov}}\left( {{X_{i,1}}{X_{i,3}}} \right) + {\rm{Cov}}\left( {{X_{i,2}}{X_{j,3}}} \right)} \right)}_{i,j = 1, \cdots ,k}} = }\\ { {\rm{Cov}} \left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_3}} \right) + {\rm{Cov}} \left( {{\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_3}} \right)} \end{array} $$ 即为3).
4) 由命题1, 可以推出
$$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{X}}_1},\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{X}}_2}} \right) = }\\ {{{\left( {{\rm{Cov}}\left( {\sum\limits_{m = 1}^k {{p_{i,m}}{X_{m,1}}} ,\sum\limits_{m = 1}^k {{q_{j,l}}{X_{l,2}}} } \right)} \right)}_{i = 1, \cdots ,p,j = 1, \cdots ,q}} = }\\ {{{\left( {\sum\limits_{m = 1}^k {\sum\limits_{l = 1}^k {{p_{i,m}}{q_{j,l}}} } {\rm{Cov}}\left( {{X_{m,1}},{X_{l,2}}} \right)} \right)}_{i = 1, \cdots ,p,j = 1, \cdots ,q}} = }\\ {\mathit{\boldsymbol{P}}{\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}} \right){\mathit{\boldsymbol{Q}}^{\rm{T}}}} \end{array} $$ 即为4).
2. 集值多元时间序列
2.1 集值多元时间序列
Wang等[19]在集值随机变量及其期望、方差、协方差等统计量的定义的基础上, 定义了集值时间序列, 并给出集值时间序列的平稳性、自协方差函数和自相关函数的定义.在Wang等[19]的基础上, 进一步给出集值多元时间序列的定义, 并讨论其性质.
对于集值多元时间序列的研究, 不能将其视为一个更高维空间中的集值时间序列.记Ω=Ω1×Ω2×…×Ωk.虽然一个u[Ω, Kk(${{\mathbb{R}}^{d}}$)]中的元素同时也是u[Ω, K(${{\mathbb{R}}^{kd}}$)]中的集值随机变量, 但直接将其视为一个集值随机变量来做进一步的讨论, 这样就忽略了集值随机向量的几何信息.因此应对其特别对待, 下面给出集值多元时间序列的定义.
定义1 称由时间{t=1, 2, …, T}生成的k维集值随机向量序列X1, X2, …, XT∈u[Ω, Kk(${{\mathbb{R}}^{d}}$)]为一个k维集值多元时间序列.
定义2 如果对于∀t=1, 2, …, T, 一个k维集值多元时间序列X1, X2, …, XT, 都有: 1) E[Xt]≡X0是一个常的集值向量, 2) Cov[Xt]=E[(Xt-X0)(Xt-X0)T]是k×k的常实值正定矩阵,那么称这个k维集值多元时间序列X1, X2, …, XT是弱平稳的.
由定义2可知, 如果一个集值多元时间序列的前两阶矩不随时间变化而变化, 那么这个序列就是弱平稳的.由于严平稳性的定义过于严格, 就使得在实际应用中很难找到满足严平稳定义的序列, 因此在这里不再讨论集值多元时间序列严平稳性的定义.进一步地, 将弱平稳简称为平稳.
下面引入k维集值多元时间序列的交叉协方差阵的定义.
定义3 滞后为l的k维集值多元时间序列的交叉协方差阵定义为
$$ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l} \buildrel \Delta \over = {\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_t},{\mathit{\boldsymbol{X}}_{t - l}}} \right) $$ 滞后为l的交叉相关阵定义为
$$ {\mathit{\boldsymbol{\gamma }}_l} \buildrel \Delta \over = {\rm{Cov}}\left( {{\mathit{\boldsymbol{X}}_t},{\mathit{\boldsymbol{X}}_{t - l}}} \right) = \mathit{\boldsymbol{D}}_t^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l}\mathit{\boldsymbol{D}}_{t - l}^{ - 1} $$ 式中${{\mathrm{D}}_{1}}=\operatorname{diag}(\sqrt{\operatorname{Var}\left({{X}_{1, t}} \right)}, \cdots, \sqrt{\operatorname{Var}\left({{X}_{k, t}} \right)})$为由Xt的每个分量的标准差组成的对角矩阵.
命题3 如果k维集值多元时间序列X1, X2, …, XT是平稳的, 那么其交叉协方差阵和交叉相关阵具有下面几个性质:
1) ${\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{ - l}}^{\text{T}}, {\mathit{\boldsymbol{\gamma }}_l} = {\mathit{\boldsymbol{\gamma }}_{ - l}}^{\text{T}}$.
2) ${\mathit{\boldsymbol{\gamma }}_l} = {\mathit{\boldsymbol{D}}_t}^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l}{\mathit{\boldsymbol{D}}_t}^{ - 1}$.
3) 对于任意的λ1, λ2, …, λT∈${{\mathbb{R}}^{k}}$, T∈{1, 2, …}, 都有$\sum\limits_{l = 1}^T {\sum\limits_{m = 1}^T {{\mathit{\boldsymbol{\lambda }}_l}^T{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{l - m}}{\mathit{\boldsymbol{\lambda }}_m}} } \geqslant 0$.
证明:
1) 由平稳性可以推出
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l} = {{\left( {{\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right)} \right)}_{i,j = 1, \cdots ,k}} = }\\ {{{\left( {{\rm{Cov}}\left( {{X_{i,t + l}},{X_{j,t}}} \right)} \right)}_{i,j = 1, \cdots ,k}} = }\\ {\left( {{\rm{Cov}}\left( {{X_{i,t}},{X_{i,t + l}}} \right)} \right)_{i,j = 1, \cdots ,k}^{\rm{T}} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{ - l}^{\rm{T}}} \end{array} $$ 同理可以推出γl=γ-lT成立.
2) 由平稳性可知Dt=Dt-l, 可推出2).
3) 由平稳性, 可以由下面的计算
$$ \begin{array}{*{20}{c}} {\sum\limits_{l = 1}^T {\sum\limits_{m = 1}^T {\mathit{\boldsymbol{\lambda }}_l^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{l - m}}{\mathit{\boldsymbol{\lambda }}_m}} } = }\\ {\sum\limits_{l = 1}^T {\sum\limits_{m = 1}^T {\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^k {{\lambda _{j,l}}{\lambda _{i,m}}} } } } {\rm{Cov}}\left( {{X_{i,t - m}},{X_{j,t - l}}} \right) = }\\ {{\rm{E}}\left( {\sum\limits_{l = 1}^T {\sum\limits_{m = 1}^T {\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^k {{\lambda _{j,l}}{\lambda _{i,m}}} } } } \int_S {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t - m}}} \right) - } \right.} } \right.}\\ {\left. {\left. {s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {\mathit{\boldsymbol{x}},{X_{j,0}}} \right)} \right){\rm{d}}\mu } \right) = }\\ {{\rm{E}}\int_S {{{\left[ {\sum\limits_{m = 1}^T {\sum\limits_{i = 1}^k {{\lambda _{i,m}}} } \left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t - m}}} \right) - s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right)} \right)} \right]}^2}} {\rm{d}}\mu \ge 0} \end{array} $$ 证得3).
2.2 平稳的集值多元时间序列统计量的估计
下面讨论集值多元时间序列期望向量, 交叉协方差阵及交叉相关阵的估计.假定X1, X2, …, XT是平稳的k维集值多元时间序列的观测值.
期望向量X0的矩估计为
$$ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_0} \buildrel \Delta \over = {{\left( {{{\hat X}_{1,0}},{{\hat X}_{2,0}}, \cdots ,{{\hat X}_{k,0}}} \right)}^{\rm{T}}} = }\\ {\frac{1}{T}\left( {{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{X}}_2} + \cdots + {\mathit{\boldsymbol{X}}_T}} \right) = }\\ {{{\left( {\frac{1}{T}\sum\limits_{t = 1}^T {{X_{1,t}}} , \cdots ,\frac{1}{T}\sum\limits_{t = 1}^T {{X_{k,t}}} } \right)}^{\rm{T}}}} \end{array} $$ 对于l=0, 1, …, L, L$ \ll $T, 滞后为l的交叉协方差阵的矩估计为
$$ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_l} = {\left( {\widehat {{\rm{Cov}}}\left( {{X_{i,t}},{X_{j,t - l}}} \right)} \right)_{i,j = 1, \cdots ,k}} $$ 式中
$$ \begin{array}{*{20}{c}} {\widehat {{\rm{Cov}}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) = }\\ {\frac{1}{{T - 1}}\sum\limits_{t = l + 1}^T {\int_S {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{i,0}}} \right)} \right)} \cdot } }\\ {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{j,0}}} \right)} \right){\rm{d}}\mu } \end{array} $$ 滞后为l的交叉相关阵的矩估计为
$$ {{\mathit{\boldsymbol{\hat \gamma }}}_l} = {{\mathit{\boldsymbol{\hat D}}}^{ - 1}}{{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_l}{{\mathit{\boldsymbol{\hat D}}}^{ - 1}} $$ 式中$\mathit{\boldsymbol{\widehat D}} = \operatorname{diag} (\sqrt {\widehat {\operatorname{Var} }\left({{X_{1, t}}} \right)}, \cdots, \sqrt {\widehat {\operatorname{Var} }\left({{X_{k, t}}} \right)})$, 以及$\hat{\operatorname{Var}}\left(X_{i, t}\right)=\frac{1}{T-1} \sum\limits_{t=1}^{T} \int_{S}\left(s\left(\mathit{\boldsymbol{x}}, X_{i, t}\right)-s\left(\mathit{\boldsymbol{x}}, \hat{X}_{i, 0}\right)\right)^{2} \mathrm{d} \mu$.
进一步地, 可通过下面的定理得出估计${{\mathit{\boldsymbol{\hat X}}}_0}$和${\mathit{\boldsymbol{ \boldsymbol{\widehat \varGamma} }}_l}$的渐近性质.
定理 期望向量和交叉协方差阵的估计${{\mathit{\boldsymbol{\hat X}}}_0}$和${\mathit{\boldsymbol{ \boldsymbol{\widehat \varGamma} }}_l}$具有下面的渐近性质:
1) ${{\mathit{\boldsymbol{\hat X}}}_0}$是一个无偏的相合估计, 即E[${{\mathit{\boldsymbol{\hat X}}}_0}$]= ${{\mathit{\boldsymbol{\hat X}}}_0}$及$\mathop {\lim }\limits_{T \to \infty } {{\mathit{\boldsymbol{\hat X}}}_0} = \mathit{\boldsymbol{X}}$成立.
2) 如果当l→∞时, Γl→0k×k, 那么${\mathit{\boldsymbol{ \boldsymbol{\widehat \varGamma} }}_l}$是一个渐近无偏估计, 即$\mathop {\lim }\limits_{T \to \infty } $E(${\mathit{\boldsymbol{ \boldsymbol{\widehat \varGamma} }}_l}$)=Γl成立.
证明:
1) 对于任意的i=1, …, k, 有
$$ {\rm{E}}\left[ {{{\hat X}_{i,0}}} \right] = {\rm{E}}\left[ {\frac{1}{T}\sum\limits_{t = 1}^T {{X_{i,t}}} } \right] = \frac{1}{T}\sum\limits_{t = 1}^T {\rm{E}} \left[ {{X_{i,t}}} \right] = {X_{i,0}} $$ 对于∀ε>0, T→∞, 由Wang等[19]中定理1和定理6可知关系式
$$ P\left\{ {{L_2}\left( {{{\hat X}_{i,0}},{X_{i,0}}} \right) \ge \varepsilon } \right\} \le \frac{{{\rm{Var}}\left( {{{\hat X}_{i,0}}} \right)}}{{{\varepsilon ^2}}} \to 0 $$ 成立, 由此可证得1)成立.
2) 只需证明
$$ \mathop {\lim }\limits_{T \to \infty } {\rm{E}}\left( {{\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right)} \right) = {\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) $$ 注意到关系式
$$ \begin{array}{*{20}{c}} {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{j,0}}} \right)} \right) = }\\ {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t}}} \right) - s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {\mathit{\boldsymbol{x}},{X_{j,0}}} \right)} \right) + }\\ {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,t}}} \right) - s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,0}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{j,0}}} \right)} \right) + }\\ {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {x,{X_{j,0}}} \right)} \right) + }\\ {\left( {s\left( {\mathit{\boldsymbol{x}},{X_{i,0}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{i,0}}} \right)} \right)\left( {s\left( {\mathit{\boldsymbol{x}},{X_{j,t - l}}} \right) - s\left( {\mathit{\boldsymbol{x}},{{\hat X}_{j,0}}} \right)} \right)} \end{array} $$ 成立, 进而由集值协方差的定义可以得出关系式
$$ \begin{array}{*{20}{c}} {\widehat {{\rm{Cov}}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) = {\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) + {\rm{Cov}}\left( {{X_{i,t}},{{\hat X}_{j,0}}} \right) + }\\ {{\rm{Cov}}\left( {{{\hat X}_{i,0}},{X_{j,t - l}}} \right) + {\rm{Cov}}\left( {{{\hat X}_{i,0}},{{\hat X}_{j,0}}} \right)} \end{array} $$ 又当l→∞时, 有Cov(Xi, t, Xj, t-l)=0, 再结合期望向量估计${{\mathit{\boldsymbol{\hat X}}}_0}$的表达式, 可以推出
$$ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{T \to \infty } {\rm{E}}\left( {\widehat {{\rm{Cov}}}\left( {{X_{i,t}},{X_{j,t - l}}} \right)} \right) = }\\ {\mathop {\lim }\limits_{T \to \infty } \frac{1}{{T - 1}}\sum\limits_{t = l + 1}^T {\rm{E}} \left[ {{\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) + } \right.}\\ {\left. {{\rm{Cov}}\left( {{X_{i,t}},{{\hat X}_{j,0}}} \right) + {\rm{Cov}}\left( {{{\hat X}_{i,0}},{X_{j,t - l}}} \right) + {\rm{Cov}}\left( {{{\hat X}_{i,0}},{{\hat X}_{j,0}}} \right)} \right] = }\\ {{\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right) + }\\ {\mathop {\lim }\limits_{T \to \infty } \frac{1}{{T - 1}}\sum\limits_{i = l + 1}^T {\frac{1}{T}} \sum\limits_{s = 1}^T {{\rm{Cov}}} \left( {{X_{i,t}},{X_{j,s}}} \right) + }\\ {\mathop {\lim }\limits_{T \to \infty } \frac{1}{{T - 1}}\sum\limits_{t = l + 1}^T {\frac{1}{T}} \sum\limits_{s = 1}^T {{\rm{Cov}}} \left( {{X_{i,s}},{X_{j,t - l}}} \right) + }\\ {\mathop {\lim }\limits_{T \to \infty } \frac{1}{{T - 1}}\sum\limits_{t = l + 1}^T {\frac{1}{{{T^2}}}} \sum\limits_{s = 1}^T {\sum\limits_{m = 1}^T {{\rm{Cov}}} } \left( {{X_{i,s}},{X_{j,m}}} \right) = }\\ {{\rm{Cov}}\left( {{X_{i,t}},{X_{j,t - l}}} \right)} \end{array} $$ 渐近无偏性2)得证.
2.3 平稳的集值多元时间序列的最优线性预测
下面讨论给定平稳的k维集值多元时间序列观测值X1, X2, …, XT后, 如何求得超前h步的最优线性预测问题, h=1, 2, ….首先,定义一个用于衡量预测质量的准则, 那么使得这个准则达到最优的X1, X2, …, XT的某一个线性组合, 即为最优线性预测.
记$\tilde{\boldsymbol{X}}_{T+h}=\left(\widetilde{X}_{1, T+h}, \cdots, \widetilde{X}_{k, T+h}\right)^{\mathrm{T}}$为任意超前h步预测, ${\boldsymbol{X}}_{T+h}=\left(X_{1, T+h}, \cdots, X_{k, T+h}\right)^{\mathrm{T}}$为T+h时刻的真实观测值.定义均方预测误差为如下的k×k矩阵
$$ \begin{array}{*{20}{c}} {{\rm{MSE}}\left( {{{\mathit{\boldsymbol{\tilde X}}}_{T + h}}} \right) = }\\ {{\rm{E}}\left[ {{{\left( {{L_2}\left( {{{\tilde X}_{1,T + h}},{X_{1,T + h}}} \right), \cdots ,{L_2}\left( {{{\tilde X}_{k,T + h}},{X_{k,T + h}}} \right)} \right)}^{\rm{T}}} \cdot } \right.}\\ {\left. {\left( {{L_2}\left( {{{\tilde X}_{1,T + h}},{X_{1,T + h}}} \right), \cdots ,{L_2}\left( {{{\tilde X}_{k,T + h}},{X_{k,T + h}}} \right)} \right)} \right]} \end{array} $$ 那么称
$$ {{\mathit{\boldsymbol{\hat X}}}_{T + h}} = {\mathit{\boldsymbol{A}}_0} + {\mathit{\boldsymbol{a}}_1}{\mathit{\boldsymbol{X}}_T} + \cdots + {\mathit{\boldsymbol{a}}_T}{\mathit{\boldsymbol{X}}_1} $$ 为最优线性预测,式中A0=(A1, 0, A2, 0, …, Ak, 0)T为k维集值向量截距, a1, a2, …, aT为k×k的实值系数矩阵, 如果${{\mathit{\boldsymbol{\hat X}}}_{T + h}}$使得均方预测误差矩阵达到最小, 即
$$ {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_{T + h}}} \right) \le {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\tilde X}}}_{T + h}}} \right) $$ 3. 区间值多元时间序列
3.1 区间与区间值随机变量
当d=1时, 将${{\mathbb{R}}^{1}}$简写为${\mathbb{R}}$, 那么K(${\mathbb{R}}$)为${\mathbb{R}}$中所有非空有界闭区间族, 即
$$ K({\mathbb{R}}) = \{ A = [\underline a , \bar a]: - \infty < \underline a \leqslant \bar a < \infty , \underline a , \bar a \in {\mathbb{R}}\} $$ 式中a和a分别为区间A的左端点和右端点.还将区间记为A=$[\underline a, \bar a]$=(ac; ar), 式中ac=(${\bar a}$+$\underline a $)/2, ar=(${\bar a}$-$\underline a $)/2分别是区间A的中心和半径.
对于任意2个闭区间A=$[\underline a, \bar a]$=(ac; ar)和B=$[\underline b, \bar b]$=(ac; ar), 加法和数乘运算可以写为
$$ A + B = \left[ {\underline a + \underline b ,\bar a + \bar b} \right] = \left( {{a^{\rm{c}}} + {b^{\rm{c}}};{a^{\rm{r}}} + {b^{\rm{r}}}} \right) $$ $$ \lambda A = \left\{ {\begin{array}{*{20}{l}} {\left[ {\lambda \underline a ,\lambda \bar a} \right],}&{\lambda \ge 0}\\ {\left[ {\lambda \bar a,\lambda \underline a } \right],}&{\lambda < 0} \end{array} = \left( {\lambda {a^{\rm{c}}};\left| \lambda \right|{a^{\rm{r}}}} \right)} \right. $$ 进一步地, 区间A=$[\underline a, \bar a]$和B=$[\underline b, \bar b]$间的L2距离为
$$ \begin{array}{*{20}{c}} {{L_2}\left( {A,B} \right) = {{\left[ {{{\left( {\underline b - \underline a } \right)}^2} + {{\left( {\bar b - \bar a} \right)}^2}} \right]}^{\frac{1}{2}}} = }\\ {{{\left[ {2{{\left( {{b^{\rm{c}}} - {a^{\rm{c}}}} \right)}^2} + 2{{\left( {{b^{\rm{r}}} - {a^{\rm{r}}}} \right)}^2}} \right]}^{\frac{1}{2}}}} \end{array} $$ 由集值随机变量的等价定义(例如, 见Li等[11]的定理1.2.2), 可以推出, 对于$X = \left[{\underline x, \overline x } \right] = ({x^{\text{c}}}; {x^{\text{r}}})$, 如果$\underline x$和$\overline x$或xc和xr是实值的随机变量, 那么X是区间值随机变量.
进一步地, 区间值随机变量X的期望可以写为
$$ {\rm{E}}\left[ X \right] = \left[ {{\rm{E}}\underline x ,{\rm{E}}\bar x} \right] = \left( {{\rm{E}}{x^{\rm{c}}};{\rm{E}}{x^{\rm{r}}}} \right) $$ u[Ω, K(${\mathbb{R}}$)]中区间值随机变量X1和X2间的D2距离可以写为
$$ \begin{array}{*{20}{c}} {{D_2}\left( {{X_1},{X_2}} \right) = {{\left[ {{\rm{E}}{{\left( {{{\underline x }_2} - {{\underline x }_1}} \right)}^2} + {\rm{E}}{{\left( {{{\bar x}_2} - {{\bar x}_1}} \right)}^2}} \right]}^{\frac{1}{2}}} = }\\ {{{\left[ {2{\rm{E}}{{\left( {x_2^{\rm{c}} - x_1^{\rm{c}}} \right)}^2} + 2{\rm{E}}{{\left( {x_2^{\rm{r}} - x_1^{\rm{r}}} \right)}^2}} \right]}^{\frac{1}{2}}}} \end{array} $$ $\mathscr{L}$2[Ω, K(${\mathbb{R}}$)]中的区间值随机变量X1、X2的方差和协方差可以写为
$$ \begin{array}{*{20}{c}} {{\rm{Var}}\left( {{X_1}} \right) = {\rm{E}}{{\left( {{{\underline x }_1} - {\rm{E}}{{\underline x }_1}} \right)}^2} + {\rm{E}}{{\left( {{{\bar x}_1} - {\rm{E}}{{\bar x}_1}} \right)}^2} = }\\ {2{\rm{E}}{{\left( {x_1^{\rm{c}} - {\rm{E}}x_1^{\rm{c}}} \right)}^2} + 2{\rm{E}}{{\left( {x_1^{\rm{r}} - {\rm{E}}x_1^{\rm{r}}} \right)}^2}} \end{array} $$ $$ \begin{array}{*{20}{c}} {{\rm{Cov}}\left( {{X_1},{X_2}} \right) = }\\ {{\rm{E}}\left[ {\left( {{{\underline x }_1} - {\rm{E}}{{\underline x }_1}} \right)\left( {{{\underline x }_2} - {\rm{E}}{{\underline x }_2}} \right) + \left( {{{\bar x}_1} - {\rm{E}}{{\bar x}_1}} \right)\left( {{{\bar x}_2} - {\rm{E}}{{\bar x}_2}} \right)} \right] = }\\ {2{\rm{E}}\left[ {\left( {x_1^{\rm{c}} - {\rm{E}}x_1^{\rm{c}}} \right)\left( {x_2^{\rm{c}} - {\rm{E}}x_2^{\rm{c}}} \right)} \right] + 2{\rm{E}}\left[ {\left( {x_1^{\rm{r}} - {\rm{E}}x_1^{\rm{r}}} \right)\left( {x_2^{\rm{r}} - {\rm{E}}x_2^{\rm{r}}} \right)} \right]} \end{array} $$ 3.2 区间值向量与区间值随机向量
由k个非空有界的闭区间A1=$[{\underline a _1}, {{\bar a}_1}]$, …, Ak=$[{\underline a _k}, {{\bar a}_k}]$构成了k维区间值向量A=(A1, A2, …, Ak)T.当k=2时, A是二维欧式空间中的矩形.当k=3时, A是三维欧式空间中的长方体.当k≥4时, A是k维的超立方体.可以发现, 相较于集值向量, 区间值向量具有更加直观的几何形状.
称向量X=(X1, X2,…, Xk)T为k维区间值随机向量, 如果X1, X2, …, Xk是K(${\mathbb{R}}$)中的区间值随机变量.记u[Ω1×Ω2×…×Ωk, Kk(${\mathbb{R}}$)]为k维区间值随机向量族.
k维区间值随机向量X的期望E[X]为
$$ \begin{array}{*{20}{c}} {{\rm{E}}\left[ \mathit{\boldsymbol{X}} \right] = {{\left( {\left[ {{\rm{E}}{{\underline x }_1},{\rm{E}}{{\bar x}_1}} \right], \cdots ,\left[ {{\rm{E}}{{\underline x }_k},{\rm{E}}{{\bar x}_k}} \right]} \right)}^{\rm{T}}} = }\\ {{{\left( {\left( {{\rm{E}}x_1^{\rm{c}};{\rm{E}}x_1^{\rm{r}}} \right), \cdots ,\left( {{\rm{E}}x_1^{\rm{c}};{\rm{E}}x_1^{\rm{r}}} \right)} \right)}^{\rm{T}}}} \end{array} $$ k维区间值随机向量的协方差阵, 交叉协方差阵及交叉相关阵形式与k维集值随机向量的相同, 在此不再给出.
进一步地, 注意到k维区间值随机向量X的任一分量${X_i} = \left[{{{\underline x }_i}, {{\bar x}_i}} \right]$都可以由其2个端点${{{\underline x }_i}}$和${{{\bar x}_i}}$或中心xic半径xir所决定, 所以可以通过实值随机变量${\underline x _1}, {{\bar x}_1}, \cdots, {\underline x _k}, {{\bar x}_k}$或$x_{1}^{\mathrm{c}}, x_{1}^{\mathrm{r}}, \cdots, x_{k}^{\mathrm{e}}, x_{k}^{\mathrm{r}}$来研究X的性质.需注意的是, 在如此分析问题时, 应保持关系式${{{\underline x }_i} \leqslant {{\bar x}_i}}$或xir≥0, 对所有的i=1, 2,…, k均成立, 否则区间值随机向量将无意义.
3.3 平稳的区间值多元时间序列
平稳的k维区间值多元时间序列由时间生成的k维区间值随机向量序列X1, X2, …, XT组成, 并且其前二阶矩不随时间变化而变化.
给定平稳的k维区间值多元时间序列观测值X1, X2, …, XT后, 可以通过极小化均方预测误差$\operatorname{MSE}\left(\widetilde{\boldsymbol{X}}_{T+h}\right)$求出最优线性预测
$$ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{T + h}} = {\mathit{\boldsymbol{A}}_0} + {\mathit{\boldsymbol{a}}_1}{\mathit{\boldsymbol{X}}_T} + \cdots + {\mathit{\boldsymbol{a}}_T}{\mathit{\boldsymbol{X}}_1} = }\\ {\left( {\begin{array}{*{20}{c}} {\left( {\left[ {{{\underline a }_{1,0}},{{\bar a}_{1,0}}} \right] + \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^k {{a_{1i,t}}} } \left[ {{{\underline x }_{i,T - t + 1}},{{\bar x}_{i,T - t + 1}}} \right]} \right)}\\ \vdots \\ {\left( {\left[ {{{\underline a }_{k,0}},{{\bar a}_{k,0}}} \right] + \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^k {{a_{ki,t}}} } \left[ {{{\underline x }_{i,T - t + 1}},{{\bar x}_{i,T - t + 1}}} \right]} \right)} \end{array}} \right)} \end{array} $$ 式中:$\boldsymbol{A}_{0}=\left(\left[\underline{a}_{1, 0}, \bar{a}_{1, 0}\right], \cdots, \left[\underline{a}_{k, 0}, \bar{a}_{k, 0}\right]\right)^{T}$为k维区间值向量截距;a1, a2, …, aT为k×k的系数矩阵.
3.4 区间值多元自回归模型
p阶的k维区间值多元自回归模型, 简记为IVAR(p)模型, 其表达式为
$$ {\mathit{\boldsymbol{X}}_t} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_0} + {\phi _1}{\mathit{\boldsymbol{X}}_{t - 1}} + {\phi _2}{\mathit{\boldsymbol{X}}_{t - 2}} + \cdots + {\phi _p}{\mathit{\boldsymbol{X}}_{t - p}} + {\mathit{\boldsymbol{Z}}_t} $$ 式中:$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{0}=\left(\left[\underline{\phi}_{1, 0}, \bar{\phi}_{1, 0}\right], \cdots, \left[\underline{\phi}_{k, 0}, \bar{\phi}_{k, 0}\right]\right)^{\mathrm{T}}$为k维区间值向量截距;ϕ1, ϕ2, …, ϕp为k×k的实值系数矩阵;Zt为不相关的同分布的k维区间值随机向量, 并且Zt与Xt-1, …, X1不相关.为讨论方便, 下面进一步假设ϕ1, ϕ2, …, ϕp的所有元素皆非负.
记Γ0=Cov(Xt)为k维区间值多元时间序列的协方差矩阵, Zt的协方差阵为Σ.由IVAR(p)模型的表达式可以推出IVAR(p)序列Xt的协方差阵为
$$ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} = {\phi _1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1} + {\phi _2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2} + \cdots + {\mathit{\boldsymbol{\phi}} _p}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p} + \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} $$ 另一方面, 对于∀l>0, 由IVAR(p)模型的表达式可以推出关系式
$$ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_l} = {\phi _1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{l - 1}} + {\phi _2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{l - 2}} + \cdots + {\phi _p}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{l - p}} $$ 成立.然后分别取l=1, 2, …, p, 联立方程组, 可以得到
$$ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0}}&{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{\rm{T}}}& \cdots &{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{p - 1}^{\rm{T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}}&{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0}}& \cdots &{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{p - 2}^{\rm{T}}}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{p - 1}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{p - 2}}}& \cdots &{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\phi _1}}\\ {{\phi _2}}\\ \vdots \\ {{\phi _p}} \end{array}} \right) $$ 式中使用了命题3的结论Γ-l=ΓlT.通过求解这个方程组, 可以得到系数矩阵ϕ1, ϕ2, …, ϕp的估计, 记为${\widehat {\boldsymbol{\phi}} _1}, {\widehat {\boldsymbol{\phi}} _2}, \cdots, {\widehat {\boldsymbol{\phi}} _p}$.进一步地, 将系数矩阵的估计代入IVAR(p)模型中推出维区间值向量截距Φ0的估计${\mathit{\boldsymbol{ \boldsymbol{\widehat \varPhi} }}_{\text{0}}}$.得到模型系数的估计之后, IVAR(p)模型的一步预测可以写为
$$ {{\mathit{\boldsymbol{\tilde X}}}_{t + 1}} = {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_0} + {{\hat \phi }_1}{\mathit{\boldsymbol{X}}_t} + {{\hat \phi }_2}{\mathit{\boldsymbol{X}}_{t - 1}} + \cdots + {{\hat \phi }_p}{\mathit{\boldsymbol{X}}_{t - p + 1}} $$ 4. 数值模拟与实证分析
4.1 数值模拟
考虑一个一阶的2维区间值多元自回归模型
$$ {\mathit{\boldsymbol{X}}_t} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_0} + {\phi _1}{\mathit{\boldsymbol{X}}_{t - 1}} + {\mathit{\boldsymbol{Z}}_t},t = 2,3, \cdots ,T $$ 式中:$\boldsymbol{\Phi}_{0}=\left(\left[\underline{\phi}_{1, 0}, \bar{\phi}_{1, 0}\right], \left[\underline{\phi}_{2, 0}, \bar{\phi}_{2, 0}\right]\right)^{\mathrm{T}}$为2维区间值向量截距;$\boldsymbol{\phi}_{1}=\left(\begin{array}{ll}{\boldsymbol{\phi}_{11, 1}} & {\boldsymbol{\phi}_{12, 1}} \\ {\boldsymbol{\phi}_{21, 1}} & {\boldsymbol{\phi}_{22, 1}}\end{array}\right)$为实值回归系数矩阵;${\boldsymbol{Z}_t} = \left( \begin{array}{l} {Z_{1,t}}\\ {Z_{2,t}} \end{array} \right) = \left( \begin{array}{l} ({z_{1,t}}^{\rm{c}};{z_{1,t}}^{\rm{r}})\\ ({z_{2,t}}^{\rm{c}};{z^{\rm{r}}}) \end{array} \right)$为与区间值时间序列Xt-1, Xt-2, …, X1不相关的噪声序列, 并且其分量的中心半径z1, tc、z2, tc与z1, tr、z2, tr分别服从正态分布N(0, σ2)与伽马分布Ga(α, λ).下面取ϕ1, 0=0.2, ϕ1, 0=0.5, ϕ2, 0=0.1, ϕ2, 0=0.3, ϕ11, 1=0.4, ϕ12, 1=0.2, ϕ21, 1=0.1, ϕ22, 1=0.5, 以及σ=0.3, α=1, λ=20.分别取T=100, 500, 1 000, 模拟1 000次, 将参数估计的均方误差列入表 1中.可以看出, 随着T增加, 各个系数估计的均方误差逐渐减小, 这说明了方法具有相合性.
表 1 系数估计的均方误差Table 1. MSEs of coefficient estimations系数 T=100 T=500 T=1 000 ϕ1, 0 0.001 7 0.001 3 0.001 1 ϕ1, 0 0.037 6 0.014 6 0.011 5 ϕ2, 0 0.001 7 0.001 9 0.001 9 ϕ2, 0 0.027 8 0.019 4 0.017 1 ϕ11, 1 0.008 0 0.001 4 0.000 8 ϕ12, 1 0.020 3 0.011 4 0.010 6 ϕ21, 1 0.017 0 0.011 8 0.010 7 ϕ22, 1 0.008 0 0.001 5 0.000 7 4.2 实证分析
本节分析2017-06-16—2017-08-08北京市的空气指数数据, 数据收集于网站http://beijingair.sinaapp.com.数据由北京市12个空气监测站所收集到的空气指数、空气水平、主要污染物、PM 2.5、PM 10、CO、NO2、SO2的质量浓度组成, 每个观测站收集到的数据都是每小时更新1次.
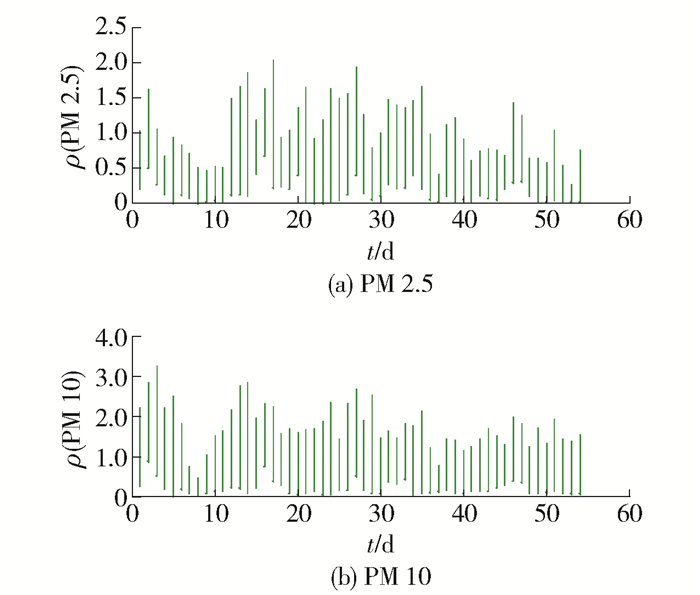
本文的研究对象是PM 2.5和PM 10的质量浓度, 取每一天里这些空气监测站收集到的PM 2.5和PM 10质量浓度的最小值和最大值作为当天的区间值随机向量观测值的端点, 并分别记每天的PM 2.5和PM 10的质量浓度为X1, t和X2, t.为计算方便, 将所有数据除以100. 图 1给出了由PM 2.5和PM 10的质量浓度组成的区间值二元时间序列.
通过计算, 可以得出区间值多元时间序列{Xt=(X1, t, X2, t)T:t=1, 2, …, 54}的协方差矩阵和自协方差矩阵的估计
$$ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_0} = \left( {\begin{array}{*{20}{c}} {0.21}&{0.17}\\ {0.17}&{0.35} \end{array}} \right),{{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_1} = \left( {\begin{array}{*{20}{c}} {0.11}&{0.10}\\ {0.10}&{0.20} \end{array}} \right) $$ 由上面的估计可以推出IVAR(1)模型系数的估计
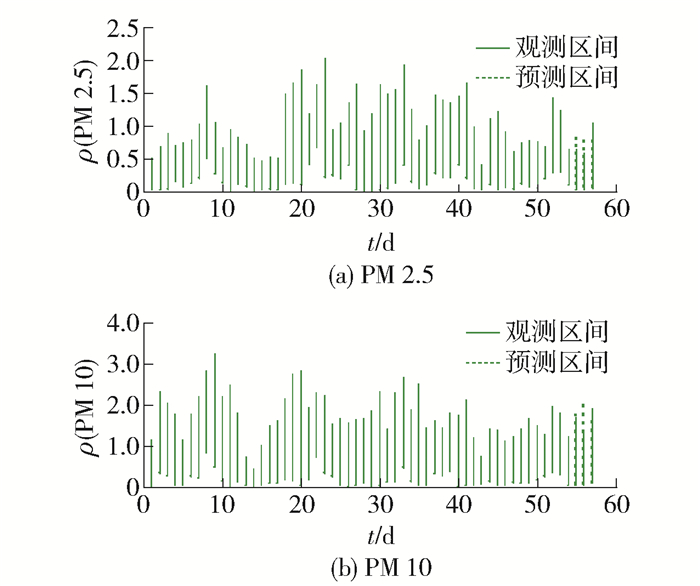
$$ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_{1,0}} = \left[ {0.0651,0.0691} \right],{{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_{2,0}} = \left[ {0.4820,0.7364} \right] $$ $$ {\widehat \phi _1} = \left( {\begin{array}{*{20}{c}} {0.5108}&{0.0243}\\ {0.0364}&{0.5559} \end{array}} \right) $$ 进一步地做了3步预测, 如图 2所示, 实线段是真实的观测区间, 虚线段是通过IVAR(1)模型得到的预测区间.可以看出,预测区间明显地反映出了接下来的趋势.进一步地, 可以计算出${{\mathit{\boldsymbol{\hat X}}}_{T + 1}}$、${{\mathit{\boldsymbol{\hat X}}}_{T + 2}}$和${{\mathit{\boldsymbol{\hat X}}}_{T + 3}}$的均方预测误差为
$$ {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_{T + 1}}} \right) = \left( {\begin{array}{*{20}{c}} {0.0494}&{0.0210}\\ {0.0210}&{0.0090} \end{array}} \right) $$ $$ {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_{T + 2}}} \right) = \left( {\begin{array}{*{20}{c}} {0.0705}&{0.1920}\\ {0.1920}&{0.5231} \end{array}} \right) $$ $$ {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_{T + 3}}} \right) = \left( {\begin{array}{*{20}{c}} {0.0561}&{0.0291}\\ {0.0291}&{0.0151} \end{array}} \right) $$ 5. 结论
1) 对于实际中多元的复杂的时间序列数据, 探讨多元集值时间序列基础理论, 建立其时间序列模型是非常必要的.由集值随机向量的定义可知, 集值随机向量是一个具有特定几何特征的集值随机变量.如果忽略这个向量形式而依旧将其视为集值随机变量来讨论相关的问题, 将会导致信息的损失, 这是一种非常粗糙的处理方式.因此, 从集值向量的定义出发, 进一步定义了集值随机向量, 并讨论了集值随机变量的期望向量、协方差阵、交叉协方差阵以及交叉相关阵的定义及性质.
2) 由于区间可以通过它的2个端点或中心半径来确定, 因此对区间值多元时间序列的讨论是一个相对更为具体的问题.相较而言集合则抽象得多, 对集值多元时间序列的讨论本质上是对区间值多元时间序列的一个推广.给出了集值多元时间序列及其平稳性的定义, 并研究了在平稳的条件下, 集值多元时间序列的期望向量、交叉协方差阵与交叉相关阵的性质, 这些统计量的估计及估计的渐近性质, 以及最优线性预测问题.以上研究为对集值多元时间序列的进一步讨论打下了理论基础.
3) 讨论了区间值情形下的随机向量和多元时间序列, 并进一步给出区间值多元自回归模型的表达形式及估计.最后, 通过一个实证分析展示了本文提出的模型及方法在实践中的应用.
-
表 1 系数估计的均方误差
Table 1 MSEs of coefficient estimations
系数 T=100 T=500 T=1 000 ϕ1, 0 0.001 7 0.001 3 0.001 1 ϕ1, 0 0.037 6 0.014 6 0.011 5 ϕ2, 0 0.001 7 0.001 9 0.001 9 ϕ2, 0 0.027 8 0.019 4 0.017 1 ϕ11, 1 0.008 0 0.001 4 0.000 8 ϕ12, 1 0.020 3 0.011 4 0.010 6 ϕ21, 1 0.017 0 0.011 8 0.010 7 ϕ22, 1 0.008 0 0.001 5 0.000 7 -
[1] BOX G E P, JENKIS G M, REINSEL G C, et al. Time series analysis:forecasting and control[M]. 5th ed. New Jersey:Wiley, 2015:47-92.
[2] TSAY R S. Multivariate time series analysis with R and financial applications[M]. New Jersey:Wiley, 2014:27-89.
[3] BROCKWELL P J, DAVIS R A. Time series:theory and methods[M]. Berlin:Springer, 2015:77-110.
[4] AUMANN R J. Integrals of set-valued functions[J]. Journal of Mathematical Analysis and Applications, 1965, 12(1):1-12. doi: 10.1016-0022-247X(65)90049-1/
[5] HIAI F, UMEGAKI H. Integrals, conditional expectations, and martingales of multivalued functions[J]. Journal of Multivariate Analysis, 1977, 7(1):149-182. doi: 10.1016/0047-259X(77)90037-9
[6] LYASHENKO N N. Statistics of random compacts in Euclidean space[J]. Journal of Mathematical Sciences, 1983, 21(1):76-92.
[7] VITALE R A. Lp metrics for compact, convex sets[J]. Journal of Approximation Theory, 1985, 45(3):280-287. doi: 10.1016/0021-9045(85)90051-6
[8] DIAMOND P. Least squares fitting of compact set-valued data[J]. Journal of Mathematical Analysis and Applications, 1990, 147(2):351-362. doi: 10.1016/0022-247X(90)90353-H
[9] LI S, OGURA Y. Convergence of set valued sub- and super-martingales in the Kuratowski-Mosco sense[J]. Annals of Probability, 1998, 26(3):1384-1402. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JAKO199811922260790
[10] LI S, OGURA Y. Convergence of set-valued and fuzzy-valued martingales[J]. Fuzzy Sets and Systems, 1999, 101(3):453-461. doi: 10.1016/S0165-0114(97)00092-4
[11] LI S, OGURA Y, KREINOVICH V. Limit theorems and applications of set-valued and fuzzy set-valued random variables[M]. Dordrecht:Kluwer Academic Publishers, 2002:1-108.
[12] GIL M, LUBIANO M, MONTENEGRO M, et al. Least squares fitting of an affine function and strength of association for interval-valued data[J]. Metrika, 2002, 56(2):97-111. doi: 10.1007/s001840100160
[13] YANG X, LI S. The Dp-metric space of set-valued random variables and its application to covariances[J]. International Journal of Innovative Computing, Information and Control, 2005, 1(1):73-82.
[14] 张文修, 李寿梅, 汪振鹏, 等.集值随机过程引论[M].北京:科学出版社, 2007:155-208. [15] WANG X, LI S. The interval autoregressive time series model[C]//Proceedings of IEEE International Conference on Fuzzy Systems. Washington D C: IEEE Computer Society, 2011: 2528-2533.
[16] GONZALEZ-RIVERA G, LIN W. Constrained regression for interval-valued data[J]. Journal of Business and Economic Statistics, 2013, 31(4):473-490.
[17] 唐娜娜.带约束条件的区间线性回归及自回归时间序列模型[D].北京: 北京工业大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10005-1018705178.htm TANG N. Interval-valued linear regression and autoregressive time series model with constrains[D]. Beijing: Beijing University of Technology, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10005-1018705178.htm
[18] 王洵.平稳集值时间序列与区间值时间序列的自回归模型的研究[D].北京: 北京工业大学, 2011. WANG X. Stationary set-valued time series and interval-valued time series autoregressive model[D]. Beijing: Beijing University of Technology, 2011. (in Chinese)
[19] WANG X, ZHANG Z, LI S. Set-valued and interval-valued stationary time series[J]. Journal of Multivariate Analysis, 2016, 145:208-223. doi: 10.1016/j.jmva.2015.12.010
[20] 章磊.多维区间值向量自回归时间序列模型理论研究和实证分析[D].北京: 北京工业大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10005-1019700868.htm ZHANG L. Theoretical research and empirical analysis of interval-valued vector autoregressive time series models[D]. Beijing: Beijing University of Technology, 2018. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10005-1019700868.htm
[21] WANG R, WANG Z. Set-valued stationary processes[J]. Journal of Multivariate Analysis, 1997, 63(1):180-198. doi: 10.1006/jmva.1997.1702
-
期刊类型引用(1)
1. 樊倩男,刘树勇,蔡云帆,宋杰,高振生. 基于Transformer的稳健电力负荷预测. 电力大数据. 2022(05): 19-27 .  百度学术
百度学术
其他类型引用(2)



 下载:
下载: