Contact Characteristics Control Method of Spiral Bevel Gears Based on Ease-off
-
摘要:
为了获得良好的传动质量，需要对螺旋锥齿轮的齿形进行合理设计以控制其接触特性.通过构建螺旋锥齿轮完全共轭齿面及对共轭差曲面进行齿形设计，在共轭齿面求解中引入预置的传动误差，利用相对曲率及线共轭曲面特性建立接触区形态参数与共轭差曲面修形量之间的关联模型，使得所有接触特性参数得以准确控制.提出了一种基于齿面特征共轭接触线修形量拟合及插值算法的共轭差曲面的设计及计算方法，该方法可避免齿根部位由于根切因素导致的修形量求解失败，同时仅需求解少量特征点修形量，便可实现整个共轭差曲面的设计，从而大大提高运算效率.最后通过齿形设计实例及齿面接触分析验证了该方法的正确性.
Abstract:To obtain good transmission quality, it is necessary to design the tooth profile of spiral bevel gears to control their contact characteristics. The tooth profile was designed through the construction of spiral bevel gear conjugate tooth profiles and ease-off tooth surface. The preset transmission errors were introduced in the solution of conjugate tooth surface, and a correlation model between the contact area morphological parameters and the ease-off tooth surface modification was established by using the relative curvature and line conjugate surface characteristics. All the contact parameters were accurately controlled. A designed method of ease-off tooth surface and contact area shape based on tooth surface characteristic conjugate contact line modification and interpolation algorithm was proposed, by which the tooth root due to modification of the factors that lead to the failure of solving undercutting can be avoided. At the same time, this method can be used to design the entire ease-off tooth surface by only a small number of feature points, which can significantly improve the computational efficiency. Finally, the correctness of the method were verified by the tooth design examples and tooth contact analysis.
-
螺旋锥齿轮是机械传动中广泛应用的基础传动零件，其接触特性直接影响齿轮副的啮合传动质量.国内外学者在螺旋锥齿轮的接触特性控制方面开展了较为系统的研究.接触特性控制主要包括接触区形态控制和传动误差控制两方面.在传动误差控制方面，Litvin等[1]、Fuentes等[2]通过将传动误差曲线设计成抛物线并限制传动误差的最大值以获得具有低噪声水平的螺旋锥齿轮. Stadtfeld等[3]将传动误差曲线设计为四阶多项式以降低螺旋锥齿轮在载荷作用下安装变形的敏感度性，并减小动载荷波动. Su等[4]发现将传动误差曲线设计为七阶多项式可以进一步减小齿轮副的齿根弯曲应力. Mermoz等[5]、Astoul等[6]通过优化齿面接触压力和传动误差控制螺旋锥齿轮传动的噪声及振动.曹雪梅等[7]控制接触迹线通过齿面预定的三点来控制传动误差.在接触区形态控制方面，Litivin[8-9]等在格里森局部共轭原理基础上提出了局部接触综合方法，通过控制齿面在接触参考点的曲率参数控制接触区的形态和传动误差的幅值；王小椿等[10-11]、吴训成等[12]又在局部接触综合理论基础上应用曲率张量和活动标架法进一步建立了齿面三阶接触特性的控制模型. Ignacio等[13]提出一种基于双重螺旋法的机床调整参数计算方法，并运用抛物线型刀具调整齿面接触区形态. Cao等[14]通过控制接触迹线过齿面预定的三点来控制接触路径. Simon[15]研究了齿形误差及安装误差对螺旋锥齿轮接触形态的影响.以上方法主要通过控制接触参考点的接触椭圆形态及其变化趋势来间接控制齿面整个啮合过程的接触状态，因此通常需要利用接触分析法，并通过反复调整才能在整个齿面上获得较为理想的接触区形态.此外这些方法涉及复杂的曲率及诱导曲率计算，需要较为深入的理论基础.
为了实现齿面在整个啮合过程中的准确控制，近年来基于共轭差曲面的螺旋锥齿轮接触特性控制方法，由于其直观的计算原理、相对简单的理论基础受到广泛关注. Shih等[16-17]研究了在螺旋锥齿轮的切齿调整计算时采用修正共轭差曲面的方法控制传动误差和接触路径.苏进展等[18]通过预置齿轮副重合度、对称抛物线型传动误差及接触椭圆参数，分别沿接触路径和啮合线对弧齿锥齿轮小轮齿面进行双向修形，得到了与大轮点接触的小轮齿面.蔡香伟等[19]、曹雪梅等[20]提出基于高阶传动误差的弧齿锥齿轮小轮齿面主动修形，设计了2个啮合点确定接触迹线并预置椭圆半长轴的长度确定沿啮合线的修形量，获得了与大轮点接触的小轮的高阶修形齿面.上述研究多侧重研究共轭差曲面的宏观设计以及实现其修形对应的切齿调整参数的计算方法，但并未给出齿轮接触特性参数与共轭差曲面的详细对应关系，而这正是保证齿面获得预定接触特性的关键.
针对这一问题，本文研究齿面接触特性参数的定义方法, 基于少量齿面特征点相对于共轭接触线修形量的拟合及插值，建立了接触特性参数与共轭差曲面修形量网格坐标的计算模型.在简化了求解过程的同时保证了接触特性与共轭差曲面对应关系的准确性以及求解过程的可靠性.
1. 共轭差曲面求解的总体思路
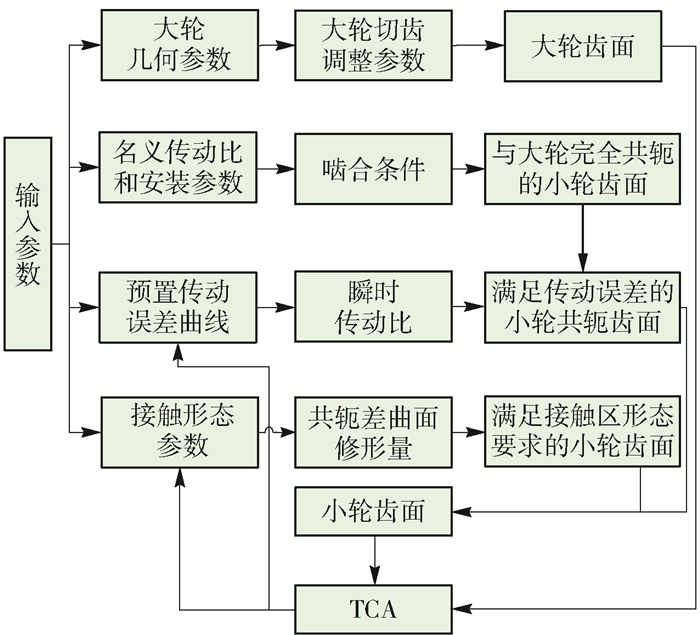
保证螺旋锥齿轮接触特性的关键在于按照接触特性参数对与大轮齿面完全共轭的小轮齿面进行适当修形得到小轮实际齿面.小轮实际齿面相对完全共轭齿面的修形量即为共轭差曲面.其求解过程如图 1所示，首先在保证大轮几何参数(压力角、螺旋角等)的基础上确定一组大轮的切齿调整参数及刀具参数，从而可获得大轮的齿面方程.利用大轮齿面方程在保证齿轮副传动条件(传动比、安装距、偏置距)下求解与大轮完全共轭的小轮齿面.再通过预置的齿轮副传动误差特性确定齿轮副啮合传动的瞬时传动比关系，并在此基础上求解基于给定传动误差的小轮共轭齿面.最后通过接触参考点位置和接触迹线方向确定共轭啮合轨迹，通过瞬时接触椭圆长度控制接触区大小，求解保证接触区形态的共轭差曲面.将其与保证传动误差下的小轮共轭齿面叠加则可获得小轮的实际齿面.
2. 与大轮共轭的小轮齿面求解
2.1 大轮齿面求解
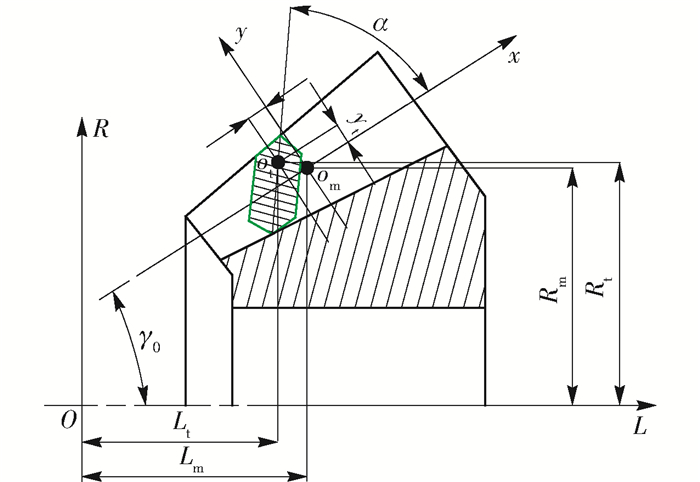
首先需要求解大轮的齿面方程，如图 2所示，建立大轮的切齿啮合坐标系Σ={o, i, j, k}，o为摇台中心，k为摇台轴线，并构建大轮坐标系Σg={og, ig, jg, kg}，og为大轮轴错交点，ig为大轮轴线矢量.构建刀盘坐标系Σc={oc, ic, jc, kc}，oc为刀盘中心，kc与k同向，则刀盘上任意一点的法矢nc、切矢tc及径矢rc可表示为
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{t}}_{\rm{c}}} = \mathit{\boldsymbol{M}}{\left( { - {\theta _{\rm{r}}}} \right)_\mathit{\boldsymbol{k}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{t}}}} \right)_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{c}}}} \right)_\mathit{\boldsymbol{k}}}{\left( {0,\sin \varphi , - \cos \varphi } \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{n}}_{\rm{c}}} = \mathit{\boldsymbol{M}}{\left( { - {\theta _{\rm{r}}}} \right)_\mathit{\boldsymbol{k}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{t}}}} \right)_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{c}}}} \right)_\mathit{\boldsymbol{k}}}{\left( {0, - \cos \varphi , - \sin \varphi } \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{r}}_{\rm{c}}} = \mathit{\boldsymbol{M}}{\left( { - {\theta _{\rm{r}}}} \right)_\mathit{\boldsymbol{k}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{t}}}} \right)_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{M}}{\left( {{\theta _{\rm{c}}}} \right)_\mathit{\boldsymbol{k}}}{\left( {0,r,0} \right)^{\rm{T}}} - b{\mathit{\boldsymbol{t}}_{\rm{c}}} \end{array} \right. $$ (1) 式中：θc为刀盘上任意一点的相位角；θt为刀倾角；θr为刀转角；$φ$为刀盘压力角；r为刀盘刀尖半径；M(θc)k为某矢量绕坐标轴k旋转θc的变换矩阵；b为刀尖沿切矢tc的反方向到瞬时接触点的距离.
将式(1)中各矢量tc、nc、rc变换到大轮坐标系Σg中，则
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{t}}_{\rm{g}}} = \mathit{\boldsymbol{M}}{\left( q \right)_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{t}}_{\rm{c}}}\\ {\mathit{\boldsymbol{n}}_{\rm{g}}} = \mathit{\boldsymbol{M}}{\left( q \right)_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{n}}_{\rm{c}}}\\ {\mathit{\boldsymbol{r}}_{\rm{g}}} = {\mathit{\boldsymbol{r}}_\mathit{\boldsymbol{d}}} + S{\left( {\cos q, - \sin q,0} \right)^{\rm{T}}} + \mathit{\boldsymbol{M}}{\left( q \right)_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{r}}_{\rm{c}}}\\ {\mathit{\boldsymbol{r}}_{\rm{d}}} = {x_{\rm{h}}}{\left( { - \cos \gamma ,0, - \sin \gamma } \right)^{\rm{T}}} - {x_{\rm{b}}}\mathit{\boldsymbol{k}} + {x_{\rm{e}}}\mathit{\boldsymbol{j}} \end{array} \right. $$ (2) 式中：q为刀盘中心相对摇台的相位角，即摇台角；S为径向刀位；xh为水平轮位；xb为床位；xe为垂直轮位；γ为机床安装根锥角；rd为大轮轴交错点到大轮的切齿啮合坐标系原点o的径矢.
式(2)中rg(q, θc, b)为切齿加工时的刀盘曲面族，其对应展成的大轮齿面应满足啮合方程，则导入啮合方程后可消去变量b，则大轮齿面方程为rg(q, θc)，当采用成形法加工时，则q为固定的角向刀位，则大轮齿面方程为rg(θc, b).
2.2 基于传动误差与大轮共轭的小轮齿面求解
求得大轮齿面方程后，可求解与其共轭的小轮齿面.在图 2中按照齿轮副传动时的安装位置要求构建小轮坐标系Σp={op, ip, jp, kp}，其中op为小轮轴错交点，ip为小轮轴线矢量，e为齿轮副的偏置距，σ为齿轮副的轴交角.偏置距e为0，对应为弧齿锥齿轮小轮共轭齿面的解.由于大小轮齿面完全共轭啮合，每一啮合瞬时大小轮均沿一条啮合线接触，设p点为某一啮合瞬时大小轮齿面接触线上的啮合点，则在p点大小轮齿面满足
$$ \left\{ \begin{array}{l} {v_{{\rm{gp}}}} \cdot \mathit{\boldsymbol{n}} = \left( {{\mathit{\boldsymbol{v}}_{\rm{g}}} - {\mathit{\boldsymbol{v}}_{\rm{p}}}} \right) \cdot {\mathit{\boldsymbol{n}}_{\rm{g}}} = 0\\ {\mathit{\boldsymbol{v}}_{\rm{g}}} = {\omega _{\rm{g}}}{\mathit{\boldsymbol{i}}_{\rm{g}}} \times \mathit{\boldsymbol{M}}{\left( {{\eta _{\rm{g}}}} \right)_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{r}}_{\rm{g}}}\\ {\mathit{\boldsymbol{v}}_{\rm{p}}} = {\omega _{\rm{p}}}{\mathit{\boldsymbol{i}}_{\rm{p}}} \times {\mathit{\boldsymbol{r}}_{\rm{p}}} \end{array} \right. $$ (3) $$ {i_{{\rm{gp}}}} = \frac{{{\omega _{\rm{p}}}}}{{{\omega _{\rm{g}}}}} $$ (4) $$ {\mathit{\boldsymbol{r}}_{\rm{p}}} = \mathit{\boldsymbol{M}}{\left( {{i_{{\rm{gp}}}} \cdot {\eta _{\rm{g}}}} \right)_\mathit{\boldsymbol{i}}}\left( {{\mathit{\boldsymbol{r}}_{\rm{g}}} + {{\left( {0,e,0} \right)}^{\rm{T}}}} \right) $$ (5) 式中：vg、vp分别为大、小轮在共轭啮合点的瞬时线速度；ωg、ωp分别为大、小轮共轭啮合时的瞬时角速度；rp为啮合点p在小轮坐标系中的矢量表示；ηg为p点处于啮合状态时大轮的转角(相位角).
当考虑大小轮的理论传动误差为0，即齿轮副按定传动比传动时有
$$ {i_{{\rm{gp}}}} = {z_{\rm{g}}}/{z_{\rm{p}}} $$ (6) 式中：zg为大轮齿数；zp为小轮齿数.
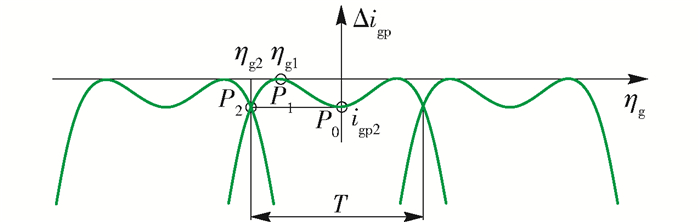
但相关文献的研究表明，这种无传动误差的齿面对齿轮加工误差及安装误差的适应性差，通常需要将齿轮副的传动误差设计为多项式的形式，常采用的为二次多项式，即传动误差曲线为抛物线型，也有将其设计为高阶多项式形式，以减小齿轮副在重合度影响下的啮合刚度波动.进行齿形设计时首先需要确定齿轮副传动误差曲线形态，并根据传动误差形态以及多项式的曲线特性，选择多项式的阶次.如图 3所示，以齿轮副啮合传动时大轮转角ηg为横坐标，传动比Δigp为纵坐标，传动误差曲线关于纵坐标对称且中间呈下凹形态，则应构建瞬时传动比函数
$$ \Delta {i_{{\rm{gp}}}} = a \times \eta _{\rm{g}}^6 + b \times \eta _{\rm{g}}^4 + c \times \eta _{\rm{g}}^2 $$ (7) 式中仅保留多项式中0~6阶的偶次项.之后确定多项式系数a、b、c，这些系数可通过给定曲线中的特征点的坐标获得.如图 3所示，可给定P0(0, igp2)、P1(ηg1, 0)、P2(ηg2, igp2)点的坐标，带入式(7)中求解方程得到多项式系数.其中ηg2=0.5T，T=360/zg为大轮啮合周期.若传动误差仅为二次多项式，此时P1=P0(0, 0)，则瞬时传动比为
$$ {i_{{\rm{gp}}}} = \Delta {i_{{\rm{gp}}}} + \frac{{{z_{\rm{g}}}}}{{{z_{\rm{p}}}}} $$ (8) 在大轮与小轮齿面的共轭接触过程中，大轮齿面也构成一个三参数的曲面族rg(q, θc, ηg).则根据大轮齿面上p点在其轴截面上的位置(R, L)代入大轮齿面方程可求解出其中的q、θc，再代入式(3)可确定大小轮齿面在p点接触时的相位角ηg.将求解的以上3个曲面族参数代入到式(5)中，并将其变换到小轮坐标系，可得与大轮共轭的小轮齿面方程
$$ {{\mathit{\boldsymbol{r'}}}_{\rm{p}}} = \mathit{\boldsymbol{M}}{\left( \sigma \right)_\mathit{\boldsymbol{j}}}{\mathit{\boldsymbol{r}}_{\rm{p}}} $$ (9) 3. 保证接触特性的共轭差曲面求解
3.1 接触特性定义
1) 接触参考点位置：在大轮轴截面内定义接触参考点的位置，建立如图 4所示二维坐标系xomy，其中以齿面中点om为原点，以齿面节锥线所在直线为x轴，垂直于节锥线为y轴.在该坐标系中任意指定接触参考点ot(xt, yt)，为了定义方便引入参数h、f表示ot相对于om在齿高和齿长方向的距离百分比，则以轴交错点为原点的大轮轴截面坐标系中的位置可表示为
$$ \left\{ \begin{array}{l} {L_{\rm{t}}} = {L_{\rm{m}}} + {x_{\rm{t}}}\cos {\gamma _0} - {y_{\rm{t}}}\sin {\gamma _0}\\ {R_{\rm{t}}} = {R_{\rm{m}}} + {x_{\rm{t}}}\sin {\gamma _0} + {y_{\rm{t}}}\cos {\gamma _0}\\ {x_{\rm{t}}} = fF\\ {y_{\rm{t}}} = hH \end{array} \right. $$ (10) ![]()
图 4 接触特性参数在大轮轴截面坐标系中的表示Figure 4. Expression of contact characteristic parameters on the topology coordinate of gear式中：Lm、Rm为齿面中点om在大轮轴截面坐标系LOR中的坐标；Lt、Rt为接触参考点ot在大轮轴截面坐标系LOR中的坐标；γ0为大轮节锥角；F为大轮齿面宽；H为大轮齿高.
2) 接触迹线：接触迹线在参考点处与齿面节锥线夹角α定义为接触迹线的倾斜方向，且假定接触迹线为直线，则接触迹线在xomy的方程可表示为
$$ y = \tan \alpha \cdot x + b $$ (11) 参数b为
$$ b = {R_1} - \tan \alpha \cdot {L_1} $$ (12) $$ \left( {{L_1},{R_1},0} \right) = \mathit{\boldsymbol{M}}{\left( \alpha \right)_\mathit{\boldsymbol{k}}} \cdot {\left( {{L_{\rm{t}}} - {L_{\rm{m}}},{R_{\rm{t}}} - {R_{\rm{m}}},0} \right)^{\rm{T}}} $$ (13) 3) 接触区长度：根据参考文献[21]齿轮副啮合产生的接触区长度主要取决于大、小轮齿面在啮合点处的相对曲率，其瞬时接触椭圆长半轴长与相对主曲率的关系为
$$ l = \frac{{\sqrt {0.025\;4\Delta k} }}{{2\Delta k}} $$ (14) 对于完全共轭的两曲面，在共轭啮合点处其理论的相对主曲率为0，瞬时接触椭圆长轴为无穷大.为了形成局部接触控制接触区长度需要借助沿瞬时接触线的适当修形获得，即需控制共轭差曲面沿接触线切向的曲率k，使其等于Δk.
3.2 共轭差曲面特征点修形量求解
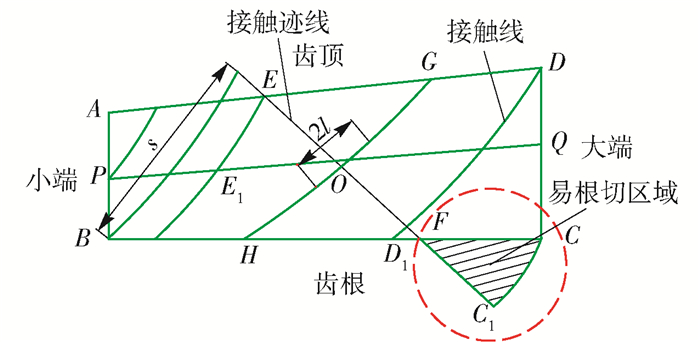
由3.1小节可知，为了控制接触区形态必须沿接触迹线EF方向对与大轮完全共轭的小轮齿面在共轭接触线方向进行修形处理.小轮齿面上的接触迹线为齿面其余部分修形的参考，其修形量为零.齿面其余点的修形量与过该点的共轭接触线到接触迹线EF的弧长相关，因此进行修形计算前必须计算出过该点的共轭接触线与接触迹线的交点.但如图 5所示，整个小轮齿面上的共轭接触线与接触迹线的交点实际会超出齿面范围，尤其在齿根C点处附近，齿面共轭接触线与接触迹线的交点有可能处于根切区域而无法进行解算，因此需利用直接求解与拟合插值推算2种方法综合进行求解.
![]()
图 5 小轮齿面上共轭接触线与接触迹线关系Figure 5. Relationship between the conjugate contact line and the contact trace on the tooth surface如3.1小节所述接触迹线参数通常是在大轮齿面上定义的，因此在求解小轮齿面特征的修形量时，首先需要计算大轮齿面上的共轭接触线与接触迹线的交点，可将式(3)共轭接触线方程与式(11)接触迹线方程联立进行求解.求解时式(11)中y、x的计算式为
$$ \left\{ \begin{array}{l} y = {\mathit{\boldsymbol{r}}_{\rm{g}}}\left( {q,{\theta _{\rm{c}}},{\eta _{\rm{g}}}} \right) \cdot {\mathit{\boldsymbol{i}}_{\rm{g}}}\\ x = {\mathit{\boldsymbol{r}}_{\rm{g}}}\left( {q,{\theta _{\rm{c}}},{\eta _{\rm{g}}}} \right) \cdot {\mathit{\boldsymbol{i}}_{\rm{g}}} \end{array} \right. $$ (15) 大轮齿面族rg(q, θc, ηg)中包含3个变量，当给定大轮齿面上任意特征点处的转角参数ηg时，方程(15)有确定的解(q, θc)，代入大轮齿面方程可得大轮齿面上共轭接触线与接触迹线交点.将其按传动比关系变换到小轮坐标系，则可得对应于小轮齿面上共轭接触线与接触迹线的交点.对应于小轮齿面接触线与接触迹线的交点满足
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_{\rm{p}}} = M{\left( {{\mathit{\boldsymbol{\eta }}_{\rm{p}}}} \right)_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{r}}_{\rm{g}}}\\ {\eta _{\rm{p}}} = {i_{{\rm{gp}}}} \cdot {\eta _{\rm{g}}} \end{array} \right. $$ (16) 由两者的交点可计算过齿面特征点的瞬时共轭接触线到接触迹线交点的弧长s.再根据设定的预置接触椭圆长半轴长l可求解瞬时共轭接触线在接触迹线点处的修形曲线曲率k.设修形曲线为标准的二次多项式，其二阶系数为a，则小轮齿面特征点处修形量的计算式为
$$ \delta = a{s^2} $$ (17) $$ k = \frac{{\left| {2a} \right|}}{{{{\left( {1 + 4{a^2}{s^2}} \right)}^{\frac{3}{2}}}}} $$ (18) 可确定如图 6所示小轮齿面上各特征点A、B、D等点的修形量δA、δB、δD.
![]()
图 6 小轮齿面网格点处的修形量求解模型Figure 6. Caculation model of pinion tooth surface modification at tooth characteristic points3.3 共轭差曲面边界线修形量的拟合
根据小轮齿面上特征点的修形量采用三点二阶多项式拟合方式可计算共轭差曲面边界线的修形量.如图 6所示，以齿高线AB为例，因A、B点修形量已知，要确定齿高线AB还需按3.2小节确定齿高线中点P修形量δP.以A点为基准，设P、B点到A点的距离为hAP、hAB，则AB边界线的修形量二次多项式的系数c1、d1、e1满足
$$ \left\{ \begin{array}{l} {\delta _B} = {d_1}h_{AB}^2 + {e_1}{h_{AB}} + {c_1}\\ {\delta _P} = {d_1}h_{AP}^2 + {e_1}{h_{AP}} + {c_1}\\ {\delta _A} = {c_1} \end{array} \right. $$ (19) 要确定齿高边界线CD修形量关系式，需首先根据齿高线AB中点P、齿面中点O及接触迹线与AD交点E所在共轭接触线与OP交点E1的修形量拟合OP线的修形量关系式，进而确定其与齿高边界线CD交点Q的修形量.同理，根据3.2小节中齿面特征点B修形量、齿面中点所在共轭接触线与齿根线BC交点H修形量及接触迹线与齿根线边界BC交点F修形量确定齿根线BC的修形量关系式.对齿根线BC修形量进行插值可确定C点的修形量.最后根据C、D、Q点修形量拟合齿高边界线CD修形量关系式.齿顶边界线AD的修形量关系式则可直接由A、D、E的修形量拟合计算.
3.4 整个共轭差曲面的修形量拟合
齿面边界的修形量关系式确定后，则可实现对共轭差曲面上任意一点修形量的求解.将齿面离散化，按齿长、齿高均匀进行网格划分，然后以某一特征点所在共轭接触线与接触迹线交点为基准点，可拟合齿面网格划分后齿长、齿高线的修形量关系式.
如图 6所示，以齿长线l为例，对齿长方向修形量拟合.首先确定l与齿高线AB、CD的交点分别为M1(RM1, LM1)、M2(RM2, LM2)，且l与接触迹线的交点为M0(RM0, LM0).然后由3.3小节中齿高线AB修形量关系和点A与M1之间距离可确定M1的修形量为δM1，同理可确定M2的修形量为δM2，则由M0、M1、M2的修形量可计算l的修形二项式系数c2、d2、e2，即
$$ \left\{ \begin{array}{l} {\delta _{{M_1}}} = {d_2}f_{{M_1}{M_0}}^2 + {e_2}{f_{{M_1}{M_0}}} + {c_2}\\ {\delta _{{M_2}}} = {d_2}f_{{M_2}{M_0}}^2 + {e_2}{f_{{M_2}{M_0}}} + {c_2}\\ {\delta _{{M_0}}} = {c_2} \end{array} \right. $$ (20) 式中fM1M0、fM2M0分别为M1、M2到M0的距离.则齿长线l1上任意网格点形量可由该二次多项式插值获得.同理可确定齿面上所有网格点的修形量.
4. 算例
为了验证本文所述基于共轭差曲面的轮齿接触特性控制方法的正确性，用该方法对一对11×41螺旋锥齿轮进行设计，其基本参数如表 1所示.
表 1 螺旋锥齿轮几何参数Table 1. Geometric parameters of the spiral bevel gear set齿轮 齿数 模数/
mm平均压力
角/(°)偏置
距/mm齿面
宽/mm外锥
距/mm轮冠
距/mm节锥
角/(°)面锥
角/(°)根锥
角/(°)螺旋
角/(°)旋向 小轮 11 4.02 19.00 23.00 27.62 88.24 79.25 19.80 23.80 18.97 49.80 左旋 大轮 41 24.00 88.18 28.08 69.30 70.15 65.15 32.12 右旋 首先根据大轮的基本几何参数，计算一组大轮的切齿调整参数(大轮采用成形法加工)，如表 2所示.
表 2 大轮切齿调整参数Table 2. Machine setting parameters of gear参数 刀盘直
径/英寸*刀错
距/mm外刀压力
角/(°)内刀压力
角/(°)机床安装
根锥角/(°)水平
轮位/mm床位/
mm垂直
轮位/mm径向
刀位基本摇台
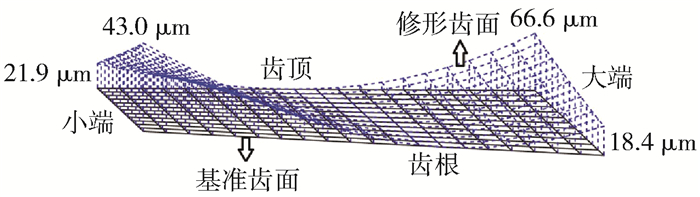
角/(°)数值 5 1.55 19.00 19.00 64.25 2.36 0 0 68.11 54.78 *1英寸=25.4 mm. 然后对齿轮副的接触区特性参数进行设定，预置传动误差曲线为二阶抛物线，其传动误差幅值为20″，预置接触参考点位于齿面中部，接触迹线与节锥线的夹角为35°，接触椭圆长轴为30%齿面宽齿面网格离散化为21×13的网格.按照上述方法分别计算满足预定传动误差的与大轮共轭的小轮齿面以及满足接触区形态的齿轮副共轭差曲面，以工作面(大轮凸面小轮凹面)为例，其共轭差曲面形态如图 7所示.
![]()
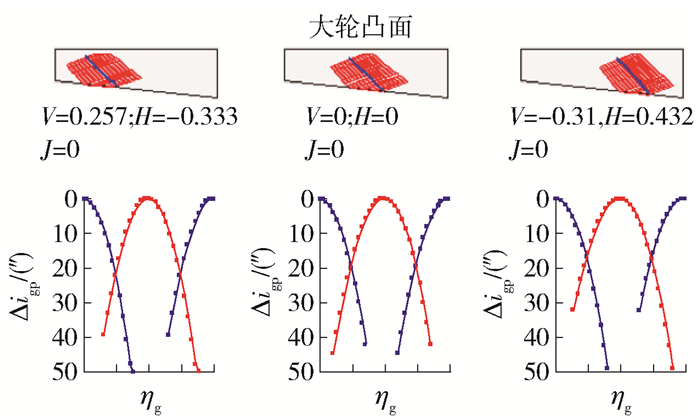
图 7 满足接触特性要求的共轭差曲面形态Figure 7. Ease-off tooth surface of ensuring the requirement of contact characteristics将两者进行叠加后获得小轮设计齿面，与大轮齿面进行齿面接触特性分析，其计算接触印痕和传动误差如图 8所示，图中V为小轮偏置距调整量，H为小轮安装距调整量.由图 8可知，其接触区位置、接触迹线倾斜程度、接触区宽度以及传动误差曲线形态和幅值均与预置参数一致.同时分析了齿轮副在小端和大端接触的情况，其接触区形态基本与中部一致，且其V、H调整量均大于0.25 mm，说明其对安装距的变动不敏感.
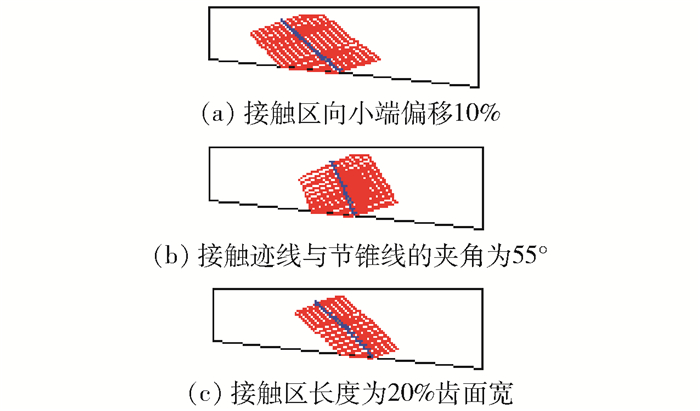
另外，为了进一步验证本文所述方法对齿面接触参数的控制能力，设置了不同的接触区位置、接触迹线的倾斜角度、接触椭圆长度进行计算，得到不同的接触区形态，如图 9所示，可见改变接触特性参数均能得到良好的接触区形态.
![]()
图 9 不同参数对应的接触区形态Figure 9. Contact area morphology corresponding to different contact characteristic parameters5. 结论
1) 建立了成形和展成切齿法统一的螺旋锥齿轮大轮齿面方程，构建了保证齿轮副传动误差特性情况下与大轮完全共轭的小轮齿面求解模型.
2) 给出了齿轮副接触区形态的数学定义方法，建立了齿轮副共轭差曲面修形量与相对曲率、共轭接触线以及接触迹线之间的联系，使得所有接触特性参数得以控制.
3) 提出了基于拟合及插值算法的共轭差曲面求解方法，采用该方法可准确控制齿轮副的接触区形态，同时可避免齿根部位由于根切因素导致的修形量求解失败，且仅需要通过少量特征点修形量求解便可将其结果映射到整个共轭差曲面，可大大提供运算效率.
-
![]()
图 4 接触特性参数在大轮轴截面坐标系中的表示
Figure 4. Expression of contact characteristic parameters on the topology coordinate of gear
![]()
图 5 小轮齿面上共轭接触线与接触迹线关系
Figure 5. Relationship between the conjugate contact line and the contact trace on the tooth surface
![]()
图 6 小轮齿面网格点处的修形量求解模型
Figure 6. Caculation model of pinion tooth surface modification at tooth characteristic points
![]()
图 7 满足接触特性要求的共轭差曲面形态
Figure 7. Ease-off tooth surface of ensuring the requirement of contact characteristics
![]()
图 9 不同参数对应的接触区形态
Figure 9. Contact area morphology corresponding to different contact characteristic parameters
表 1 螺旋锥齿轮几何参数
Table 1 Geometric parameters of the spiral bevel gear set
齿轮 齿数 模数/
mm平均压力
角/(°)偏置
距/mm齿面
宽/mm外锥
距/mm轮冠
距/mm节锥
角/(°)面锥
角/(°)根锥
角/(°)螺旋
角/(°)旋向 小轮 11 4.02 19.00 23.00 27.62 88.24 79.25 19.80 23.80 18.97 49.80 左旋 大轮 41 24.00 88.18 28.08 69.30 70.15 65.15 32.12 右旋 
下载: 导出CSV
表 2 大轮切齿调整参数
Table 2 Machine setting parameters of gear
参数 刀盘直
径/英寸*刀错
距/mm外刀压力
角/(°)内刀压力
角/(°)机床安装
根锥角/(°)水平
轮位/mm床位/
mm垂直
轮位/mm径向
刀位基本摇台
角/(°)数值 5 1.55 19.00 19.00 64.25 2.36 0 0 68.11 54.78 *1英寸=25.4 mm.
下载: 导出CSV
-
[1] LITVIN F L, FUENTES A, FAN Q. Computerized design, simulation of meshing, and contact and stress analysis of face-milled formate generated spiral bevel gears[J]. Journal of Mechanical Design, Transactions of the SAME, 2002, 37(5):441-459. http://cn.bing.com/academic/profile?id=b519e47a494f549dd928e638bc16a472&encoded=0&v=paper_preview&mkt=zh-cn
[2] FUENTES A, LITVIN F L, MULLINS B R. Design and stress analysis of low-noise adjusted bearing contact spiral bevel gears[J]. Journal of Mechanical Design, Transactions of the SAME, 2002, 124(9):523-532. http://cn.bing.com/academic/profile?id=4043fa2dc26ab1c1cfba934c2fc5434a&encoded=0&v=paper_preview&mkt=zh-cn
[3] STADTFELD H J, GAISER U. The ultimate motion graph[J]. Journal of Mechanical Design, Transactions of the SAME, 2000, 122(3):317-322. http://cn.bing.com/academic/profile?id=e76ad46ffcf532559ac4b5c0d09306ed&encoded=0&v=paper_preview&mkt=zh-cn
[4] SU J Z, FANG Z D, CAI X W. Design and analysis of spiral bevel gears with seventh-order function of transmission error[J]. Chinese Journal of Aeronautics, 2013, 26(5):1310-1316. doi: 10.1016/j.cja.2013.07.012
[5] MERMOZ E, ASTOUL J, SARTOR M, et al. A new methodology to optimize spiral bevel gear topography[J]. CIRP Annals-Manufacturing Technology, 2013(62):119-122. http://cn.bing.com/academic/profile?id=028a3f7ed88687549b6c697738cb6013&encoded=0&v=paper_preview&mkt=zh-cn
[6] ASTOUL J, MERMOZ E, SARTOR M. New methodology to reduce the transmission error of the spiral bevel gears[J]. CIRP Annals Manufacturing Technology, 2014(63):165-168. http://cn.bing.com/academic/profile?id=fa126a90713de3585535c368706650eb&encoded=0&v=paper_preview&mkt=zh-cn
[7] 曹雪梅, 方宗德, 邓效忠, 等.弧齿锥齿轮的齿面主动设计[J].机械工程学报, 2007, 43(8):155-158. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb200708027 CAO X M, FANG Z D, DENG X Z, et al. Function-oriented active tooth surface design of spiral bevel gears[J]. Journal of Mechanical Engineering, 2007, 43(8):155-158. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb200708027
[8] LITVIN F L, GUTMAN Y. A method of local synthesis of gears grounded on the connections between the principal and geodetic curvatures of surfaces[J]. Journal of Mechanical Design, Transcations of the ASME, 1981, 103(l):114-125. http://cn.bing.com/academic/profile?id=eced4333e50f3093d5de2f9d8a53f226&encoded=0&v=paper_preview&mkt=zh-cn
[9] LITVIN F L. Gear geometry and applied theory[M]. 2nd ed. Cambridge:Cambridge University Press, 2004:245-249.
[10] 王小椿.点啮合曲面的三阶接触分析[J].西安交通大学学报, 1983, 17(3):1-13. http://www.cnki.com.cn/Article/CJFDTotal-JXCD198604005.htm WANG X C. Third order contact analysis of point contact surfaces[J]. Journal of Xi'an Jiaotong University, 1983, 17(3):1-13. (in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-JXCD198604005.htm
[11] 王小椿, 吴序堂.弧齿锥齿轮和双曲线齿轮的三阶接触分析和优化切齿计算[J].齿轮, 1989, 13(2):1-10. http://www.cnki.com.cn/Article/CJFDTotal-ZHJC201502001.htm WANG X C, WU X T. Third order contact analysis of spiral bevel gear and hyperbolic gear and optimization of tooth cutting[J]. Gear, 1989, 13(2):1-10. (in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-ZHJC201502001.htm
[12] 吴训成, 毛世民, 吴序堂.点啮合齿面主动设计研究[J].机械工程学报, 2000, 36(4):70-73. http://bianke.cnki.net/onlineread/Home/BianKeOnlineView?id=5305 WU X C, MAO S M, WU X T. Research on active design of point meshing tooth surface[J]. Journal of Mechanical Engineering, 2000, 36(4):70-73. (in Chinese) http://bianke.cnki.net/onlineread/Home/BianKeOnlineView?id=5305
[13] IGNACIO G P, FUENTES A, KAHRAMAN A. Computerized design and tooth contact analysis of spiral bevel gears generated by the duplex helical method[C]//Proceedings of the ASME 2011 International Design Engineering Technical Conference & Computers and Information in Engineering Conference. New York: ASME, 2011: 1-10.
[14] CAO X M, FANG Z D, XU H, et al. Design of pinion machine tool-settings for spiral bevel gears by controlling contact path and transmission errors[J]. Chinese Journal of Aeronautics, 2008, 21(2):179-186. doi: 10.1016/S1000-9361(08)60023-0
[15] SIMON V. Influence of tooth errors and misalignments on tooth contact in spiral bevel gears[J]. Mechanism and Machine Theory, 2008, 43(10):1253-1267. doi: 10.1016/j.mechmachtheory.2007.10.012
[16] SHIH Y P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears[J]. Mechanism and Machine Theory, 2010, 45(8):1108-1124. doi: 10.1016/j.mechmachtheory.2010.03.010
[17] SHIH Y P, FONG Z H. Flank modification methodology for face-hobbing hypoid gears based on ease-off topography[J]. Journal of Mechanical Design, Transactions of the ASME, 2017, 129(12):1294-1302. http://cn.bing.com/academic/profile?id=cd3622dc8ce9794f2b3e08d490b01f46&encoded=0&v=paper_preview&mkt=zh-cn
[18] 苏进展, 贺朝霞.弧齿锥齿轮齿面的高精度修形方法[J].华南理工大学学报(自然科学版), 2014, 42(4):91-96, 104. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hnlgdxxb201404014 SU J Z, HE Z X. High-precision modification of tooth surface for spiral bevel gears[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(4):91-96, 104. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hnlgdxxb201404014
[19] 蔡香伟, 方宗德.弧齿锥齿轮机床加工参数逆向求解的算法研究[J].机械传动, 2015, 39(3):5-8, 14. http://www.cqvip.com/QK/92228A/201503/664132505.html CAI X W, FANG Z D. Research on inversion algorithm of machine-tool machining parameter for spiral bevel gear[J]. Journal of Mechanical Transmission, 2015, 39(3):5-8, 14. (in Chinese) http://www.cqvip.com/QK/92228A/201503/664132505.html
[20] 曹雪梅, 邓效忠, 聂少武.基于共轭齿面修正的航空弧齿锥齿轮高阶传动误差齿面拓扑结构设计[J].航空动力学报, 2015, 30(1):195-200. http://cdmd.cnki.com.cn/Article/CDMD-10497-2009103183.htm CAO X M, DENG X Z, NIE S W. Ease-off topology design for aviation spiral bevel gears with higher-order transmission error by modification of conjugate flank[J]. Journal of Aeronautics, 2015, 30(1):195-200. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10497-2009103183.htm
[21] 郑昌启.弧齿锥齿轮和准双曲面齿轮[M].北京:机械工业出版社, 1988:320-370. -
期刊类型引用(11)
1. 李建国，徐国胜. 高接触比螺旋锥齿面修形方法及动态特性研究. 机床与液压. 2024(01): 98-104 . 
百度学术
2. 耿龙龙，聂少武，蒋闯. 基于定量失配的弧齿锥齿轮齿面修形设计及实验验证. 机械传动. 2023(11): 73-79 . 百度学术
3. 姜志宏，王兴卫，池汉佳，赵小涛. 遗传算法下弧齿锥齿轮齿面接触特性优化. 机械科学与技术. 2022(03): 409-413 . 百度学术
4. 明显诚，许博. 针对全地形车覆盖件表面复杂曲面拟合算法的改进设计. 现代电子技术. 2021(04): 111-114 . 百度学术
5. 蒋进科，方宗德，刘红梅. Ease-off拓扑修形准双曲面齿轮齿面数控修正. 重庆大学学报. 2021(02): 25-33 . 百度学术
6. 蒋进科，刘钊，彭先龙. Ease-Off修形准双曲面齿轮减振优化设计. 华南理工大学学报(自然科学版). 2020(05): 134-141+148 . 百度学术
7. 孙月海，唐二星. 弧齿锥齿轮基本参数优化设计. 工程设计学报. 2020(05): 616-624 . 百度学术
8. 蒋进科，方宗德，刘钊. Ease-off拓扑修形准双曲面齿轮齿面多目标优化设计方法. 西安交通大学学报. 2019(06): 44-53 . 百度学术
9. 李宁. 基于ADAMS GearAT直齿轮接触特性研究. 煤矿机械. 2019(10): 62-64 . 百度学术
10. 敬正彪，龚一龙，冉龙姣，陈廷兵. 准双曲面齿轮接触疲劳有限元仿真. 煤矿机械. 2019(11): 189-192 . 百度学术
11. 惠宇. 加工误差对面齿轮接触特性影响研究. 中国金属通报. 2018(10): 165+167 . 百度学术
其他类型引用(9)
计量
- 文章访问数: 180
- HTML全文浏览量: 5
- PDF下载量: 55
- 被引次数: 20
