Method of Error Sensitivity Analysis of Machine Tools
-
摘要:
目前精度设计依然停留在以设计人员感官经验设计为主的层面，已开展的误差敏感度分析工作无法对精度设计提供直接的量化指导.针对上述问题，展开了机床误差敏感度分析方法的研究.首先，基于多体系统理论建立了数控机床的空间运动误差模型，同时构造了基于零部件公差的几何误差源参数的预估模型，在此基础上，进一步提出了基于部件运动增量的误差敏感度分析方法.以CA摆头五轴数控铣床为研究对象，以"S"试件为加工对象进行试验验证，利用基于机床部件运动增量的误差敏感度分析方法对五轴加工中心进行误差敏感度分析.结果表明：εy（x）、q6e、εx（x）、q5e、θCe、εzx45这6项误差源参数对应的误差敏感度系数之和为0.95，其他误差源参数的敏感度系数之和仅为0.05，因此该方法可以有效地识别出对数控机床加工精度影响较大的关键零部件，为提升数控机床的加工精度奠定了理论基础.
Abstract:At present, the accuracy design remains at the level of the designer's sensory experience, and the developed error sensitivity analysis cannot provide direct quantitative guidance for accuracy design. In view of the above problems, the error increment equation was first established based on the theory of the multi-body system. Meanwhile, the prediction model of component tolerance and geometric error source parameters was constructed. Furthermore, a method of error sensitivity analysis based on component motion was proposed. Taking CA swing head five-axis NC milling machine as the subject, and taking "S" specimen as the object of processing, the error sensitivity analysis of five axis machining center was carried out by using the method of error sensitivity analysis based on the increment of machine tool component motion. The experimental results show that the sum of the error sensitivity coefficients of the six error source parameters εy(x)、q6e、εx(x)、q5e、θCe and εzx45 is 0.95 and the sum of sensitivity coefficients of other error source parameters is only 0.05. Therefore, this method can effectively identify the key parts that affect the machining accuracy of CNC machine tools, and lay a theoretical foundation for improving the machining accuracy of CNC machine tools.
-
近年来，随着多轴联动机床各项技术的不断成熟，大型复杂曲面零件的可加工性和加工精度大幅提高，加工零件的日益复杂，机床结构的多样化，使得对于如何提高机床的加工精度等需要进行更深入的研究.
目前，国内外学者已经开展了许多关于机床精度建模方法的研究[1-8]，先后出现了二次关系模型法、几何建模法、误差矩阵法、刚体运动学法和多体系统理论法.数控机床误差敏感度分析是近年来新兴的一种研究方法，该方法研究的主要目的是找出对机床加工精度产生重要影响的误差源参数. Li等[9]运用数值模拟的方法对五轴机床进行了敏感度分析. Peng等[10]提出了一种基于辨识矩阵灵敏度分析的优化方法，以获得激光干涉仪的最佳安装位置，减小安装误差的影响, 并进行了实验验证.李小雷等[11]利用多刚体系统理论建立了数控刻楦机空间误差计算模型并结合误差灵敏度分析，对主要部件的精度进行分配，提高了系统的加工精度.程强等[12]提出了用矩阵微分法建立四轴数控机床敏感度分析模型的方法，并推导出精密卧式加工中心的敏感度分析模型.程刚等[13]提出了一种通过归一化描述灵敏度的新方法，并建立了灵敏度系数数学模型.现有的数控机床误差敏感度分析方法，没有考虑到机床误差源参数随机床位置变化而变化的特性，其分析结果不能正确指导机床的精度设计.现有的方法存在2个问题，其一是误差源参数有2类：线性误差源和角度误差源，这2种误差源参数对机床加工误差影响的量纲不同，不好直接放在一起比较；其二真正影响机床加工精度的是误差源参数随着部件运动的变化量，如果导轨在装配中存在平移误差，由于加工前对刀的存在，因此不会对加工误差产生影响.而现有敏感度分析中假设各个位置处误差源参数增量为单位1，就属于这种情况，因此它不能真实反映出误差参数对机床加工精度的影响规律.
通过深入分析机床实际加工误差产生的原因，发现误差源参数是随着机床的运动而相对变化的，因此本文提出了一种基于部件运动增量的误差敏感度分析的方法.首先基于多体系统理论建立了数控机床的空间运动误差模型，同时构造了基于零部件公差的几何误差源参数的预估模型，在此基础上，进一步提出了基于部件运动增量的误差敏感度分析方法.以CA摆头五轴数控铣床为研究对象，以“S”试件为加工对象进行试验验证，利用基于机床部件运动增量的误差敏感度分析方法对五轴加工中心进行误差敏感度分析，从而实现了机床关键零部件的辨识.
1. 基于多体系统运动学理论的数控机床空间运动误差模型
数控机床运动误差建模是数控机床精度设计、精度分配和误差补偿的重要环节之一.数控机床是多体系统的一个特例，将多体系统运动学理论运用于数控机床的误差建模和误差分析中，不仅可以解决数控机床运动误差建模现存的问题，同时也拓宽了多体系统运动学理论在工程领域的应用范围.
1.1 CA摆头五轴龙门数控机床结构示意图
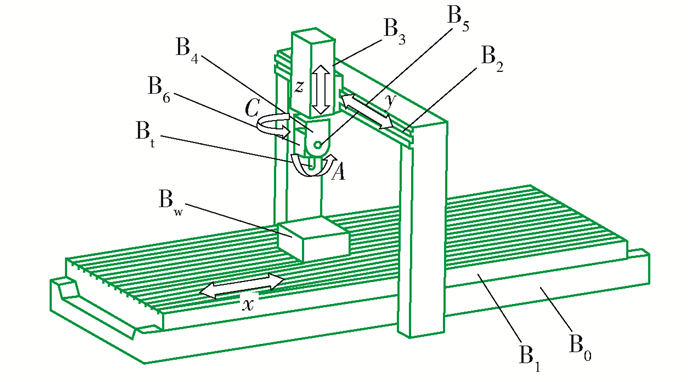
该类机床由工作台、平动轴、转动轴、主轴单元、床身等零部件组成，如图 1所示.
![]()
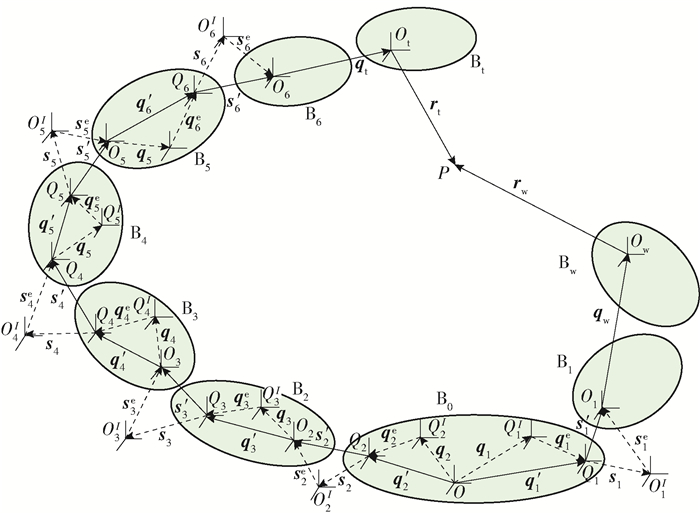
图 1 CA摆头五轴龙门数控机床结构B0—床身; B1—x轴; B2—y轴; B3—z轴; B4—C轴; B5—A轴; B6—主轴; Bw—工件; Bt—刀具Figure 1. Schematic of the five-axis gantry machining center structure为简化复杂的机械系统，方便多体系统的研究，将机床各组成零部件分成2个分支，如图 2所示，B0-B2-B3-B4-B5-B6-Bt为刀具分支，B0-B1-Bw为工件分支.
根据刚体六自由度假设理论，刚体在三维空间中运动必然会产生6项误差(3项线位移误差、3项角位移误差)，共36项与位置点有关的误差，在生产实际中，x、y、z三条导轨间存在3项不垂直度误差，分别为εxy02、εxz23、εyz23，C轴与x、y轴，A轴与y、z轴以及主轴与x、y轴之间共存在6项垂直度误差，依次为εxz34、εyz34、εxy45、εzx45、εxz56、εyz56，A、C轴转角误差分别为(θA)e、(θC)e以及qke(k=1、2、3、4、5、6)依次为x、y、z、A、C轴和主轴的装配位置误差，因此共53项误差，如表 1所示.
表 1 CA摆头五轴龙门数控铣床几何误差Table 1. Geometric errors for the five-axis gantry machining center项目 误差 沿x轴平动 εx(x) εy(x) εz(x) δx(x) δy(x) δz(x) 沿y轴平动 εx(y) εy(y) εz(y) δx(y) δy(y) δz(y) 沿z轴平动 εx(z) εy(z) εz(z) δx(z) δy(z) δz(z) 绕C轴转动 εyz(θC) εxz(θC) εxy(θC) δx(β) δy(β) δz(β) 绕A轴转动 εyz((θA)) εxz(θA) εxy(θA) δx(α) δy(α) δz(α) 主轴转动 εyz(φ) εxz(φ) εxy(φ) δx(φ) δy(φ) δz(φ) 垂直度 εxy02、εxz23、εyz23、εxz34、εyz34、εxy45、εzx45、εxz56、εyz56 装配位置误差 q1e、q2e、q3e、q4e、q5e、q6e A、C轴转角误差 (θA)e(θC)e 1.2 CA摆头五轴龙门数控铣床空间运动误差模型
为方便建立机床模型展示机床各部件之间的位置关系，设定O为B0的体坐标系的原点，j=1, 2, …, 6，Qjl和Qj分别为Bj的理想运动参考坐标系和实际运动参考坐标系，Ojl和Oj分别为Bj的理想体参考坐标系和实际体参考坐标系，qj和q′j分别为Bj相对于Bj-1的理想位置矢量和实际位置矢量，qje为位置误差矢量，sj和s′j分别为Bj相对于Bj-1的理想位移矢量和实际位移矢量，sje为位移误差矢量. qw和qt分别为工件相对于工作台的定位坐标和刀具相对于主轴的定位坐标，rw和rt分别为数控指令到工件坐标系和刀具坐标系的投影.
根据数控机床各部件之间的运动关系，可建立各相邻体之间的变换矩阵如表 2所示，考虑篇幅有限，仅以x、y轴为例，其余各轴以此类推.
表 2 各位置矢量、位移矢量和变换矩阵(部分)Table 2. Position vectors, displacement vectors and transform matrices (part)相邻体 体间实际结构变换矩阵 体间实际运动变换矩阵 位移矢量 大地—0 Hpe0=I 无 无 0—1 Hpe1=I $\mathit{\boldsymbol{H}}_{{\rm{se}}}^1 = \left[{\begin{array}{*{20}{c}} 1&{ - {\varepsilon _z}\left(x \right)}&{{\varepsilon _y}\left(x \right)}\\ {{\varepsilon _z}\left(x \right)}&1&{ - {\varepsilon _x}\left(x \right)}\\ { - {\varepsilon _y}\left(x \right)}&{{\varepsilon _x}\left(x \right)}&1 \end{array}} \right]$ $s{\prime _1} = {s_1} + s_1^{\rm{e}} = \left( {\begin{array}{*{20}{c}} {x + {\delta _x}\left( x \right)}\\ {{\delta _y}\left( x \right)}\\ {{\delta _z}\left( x \right)} \end{array}} \right)$ 0—2 $\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2 = \left[{\begin{array}{*{20}{c}} 1&{ - \varepsilon _{xy}^{02}}&0\\ {\varepsilon _{xy}^{02}}&1&{ - {\varepsilon _x}0\left(x \right)}\\ 0&0&1 \end{array}} \right]$ $\mathit{\boldsymbol{H}}_{{\rm{se}}}^2 = \left[{\begin{array}{*{20}{c}} 1&{ - {\varepsilon _z}\left(y \right)}&{{\varepsilon _y}\left(y \right)}\\ {{\varepsilon _z}\left(y \right)}&1&{ - {\varepsilon _x}\left(y \right)}\\ { - {\varepsilon _y}\left(y \right)}&{{\varepsilon _x}\left(y \right)}&1 \end{array}} \right]$ $s{\prime _2} = {s_2} + s_2^{\rm{e}} = \left( {\begin{array}{*{20}{c}} {{\delta _x}\left( y \right)}\\ {y + {\delta _y}\left( y \right)}\\ {{\delta _z}\left( y \right)} \end{array}} \right)$ 工件坐标系上任意一点到大地坐标系的位置矢量为
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{\rm{w}}} = {\mathit{\boldsymbol{q}}_1} + \mathit{\boldsymbol{q}}_1^{\rm{e}} + {\mathit{\boldsymbol{s}}_1} + \mathit{\boldsymbol{s}}_1^{\rm{e}} + {\mathit{\boldsymbol{q}}_{\rm{w}}} + {\mathit{\boldsymbol{R}}_{\rm{w}}} = }\\ {\mathit{\boldsymbol{H}}_{{\rm{pe}}}^0{\mathit{\boldsymbol{q}}_1} + \mathit{\boldsymbol{H}}_{{\rm{pe}}}^1{\mathit{\boldsymbol{s}}_1} + \mathit{\boldsymbol{H}}_{{\rm{se}}}^1\left( {{\mathit{\boldsymbol{q}}_{\rm{w}}} + {\mathit{\boldsymbol{R}}_{\rm{w}}}} \right)} \end{array} $$ (1) 式中:Hpe0表示大地与床身之间的体间实际结构变换矩阵; Hpe1表示床身与x轴之间的体间实际结构变换矩阵; Hse1表示床身与x轴之间的体间实际运动变换矩阵.
刀具中心点到大地坐标系的位置矢量为
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{\rm{t}}} = {\mathit{\boldsymbol{q}}_2} + \mathit{\boldsymbol{q}}_2^{\rm{e}} + {\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{s}}_2^{\rm{e}} + {\mathit{\boldsymbol{q}}_3} + \mathit{\boldsymbol{q}}_3^{\rm{e}} + {\mathit{\boldsymbol{s}}_3} + \mathit{\boldsymbol{s}}_3^{\rm{e}} + }\\ {{\mathit{\boldsymbol{q}}_4} + \mathit{\boldsymbol{q}}_4^{\rm{e}} + {\mathit{\boldsymbol{s}}_4} + \mathit{\boldsymbol{s}}_4^{\rm{e}} + {\mathit{\boldsymbol{q}}_5} + \mathit{\boldsymbol{q}}_5^{\rm{e}} + {\mathit{\boldsymbol{s}}_5} + \mathit{\boldsymbol{s}}_5^{\rm{e}} + }\\ {{\mathit{\boldsymbol{q}}_6} + \mathit{\boldsymbol{q}}_6^{\rm{e}} + {\mathit{\boldsymbol{s}}_6} + \mathit{\boldsymbol{s}}_6^{\rm{e}} + {\mathit{\boldsymbol{q}}_{\rm{t}}} + {\mathit{\boldsymbol{r}}_{\rm{t}}}} \end{array} $$ (2) 由于在实际操作中，直接检测到的是机床空间运动相对于工件坐标系或者工作台坐标系的误差，而非相对于大地坐标系的误差，所以实际情况下数控指令到工件坐标的映射:
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{wactual}}}} = \mathit{\boldsymbol{H}}_{{\rm{se}}}^1\left( {{\mathit{\boldsymbol{q}}_2} - {\mathit{\boldsymbol{s}}_1}} \right) + \mathit{\boldsymbol{H}}_{{\rm{se}}}^1\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2{\mathit{\boldsymbol{s}}_2} + }\\ {\mathit{\boldsymbol{H}}_{{\rm{se}}}^1\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2\mathit{\boldsymbol{H}}_{{\rm{se}}}^2\left( {{\mathit{\boldsymbol{q}}_3} + \mathit{\boldsymbol{H}}_{{\rm{pe}}}^3{\mathit{\boldsymbol{s}}_3}} \right) + \mathit{\boldsymbol{H}}_{{\rm{se}}}^1\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2\mathit{\boldsymbol{H}}_{{\rm{se}}}^2}\\ {\mathit{\boldsymbol{H}}_{{\rm{pe}}}^3\mathit{\boldsymbol{H}}_{{\rm{se}}}^3\left( {{\mathit{\boldsymbol{q}}_4} + \mathit{\boldsymbol{H}}_{{\rm{pe}}}^4{\mathit{\boldsymbol{s}}_4}{\mathit{\boldsymbol{q}}_5}} \right) + }\\ {\mathit{\boldsymbol{H}}_{{\rm{se}}}^1\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2\mathit{\boldsymbol{H}}_{{\rm{se}}}^2\mathit{\boldsymbol{H}}_{{\rm{pe}}}^3\mathit{\boldsymbol{H}}_{{\rm{se}}}^3\mathit{\boldsymbol{H}}_{{\rm{pe}}}^4{\mathit{\boldsymbol{s}}_4}\mathit{\boldsymbol{H}}_{{\rm{pe}}}^5{\mathit{\boldsymbol{s}}_5}\left( {{\mathit{\boldsymbol{q}}_6} + \mathit{\boldsymbol{H}}_{{\rm{pe}}}^6{\mathit{\boldsymbol{R}}_{\rm{t}}}} \right) - {\mathit{\boldsymbol{q}}_{\rm{t}}}} \end{array} $$ (3) 式中:Hpe2表示床身与y轴之间的体间实际结构变换矩阵; Hse2表示床身与y轴之间的体间实际运动变换矩阵; Hpe3表示y轴与z轴之间的体间实际结构变换矩阵; Hse3表示y轴与A轴之间的体间实际运动变换矩阵; Hpe4表示z轴与C轴之间的体间实际结构变换矩阵; Hpe5表示A轴与C轴之间的体间实际结构变换矩阵; Hpe6表示主轴与A轴之间的体间实际结构变换矩阵.
理想情况下，数控指令到工件坐标的映射为
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_{{\rm{wideal}}}} = {\mathit{\boldsymbol{q}}_2} + {\mathit{\boldsymbol{s}}_2} + {\mathit{\boldsymbol{q}}_3} + {\mathit{\boldsymbol{s}}_3} + {\mathit{\boldsymbol{q}}_4} + {\mathit{\boldsymbol{s}}_4} + {\mathit{\boldsymbol{q}}_5} + }\\ {{\mathit{\boldsymbol{s}}_5} + {\mathit{\boldsymbol{q}}_6} + {\mathit{\boldsymbol{s}}_6} + {\mathit{\boldsymbol{q}}_{\rm{t}}} + {\mathit{\boldsymbol{r}}_{\rm{t}}} - {\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{s}}_1} - {\mathit{\boldsymbol{q}}_{\rm{w}}}} \end{array} $$ (4) 数控机床空间运动误差模型为
$$ \mathit{\boldsymbol{E}}_{\rm{P}}^{\rm{w}} = {\mathit{\boldsymbol{r}}_{{\rm{wactual}}}} - {\mathit{\boldsymbol{r}}_{{\rm{wideal}}}} = {\left[ {\begin{array}{*{20}{c}} {{E_x}}&{{E_y}}&{{E_z}} \end{array}} \right]^{\rm{T}}} $$ (5) 2. 基于零部件公差的数控机床误差源参数预估模型
为了绕过机床误差源参数未知的问题，一些学者引入误差敏感度分析的概念，采用误差源参数增量处处为1的假设.因为误差源参数对机床运动误差的影响取决于2个因素：运动位置和误差参数的局部相对变化.误差源参数增量均为1的假设实际代表的是机床导轨整体平移的概念，它根本无法反映机床误差参数的局部变化，导致误差分析大大失真.目前机床的误差敏感度分析，对机床的设计造成了很大的盲目性.为更好地反映误差源参数的局部相对变化以及机床各轴在各运动位置处误差源参数的值，构造了零部件公差与机床误差源参数的关系模型.
以CA摆头五轴数控机床为例，由零部件公差的概念以及机床误差源参数的真实规律，可知机床误差源参数的变化可由正余弦函数拟合，本节提出了公差与误差源参数间的关系模型，现以y轴导轨为例加以说明，其余各轴以此类推. y轴与x轴的不垂直度误差本身就是不垂直度公差的反映可直接由εxy表示，单位mm，装配误差本身就是装配公差的反映可直接由q1e、q2e、q3e、q4e、q5e、q6e表示，单位mm.
$$ {\delta _x}\left( y \right) = \frac{{{k_{y1}}}}{{{m_1}}}\sin \left( {\frac{{{n_1}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right) $$ (6) 式中：δx(y)为部件沿y轴运动时，在x方向产生的不直度误差；ky1为y向导轨在xy平面内的不直度公差；Ly为y向导轨的整个行程；n1决定导轨弯曲波动次数.在1~8间取值，一般取1或2；m1决定公差对y向导轨波动幅度的影响形式，当n1取1时，m1=1；当n1大于1时，m1=2.
同理，y向导轨的其他误差源参数与公差的关系为
$$ {\delta _y}\left( y \right) = \frac{{{k_{y2}}}}{{{m_2}}}\sin \left( {\frac{{{n_2}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right) + {K_y}\frac{y}{{{L_y}}} $$ (7) $$ {\delta _z}\left( y \right) = \frac{{{k_{y3}}}}{{{m_3}}}\sin \left( {\frac{{{n_3}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right) $$ (8) $$ {\varepsilon _x}\left( y \right) = \frac{{{\delta _z}\left( {y - {b_y}} \right) - {\delta _z}\left( y \right)}}{{{b_y}}} $$ (9) $$ {\varepsilon _y}\left( y \right) = \frac{{{k_{y4}}}}{{{w_y}}}\sin \left( {\frac{{{n_4}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right) $$ (10) $$ {\varepsilon _z}\left( y \right) = - \frac{{{\delta _x}\left( {y - {b_y}} \right) - {\delta _x}\left( y \right)}}{{{b_y}}} $$ (11) 式中：by为y向工作台前后导轨运动副之间的距离；ky4为2条y向导轨之间的扭曲公差，公差值参考CA摆头五轴龙门数控机床精度检测国家标准；wy为2条y向导轨的间距，其他运动部件误差源参数与公差的关系模型与上述形式类似，这里不一一赘述.
3. 基于局部运动增量的数控机床误差敏感度分析新方法
为了确定误差源参数对数控机床空间运动误差的影响程度，一些学者开展了数控机床误差敏感度分析的研究工作.遗憾的是现有的误差敏感度模型，仅是利用空间运动误差模型对误差源参数求偏导而求得，并假设误差源参数的变化均为1，实际代表的是机床导轨整体平移的概念，它根本无法反映机床误差参数的局部变化，如果导轨在装配中存在平移误差，由于加工前对刀的存在，因此不会对加工误差产生影响，使得分析工作严重失真，无法准确地反映出误差参数对数控机床空间运动误差的真实影响.
该二次偏导数的误差敏感度分析模型，即用数控机床空间运动误差模型依次对各误差源参数求一次偏导数，再用该误差源参数对运动增量求一次偏导数，从而，可以依次确定出各个误差源参数在机床运动过程中对空间误差的影响程度.由数控机床空间运动误差方程(5)，可推导出基于局部运动增量的误差敏感度方程
$$ \Delta E_{\rm{P}}^{\rm{w}} = \frac{{\partial E_{\rm{P}}^{\rm{w}}}}{{\partial {\delta _i}}}\frac{{{\rm{d}}{\delta _i}}}{{{\rm{d}}{s_i}}}\Delta {s_i} $$ (12) 式中：δi为数控机床第i项误差源参数；si为与第i项误差源参数有关的数控机床运动量.
对于与运动量无关的装配误差，默认误差参数增量为单位1.
$$ \Delta {\delta _i} = \frac{{{\rm{d}}{\delta _i}}}{{{\rm{d}}{s_i}}}\Delta {s_i} = 1 $$ (13) 针对如图 1所示的具有CA摆头的五轴龙门数控铣床，由于各轴计算分析方法相同，以下仅给出与y向滑台运动有关的一个线性以及一个转角误差源参数的误差敏感度表达方程.
误差源参数δx(y)的误差敏感度表达方程为
$$ \begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {\Delta {E_x}}\\ {\Delta {E_y}}\\ {\Delta {E_z}} \end{array}} \right) = \frac{{\partial E_{\rm{P}}^{\rm{w}}}}{{\partial {\delta _x}\left( y \right)}}\frac{{{\rm{d}}{\delta _x}\left( y \right)}}{{{\rm{d}}y}}\Delta y = }\\ {\left( {\begin{array}{*{20}{c}} 1\\ 0\\ 0 \end{array}} \right)\frac{{{k_{y2}}}}{{{m_2}}}\frac{{{n_2}{\rm{ \mathsf{ π} }}}}{{{L_y}}}\cos \left( {\frac{{{n_2}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right)} \end{array} $$ (14) 误差源参数εx(y)的误差敏感度表达方程为
$$ \begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {\Delta {E_x}}\\ {\Delta {E_y}}\\ {\Delta {E_z}} \end{array}} \right) = \frac{{\partial E_{\rm{P}}^{\rm{w}}}}{{\partial {\delta _x}\left( y \right)}}\frac{{{\rm{d}}{\delta _x}\left( y \right)}}{{{\rm{d}}y}}\Delta y = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&{ - 1}\\ 0&0&0 \end{array}} \right]\left[ {\left( {\begin{array}{*{20}{c}} {{q_{{\rm{w}}x}}}\\ {{q_{{\rm{w}}y}}}\\ {{q_{{\rm{w}}z}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{r_{{\rm{w}}x}}}\\ {{r_{{\rm{w}}y}}}\\ {{r_{{\rm{w}}z}}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{q_{{\rm{2}}x}}}\\ {{q_{{\rm{2}}y}}}\\ {{q_{{\rm{2}}z}}} \end{array}} \right)} \right] \cdot }\\ {\frac{{{k_{y3}}}}{{{m_3}}}\frac{{{n_3}{\rm{ \mathsf{ π} }}}}{{{L_y}{b_y}}}\left( {\cos \left( {\frac{{{n_3}{\rm{ \mathsf{ π} }}\left( {y - {b_y}} \right)}}{{{L_y}}}} \right) - \cos \left( {\frac{{{n_3}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right)} \right)\Delta y + }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&1&0 \end{array}} \right]\left[ {\left( {\begin{array}{*{20}{c}} {{q_{{\rm{3}}x}}}\\ {{q_{{\rm{3}}y}}}\\ {{q_{{\rm{3}}z}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{q_{{\rm{4}}x}}}\\ {{q_{{\rm{4}}y}}}\\ {{q_{{\rm{4}}z}}} \end{array}} \right) + } \right.}\\ {\left[ {\begin{array}{*{20}{c}} {c{\theta _C}}&{ - s{\theta _C}}&0\\ {s{\theta _C}}&{c{\theta _C}}&0\\ 0&0&1 \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{q_{{\rm{5}}x}}}\\ {{q_{{\rm{5}}y}}}\\ {{q_{{\rm{5}}z}}} \end{array}} \right) + }\\ {\left[ {\begin{array}{*{20}{c}} {c{\theta _C}}&{ - s{\theta _C}}&0\\ {s{\theta _C}}&{c{\theta _C}}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{c{\theta _A}}&{ - s{\theta _A}}\\ 0&{s{\theta _A}}&{c{\theta _A}} \end{array}} \right] \cdot }\\ {\left. {\left[ {\left( {\begin{array}{*{20}{c}} {{q_{{\rm{6}}x}}}\\ {{q_{{\rm{6}}y}}}\\ {{q_{{\rm{6}}z}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ { - 1} \end{array}} \right)} \right]} \right]\frac{{{k_{y3}}}}{{{m_3}}}\frac{{{n_3}{\rm{ \mathsf{ π} }}}}{{{L_y}{b_y}}} \cdot }\\ {\left( {\cos \left( {\frac{{{n_3}{\rm{ \mathsf{ π} }}\left( {y - {b_y}} \right)}}{{{L_y}}}} \right) - \cos \left( {\frac{{{n_3}{\rm{ \mathsf{ π} }}y}}{{{L_y}}}} \right)} \right)\Delta y} \end{array} $$ (15) 依照上述方法，在机床工作空间内，对每项误差源参数进行敏感度分析，并以每个误差源参数对机床空间误差敏感度的波动范围为指标，列出误差源参数敏感度队列.
4. 计算与试验分析
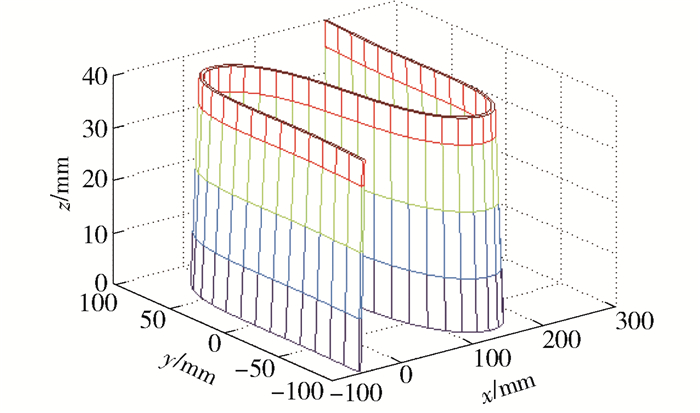
为了验证基于局部运动增量的数控机床误差敏感度分析新方法的准确性与可靠性，本文以CA摆头五轴数控机床为研究对象，以“S”试件为加工对象进行试验验证，“S”试件的现场加工图如图 3所示.利用德国蔡司公司生产的CONTURA G2 RDS桥式三坐标测量机对“S”试件上的50条母线并且每条母线上取5个点进行测量，如图 4所示.利用自主编写的程序借助MATLAB软件，得出各个误差源参数对机床误差的影响如图 5所示(考虑篇幅有限，仅列出影响程度较大的误差源参数). “S”试件三维模型如图 6所示.机床的基本参数参如表 3所示.
![]()
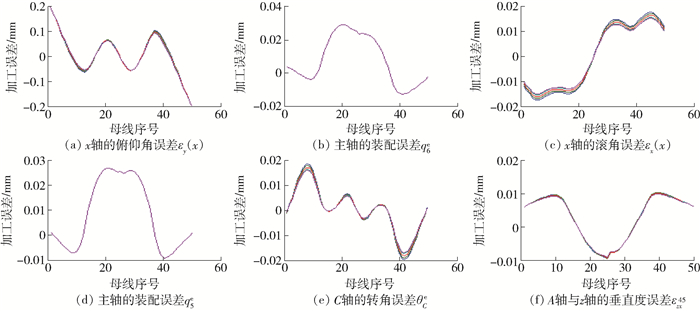
图 5 单项误差源参数引起的加工误差Figure 5. Machining errors caused by individual error source parameter表 3 五轴龙门机床基本参数Table 3. Basic parameters of the five-axis gantry machining center参数 数值/mm q1 [0 0 0]T q3 [-5 800 -60 2 000]T q5 [-0 0 -3 700]T qw [3 000 1 940 250]T Lx 6 000 Lz 3 000 by 4 000 wx 3 880 wz 500 q2 [6 000 4 500 3 950]T q4 [-170 -190 -3 700]T q6 [0 0 -200]T rt 4 500 Ly 4 500 bx 5 200 bz 2 500 wy 1 800 对“S”试件上选取的50条母线并且每条母线上选取5个点进行计算，计算结果如图 5所示用5种不同颜色的曲线表示每条母线上的5个点的加工误差值.每个单项误差源参数对机床加工精度影响程度各不相同，以下几种误差源参数对机床加工精度影响以及在“S”试件上的加工特征比较明显，故加以说明.
1) x轴的俯仰角误差，如图 5(a)所示，在取样区间1~10、37~50，加工误差从正到负呈现单调递减的趋势.这2个区域是“S”试件的2个右侧面，其加工误差为±0.2 mm.
2) 主轴装配误差源参数，如图 5(b)所示，由于每条母线上的5个测点处由主轴装配运动误差引起的加工误差近似相等，所以图 5(b)为一条单一的曲线.在取样区间内，“S”试件上形成的加工误差特征为n型，由于主轴装配位置误差，使得当C轴旋转时，带着主轴产生摆动，这时，8、40处出现误差负极值，20处出现误差正极致，8、40处的误差与20处的误差呈现反向状态.
3) C轴转角误差源参数，如图 5(e)所示，在“S”试件上形成的加工误差特征为，在加工点8、43处存在极值，这是由于C角误差以及“S”试件加工面朝向的综合作用结果所致.
由以上分析结果表明，加工误差的波动范围越大，该项误差对机床加工精度的影响也越大，为了更直观地辨别出关键性误差源参数，将各个误差源参数引起的机床加工精度进行归一化处理，即
$$ {S_n} = \frac{{{E_n}}}{{\sum {{E_n}} }}\;\;\;\;\;\left( {n = 1,2, \cdots ,53} \right) $$ (16) 式中：Sn为第n项误差源参数对应的误差敏感度系数，系数之和等于1；En为第n项误差源参数对应的机床加工误差的绝对范围.
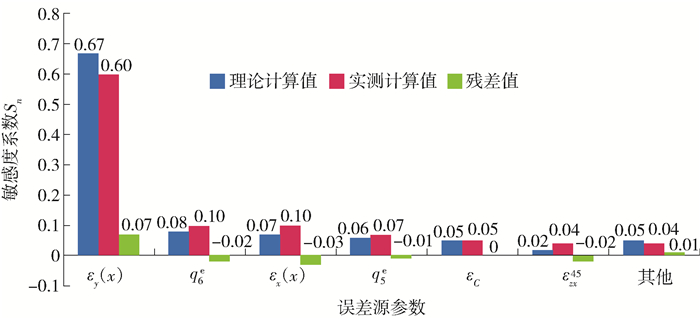
图 7为机床误差源参数对应的敏感度系数对比图，可以看出εy(x)、q6e、εx(x)、q5e、θCe、εzx45这6项误差源参数对应的误差敏感度系数之和为0.95，其他误差源参数的敏感度系数之和仅为0.05，残差绝对值的最大值为0.07，最小值为0.由此可得实测计算值的误差源参数敏感度排序与理论计算值的误差源参数敏感度排序结果一致，表明了理论分析的正确性.
以上分析表明：x轴的俯仰角误差、主轴的装配误差、x轴的滚角误差、A轴装配误差、C轴的转角误差以及A轴与C轴在xz平面的不垂直度误差等这几项误差源参数对机床加工误差的敏感度较大，即在机床各个零部件中，对最终机床加工精度起到关键性作用的为x轴导轨、A、C摆头以及主轴，所以在数控机床精度设计时应着重考虑.
5. 结论
1) 基于多体系统理论，将机床的各种几何误差考虑其中，建立了CA摆头五轴数控机床的运动误差模型.
2) 构造了基于零部件公差的几何误差源参数的预估模型，成功将公差要素引入到数控机床空间运动误差计算模型中，为基于机床部件运动增量的误差敏感度分析新方法的研究奠定基础.
3) 该二次偏导数的误差敏感度分析模型，由数控机床空间运动误差模型和误差源参数的预估模型，提出了基于局部运动增量的误差敏感度分析新方法，该方法有效地解决了由于误差源参数增量均为1的假设所造成的分析结果严重失真的问题.
4) 以“S”试件的加工为例，同时借助MATLAB对五轴加工中心进行误差敏感度分析，由此得出εy(x)、q6e、εx(x)、q5e、θCe、εzx45这6项误差源参数对应的误差敏感度系数之和为0.95，其他误差源参数的敏感度系数之和仅为0.05，有效地识别出对数控机床精度影响较大的关键零部件，进而通过实验验证了基于局部运动增量的误差敏感度分析新方法的准确性与可靠性，为之后数控机床的精度设计奠定了坚实的理论基础.
-
![]()
图 1 CA摆头五轴龙门数控机床结构
B0—床身; B1—x轴; B2—y轴; B3—z轴; B4—C轴; B5—A轴; B6—主轴; Bw—工件; Bt—刀具
Figure 1. Schematic of the five-axis gantry machining center structure
![]()
图 5 单项误差源参数引起的加工误差
Figure 5. Machining errors caused by individual error source parameter
表 1 CA摆头五轴龙门数控铣床几何误差
Table 1 Geometric errors for the five-axis gantry machining center
项目 误差 沿x轴平动 εx(x) εy(x) εz(x) δx(x) δy(x) δz(x) 沿y轴平动 εx(y) εy(y) εz(y) δx(y) δy(y) δz(y) 沿z轴平动 εx(z) εy(z) εz(z) δx(z) δy(z) δz(z) 绕C轴转动 εyz(θC) εxz(θC) εxy(θC) δx(β) δy(β) δz(β) 绕A轴转动 εyz((θA)) εxz(θA) εxy(θA) δx(α) δy(α) δz(α) 主轴转动 εyz(φ) εxz(φ) εxy(φ) δx(φ) δy(φ) δz(φ) 垂直度 εxy02、εxz23、εyz23、εxz34、εyz34、εxy45、εzx45、εxz56、εyz56 装配位置误差 q1e、q2e、q3e、q4e、q5e、q6e A、C轴转角误差 (θA)e(θC)e 
下载: 导出CSV
表 2 各位置矢量、位移矢量和变换矩阵(部分)
Table 2 Position vectors, displacement vectors and transform matrices (part)
相邻体 体间实际结构变换矩阵 体间实际运动变换矩阵 位移矢量 大地—0 Hpe0=I 无 无 0—1 Hpe1=I $\mathit{\boldsymbol{H}}_{{\rm{se}}}^1 = \left[{\begin{array}{*{20}{c}} 1&{ - {\varepsilon _z}\left(x \right)}&{{\varepsilon _y}\left(x \right)}\\ {{\varepsilon _z}\left(x \right)}&1&{ - {\varepsilon _x}\left(x \right)}\\ { - {\varepsilon _y}\left(x \right)}&{{\varepsilon _x}\left(x \right)}&1 \end{array}} \right]$ $s{\prime _1} = {s_1} + s_1^{\rm{e}} = \left( {\begin{array}{*{20}{c}} {x + {\delta _x}\left( x \right)}\\ {{\delta _y}\left( x \right)}\\ {{\delta _z}\left( x \right)} \end{array}} \right)$ 0—2 $\mathit{\boldsymbol{H}}_{{\rm{pe}}}^2 = \left[{\begin{array}{*{20}{c}} 1&{ - \varepsilon _{xy}^{02}}&0\\ {\varepsilon _{xy}^{02}}&1&{ - {\varepsilon _x}0\left(x \right)}\\ 0&0&1 \end{array}} \right]$ $\mathit{\boldsymbol{H}}_{{\rm{se}}}^2 = \left[{\begin{array}{*{20}{c}} 1&{ - {\varepsilon _z}\left(y \right)}&{{\varepsilon _y}\left(y \right)}\\ {{\varepsilon _z}\left(y \right)}&1&{ - {\varepsilon _x}\left(y \right)}\\ { - {\varepsilon _y}\left(y \right)}&{{\varepsilon _x}\left(y \right)}&1 \end{array}} \right]$ $s{\prime _2} = {s_2} + s_2^{\rm{e}} = \left( {\begin{array}{*{20}{c}} {{\delta _x}\left( y \right)}\\ {y + {\delta _y}\left( y \right)}\\ {{\delta _z}\left( y \right)} \end{array}} \right)$
下载: 导出CSV
表 3 五轴龙门机床基本参数
Table 3 Basic parameters of the five-axis gantry machining center
参数 数值/mm q1 [0 0 0]T q3 [-5 800 -60 2 000]T q5 [-0 0 -3 700]T qw [3 000 1 940 250]T Lx 6 000 Lz 3 000 by 4 000 wx 3 880 wz 500 q2 [6 000 4 500 3 950]T q4 [-170 -190 -3 700]T q6 [0 0 -200]T rt 4 500 Ly 4 500 bx 5 200 bz 2 500 wy 1 800
下载: 导出CSV
-
[1] 王波雷.数控机床热误差补偿技术的研究[D].北京: 北京工业大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1787727 WANG B L. The study on thermal errors compensation of NC machine tools[D]. Beijing: Beijing University of Technology, 2010. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1787727
[2] 李圣怡, 戴一帆, 尹自强, 等.精密和超精密机床精度建模技术[M].长沙:国防科技大学出版社, 2007:23. [3] 刘志峰, 刘广博, 程强, 等.基于多体系统理论的精密立式加工中心精度建模与预测[J].吉林大学学报(工学版), 2012, 42(2):388-391. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jlgydxzrkxxb201202023 LIU Z F, LIU G B, CHENG Q, et al. Precision modeling and prediction of precise vertical machining center based on theory of multi-body system[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(2):388-391. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jlgydxzrkxxb201202023
[4] 范晋伟, 王鸿亮, 张兰清, 等.数控凸轮轴磨床运动误差分析与建模技术[J].北京工业大学学报, 2017, 43(2):203-209. http://www.bjutxuebao.com/bjgydx/CN/abstract/abstract3990.shtml FAN J W, WANG H L, ZHANG L Q, et al. Motion error analysis and modeling technology of CNC camshaft grinder[J]. Journal of Beijing University of Technology, 2017, 43(2):203-209. (in Chinese) http://www.bjutxuebao.com/bjgydx/CN/abstract/abstract3990.shtml
[5] LI J, XIE F, LIU X J, et al. Geometric error identification and compensation of linear axes based on a novel 13-line method[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(5/6/7/8):2269-2283. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9fcd65750bf0afc0f9a16beb108ac047
[6] 唐宇航, 范晋伟, 陈东菊, 等.基于蒙特卡洛模拟的机床关键几何误差溯源方法[J].北京工业大学学报, 2017, 43(11):1619-1628. doi: 10.11936/bjutxb2016120032 TANG Y H, FAN J W, CHEN D J, et al. Tracing method for key geometric errors of a machine tool based on monte carlo simulation[J]. Journal of Beijing University of Technology, 2017, 43(11):1619-1628. (in Chinese) doi: 10.11936/bjutxb2016120032
[7] 阎艳, 王戈, 张发平, 等.基于误差传递模型的精密装配几何误差灵敏度分析[J].北京理工大学学报, 2017, 37(7):682-686. http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201707005 YAN Y, WANG G, ZHANG F P, et al. Precision assembly geometric error sensitivity analysis based on the error transformation model for precision assembly[J]. Journal of Beijing Institute of Technology, 2017, 37(7):682-686. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201707005
[8] DING G B, ZHU S W, YAHYA E, et al. Prediction of machining accuracy based on a geometric error model in five-axis peripheral milling process[J]. Proceedings of the Institution of Mechanical Engineers:Part B Journal of Engineering Manufacture, 2014, 228(10):1226-1236. doi: 10.1177/0954405413516611
[9] LI J, XIE F J, LIU X J. Geometric error modeling and sensitivity analysis of a five-axis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82:2037-2051. doi: 10.1007/s00170-015-7492-5
[10] PENG W C, XIA H J, WANG S J, et al. Measurement and identification of geometric errors of translational axis based on sensitivity analysis for ultra-precision machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94:2905-2917. doi: 10.1007/s00170-017-1095-2
[11] 李小雷, 童水光, 金涛, 等.新型数控刻楦机的误差分析和精度综合[J].浙江大学学报, 2006, 40(6):991-996. doi: 10.3785/j.issn.1008-973X.2006.06.015 LI X L, TONG S G, JIN T, et al. Error analysis and accuracy synthesis of new numerical control shoe last machine[J]. Journal of Zhejiang University, 2006, 40(6):991-996. (in Chinese) doi: 10.3785/j.issn.1008-973X.2006.06.015
[12] 程强, 刘广博, 刘志峰, 等.基于敏感度分析的机床关键性几何误差源识别方法[J].机械工程学报, 2012, 48(4):92-100. http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201207023 CHENG Q, LIU G B, LIU Z F, et al. An indentification approach for key geometric error sources of machine tool based on sensitivity analysis[J]. Journal of Mechanical Engineering, 2012, 48(4):92-100. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201207023
[13] 程刚, 葛世荣. 3-RPS对称并联式机械腿误差模型及分析[J].中国矿业大学学报, 2009, 38(1):50-55. doi: 10.3321/j.issn:1000-1964.2009.01.011 CHENG G, GE S R. Error model and analysis of 3-RPS symmetrical parallel robot leg with three degree-of-freedom[J]. Journal of China University of Mining & Technology, 2009, 38(1):50-55. (in Chinese) doi: 10.3321/j.issn:1000-1964.2009.01.011
计量
- 文章访问数: 311
- HTML全文浏览量: 5
- PDF下载量: 52
