Adaptive Testing of Network Security Awareness Based on IRT
-
摘要:
为有效度量个人网络安全意识状态,根据项目反应理论和多阶段测验理论提出了网络安全意识自适应测试技术.首先,设计了基于"行业、岗位、人员"层级的知识库模型,根据模型给出了测试项目参数的计算方法.然后,引入反应时间的概念改进了逻辑斯蒂三参数模型.最后,提出了基于滑动窗口的组卷策略并给出了状态评估模型.结果表明:基于模型改进后的自适应测试的效能较传统模型测试和原逻辑斯蒂三参数模型的测试效能分别提高了34.9%和8.7%,为网络安全意识测试领域和其他领域计算机自适应测试技术的研究提供了参考.
-
关键词:
- 网络安全意识 /
- 自适应测试 /
- IRT /
- Logistic模型 /
- 组卷策略
Abstract:To effectively measure the status of personal network security awareness, this paper proposed an adaptive testing of the network security awareness based on the items response theory (IRT) and multi-stage testing theory. First, a knowledge library model based on "industry, job, and personnel" was designed. According to the model, the calculation method of the item parameters was given. Second, the concept of reaction time was imported to improve the logistic-3-parameter model. Finally, the grouping strategy based on the sliding window and the state evaluation model was given. Results show that the improved adaptive testing performance is 34.9% and 8.7% higher than the traditional model testing and the original logistic-3-parameter model testing, respectively. It provides a reference for the field of testing on network security awareness and computerized adaptive testing technology.
-
近年来,在世界范围内发生了多起网络诈骗、网络勒索和信息泄露等重大社会安全问题,造成了国家、企业和个人的巨大损失.研究表明,人员作为网络空间安全链条的薄弱环节,其所遭受的风险远远大于技术,因社会工程学攻击而引发的损失也越来越大.因此,网络安全意识逐渐得到了社会的广泛关注[1],并作为国家网络安全战略的重要内容之一.
网络安全意识形而上地影响着个人的网络空间行为,准确而有效地度量个人网络安全意识水平将有助于对网络空间的威胁及时预警,从而减少或避免造成较大的损失.同时,根据网络安全意识的度量情况,还可针对性地编制教育方案,从而高效地提高个人网络安全意识.
现有的网络安全意识测试方式较为单一,一般仅有知识考试和意识测评2类较为独立的方案,2类方案缺乏联系从而难以对意识水平做定量分析.缺乏定量分析就难以根据数据从科学的角度做进一步解析,就无法了解技术的进步空间[2].
知识考核系统是量化网络安全意识水平的关键,因网络技术的快速发展使得知识体系变得极度繁杂,知识库构建难度加剧. “千人一卷”的传统考试很难有效判别被测人员的知识掌握程度,水平低的人员根本无法作答难度大的题目,水平高的人员作答简单题目又测不出真实水平.目前的考试模式大多采用这种基于计算机平台的传统测试,题目、试卷质量和估计的准确度难以得到保障.为弥补经典测量理论的不足,衍生了计算机自适应测试(computerized adaptive testing,CAT),可根据考生能力和答题状况动态抽取下一道考题,形成了“因人而异”的计算机自适应测试系统,在教育领域应用较多,诸如GRE、TOEFL.
现有的自适应测试系统多基于项目反应理论(item response theory,IRT)[3],系统可根据被测人员的能力水平自动选择测试题,最终做出对被试能力的准确估计.但由于网络安全意识涵盖的知识点复杂、逻辑性强,现有的网络安全意识自适应测试方法在题库的设计上仍有不足,各个行业领域之间的意识要求界限并不分明,难以准确评估.
自适应测试技术自发展以来仍然存在不足,因其测试题目研制成本高、周期长、更新慢,应用受到了很多限制.自适应测试的单位时间长短会影响能力估计准确度[4],但目前IRT时间模型研究较少,已有的模型[5]在实践中适用性不强.其次,能力估计的精确度同网络安全知识体系的完善与否密切相关,目前国内外针对网络安全意识体系仍然缺乏系统认知,据现有的知识体系[6]难以构建完整的试题库.
为尽可能减少自适应测试的缺陷,提高网络安全意识的测试效率,本文构建了一种基于“行业、岗位、人员”的三层三维知识库模型,能够囊括和分解知识点,便于量化,同时提出并论证了IRT-3PL-T模型的可行性,阐述了基于滑动窗口的组卷策略,最后通过工程实验证明了改进后的自适应测试技术的可用性及其效率的提高,为自适应测试技术和网络安全意识的发展提供了参考.
1. 试题库建库分析
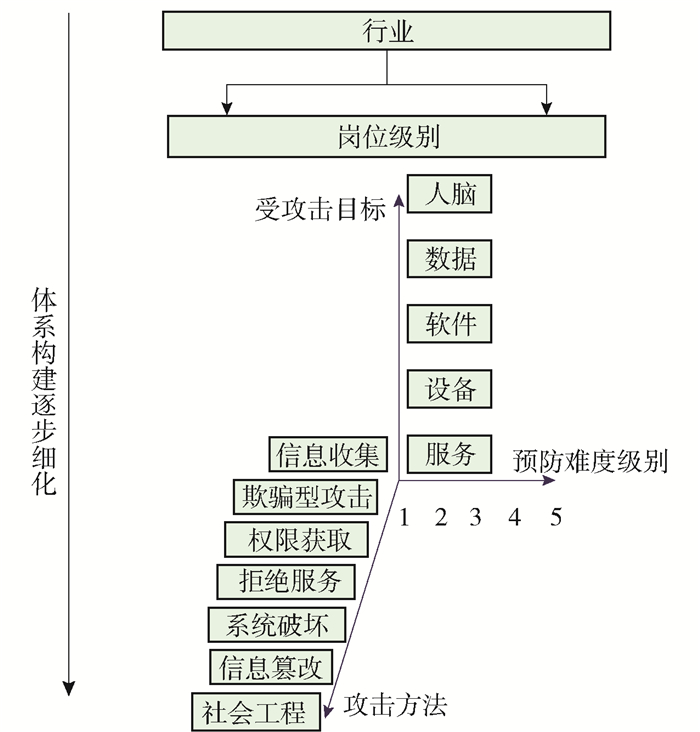
题库是测试的基础,高质量的题库应具备优质、丰富、等值、动态可扩充等重要特性.网络安全相关知识随着技术发展不断更新,依照目前现有的知识体系很难构建一个完备的知识库.综合分析国内外网络安全知识体系分类标准[6],结合具体行业领域规范,同时为方便测试的选题,本文构建了以“行业、岗位、角色”为分类层次的三维知识库,如图 1所示.
首先,根据行业网络安全规范的差异进行知识点聚类,确定该行业需求的知识点,再根据该行业中岗位的具体要求生成知识图谱,将三维知识库中可定位的具体试题填充至图谱中,自主生成了该角色的适应性题库,便于测试的题目抽取,提高了效率和准确性,一定程度降低了组卷算法的复杂度.
三维知识库,将单一的网络安全知识点定位在立方体模型中的一个区域,保证了知识的精确性,提供了足够的空间涵盖目前已知的知识点,并为未来知识点的拓展提供了空间.根据网络安全规范,不同角色对网络安全意识要求的程度不同,这相当于规定了角色考核试题的难度以及角色所要求的能力,进一步为确定试题的参数提供了参考,方便了组卷策略的制定.
在知识点的相应区域填充高质量试题是试题库建库的核心阶段,虽然人工制定的试题质量高但消耗的资源过多,制题的效率很难赶上网络安全技术的发展速度.为提高制题效率,知识库模型仅在高威胁、实时性强的知识点上采用人工制题,其余试题均采用网络爬虫的方法,制定合适的抓取策略,利用搜索引擎定期从网络空间中抓取含有关键词且符合主题和语义模型的考题,系统自动计算试题参数并及时填充到知识库中,通过对不同试题参数值迭代分析,舍弃质量较差的试题,同时根据需要调整区域关键词进一步“爬取”高质量试题.
诸如选择、判断等客观题型具有设计简单、判别容易、便于量化计算等优势,所以现有的计算机自适应测试的题型一般仅限于客观题,但客观题无法完全量化被试人员的能力和掌握情况.本文通过分解实操步骤和提取关键词等技术,设计了便于量化的主观题型.简答题的答案可根据语义分析确定关键词作为其得分要点,采集被试人员的测试结果,利用相同的语义分析提取关键词并同答案词对比进而确定成绩.应用技能题将实训内容划分不同的步骤,每一步骤设置可量化的确定结果并进行监听,被试人员操作到哪一步,哪一步就计入成绩,从而实现操作的考核量化.依具体测试要求和客观实际,设计特定的试题数据库表单模型如表 1所示.
表 1 试题表单设计Table 1. Item designing题型 设计内容 选择题(不定项选择) 题号 题目 选项A 选项B 选项C 选项D 选项E 答案 难度 区分度 可信度 优先级 关键词 录入日期 判断题 题号 题目 答案 难度 区分度 可信度 优先级 关键词 录入日期 简答题 题号 题目 答案词1 答案词2 答案词3 答案词4 答案词5 难度 区分度 可信度 优先级 关键词 录入日期 应用技能题 题号 题目 步骤1 步骤2 步骤3 步骤4 步骤5 难度 区分度 可信度 优先级 关键词 录入日期 难度(difficulty)指考生完成题目的困难程度,也称统计难度,根据同一试题在样本中的错误率来确定初始难度,错误率越高试题越难,难度系数用符号d表示.计算表达式为
$$ d=1-\frac{\sum\limits_{i=1}^{n} X_{i}}{n X_{\max }} $$ (1) 式中:Xi为第i名考生对该题获得的分数;n为指测试总人数;Xmax为指该题满分值.式(1)表明,难度越高,考生得分越低,即Xi值越大,d越小. d取值范围是0≤d≤1.
区分度(partition)是区分不同层次考生水平能力的指标,通常由试题得分和考生能力值的关系确定.假设试题区分度高,则能力值高的考生在该题得分就高,能力值低的考生在该题得分就低,从而将不同考生区分开来.试题的初始区分度等同于知识库的预防难度级别,通过预防难度级别区分考生能力水平,避免了通用CAT测试方法中舍弃区分度低的试题从而引发高曝光率降低测试准确性,同时减小了系统计算量,提高了试题入库效率.
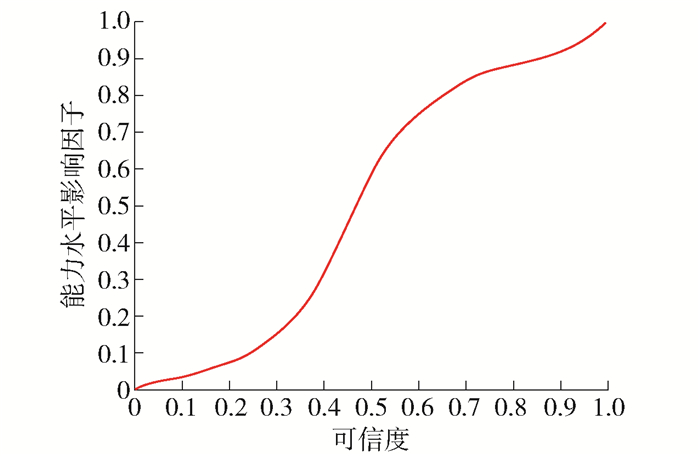
可信度(reliability)是指该题测试结果的稳定程度[7],即信度高的试题应满足在任何位置、任何时间测试都可以获得一致的结果,换句话说,可信度低的试题无论水平高低都容易猜对.关于能力值计算的影响曲线如图 2所示.
只有可信度较高的试题才会对能力估计产生影响,而可信度较低的试题对于估计被试人员的能力水平产生了干扰,试题测试结果不应纳入能力水平计算,所以在题库中应尽可能舍弃可信度较低的试题,从而提高组卷的效率.
可信度的概念是理论上的构想,实际上很难直接测量得到,通常采用统计理论中的估计法计算表示可信度大小[7].本文初始参数测试方法结合网络安全试题参数设计,基于库里法[8]改进了Kuder-Richardson-21公式,其应用规则表现为能力高的人在作答相应题目时取得正确的成绩,对满足正态分布的能力值不同的人员进行测试同一试题,利用θ/X作为项目匹配比(能力对正确反应的相关性)的参数,进而综合全部的项目匹配比估计试题的可信度r,计算式为
$$ r=\frac{n}{n-1} \left( \begin{array}{c}\frac{{\sum\limits_{i=1}^{n} \frac{\theta_{i}}{X_{i}}}} {{\sum\limits_{i=1}^{n} \frac{\theta_{\max }}{X_{\max }}}}\end{array}\right)=\frac{\sum\limits_{i=1}^{n} \frac{\theta_{i}}{X_{i}}}{(n-1) \frac{\theta_{\max }}{X_{\max }}} $$ (2) 式中:Xi为第i名考生该题获得的分数;θi为第i名考生的能力值;n为指测试总人数;Xmax为指该题满分值;θmax为考生的能力最大值.
由于试题初始参数可能同被试人员的能力估计函数不匹配,为了尽可能提高估计准确度,利用GA-BP(遗传算法-优化神经网络)算法[9]求解模型项目参数,对初始参数进行修正,以提高收敛能力和精度.
2. Logistic-3PL-T模型
RT的基本思想是指被测人员的某种潜在特质与对项目的反应之间存在一定联系,这种联系可以通过数学模型表示. IRT数学模型至今已经发展了20多种,Logistic模型是伯恩鲍姆提出的一种二级评分模型[10],此模型与实际测验结果匹配较好,所以应用也最为广泛.
Logistic模型一般分为单参数、双参数、三参数(3PL)和四参数模型.其中,三参数模型是迄今为止使用最多的模型[10],三参数Logistic模型
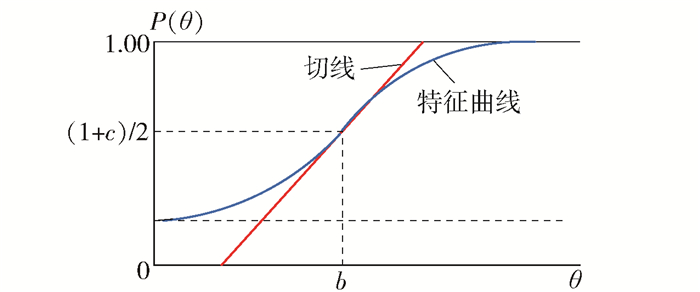
$$ P(\theta)=c+(1-c) \frac{1}{1+\mathrm{e}^{-D a(\theta-b)}} $$ (3) 式中:D=1.702常量;θ为被测人员的能力估计值;P(θ)为能力大小为θ的人答对此题的概率;a为项目区分度,即特征曲线的斜率,它的值越大说明题目对受测者的区分程度越高;b为项目难度,即特征曲线在横坐标上的投影;c为项目猜测系数,即特征曲线的截距.
Logistic 3PL模型特征曲线如图 3所示.
IRT模型的核心就是对被试人员能力的估计,但是在实测过程中发现,人员思考试题时间的长短会影响测试结果,中低及以下能力水平的被试人员对思考时间的影响可能由于知识掌握不牢靠所以表现不是很明显,中等及以上能力水平的被试人员思考问题的时间越长,试题作答的正确率越高,而思考时间对于高水平被试人员的影响尤为突出.为提高能力估计的精确度,针对原模型对试题作答时间参数考虑不足,本文提出了反应时间(response time)假设,对3PL模型做了相应的改进,同时将信度代替猜测度.由于项目时间作为难度、区分度的辅助参数,处于e的指数位,同时项目时间不能对能力估计产生较大程度的影响,故时间对能力估计值的影响处于正态分布,但由于μ=0时该值未处于峰值且t对Dp(θ-d+m)的影响因其正负变换产生翻折不符合实际.模型的解决方法是利用阶数为2的矩形窗向右1个单位截取时间参数,即t=1作为峰值点,根据Dp(θ-d+m)的正负关系变换t函数,其完整计算模型为
$$ \begin{array}{c} P(\theta ) = \\ \left\{ {\begin{array}{*{20}{l}} {(1 - r) + r\frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m)t}}}}, \quad \;\;\;\;\theta - d + m≥0}\\ {(1 - r) + r\frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m)(2 - t)}}}}, \quad \theta - d + m < 0} \end{array}} \right. \end{array} $$ (4) 式中:D=1.702常量;θ为能力估计值,θ∈(-3, 3);p为项目区分度,对知识库预防难度级别做归一化处理,p∈(0, 1];d为项目难度,d∈(0, 1];r为可信度,r∈(0, 1];t为反应时间,对项目反应时间做归一化处理,t∈(0, 1];m为修正参数,一般默认m=0,可以根据项目规模自主调整.
3PL-T模型中,个人能力只有高于测试项目的难度才会增加正确反应的概率.综合其他因素以及实际测试表明,能力水平略高于试题难度的测试正答率并不高,而是以(1-r/2)的概率显示,能力极高的被试对于高难度试题也无法达到100%的正确率,其指数收敛于Dp(θ-d+m),传统模型可以视为该模型的极限情况.相比于原3PL模型,改进模型在时间的分析上提高了能力估计的精确度,反应(思考)时间在规定范围内越长,正确反馈的概率越大,但不会大幅提高能力估计值.
根据测试的实际情况,3PL-T模型具备如下性质.
性质1 被试反应时间越长,正确反馈概率越大
证明:利用概率差值比较反应时间同概率之间的关系
$$ \begin{array}{*{20}{c}} {\mathit{\Delta } = {P_1}(\theta ) - {P_2}(\theta ) = }\\ {\left[ {(1 - r) + r\frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_1}}}}}} \right] - }\\ {\left[ {(1 - r) + r\frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_2}}}}}} \right] = } \\ {r\left[ {\frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_1}}}}} - \frac{1}{{1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_2}}}}}} \right] = }\\ {r\left[ {\frac{1}{{\left( {1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_1}}}} \right)\left( {1 + {{\rm{e}}^{ - Dp(\theta - d + m){t_2}}}} \right)}}} \right] \cdot }\\ {\frac{{{{\rm{e}}^{Dp(\theta - d + m){t_1}}} - {{\rm{e}}^{Dp(\theta - d + m){t_2}}}}}{{{{\rm{e}}^{Dp(\theta - d + m){t_1}}}{{\rm{e}}^{Dp(\theta - d + m){t_2}}}}}} \end{array} $$ 式中:r∈(0, 1];1/[(1+e-Dp(θ-d+m)t1)(1+e-Dp(θ-d+m)t2)]>0;eDp(θ-d+m)t1eDp(θ-d+m)t2>0,因此Δ的符号由eDp(θ-d+m)t1-eDp(θ-d+m)t2决定,其讨论情况如下.
$$ \begin{equation} \begin{array}{l}{t_{1}>t_{2}, \mathrm{e}^{D p(\theta-d+m) t_{1}}-\mathrm{e}^{D p(\theta-d+m) t_{2}}>0} \\ {t_{1}=t_{2}, \mathrm{e}^{D p(\theta-d+m) t_{1}}-\mathrm{e}^{D p(\theta-d+m) t_{2}}=0} \\ {t_{1}<t_{2}, \mathrm{e}^{D p(\theta-d+m) t_{1}}-\mathrm{e}^{D p(\theta-d+m) t_{2}}<0}\end{array} \end{equation} $$ 所以,上述证明过程指出正确作答概率同项目反应时间呈正相关,即测试人员思考的时间越长,正确反馈的概率就越大.
性质2 被试反应时间对能力估计的增幅可控制在一定范围内
证明:采用极大似然估计对被试能力水平估计,项目反应为ui,正确值为1,错误值为0.局部独立假设,项目反应为联合概率
$$ \begin{array}{*{20}{c}} {L\left( {{u_1}, {u_2}, \cdots , {u_n}|\theta } \right) = }\\ {P\left( {{u_1}|\theta } \right)P\left( {{u_2}|\theta } \right) \cdots P\left( {{u_n}|\theta } \right) = \prod\limits_{i = 1}^n {P_i^{{u_i}}} Q_i^{1 - {u_i}}} \end{array} $$ (5) 式中:n为项目数量;Piui为第i个项目的正确概率;Qiui为第i个项目的错误概率.通过方程$\frac{\mathrm{d}}{\mathrm{d} \theta} \ln L(\theta)=0$求得θ的极大似然估计值,为利用计算机求解方便通常采用Newton-Raphson迭代法对似然函数求解.在保证其他参数不变的情况下,仅改变时间参数值,做差表示其增幅,则有
$$ \begin{array}{*{20}{c}} {\mathit{\Delta } = {\mathop{\rm abs}\nolimits} \left( {{\theta _{t2}} - {\theta _{t1}}} \right) = }\\ {\left| {\frac{{{P_i}{r_i}\sum\limits_{i = 1}^n {\left( {{u_i} - {P_i}} \right)} }}{{D\sum\limits_{i = 1}^n {{p_i}} \left( {{u_i}\left( {1 - {r_i}} \right) - P_i^2} \right){Q_i}}}} \right|}\\ \end{array} $$ 假设二者均正确作答,即ui=1,各项参数均取极值可得0 < Δ≤1/D,增幅在可控范围内,符合实际,确保不会影响能力估计的精确度.
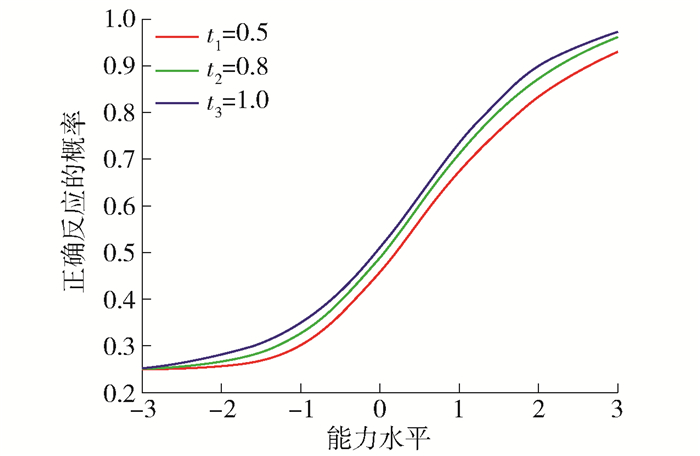
自适应测试中,采用3PL-T模型,3次被试对同一个测试项目做出了反应,结果一致,但时间略有区分,如表 2所示. t=1时,模型即为原3PL参数模型,其值域范围高于其他t参数时刻的值,是3PL-T模型的特殊情形.相比于原模型,改进后的模型更能体现出项目反应时间对能力参数估计的影响,有效提高了能力参数估计的精度.
表 2 反应时间测试案例Table 2. Test of different response times参数 难度d 区分度p 可信度r 修正参数m 反应时间系数t 数值 0.5 0.8 0.75 0 0.5
0.8
1.0上述测试案例的项目特征曲线如图 4所示.
3. 组卷策略
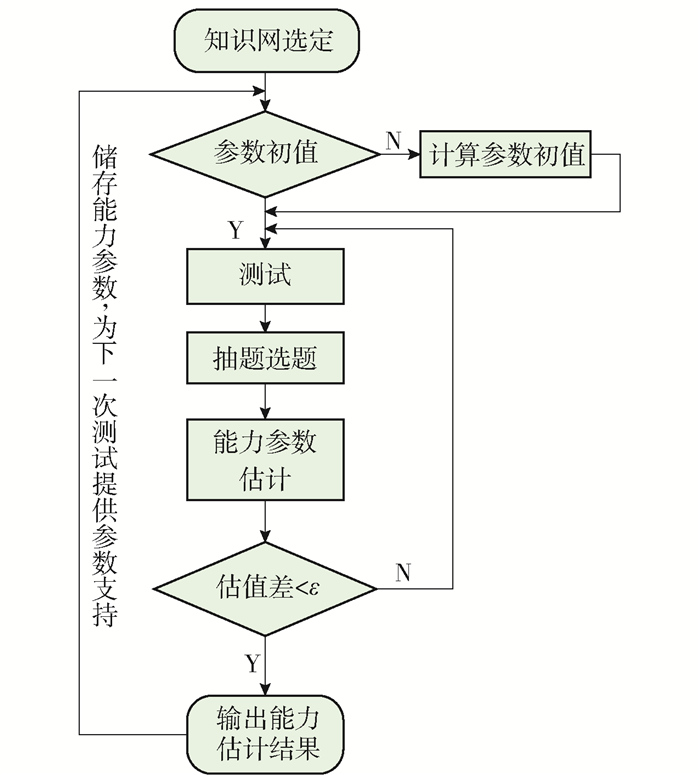
只有当被试能力水平大于项目难度时,提供的信息量才最大,且测验结果的效度和信度以及被试接受测验的积极性均可有效提高,这就是自适应测试中抽选试题的理论依据. CAT测试的优势在于可以根据实时测试的情况估计被试的能力参数,从而动态调整试题的难度,达到高效、快捷、准确的目的.测试算法流程如图 5所示,据步骤进行组卷优化.
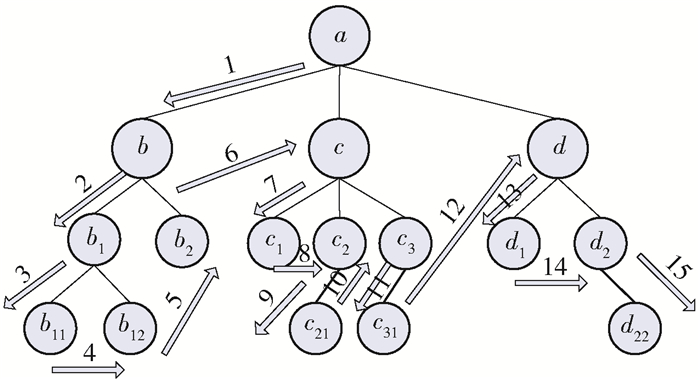
根据被试的行业、岗位和角色要求,依知识库选取相应的知识点生成知识考核网络,参考图论中二叉树的先序遍历算法,从而提高试题间的逻辑性,便于优化组卷,如图 6所示.针对某一知识网络,为全面、综合考核被试的知识掌握水平及其能力,应尽可能遍历考核知识点,同时保证知识的连贯性,避免因打破知识间的逻辑而降低估计的收敛速度.
在项目参数初始值尚未确定时,一般可采用Mislevy的边际贝叶斯估计法[11],而能力参数估计不仅可以采用上述证明中应用的极大似然估计,也可以采用贝叶斯定理,通过最大后验估计和期望后验估计2个过程调整能力参数.假设ξ为项目参数向量,y(ξ)表示第i个项目参数的先验分布,f(θ)表示能力的先验分布,则有
$$ \begin{array}{*{20}{c}} {h(u|\mathit{\boldsymbol{\xi }}, \theta ) \propto L(u|\mathit{\boldsymbol{\xi }}, \theta )y(\mathit{\boldsymbol{\xi }})f(\theta )}\\ {L(u|\mathit{\boldsymbol{\xi }}, \theta ) = \prod\limits_{i = 1}^N {\prod\limits_{j = 1}^m {{P_j}} } {{\left( {{\theta _i}} \right)}^{{u_i}}}{Q_j}{{\left( {{\theta _i}} \right)}^{1 - {u_i}}}y(\mathit{\boldsymbol{\xi }})f(\theta ) = }\\ {\prod\limits_{i = 1}^N P \left( {{u_i}|{\theta _i}, \mathit{\boldsymbol{\xi }}} \right)y(\mathit{\boldsymbol{\xi }})f(\theta )} \end{array} $$ (6) 对式(6)取对数,可以得到似然函数
$$ \ln L = \sum\limits_{i = 1}^N {\ln } P\left( {{u_i}|{\theta _i}, \mathit{\boldsymbol{\xi }}} \right) + \ln y(\mathit{\boldsymbol{\xi }}) + \ln f(\theta ) $$ (7) 通过对式(7)求偏导,计算出能力估计参数.在假定已知能力参数的条件下,可估算出相应的试题参数.再将2个参数中一个条件估计的结果作为另一个条件估计的参数,如此反复执行EM迭代算法形成训练模型,使得全部参数收敛并逼近真值.
能力估计选题,能力真值做题.在CAT测试中,每作答一道试题后都会计算出新的能力估计参数,根据该临时参数选择试题库中信息量最大的一个作为其下一个测试项目,以提高测试的精确度.
本文使用项目信息函数作为分析测验的参考,根据临时能力值预估备选试题的正确率,从而选取能力值与正确率相适应的试题,即信息函数最大的试题将作为下一道测试项目,信息函数表示为
$$ \begin{equation} \begin{array}{c}{I_{i}\left(\theta^{\prime}\right)=\frac{\left[P_{i}^{\prime}\left(\theta^{\prime}\right)\right]^{2}}{P_{i}\left(\theta^{\prime}\right) Q_{i}\left(\theta^{\prime}\right)}=} \\ {\frac{\left[P_{i}^{\prime}\left(\theta^{\prime}\right)\right]^{2}}{P_{i}\left(\theta^{\prime}\right)\left[1-P_{i}\left(\theta^{\prime}\right)\right]}}\end{array} \end{equation} $$ (8) 式中:θ′为测试过程的临时能力估计值;Pi(θ′)为反应正确的概率.研究表明,同一项目对不同能力值提供的信息量不同,不同的项目对相同能力值提供的信息量也不相同,以此为依据可有效遴选在能力值附近的试题,提高估计精确度.
但此种策略由于每次能力估计都会消耗内存,尤其是多测试的并行运算会随着测试项目的增加而提升运算量,对于测试系统的响应时间、反馈效率以及云系统的运算能力都提出了非常高的要求.
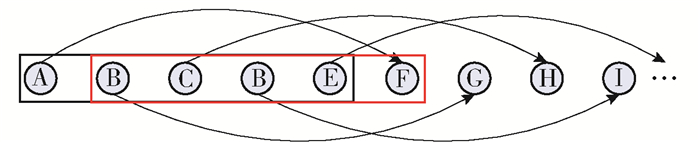
为提高测试系统的健壮性、连贯性,本文提出了在b-CBUI[10]方法的基础上建立数量为5的滑动窗口策略.即根据初始能力值先在题库中选取参数匹配的5道试题,随后根据第1题的测试结果,估算其能力值并动态调整第6道试题的内容,如此往复,从而为系统运算提供了时间.简单讲,就是根据第i题决定第i+5题的内容,形成滑动窗口,如图 7所示.另外,可以根据系统的具体运算情况,更改每次调整试题的数量,但数量不得大于滑动窗口数目.调整试题若超过1道,试题的难度变化应控制在[d′-0.1, d′+0.1],其中d′为依据临时估计的能力参数而选定的试题难度值.
前5道试题的选择由于缺乏调整的可能性,为了保证能力估计参数计算的有效性,可首先确定初始难度d0,则前5道题目的难度分别为[d0-0.1,d0-0.1, d0, d0+0.1, d0+0.1], 根据试题难度安排选取策略可以有效减少参数估计的运算量,进而提高组卷效率.
为降低高质量、高区分度试题的曝光率,引入了优先级的概念,即将某一知识点题库内的同一难度级别的试题进行优先级排序,由于知识库设置在云服务器上,不同的被试调用的相同知识点的试题时,均选取优先级最高的试题,则被选取的试题优先级置0,其他试题的优先级均做“+1”运算,从而保障了试题内容的均衡问题、控制了曝光率,减小了测度误差.
测试的终止条件在一定程度上决定了测试的效率,目前终止条件一般有按照试题数目、测试时间和能力估计的标准差等方式,前者缺点是能力估计的精度较低,后者是测试可能过长.综合来看,测试终止条件可同时结合多种方法,如果能力估计值持续(≥3)高于某一定值,且根据能力参数调整的下一题出现作答错误,则可以终止测试,并最终估计其本次测试的能力值.若估计精度的指标小于定值,也可作为终止条件. 2种方式无论哪一种先达到标准均可停止测试.
估计精度一般采用平均绝对偏差(ABS)和平均偏移均方根(RMSD)2个指标,具体公式为
$$ \begin{equation} \mathrm{ABS}=\sum\limits_{r-1}^{R}\left(\sum\limits_{i-1}^{K} | x_{i}-\hat{x}_{i r} / K\right) / R \end{equation} $$ (9) $$ \mathrm{RMSD}=\sqrt{\sum\limits_{r-1}^{R} \sum\limits_{i-1}^{K}\left(x_{i}-\hat{x}_{i r}\right)^{2} / K R} $$ (10) 式中:$\hat{x}_{i r}$为根据xi的第r次测试计算的估计;xi为模拟真值;K为测试题数量;R表示测试次数,测试方法中R=1. ABS指标反映了估计与真值的平均偏差,RMSD指标反映了偏移均方根的平均,所以值越小,估计的准确性越高.
4. 测试分析
以3PL-T模型和组卷策略为基础的网络安全意识自适应测试系统为例,在同一服务器和同一运算能力的计算机环境下,对教研室8名教师测试其网络安全意识水平.测试结果表明,本系统平均测试时间相比于传统测试和以原测试模型为基础的自适应测试分别减少了约35 min和约14 min,平均测试试题数目分别减少了95.3道题和44.7道题,大大提高了测试效率和准确度,详细测试结果如表 3所示.
表 3 不同方案的测试效能对比Table 3. Comparison of testing effectiveness测试项目 平均时间/min 平均数量 能力值估计 效能比/% 传统测试 100 260.0 8.500 44.70 原模型的自适应测试 79 209.4 8.232 70.93 3PL-T的自适应测试 65 164.7 8.197 79.67 由此可知,同传统测试和基于原模型的自适应测试相比,基于3PL-T模型的自适应测试方案极大地缩减了测试时间和测试题目数量,同时提高了能力估计的精度,自适应测试系统也更加高效.
5. 结论
1) 该计算机自适应测试技术基本满足量化要求,能够根据被试的能力层次动态抽取试题从而快捷高效地判定被试的网络安全意识水平,进一步为预警和定制化教育提供数据支持.相比于传统的测试和目前现有的自适应智能组卷系统,本文提出的3PL-T模型和基于滑动窗口的组卷策略,提高了能力估计的精确度和效率,同比降低了试卷的规模.测试的结果数据同时可作为网络安全态势感知的人为因素数据源,为网络攻击的预防和网络系统的效能评估等提供数据参考.
2) 该网络安全知识库模型能够适应技术要求,模型基本囊括网络安全相关知识点,划分界限较为明显,有助于提供知识体系或知识图谱的支撑.
3) 基于滑动窗口的组卷策略和停测条件模型能够有效减少自适应测试的运算量,在以改变少量精准度的代价下提高了测试效率,增加了技术的可用性.
4) 该自适应测试系统具有较高的移植性和拓展性,不仅可以应用到网络安全意识领域,也同时可以在其他教育领域进行广泛使用.
-
表 1 试题表单设计
Table 1 Item designing
题型 设计内容 选择题(不定项选择) 题号 题目 选项A 选项B 选项C 选项D 选项E 答案 难度 区分度 可信度 优先级 关键词 录入日期 判断题 题号 题目 答案 难度 区分度 可信度 优先级 关键词 录入日期 简答题 题号 题目 答案词1 答案词2 答案词3 答案词4 答案词5 难度 区分度 可信度 优先级 关键词 录入日期 应用技能题 题号 题目 步骤1 步骤2 步骤3 步骤4 步骤5 难度 区分度 可信度 优先级 关键词 录入日期 表 2 反应时间测试案例
Table 2 Test of different response times
参数 难度d 区分度p 可信度r 修正参数m 反应时间系数t 数值 0.5 0.8 0.75 0 0.5
0.8
1.0表 3 不同方案的测试效能对比
Table 3 Comparison of testing effectiveness
测试项目 平均时间/min 平均数量 能力值估计 效能比/% 传统测试 100 260.0 8.500 44.70 原模型的自适应测试 79 209.4 8.232 70.93 3PL-T的自适应测试 65 164.7 8.197 79.67 -
[1] 齐斌, 王宇, 邹红霞, 等.解析网络空间武器威胁[J].保密科学技术, 2017(6):28-32. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20172017080200003481 QI B, WANG Y, ZOU H X, et al. The analyses on threat of cyber weapons[J]. Journal of Secret Science and Technology, 2017(6):28-32. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20172017080200003481
[2] BOWEN B M, DEVARAJAN R, STOLFO S. Measuring the human factor of cyber security[C]//IEEE International Conference on Technologies for Homeland Security. NewYork: IEEE, 2011: 230-235. https://www.researchgate.net/publication/232747655_Measuring_the_Human_Factor_of_Cyber_Security
[3] LORD F M. Applications of item response theory to practical testing problems[J]. Erlbaum, 1980, 1:274. http://cn.bing.com/academic/profile?id=7cbc44b4a53d130919c53f14a5a0abdb&encoded=0&v=paper_preview&mkt=zh-cn
[4] HOL A M, VORST H C M, MELLENBERGH G J. Computerized adaptive testing of personality traits[J]. Zeitschrift Für Psychologie, 2008, 216(1):12-21. http://cn.bing.com/academic/profile?id=7526d383495b25478e1495837aeae30d&encoded=0&v=paper_preview&mkt=zh-cn
[5] PRIMI C, MORSANYI K, CHIESI F, et al. The development and testing of a new version of the cognitive reflection test applying item response theory (IRT)[J]. Journal of Behavioral Decision Making, 2016, 29(5):453-469. doi: 10.1002/bdm.v29.5
[6] 齐斌, 邹红霞, 王宇, 等.浅析国内外网络安全意识教育知识体系[J].网络安全技术与应用, 2017(6):18-20. doi: 10.3969/j.issn.1009-6833.2017.06.013 QI B, ZOU H X, WANG Y, et al. The analyses of the domestic and foreign network security awareness education knowledge system[J]. Journal of Network Security Technology and Applications, 2017(6):18-20. (in Chinese) doi: 10.3969/j.issn.1009-6833.2017.06.013
[7] KIM S, FELDT L S. The estimation of the IRT reliability coefficient and its lower and upper bounds, with comparisons to CTT reliability statistics[J]. Asia Pacific Education Review, 2010, 11(2):179-188. doi: 10.1007/s12564-009-9062-8
[8] PARTHIBAN S, RODRIGUES P. Kuder-Richardson reputation coefficient based reputation mechanism for isolating root node attack in MANETs[J]. Indian Journal of Science & Technology, 2015, 8(15):1-9. http://cn.bing.com/academic/profile?id=9e31d848fcc3a62051600dab27254941&encoded=0&v=paper_preview&mkt=zh-cn
[9] XU P, LIN W, LIU F, et al. Competitive regulation of IPO4 transcription by ELK1 and GABP[J]. Gene, 2017, 613:30-38. doi: 10.1016/j.gene.2017.02.030
[10] 路鹏.计算机自适应测试若干关键技术研究[D].长春: 东北师范大学, 2012. LU P. The research on technologies of computer adaptive testing[D]. Changchun: Northeast Normal University, 2012.
[11] ÜNLÜ A, SCHREPP M. Untangling comparison bias in inductive item tree analysis based on representative random quasi-orders[J]. Mathematical Social Sciences, 2015, 76:31-43. doi: 10.1016/j.mathsocsci.2015.03.005
-
期刊类型引用(3)
1. 马玥璐,王平,谢姒,胡霞,宫黎明. 基于IRT的有效学习的翻转课堂教学模式的构建. 山西能源学院学报. 2021(03): 23-24+34 .  百度学术
百度学术
2. 梁珊. 自适应英语测试系统的效率分析与进度验证. 信息技术. 2021(12): 95-99+105 .  百度学术
百度学术
3. 郑瑞刚,许暖,韩志峰. 一种自适应安全防护技术实现. 信息技术与信息化. 2020(12): 178-180 .  百度学术
百度学术
其他类型引用(1)



 下载:
下载: