Numerical Simulation of Magnetization and Mechanical Properties for High Temperature Superconducting Strip With Defect
-
摘要:
为了分析缺陷对带材磁化及力学性能的影响，基于Bean临界态模型和最小磁能泛函方法，研究了含不同类型缺陷高温超导带材的电磁特性，数值模拟了磁化过程中高温超导带材的应力分布和磁致伸缩行为.研究结果表明：当缺陷偏离带材几何中心时，磁化强度出现水平分量；电磁体力使超导带材发生磁致伸缩；最大应力出现在缺陷附近，当缺陷在带材表面时，最大拉应力出现在外磁场下降阶段；当缺陷位于带材内部时，最大拉应力出现在外磁场最大时刻.根据分析结果可知，垂直磁场中的高温超导带材，其磁化及力学性能受缺陷尺寸和位置影响较大.
Abstract:To analyze the influence of defect on magnetization and mechanical properties, a study of the electromagnetic properties of various high temperature superconducting strips containing different types of defects based on the Bean critical state model and the minimum magnetic energy variation method was presented. The magnetostrictive behavior and the stress distribution of the high temperature superconducting strip were numerically simulated. Results show that a horizontal component of the magnetization appears as the defect deviates from the centre of the strip. The strip exhibits a magnetostrictive phenomenon and the maximum stress arises nearby the defect on account of the action of electromagnetic body force. The moment of the maximum tensile stress appears in the magnetic field decreasing stage when a strip contains a surface defect. For the case of an interior defect, the tensile stress in a strip reaches its extreme value at the highest magnetic field. The analysis results indicate the magnetization and mechanical properties of a strip in perpendicular magnetic field have distinct dependence on the dimension and location of the defect.
-
高温超导体(high temperature superconductor，HTS)在高磁场下具有卓越的载流能力进而能够俘获较高的磁场，在工程领域具有广阔的应用前景[1-3].目前，以钇钡铜氧和二硼化镁为代表的高温超导带材是高温超导材料大规模应用的主要趋势[4]，主要用于限流器、电缆、变压器、电机等超导电力领域.超导技术的大规模应用一方面要求降低带材损耗，提高载流能力，另一方面要求超导带材具有较好的力学性能.但在制备和后处理过程中受工艺所限，高温超导材料内部易产生微裂纹和孔洞缺陷[5-6].与此同时，超导材料具有较高的临界电流密度，因此在高磁场中承受较大的电磁体力.电磁体力的存在极易导致超导材料裂纹扩展甚至破裂，严重威胁了高温超导体的机械稳定性.所以研究含缺陷高温超导带材的电磁和力学性能，详细分析缺陷对各类性能的影响非常重要.
临界态理论首先由Bean[7]提出，认为外部磁场大于临界磁场条件下，外部磁场以磁通量子涡旋线的形式渗透至超导体内一定深度.此时，超导体内部产生体感应电流，磁通涡旋线受到一对平衡力的作用，即钉扎力和Lorentz力.由临界态的定义可知，超导体内的感应电流密度即为临界电流密度Jc，且Jc的大小由钉扎力决定，与温度和磁感应强度密切相关.根据这一理论，有学者提出多种临界态模型用以描述磁通涡旋线在超导体内的运动[7-11].其中，Bean模型假定超导体内临界电流密度Jc与磁场无关为一常数[7-8].根据临界态定义可知，当磁通涡旋线在超导体内运动时，超导体承受电流与磁场相互作用的电磁体力，并在内部产生应变和应力. Ikuta等[12-13]首先于实验中测量到超导体内的相对变形达10－4量级，并将这一现象命名为磁致伸缩. Ren等[14]测量MT-YBCO小圆盘的俘获场时发现，在外磁场下降阶段超导体内会形成裂纹.基于临界态模型，Johansen理论分析了不同冷却条件下各类超导样品的磁致伸缩特性，给出外磁场下降阶段超导体内存在正应力，超导体内易产生裂纹并破坏的结论[15-20]. Koziol等[21]计算了平行磁场下无限大超导平板的复杂磁致伸缩行为. Yong等[22-23]对含颗粒夹杂的超导圆柱及载流超导带材的应力和变形问题进行了详细的研究.以上对超导结构的研究均在一维情形下展开，而在实际的超导装置或设备中，超导块材均为有限尺寸，退磁效应使得它们沿外磁场方向非均匀磁化，因此计算内部的感应电流十分困难.只有当超导体几何形状规则且感应电流方向已知时，可以采用特殊方法进行处理.其中，Brandt[24-25]根据第一性原理，通过求解积分方程对有限高超导圆柱的感应电流进行了数值分析. Prigozhin[26-27]采用最小化特定泛函的方法得到超导体内的感应电流.基于后一理论和临界态模型，Sanchez等[28-29]、Navau等[30]计算了有限高超导圆柱和圆盘的磁化强度，分析了超导带材及带材矩阵的磁化和悬浮特性[31-32]. Huang等[33]和Liu等[34]给出了含洞高温超导圆柱及圆环矩阵的磁化强度及力学特性的数值解.
由于在超导结构的制备中，材料内部会出现缺陷及微裂纹等，而对含缺陷超导带材的磁化规律仍需进一步的探讨.基于此，本文结合超导材料的Bean临界态模型，采用最小磁能泛函方法，开展了不同类型缺陷下超导带材内感应电流的数值模拟，给出了超导带材内电磁体力大小.最后采用有限元方法分析给定边界条件下超导带材的变形和应力分布，详细讨论了缺陷对超导带材磁化和力学性能的影响.本文计算结果可以为超导系统的设计和生产提供指导.
1. 数值模型和计算原理
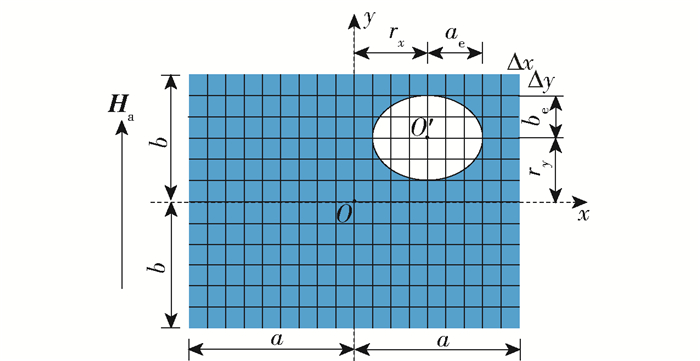
如图 1所示，考虑一含缺陷的无限长高温超导带材，宽度为2a，高度为2b，外部均匀磁场Ha(Ha=Hacos tj)随时间变化.带材存在缺陷且缺陷截面为椭圆形，图示坐标系下，缺陷可用方程(x－rx)2/ae2+(y－ry)2/be2=1描述.其中，r=rxi+ryj为缺陷中心O'点的矢径，i、j、k分别为沿x、y、z轴正向的单位矢量.
![]()
图 1 均匀外磁场下含缺陷高温超导带材的离散单元示意图Figure 1. Schematic view of discrete unites of a HTS strip containing defect in uniform magnetic field当外部磁场Ha从零开始稳定增加，超导体由两侧向内逐渐产生感应电流以屏蔽外磁场.假定超导材料电磁本构关系符合Bean临界态模型，超导体内临界电流密度J=Jk的大小J与磁场无关为一常数，即
$$ J = {J_{\rm{c}}} $$ (1) 本文采用最小磁能泛函法来计算图 1中带材内部感应电流的分布，其核心思想为超导系统内部动能增加与势能减小的相互平衡，计算中通过执行超导体的某一特定泛函最小化求解感应电流.对于图 1所示外磁场中的超导带材，给定特定磁能泛函F[J][31-32]，且
$$ \begin{array}{l} F\left[J \right] = \frac{1}{2}\int_S {J\left( \mathit{\boldsymbol{r}} \right){A_J}} \left( \mathit{\boldsymbol{r}} \right){\rm{d}}S - \int_S {J\left( \mathit{\boldsymbol{r}} \right){{\hat A}_J}} \left( \mathit{\boldsymbol{r}} \right){\rm{d}}S + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_S {J\left( \mathit{\boldsymbol{r}} \right)\left[{{A_{\rm{a}}}\left( \mathit{\boldsymbol{r}} \right)-{{\hat A}_a}\left( \mathit{\boldsymbol{r}} \right)} \right]} {\rm{d}}S \end{array} $$ (2) 式中：dS表示超导体面积横截面的面积微元；A(r)为磁矢势；符号"^"表示上一时间层的磁性参量.需要指出的是对于式(2)，计算中必须满足约束条件|J|≤Jc且$ \int_S {J{\rm{d}}S} = 0 $.
若定义感应电流密度增量$ {\rm{ \mathsf{ δ} }}J = J - \hat J $，则可得到一个与式(2)等价的泛函F'[δJ]
$$ \begin{array}{l} F'\left[{{\rm{ \mathit{ δ} }}J} \right] = \frac{1}{2}\int_S {{\rm{ \mathit{ δ} }}J\left( \mathit{\boldsymbol{r}} \right)} {A_{{\rm{ \mathit{ δ} }}J}}\left( \mathit{\boldsymbol{r}} \right){\rm{d}}S + \\ \;\;\;\int_S {{\rm{ \mathit{ δ} }}J\left( \mathit{\boldsymbol{r}} \right)} \left[{{A_a}\left( \mathit{\boldsymbol{r}} \right)-{{\hat A}_a}\left( \mathit{\boldsymbol{r}} \right)} \right]{\rm{d}}S \end{array} $$ (3) 由于含有$ {\hat J} $的项在上一时间层已被最小化，式(3)中已排除含有$ {\hat J} $的项.
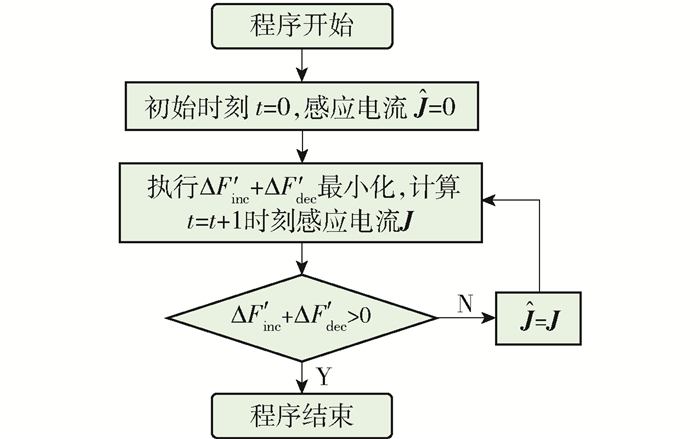
本文采用离散单元法计算超导带材体内感应电流.结合超导带材特点，将计算模型划分为N=2nx×2ny(2nx列、2ny行)个横截面为矩形且沿z轴无限长的棱柱单元，如图 1所示，每个单元的横截面积为ΔS(ΔS=Δx×Δy=a/nx×b/ny)，分别用下标i=1~N标记.进行单元划分时，为确保结果满足精度要求，应使棱柱单元横截面接近正方形即Δx≈Δy.当超导带材在某时间点位于外磁场$ {{\mathit{\boldsymbol{\hat H}}}_{\rm{a}}} $中且超导体内感应电流密度为$ {\hat J} $(初始时刻$ {\hat J} $=0)，下一时间点外磁场增加至Ha后，执行式(3)最小化可得到下一时间点感应电流密度$ J = {\rm{ \mathsf{ δ} }}J + \hat J $.具体过程如下：首先，定义电流增量ΔI=δJΔxΔy.接着在某一单元处给定电流增量ΔI，引起F'的增量记作ΔF'inc，另一单元处给定电流增量－ΔI，引起F'的增量记作ΔF'dec，计算ΔF'inc+ΔF'dec.反复循环，在所有单元中找出ΔF'inc+ΔF'dec的值为最小且满足条件ΔF'inc+ΔF'dec＜0的一对单元，在此两单元处分别增加电流ΔI和－ΔI.最后，重复以上步骤直至ΔF'inc+ΔF'dec的和不再减小，即可得到超导带材体内的感应电流，计算流程见图 2.通过计算检验可发现，在执行泛函增量之和ΔF'inc+ΔF'dec最小化的过程中，电流增量ΔI足够小(电流密度增量δJ足够小且单元数量N足够大)即可保证计算精度. 图 1所示的所有单元中，面积位于超导区域的单元始终参与计算且满足条件|J|≤Jc.面积位于缺陷区域的单元忽略不记，即J=0.对于超导与缺陷边界处的单元，做如下处理：若单元几何中心位于超导区域内，按上述前一种单元操作.反之若中心位于缺陷区域或边界处，按后一种单元操作.其中，i单元处给定电流增量ΔI后，泛函F'[δJ]的增量ΔF'[δJ]的离散化表达式[31-32]为
$$ \begin{array}{l} \Delta {{F'}_i}\left( {{\rm{ \mathsf{ δ} }}J} \right) = \Delta S\Delta I\sum\limits_{k = 1}^N {{C_{ki}}} {\rm{ \mathsf{ δ} }}{J_k} + \frac{1}{2}{C_{ii}}{\left( {\Delta I} \right)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta I\left[{{G_{{\rm{a, i}}}}-{{\hat G}_{{\rm{a, i}}}}} \right] \end{array} $$ (4) 式中：δJk为k单元处电流密度增量；$ {C_{ki}}\left( {{{\hat C}_{ki}}} \right) $、$ {G_{{\rm{a}},{\rm{i}}}}\left( {{{\hat G}_{{\rm{a}},{\rm{i}}}}} \right) $分别表示k单元的单位电流和外磁场Ha($ {{\hat H}_{\rm{a}}} $)在超导单元i中心处的磁矢势.
通过执行磁能泛函最小化步骤得到超导带材内感应电流密度J后，可根据Biot-Savart定律计算出空间任意位置处的磁感应强度B.由Lorentz力计算法则可知，超导体内任意单元中心处作用的电磁体力f为
$$ \begin{array}{l} \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{J}} \times \mathit{\boldsymbol{B}} = - J\left( {x, y} \right){B_y}\left( {x, y} \right)\mathit{\boldsymbol{i}} + \\ \;\;\;\;\;\;\;\;\;J\left( {x, y} \right){B_x}\left( {x, y} \right)\mathit{\boldsymbol{j}} \end{array} $$ (5) 式中J和B分别为该单元几何中心处的感应电流密度和磁感应强度.
2. 计算结果和讨论
基于第1节的模型，本节给出并讨论含缺陷高温超导带材的磁化性能和力学特性.具体计算中选取超导带材临界电流密度为3×107 A/m2，杨氏模量为100 GPa，泊松比为0.25.为了系统地呈现分析结果，所有长度量统一用a进行归一化，所有磁场量用Hp=Jca进行归一化[31]，记α=ae/a，β=be/a，γ=b/a，λ=rx/a，η=ry/a.应力用σ0=16μ0Hp2进行归一化[35].在实际的材料制备加工中，缺陷随机分布在超导体中，本文根据位置的不同，将缺陷分为2类：表面缺陷和内部缺陷.
磁化强度M定义为单位体积的磁矩，因此先计算超导带材单位长度的磁矩m.结合最小磁能泛函法，采用特殊方法计算超导带材整体磁化强度，即按照第1节所述计算电流分布时，每次在单元i和j处给定电流增量ΔI和－ΔI后，等效于带材的内部增加一无限长电流回路，产生磁矩增量为Δm=rji×(ΔIk)(rji为j单元中心指向i单元中心的矢量)，因此，可得出单位长度超导带材磁化强度的计算公式为
$$ \mathit{\boldsymbol{M}} = \frac{{\sum {\Delta \mathit{\boldsymbol{m}}} }}{{{S_{xy}}}} = \frac{{\sum {\Delta {m_x}\mathit{\boldsymbol{i}}} + \sum {\Delta {m_y}\mathit{\boldsymbol{j}}} }}{{{S_{xy}}}} = {m_x}\mathit{\boldsymbol{i}} + {m_y}\mathit{\boldsymbol{j}} $$ (6) 式中Sxy为带材横截面的有效面积.为方便讨论，假定表面缺陷几何中心位于带材表面，即γ=η=0.8，Sxy=4ab－0.5πaebe.对于内部缺陷，Sxy=4ab－πaebe. Mx和My分别为磁化强度M沿x轴和y轴的分量.此外，本文还研究了外磁场循环周期内超导带材的磁致伸缩和应力分布规律.
2.1 表面缺陷
图 3给出了外部磁场从零增加至Ha=0.08Hp和Ha=0.4Hp时刻含表面缺陷超导带材的感应电流和磁场线分布，具体几何参数为α=0.4，β=0.4，γ=0.8，λ=0，η=0.8.图中青色和黄色表示不同方向的感应电流.由图 3(a)可见，在Ha=0.08Hp时刻，因为外磁场强度较小，磁通涡旋线未运动至缺陷边缘处，感应电流和磁场分布与无缺陷带材的计算结果几乎一致.但当外磁场增加至Ha=0.4Hp时，如图 3(b)所示，此时带材内部存在磁场强度为零的"零场区域"，这是因为感应电流在该区域内产生大小为0.4Hp且与外部磁场反向的均匀磁场，该磁场与外部磁场相互抵消.随着外部磁场的不断增大，这一区域的面积持续缩减最后为零，超导带材完全磁化.由图 3可见，当带材截面关于y轴对称时，磁场线和超导电流分布也关于y轴对称.
![]()
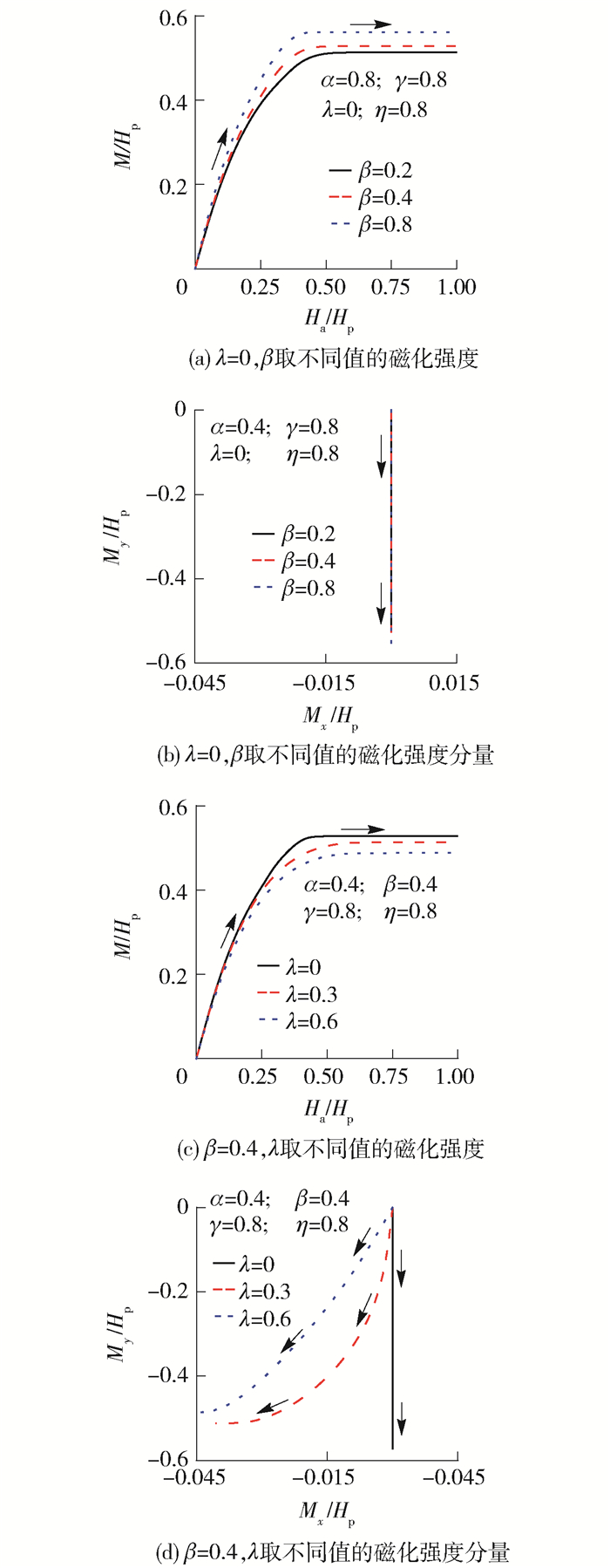
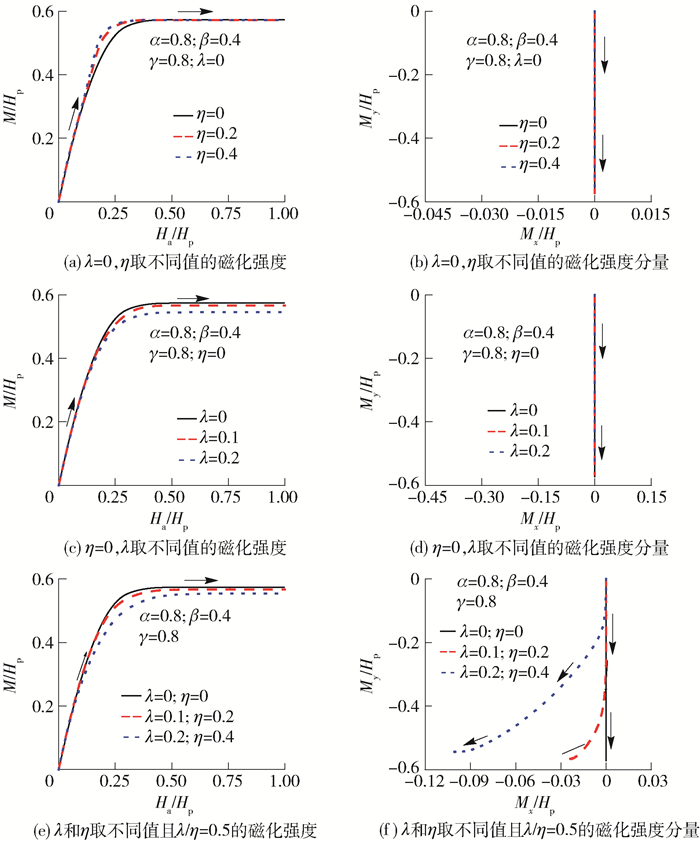
图 3 含表面缺陷HTS带材的磁场线及感应电流Figure 3. Magnetic field line and current profile for a HTS strip containing surface defect图 4给出了磁场上升阶段含表面缺陷带材的磁化强度曲线和分量曲线，其中α=0.4，η=γ=0.8保持不变.如式(6)所描述，超导带材磁化强度M的大小$ M = \sqrt {M_x^2 + M_y^2} $，M的方向可用Mx和My的比值来表示. 图 4(a)表明，外磁场从零开始增加后，带材磁化强度绝对值单调增加，最后达到一饱和值. β越大或λ越小，磁化强度曲线的斜率越大，超导带材越易被外磁场磁化.这是因为缺陷面积增加会使带材体积减小，削弱其抵抗外磁场的能力，但单位体积的磁矩却因有效体积的减小而增大.这一结果与超导圆柱体的变化趋势一致[33].在缺陷面积一定的条件下，缺陷越靠近几何中心，带材两侧的感应电流产生磁场和磁矩越大，此时带材可在较小的磁场中完全磁化且获得较大的磁化强度. 图 4(b)给出了磁化强度M分量Mx和My的相对变化情况，由图 4(b)可见，当存在表面缺陷且缺陷位于表面中心(λ=0)时，Ha从零增加至Hp的过程中，3条直线重合，My的绝对值逐渐增大而Mx始终为零.此结果说明带材的磁化强度M始终与外部磁场Ha平行但方向相反. 图 4(d)给出了表面缺陷尺寸不变，而位置水平改变后的计算结果.由图 4可见，当外磁场逐渐增大，My的绝对值随Ha的增大而增大. Mx开始为零，当Ha足够大，Mx绝对值由零开始增加.磁化的最后阶段，Mx的增幅明显大于My，曲线斜率接近零. λ越大，Mx出现越早.这是因为外部磁通线运动至缺陷边缘时，若缺陷偏离截面中心导致带材截面几何不对称，则每增加一对电流增量，形成的无限长电流回路与y轴不平行，最终表现为磁化强度M与外磁场Ha出现一个夹角.
![]()
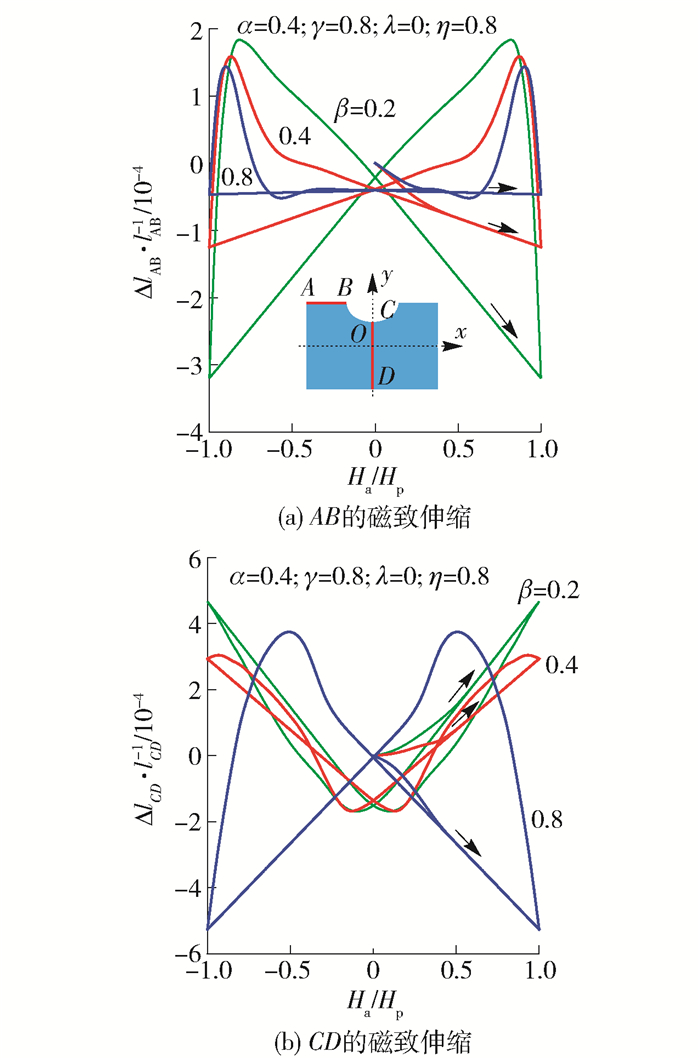
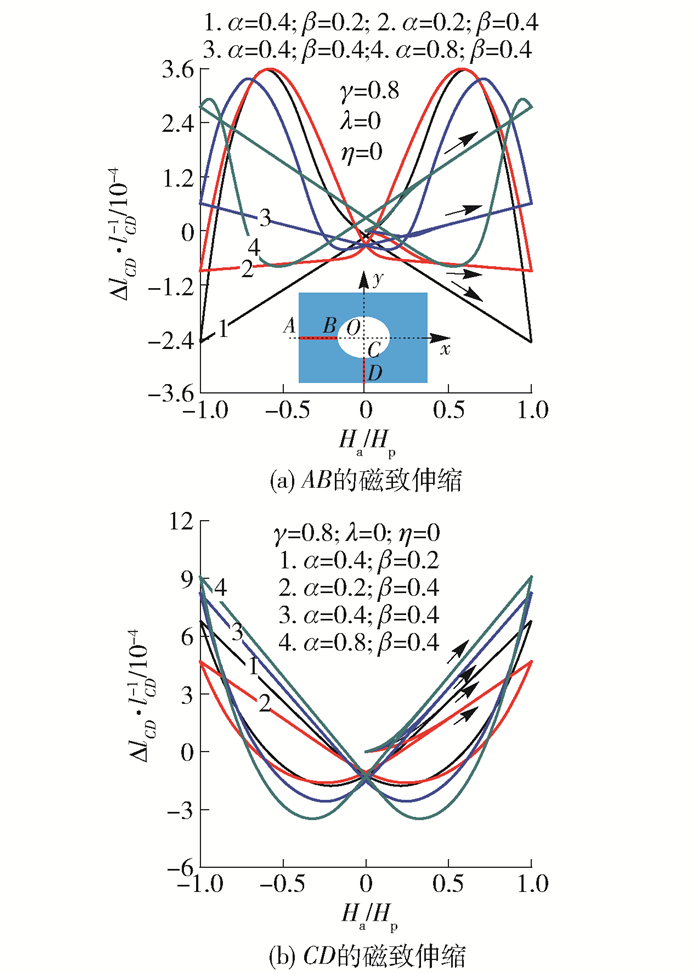
图 4 外部磁场从零增大至Hp过程中含表面缺陷HTS带材的磁化强度及分量Figure 4. Calculated magnetizations and their components for HTS strips containing surface defects during the field rise from zero to Hp图 5、6给出了含表面缺陷超导带材(α=0.4，γ=0.8，λ=0，η=0.8, β取不同值)中特定线段AB和CD的磁致伸缩曲线及应力分布云图.针对问题的对称性，同时为了控制刚体位移，数值模拟中补充约束条件：D点的位移Ux=Uy=0.由图 5可见，外磁场Ha从零增加后，带材两侧产生感应电流，根据左手螺旋法则可知，感应电流的存在使得该区域内承受电磁体力，带材出现宏观变形.随着Ha的增加，磁通涡旋线由外逐渐运动至带材内部，电流穿透区域增大，此过程中AB和CD的变形量也增大，并在Ha=Hp时刻达到极值.当Ha开始下降后，AB和CD的变形量减小至零后又逐渐增大. β由0.2增大至0.8后，图 5中AB在外场上升阶段的变形量明显减小，而CD的磁致伸缩曲线发生了"翻转"现象，在磁场最大时刻变形由拉伸状态转变为压缩状态.由此可知，缺陷的尺寸对磁化过程中带材的宏观变形产生较大影响.
![]()
图 5 含表面缺陷HTS带材的磁致伸缩Figure 5. Simulated magnetostriction curves calculated for HTS strips containing surface defects![]()
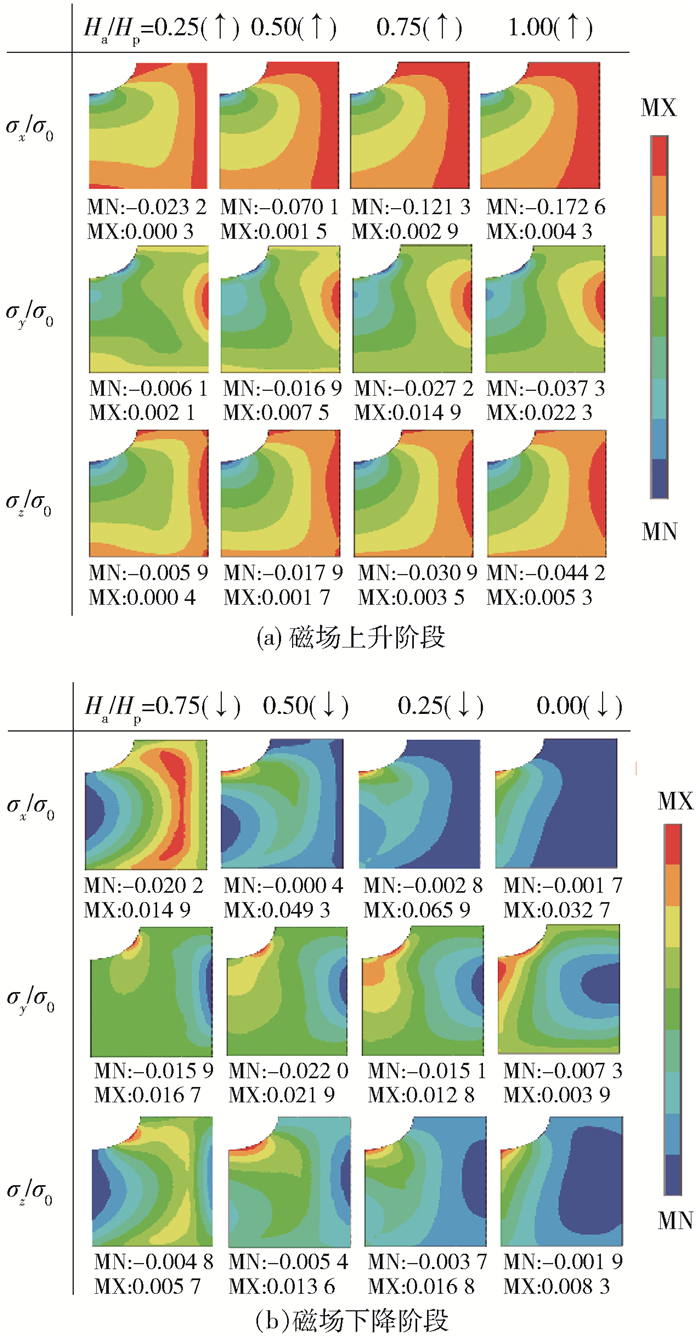
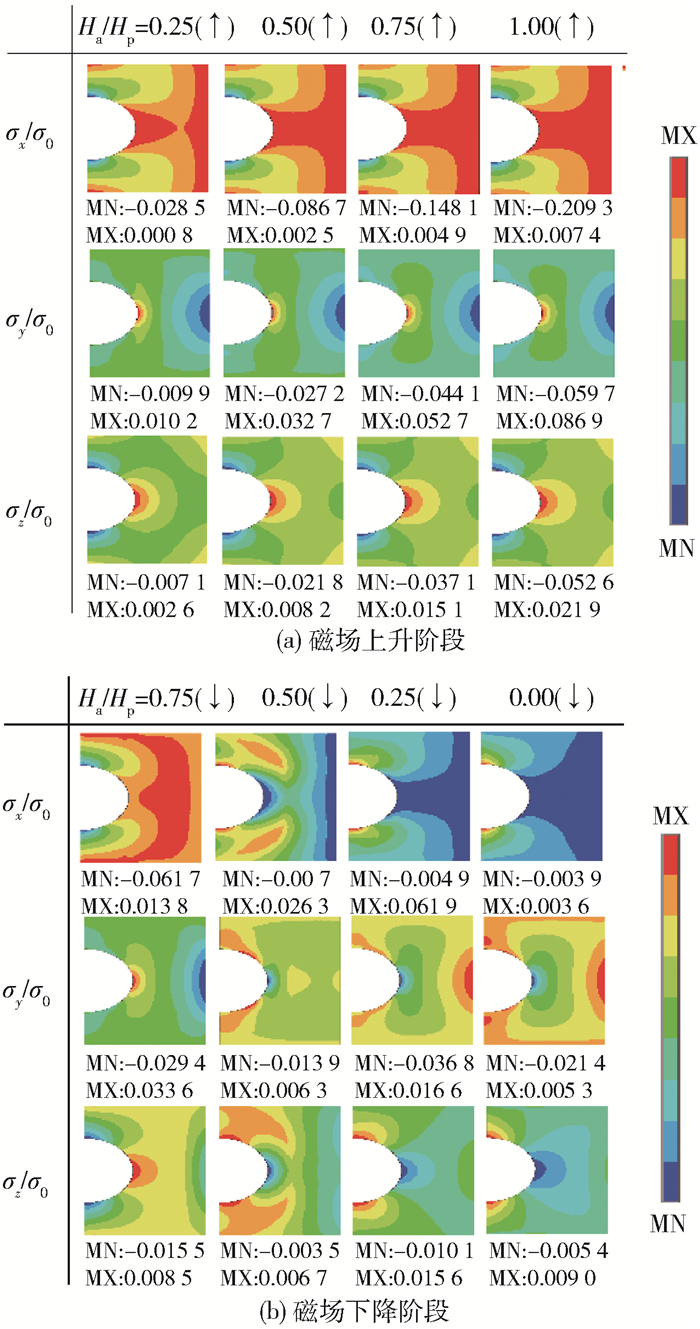
图 6 磁化过程中含表面缺陷HTS带材的正应力σx、σy、σz云图Figure 6. Contours of normal stresses σx, σy, and σz for a HTS strip containing surface defect外磁场不断变化的过程中，超导带材内部电磁体力分布状况也随之改变，情况十分复杂.因此，分析超导样品最易断裂破坏时刻的应力分布规律非常有意义.针对含表面缺陷的特定带材试样(α=0.4，β=0.4，γ=0.8，λ=0，η=0.8)，图 6给出了外磁场从零增加至Hp后再减小为零过程中，采用有限元方法得到的不同磁化状态下带材试样内正应力分布. 图 6中，根据轴对称性仅绘制了1/2带材模型.各应力云图左侧边线对应图 1中y轴. MX和MN分别代表不同时刻的最大和最小应力，所有应力用σ0=16μ0Hp2归一化处理.由图 6可见，任意磁化状态下带材内均出现应力集中现象.外磁场上升阶段，体内各向应力绝对值随着外磁场Ha的增大而增大且均为负值，仅在外侧局部区域出现拉应力，表明此过程中带材体内以压应力为主，而拉应力极值σy=0.022 3σ0出现在Ha=Hp时刻.外磁场下降阶段，体内各向压应力减小而x和z向拉应力迅速增加. Ha=0.25Hp前后，缺陷边缘处出现另一拉应力极值σx=0.065 9σ0.根据以上结果可知，外磁场最大时刻和下降过程中，带材边缘与缺陷处存在较大拉应力，易出现裂纹甚至断裂，需特别注意.
2.2 内部缺陷
图 7给出了外磁场上升阶段不同位置的含内部缺陷超导带材的感应电流和磁场线分布.为了与图 3进行比较，选取Ha=0.08Hp和Ha=0.4Hp两时刻不变，带材几何参数为α=0.4，β=0.4，γ=0.8. 图 7(a)和(b)中内部缺陷位于带材截面几何中心，λ=η=0. 图 7(c)和(d)中内部缺陷位于截面右上角，λ=η=0.3.可见图 7(a)和(c)中电流分布相同，与图 7(a)结果无差异，这与2.1小节的结论相符，即在外部磁通涡旋线未渗透至缺陷边缘时，缺陷不影响感应电流及磁通线分布.当外磁场增加至一较大值(Ha=0.4Hp)后，由图 7(b)和(d)可见感应电流、磁通线及零场区域分布明显不同.与图 3(b)相似，图 7(b)中缺陷位于截面中心处(λ=0，η=0)，而截面关于y轴对称时，电流和磁通线关于y轴对称分布. 图 7(d)中，内部缺陷位于截面右上角，因此截面关于y轴非对称，而带材内的电流与磁通线也呈现非对称分布形态.结合图 3综合分析可知，变化外磁场中，不同类型的缺陷影响超导带材内部的磁通线及感应电流分布.
![]()
图 7 含内部缺陷HTS带材的磁场线及感应电流Figure 7. Magnetic field line and current profile for HTS strips containing interior defects图 8给出了不同内部缺陷下超导带材的磁化强度曲线及分量曲线，其中参数为α=0.8，β=0.4，γ=0.8保持不变. λ或η从零增大分别表示内部缺陷从截面中心竖向向上或沿水平向右移动.而λ和η按比例增加表示沿固定方向斜向上移动. 图 8(a)中结果表明，内部缺陷位置竖向改变后，最终得到的饱和磁化强度大小不变，但磁化强度达到饱和所需的外磁场有差异. 图 8(c)和(e)中结果表明，当内部缺陷位置沿水平或右上方改变时，偏离带材中心越远，饱和磁化强度绝对值越小，这一结论与表面缺陷一致.采用相同方法分析可知，缺陷尺寸一定时，偏心距|r|越小，有效面积集中于带材四周，因而磁矩越大.值得注意的是，同图 4(b)类似，当内部缺陷位置水平或竖向改变后，见图 8(b)和(d)，Mx始终为零，这表明磁化过程中M与Ha反向.而内部缺陷位于带材截面右上方时，Mx不为零表明二者间的夹角随外磁场Ha而变化.综上可知，当带材截面几何不对称时，其磁化强度的大小及其方向与所含缺陷的尺寸和位置密切相关，此结果与文献[36-38]中的理论结果一致.
![]()
图 8 外部磁场从零增大至Hp过程中含内部缺陷HTS带材的磁化强度及分量Figure 8. Calculated magnetizations and their components for HTS strips containing interior defects during the field rise from zero to Hp图 9、10给出了含内部缺陷超导带材(γ=0.8，λ=0，η=0, α和β分别取不同值)中特定线段AB和CD的磁致伸缩曲线及正应力分布云图，其边界约束条件同图 5、6.由图 9(a)可见，AB的磁致伸缩曲线呈现"蝴蝶"样式且变形趋势随α或β的改变不断变化.而CD的曲线形状不随α或β改变，但变形量仍受影响.
![]()
图 9 含内部缺陷HTS带材的磁致伸缩Figure 9. Simulated magnetostriction curves calculated for HTS strips containing interior defects![]()
图 10 磁化过程中含内部缺陷HTS带材的正应力应力σx、σy、σz云图Figure 10. Contours of normal stresses σx, σy, and σz for a HTS strip containing interior defect结合图 5、9分析可知，不论含内部缺陷还是含表面缺陷的超导带材，缺陷尺寸的改变使磁致伸缩曲线的垂直宽度发生变化，尤其在增大缺陷的竖向尺寸β后，磁致伸缩曲线的垂直宽度会明显增加.这是因为样品厚度的减小会增大样品的退磁效应，也就增大了样品内竖向电磁体力的大小.
图 10给出了不同磁化状态下含内部缺陷超导带材试样(α=0.4, β=0.4, γ=0.8, λ=0, η=0)的正应力云图.与图 6比较可知，同一外磁场下带材体内的应力分布规律基本相同.不同之处为内部缺陷引起的应力集中效应更明显，上升场阶段Ha=Hp时刻缺陷边缘处出现拉应力极值σy=0.086 9σ0.外磁场下降过程中，y和z向拉应力减小而x向拉应力增加. Ha=0.25Hp前后，缺陷边缘处出现另一拉应力极值σx=0.061 9σ0，这与含表面缺陷带材的计算结果一致.
3. 结论
1) 外磁场中的超导带材，其磁化强度的大小和方向与缺陷尺寸及位置密切相关.增大缺陷面积或减小水平偏心距使带材的完全穿透磁场降低，产生较大的饱和磁化强度.同时，带材磁化强度的方向随外部磁场的变化而改变.
2) 超导带材的磁致伸缩曲线出现"翻转"现象，其变形趋势同样受缺陷尺寸的影响.磁化过程中应力极值始终出现在缺陷边缘.对于存在表面缺陷的带材，最大拉应力出现在外部磁场达到最大后开始下降的过程中.对于存在内部缺陷的带材，最大拉应力出现在外部磁场最大时刻.
3) 本文的计算方法适用于分析缺陷形状复杂及存在多个缺陷的超导带材，并可推广到非均匀磁场、各向异性及含填充材料的超导磁体.
-
![]()
图 1 均匀外磁场下含缺陷高温超导带材的离散单元示意图
Figure 1. Schematic view of discrete unites of a HTS strip containing defect in uniform magnetic field
![]()
图 3 含表面缺陷HTS带材的磁场线及感应电流
Figure 3. Magnetic field line and current profile for a HTS strip containing surface defect
![]()
图 4 外部磁场从零增大至Hp过程中含表面缺陷HTS带材的磁化强度及分量
Figure 4. Calculated magnetizations and their components for HTS strips containing surface defects during the field rise from zero to Hp
![]()
图 5 含表面缺陷HTS带材的磁致伸缩
Figure 5. Simulated magnetostriction curves calculated for HTS strips containing surface defects
![]()
图 6 磁化过程中含表面缺陷HTS带材的正应力σx、σy、σz云图
Figure 6. Contours of normal stresses σx, σy, and σz for a HTS strip containing surface defect
![]()
图 7 含内部缺陷HTS带材的磁场线及感应电流
Figure 7. Magnetic field line and current profile for HTS strips containing interior defects
![]()
图 8 外部磁场从零增大至Hp过程中含内部缺陷HTS带材的磁化强度及分量
Figure 8. Calculated magnetizations and their components for HTS strips containing interior defects during the field rise from zero to Hp
![]()
图 9 含内部缺陷HTS带材的磁致伸缩
Figure 9. Simulated magnetostriction curves calculated for HTS strips containing interior defects
-
[1] MURAKAMI M. Progress in applications of bulk high temperature superconductors[J]. Superconductor Science and Technology, 2000, 13(5):448-450. doi: 10.1088/0953-2048/13/5/302
[2] SUNG T H, HAN S C, HAN Y H, et al. Designs and analyses of flywheel energy storage systems using high-Tc superconductor bearings[J]. Cryogenics, 2002, 42(6/7):357-362. http://www.sciencedirect.com/science/article/pii/S0011227502000577
[3] HULL J R. Superconducting bearings[J]. Superconductor Science and Technology, 2000, 13(2):R1-R15. doi: 10.1088/0953-2048/13/2/201
[4] 王秋良.高磁场超导磁体科学[M].北京:科学出版社, 2008:16. [5] YONG H D, YANG Y, ZHOU Y H. Dynamic fracture behavior of a crack in the bulk superconductor under electromagnetic force[J]. Engineering Fracture Mechanics, 2016, 158:167-178. doi: 10.1016/j.engfracmech.2016.03.004
[6] JOHANSEN T H, WANG C, CHEN Q Y, et al. Enhancement of tensile stress near a hole in superconducting trapped-field magnets[J]. Journal of Applied Physics, 2000, 88(5):2730-2733. doi: 10.1063/1.1287123
[7] BEAN C P. Magnetization of hard superconductors[J]. Physical Review Letters, 1962, 8(6):250-253. doi: 10.1103/PhysRevLett.8.250
[8] BEAN C P. Magnetization of high-field superconductors[J]. Reviews of Modern Physics, 1964, 36(1):31-39. doi: 10.1103/RevModPhys.36.31
[9] KIM Y B, HEMPSTEAD C F, STRNAD A R. Magnetization and critical super currents[J]. Physical Review, 1963, 129(2):528-535. doi: 10.1103/PhysRev.129.528
[10] FIETZ W A, BEASLEY M R, SILCOX J, et al. Magnetization of superconducting Nb-25% Zr wire[J]. Physical Review, 1964, 136(2A):335-345. doi: 10.1103/PhysRev.136.A335
[11] FIETZ W A, WEBB W W. Hysteresis in superconducting alloys-temperature and field dependence of dislocation pinning in niobium alloys[J]. Physical Review, 1969, 178(2):657-667. doi: 10.1103/PhysRev.178.657
[12] IKUTA H, HIROTA N, NAKAYAMA Y, et al. Giant magnetostriction in Bi2Sr2CaCu2O8 single crystal in the superconducting state and its mechanism[J]. Physical Review Letters, 1993, 70(14):2166-2169. doi: 10.1103/PhysRevLett.70.2166
[13] IKUTA H, KISHIO K, KITAZAWA K. Critical state models for flux-pinning-induced magnetostriction in type-Ⅱ superconductors[J]. Journal of Applied Physics, 1994, 76(8):4776-4786. doi: 10.1063/1.357249
[14] REN Y, WEINSTEIN R, LIU J, et al. Damage caused by magnetic pressure at high trapped field in quasi-permanent magnets composed of melt-textured Y-Ba-Cu-O superconductor[J]. Physica C, 1995, 251:15-16. doi: 10.1016/0921-4534(95)00398-3
[15] JOHANSEN T H, BRATSBERG H, LOTHE J. Flux-pinning-induced magnetostriction in cylindrical superconductors[J]. Superconductor Science and Technology, 1998, 11:1186-1189. doi: 10.1088/0953-2048/11/10/062
[16] JOHANSEN T H. Flux-pinning-induced stress and strain in superconductors:long rectangular slab[J]. Physical Review B, 1999, 59(17):11187-11190. doi: 10.1103/PhysRevB.59.11187
[17] JOHANSEN T H. Flux-pinning-induced stress and magnetostriction in bulk superconductors[J]. Superconductor Science and Technology, 2000, 13(10):R121-R137. doi: 10.1088/0953-2048/13/10/201
[18] JOHANSEN T H, LOTHE J, BRATSBERG H. Shape distortion by irreversible flux-pinning-induced magnetostriction[J]. Physical Review Letters, 1998, 80(21):4757-4760. doi: 10.1103/PhysRevLett.80.4757
[19] JOHANSEN T H. Flux-pinning-induced stress and strain in superconductors:case of a long circular cylinder[J]. Physical Review B, 1999, 60(13):9690-9703. doi: 10.1103/PhysRevB.60.9690
[20] JOHANSEN T H, SHANTSEV D V. Magnetostrictive behaviour of thin superconducting disks[J]. Superconductor Science and Technology, 2003, 16(9):1109-1114. doi: 10.1088/0953-2048/16/9/324
[21] KOZIOL Z, DUNLAP R. Magnetostriction of a superconductor:results from the critical-state model[J]. Journal of Applied Physics, 1996, 79(8):4662-4664. doi: 10.1063/1.361697
[22] YONG H D, ZhOU Y H. Effect of nonsuperconducting particles on the effective magnetostriction of bulk superconductors[J]. Journal of Applied Physics, 2008, 104(4):043907. doi: 10.1063/1.2952042
[23] YONG H D, ZHOU Y H. Stress distribution in a flat superconducting strip with transport current[J]. Journal of Applied Physics, 2011, 109(7):073902. doi: 10.1063/1.3561366
[24] BRANDT E H. Superconductor disks and cylinders in an axial magnetic field. I. flux penetration and magnetization curves[J]. Physical Review B, 1998, 58(10):6506-6522. doi: 10.1103/PhysRevB.58.6506
[25] BRANDT E H. Superconductor disks and cylinders in an axial magnetic field. Ⅱ. nonlinear and linear ac susceptibilities[J]. Physical Review B, 1998, 58(10):6523-6533. doi: 10.1103/PhysRevB.58.6523
[26] PRIGOZHIN L. Analysis of critical-state problems in type-Ⅱ superconductivity[J]. IEEE Transactions on Applied Superconductivity, 1997, 7(4):3866-3873. doi: 10.1109/77.659440
[27] PRIGOZHIN L. Solution of thin film magnetization problems in type-Ⅱ superconductivity[J]. Journal of Computational Physics, 1998, 144(1):180-193. doi: 10.1006/jcph.1998.5978
[28] SANCHEZ A, NAVAU C. Influence of demagnetizing effects in superconducting cylinders[J]. IEEE Transactions on Applied Superconductivity, 1999, 9(2):2195-2198. doi: 10.1109/77.784904
[29] SANCHEZ A, NAVAU C. Magnetic properties of finite superconducting cylinders. I. uniform applied field[J]. Physical Review B, 2001, 64(21):214506. doi: 10.1103/PhysRevB.64.214506
[30] NAVAU C, SANCHEZ A, PARDO E, et al. Critical state in finite type-Ⅱ superconducting rings[J]. Physical Review B, 2005, 71(21):214507. doi: 10.1103/PhysRevB.71.214507
[31] PARDO E, SANCHEZ A, NAVAU C. Magnetic properties of arrays of superconducting strips in a perpendicular field[J]. Physical Review B, 2003, 67(10):104517. doi: 10.1103/PhysRevB.67.104517
[32] SANCHEZ A, DEL VALLE N, PARDO E, et al. Magnetic levitation of superconducting bars[J]. Journal of Applied Physics, 2006, 99(11):113904. doi: 10.1063/1.2201767
[33] HUANG C G, ZHOU Y H. Magnetic and magnetostrictive properties of finite superconducting cylinders containing a cavity[J]. Journal of Applied Physics, 2014, 115(3):033904. doi: 10.1063/1.4862856
[34] LIU J, HUANG C G, YONG H D, et al. Simulation of magnetization and levitation properties of arrays of ring-shaped type-Ⅱ superconductors[J]. Physica C, 2017, 534:55-60. doi: 10.1016/j.physc.2017.01.002
[35] 黄晨光. 复杂高温超导结构的交流损耗和力学特性[D]. 兰州: 兰州大学, 2015. HUANG C G. AC losses and mechanical properties of complex high temperature superconducting structures[D]. Lanzhou: Lanzhou University, 2015. (in Chinese)
[36] HUANG C G, LIU J. Magnetic and mechanical properties of a finite-thickness superconducting strip with a cavity in oblique magnetic fields[J]. Journal of Applied Physics, 2017, 121(1):023905. http://adsabs.harvard.edu/abs/2017JAP...121b3905H
[37] MIKITIK G P, BRANDT E H, INDENBOM M.Superconducting strip in an oblique magnetic field[J]. Physical Review B, 2004, 70:014520. doi: 10.1103/PhysRevB.70.014520
[38] YONG H D, ZHOU Y H. Elliptical hole in a bulk superconductor under electromagnetic forces[J]. Superconductor Science and Technology, 2009, 22:025018. doi: 10.1088/0953-2048/22/2/025018
下载:
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
