Aeroelastic Stability Analysis of Composite Laminated Plate in Subsonic Airflow
-
摘要:
为了研究复合材料层合板结构在亚音速气流作用下的气动弹性稳定性, 基于线性势流理论建立适用于三维复合材料层合板结构的亚音速气动力模型, 采用经典层合板理论, 根据Hamilton变分原理, 建立亚音速下三维复合材料层合板的运动方程.采用假设模态法, 将偏微分方程离散成常微分方程组, 通过求解广义特征值问题分析其气动弹性特性.通过计算层合板结构在不同来流速度时的固有频率, 得到层合板结构在亚音速气流作用下的临界失稳速度.研究表明:该亚音速气动力模型适用于三维薄板结构.在气流作用下, 层合板结构刚度降低导致结构失稳.
-
关键词:
- 亚音速气流 /
- 复合材料层合板 /
- 临界失稳速度 /
- Hamilton原理 /
- 假设模态法
Abstract:In this paper, the aeroelastic stability of the laminated composite plate in subsonic airflow was analyzed.A subsonic aerodynamic model fit for the three-dimensional (3D) composite laminated plate was established by the linear potential flow theory.The equation of motion of the 3D composite laminated plate was obtained by Hamilton's principle and the classical laminated composite plate theory.The equation of motion was discretized to the ordinary differential equations by using the assumed mode method.The aeroelastic characteristics were analyzed by solving the generalized eigenvalue problem.The critical instability speeds of the laminated composite plate in subsonic airflow were obtained by calculating its natural frequencies at different flow velocities.The investigation results show that the subsonic aerodynamic model established in this paper is fit for the 3D plate structures.In subsonic airflow, the structural stiffness of the laminated plate is reduced, which results in the instability of the laminated plate structure.
-
复合材料结构具有质量轻、比强度高和比刚度大等优点, 以及耐压、耐高温、耐腐蚀等特性, 近年来被广泛应用于航空航天、风机叶片、高铁及汽车制造等领域.在实际应用中, 这些领域的工程结构经常受到气动力的作用而发生振动, 这将导致结构出现疲劳损伤和破坏[1].因此研究复合材料层合板结构在亚音速气流作用下的振动特性、计算结构的临界失稳速度, 对于亚音速运行的运载器结构的动力学分析和设计具有重要意义.
关于气动弹性问题的研究, 许多学者已经做了很多有意义的工作, 但大多数是针对超音速气动弹性问题进行研究.例如, Song等[2]研究了复合材料夹芯板在超音速气流中的气动热弹性问题, 采用频域法分析了不同夹芯参数对整体结构气动热弹性的影响, 并对采用二维夹芯和三维夹芯时结构的气动热弹性进行了对比.Mahmoudkhani等[3]研究了复合材料层合圆柱壳在超音速气流中的气动热弹性问题, 考虑了预应变对壳体气弹稳定性的影响.Vedeneev[4]通过讨论特征值问题研究了半无限大平板在单侧超音速气流作用下的气动弹性问题.
对于亚音速气动弹性问题, Bisplinghoff等[5]进行了系统研究.之后, 很多学者采用Bisplinghoff等的亚音速二维薄板气动力模型对二维板结构的气动弹性稳定性以及非线性振动等进行了研究, 其中Dugundji等[6]采用Galerkin法研究了亚音速下对边简支、具有弹性支撑二维薄板的临界失稳与颤振问题.Tang等[7]采用基于升力面理论的涡格法气动力模型, 研究了亚音速下一端固支, 另一端自由二维薄板的极限环运动.在此基础上, Tang等[8-9]研究了悬臂板尾流对其极限环运动的影响.Zhao等[10]研究了悬臂板在发生气动失稳后其模态的变化, 并与实验结果进行了对比.Weaver等[11]采用对速度势函数Laplace方程进行Fourier变换方法, 研究了对边简支二维薄板的流固耦合稳定性问题.Korbahti等[12]基于线性势流理论的可压缩气动力模型, 研究了亚音速流场内正交各向异性板的气动弹性稳定性问题, 讨论了板的不同长厚比对失稳速度的影响.Yao等[13]研究了四边简支二维复合材料层合板结构在亚音速气流作用下的动力学稳定性和非线性振动问题.Yao等[14]对亚音速下复合材料层合开口圆柱壳进行了气动弹性稳定性分析.Li等[15-16]研究了一边固定、对边非线性弹簧约束的二维平板在亚音速气流作用下的极限环振动以及分叉问题.
目前已有的研究主要集中在超音速下板壳结构的气动弹性分析, 而对于三维板壳结构亚音速气动弹性问题的研究相对较少.对于亚音速下的薄板结构, 目前通常采用的气动力模型为基于线性势流理论的二维薄板气动力模型, 这种气动力模型一般为复杂的积分-微分形式, 且不能适用于三维薄板结构, 这为理论分析和数值计算带来诸多不便.所以有必要建立适用于理论分析和数值计算的三维亚音速气动力模型.本文采用经典复合材料层合板理论, 针对亚音速气流作用下四边简支复合材料层合板, 基于线性势流和假设模态法, 建立适用于三维复合材料层合板结构的亚音速气动力模型, 通过Hamilton原理建立结构运动方程, 分析结构基频随来流速度的变化情况, 得到结构的临界失稳速度.
1. 复合材料层合板运动方程
1.1 结构本构方程及边界条件
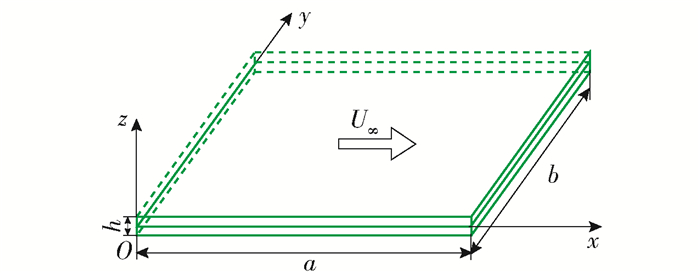
考虑图 1所示的亚音速下四边简支复合材料层合板, 板的长、宽、厚分别为a、b、h, 其中h«min{a, b}, U∞为来流速度, 设板的横向位移为w, 以板的中面作为xOy面构建直角坐标系.
对于薄板结构, 采用Kirchhoff板理论来模拟结构的位移场, 可以表示为
$$ u = - z\frac{{\partial w}}{{\partial x}},v = - z\frac{{\partial w}}{{\partial y}},w = w $$ (1) 式中:u和v为结构上任一点沿x和y方向的面内位移; w为结构的横向位移.
平板结构的应变-位移关系即几何方程表示为
$$ {\varepsilon _x} = \frac{{\partial u}}{{\partial x}},{\varepsilon _y} = \frac{{\partial v}}{{\partial y}},{\gamma _{xy}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} $$ (2) 式中εx、εy和γ分别为正应变和切应变.
将结构的位移场(1)代入几何方程(2), 可将应变-位移关系表示为
$$ \mathit{\boldsymbol{\varepsilon }} = {\left[ {{\varepsilon _x},{\varepsilon _y},{\gamma _{xy}}} \right]^{\rm{T}}} = z\mathit{\boldsymbol{k}} $$ (3) 式中:ε为应变向量; k为曲率向量, 表示为
$$ \mathit{\boldsymbol{k}} = {\left[ { - \frac{{{\partial ^2}w}}{{\partial {x^2}}}, - \frac{{{\partial ^2}w}}{{\partial {y^2}}}, - 2\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \right]^{\rm{T}}} $$ (4) 对于复合材料层合板的单层板, 其本构方程表示为
$$ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{Q\varepsilon }} $$ (5) 其中:σ为应力向量; ε为应变向量; Q为刚度系数矩阵, 表示为
$$ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&0\\ {{Q_{12}}}&{{Q_{22}}}&0\\ 0&0&{{Q_{66}}} \end{array}} \right] $$ (6) 式中:${Q_{66}} = {G_{12}}{Q_{11}} = \frac{{{E_1}}}{{1 - {v_{12}}{v_{21}}}};\;{Q_{22}} = \frac{{{E_2}}}{{1 - {v_{12}}{v_{21}}}};\;{Q_{12}} = \frac{{{v_{12}}{E_1}}}{{1 - {v_{12}}{v_{21}}}}$.其中E1、E2和G12分别为弹性模量和剪切模量, v12和v21为泊松比.
对于复合材料层合结构, 各单层板的纤维方向不一定与整体坐标系中坐标轴方向一致.为了求得材料参数在整体坐标系中的本构关系, 需要进行坐标转换.经过坐标转换后的材料参数矩阵表示为
$$ \mathit{\boldsymbol{\bar Q}} = {\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{T}}^{ - {\rm{T}}}} $$ (7) 式中:Q为刚度系数矩阵; T为坐标转换矩阵, 它的展开形式可表示为
$$ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{{\cos }^2}\beta }&{{{\sin }^2}\beta }&{ - 2\sin \beta \cos \beta }\\ {{{\sin }^2}\beta }&{{{\cos }^2}\beta }&{2\sin \beta \cos \beta }\\ {\sin \beta \cos \beta }&{ - \sin \beta \cos \beta }&{{{\cos }^2}\beta - {{\sin }^2}\beta } \end{array}} \right] $$ (8) 式中β为纤维方向与整体坐标轴的夹角.
层合板结构横截面上单位长度合内力矩M可由各单层板的力矩沿厚度方向积分求得, 其表示为
$$ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{Dk}} $$ (9) 式中D为弯曲刚度矩阵, 其表示为
$$ \mathit{\boldsymbol{D}} = \sum\limits_{k = 1}^s {\int_{{z_{k - 1}}}^{{z_k}} {\mathit{\boldsymbol{\bar Q}}\left( {{\beta _k}} \right){z^2}{\rm{d}}z} } $$ (10) 式中:s为层合板的层数; βk为第k层板的铺设角度; zk-1与zk分别为第k层板的下表面和上表面横向坐标; Q(βk)为铺设角度为βk时的刚度系数矩阵.
结构的应变能U表示为
$$ U = \frac{1}{2}\int {\int_A {{\mathit{\boldsymbol{k}}^{\rm{T}}}\mathit{\boldsymbol{M}}{\rm{d}}x{\rm{d}}y} } = \frac{1}{2}\int {\int_A {{\mathit{\boldsymbol{k}}^{\rm{T}}}\mathit{\boldsymbol{Dk}}{\rm{d}}x{\rm{d}}y} } $$ (11) 结构的动能T可表示为
$$ T = \frac{1}{2}\int {\int_A {{\rho _{\rm{m}}}h{{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}{\rm{d}}x{\rm{d}}y} } $$ (12) 式中ρm为板的密度.
外力虚功δW可表示为
$$ \delta W = \int {\int_A {\Delta P\delta w{\rm{d}}x{\rm{d}}y} } $$ (13) 式中ΔP为亚音速气动力.
板的四边简支边界条件为
$$ \left\{ \begin{array}{l} w = 0,\frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0\;\;\;\;\left( {当\;x = 0\;与\;x = a} \right)\\ w = 0,\frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0\;\;\;\;\left( {当\;y = 0\;与\;y = b} \right) \end{array} \right. $$ (14) 根据假设模态法, 横向位移可表示为
$$ \begin{array}{*{20}{c}} {w\left( {x,y,t} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W_{mn}}\left( {x,y} \right){q_{mn}}\left( t \right)} } = }\\ {{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {x,y} \right)\mathit{\boldsymbol{q}}\left( t \right)} \end{array} $$ (15) 式中:W(x, y)为满足边界条件的位移形函数; q(t)为广义坐标.根据四边简支边界条件, 位移形函数表示为
$$ \begin{array}{*{20}{c}} {{W_{mn}} = \sin \left( {\frac{{m{\rm{ \mathsf{ π} }}x}}{a}} \right)\sin \left( {\frac{{n{\rm{ \mathsf{ π} }}y}}{b}} \right)}\\ {\left( {m = 1,2, \cdots ,M;n = 1,2, \cdots ,N} \right)} \end{array} $$ (16) 1.2 薄板的亚三维音速气动力模型
假设亚音速气流为无旋、无黏且不可压缩的理想气体, 则其流动为有势流动, 流场可描述为如下的Laplace方程
$$ \frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {z^2}}} = 0 $$ (17) 式中φ为速度势函数.根据线性Bernoulli方程, 亚音速流固耦合气动力可表示为
$$ \Delta P = {\rho _\infty }{\left( {\frac{{\partial \varphi }}{{\partial t}} + {U_\infty }\frac{{\partial \varphi }}{{\partial x}}} \right)_{z = \frac{h}{2}}} $$ (18) 式中ρ∞和U∞分别为无穷远处来流的密度和速度.
气流与平板上表面的耦合关系可表示为
$$ \left( {\frac{{\partial \varphi }}{{\partial z}}} \right)\left| {_{z = \frac{h}{2}}} \right. = \left( {\frac{{\partial w}}{{\partial t}} + {U_\infty }\frac{{\partial w}}{{\partial x}}} \right) $$ (19) 速度势函数可表示为
$$ \varphi \left( {x,y,z,t} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W_{mn}}\left( {x,y} \right){\psi _{mn}}\left( z \right){f_{mn}}\left( t \right)} } $$ (20) 式中ψmn(z)与fmn(t)是关于z与t的函数.将式(20)代入式(18)得到气动力表达式
$$ \begin{array}{*{20}{c}} {\Delta P = {\rho _\infty }\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\{ {{\psi _{mn}}\left( {\frac{h}{2}} \right)\left[ {{W_{mn}}{{\dot f}_{mn}}\left( t \right) + } \right.} \right.} } }\\ {\left. {\left. {{U_\infty }\frac{{\partial {W_{mn}}}}{{\partial x}}{f_{mn}}\left( t \right)} \right]} \right\}} \end{array} $$ (21) 将式(15)(20)代入到气流与平板的耦合关系式(19)中, 得到
$$ \begin{array}{*{20}{c}} {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left[ {{W_{mn}}{f_{mn}}\left( t \right)} \right]} } = }\\ {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\{ {\frac{1}{{{{\psi '}_{mn}}\left( {h/2} \right)}}\left[ {{W_{mn}}{{\dot q}_{mn}}\left( t \right) + {U_\infty }\frac{{\partial {W_{mn}}}}{{\partial x}}{q_{mn}}\left( t \right)} \right]} \right\}} } } \end{array} $$ (22) 将式(22)代入式(21)得到气动力表达式
$$ \begin{array}{*{20}{c}} {\Delta P = {\rho _\infty }\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\{ {\frac{{{\psi _{mn}}\left( {h/2} \right)}}{{{{\psi '}_{mn}}\left( {h/2} \right)}} \cdot } \right.} } }\\ {\left. {\left[ {{W_{mn}}{{\ddot q}_{mn}}\left( t \right) + 2{U_\infty }\frac{{\partial {W_{mn}}}}{{\partial x}}{{\dot q}_{mn}}\left( t \right) + U_\infty ^2\frac{{{\partial ^2}{W_{mn}}}}{{\partial {x^2}}}{q_{mn}}\left( t \right)} \right]} \right\}} \end{array} $$ (23) 为了确定表达式中的未知函数ψmn(z), 可将速度势函数式(20)代入到Laplace方程(17), 考虑到当z趋于无穷大时速度势为有限值, 则有
$$ {\psi _{mn}}\left( z \right) = \exp \left( { - \sqrt {\frac{{{m^2}{{\rm{ \mathsf{ π} }}^2}}}{{{a^2}}} + \frac{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}{{{b^2}}}z} } \right) $$ (24) 所以四边简支板亚音速气动力模型表示为
$$ \begin{array}{*{20}{c}} {\Delta P = {\rho _\infty }\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\{ {\frac{{ - ab}}{{{\rm{ \mathsf{ π} }}\sqrt {{m^2}{b^2} + {n^2}{a^2}} }} \cdot } \right.} } }\\ {\left. {\left[ {{W_{mn}}{{\ddot q}_{mn}}\left( t \right) + 2{U_\infty }\frac{{\partial {W_{mn}}}}{{\partial x}}{{\dot q}_{mn}}\left( t \right) + U_\infty ^2\frac{{{\partial ^2}{W_{mn}}}}{{\partial {x^2}}}{q_{mn}}\left( t \right)} \right]} \right\}} \end{array} $$ (25) 1.3 流固耦合结构系统的运动方程
采用Hamilton原理建立亚音速气流作用下三维复合材料层合板的运动方程
$$ \int_{{t_1}}^{{t_2}} {\left( {\delta T - \delta U} \right){\rm{d}}t} + \int_{{t_1}}^{{t_2}} {\delta W{\rm{d}}t} = 0 $$ (26) 式中t1和t2分别为对时间积分的下、上限.
将应变能(11)、动能(12)和外力虚功(13)代入Hamilton原理, 对位移进行变分运算, 可以得到亚音速气流作用下层合板的运动方程为
$$ \begin{array}{*{20}{c}} {\int {\int_A {{\rho _{\rm{m}}}hw\frac{{{\partial ^2}w}}{{\partial {t^2}}}{\rm{d}}A} } + \int {\int_A {w\left( {{D_{11}}\frac{{{\partial ^4}w}}{{\partial {x^4}}} + {D_{22}}\frac{{{\partial ^4}w}}{{\partial {y^4}}} + } \right.} } }\\ {2{D_{12}}\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + 4{D_{16}}\frac{{{\partial ^4}w}}{{\partial {x^3}\partial y}} + 4{D_{26}}\frac{{{\partial ^4}w}}{{\partial x\partial {y^3}}} + }\\ {\left. {4{D_{66}}\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}}} \right){\rm{d}}A - \int {\int_A {w\Delta P{\rm{d}}A} } = 0} \end{array} $$ (27) 2. 运动方程的求解
采用假设模态法, 将式(15)代入式(27)并整理写成如下矩阵形式的方程
$$ \mathit{\boldsymbol{M\ddot q}}\left( t \right) + \mathit{\boldsymbol{C\dot q}}\left( t \right) + \mathit{\boldsymbol{Kq}}\left( t \right) = 0 $$ (28) 式中M、C和K分别为质量矩阵、阻尼矩阵和刚度矩阵, 它们中的元素表示为
$$ {M_{mn}} = \int {\int_A {\left( {{\rho _{\rm{m}}}h - {\rho _\infty }\frac{{ - ab}}{{{\rm{ \mathsf{ π} }}\sqrt {{m^2}{b^2} + {n^2}{a^2}} }}} \right){W_{mn}}{W_{mn}}{\rm{d}}A} } $$ (29) $$ {C_{mn}} = - \int {\int_A {2{\rho _\infty }{U_\infty }\frac{{ - ab}}{{{\rm{ \mathsf{ π} }}\sqrt {{m^2}{b^2} + {n^2}{a^2}} }}\frac{{\partial {W_{mn}}}}{{\partial x}}{W_{mn}}{\rm{d}}A} } $$ (30) $$ \begin{array}{*{20}{c}} {{K_{mn}} = \int {\int_A {\left( {{D_{11}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial {x^4}}} + {D_{22}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial {y^4}}} + 2{D_{12}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial {x^2}\partial {y^2}}} + } \right.} } }\\ {4{D_{16}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial {x^3}\partial y}} + 4{D_{26}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial x\partial {y^3}}} + 4{D_{66}}\frac{{{\partial ^4}{W_{mn}}}}{{\partial {x^2}\partial {y^2}}} - }\\ {\left. {{\rho _\infty }U_\infty ^2\frac{{ - ab}}{{{\rm{ \mathsf{ π} }}\sqrt {{m^2}{b^2} + {n^2}{a^2}} }}\frac{{{\partial ^2}{W_{mn}}}}{{\partial {x^2}}}} \right){W_{mn}}{\rm{d}}A} \end{array} $$ (31) 式(28)的稳态解形式为
$$ \mathit{\boldsymbol{q}} = {\mathit{\boldsymbol{q}}_0}{{\rm{e}}^{\lambda t}} $$ (32) 式中q0和λ分别为系统的特征向量与特征值.
将式(32)代入到式(28), 得到广义特征值问题
$$ \left( {\mathit{\boldsymbol{M}}{\lambda ^2} + \mathit{\boldsymbol{C}}\lambda + \mathit{\boldsymbol{K}}} \right){\mathit{\boldsymbol{q}}_0} = 0 $$ (33) 方程有非零解的充要条件为
$$ \left| {\mathit{\boldsymbol{M}}{\lambda ^2} + \mathit{\boldsymbol{C}}\lambda + \mathit{\boldsymbol{K}}} \right| = 0 $$ (34) 通过求解式(34), 可得不同来流速度下结构的各阶固有频率.
由式(31)可见, 当考虑气动压力时, 结构系统的刚度中包含了气动刚度项, 随着来流速度的逐渐增加, 结构系统的刚度将逐渐变小, 由此导致系统的各阶固有频率也将逐渐减小.当结构的基频减小到0时, 结构将处于临界失稳状态, 此时对应的来流速度即为临界失稳速度.在实际应用中, 应根据复合材料层合板结构所处力学环境, 合理设计结构参数, 避免出现在气流作用下结构发生失稳问题.
3. 数值计算
研究如图 1所示的亚音速气流作用下复合材料层合板结构, 通过讨论系统固有频率随来流速度的变化情况, 分析不同结构尺寸以及铺设角度对层合板结构气动弹性稳定性的影响.
3.1 算法有效性验证
将采用本文方法的计算结果与已有文献结果加以对比, 以验证本文建立的气动力模型和结构运动方程的合理性, 以及数值算法和程序的正确性.由于我们尚未查到有关复合材料层合板结构亚音速相关问题的研究结果, 所以与各向同性薄板的相关研究结果加以比较.令E1=E2=E, μ12=μ21=μ, G12=E/[2(1+μ)], 则层合板结构退化为各向同性薄板, 再令b→+∞, 则三维薄板进一步退化为二维薄板.材料和结构参数取为E=70 GPa, μ=0.3, ρ∞=1.29 kg/m3, a=0.8 m, 表 1给出了采用本文方法计算得到的不同结构参数下薄板的临界失稳速度, 并与文献[6]中的结果进行了对比.
表 1 不同结构尺寸薄板的临界失稳速度Table 1. Critical instability velocities of the plate with different structural sizes项目 本文结果 文献[6] 平板宽度b/m 1 3 10 30 →∞ 失稳速度/(m·s-1) 167.29 98.22 90.87 90.21 90.14 从表 1可以看出, 随着板宽度b逐渐增大, 薄板的临界失稳速度逐渐降低, 当b=30 m时, 临界失稳速度与文献[6]的结果相差不到0.1%, 从而验证了本文研究方法和计算结果的有效性.
3.2 三维层合板气动稳定性分析
研究亚音速气流下三维层合板结构的气动弹性稳定性.取参数为E1=140 GPa, E2=9.1 GPa, G12=7.2 GPa, μ12=0.019 4, μ21=0.3, a=0.8 m, ρm=1 600 kg/m3, ρ∞=1.29 kg/m3.层合板的铺设角度为[β/-β/β], 其中β变化从0°到90°.
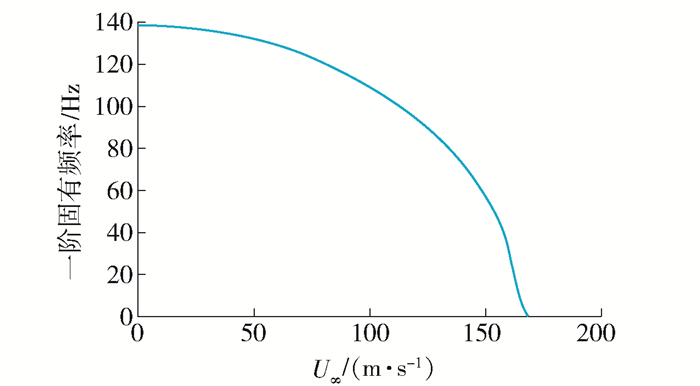
通过求解式(34), 可以得到系统固有频率随来流速度的变化曲线.图 2、3为铺设角30°层合板基频随来流速度的变化情况.
![]()
图 2 结构基频随来流速度的变化Figure 2. Variation of the first natural frequencies with respect to the flow velocity![]()
图 3 结构基频随来流速度的变化(不同宽度)Figure 3. Variation of the first natural frequencies with respects to the flow velocity (different width)从图 2中可以看出, 随着来流速度的增加, 结构的基频逐渐减小, 当基频减小到0时, 此时对应的来流速度为结构的临界失稳速度, 此时临界失稳速度约为168 m/s.
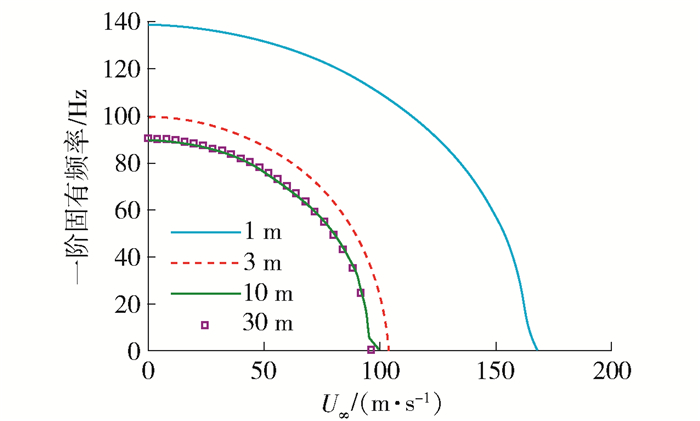
从图 3可以看出, 当层合板宽度分别为b=1、3、10、30 m时, 结构的临界失稳速度分别为168、104、98、98 m/s.对比可知, 当层合板宽度越大时, 其越接近于二维平板, 以至于结构的临界失稳速度越低, 结构越容易失稳.
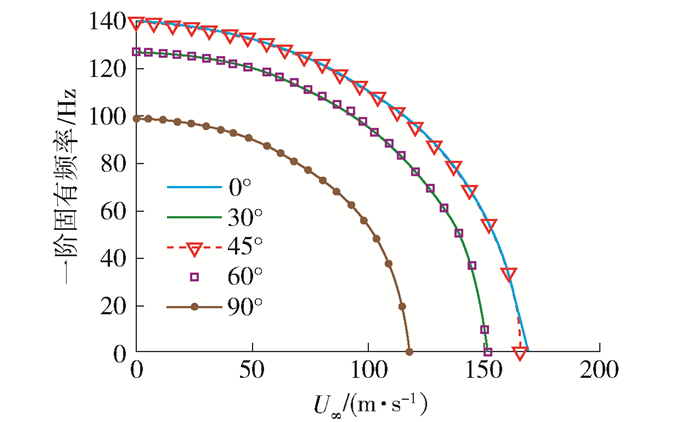
图 4为针对宽度为1 m, 铺设角为0°、30°、45°、60°、90°情况时, 层合板结构基频随来流速度的变化曲线.
![]()
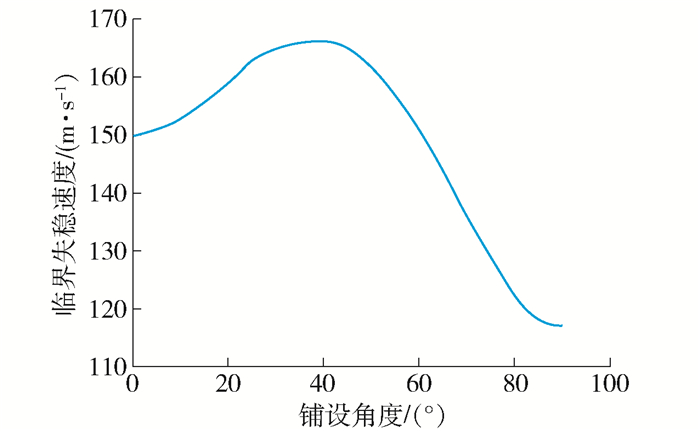
图 4 结构基频随来流速度的变化(不同铺设角)Figure 4. Variation of the first natural frequencies with respect to the flow velocity (with different ply angles)图 5为临界失稳速度随铺设角度的变化曲线.可见, 随着层合板铺设角度的逐渐增大, 板的临界失稳速度先增大后减小, 这一结论在图 4中也可得到, 可见存在最优铺设角度.层合板的最优铺设角度与其自身的结构尺寸有关, 通过本文研究发现, 对于任意尺寸的三维层合板结构, 在亚音速气流作用下存在最优铺设角度, 可以通过计算临界失稳来流速度随层合板铺设角度的变化曲线, 确定最优铺设角度.
![]()
图 5 临界失稳速度随铺设角度的变化Figure 5. Critical instability velocities of the plate with respect to the ply angles4. 结论
本文研究了亚音速气流作用下复合材料层合板结构的气动弹性稳定性.通过计算层合板结构在不同来流速度时的固有频率, 得到层合板在亚音速气流作用下的临界失稳速度, 分析了不同结构尺寸和铺设角度对临界失稳速度的影响.通过本文研究, 得到以下结论:
1) 随着板沿y方向宽度的逐渐增大, 三维板的临界失稳速度趋近于二维板的临界失稳速度, 验证了本文研究方法和计算结果的可行性.
2) 在亚音速气流作用下, 随着来流速度的逐渐增大, 结构系统的固有频率会逐渐减小.当基频减小到零时, 层合板结构会发生失稳, 主要是由于气流的作用使结构的刚度发生了变化.
3) 随着层合板的铺设角度逐渐增大, 结构临界失稳速度先增大后减小, 存在最优铺设角度.因此对于任意给定尺寸的三维复合材料层合板, 可采用本文方法计算其最优铺设角度.
-
![]()
图 2 结构基频随来流速度的变化
Figure 2. Variation of the first natural frequencies with respect to the flow velocity
![]()
图 3 结构基频随来流速度的变化(不同宽度)
Figure 3. Variation of the first natural frequencies with respects to the flow velocity (different width)
![]()
图 4 结构基频随来流速度的变化(不同铺设角)
Figure 4. Variation of the first natural frequencies with respect to the flow velocity (with different ply angles)
![]()
图 5 临界失稳速度随铺设角度的变化
Figure 5. Critical instability velocities of the plate with respect to the ply angles
-
[1] IONITA S.A chaos theory perspective on system's failure[J].Information Sciences, 2000, 127(3/4):193-215. http://www.sciencedirect.com/science/article/pii/S0020025500000372
[2] SONG Z G, LI F M.Aerothermoelastic analysis of lattice sandwich composite panels in supersonic airflow[J].Meccanica, 2016, 51:877-891. doi: 10.1007/s11012-015-0240-y
[3] MAHMOUDKHANI S, SADEGHMANESH M, HADDADPOUR H.Aero-thermo-elastic stability analysis of sandwich viscoelastic cylindrical shells in supersonic airflow[J].Composite Structures, 2016, 147:185-196. doi: 10.1016/j.compstruct.2016.03.020
[4] VEDENEEV V V.Flutter of a wide strip plate in a supersonic gas flow[J].Fluid Dynamics, 2005, 40(5):805-817. doi: 10.1007/s10697-005-0118-0
[5] BISPLINGHOFF R L, ASHLEY H, HALFMAN R L.Aeroelasticity[M].Cambridge:Cambridge University Press, 1955:285-326.
[6] DUGUNDJI J, DOWELL E H, PERKIN B.Subsonic flutter of panels on continuous elastic foundations[J].AIAA Journal, 1963, 5(1):1146-1154. http://adsabs.harvard.edu/abs/1963AIAAJ...1.1146D
[7] TANG D M, DOWELL E H, Limit cycle oscillations of two-dimensional panels in low subsonic flow[J].International Journal of Non-Linear Mechanics, 2002, 37(7):1199-1209. doi: 10.1016/S0020-7462(01)00140-8
[8] TANG L, PAIDOUSSIS M P, JIANG J.The dynamics of variants of two-dimensional cantilevered flexible plates in axial flow[J].Journal of Sound and Vibration, 2009, 323(1/2):214-231. https://www.researchgate.net/publication/239289992_The_dynamics_of_variants_of_two-dimensional_cantilevered_flexible_plates_in_axial_flow
[9] TANG L, PAIDOUSSIS M P.The influence of the wake on the stability of cantilevered flexible plates in axial flow[J].Journal of Sound and Vibration, 2008, 310(3):512-526. doi: 10.1016/j.jsv.2007.09.025
[10] ZHAO W, PAIDOUSSIS M P, TANG L.Theoretical and experimental investigations of the dynamics of cantilevered flexible plates subjected to axial flow[J].Journal of Sound and Vibration, 2012, 331(3):575-587. doi: 10.1016/j.jsv.2011.08.014
[11] WEAVER D S, UNNY T E.The hydroelastic stability of a flat plate[J].Journal of Applied Mechanics, 1970, 37(1):823-827. http://appliedmechanics.asmedigitalcollection.asme.org/article.aspx?articleid=1399525
[12] KORBAHTI B, UALl E.Vibrations of an anisotropic plate under fluid flow in a channel[J].Journal of Vibration and Control, 2007, 13(8):1191-1204. doi: 10.1177/1077546307076897
[13] YAO G, LI F M.Nonlinear vibration of a two-dimensional composite laminated plate in subsonic airflow[J].Journal of Vibration and Control, 2015, 21(4):662-669. doi: 10.1177/1077546313489718
[14] YAO G, LI F M.The stability analysis and active control of a composite laminated open cylindrical shell in subsonic airflow[J].Journal of Intelligent Material Systems and Structures, 2014, 25(3):259-270. doi: 10.1177/1045389X13491020
[15] LI P, YANG Y.Nonlinear flutter behavior of a plate with motion constraints in subsonic flow[J].Meccanica, 2014, 49:2797-2815. doi: 10.1007/s11012-014-0041-8
[16] LI P, YANG Y.Hopf and two-multiple semi-stable limit cycle bifurcations of a restrained plate subjected to subsonic flow[J].Journal of Sound and Vibration, 2015, 335:286-303. doi: 10.1016/j.jsv.2014.09.024
下载:
计量
- 文章访问数: 159
- HTML全文浏览量: 2
- PDF下载量: 39
