我国城市轨道交通尚缺乏有效的车载客流检测设备，导致无法实时获取断面客流信息.该信息缺失成为制约轨道交通动态运营管理实施的关键障碍.基于动态交通分配(dynamic traffic assignment，DTA)的预测方法为断面流获取提供了新思路^[1-2]，即首先预测短时内路网起讫点(origin-destination，OD)矩阵，然后将OD矩阵动态分配至路网，进而得到断面流分布状态.考虑到分配模型的时效性，主要采用仿真方法进行动态交通分配，代表性应用如DynaMIT^[3]、DynaSmart-X^[4].然而，在仿真预测系统中的需求生成阶段，由于输入OD矩阵的时间跨度(较长)与需求生成时间粒度(较短)往往不一致，导致生成的客流需求(乘客个体)与实际客流到达规律存在较大偏差，进而影响断面流预测精度.

基于DTA的客流仿真预测系统涉及两大关键问题：一是短时OD矩阵预测，即利用实时采集客流信息反推OD矩阵，因为轨道交通可实时采集的客流信息有限，所以难以对短时OD矩阵进行有效预测.文献[5]研究结果显示，当时间粒度缩短至15 min时，预测误差达35.5%.二是动态客流分配，即如何将预测到的OD矩阵动态分配至路网，从而获取断面客流的时变分布状态，文献[1, 6]研究了如何从乘客个体出行视角实现动态客流分配.短时OD矩阵预测结果是动态客流分配的输入.除此之外，在仿真预测过程中还涉及另一重要问题，即需求生成问题.需求生成是衔接上述2个关键问题的纽带，本文中需求生成是指利用已知OD矩阵来生成符合一定特征的出行个体或群体，作为动态客流分布预测仿真系统中的输入.

既有仿真系统中常常假设乘客个体到达间隔时间服从特定概率分布，如均匀分布或泊松分布.当OD矩阵时间跨度较短(如5 min)时，该方法具有良好的适用性；然而当OD矩阵时间跨度较长时，所生成需求与实际需求存在较大偏差.原因在于该方法忽略了时段内需求的时变波动特征.目前，关于需求生成研究十分匮乏.林勇等^[7]较早针对该问题进行了研究，将OD矩阵时段离散化为等长子时段，采用直方图逼近方式来优化需求生成过程，所提出方法可应用于离线参数估计；虞治涵等^[8]从随机数生成角度研究了需求生成问题，认为特赛特旋转(mersenne twister，MT)演算法发生器比线性同余发生器更优；周光伟等^[9]对需求生成模块的功能进行了分析，但缺乏相应的需求生成方法.为此，本文充分考虑轨道交通运营特征及技术条件，借鉴文献[7]的基本思路，将OD矩阵时间跨度离散化为细小的子时段，利用自动售检票机(automaic fare collection，AFC)实时获取的进站量对未来短时范围内进站量进行预测，从而确定子时段内需求分配比例，使得在需求生成时沿着子时段流量波动轨迹变化，逼近真实客流到达过程.该研究目的是使仿真系统中需求生成结果尽可能贴近实际客流到达过程，从而提高断面流预测精度.

1.   需求生成过程

定义T为OD矩阵涵盖的时间跨度(一般大于15 min)；假设OD矩阵已知(通过短时OD矩阵预测获取)，定义为Q，Q=[q_ij]^N×N，其中：N为路网车站集合；i、j为车站编号，i∈N, j∈N；q_ij为从车站i出发去往车站j的客流量.假设仿真系统中需求生成的单位时间粒度为Δt^*(一般较小，如1 min)，那么在Δt^*仿真步长内生成一次乘客个体.

需求生成过程应满足：1)需求总量的时间分布特征符合实际客流到达规律；2)需求的空间分布(目的车站选择)满足OD矩阵对应的分布结构.需求生成过程可拆为需求总量生成和目的车站选择2个步骤，可近似理解为四阶段法中的交通生成和交通分布.以车站i为例描述需求生成过程，单位时间Δt^*内需求生成强度可表示为

式中λ_i为车站i在单位时间内的需求生成强度.假设乘客到达时间间隔服从均匀分布，单位时间内生成的乘客个体数则为λ_i.

既有仿真系统或排队论中常假设乘客到达间隔时间服从特定概率分布，最为常见的为泊松分布.在此，以泊松分布为例，以式(1)得到的需求生成强度λ为参数，即可确定单位时间内到达车站乘客数的概率分布函数

式中k为乘客数.

在确定到达乘客总数的基础上，需进一步确定每一乘客的出行目的地.对某乘客而言，其选择车站j为目的车站的概率为

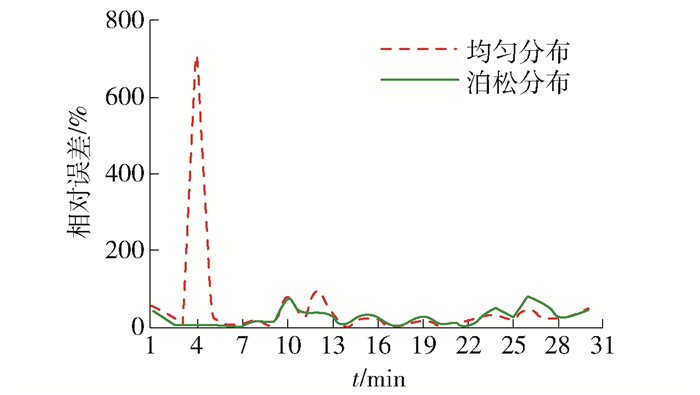
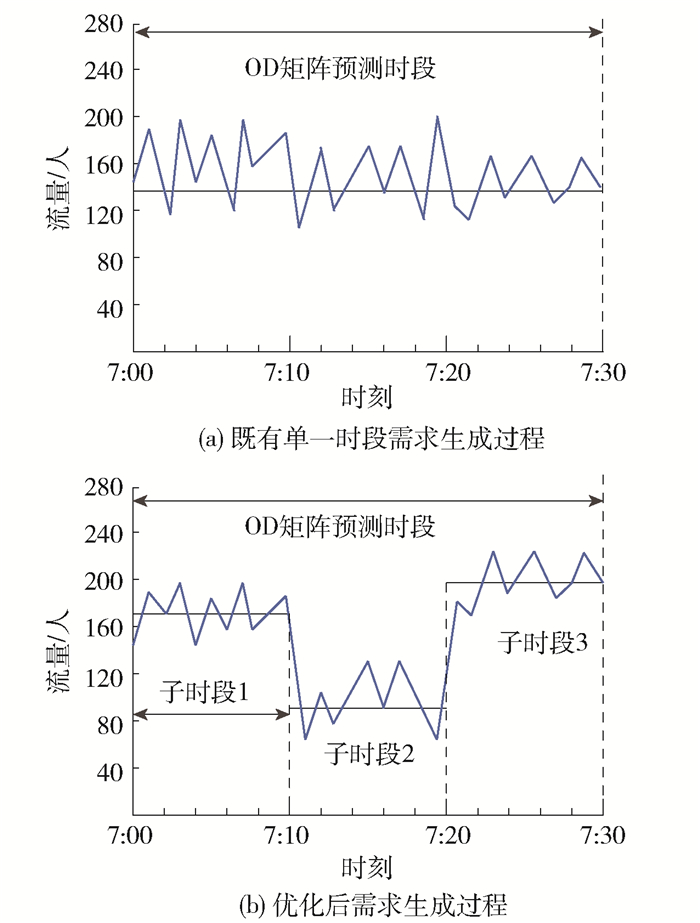
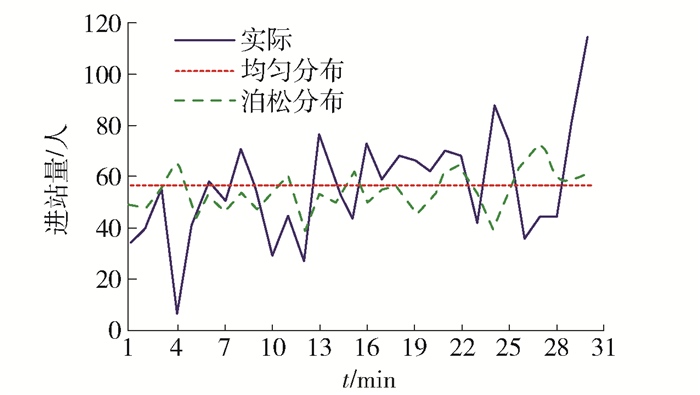
既有基于概率分布的需求生成忽略了时段内需求时变波动特征，在OD矩阵时间跨度内采用统一的需求生成强度.不难推测，当OD矩阵时段跨度较长、需求波动明显时，所生成需求与实际客流到达过程存在较大偏差.对北京地铁某站AFC数据统计结果进行分析，30 min范围内客流到达强度为56.9人/min，以此为参数生成服从均匀分布和泊松分布的随机流，并以1 min为粒度统计实际进站量. 图 1给出生成客流与实际客流的分布结果，图 2给出生成客流与实际客流的相对偏差，可以看出：泊松分布能较好地刻画客流的随机到达过程，但其与实际客流的平均相对误差仍达57%.

图  1  需求生成量与实际量对比

Figure  1.  Comparation between generation and real flows

下载: 全尺寸图片 幻灯片

图  2  需求生成量与实际量的相对误差

Figure  2.  Relative errors between generation and real flows

下载: 全尺寸图片 幻灯片

2.   需求生成过程优化

2.1   组合生成策略

提高需求生成精度的方法主要包含两方面：一是缩短OD矩阵预测时段长度，二是优化需求生成过程.既有研究结果显示^[5]，由于轨道交通可实时采集的客流信息有限，难以对较短时间粒度下的OD矩阵进行预测.因此，从缩短OD矩阵预测时段长度方面不具有可行性.为此，本文从需求生成过程优化角度出发，基本思路是将较长OD矩阵时间跨度离散化为细小子时段，通过对子时段内进站量进行短时预测来计算子时段内对应的需求分配比例，从而在每个子时段内采用不同的需求强度参数来生成对应的需求量.结合前述需求生成过程可知，本文对需求生成过程优化体现在第1阶段，即需求总量生成. 图 3为需求生成过程优化示意图.

图  3  需求生成过程优化示意图

Figure  3.  Schematic diagram of optimization processes for travel demand generation

下载: 全尺寸图片 幻灯片

将OD矩阵时间跨度T离散化为等长子时段，T={1, 2, …, t}；M为子时段集合数；Δt为子时段长度.假设子时段内进站量预测值为q_t，定义ϕ_t为子时段内需求分配比例，即

子时段内需求生成强度为

式中λ_it为车站i在子时段t内的需求生成强度.

因此，在利用式(2)进行需求生成时即可采用不同的需求生成强度参数

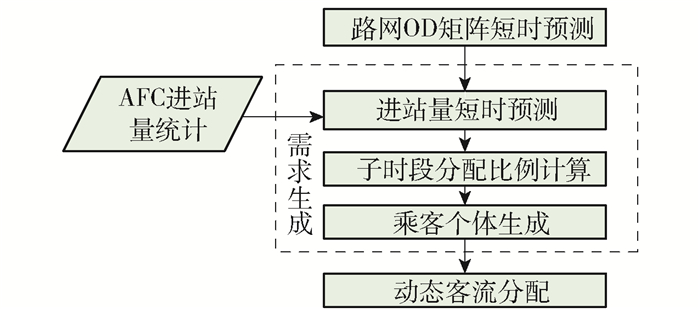
图 4给出了优化后仿真过程中的需求生成流程.不难理解，该组合需求生成过程可视为将较长时间跨度的OD矩阵虚拟化为多个较短时间粒度的OD矩阵，其中，确定各子时段内的分配比例可通过进站量短时预测予以实现.对于在线仿真预测系统，实时客流信息能否有效获取至关重要.目前，AFC系统尚不能实时传输完整的乘客出行记录(如卡信息、OD等)，但能获取短时内进站量统计结果.因此，该策略具备实施技术条件.另外，进站量短时预测属于局部预测，难度低，预测精度高，相关模型的计算效率能够满足在线应用需求，因此，该策略也具备理论可行性.

图  4  优化后需求生成流程

Figure  4.  Demand generation processes after optimization

下载: 全尺寸图片 幻灯片

2.2   进站量短时预测

由前述分析可知，进站量短时预测是优化的关键.前期关于进站量短时预测的研究已较为丰富^[10-13]，对比既有研究，文中进站量短时预测具有如下特点：1)多步预测，需同时对未来多个子时段内进站量进行预测；2)时间粒度小，预测时间粒度一般不超过5 min；3)对模型计算效率具有较高要求，全路网所有车站的总体预测时间应控制在秒级范围.本文选取计算效率较优的自回归滑动平均(auto-regressive and moving average，ARMA)、卡尔曼滤波以及分别与小波分析(wavelet analysis，WA)相结合的组合模型进行分析.

1) ARMA模型

ARMA模型的基本思想是：假设数据序列是依赖于时间的一簇变量，构成该时序的单个值虽然具有不确定性，但整个序列具有一定内在规律性，可用相应数学模型近似描述，进而从本质上认识这些数据的内在结构和演变规律，达到最小方差意义下的最优预测^[11].

设{x_t, t=0, ±1, ±2, …}是零均值的平稳时间序列，满足

式中：{ε_t-j}表示均值为0、方差为σ_ε²的平稳白噪声序列；p、q为预测阶数，可通过序列样本的自相关函数和偏自相关函数确定；φ=[φ₁, φ₂, …, φ_p]^T，θ=[θ₁, θ₂, …, θ_q]^T，为预测参数.

完成阶数及参数计算后，即可完成模型构建，将数据序列模型表示为ARMA(p, q).根据{x_t-1, x_t-2, …}即可对t时段内的变量x_t进行预测，预测值$ {{\mathit{\hat{x}}}_{\mathit{t}}}$可表示为

2) 卡尔曼滤波模型

卡尔曼滤波模型的基本思想是：利用状态方程和观测方程组成的线性随机系统的状态空间模型来描述滤波器，根据线性无偏最小均方误差估计准则，采用一套递推算法对该滤波器的状态变量做最佳估计，从而求得滤掉噪声的有用信号的最佳估计^[14].卡尔曼滤波模型中状态转移方程为

量测方程为

式中：x(t)为时段t内状态变量矩阵形式，x(t)=[x_t, x_t-1, …, x_t-n]^T，n可理解为预测过程中包含的前向分析时段数；y(t+1)为量测矩阵；w(t+1)、v(t+1)为零均值高斯白噪声序列；F、H为状态转移矩阵，本文中H为单位矩阵.

w(t)和v(t)分别表示系统的激励噪声和量测噪声，满足

式中：γ_kt为Kronecker Delta系数(k=t时，γ_kt=1，否则γ_kt=0)；Q和R为白噪声对应的协方差矩阵.

卡尔曼滤波递推过程包含自回归反馈调节机制，利用协方差矩阵将前期估计效果用于后期预测中.递推过程可概括为两大步：1)系统状态初始推算，包括先验预测推算和先验协方差矩阵计算；2)系统状态修正，包括卡尔曼滤波增益计算、先验预测修正和后验协方差矩阵更新.具体算法参见文献[15].

3) 小波分析模型

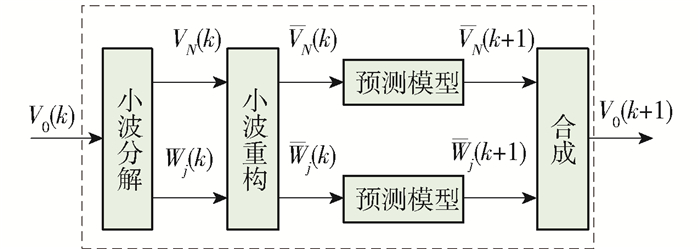
随着预测时段缩短，交通流波动性增强，规律性也随之降低.本文采用分解—单支重构—预测—合成的顺序进行预测.基于小波分析预测交通流的基本流程如图 5所示.小波分解与重构是将包括多组信息的交通流信号V₀(v_i∈V₀)分解到不同的信息子空间{W₁, W₂, …, W_N, V_N}，得到不同分辨率的分解信号^[16].其中，v_k^N∈V_N是在第N分辨率时对v_i∈V₀的近似信息，表示交通流变化趋势的基本信号；W_j是干扰信号.通过多分辨率分析将表征交通流本质变化趋势的基本信号与高频干扰信号相分离，再利用其他预测方法对基本信号与干扰信号进行预测.

图  5  基于小波分析的交通流预测流程

Figure  5.  Prediction processes for traffic flow based on wavelet analysis

下载: 全尺寸图片 幻灯片

3.   案例分析

选取北京市轨道交通某站进行案例分析，研究时段范围为06:00—12:00.假定OD矩阵短时预测时间跨度为30 min，以5 min为单位时长将OD时段分为6个子时段.以原始AFC记录为基础数据，统计获取实际进站客流分布及预测模型参数.

3.1   进站量预测分析

首先，评估子时段内进站量预测结果精度，从而选取恰当的进站量预测模型.预测范围为未来一个OD矩阵所对应的时间跨度，即6个子时段，单位预测时间长度为5 min.为评估模型在不同客流特征下的适应性，分别对工作日和周末的进站量进行预测.选取平均相对误差

均方根相对误差

相关系数

3个指标来综合评估预测结果.式中：q_t^*为子时段t内实际进站量；q_t为预测值；q和q^*分别为实际值和预测值的均值.在普通计算机上(Intel Core I5, 4 GB RAM, 3.2 GHz)，运用Matlab 2010编写程序进行进站量预测.

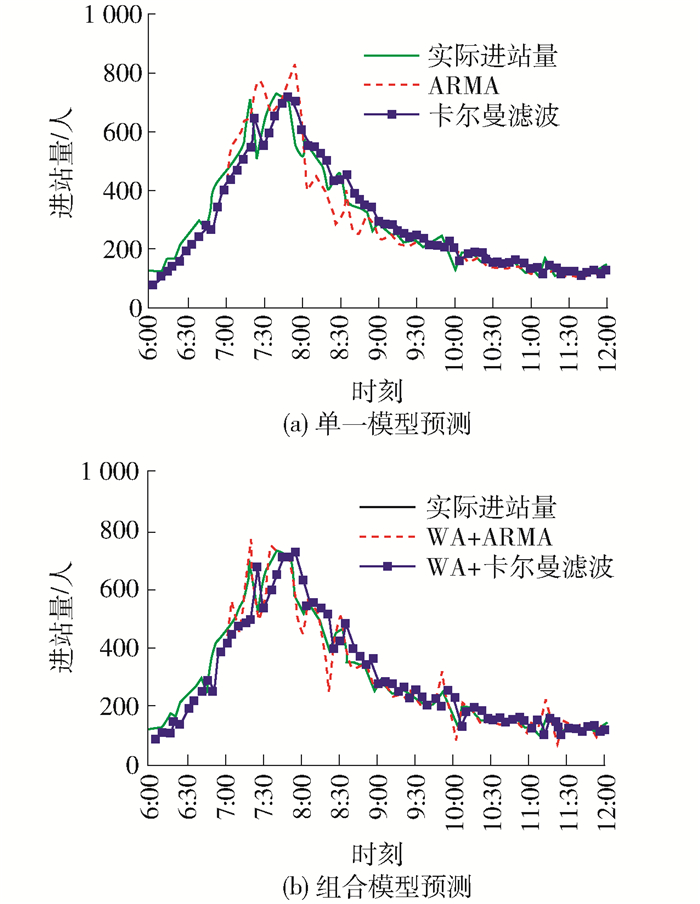
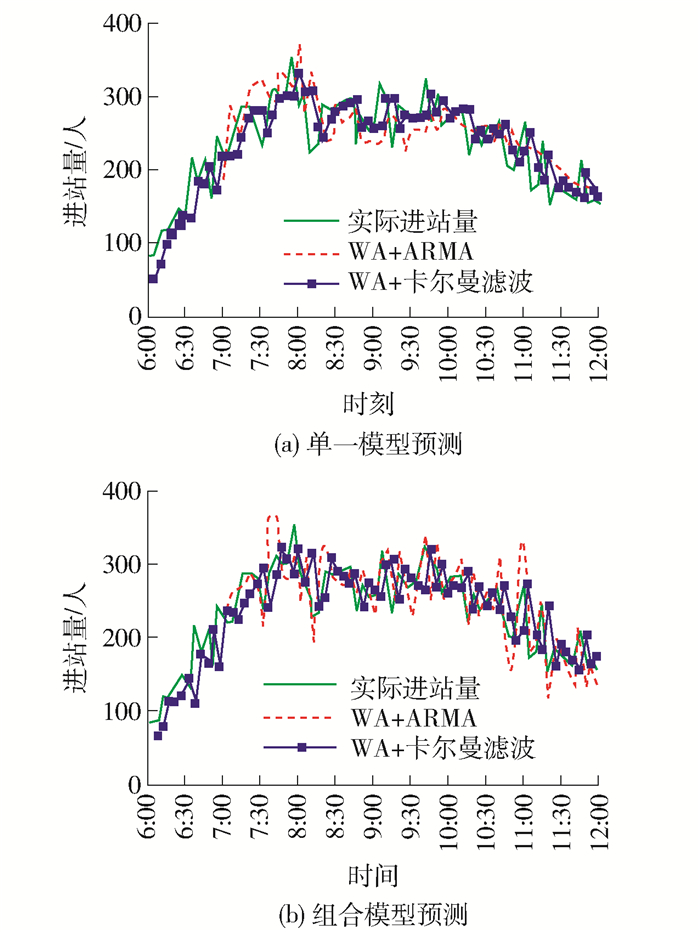
图 6、7分别给出工作日和周末的预测结果，不同模型间详细对比见表 1.

图  6  工作日进站量预测结果

Figure  6.  Forecasting results of station inflows in a weekday

下载: 全尺寸图片 幻灯片

图  7  周末进站量预测结果

Figure  7.  Forecasting results of flows in a weekend day

下载: 全尺寸图片 幻灯片

表  1  不同模型预测结果对比

Table  1.  Comparison of results for different models

模型	MAPE/%			RMSPE			CC			运算时间/s
	工作日	周末		工作日	周末		工作日	周末		工作日	周末
ARMA	16.42	14.63		0.21	0.18		0.94	0.72		8.24	8.31
卡尔曼滤波	15.04	13.15		0.19	0.18		0.96	0.83		0.02	0.01
WA+ARMA	8.95	8.81		0.12	0.11		0.98	0.91		45.97	44.54
WA+卡尔曼滤波	18.99	16.81		0.25	0.23		0.94	0.76		0.05	0.04

下载: 导出CSV 

| 显示表格

由表 1可以看出：

1) 从单一预测模型精度来看，卡尔曼滤波模型优于ARMA模型；从计算效率来看，卡尔曼滤波模型运算时间能够控制在毫秒级范围内，明显优于ARMA模型，能够满足在线实时预测的需求.

2) 在单一预测模型基础上增加小波分析，ARMA模型预测精度大幅提高，但计算效率降低明显，而卡尔曼滤波模型在精度和效率方面均存在一定幅度的降低.主要原因在于：小波分解和重构过程在于捕捉复合时间序列的本质信号与干扰信号的规律，ARMA模型预测核心在于捕捉时间序列的变化趋势，与WA一致；而卡尔曼滤波模型仅以前后2步递推过程为依据，对序列变化趋势捕捉能力较弱.

3) 针对不同客流特征日，从MAPE指标来看，模型对周末的预测精度高于工作日，原因在于周末客流波动性较弱(无明显高峰)；从CC指标来看，模型对工作日的整体预测精度要高于周末，CC指标反映的是整体预测的拟合程度，造成该现象的原因在于工作日客流分布规律性(趋势)更强，因此，预测结果与实际客流特征相吻合.

综上分析，WA与ARMA的组合模型具有最佳预测精度，但运算效率难以满足在线预测需求，从精度和运算效率两方面综合考虑，认为卡尔曼滤波模型最佳.

3.2   需求生成分析

仿真系统中需求生成的结果为独立出行的乘客个体，其包含到站时间及目的车站信息.本文需求生成过程优化体现在需求总量生成方面，即确定时变的到站客流量(乘客到站时间分布).因此，暂不对所生成乘客个体的空间结构(目的站选择)进行分析，乘客的目的车站可根据式(3)确定.

假设仿真系统中需求生成时间粒度为1 min，已知30 min粒度的短时OD矩阵预测结果，即30 min内进入某站的客流量.选取卡尔曼滤波模型进行进站量短时预测(5 min时间粒度)，采用式(4)计算子时段内需求分配比例，再利用式(5)(6)生成子时段内到达客流量.将生成的需求到达分布与实际AFC记录统计结果进行对比分析.

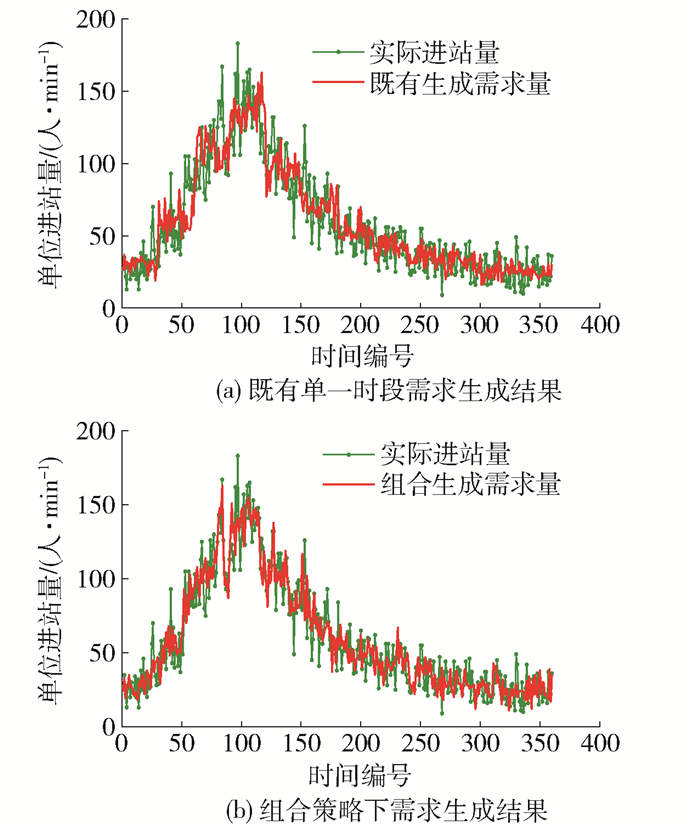
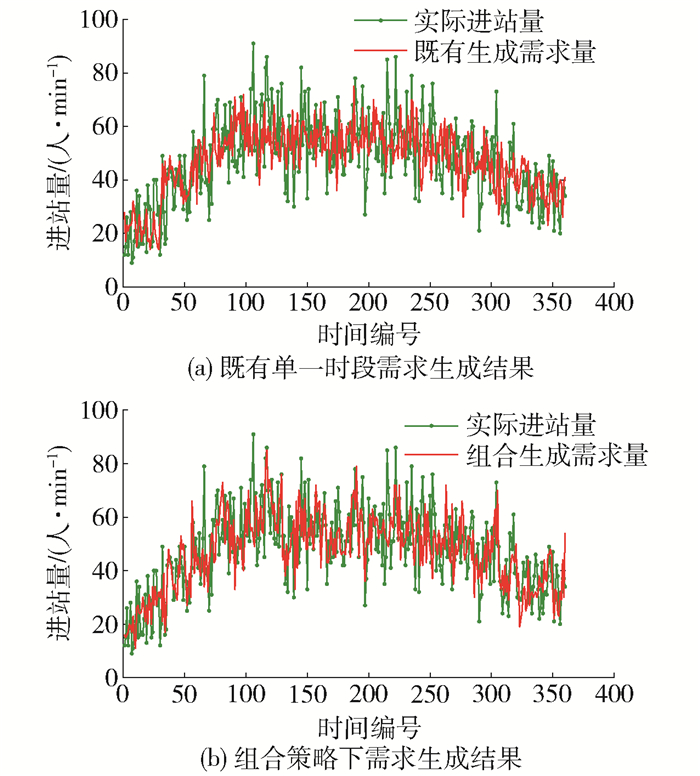
图 8、9分别给出了工作日、周末需求生成结果与实际AFC数据统计结果的对比情况，可以看出，基于组合策略的需求生成过程能够较好地贴近实际客流到达过程，而既有单一时段需求生成曲线呈现明显的阶梯跳跃特征.

图  8  需求生成结果对比(工作日)

Figure  8.  Results of demand generation for weekday

下载: 全尺寸图片 幻灯片

图  9  需求生成结果对比(周末)

Figure  9.  Results of demand generation for weekend

下载: 全尺寸图片 幻灯片

表 2给出了不同生成策略与实际统计结果的平均相对误差.可以看出：对比既有单一时段需求生成方法，组成需求生成策略与实际客流的吻合度平均提高22.89%，因此，所构建方法能较大幅度提高需求生成精度.需求生成结果作为动态客流分配的输入，其精度提高必将对断面流预测精度提升起到积极作用.

表  2  生成需求量与实际需求量平均相对误差

Table  2.  Relative deviations between generation and real demand

%
分析日	既有生成	组合生成	误差变化
工作日	47.76	23.36	-24.40
周末	48.16	26.78	-21.38
均值	47.96	25.07	-22.89

下载: 导出CSV 

| 显示表格

4.   结论

1) 本文针对轨道交通断面流在线仿真预测系统中的需求生成问题展开研究.通过融合进站量预测，构建了组合需求生成策略，有效解决了输入OD矩阵时段跨度与需求生成时间粒度的不一致问题，提高了需求生成过程与实际客流到达规律间的吻合度.

2) 北京地铁实证分析表明，所构建策略具有良好的时效性与准确性，认为在进行进站量预测时卡尔曼滤波模型效果最佳；通过生成需求量与实际AFC统计结果对比，显示所构建策略与实际客流的吻合度平均提高22.89%.

3) 城市轨道交通路网断面流短时在线预测是一项极具挑战的研究，目前很多问题尚未有效解决.提高断面客流预测精度需从多方面考虑，本研究仅针对预测系统中的需求生成问题展开，后续可针对短时OD矩阵实时估计、预测与校准以及精细化动态客流分配展开进一步研究.