Accelerating CNN Models for Face Verification With Convolution Theorem
-
摘要:
针对人脸验证系统中复杂卷积神经网络(convolutional neural network,CNN)模型的计算负担大、运算速度慢的问题,提出使用卷积定理来加速人脸特征提取中的CNN卷积层计算,从而提升人脸验证的速度.卷积定理中,空域中的卷积运算等价于频域中的乘积运算.将耗时的卷积计算转化为频域中的乘积计算后,可能会显著减少计算量,且无精度损失.分析了用卷积定理计算卷积的时间复杂度,给出了卷积定理加速的适用条件.在进行傅里叶变换后,详细探讨了如何高效、并行地计算频域中的乘积求和,以便利用现有的并行线性代数运算库,充分发挥图形处理单元(graphics processing uni,GPU)的并行计算能力.实验结果表明:该方法对人脸验证取得了明显的加速效果,具有一定实用价值.
Abstract:In order to alleviate the computational burden of large CNN (convolutional neural network) models in current face verification systems, convolution theorem was proposed, which suggested that convolution in the spatial domain was equivalent to product in the frequency domain, to speed up the convolutional layers in CNN, and consequently accelerate face verification systems. By transforming time-consuming convolutions into product operations in the frequency domain, much computation was saved without loss of accuracy. The computational complexities of convolution by using the convolution theorem and the direct computation were compared, and the conditions under which acceleration can be achieved by convolution theorem were given. After Fourier transform, the way of fulfillment of the product/sum operations in parallel was explored in detail, with the goal to fully utilize the power of GPU (graphics processing unit). Results show that the proposed algorithm has achieved apparent speedups for some recent face verification models, demonstrating its effectiveness.
-
人脸验证是目前计算机视觉中的一个热点研究方向,目标是判断2张人脸图片是否为同一个人,是一个二分类的模式识别问题.人脸验证系统由人脸图像预处理、特征提取、分类器等3部分组成,典型流程如下:先通过定位面部关键点来进行人脸图像裁剪,然后使用卷积神经网络(convolutional neural network,CNN)提取人脸特征,再使用余弦来度量2个人脸特征向量的相似性,并使用支持向量机(support vector machine,SVM)等分类器来进行验证分类.人脸验证技术在很多场景中有着广泛应用,比如登陆验证、身份识别等.
最近几年,由于CNN在图像识别领域应用的巨大成功,陆续有一些学者和机构尝试将CNN应用于人脸验证领域,以取得更高的正确率. Sun等提出的DeepID[1]使用大规模人脸数据集来训练CNN,将CNN的输出作为人脸特征,并据此特征进行分类. DeepID也组合了多个CNN来提取特征. DeepID2[2]在DeepID的基础上改进了训练方法,联合分类和验证2个目标来训练CNN. DeepID2+[3]则进一步改进了训练方法. DeepID3[4]使用了更深层的CNN,在LFW数据集[5]上正确率达到99.53%. VGG FACE[6]介绍了一种收集大规模人脸数据的方法,研究了不同的CNN结构、训练数据集以及预处理方法等对人脸验证性能的影响,最终在LFW数据集上取得了99.13%的正确率. FaceNet[7]不使用CNN中某一层的输出作为特征表示,而是学习一个从图像到欧式空间的编码方法,并根据编码进行人脸验证,在LFW数据集上的正确率达到了99.63%. DeepFace[8]提出使用3D对齐方法来预处理人脸图像. CASIA-WebFace[9]和MegaFace[10]提供了公开的大规模人脸数据库,可用于训练人脸验证的CNN模型.
上述工作主要是提出了新的网络结构、训练方法、特征表示方法,或者新的人脸预处理方法等,并构建了大规模人脸图像数据集进行训练,首要目的是提升模型在LFW数据集上的测试正确率.但另一方面,为了提高正确率,人脸验证算法中CNN模型的层数不断加深,参数不断增多,用以提升模型的拟合能力.这些复杂的CNN模型导致的一个主要问题是计算负担很大,尽管使用图形处理单元(graphics processing unit,GPU)等高速计算设备,人脸验证系统的速度仍有待改进.与此同时,实际应用中有海量的人脸数据需要进行处理,并且很多场景中要求人脸验证的实时性.因此,在基于CNN的人脸验证算法研究中,除了不断提升人脸验证的正确率外,加快人脸验证的速度也是非常必要的.
对于人脸验证系统的加速,目前主要有3个研究方向.一个方向是对CNN网络结构进行改进,在保持很高正确率的前提下,简化CNN结构,从而减少网络参数. Wu等提出了轻型人脸CNN模型[11],网络参数大幅减少. Sun等提出的Sparse ConvNets[12]在训练完毕的复杂CNN模型基础上,逐层减少神经元间的连接并重新训练,使得CNN结构变得稀疏.另一个方向是采用并行计算设备来加速CNN计算. Caffe[13]等主流CNN框架利用GPU具有众多运算核心的特点来加速计算,比CPU实现快几十倍[14]. NVIDIA公司的cuDNN[15]基于对GPU架构特点的充分了解,高度优化CNN实现代码,进一步提升了计算效率. Ferry等[16]采用FPGA平台来并行实现CNN模型.最后一种加速CNN的方法是采用卷积定理来计算卷积.卷积层的计算量约占整个CNN计算量的90%~95%[17],因此,加速卷积计算可以达到显著加速CNN的目的. Dubout等[18]曾在目标检测问题上提出使用卷积定理来加速卷积计算,但只有CPU加速版本. Vasilache等提出了fbfft[19],在GPU上应用卷积定理完成卷积加速,在某些条件下取得较高的加速比.
本文提出使用卷积定理来加速人脸验证算法中的CNN卷积层计算,从而提升人脸验证中特征提取的速度.卷积层是整个CNN结构中最耗时的环节,因此,加速CNN的关键就是加速卷积层的计算.卷积定理表明,空域中的卷积等价于频域中的乘积.将耗时的卷积计算转化为频域中的乘积计算后,可能会显著减少计算量,且无精度损失.尽管卷积定理在信号处理和图像处理学科中应用广泛,在如何并行实现卷积运算方面也有较多工作,但在深度学习的背景下,分析哪些CNN模型能用卷积定理来实现加速,如何在现有GPU平台上高效、并行地计算频域中的乘积求和(由于深度学习中每一层往往有多个输入通道,除了传统卷积定理中频域的乘积运算外,还存在频域中的求和运算,详见1.1),以及实际的CNN加速效果到底有多大等,这些问题在传统的信号处理和图像处理中并无现成答案,相关工作在深度学习中也才刚刚开始.因此,对这些问题的研究仍然具有一定理论意义和重要实用价值,也是本文的主要研究内容.
本文首先分析了卷积定理计算卷积的时间复杂度,并给出了CNN中卷积层能获得加速的条件,然后详细阐述了卷积定理计算卷积的算法原理与流程.在傅里叶变换转换到频域后,问题就转变为如何高效、并行地计算频域中的乘积求和.因此,利用卷积定理计算卷积的主要工作和难度体现在并行实现方法上.不同的并行实现方法,比如并行度的大小不同以及是否采用GPU共享内存等,有可能产生明显不同的加速效果.如何高效地并行计算频域中的乘积求和并非一目了然,需要对GPU平台有深入的了解和一定的优化技巧.本文的思路是利用GPU厂商提供的高度优化过的并行线性代数运算库,通过一些技巧将频域中的乘积求和计算转换为矩阵乘积,以便充分利用现有GPU运算库的并行优化,而无须从零开始实现GPU并行.最后,本文将卷积定理加速应用于人脸验证问题上.实验结果表明:本文方法对一个近期的人脸验证CNN模型[11]可加速约2.2倍,对另一相关的复杂模型VGG FACE[6]可加速约13.2倍.
1. 计算复杂度的分析
下面从计算时间复杂度的角度比较标准卷积计算方法和采用卷积定理计算卷积的方法. 表 1定义了本文所使用的符号.
表 1 本文所使用符号Table 1. Symbols used in this paper符号 含义 x 输入图像 w 卷积核 S 批量输入图像数量 K 输入图像通道数量 L 卷积核数量 M 输入图像尺寸 P 卷积核尺寸 Q 输入图像扩展尺寸 Q′ 卷积核扩展尺寸 1.1 标准卷积计算的时间复杂度
在CNN中,输入图像和卷积核一般都为正方形.尺寸为M×M的输入图像x和尺寸为P×P的卷积核w的二维离散卷积表示为x*w,其第m行第n列的元素定义为
$$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}\left( {m,n} \right) = \left( {\mathit{\boldsymbol{x}} * \mathit{\boldsymbol{w}}} \right)\left( {m,n} \right) = }\\ {\sum\limits_{i = 0}^{P - 1} {\sum\limits_{j = 0}^{P - 1} {\mathit{\boldsymbol{x}}\left( {m + i,n + i} \right)\mathit{\boldsymbol{w}}\left( {P - 1 - i,P - 1 - j} \right)} } ,}\\ {\left( {m,n = 0,1,2, \cdots ,M - P} \right)} \end{array} $$ (1) 在CNN的各个卷积层中,每一批数据可能会有多幅输入图像,而每幅输入图像可能有多个通道,此外卷积核一般也有多个.此时,第s幅输入图像与第l个卷积核的卷积定义为
$$ \begin{array}{l} {\mathit{\boldsymbol{y}}_{s,l}} = \sum\limits_{k = 0}^{K - 1} {{\mathit{\boldsymbol{x}}_{s,k}} * {\mathit{\boldsymbol{w}}_{l,k}}} ,\\ \left( {s = 0,1,2, \cdots ,S - 1;l = 0,1,2, \cdots ,L - 1} \right) \end{array} $$ (2) 与式(1)相比,式(2)中多了对通道的求和.标准的卷积计算方法是采用四重循环嵌套来计算式(1),其计算时间复杂度为
$$ {C_{{\rm{std}}}} \approx {M^2}{P^2} $$ (3) 若CNN的一个卷积层有K个输入通道和L个卷积核,则单幅图像卷积计算的时间复杂度为
$$ \begin{array}{l} {C_{{\rm{std}}\_{\rm{layer}}}} \approx KL{C_{{\rm{std}}}} \end{array} $$ (4) 由于多重循环计算卷积的效率较低,为了充分利用并行计算资源,Caffe将标准卷积计算过程转化为2个矩阵相乘[20],矩阵尺寸分别为(M×M, P×P×K)和(L, P×P×K),但卷积计算的时间复杂度并未改变.
1.2 用卷积定理计算卷积的时间复杂度
除了根据卷积定义直接计算卷积外,还可以根据卷积定理计算卷积.卷积定理是指空域中的卷积运算等价于频域中的乘积运算,即
$$ \mathit{\boldsymbol{x}} * \mathit{\boldsymbol{w}} = {F^{ - 1}}\left( {F\left( \mathit{\boldsymbol{x}} \right) \circ \left( {F\left( \mathit{\boldsymbol{w}} \right)} \right)} \right) $$ (5) 式中:F为傅里叶变换;F-1为傅里叶反变换;º为对应频域元素的乘积操作.运用上述卷积定理,可由式(2)得到
$$ F\left( {{\mathit{\boldsymbol{y}}_{s,l}}} \right) = \sum\limits_{k = 0}^{K - 1} {F\left( {{\mathit{\boldsymbol{x}}_{s,k}}} \right) \circ F\left( {{\mathit{\boldsymbol{w}}_{l,k}}} \right)} $$ (6) 以分量形式表示时,第m行和第n列处的结果为
$$ \begin{array}{*{20}{c}} {F\left( {{\mathit{\boldsymbol{y}}_{s,l}}} \right)\left( {m,n} \right) = }\\ {\sum\limits_{k = 0}^{K - 1} {F\left( {{\mathit{\boldsymbol{x}}_{s,k}}} \right)\left( {m,n} \right) \cdot F\left( {{\mathit{\boldsymbol{w}}_{l,k}}} \right)\left( {m,n} \right)} } \end{array} $$ (7) 快速傅里叶变换(fast Fourier transform, FFT)的时间复杂度约为[21]
$$ {C_{{\rm{FFT}}}} \approx 2.5{M^2}{\log _2}{M^2} $$ (8) 频域乘积的时间复杂度为
$$ {C_{{\rm{mul}}}} \approx 4{M^2} $$ (9) 式(9)中的系数4是因为傅里叶变换后有实部和虚部.采用卷积定理来计算卷积,需要进行输入图像和卷积核的傅里叶变换、频域乘积以及乘积结果的傅里叶反变换等操作.对单个输入通道和单个卷积核的情形,采用卷积定理计算卷积的时间复杂度为
$$ {C_{{\rm{conv}}}} \approx 3{C_{{\rm{FFT}}}} + {C_{{\rm{mul}}}} $$ (10) 在实际应用时,采用训练完毕的CNN来提取人脸特征,其卷积核的数值已固定,因此,卷积核的快速傅里叶变换(fast Fourier transform,FFT)可以事先计算好,从而将其从时间复杂度中去除.综合起来,对一个有K个输入通道和L个卷积核的卷积层,采用卷积定理对单幅图像进行卷积计算的时间复杂度为
$$ {C_{{\rm{conv}}\_{\rm{layer}}}} \approx K{C_{{\rm{FFT}}}} + L{C_{{\rm{FFT}}}} + KL{C_{{\rm{mul}}}} $$ (11) 通过Cstd_layer和Cconv_layer的对比可得出,当K+L≪KL时,采用卷积定理计算卷积能显著减少计算量.此外,采用卷积定理计算卷积的时间复杂度与卷积核尺寸P无关,这说明卷积核尺寸较大的卷积层采用卷积定理计算能获得更高的加速比.作为一个例子,选取卷积层中常见的一组参数取值:M=60,K=64,L=96,P=9,由式(4)(11)可算出,采用卷积定理计算卷积可以获得约17倍的理论加速比.
2. 采用卷积定理计算卷积的算法流程
2.1 输入图像和卷积核的尺寸扩充
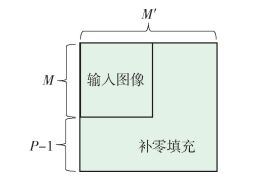
由于卷积层中输入图像和卷积核的尺寸通常不相等,为了应用卷积定理计算卷积,首先要将输入图像和卷积核扩充至相同尺寸.为了避免因为周期性问题而导致的混淆错误,扩充尺寸M′要求满足
$$ M' \ge M + P - 1 $$ (12) 扩充后在原数据右下方补零填充,如图 1所示.
类似于Caffe,本文采用四维数组来存储卷积层的输入和输出.假设卷积层的输入x的各维尺寸为S×K×M×M,则尺寸扩充操作可表示为
$$ {\mathit{\boldsymbol{x}}_{S \times K \times M \times M}}\xrightarrow{{扩充}}{{\mathit{\boldsymbol{x'}}}_{S \times K \times \left( {M + Q} \right) \times \left( {M + Q} \right)}} $$ (13) 卷积核w的尺寸为L×K×P×P,尺寸扩充操作为
$$ {\mathit{\boldsymbol{w}}_{L \times K \times P \times P}}\xrightarrow{{扩充}}{{\mathit{\boldsymbol{w'}}}_{L \times K \times \left( {P + Q'} \right) \times \left( {P + Q'} \right)}} $$ (14) 输入图像和卷积核延拓后尺寸相同,即
$$ M + Q = P + Q' $$ 2.2 输入图像和卷积核的傅里叶变换
利用傅里叶变换将图像从空域变换至频域时,根据Hermitian对称性,傅里叶变换后的数据存在一半的冗余,因此,只需存储和计算一半数据,从而可减少计算量.对图像进行傅里叶变换
$$ {{\mathit{\boldsymbol{x'}}}_{S \times K \times \left( {M + Q} \right) \times \left( {M + Q} \right)}}\xrightarrow{{{\rm{FFT}}}}{{\mathit{\boldsymbol{x''}}}_{S \times K \times \left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right)}} $$ (15) 对卷积核进行傅里叶变换,得到
$$ {{\mathit{\boldsymbol{w'}}}_{L \times K \times \left( {P + Q'} \right) \times \left( {P + Q'} \right)}}\xrightarrow{{{\rm{FFT}}}}{{\mathit{\boldsymbol{w''}}}_{L \times K \times \left( {P + Q'} \right) \times \left( {\left\lfloor {\frac{{P + Q'}}{2}} \right\rfloor + 1} \right)}} $$ (16) 本文采用NVIDIA公司的CUDA软件包所提供的cuFFT库来实现傅里叶变换.
2.3 频域中的乘积求和计算
对式(7)所示的频域中的乘积求和,直接的方法是采用循环嵌套进行计算,但无疑效率较低.为了充分利用GPU的并行计算能力,本文采用矩阵相乘来完成频域中的乘积求和计算.由式(7)可见,当只考察单个像素位置(m, n)时,如果把在(m, n)处的所有输入图像的所有通道的F(xs, k)(即xs, k″)值组成一个矩阵A,其行数和列数分别为S和K,再把(m, n)处的所有卷积核的所有通道的wl, k″值组成另一个矩阵B,其行数和列数分别为L和K,则用矩阵乘积A·BT就可以一次性求出所有S个输入图像和所有L个卷积核在(m, n)处的卷积结果.矩阵乘法可以通过GPU上的cuBLAS并行线性代数计算库来实现,且不同像素位置处的矩阵乘积计算可以成批进行,从而可以高效地完成频域中的乘积求和计算.
为了用cuBLAS库来实现矩阵相乘,在将同一像素位置处的{xs, k″ (m, n)|s=0, 1, 2, …, S-1;k=0, 1, 2, …, K-1}组成一个矩阵时,需要它们在内存中连续存储.但在完成傅里叶变换后,x″是以行为主存储的,即在内存中依次按(s, k, m, n)的次序存储,先存储第0幅图像第0通道的各个傅里叶系数值,之后存储第0幅图像第1通道的各个傅里叶系数值,依次类推;因此,在内存中{xs, k″ (m, n)|s=0, 1, 2, …, S-1;k=0, 1, 2, …, K-1}并不连续存储,需要先将数据重新排列,使其转换为在内存中以(m, n, s, k)的次序来存储,从而{xs, k″ (m, n)|s=0, 1, 2, …, S-1;k=0, 1, 2, …, K-1}变为连续存储.
综上所述,频域中的乘积求和计算包括3个步骤:输入图像和卷积核数据的重排列,批量矩阵相乘及乘积结果反重排列.
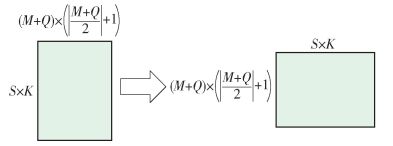
数据重排列可以通过矩阵转置来实现.以x″为例,将x″的四维数组看作一个矩阵,前两维(s, k)和后两维(m, n)分别作为矩阵的行和列.将x″进行矩阵转置后得到x''',则x'''的每行(m, n)对应于该像素位置处的{xs, k″|s=0, 1, 2, …, S-1;k=0, 1, 2, …, K-1}集合.在以行为主存储时矩阵中每行的数据是连续存储的,因此,{xs, k″ (m, n)|s=0, 1, 2, …, S-1;k=0, 1, 2, …, K-1}将连续存储.上述数据重新排列过程如图 2所示.
输入图像的重排列可表示为
$$ {{\mathit{\boldsymbol{x''}}}_{S \times K \times \left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right)}}\xrightarrow{{重排列}}{{\mathit{\boldsymbol{x'''}}}_{\left( {M + Q} \right)\left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right)SK}} $$ (17) 卷积核的重排列表示为
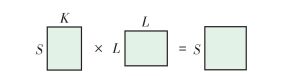
$$ {{\mathit{\boldsymbol{w''}}}_{LK \times \left( {P + Q'} \right)\left( {\left\lfloor {\frac{{P + Q'}}{2}} \right\rfloor + 1} \right)}}\xrightarrow{{重排列}}{{\mathit{\boldsymbol{w'''}}}_{\left( {P + Q'} \right)\left( {\left\lfloor {\frac{{P + Q'}}{2}} \right\rfloor + 1} \right)LK}} $$ (18) 在完成数据重排列后,将w'''的(m, n)处后两维(s, k)看作一个大小为(S, K)的矩阵,w'''的(m, n)处后两维(l, k)看作另一个大小为(L, K)的矩阵,进行矩阵相乘,如图 3所示.如此便完成了(m, n)像素位置处的频域乘积求和计算.
将矩阵乘积运算对(M+Q)·((M+Q)/2+1)个像素进行重复,便完成了全部数据的频域乘积求和计算,即
$$ \begin{gathered} {{\mathit{\boldsymbol{x'''}}}_{\left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right) \times S \times K}}\xrightarrow{{乘积求和}} \hfill \\ {{\mathit{\boldsymbol{w'''}}}_{\left( {P + Q'} \right) \times \left( {\left\lfloor {\frac{{P + Q'}}{2}} \right\rfloor + 1} \right) \times L \times K}} \hfill \\ \;\;\;\;\;\;{\mathit{\boldsymbol{y}}_{\left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right) \times S \times L}} \hfill \\ \end{gathered} $$ (19) 式中y为乘积计算后的结果.最后将y进行反重排列操作,即
$$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_{\left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right) \times S \times L}}\xrightarrow{{反重排列}}} \\ {{{\mathit{\boldsymbol{y'}}}_{S \times L \times \left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right)}}} \end{array} $$ (20) 2.4 傅里叶反变换
对y′进行傅里叶反变换前,先根据Hermitian对称性填充另一半数据,然后再做傅里叶反变换,得到
$$ {{\mathit{\boldsymbol{y'}}}_{S \times L \times \left( {M + Q} \right) \times \left( {\left\lfloor {\frac{{M + Q}}{2}} \right\rfloor + 1} \right)}}\xrightarrow{{{\rm{IFFT}}}}{{\mathit{\boldsymbol{y''}}}_{S \times L \times \left( {M + Q} \right) \times \left( {M + Q} \right)}} $$ (21) 2.5 输出结果的裁剪
由于在进行傅里叶变换前,将输入图像和卷积核的尺寸都进行了扩充,所以,需要对计算结果的右下方进行裁剪.由卷积的定义式(1)中(m, n)的取值范围可以看出,应保留尺寸为M-P+1,即
$$ {{\mathit{\boldsymbol{y''}}}_{S \times L \times \left( {M + Q} \right) \times \left( {M + Q} \right)}}\xrightarrow{{{\rm{Crop}}}}{{\mathit{\boldsymbol{y'''}}}_{S \times L \times \left( {M - P + 1} \right) \times \left( {M - P + 1} \right)}} $$ (22) y'''即为卷积运算的最终结果.
3. 进一步优化
3.1 多个卷积层间的缓存共享
应用卷积定理计算卷积时,需要对输入图像和卷积核的尺寸进行扩充,因此,需要额外的缓存空间.每个卷积层的参数不同,需要的缓存空间大小也不同.为了避免消耗过多内存,在初始化时离线计算出各卷积层需要的缓存空间,一次性分配其中的最大值.在运行时各卷积层共用这一块缓存区域,而不再为它们单独分配缓存,以此节省内存.
3.2 卷积核的FFT变换的离线计算
完成训练后,卷积核的数值将不再改变,因此,可以预先进行各卷积层的卷积核尺寸扩充和傅里叶变换计算,并将结果保存起来留待测试时使用,从而节约计算时间.
3.3 卷积定理的择优使用
预先分别用卷积定理和直接方法计算各个卷积层的用时.运行时,各卷积层只有在卷积定理计算快于直接方法的情况下才采用卷积定理进行加速.
4. 实验结果
本节分别利用卷积定理计算卷积方法和Caffe卷积计算方法来进行CNN前向运算,以验证卷积定理计算方法的加速效果.
4.1 实验环境
本文采用的实验环境为:CPU为I5-4200H,GPU为GTX 860M,CUDA为7.0版.图像和卷积核都采用float类型,在测试速度时,每幅图像的像素值随机生成. 4.2中每批输入图像的数量为32,4.3中每批输入图像的数量为8,共输入1 000批图像进行实验.
4.2 用卷积定理计算卷积的速度和精度
1.2中已经分析过,当选取M=60,K=64,L=96,P=9等参数值时,采用卷积定理计算卷积可以获得约17倍的理论加速比.下面将给出相对于Caffe卷积计算方法的实际加速比.本文实验得到2种方法的总用时如下:用卷积定理计算卷积方法用时32.645 s,用Caffe卷积计算方法计算卷积用时281.131 s.由此得到实际加速比为8.61,表明采用卷积定理计算卷积能获得较高的加速比.实际加速比低于理论加速比的主要原因在于,时间复杂度公式中的系数只是估计值,以及卷积定理计算过程中数据扩充、裁剪等操作也存在耗时等.
为了验证卷积定理计算的正确性,本文也计算了卷积定理计算结果与Caffe卷积计算结果的误差平方和.实验中,卷积计算的输出共有8 306 688个元素,总误差平方和只有0.285.因此,卷积定理计算的结果正确,极小的误差是由于float类型数据的精度有限造成的.
4.3 人脸验证CNN模型的加速
选取文献[11]中的modelA CNN模型作为实验模型来测试本文方法的加速效果.选取modelA作为实验模型的主要原因如下:1) modelA是轻型CNN模型,与VGG FACE等网络相比参数大幅减少,运算速度较快. 2)卷积层中的卷积核尺寸较大,满足卷积定理加速条件. 3) modelA是单CNN模型,而非多CNN组合,从而适合用来测试单个CNN的加速效果. 4) modelA在LFW数据集上取得了97.77%的正确率,为单个CNN的当前顶尖水平. 5)训练完毕的modelA模型已经开源,可以在此基础上微调,节省训练时间. modelA的网络结构如表 2所示.
层名称 卷积核(池化)
尺寸/跨度输出尺寸(宽、高、
通道数)input 128×128×1 conv1 9×9/1 120×120×96 pool1 2×2/2 60×60×96 mfm1 60×60×48 conv2 5×5/1 56×56×192 pool2 2×2/2 28×28×192 mfm2 28×28×96 conv3 5×5/1 24×24×256 pool3 2×2/2 12×12×256 mfm3 12×12×128 conv4 4×4/1 9×9×384 pool4 2×2/2 5×5×384 mfm4 5×5×192 fc1 256 fc2 10 575 softmax 10 575 4.3.1 卷积层运算用时所占比重
对modelA网络进行前向运算,使用Caffe卷积计算方法,测量所有卷积层运算用时所占的比重,实验结果如下:卷积层用时60.478 s,网络总用时62.432 s,由此得到卷积层用时所占比重为96.87%.上述结果表明,卷积层为整个卷积神经网络中最为耗时的环节,对卷积层进行加速能有效提高整个网络的速度.
4.3.2 用卷积定理计算卷积的加速效果
分别采用卷积定理计算卷积方法和Caffe卷积计算方法,对modelA网络进行前向运算.各个卷积层的用时和总用时见表 3.
表 3 用卷积定理计算卷积的加速效果Table 3. Acceleration effect of computing convolutions with convolution theorem测量部分 用卷积定理
计算卷积的
用时/s用Caffe计算
卷积的
用时/s加速比 conv1 19.925 7.013 0.35 conv2 10.560 38.519 3.65 conv3 5.297 10.830 2.04 conv4 3.238 4.116 1.27 所有卷积层 39.020 60.478 1.55 整个网络 40.974 62.432 1.52 根据表 3中的实验结果,conv1卷积层用卷积定理无法获得加速,后3个卷积层则能获得明显加速.
若择优选择卷积计算方案,则第1个卷积层采用直接方法计算,后3个卷积层采用卷积定理计算,结果见表 4.
表 4 择优计算方案的加速效果Table 4. Acceleration effect of optimized scheme测量部分 择优计算
方案的
用时/sCaffe卷积
计算方法的
用时/s加速比 卷积层 26.108 60.478 2.32 整个网络 28.062 62.432 2.22 表 4中的结果表明,相较于单纯采用卷积定理计算卷积,择优计算方案能获得更高加速比.
4.3.3 与VGG FACE模型的速度比较
VGG FACE[6]是一个复杂的相关人脸验证CNN模型.几种方法的用时比较见表 5.
表 5 与VGG FACE的速度对比Table 5. Speed comparison with VGG FACE方案 网络总用时/s 加速比 VGG FACE网络 371.596 modelA网络 62.432 5.95 modelA网络卷积
定理加速28.062 13.20 表 5表明,采用卷积定理对modelA网络加速后,比VGG FACE快13.2倍.
4.4 人脸验证正确率的改进
本文对文献[11]中modelA的人脸验证流程进行了改进,取得了更高的验证正确率. 表 6比较了几种不同方案的人脸验证正确率.表中后3种方案的流程类似,都采用CASIA-WebFace数据集来训练CNN.首先采用文献[22]中的算法进行面部关键点检测,完成人脸图像的裁剪等预处理.然后对modelA CNN进行微调,学习速率设置为0.000 05,迭代8个时期(epoch).微调后的模型称为modelA-finetune.最后将全连接层fc1的256维输出作为人脸特征,采用余弦相似度来度量特征差异,并使用SVM分类器来完成分类.本文采用LFW数据集进行测试,测试类型为:Unrestricted, Labeled Outside Data[5],采用十重交叉验证. LFW数据集采用与训练时一样的预处理过程.
表 6 几种人脸验证模型在LFW数据集上的正确率Table 6. Accuracies of several face verification models on LFW dataset测试方案 正确率/% 文献[11]中modelA 97.77 方案1:modelA+ cosine + SVM 97.62 方案2:modelA-finetune+ cosine + SVM 97.67 方案3:modelA-finetune+PCA+cosine+SVM 98.02 表 6中,方案1与文献[11]中modelA采用了一样的流程,它们之间正确率的少量差异应该是由不同的预处理细节导致的.方案2的正确率比方案1的有所提升,表明CNN模型的微调取得一定效果.方案3采用PCA算法将特征降至120维,然后再采用余弦相似度度量和SVM完成分类,使得验证正确率明显提升.
5. 结论
1) 本文提出用卷积定理计算卷积来加速人脸验证CNN模型.分析了用卷积定理计算卷积的时间复杂度,给出了卷积定理加速的适用条件.利用cuBLAS并行线性代数运算库,高效、并行地实现了频域中的乘积求和计算.
2) 实验结果表明,本文方法对近期的轻型人脸验证CNN模型可加速约2.2倍,比VGG FACE可加速约13.2倍.本文研究成果对人脸验证系统的加速具有一定实际意义.
-
表 1 本文所使用符号
Table 1 Symbols used in this paper
符号 含义 x 输入图像 w 卷积核 S 批量输入图像数量 K 输入图像通道数量 L 卷积核数量 M 输入图像尺寸 P 卷积核尺寸 Q 输入图像扩展尺寸 Q′ 卷积核扩展尺寸 层名称 卷积核(池化)
尺寸/跨度输出尺寸(宽、高、
通道数)input 128×128×1 conv1 9×9/1 120×120×96 pool1 2×2/2 60×60×96 mfm1 60×60×48 conv2 5×5/1 56×56×192 pool2 2×2/2 28×28×192 mfm2 28×28×96 conv3 5×5/1 24×24×256 pool3 2×2/2 12×12×256 mfm3 12×12×128 conv4 4×4/1 9×9×384 pool4 2×2/2 5×5×384 mfm4 5×5×192 fc1 256 fc2 10 575 softmax 10 575 表 3 用卷积定理计算卷积的加速效果
Table 3 Acceleration effect of computing convolutions with convolution theorem
测量部分 用卷积定理
计算卷积的
用时/s用Caffe计算
卷积的
用时/s加速比 conv1 19.925 7.013 0.35 conv2 10.560 38.519 3.65 conv3 5.297 10.830 2.04 conv4 3.238 4.116 1.27 所有卷积层 39.020 60.478 1.55 整个网络 40.974 62.432 1.52 表 4 择优计算方案的加速效果
Table 4 Acceleration effect of optimized scheme
测量部分 择优计算
方案的
用时/sCaffe卷积
计算方法的
用时/s加速比 卷积层 26.108 60.478 2.32 整个网络 28.062 62.432 2.22 表 5 与VGG FACE的速度对比
Table 5 Speed comparison with VGG FACE
方案 网络总用时/s 加速比 VGG FACE网络 371.596 modelA网络 62.432 5.95 modelA网络卷积
定理加速28.062 13.20 表 6 几种人脸验证模型在LFW数据集上的正确率
Table 6 Accuracies of several face verification models on LFW dataset
测试方案 正确率/% 文献[11]中modelA 97.77 方案1:modelA+ cosine + SVM 97.62 方案2:modelA-finetune+ cosine + SVM 97.67 方案3:modelA-finetune+PCA+cosine+SVM 98.02 -
[1] SUN Y, WANG X, TANG X. Deep learning face representation from predicting 10, 000 classes[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC:IEEE Computer Society, 2014:1891-1898.
[2] SUN Y, WANG X, TANG X. Deep learning face representation by joint identification-verification[J]. Advances in Neural Information Processing Systems, 2014, 27:1988-1996. http://www.wenkuxiazai.com/doc/4548d917f7ec4afe04a1dfed-2.html
[3] SUN Y, WANG X, TANG X. Deeply learned face representations are sparse, selective, and robust[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Washinpton, DC:IEEE Computer Society, 2015:2892-2900.
[4] SUN Y, LIANG D, WANG X, et al. Deepid3:face recognition with very deep neural networks[J/OL].[2016-07-10]. https://arxiv.org/abs/1502.00873.
[5] University of Massachusetts. LFW result[EB/OL].[2016-06-08]. http://vis-www.cs.umass.edu/lfw/results.html.
[6] PARKHI M, VEDALDI A, ZISSERMAN A. Deep face recognition[C]//Proceedings of British Machine Vision Conference 2015. London:BMVA Press, 2015:41.1-41.12
[7] SCHROFF F, KALENICHENKO D, PHILBIN J. FaceNet:a unified embedding for face recognition and clustering[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC:IEEE Computer Society, 2015:815-823.
[8] TAIGMAN Y, YANG M, RANZATO M, et al. DeepFace:closing the gap to human-level performance in face verification[C]//Proceddings of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC:IEEE Computer Society, 2014:1701-1708.
[9] YI D, LEI Z, LIAO S, et al. Learning face representation from scratch[J/OL].[2016-07-10]. https://arxiv.org/abs/1411.7923.
[10] MILLER D, BROSSARD E, SEITZ S, et al. MegaFace:a million faces for recognition at scale[J/OL].[2016-07-20]. https://arxiv.org/abs/1505.02108.
[11] WU X, HE R, SUN Z. A lightened CNN for deep face representation[J/OL].[2016-07-20]. https://arxiv.org/abs/1511.02683.
[12] SUN Y, WANG X, TANG X. Sparsifying neural network connections for face recognition[J/OL].[2016-07-20]. https://arxiv.org/abs/1512.01891.
[13] JIA Y. Caffe project[CP/OL].[2016-07-10]. http://caffe.berkeleyvision.org/.
[14] STRIGL D, KOFLER K, PODLIPNIG S. Performance and scalability of GPU-based convolutional neural networks[C]//Proceddings of the 2010 Euromicro International Conference on Parallel, Distributed, and Network-Based Processing. Piscataway:IEEE, 2010:317-324.
[15] Nvidia Company. cuDNN project[CP/OL].[2016-07-20]. https://developer.nvidia.com/cudnn/.
[16] FERRY C. Hardware accelerated convolutional neural networks for synthetic vision systems[C]//IEEE International Symposium on Circuits and Systems. Piscataway:IEEE, 2010:257-260.
[17] KRIZHEVSKY A. One weird trick for parallelizing convolutional neural networks[J/OL].[2016-07-20]. https://arxiv.org/abs/1404.5997.
[18] DUBOUT C, FLEURET F. Exact acceleration of linear object detectors[C]//Proceedings of the European Conference on Computer Vision. Berlin:Springer International Publishing, 2012:301-311.
[19] VASILACHE N, JOHNSON J, MATHIEU M, et al. Fast convolutional nets with fbfft:a GPU performance evaluation[J/OL].[2016-07-20]. https://arxiv.rg/abs/1412.7580.
[20] CHELLAPILLA K, PURI S, SIMARD P. High performance convolutional neural networks for document processing[C]//Proceedings of the Tenth International Conference on Frontiers in Handwriting Recognition. Washington, DC:IEEE Computer Society, 2006:1-6.
[21] FRIGO M, JOHNSON G. The design and implementation of FFTW3[J]. Proceedings of the IEEE, 2005, 93(2):216-231. doi: 10.1109/JPROC.2004.840301
[22] SUN Y, WANG X, TANG X. Deep convolutional network cascade for facial point detection[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC:IEEE Computer Society, 2013:3476-3483.
-
期刊类型引用(2)
1. 刘海,张昊,崔国旭,李洪亮,景国玺,何悦波. TGDI汽油机噪声源时域分离方法研究. 内燃机学报. 2023(02): 158-165 .  百度学术
百度学术
2. 李博,江朝晖,谢军,饶元,张武. 基于迁移学习的园艺作物叶部病害识别及应用. 中国农学通报. 2021(07): 138-143 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: