Objective Segmentation Based on Shape Prior and Contour Pre-positioning
-
摘要:
针对单帧图像中特定目标的分割一直面临着由于背景复杂和光照变化等因素带来的分割精度偏低的问题,提出一种基于轮廓预定位的先验局部二值拟合(local binary fitting,LBF)算法,用于人体上肢图像的分割.首先,利用浅层卷积神经网络对上肢形状模板进行筛选和预定位,得到分割目标的粗轮廓曲线;然后,利用基于先验形状的LBF算法对粗轮廓曲线进行演化,得到分割目标的精确轮廓曲线.实验结果显示算法的成功率在90%以上,表明该方法对于背景复杂和光照变化情况下的特定目标分割具有良好的效果.
-
关键词:
- 上肢图像分割 /
- 轮廓预定位 /
- 局部二值拟合(local binary fitting, LBF) /
- 形状先验
Abstract:The segmentation of a specific object in a single frame image has been faced with the problem of low segmentation accuracy due to background complexity and illumination variation. In this paper, a shape prior local binary fitting (LBF) based on contour pre-positioning was proposed for segmentation of human upper-limb images. Firstly, the upper-limb contour template was selected and pre-positioned by a kind of shallow convolutional neural network, and the coarse contour was obtained. Then, the LBF algorithm based on a prior shape was used to evolve the coarse contour, and the precise contour was obtained. Experimental results show that the success rate of the algorithm is over 90%, which shows that the method has good effect on the segmentation of a specific object in a single frame image faced with background complexity and illumination variation.
-
脑卒中通常被称为“中风”,是指由急性脑血管疾病引起的持续性的大脑神经功能缺损,患病者中有85%引起偏瘫症状,尤其在老年人中居多[1].如何帮助中风患者恢复肢体运动功能,重新获得独立生活的能力是一项非常具有现实意义的课题.目前的传统康复训练面临很多问题,如康复训练师资源匮乏,训练方式单调、缺乏趣味性,训练动作的准确性和效果无量化标准等.智能运动康复设备是一个机器人科学与康复医学相结合的研究领域,目的是为肢体功能障碍患者提供辅助康复训练,同时承载着解决传统康复训练中诸多问题的任务.
在智能康复设备的研究领域中,如何将感兴趣区域(如人体上肢)从单帧图像中精确分割出来是一个重要的问题,为患者的患肢定位和病情诊断奠定了基础.图像分割一直是图像领域的经典难题,早期的图像分割算法主要是基于底层的图像数据信息(如灰度、边缘和纹理等),分割效果受遮挡、光照和背景的影响较大.要解决这个问题就需要结合高层的先验信息来辅助图像分割,其中利用先验形状信息就是一种有效的方法[2].
以活动轮廓模型[3](active contour model, ACM)为基础的一类算法,可以将先验形状作为一个约束项融合到能量模型中,能有效提高模型的分割精度.最早的活动轮廓模型就是snake模型[3],由于它以参数化形式来表达轮廓,导致其无法灵活处理曲线拓扑结构的变化.几何活动轮廓模型[4]和测地线活动轮廓模型[5]都是snake模型的拓展,它们将水平集函数引入到能量泛函中,有效解决了轮廓曲线拓扑结构的演变问题.但因其外部能量函数是基于边缘梯度信息,所以轮廓曲线很容易穿透弱边缘,造成分割失败. M-S模型[6]和CV模型[7]是利用区域信息来引导曲线向轮廓逼近,由于M-S模型过于复杂,并没有得到实际应用. CV模型简化了M-S模型,该模型适用于梯度有意义和无意义的轮廓检测,同时对弱边缘也有很好的分割效果.但其对灰度不均匀的图像分割结果不理想,并且在曲线的演化过程中需定期重新初始化零水平集的符号距离函数.
针对以上情况,本文提出一种针对局部二值拟合[8](local binary fitting,LBF)改进的先验轮廓模型,主要用于人体上肢的图像分割. LBF模型也是一种基于水平集的活动轮廓模型,有效解决了曲线演化过程中符号距离函数的重新初始化问题,并对灰度不均匀图像有很好的分割效果.但该方法非常依赖于初始轮廓位置,不当的初始轮廓会导致分割时间较长甚至分割失败.为了解决这一问题,本文提出了一种水平集初始轮廓预定位算法,使LBF模型在进行曲线演化之前,就有一个较好的初始轮廓,从而提高了整体模型的鲁棒性和收敛速度.
1. 人体上肢分割算法
1.1 LBF模型
1.1.1 模型介绍
考虑到局部图像信息在灰度不均匀图像分割中起的作用,Li等[8]于2007年提出了LBF模型. LBF模型引入了一种称之为局部二值拟合能量的泛函,代替了CV模型中的全局二值拟合能量.由于LBF有较高的分割精度,在当时引起了广泛的关注.
Li通过引入高斯核函数来定义局部二值拟合能量.用2个拟合函数f1(x)和f2(x)来拟合轮廓里和轮廓外的灰度值,以代替CV模型中的平均灰度值C1和C2. LBF的外部能量泛函定义为
$$ \begin{array}{*{20}{c}} {\varepsilon _x^{{\rm{LBF}}}\left( {\phi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = }\\ {{\lambda _1}\int_{{\rm{in}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_1}\left( x \right)} \right|}^2}{\rm{d}}y} + }\\ {{\lambda _2}\int_{{\rm{out}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_2}\left( x \right)} \right|}^2}{\rm{d}}y} } \end{array} $$ (1) 式中:K(x-y)为高斯核函数;I(y)为图像域Ω上的点;x为水平集轮廓Φ上的点;λ1和λ2为能量的权重系数;C为演化曲线.高斯核函数有局部性质且非负单减,当核函数值比较大时,点y接近点x,会对函数f1和f2的值有很大影响;相反,当核函数的值接近0时,点y远离点x,对函数f1和f2的值基本没有影响.
为了解决曲线C的拓扑结构变化问题,模型中引入了水平集函数. LBF能量泛函的水平集可表示为
$$ \begin{array}{*{20}{c}} {\varepsilon _x^{{\rm{LBF}}}\left( {\phi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = }\\ {{\lambda _1}\int_{{\rm{in}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_1}\left( x \right)} \right|}^2}H\left( \phi \right){\rm{d}}y} + }\\ {{\lambda _2}\int_{{\rm{out}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_2}\left( x \right)} \right|}^2}\left( {1 - H\left( \phi \right)} \right){\rm{d}}y} } \end{array} $$ (2) 为了避免水平集符号距离函数的周期性初始化,LBF应用了无需重新初始化符号距离函数的方法[9],在模型中加入了距离正则项, 使得水平集函数在演化的过程中始终满足符号距离函数的性质|Δφ(x)|=1.距离正则项为
$$ \mu \int_\mathit{\Omega } {\frac{1}{2}{{\left( {\left| {\nabla \phi \left( x \right)} \right| - 1} \right)}^2}{\rm{d}}x} $$ (3) 整合以上分析,最终Li提出的变分模型的水平集表达式为
$$ \begin{array}{*{20}{c}} {E_x^{{\rm{LBF}}}\left( {\phi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = }\\ {\varepsilon _x^{{\rm{LBF}}} + v\int_\mathit{\Omega } {\delta \left( {\phi \left( x \right)} \right)\left| {\nabla \phi \left( x \right)} \right|{\rm{d}}x + } }\\ {\mu \int_\mathit{\Omega } {\frac{1}{2}{{\left( {\left| {\nabla \phi \left( x \right)} \right| - 1} \right)}^2}{\rm{d}}x} } \end{array} $$ (4) 1.1.2 模型的数值解法
因为LBF模型的能量函数是一个泛函,所以要通过欧拉-拉格朗日方程推导出对应的梯度下降流来求解.当能量函数取得全局极小值时,所得的水平集轮廓就是所求轮廓.
先固定水平集函数Φ,利用变分法最小化能量泛函,得到f1(x)和f2(x)的表达式分别为
$$ {f_1}\left( x \right) = \frac{{K\left( x \right)\left[ {H\left( {\phi \left( x \right)} \right)I\left( x \right)} \right]}}{{K\left( x \right)H\left( {\phi \left( x \right)} \right)}} $$ (5) $$ {f_2}\left( x \right) = \frac{{K\left( x \right)\left[ {\left( {1 - H\left( {\phi \left( x \right)} \right)} \right)I\left( x \right)} \right]}}{{K\left( x \right)\left[ {1 - H\left( {\phi \left( x \right)} \right)} \right]}} $$ (6) 接下来固定f1(x)和f2(x),根据欧拉-拉格朗日方程推导出水平集的演化方程为
$$ \begin{array}{*{20}{c}} {\frac{{\partial \phi }}{{\partial t}} = v\delta \left( \phi \right){\rm{div}}\left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right) - \delta \left( \phi \right)\left( {{\lambda _1}{e_1} - {\lambda _2}{e_2}} \right) + }\\ {\mu \left( {{\nabla ^2}\phi - {\rm{div}}\left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right)} \right)} \end{array} $$ (7) 其中
$$ {e_1}\left( x \right) = \int_{{\rm{in}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_1}\left( x \right)} \right|}^2}{\rm{d}}y} $$ (8) $$ {e_2}\left( x \right) = \int_{{\rm{out}}\left( C \right)} {K\left( {x - y} \right){{\left| {I\left( y \right) - {f_2}\left( x \right)} \right|}^2}{\rm{d}}y} $$ (9) 1.1.3 分割结果
对于简单图形的分割结果如图 1所示.在复杂背景下,对人体上肢的分割结果如图 2所示.
可以看出,对于简单背景LBF模型的分割效果是很好的,但是对于复杂背景,分割效果就不尽人意了.
1.2 先验形状的表示及其与LBF模型的融合
LBF模型能够很好地分割灰度不均匀的图像,但是如果遇到复杂背景、遮挡、底层特征信息缺失等问题时,该模型很难达到预期的分割效果.在模型中加入形状先验信息能在一定程度上解决这些问题.最直接的做法就是在能量函数中加入一个形状能量项来约束曲线的演化.新的能量泛函可以表示为
$$ E = {E_{\rm{i}}} + \lambda {E_{\rm{p}}} $$ (10) 式中:Ei为原始的LBF模型;Ep为形状先验项;λ为先验项的在分割中所占的权重系数.
1.2.1 先验形状构建
Chan等[10]中提出用符号距离函数表示先验形状,并在CV模型中增加形状约束项,通过计算演化曲线与先验形状对应的水平集函数的Heaviside函数差来表示形状约束项的能量大小.该文章中的形状约束项的表达式为
$$ {E_{\rm{p}}}\left( \phi \right) = \int_\mathit{\Omega } {{{\left( {H\left( \phi \right) - H\left( {{\phi _0}} \right)} \right)}^2}{\rm{d}}x{\rm{d}}y} $$ (11) 本文也采用符号距离函数来表示人体上肢的形状样本.同时考虑到由于不同人的上肢形状和大小都略有区别,所以必须考虑先验形状的变化问题.这里考虑的形状变化是缩放、平移和旋转,可表述为
$$ \begin{array}{*{20}{c}} {\psi \left( {x,y} \right) = r{\psi _0}\left[ {\frac{{\left( {x - a} \right)\cos \theta + \left( {y - b} \right)\sin \theta }}{r},} \right.}\\ {\left. {\frac{{ - \left( {x - a} \right)\sin \theta + \left( {y - b} \right)\cos \theta }}{r}} \right]} \end{array} $$ (12) 式中:ψ0是形状模板库中的水平集函数;ψ为经过仿射变换后用于图像分割的水平集函数,a、b、r、θ为仿射变换参数,分别对应形状的水平平移、垂直平移、形状缩放和形状旋转.于是式(11) 可以写成
$$ {E_{\rm{p}}}\left( {\phi ,\psi } \right) = \int_\mathit{\Omega } {{{\left( {H\left( \phi \right) - H\left( \psi \right)} \right)}^2}{\rm{d}}x{\rm{d}}y} $$ (13) 1.2.2 模型的数值解法
形变模板ψ0进行仿射变换后的形状模板ψ的各仿射变换参数对应的梯度下降流公式分别为
$$ \begin{array}{*{20}{c}} {\frac{{\partial a}}{{\partial t}} = \int_\mathit{\Omega } {\left( {H\left( \psi \right) - H\left( \phi \right)} \right)\left[ {{\psi _{0x}}\left( {{x^ * },{y^ * }} \right)\cos \theta - } \right.} }\\ {\left. {{\psi _{0y}}\left( {{x^ * },{y^ * }} \right)\sin \theta } \right]\delta \left( \psi \right){\rm{d}}x{\rm{d}}y} \end{array} $$ (14) $$ \begin{array}{*{20}{c}} {\frac{{\partial b}}{{\partial t}} = \int_\mathit{\Omega } {\left( {H\left( \psi \right) - H\left( \phi \right)} \right)\left[ {{\psi _{0x}}\left( {{x^ * },{y^ * }} \right)\sin \theta - } \right.} }\\ {\left. {{\psi _{0y}}\left( {{x^ * },{y^ * }} \right)\cos \theta } \right]\delta \left( \psi \right){\rm{d}}x{\rm{d}}y} \end{array} $$ (15) $$ \begin{array}{*{20}{c}} {\frac{{\partial r}}{{\partial t}} = \int_\mathit{\Omega } {\left( {H\left( \psi \right) - H\left( \phi \right)} \right)\left[ { - {\psi _0}\left( {{x^ * },{y^ * }} \right) + } \right.} }\\ {\left. {{\psi _{0x}}\left( {{x^ * },{y^ * }} \right){x^ * } + {\psi _{0y}}\left( {{x^ * },{y^ * }} \right){y^ * }} \right]\delta \left( \psi \right){\rm{d}}x{\rm{d}}y} \end{array} $$ (16) $$ \begin{array}{*{20}{c}} {\frac{{\partial \theta }}{{\partial t}} = \int_\mathit{\Omega } {\left( {H\left( \psi \right) - H\left( \phi \right)} \right)\left[ { - r{\psi _{0x}}\left( {{x^ * },{y^ * }} \right){y^ * } + } \right.} }\\ {\left. {r{\psi _{0y}}\left( {{x^ * },{y^ * }} \right){x^ * }} \right]\delta \left( \psi \right){\rm{d}}x{\rm{d}}y} \end{array} $$ (17) 式中
$$ {x^ * } = \frac{{\left( {x - a} \right)\cos \theta + \left( {y - b} \right)\sin \theta }}{r} $$ (18) $$ {y^ * } = \frac{{ - \left( {x - a} \right)\sin \theta + \left( {y - b} \right)\cos \theta }}{r} $$ (19) $$ {\psi _{0x}} = \frac{{\partial {\psi _0}}}{{\partial x}},{\psi _{0y}} = \frac{{\partial {\psi _0}}}{{\partial y}} $$ (20) 根据式(14)~(20),通过不断地将变形模板与水平集演化函数进行比较,更新a、b、r、θ参数,从而实现形状模板与目标的匹配.具体操作步骤如下:
步骤1 选择初始水平集函数.
步骤2 计算f1(x)和f2(x).
步骤3 选择先验形状模板,并构建对应的符号距离函数.
步骤4 求解仿射变换参数,生成ψ的符号距离函数.
步骤5 进行曲线演化.
步骤6 重复步骤2~5,直到模型收敛,或达到限定的迭代次数.
1.2.3 分割结果
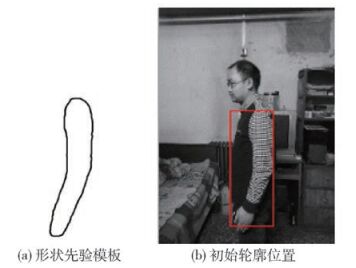
选择合适的形状先验模板和适当的水平初始轮廓,如图 3所示.
在复杂背景下,基于形状先验的LBF算法对人体上肢的分割结果如图 4所示.
可以看到,如果已知所需的形状先验模板和合适的初始轮廓位置,基于形状先验的LBF模型有很好的分割效果.
1.3 水平集初始轮廓的预定位
在LBF模型中加入形状先验信息可以提高图像分割的精度,但是由于LBF模型过于依赖初始轮廓的位置,不当的初始轮廓位置可能使模型收敛到局部极小值,造成模型分割失败.并且模板的选择也是一个很大的问题,如果模板库过于庞大,遍历每个模板非常耗时,且目前并没有找到自动评估分割效果的方法.为了解决这些问题,需要让算法自动选择一个合适的模板作为初始轮廓,并对其进行预定位,使初始轮廓能够达到粗略分割人体上肢的效果,再用基于先验形状的LBF模型,使模型达到全局极小值,完成目标的精确分割.这样一方面解决了模型收敛到局部极小的问题,同时也解决了LBF模型收敛速度过慢的问题.
1.3.1 轮廓预定位算法的理论基础
轮廓预定位算法本质上是一种多尺度轮廓匹配方法,通过找寻与原始图像I0的局部区域相似程度最大的轮廓模板来确定初始水平集函数的形状和位置,以达到粗略分割人体上肢的目的.
每个上肢模板都是一个简单的二值轮廓图像,通过双线性插值算法对轮廓模板进行缩放,可以得到不同的模板尺度图.待匹配图像I0为彩色图像,所含信息量较大,先将其转化为灰度图像I1,再通过sobel算子得到整幅图像的二值轮廓图像I2. I2中不仅包含上肢的轮廓信息,同时也包含背景和其他前景的轮廓信息.需要在含有噪声的轮廓图像I2中,找到与其所匹配的轮廓模板及其对应的尺度大小.
在图像空间中,局部的像素联系较为紧密,卷积核可以被视为局部特征的模板,图像中一个局部窗口与卷积核做内积,可以理解为计算局部窗口与卷积核的相似程度,相似度越高则内积值越大,那么这个局部窗口就更有可能是该卷积核所表示的特征.将上肢轮廓模板视为卷积核,计算其与轮廓图像I2的卷积,得到相应的特征矩阵,其中矩阵值越大的地方就有越大的概率成为与模板匹配的上肢区域.将多个模板的多个尺度卷积核与轮廓图像I2进行卷积计算,得到特征矩阵组.只要找到特征矩阵组的全局极大值,就求得了轮廓模板选择问题和预定位问题的可行解.
轮廓预定位算法可以通过浅层卷积神经网络[11]来实现.首先将含有噪声的轮廓图像I2作为输入层;m×n个卷积核作为卷积层,其中m为模板个数,n为单个模板的尺度层数;由ReLU函数组成激励层.卷积层和激励层负责计算图像I2的局部窗口与模板卷积核的相似度,得到m×n个特征矩阵.将激励层的输出送入到全连接层,用来计算特征矩阵组的全局极大值,并将全局极大值的坐标和所属卷积核作为输出.对应的坐标即为初始水平集函数的中心坐标,对应的卷积核即为初始水平集函数的形状,同时也是水平集演化函数的形状先验约束项.
1.3.2 具体步骤
本文提出了一种水平集初始轮廓的预定位算法.具体操作步骤如下:
步骤1 将原图像I0转换为灰度图像I1,通过sobel边缘提取算子对原图像I1进行滤波,得到含有噪声的轮廓图像I2,作为浅层卷积神经网络的输入.
步骤2 通过双线性插值算法对人体上肢的形状先验模板进行缩放,得到多尺度形状先验模板.如果有m个模板,每个模板有n个尺度,那么卷积层就有m×n个卷积核,每个卷积核可表示为σi×j (i=1, 2, 3, …,m; j=1, 2, 3, …,n).
步骤3 使轮廓图像I2先通过由σi×j组成的多卷积计算层,再通过由ReLU函数组成的激励层.这里的卷积计算层满足卷积神经网络的局部感知和权值共享特性,并且权值也基本固定,达到了深度神经网络预训练的效果.
步骤4 将激励层的输出送入全连接层和输出层.输出层有4个神经元,分别表示卷积核σi×j的下标(i, j)的值和轮廓图像I2中的一个点(x, y).
步骤5 通过BP算法对整个网络进行调整.训练样本为标记过的噪声轮廓图像I2,其中每个I2标记为其所对应的卷积核σi×j和卷积核在I2中取得极大值的位置坐标(x, y).由于卷积计算层已基本收敛,所以不做调整或者只做微调即可,BP算法主要用于调整全连接层的权值.
网络训练好后,可以将其放到初始轮廓预定位的应用中.给定一幅待分割图像I0,先对其进行灰度图转换和sobel滤波,将所得图像I2输入到网络中,即得到其所对应的卷积核σi×j和坐标(x, y).卷积核σi×j即为水平集的初始轮廓,(x, y)即为初始轮廓的中心坐标.
1.3.3 分割结果
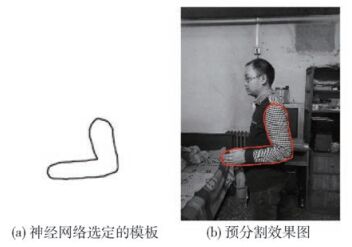
通过浅层神经网络自动选定的模板如图 5(a)所示,选定的轮廓模板即为水平集的初始轮廓,将其按照(x, y)坐标加载到待分割图像中,效果图如图 5(b)所示.
用基于形状先验的LBF模型对初始轮廓进行演化,得到的精确分割结果如图 6所示.
实验结果表明,算法是有效的,分割的精确度达到了理想的效果.
2. 实验结果
算法性能的评估主要分为2个部分:一是对分割质量的评估,二是对分割所需时间的评估.对于图像的分割质量采用的是主观评价法,将分割质量分为3个等级:准确、略差、失败.定义无效分割率公式为
$$ 无效分割率 = \frac{{\left| {实际轮廓面积 - 分割轮廓面积} \right|}}{{实际轮廓面积}} $$ (21) 当无效分割率≤0.05时,分割质量视为精确;当0.05<无效分割率≤0.15时,分割质量视为略差;当无效分割率>0.15时,分割质量视为失效.
分别对LBF、基于形状先验的LBF、基于轮廓预定位的先验LBF三种算法进行了对比评估.分割时间的评估指标采用的是水平集演化的迭代次数n.由于单纯的LBF算法在复杂背景下的分割效果很差,在分割时间评估中,只计算了基于先验形状的LBF和基于轮廓预定位的先验LBF的迭代次数.分割失败的迭代次数是一个无意义的值,所以也没有计算在内.
本文采用的样本数据库是由北京工业大学NNIR实验室提供.数据库是由10个同学的连续摆臂动作组成,每个同学取30张,共计300张摆臂图片.从中随机抽取了50张图片作为测试样本.评估结果如表 1、2所示.
表 1 分割质量对应图片数Table 1. Segmentation quality correspords to the number of pictures算法 准确 略差 失败 LBF 0 0 50 先验形状 23 1 26 轮廓预定位 41 7 2 表 2 水平集演化的迭代次数Table 2. Number of iterations of level set evolution算法 准确 略差 先验形状 113.7 132.1 轮廓预定位 35.6 47.3 从表 1中可以看出,单纯的LBF算法对于复杂背景下特定目标的分割能力基本为0.当加入形状先验信息后,分割成功率提升到50%左右,但是由于LBF算法对轮廓初始位置比较敏感,仍不能保证分割的成功率.当加入轮廓预定位的处理过程之后,分割成功率上升到90%,在确保分割精度的前提下,算法也有了很好的鲁棒性.
表 2主要体现了算法的时间性能,基于形状先验的LBF算法由于初始轮廓只是一个矩形,算法收敛的平均迭代次数在100次以上.当通过预定位算法对初始轮廓进行过处理后,初始的水平集函数基本收敛到待分割目标,从而使耗时的水平集演化操作的平均迭代次数降到了40以下.
3. 结论
1) 提出了一种基于轮廓预定位的先验LBF算法.该算法先利用浅层卷积神经网络得到待分割目标的轮廓模板,实现轮廓模板在待分割图像中的预定位;然后利用基于形状先验的LBF算法对模板进行演化,最终达到精确分割特定目标的目的.
2) 实验结果表明:基于轮廓预定位的先验LBF算法是一种鲁棒性强且分割精度高的特定目标分割算法.轮廓预定位的处理过程将整体算法的成功率提升到90%,并使得耗时的LBF算法的迭代次数降到了40以下.
-
表 1 分割质量对应图片数
Table 1 Segmentation quality correspords to the number of pictures
算法 准确 略差 失败 LBF 0 0 50 先验形状 23 1 26 轮廓预定位 41 7 2 表 2 水平集演化的迭代次数
Table 2 Number of iterations of level set evolution
算法 准确 略差 先验形状 113.7 132.1 轮廓预定位 35.6 47.3 -
[1] 黄如训, 苏镇培.脑卒中[M].北京:人民卫生出版社, 2001:1-2, 298. [2] ZHANG S, ZHAN Y, DEWAN M, et al. Towards robust and effective shape modeling:sparse shape composition[J]. Medical Image Analysis, 2012, 16(1):265-277. doi: 10.1016/j.media.2011.08.004
[3] KASS M, WITKIN A, TERZOPOULOS D. Snakes:active contour models[J]. International Journal of Computer Vision, 1988, 1(4):321-331. doi: 10.1007/BF00133570
[4] CASELLES V, CATTE F, COLL T, et al. A geometric model for active contours in image processing[J]. Numerische Mathematik, 1993, 66(1):1-31. doi: 10.1007/BF01385685
[5] CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1):61-79. doi: 10.1023/A:1007979827043
[6] MUMFORD D, SHAH J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics, 1989, 42(5):577-685. doi: 10.1002/(ISSN)1097-0312
[7] CHAN T F, VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2):266-277. doi: 10.1109/83.902291
[8] LI C, KAO C Y, GORE J C, et al. Implicit active contours driven by local binary fitting energy[C]//2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis:IEEE, 2007:1-7.
[9] LI C, XU C, GUI C, et al. Level set evolution without re-initialization:a new variational formulation[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). San Diego:IEEE, 2005, 1:430-436.
[10] CHAN T, ZHU W. Level set based shape prior segmentation[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). San Diego:IEEE, 2005, 2:1164-1170.
[11] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems. New York:Curran Associates, 2012:1097-1105.
-
期刊类型引用(2)
1. 韩红桂,甄晓玲,李方昱,杜永萍. 基于多尺度卷积神经网络的手机表面缺陷识别方法. 北京工业大学学报. 2023(11): 1150-1158 .  本站查看
本站查看
2. 韩红桂,甄琪,任柯燕,伍小龙,杜永萍,乔俊飞. 基于孪生卷积神经网络的手机型号识别方法. 北京工业大学学报. 2021(02): 112-119 .  本站查看
本站查看
其他类型引用(0)



 下载:
下载: