MBO-Based Method With Parameter Optimization to Predict 3D Chromatin Structure
-
摘要:
认识染色体的三维空间结构对于理解细胞核内基因组的表达、调控等具有重要作用.针对Hi-C数据稀疏和含有噪声的特点，提出了基于流形优化（manifold based optimization，MBO）与参数优化相结合的染色体三维结构预测方法——变参数的基于流形优化的算法（variable-parameter MBO，VMBO）.通过黄金分割算法迭代优化转换参数，将染色体片段间的接触频率转换为空间距离值；然后用MBO算法重构染色体的三维平均结构（consensus structures）.在实验部分用模拟数据集和真实的Hi-C数据集进行三维结构预测，预测结果的均方根误差（root mean squared deviation，RMSD）和距离的斯皮尔曼相关系数（distance Spearman correlation coefficient，dSCC）说明了VMBO算法的有效性和鲁棒性.
-
关键词:
- Hi-C接触频率 /
- 基于流形最优化(MBO) /
- 染色体结构的预测 /
- 平均结构 /
- 变参数的基于流形优化的算法(VMBO)
Abstract:Having known the 3D structures of chromosomos is of great importance to the understanding of gene expression and regulation in nuclei. Hi-C technology has been developed to capture genome-wide interactions and generate contact frequency data. Based on the characteristic of the sparse and noisy interaction sampling in Hi-C data, a MBO-based method with parameter optimization, named VMBO, was proposed to predict a 3D chromatin structure. First, for converting the interaction frequency to spatial distance between two chromosome fragments the conversion factor was optimized by golden section search. Second, manifold based optimization (MBO) was applied to reconstruct a consensus 3D structure. The VMBO accuracy and robustness were validated on both simulation data and real Hi-C data. The results of structure similarity measures, root mean squared deviation and distance Spearman correlation coefficient, indicate that the proposed method can well reconstruct 3D chromatin structures.
-
染色体在三维空间的折叠结构极大影响着细胞内DNA的复制、基因的表达和调控.目前，主要是染色体构象捕获技术及其衍生技术用于基因组三维数据的测定，可获得大量的染色质交互作用数据.其中，Hi-C技术能高通量地获取多个物种的全基因组的交互作用信息，进行数据处理和分析后得到接触频率数据，可用于推断染色体的三维结构.该构象能极大地拓展人们对于基因组空间结构的认识，为更好地了解染色质的调控功能提供结构上的依据[1-2].
目前Hi-C技术的研究对象主要分为2类：一是群体细胞，捕获的Hi-C数据反映的是群体细胞空间结构呈现的总体趋势；二是单个细胞，单细胞Hi-C技术可捕获单个细胞的交互信息，用于某种特殊形态或稀少细胞的染色体三维结构的解析.基于群体细胞的Hi-C数据进行建模研究可以构建出染色体的平均结构，也可以构建群体结构(ensemble structures)[3].平均结构呈现的是细胞系中染色体结构呈现的一致性或总体趋势，无法反映染色体之间空间结构的随机性和差异性；而群体结构将展示细胞系中染色体结构的多样性和存在的各种可能性.
利用Hi-C数据或单细胞Hi-C数据预测染色体的三维结构，根据构建模型原理的不同，建模方法主要分为概率模型(probabilistic models)和距离约束模型(restraint-based models)[4].概率模型设定染色体3D结构服从某种概率分布，以一定概率值存在. Rousseau等[5]于2011年提出了MCMC5C的预测方法.其假设2个片段间的接触频率和空间距离服从正态分布，通过马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)抽样方法模拟染色体的群体结构. Hu等[6]于2013年提出BACH方法，为了减少原始Hi-C数据中存在的系统偏差(bias)，利用泊松分布归一化Hi-C数据，然后将贝叶斯统计推理方法用于建立染色体三维结构.在距离约束模型中，原理是首先计算出染色体的每个片段的三维空间坐标，然后对染色体结构进行三维可视化. Zhang等[7]于2013年提出了ChromSDE方法，该方法针对群体细胞的Hi-C数据的特点，首次在从接触频率到3D距离的转化函数中引入了转化参数α，并用半正定规划(semi-define programming，SDP)[8]算法定位染色体的空间位置信息. Lesne等[8]于2014年提出了一个包含2个步骤的算法ShRec3D，它将网络最短通路算法和经典的多维定标(multidimensional scaling，MDS)算法有机结合，该算法效率更高且可有效避免传统优化算法的收敛问题.另一方面，针对单细胞Hi-C数据稀疏性和高噪声的特点，Paulsen等[9]于2015年首次将基于流形的优化算法用于构建单个细胞的染色体结构.该方法利用低秩矩阵填充理论恢复了距离矩阵中缺失的元素，从而构建染色体的三维结构模型.
本文提出了一种基于流形技术的最优化和参数优化的染色体3D重构方法——变参数的基于流形优化的算法(variable parameter manifold based optimization，VMBO)，作用于群体细胞的Hi-C数据预测染色体的平均结构.其基本原理是，根据染色体片段间的交互频率与空间距离呈现幂律的分布递减关系，首先在接触频率到空间距离的转换函数中引入转换参数，并用黄金分割算法迭代优化参数；然后依据Hi-C接触频率矩阵稀疏性和噪声复杂性的特点，将MBO算法用于构建群体细胞的染色体平均结构.实验中将该方法应用于模拟数据集和群体细胞的Hi-C数据集，通过与ChromSDE和ShRec3D方法比较，证明了VMBO能有效预测染色体的三维结构.
1. VBMO方法
1.1 模型的表示
利用Hi-C数据预测染色体的三维结构，首先需要将生物学意义的染色体结构表示成数学模型.假设染色体或者染色体的部分区域是由多个“线珠结构”(beads-on-string)的物理模型结构构成.例如，假设数据的分辨率为1 Mbit，就是将染色体打断成N个连续的、长度为1 Mbit长度的片段.假设某条染色体上的N个连续的片段，根据这些片段可得到N×N的接触频率矩阵(Fij)N×N，该矩阵为对称半定的，其中Fij代表第i个片段和第j个片段之间的接触频率值.定义N个连续染色体片段在三维空间中的坐标矩阵为X=(x1, x2, …, xn)∈ℝ3×n，式中xi∈ℝ3代表第i个片段的三维坐标.
1.2 变参数的转换函数：从接触频率矩阵F到空间距离矩阵D
Lieberman-Aiden等[10]于2009年发表的研究成果表明：三维空间中染色体各个片段间距离值越大，其接触频率值越小；空间距离越近的片段间产生的接触频率值越大.即接触频率和空间距离间遵循幂律关系：F(i, j)=f(D(i, j)).在ChromSDE方法中Zhang等[7]首次在转换函数关系的幂函数中引入指数参数α(α>0)，且理论上证明参数的绝对值与Hi-C数据分辨率成正比关系.本文基于以上理论定义了式(1)的转换函数，进一步用MBO解决距离矩阵的填充问题：已知部分矩阵元素来恢复整个矩阵；考虑到MBO的应用条件，将无接触的片段之间的欧氏距离暂定为0.所以其转换函数定义为
$$ \mathit{\boldsymbol{D}}_{ij}^{\rm{t}}\left\{ \begin{array}{l} \mathit{\boldsymbol{F}}_{ij}^{-\alpha }, \;\;\;\;{\mathit{\boldsymbol{F}}_{ij}} > 0\\ 0, \;\;\;\;\;\;\;\;\;其他 \end{array} \right. $$ (1) 式中Dijt为i, j两个染色体片段对应的距离.
接下来有2个问题需要解决：1)确定参数α；2)对接触频率矩阵中零值元素的处理. α可用黄金分割算法迭代优化.对于问题2)通常有2个解决办法：其一，将非接触的染色体片段之间赋予很大的距离值和对应小的权重值，因接触频率值越小代表可信度越低；其二，利用ShRec3D算法的思想，用最短路径算法恢复缺失的距离值，但这样会导致缺失元素获得一个大的距离值，影响建模效果[9].
本文结合两者的特点，首先假设参数α已知，利用Floyd-Warshall算法，用已知距离推断出的距离填充零值，从而将Dt转换为空间矩阵D.然后引入权重矩阵H，将有连接的片段间的距离赋予权重1，恢复的距离赋予极小的权重，从而加大接触频率大的空间距离的可信度.接下来可用MBO算法求取染色体片段的三维坐标值.
1.3 MBO算法：从距离矩阵D到三维空间坐标矩阵X
针对距离矩阵稀疏的特性，借鉴矩阵填充理论的研究成果[11-12]，用MBO算法解决凸优化问题.考虑到三维染色体建模的原理，矩阵填充理论可表示成如
$$ \mathop {\min }\limits_{{\mathit{\boldsymbol{D}}^r} \in {\xi ^n}\left( r \right)} \frac{1}{2}{\left\| {\mathit{\boldsymbol{H}} \odot \left( {{\mathit{\boldsymbol{D}}^r}-\mathit{\boldsymbol{D}}} \right)} \right\|^2} $$ (2) 的无约束优化问题.式中：ξn(r)为嵌入维数小于或等于r的欧氏距离集合；Dr为ξn(r)的元素；H为距离矩阵D对应的权重矩阵；⊙表示矩阵中元素的Hadamard积.
权重矩阵中的元素值代表空间距离值对应的染色体片段间的接触频率的可信赖程度，接触频率值越小，可信赖程度越低，对应的权重越小.权重矩阵用
$$ {\mathit{\boldsymbol{H}}_{ij}} = {\mathit{\boldsymbol{H}}_{ji}} = \left\{ \begin{array}{l} n_{ij}^{-q}, \;\;\;\;\mathit{\boldsymbol{D}}_{ij}^t = 0\\ 1\;\;\;\;\;\;\;\;\mathit{\boldsymbol{D}}_{ij}^{\rm{t}} \ne 0 \end{array} \right. $$ (3) 求解.式中：nij表示连接片段i和j之间的路径的条数；q是一个待优化的参数，用于调节无连接边与连接边的权重比.式(3)求出的权重矩阵，使得有接触片段间的距离值的权重变大，加大了接触频率高的片段对应的空间距离的拟合权重.
式(2)在理论上可定义为一个关于半正定矩阵集合S+n(r)的最优化问题，则S+n(r)到距离矩阵集合ξn(r)的映射关系可表示为
$$ {\mathit{\boldsymbol{D}}^2} = \kappa \left( \mathit{\boldsymbol{B}} \right) = \mathit{\boldsymbol{b}}{\mathit{\boldsymbol{e}}^{\rm{T}}} + \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{b}}^{\rm{T}}}-2\mathit{\boldsymbol{B}} $$ (4) 式中：b=diag B=(B⊙I)e；向量e∈ℝn的分量全为1；b为列向量；矩阵B为对角的.秩为r的半定矩阵可以分解为B=XXT，式中X∈ℝn×r且rank X=r.因此式(2)可转换为最小化如
$$ f\left( \mathit{\boldsymbol{X}} \right) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{H}} \odot \left( {\sqrt {\kappa \left( {\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}} \right)}-\mathit{\boldsymbol{D}}} \right)} \right\|^2} $$ (5) 所示的代价函数的优化问题.因此求解式(5)的无约束最优化问题获得最优的空间坐标矩阵X，即为三维空间中染色体片段的坐标.
求解式(5)的目标函数通常有2种常用方法：梯度下降算法和信赖域方法，两者都可用于无约束最优化问题的求解.本文用Matlab中的MBO算法中的优化工具箱：Manopt toolbox，选择信赖域的求解方法求解.
1.4 黄金分割算法：迭代优化转换参数α
重构染色体结构的第一个关键是有效地将接触频率转换为空间距离，转换函数(1)中不同的数据集对应不同的参数α，需优化获得每个数据集的最优参数.本文定义目标函数
$$ {\rm{error}}\left( {\mathit{\boldsymbol{F, }}\alpha } \right) = \left\| {\mathit{\boldsymbol{F-}}{\mathit{\boldsymbol{F}}^{\rm{r}}}} \right\| $$ (6) 使重构后的接触频率和初始接触频率的误差最小. 式中：F为输入的接触矩阵；Fr为预测结构的接触矩阵Fijr=(1/Dijr)(1/α)，Dijr由重构后的3D坐标信息X计算得到.要寻找使式(6)的误差值最小的参数α.由于无法获得误差函数的梯度信息，本文将利用黄金分割算法迭代搜索参数α的值. α不能太小，否则F将变成与指数无关的量(如α→0)；同理α不能太大，否则可信度较小的F值对应的距离值将占据较大作用.经实验选取0.1 < α < 3.0.
2. 模型的评估指标
三维基因组学的研究不断成熟，但仍无法得到精确的染色体三维结构模型来评估建模方法构建的3D结构的准确性.当前主要是通过进行交叉验证来进行评估，即比较同一细胞系的不同数据集来预测结构的可重复性或重叠的一致性[13].本文使用了2个指标即均方根误差和斯皮尔曼相关系数来量化所构建染色体三维结构的相似性，以此来评估建模方法的性能.
2.1 均方根误差
经过MBO算法求得的是染色体片段的相对坐标值，所以可将同一细胞系的2个数据集对应的2个重构结构进行最大化的重叠，将一个三维结构进行刚性的平移、旋转和伸缩，采用最小平方拟合的方法，使一个结构最大化地叠置到另一个结构上. RMDS的计算公式为
$$ {\rm{RMSD = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {{q_i}-p_i^{\rm{t}}} \right\|}^2}} } $$ (7) 假设2个结构的染色体片段分别由连续的三维坐标点确定，2个结构分别为P=(p1, p2，…, pN)和Q=(q1, q2，…, qN).将P通过公式Pt=sRP-t在三维空间中进行坐标变换，式中：Pt∈ℝ3×N为结构P变换后的结果；t∈ℝ3为平移变换向量；R∈ℝ3×3为旋转变换矩阵；s表示变换的缩放系数.通过最小二乘算法，使结构Pt和Q的重叠误差最小，即式(7)数值最小. RMSD数值越小，则表示建模方法对相同结构的不同数据的三维结构重构的重复性越高，该方法预测三维结构的性能越好.
2.2 斯皮尔曼相关系数
斯皮尔曼相关系数可消除不同数据的转换参数的影响，因此本文采用斯皮尔曼相关系数，而不是皮尔森相关系数，去比较2组数据重建的距离矩阵的相关性. dSCC的取值在-1~+1，相关系数的值越接近1，则说明2个重构三维结构的相似度越高，则该方法的预测性能越好.
3. 实验结果
3.1 数据来源
本文采用结构已知的模拟数据集和真实的Hi-C数据集，通过实验验证VMBO算法的性能.
3.1.1 模拟数据集
本文用计算机模拟产生了3种三维结构模型，其结构由简单到复杂分别为：1)螺旋结构；2)布朗运动点形成的结构；3)一个立方体内随意运动点形成的结构.假设每个结构由100个点组成，Hi-C技术能有效捕获最近邻的50个点，这样能够得到连通的拓扑结构和稀疏的接触频率矩阵.计算两点的接触频率的公式为fij=(1/dij)1/α，式中dij为欧几里得距离，这里取α=1，并规定接触频率矩阵元素之和为106，以便模拟的Hi-C数据更加真实.
3.1.2 Hi-C数据集
原始的Hi-C数据存在系统偏差和复杂的噪声.本文实验Hi-C数据部分来源于网站http://www.people.fas.harvard.edu/~junliu/HiCNorm/，包括人类GM06990细胞系的23个染色体和小鼠胚胎干细胞的20个染色体的接触频率数据，使用Yaffe等[14]提出的去除偏差的方法得到归一化的接触矩阵，分别记为GM-YT和mESC.另一部分实验数据是使用HiCNorm归一化方法获得的人类GM06990细胞系的归一化数据，记为GM-HiCNorm，源自网站http://compgenomics.weizmann.ac.il/tanay/?page_id=283. 3个数据集的每个染色体的结构都包括Hind3和Ncol两种酶切数据，用于比较两者构建同一条染色体结构的重叠度.
3.2 参数q值的确定
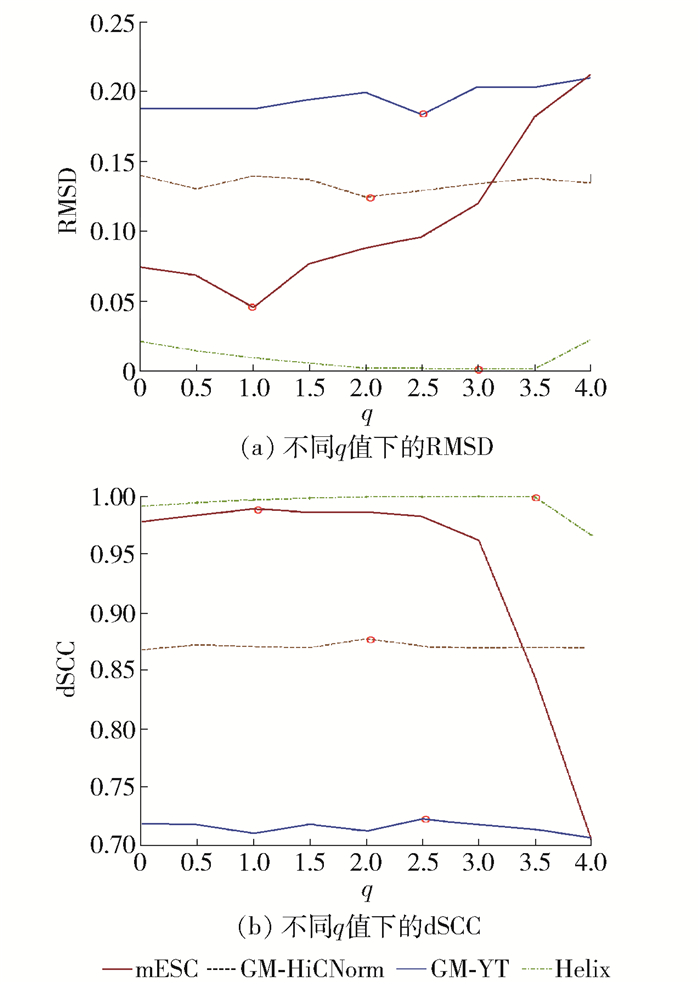
在MBO算法应用中，求解权重矩阵H时在式(3)中引入待优化参数q. q用于调节无连接边与连接边的权重比，因此不同的数据集对应不同的q.本文令0 < q < 4，求取每个数据集中使真实结构与重构结构的重叠度最大的q，即对应的RMSD值最小和dSCC值最大. 图 1所示为不同的q值下，4个数据集的RMSD和dSCC的变化，其中红色圆圈代表最优值.从图 1可以看出，模拟数据集以螺旋结构为代表，其q=3.0.真实的Hi-C数据集中，以每个数据集中第2条染色体内的数据为代表，寻找q的最优值.其中mESC数据集q=1.0，从图 1可以看出，q值的变化对于GM-YT和GM-HiCNorm数据集建模性能影响很小，为了计算方便，统一令q=2.0.
3.3 参数α的确定
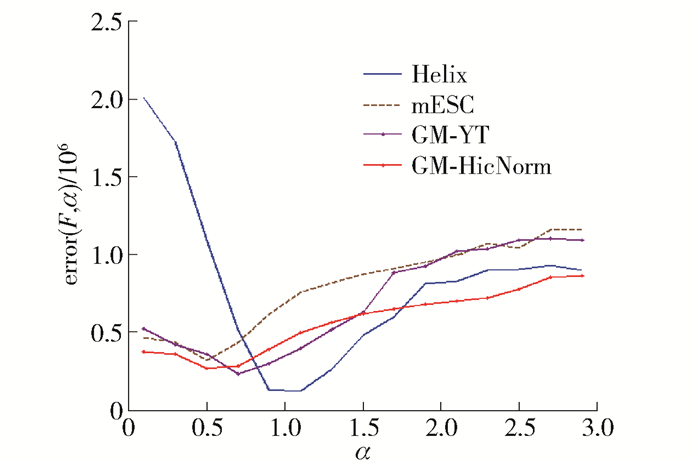
VMBO算法中，在转化函数(1)中引入参数α，对于不同的数据集采用黄金分割算法迭代优化参数，最小化重构后的接触频率和初始接触频率之间的误差，也即最小化式(6).对于模拟数据集、mESC和GM06996细胞系的Hi-C数据集，误差函数error(F, α)随参数α的变化如图 2所示.从图 2可以看出误差函数在α∈(0.1, 3)区间内存在最小值.模拟数据集采用螺旋结构Helix数据，转化参数真实值为1，经黄金分割算法优化得到α值接近1. Hi-C数据集以mESC和GM06996中的1号染色体为例，mESC的最值在0.5附近，GM06996对应的最优值在0.7附近.从中可以看出，不同数据集对应不同的转化参数；同样，从图 2可以看出，α在其最优值附近的变化对应的误差函数值的变化很小，表明误差值在参数最优值附近对α的变化不灵敏.
3.4 模拟数据集实验结果
3.4.1 无噪声下VMBO重构模拟结构的性能
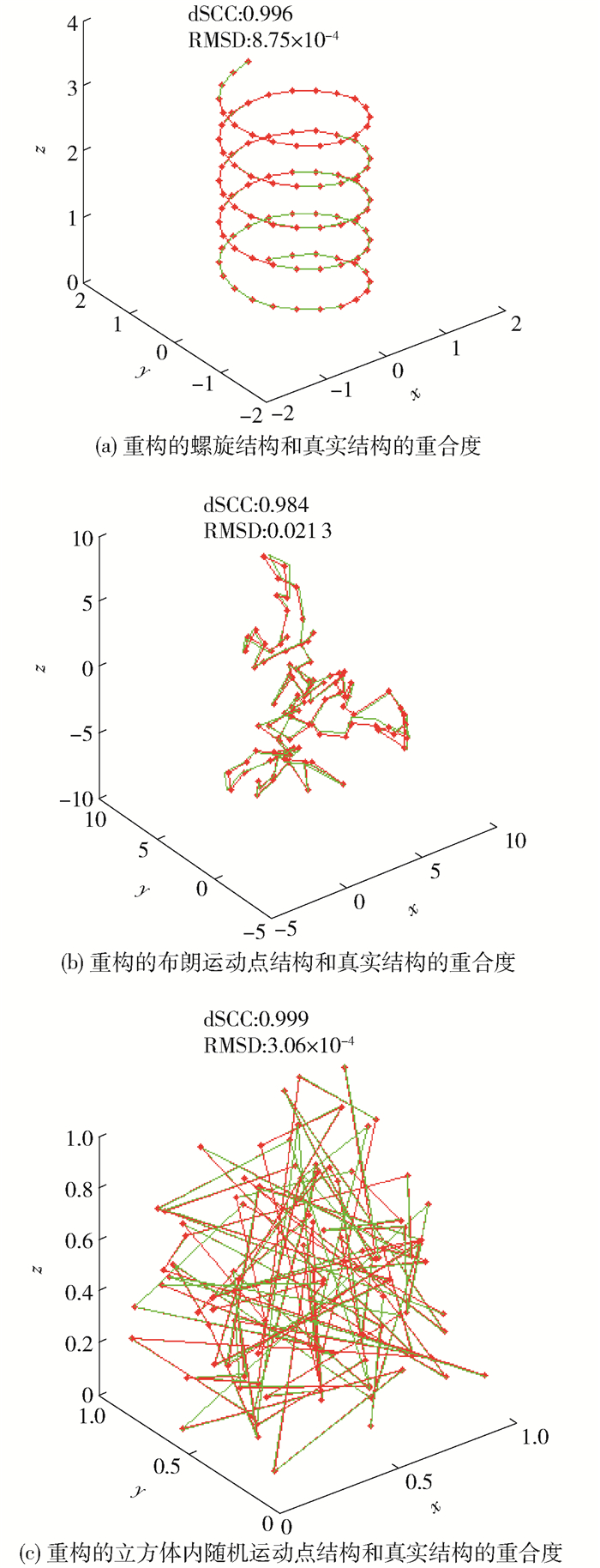
利用VMBO算法重构3种模拟结构.如图 3所示，红色曲线代表真实结构，绿色代表重构结构，RMSD和dSCC量化3种结构的重叠度.从图 3可以看出，对于简单螺旋结构和立方体内随意运动点形成的结构，dSCC数值接近1，VMBO算法能很好地重构真实结构.对于复杂的布朗运动点形成的结构，VMBO算法能捕获每个点的真实位置，对真实结构有很好的建模效果.说明VMBO算法在无噪声下，重构三维结构的有效性.
![]()
图 3 3种模拟数据集的真实结构和重构结构的对比Figure 3. Predicted vs true structures from three sets of simulation data3.4.2 VMBO的鲁棒性
真实的Hi-C数据中存在复杂的噪声，因此需要测试VMBO在不同的噪声水平下，构建模拟结构的性能.设含有噪声的接触频率矩阵可由
$$ \mathit{\boldsymbol{\tilde F = }}\left( {1 + \delta } \right)\mathit{\boldsymbol{F}} $$ (8) 计算得到.式中：δ为符合均匀分布的随机噪声值，δ=(2r-1)S，r∈(0, 1)为随机数；S∈(0, 1)表示噪声水平；F为无噪声的接触矩阵，Fij=1/dij，dij为欧几里得距离.
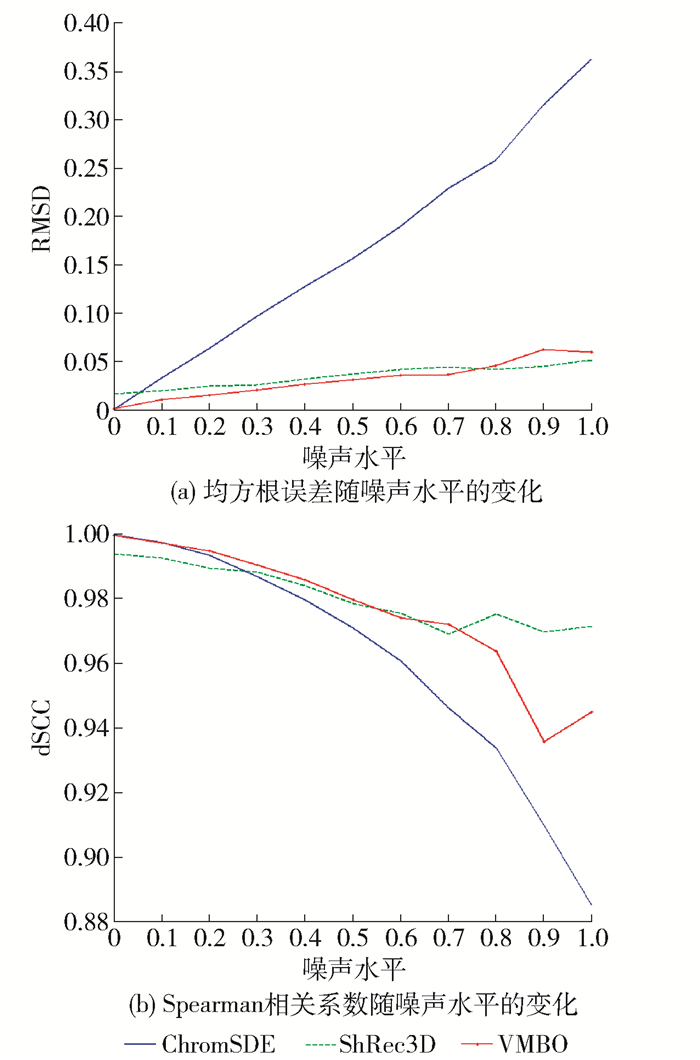
图 4所示为在不同的噪声下，对简单的螺旋结构数据集，用ChromSDE、ShRec3D和VMBO三种方法重构模拟结构的性能.由于VMBO算法中信赖域方法的应用导致结果具有随机性，因此对实验中的每个数据集进行10次实验，VMBO的结果是取RMSD和dSCC的平均值.从图 4可看出，3种方法预测的模拟结构，总体上随着噪声值的增加，重构结构和真实结构之间的重叠度减小，表现在RMSD值增大，dSCC值减小，不能很好预测三维结构.在噪声值很小时，ChromSDE方法的性能优于其他2种方法，这也验证了Zhang等[7]的理论：ChromSDE方法在无噪声下能唯一定位(uniquely localizable)数据集中每个点的三维坐标值，从而可以重构唯一结构.但随着噪声的增加，ChromSDE表现出明显的劣势.总体上，ShRec3D和VMBO方法具有相似的性能，2个参数值RMSD < 0.06, dSCC>0.93，说明重构结构的有效性.但在噪声值较小时，VMBO算法的性能优于ShRec3D.从而证明了VMBO在一定的噪声水平下能有效重构三维结构，具有良好的鲁棒性.从大量的无噪声和有噪声的模拟数据集实验结果可看出，VMBO算法能更精确构建复杂度不同的三维结构.在MBO基础上引入指数可变的转换函数，可以使VMBO算法对不同分辨率下的数据集的结构进行预测.但是Hi-C数据中存在的噪声分布较为复杂，需要进一步验证VMBO重构染色结构的性能.
![]()
图 4 3种方法构建模拟结构的性能Figure 4. Performance of the three methods undervarious level of noise (from simulation data)3.5 Hi-C数据集实验结果
实验采用了3组Hi-C数据集，其中mESC来自老鼠的胚胎干细胞系，共20条染色体；而GM-YT和GM-HiCNorm都来自人类的GM06990细胞系的23条染色体的数据，利用不同去除偏差方法得到归一化数据.本部分将VMBO算法与ChromSDE和ShRec3D进行比较实验，通过RMSD和dSCC两个指标进行建模性能分析.同样，VMBO对于每个数据集中每条染色体的Hi-C数据都进行10次实验，用2个指标的平均值来衡量建模效果，消除信赖域搜索带来的随机性. 表 1~3所示为每个细胞系中构建的所有染色体结构的RMSD和dSCC的平均值.
表 1 mESC数据集Table 1. mESC data项目 ChromSDE ShRec3D VMBO dSCC 0.974 0.982 0.988 RMSD 0.078 0.051 0.044 表 2 GM-YT数据集Table 2. GM-YT data项目 ChromSDE ShRec3D VMBO dSCC 0.857 0.687 0.715 RMSD 0.148 0.184 0.163 表 3 GM-HiCNorm数据集Table 3. GM-HiCNorm data项目 ChromSDE ShRec3D VMBO dSCC 0.952 0.836 0.874 RMSD 0.065 0.173 0.148 从表 1可以看出，3种方法对mESC数据集的结构预测性能都较好，距离相关系数的平均值都大于0.97.从结果看2个参数具有一致性：dSCC值越小，RMSD越大，建模效果越好.从数值看VMBO算法相对于ShRec3D和ChromSDE算法对于mESC细胞系的结构预测性更优，ShRec3D方法略优于ChromSDE.从表 2、3可以看出，VMBO对于GM细胞系的2个数据集的结构预测性能都优于ShRec3D方法，但是低于ChromSDE方法.比较表 2、3，相比于文献[14]提出的归一化方法，对于HiCNorm归一化方法得到的数据集，3种方法获得的重构结构的重叠度都较高，也说明不同去除偏差的方法也影响算法的建模性能，HiCNorm去除偏差的方法更适用于构建GM细胞系的平均结构.再者，将表 1与表 2、3进行比较可以看出，mESC细胞系的重构结构的性能总体上优于GM06990细胞系的2个数据集，一定程度验证了ChromSDE方法中的结论：mESC细胞系中的染色体总体上趋于一个平均结构，而GM细胞系中的染色体结构差异性大，Hi-C数据中噪声分布更加复杂.
本文提出的VMBO算法用于构建群体细胞染色体的平均结构，从RMSD和dSCC两个模型评估指标看，VMBO对于不同细胞系的数据集，构建染色体结构的性能有一定的差别，结果看出其主要受噪声的影响.同样，对于不同的Hi-C数据集，3种方法预测的结构也不同，VMBO方法更适用于细胞系中染色体结构趋于一致性的结构预测.
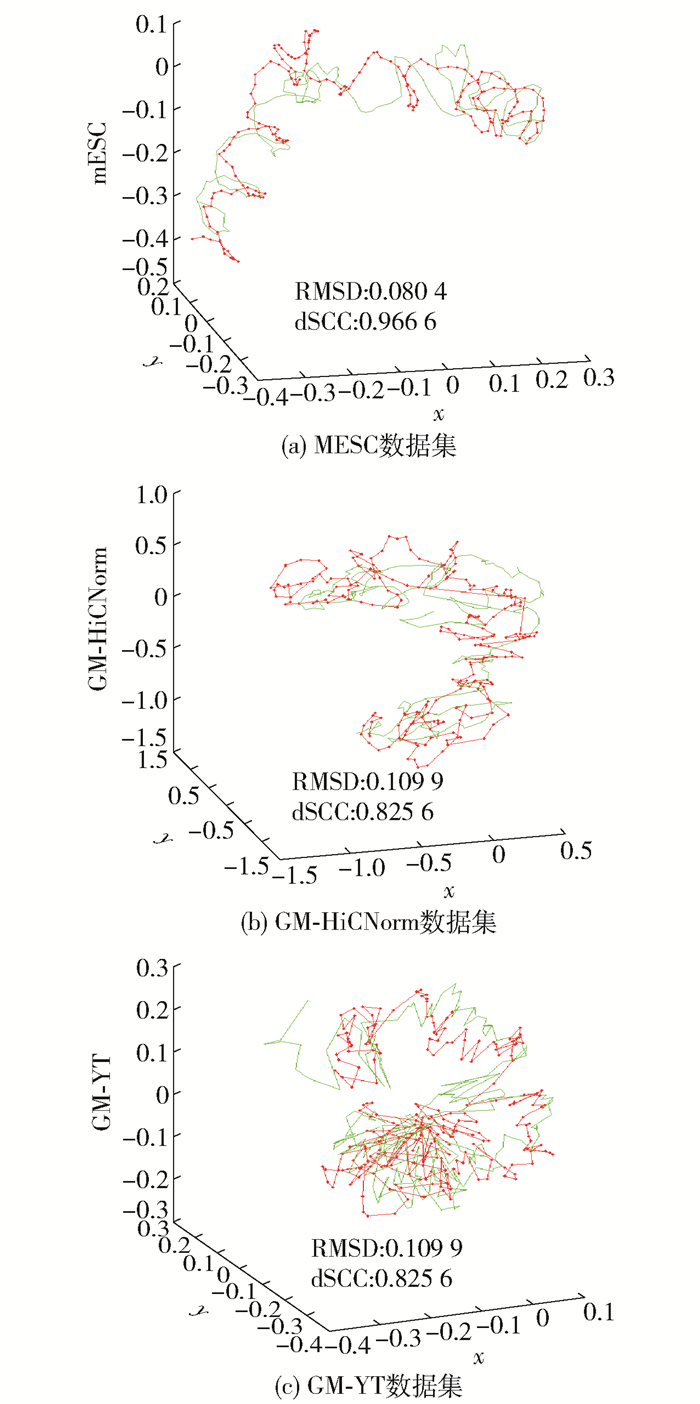
如果将染色体片段用不断折叠的实线表示，则可形象展示染色体的三维折叠结构，同样可视化2个结构的重叠状态.如图 5所示，以mESC、GM-YT和GM-HiCNorm数据集中第2条染色体为代表，用VMBO算法预测染色体片段的三维坐标值，然后构建染色体空间的折叠结构，图 5展示了Hind3酶的Hi-C数据(红色曲线)和NcoI酶的Hi-C数据(绿色曲线)重构的染色体3D结构的折叠状态和重合度，并注解了单条染色体的RMSD和dSCC数值.
![]()
图 5 3种数据集中重构的2号染色体的三维结构Figure 5. Reconstructed structures of chromosome 2 from three datasets4. 结论
1) 将VMBO算法应用到Hi-C接触频率数据，通过实验对比分析表明，其可有效构建染色体的平均结构.
2) 对于复杂度不同的模拟结构，在一定的噪声水平下VMBO算法能有效重构三维结构，鲁棒性较好.
3) 对于归一化的Hi-C数据集，VMBO算法可构建不同细胞系的染色体的三维结构，效果良好；对原始Hi-C数据的归一化处理，同样影响算法的结构预测能力.
-
![]()
图 3 3种模拟数据集的真实结构和重构结构的对比
Figure 3. Predicted vs true structures from three sets of simulation data
![]()
图 4 3种方法构建模拟结构的性能
Figure 4. Performance of the three methods undervarious level of noise (from simulation data)
![]()
图 5 3种数据集中重构的2号染色体的三维结构
Figure 5. Reconstructed structures of chromosome 2 from three datasets
表 1 mESC数据集
Table 1 mESC data
项目 ChromSDE ShRec3D VMBO dSCC 0.974 0.982 0.988 RMSD 0.078 0.051 0.044 
下载: 导出CSV
表 2 GM-YT数据集
Table 2 GM-YT data
项目 ChromSDE ShRec3D VMBO dSCC 0.857 0.687 0.715 RMSD 0.148 0.184 0.163
下载: 导出CSV
表 3 GM-HiCNorm数据集
Table 3 GM-HiCNorm data
项目 ChromSDE ShRec3D VMBO dSCC 0.952 0.836 0.874 RMSD 0.065 0.173 0.148
下载: 导出CSV
-
[1] 李国亮, 阮一骏, 谷瑞升, 等.起航三维基因组学研究[J].科学通报, 2014, 59(13):1165-1172. doi: 10.1360/N972014-00163 LI G L, RUAN Y J, GU R S, et al. Open three-dimensional genome research[J]. Chinese Science Bulletin, 2014, 59(13):1165-1172. doi: 10.1360/N972014-00163
[2] 彭城, 李国亮, 张红雨, 等.染色质三维结构重建及其生物学意义[J].中国科学:生命科学, 2014, 44(8):794-802. https://www.researchgate.net/profile/Guoliang_Li/publication/270953522_Reconstruction_of_Three-Dimensional_Structures_of_Chromatin_and_Its_Biological_Implications/links/5527968a0cf229e6d6362a53.pdf PENG C, LI G L, ZHANG H Y, et al. Reconstruct 3D chromatin structure and explore the biological significance[J]. Scientia Sinica Vitae, 2014, 44(8):794-802. https://www.researchgate.net/profile/Guoliang_Li/publication/270953522_Reconstruction_of_Three-Dimensional_Structures_of_Chromatin_and_Its_Biological_Implications/links/5527968a0cf229e6d6362a53.pdf
[3] VAROQUAUX N, AY F, NOBLE W S, et al. A statistical approach forinferring the 3D structure of the genome[J]. Bioinformatics, 2014, 30:26-33. doi: 10.1093/bioinformatics/btu268
[4] SERRA F, DI STEFANO M, SPILL Y G, et al. Restraint-based three-dimensional modeling of genomes and genomic domains[J]. FEBS Letter, 2015, 20(589):2987-2995. https://www.researchgate.net/publication/276851437_Restraint-based_three-dimensional_modeling_of_genomes_and_genomic_domains
[5] ROUSSEAU M, FRASER J, FERRAIUOLO M A, et al. Three-dimensional modeling of chromatinstructure from interactionfrequency data using Markov chain Monte Carlo sampling[J]. BMC Bioinformatics, 2011, 12(1):414. doi: 10.1186/1471-2105-12-414
[6] HU M, DENG K, QIN Z, et al. Bayesian inference of spatial organizations of chromosomes[J]. PLoS Comput Biol, 2013, 9:14-29. https://www.researchgate.net/profile/Jun_Liu54/publication/235402588_Bayesian_Inference_of_Spatial_Organizations_of_Chromosomes/links/004635165bb5d5d806000000.pdf
[7] ZHANG Z, LI G, Toh K C, et al. 3D chromosome modeling with semi-definite programming and Hi-C data[J]. ComputBiol, 2013, 20:831-846. https://www.researchgate.net/profile/Kim-Chuan_Toh/publication/258334676_3D_Chromosome_Modeling_with_Semi-Definite_Programming_and_Hi-C_Data/links/5583cc2308ae89172b85f47b.pdf
[8] LESNE A, RIPOSO J, ROGER P, et al. 3D genome reconstruction from chromosomal contacts[J]. Nat Methods, 2014, 11:1141-1143. doi: 10.1038/nmeth.3104
[9] PAULSEN J, GRAMSTAD O, COLLAS P. Manifold based optimization for single-cell 3D genome reconstruction[J]. Computational Biology, 2015, 11(8):e1004396. http://adsabs.harvard.edu/abs/2015PLSCB..11E4396P
[10] LIEBERMAN-AIDEN E, VAN BERKUM N L, WILLIAMS L, et al. Comprehensivemapping of long-range interactions reveals folding principles of the human genome[J]. Science, 2009, 326:289-293. doi: 10.1126/science.1181369
[11] JOURNÉE M, BACH F, ABSIL P, et al. Low-rank optimization on the cone of positive semidefinitematrices[J]. SIAM J Optim, 2010; 20(5):2327-2351. doi: 10.1137/080731359
[12] MISHRA B, MEYER G, SEPULCHRE R. Low-rank optimization for distance matrix completion[C]//Orlando, FL, USA Proceedings of the 50th IEEE Conference on Decision and Control. New York: IEEE, 2011: 4455-4460.
[13] 张卫. 基于Hi-C数据的预测染色体三维结构的方法研究[D]. 北京: 北京工业大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10005-1016785529.htm ZHANG W. The research for predicting three-dimensional structure of chromsomes based on Hi-C data[D]. Beijing: Beijing University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10005-1016785529.htm
[14] YAFFE E, TANAY A. Probabilistic modeling of Hi-C contact maps eliminates systematic biases to characterize global chromosomal architecture[J]. Nat Genet, 2011, 43:1059-1065. doi: 10.1038/ng.947
-
期刊类型引用(2)
1. 何存富，王永慷，高杰，张义政，吕炎. 表面波相控变频电磁声传感器的研制. 仪器仪表学报. 2024(05): 90-98 . 
百度学术
2. 张金，赵亮，石文泽，王鑫，董子华. 曲折线圈电磁超声换能器激励性能优化设计. 传感技术学报. 2019(08): 1182-1188 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 171
- HTML全文浏览量: 3
- PDF下载量: 36
- 被引次数: 4
