水体光场具有方向特性,即二向性,水面遥感反射率 R _rs的二向性不容忽视 . 以往做法是将卫星遥感影像经过大气校正后获得的 R _rs直接代入水质参数模型反演出水色产品,往往省略了二向性校正这个步骤 . 二向性校正可以将不同太阳位置下不同观测方向的 R _rs校正到归一化遥感反射率,从而提高水色产品的精度 . 因内陆水体光学特性的复杂,针对内陆水体二向性的校正还不成熟,以往大多数水质参数反演模型中都忽略了二向性的影响,降低了水质参数遥感反演的精度 . 随着卫星应用产品精度的不断提高,各类静止卫星、多角度卫星和宽幅卫星的不断发展,向内陆水体的二向性研究提出了新的需求 .

水体光场的二向性研究始于大洋清洁水体 . 早在20世纪60年代就有实验证明大洋水体光场存在二向性 ^{[ 1 - 2]} ,不过直到最近30年才出现和发展了大洋水体光场二向性的理论分析和建模 ^{[3 - 9]} . 这些研究都是使用Monte Carlo方法模拟大洋水体光场,进而分析其二向性分布规律 . 早先的Monte Carlo方法是基于以叶绿素a(Chla)质量浓度为参数的固有光学量(inherent optical parameters,IOPs)模型和水分子及颗粒物散射相函数 ^{[ 4 - 5]} ,这种方法的缺点是只能准确地模拟Chla质量浓度小于1mg/m ³的水体光场 . 后来修改了以Chla质量浓度为参数的IOPs模型,并可以根据Chla质量浓度的变化选择不同的散射相函数,修改后的Monte Carlo方法可以准确地模拟各种Chla质量浓度的水体光场 ^{[ 9]} . 有关水体光场二向性的研究,理论模拟采用Monte Carlo方法的占多数,使用商业软件Hydrolight的则较少 . 相比Monte Carlo方法,Hydrolight具有运行速度快、求解辐射传输方程时没有统计噪声等优势 .

与相对成熟的大洋水体光场的二向性研究相比,内陆和近海水体光场的二向性分布规律将比大洋水体复杂得多,相关研究才刚刚起步 ^{[ 10 - 13]} . 水体光场的二向性不仅与波长、太阳天顶角、观测天顶角、观测方位角有关,还与水体IOPs有关 ^{[ 14]} . 值得注意的是,水色遥感中唯一可获得的量是 R _rs,因此水体的IOPs仅能通过 R _rs反演得到,同时需输入IOPs等参量才能完成 R _rs的二向性校正;但是二向性校正的终极目的是为了反演估算准确的IOPs和水体组分 . 由此可见,这个过程是相互缠绕的,困境在于先由 R _rs求解IOPs,还是先完成二向性校正 . 对于大洋水体 ^{[ 5, 9, 15]} 的解决思路是,先由 R _rs粗略估算Chla质量浓度,由Chla质量浓度和先验IOPs模型作为参数,在事先构建好的查找表中得到二向性校正因子,进而完成二向性校正,再由校正后的 R _rs估算Chla质量浓度,不断迭代 . 然而对于内陆水体,光学特性复杂,缺乏可靠的IOPs先验模型,对其进行二向性校正是较为困难的,还有待进一步研究 .

本文选取了太湖5次水体综合试验采集的共250个采样点的实测数据,其中单位固有光学量数据是取了平均值,水质参数是取了测量值分布范围作为输入的初始数据集 . 同时,将这些参数代入水体辐射传输软件Hydrolight模拟了内陆水体光场二向性数据 . 基于该数据,分析了内陆水体光场的二向性分布规律和主要影响要素,可以为下一步建立内陆水体二向性校正模型提供依据,并最终提高水质参数反演精度 .

1 Hydrolight模拟水体光场二向性

1.1 二向性因子及其影响要素

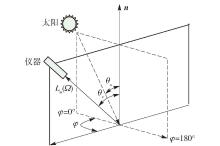
离水辐亮度( L _w, W·m ^{- 2}· sr ^{- 1})不仅随波长变化和随水体组分变化,还随几何角度 θ _s、 θ _v、 φ(用 Ω共同表示)变化, θ _s为太阳天顶角; θ _v为传感器相对星下点观测方向的天顶角; φ为传感器观测方向垂直平面与太阳入射垂直平面的夹角,实际上是相对观测方位角,统一简称为观测方位角 .

为了能够校正离水辐亮度 L _w( λ, Ω)的角度变化,引入了一个假想的物理量——归一化离水辐亮度[ L _w( λ)] _N ,它是假设太阳天顶角和观测天顶角均为零、黑天空(在太阳与水体之间不存在大气)条件下的 L _w . 将 L _w( λ, Ω)转换为[ L _w( λ)] _N 的关系式可以表达为

$\begin{array}{c}\frac{[L_w{\left(\lambda \right)]}_N}{L_w(\lambda ,\Omega )}\end{array}$ = $\begin{array}{c}\frac{F_0\left(\lambda \right)}{E_d(0^{+},\mathit{\lambda },{\theta }_s)}\end{array}\begin{array}{c}\frac{{\left[R\right]}_N}{R({\theta }_s,{\theta }_v)}\end{array}\begin{array}{c}\frac{[f{\left(\lambda \right)]}_N}{f(\lambda ,{\theta }_s)}\end{array}\begin{array}{c}\frac{Q(\lambda ,\Omega )}{[Q{\left(\lambda \right)]}_N}\end{array}$ (1)

式中: F ₀( λ)为日地平均距离下大气层外太阳辐照度,W·m ^{- 2}; E _d(0 ⁺ , λ, θ _s)是当测量 L _w时对应的水面以上下行辐照度;R表示了上行辐亮度由水体进入空气中的界面效应,可以由几何角度计算得到; f为联系水面以下辐照度反射率 R(0 ^- ) = $\begin{array}{c}\frac{E_u(0^{-},{\theta }_s,\lambda )}{E_d(0^{-},{\theta }_s,\lambda )}\end{array}$ 与固有光学量(总吸收系数 a和总后向散射系数 b _b)之间的参量,即 R(0 ^- ) =f $\begin{array}{c}\frac{a+b_b}{b_b}\end{array}$ ; Q表示水面以下上行辐照度与 L _w( λ, Ω)对应的上行辐亮度之间的比值, Q(0 ^- , λ, Ω) = $\begin{array}{c}\frac{E_u(0^{-},\lambda )}{L_u(0^{-},\lambda ,\mathit{\Omega \text{'}})}\end{array}$ .

遥感反射率( R _rs, sr ^{- 1})定义为水面以上上行辐亮度与下行辐照度的比值, R _rs( λ, Ω) = $\begin{array}{c}\frac{L_w(0^{+},\lambda ,\Omega )}{E_d(0^{+},\mathit{\lambda },{\theta }_s)}\end{array}$ . R _rs( λ, Ω)与归一化遥感反射率[ R _rs( λ)] _N 的关系式为

$\begin{array}{c}\frac{[R_{\mathit{rs}}{\left(\lambda \right)]}_N}{R_{\mathit{rs}}(\lambda ,\Omega )}\end{array}$ = $\begin{array}{c}\frac{{\left[R\right]}_N}{R({\theta }_s,{\theta }_v)}\end{array}\begin{array}{c}\frac{[f{\left(\lambda \right)]}_N}{f(\lambda ,{\theta }_s)}\end{array}\begin{array}{c}\frac{Q(\lambda ,\mathit{\Omega })}{[Q{\left(\lambda \right)]}_N}\end{array}$ =G( λ, Ω) (2)

将 L _w( λ, Ω)转换为[ L _w( λ)] _N 或将 R _rs( λ, Ω)转换为[ R _rs( λ)] _N 的二向性校正,归结为确定二向性因子 $\begin{array}{c}\frac{{\left[R\right]}_N}{R({\theta }_s,{\theta }_v)}\end{array}\begin{array}{c}\frac{[f{\left(\lambda \right)]}_N}{f(\lambda ,{\theta }_s)}\end{array}\begin{array}{c}\frac{Q(\lambda ,\mathit{\Omega })}{[Q{\left(\lambda \right)]}_N}\end{array}$ ,这里用综合性因子 G( λ, Ω)统一表示 . 式中的 $\begin{array}{c}\frac{{\left[R\right]}_N}{R({\theta }_s,{\theta }_v)}\end{array}$ 可以求解 . 剩余的未知量是 f( λ, θ _s)和 Q( λ, Ω) . 因此研究水体的二向性校正,就是求解二向性因子 f( λ, θ _s)、 Q( λ, Ω)(以下简写为 f、 Q)或者综合性因子 G( λ, Ω),进而将 L _w( λ, Ω)转换为[ L _w( λ)] _N 或将 R _rs( λ, Ω)转换为[ R _rs( λ)] _N.

事实上, f、 Q受到很多要素的影响,不仅随波长、观测角度变化,还与气溶胶光学厚度 τ _a,风速 W,水体自身IOPs尤其是散射相函数 ^{[ 16 - 17]} 等有关 . f、 Q可以分别写成随变量变化的函数形式 Q[ λ, Ω, τ _a, W,IOPs] , f[ λ, θ _s, τ _a, W,IOPs] . 本文将这些影响要素分为2类:首先, f、 Q随波长、观测天顶角、观测方位角表现出差异变化;其次,太阳天顶角、气溶胶光学厚度、风速、水体固有光学特性等属于二向性因子的驱动型影响要素 . 以下将分别讨论二向性因子随观测角度和波长的变化规律,以及二向性因子受驱动要素的影响规律 . 以及采用了变异系数,即标准差 /平均值表征各个要素对二向性因子 f、 Q的影响程度 .

1.2 辐射传输模拟原理与参数设置

1 .2 .1 Hydrolight模拟原理

采用Hydrolight模拟水体光场分布,一方面研究 f、 Q随观测方向、波段的变化规律,有助于选择更合理的观测方向和波段,降低二向性对于水质参数反演的影响;一方面明确哪些驱动要素是影响水体光场二向性的主导要素,会对水质参数反演精度产生较大影响 .

Hydrolight是美国海洋光学学者Mobley用Fortran语言编写的一套水体光学辐射传输软件,当入射的太阳光、水体各组分的IOPs、边界条件都已知后,Hydrolight采用不变嵌入法解算辐射传输方程,以获得水面以上和水下光场随水深、天顶角、方位角、波长变化的分布情况 .

在设定Hydrolight模拟条件时,需要注意:

1) 坐标系的设定

本文的观测坐标系规定如下:当观测方向铅锤向上时 θ _v为0 °,当观测方向与太阳入射光方向一致时,即背对太阳进行观测时 φ为0 °,当观测方向正对太阳入射光方向时, φ为180 °. φ定义与Hydrolight一致,与唐军武 ^{[ 7]} 的规定则相差180 °. 角度坐标系如 图1所示 . 在讨论 f、 Q随观测方向的变化分析时,采用了该角度坐标系 .

图  1  角度坐标系

Figure  1.  Angle coordinate system

下载: 全尺寸图片 幻灯片

2) 波段的设定

Hydrolight解算辐射传输方程时,是以光学深度 ζ为深度分辨率来运算的,它和几何深度 z的关系是 ζ=c*z, c为光束衰减系数 . 因为在近红波段以后纯水强吸收(在970nm处的吸收系数达到45m ^{- 1})而使 c很大,从而使 ζ很大,而 ζ越大,运行时间越长 . 因此为了保证较快的计算时间,在模拟内陆水体时,除非必要,运行Hydrolight时尽量少地选择红或者近红波段(尤其是超过750nm谱段) .

1 .2 .2 参数设置

为实现水体光场二向性分布规律的研究,首先基于一套具有代表性的数据集作为初始输入条件,然后只变动一个影响因素并固定其他所有因素不变,从而定量分析每个因素对光场二向性的影响 . 因此,需要根据典型内陆水体——太湖的实测数据和经验数据设定了一套初始不变的输入数据集 .

这里选择了太湖水体遥感反射率的特征波长442、467、496、571、632、652、678、697、732、807、831nm作为输出波长 . 太湖大部分湖区的悬浮物浓度较高、透明度较低,光往往在到达湖底之前就已经被散射和吸收了,因此这里设定为光学深水,选择输出深度分别为0、0 .2、0 .6、1 .0m . 水面以上光谱测量规范 ^{[18 - 20]} 中要求 θ _v为30 °~45 °, φ为45 °~90 °,典型的几何设置推荐是 θ _v =40 °, φ=45 °.

Hydrolight中总是默认太阳所处方位角 φ=0 °. θ _s =30 °是太阳天顶角的初始值,取值为0 °、30 °、45 °、60 °、75 °. 因为对于航天光学遥感器来说,过境往往在当地地方时10:00—14:00,因此 θ _s极少会大于75 °. 除了太阳位置,共同确定进入水体的入射光信息的输入参量还包括:水体折射率默认为常数1 .34,气压101 .325kPa、24h平均风速5m/s、相对湿度80 %、平均水平能见度15km、大气可降水量2 .5cm、总臭氧含量330 DU、大气质量类型10(取

值1 ~10,1表示海洋型,10表示大陆型),积日选为第266天(秋分日) . 云量初始值设为0,认为是晴空,变化值为0 %、50 %、100 %. 这里的云量主要是带入Hydrolight的天空辐照度模型RADTRAN-X中简化的经验公式 ^{[ 21]} ,以此修正下行辐照度 . 风速初始值为5m/s,取值为0、5、10、15m/s . 需要说明的是,风速和24h平均风速是2个不同的参量,前者主要是影响水 -气界面粗糙度,后者则主要是影响大气条件进而影响到入射光 . 天空漫射下行辐照度与总下行辐照度的比例,简称漫总比 $\begin{array}{c}{F_{\mathit{dif}}}^{\left[22\right]}\end{array}$ ,该参数在Hydrolight中不能直接设定,通过输入以上参数得到能见度15km和8km分别对应的 F _dif为36 %,52 %.

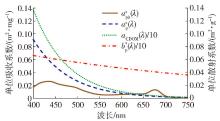
以水体4种组分的固有光学量作为输入,4种组分分别是纯水、悬浮物颗粒、浮游植物颗粒和有色溶解性有机物(color dissolved organic matter, CDOM) . 这里简化的认为水体组分的质量浓度,包括Chla质量浓度 C _Chla、悬浮物质量浓度 C _s、CDOM在440nm处吸收系数 a _CDOM都不随水深变化 . 根据2006年1月、2006年7月、2006年10月、2007年1月和2007年4月在太湖开展了5次试验,每次试验各获取了50个采样点数据,共计250个采样点数据,包括水质参数数据、固有光学量数据 . 统计太湖水体3种组分质量浓度如 表1所示 . 因此初始值 C _Chla =50μg/L, C _s =50mg/L, a _CDOM(440) = 1m ^{- 1} . 3种组分的变化范围分别是: C _Chla的变化值1、10、50、100、1000μg/L; C _s的变化值5、10、50、100、300mg/L; a _CDOM(440) =0 .2、0 .5、1 .0、3 .0m ^{- 1},如 表2所示 .

表  1  太湖的3种水体组分浓度统计情况

Table  1.  Three types of components concentrations in water body of Taihu Lake

3种水体组分	最小值	最大值	均值	方差
C Chla / (μg·L -1)	4 .018	942 .567	42 .659	93 .188
C s /(mg·L - 1)	10 .320	285 .600	74 .842	57 .332
a CDOM(440) /(m - 1)	0 .226	2 .384	0 .818	0 .300

下载: 导出CSV 

| 显示表格

对太湖实测的3种组分单位固有光学量数据求平均作为输入 . 浮游植物色素单位吸收系数 $\begin{array}{c}{a}_{\mathit{ph}}^{*}\end{array}$ ( λ),悬浮物单位吸收系数 $\begin{array}{c}{a}_p^{*}\end{array}$ ( λ),CDOM吸收系数 a _CDOM( λ),悬浮物单位散射系数 $\begin{array}{c}{b}_p^{*}\end{array}$ ( λ)如 图2所示 . 其中, $\begin{array}{c}{a}_{\mathit{ph}}^{*}\end{array}$ (675) =0 .0131, $\begin{array}{c}{a}_{\mathit{ph}}^{*}\end{array}$ (430) / $\begin{array}{c}{a}_{\mathit{ph}}^{*}\end{array}$ (675) =1 .9926; a _CDOM(440) =0 .82,拟合斜率 S _CDOM =0 .0130(当采用模型为 a _CDOM( λ) =a _CDOM(440)·exp( -S _CDOM)·( λ-440)时); $\begin{array}{c}{a}_p^{*}\end{array}$ (440) =0 .056,拟合斜率 S _ap =0 .0123(当采用模型为 $\begin{array}{c}{a}_p^{*}\end{array}$ ( λ) = $\begin{array}{c}{a}_p^{*}\end{array}$ (440)exp( -S _ap)·( λ-440)时); $\begin{array}{c}{b}_p^{*}\end{array}$ (440) =0 .618,拟合斜率 S _bp =0 .00175(当采用模型为 $\begin{array}{c}{b}_p^{*}\end{array}$ ( λ) = $\begin{array}{c}{b}_p^{*}\end{array}$ (440)exp( -S _bp)·( λ-440)时) .

图  2  实测采样点的固有光学量平均值

Figure  2.  Average of the measured inherent optical parameters of sampling points

下载: 全尺寸图片 幻灯片

除去图中提供的单位固有光学量,还需要提供叶绿素单位散射系数、叶绿素散射相函数、悬浮物散射相函数 .

叶绿素单位散射系数 $\begin{array}{c}{b}_{\mathit{ph}}^{*}\end{array}$ 没有实测数据支持,因此采用可以适用于2类水体的GAM模型 ^{[ 23]} :

$\begin{array}{c}{b}_{\mathit{ph}}^{*}\end{array}$ ( λ) =b ₀ X ⁿ $\begin{array}{c}\frac{\mathit{m\lambda }+i}{m{\lambda }_0+i}\end{array}$ (3)

式中: b ₀ =0 .5; X=C _chla; n=0 .62; m=-0 .001126; i=1 .62517; λ ₀ =550 .

叶绿素散射相函数、悬浮物散射相函数没有实测数据 . 按照经验给出后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$ =0 .005, $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ =0 .04,从而Hydrolight会自动调用该后向散射概率对应的散射相函数 ^{[24 - 25]} ,进而积分求得后向散射系数 .

需要说明的是,本文没有考虑水体的非弹性散射,包括Raman散射、叶绿素荧光、CDOM荧光、生物体发光 . 因为对于太湖这类较浑浊的水体,非弹性散射往往会被高强度的散射作用所掩盖 .

表  2  模拟太湖水体光场的输入变量

Table  2.  Input variables of the simulation of water body light field in Taihu Lake

	变量	输入
表现要素	波长 /nm	442,467,496,571,632,652,678,697,732,807,831
	θ v /(°)	0,10 .0,20 .0,30 .0,40.0,50 .0,60 .0,70 .0,80 .0,87 .5
	φ/( °)	0, 15, 30,45, 60, 75, 90, 105, 120, 135, 150, 165,180
		195, 210, 225, 240, 255, 270, 285, 300, 315, 330, 345, 360
驱动要素	θ s /(°)	0,30,45,60,75
	C chla/(μg·L -1)	1,10,50,100,1000
	C s /(mg·L - 1)	5,10,50,100,300
	a CDOM(440) /(m - 1)	0 .2,0 .5,1.0,3 .0
	叶绿素后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$	0 .001,0.005, 0 .010
	悬浮物后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$	0 .010, 0 .018, 0 .030,0.040
	天空漫射下行辐照度与总下行辐照度的比例 /%	F dif(430 ~454) =36,52
	云量 /%	0,50,100
	风速 /(m·s - 1)	0,5,10,15
	水深 /m	0,0 .2,0 .6,1 .0
注:下文中如不做出特殊说明,初始数据集默认选择表中加黑的参数设置 .

下载: 导出CSV 

| 显示表格

2 分析

2.1 二向性因子随观测角度和波长的变化分析

根据 表1的初始数据集的输入参数,得到模拟的太湖水体光场分布,不同角度的 R _rs光谱如 图3所示 . 初步分析多角度 R _rs得到, R _rs( θ _v:60, φ:90) >R _rs( θ _v:60, φ:45) >R _rs( θ _v:30, φ:90) >R _rs( θ _v:30, φ:45) >R _rs( θ _v:0),观测天顶角越大、观测方位角越大, R _rs的值一般也越大 .

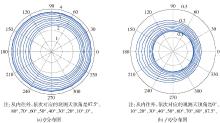
由于波长571nm对应的 R _rs较大,也就是说能够较好地呈现不同观测角度下的差异 . 本文选取了波长571nm处 Q、 f/Q,绘制了极坐标图讨论 Q、 f/Q随观测方位角的变化,如 图4所示 . 极坐标图的极角表示观测方位角,极径表示二向性因子 Q、 f/Q的数值 . 如果圆形越规则,表明朗伯性越好;椭圆形变形越大朗伯性越差,二向性越明显 . 由 图4可以观察得出,随观测天顶角增大、观测方位角增大, Q不断减小, f/Q不断增大,且水体光场二向性越强 . f/Q的变化更多地体现在观测方位角90 °~270 °的范围,尤其体现在观测方位角150 °~210 °内,但是 f/Q随观测方位角的变化没有观测天顶角的大 .

图  3  模拟的多角度 R _rs光谱

Figure  3.  Simulation of multi-angular R _rs spectra

下载: 全尺寸图片 幻灯片

图  4  571nm处不同观测天顶 Q、 f/Q随观测方位角变化

Figure  4.  Different viewing zenith angles Q, f/Q change with viewing azimuth angles at 571nm

下载: 全尺寸图片 幻灯片

由模拟结果计算得出:当波段固定在某一位置,如571nm处,观测天顶角在0 °~40 °变化, f/Q的变化都大于3 .39 %,最大达到6 .02 %;当波段固定在某一位置,如571nm处,观测方位角在0 °~180 °变化, f/Q的变异系数在2 .63 %以内 .

当 θ _v固定在40 °时, φ在0 °~180 °变化, f/Q的变异系数如 表3所示 . 由 表3得出, f/Q在每个不同波段内随观测方位角的变化在3 .5 %以内,其中变化最大的是 f/Q(732nm),达到3 .37 %.

表  3  θ _v =40°, φ=0°~180° 内不同波段 f/Q的变异系数

Table  3.  θ _v=40°, φ=0°~180°, the coefficients of variation of f/Q at different wavelengths

波段 /nm	442	467	496	571	632	652	678	697	732	807	831
(标准差 /均值) /%	3 .08	3 .15	3 .13	2 .63	2 .70	2 .75	3 .05	2 .84	3 .37	3 .41	3 .23

下载: 导出CSV 

| 显示表格

当 φ固定在45 °时, θ _v在0 °~40 °或0 °~87 .5 °变化, f/Q的标准差 /均值如 表4所示 . 由 表4得出: 1) 当观测天顶角的变化范围越大,观测方向对于 f/Q的影响越大; 2) 观测天顶角在0 °~87 .5 °变化, f/Q的变异系数在10 %以上;观测天顶角在0 °~40 °变化, f/Q的变异系数在5 %量级 .

表3、4还表明:1) f/Q随观测天顶角的变化大于随方位角的变化; 2) 观测方向对所有波长的 f/Q都有影响,对蓝光波长范围和近红波长范围的 f/Q的影响大于对绿光和红光的影响 . 该规律引申到水质参数反演上面,仅考虑二向性影响,尽量选用绿光和红光波长范围内的遥感反射率优于蓝光和近红波长范围内的遥感反射率 .

当 θ _v固定在40 °时,波长在442 ~831nm内变化, f/Q的变异系数如 表5所示 . 由 表5得, f/Q在每个观测方位角内随波段的变化都很大,且都大于8 .50 %,最大达到9 .54 %,对应的是75 °观测方位角 .

当 φ固定在45 °时,波长在442 ~831nm变化, f/Q的标准差 /均值如 表6所示 . 由 表6得, f/Q在每个观测天顶角内随波段的变化较大,都大于4 .00 %;观测天顶角越小, f/Q受波段变化的影响越大,最大达到10 .83 %.

表  4  φ=45°, θ _v =0°~40°或87.5° 内不同波段 f/Q的变异系数

Table  4.  Coefficients of variation of f/Q at different wavelengths when φ=45°, θ _v=0°~40° or 87.5°

波长 /nm		442	467	496	571	632	652	678	697	732	807	831
(标准差 /均值) /%	θ v =0 °~87 .5 °	19 .90	18 .23	16 .52	12 .18	12 .11	12 .20	13 .63	12 .40	16 .14	16 .69	18 .86
	θ v =0 °~40 °	5 .01	4 .80	4 .53	3 .57	3 .56	3 .59	3 .95	3 .65	4 .43	4 .50	4 .70

下载: 导出CSV 

| 显示表格

表  5  θ _v =40°, 在11个特征波段内不同观测方位 f/Q的变异系数

Table  5.  Coefficients of variation of f/Q at different viewing azimuth angles in 11 wavelengths, θ _v=40°

观测方位 φ/( °)	0	15	30	45	60	75	90	105	120	135	150	165	180
(标准差 /均值) /%	9 .29	9 .31	9 .37	9 .45	9 .51	9 .54	9 .50	9 .40	9 .25	9 .07	8 .90	8 .79	8 .75

下载: 导出CSV 

| 显示表格

表  6  φ=45°, 在11个特征波段内不同观测天顶角 f/Q的变异系数

Table  6.  Coefficients of variation of f/Q at different viewing zenith angles in 11 wavelengths, φ=45°

观测天顶 θ v /( °)	0	10	20	30	40	50	60	70	80	87 .5
(标准差 /均值) /%	10 .83	10 .65	10 .40	10 .02	9 .45	8 .60	7 .39	5 .90	4 .48	4 .13

下载: 导出CSV 

| 显示表格

表5、6的结果表明:1) f/Q随波段的变化大于随观测天顶角和观测方位角的变化; 2) 一直以来将 f/Q看作不随波段变化的常量的简化做法,需要改进 .

综上所述,得出:1) 观测天顶角越大、观测方位角越大, R _rs越大, Q不断减小, f/Q不断增大 . 2) f/Q随波段的变化大于随观测天顶角的变化, f/Q随观测天顶角变化大于随观测方位角的变化 . 3) 观测方向对不同波长的 f/Q影响不同,对蓝光和近红波段 f/Q的影响大于对绿光和红光 f/Q的影响 . 4) 当观测天顶角的变化范围越大,观测方向对于 f/Q的影响越大 . 观测天顶角在0 °~40 °内变化, f/Q的变异系数在5 %量级 . 观测天顶角在0 °~87 .5 °内变化, f/Q的变异系数在10 %以上 . 5) 当观测方位角在90 °~270 °,尤其在150 °~210 °,观测方向对于 f/Q的影响较大 .

2.2 驱动要素对二向性因子的影响分析

影响水体光场二向性的驱动要素主要包括太阳天顶角、气溶胶光学厚度、风速、水体固有光学特性等 . 其中,气溶胶光学厚度影响了气 -水界面以上的入射光,进而影响了水体光场的分布 . 而漫总比也是受大气状况决定的物理量,因此这里用该因素替代气溶胶光学厚度,讨论对二向性因子的影响 . 以下将逐个讨论太阳天顶角、水体成分的质量浓度( C _Chla、 C _s、 a _CDOM)、叶绿素后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$ 、悬浮物后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ 、漫总比、云量、水面粗糙度(风速)等各因素对光场二向性因子 Q、 f/Q的影响规律 .

综上得出,观测方向对于蓝光和近红波段的 f/Q影响较大,又因为常用的太湖悬浮物浓度反演波段是近红波段 ^{[ 26 - 28]} ,因此下文如不特别指出,则默认为807nm处的 Q、 f/Q参与讨论,同时将观测几何固定为 θ _v =40 °, φ=45 °.

太阳天顶角 θ _s为0 °~75 °时, Q的变异系数是6 .43 %, f/Q的变异系数是4 .66 %. 但是遥感器过境时一般都是地方时中午附近,太阳天顶角不会过大,太阳天顶角最大取值往往对应当地冬季,例如冬季太湖正午14时的太阳天顶角能达到60 °. 当 θ _s为0 °~60 °时, Q的变异系数为5 .69 %, f/Q的变异系数为3 .85 %. 当 θ _s为0 °~45 °时, Q的变异系数为4 .68 %, f/Q的变异系数为2 .98 %. 由此可见,太阳天顶角是一个不容忽视的影响水体光场二向性的驱动要素,应尽量选择太阳天顶角较小时的遥感影像,会引入较少的二向性误差,从而提高水质参数的反演精度 .

悬浮物质量浓度 C _s为5 ~300mg/L时,同时假定悬浮物单位吸收系数、悬浮物单位散射系数、悬浮物后向散射概率都不变,此时 f/Q的变异系数为20 .93 %, Q的变异系数为4 .25 %. 随着 C _s增大, Q不断减小, f/Q不断增大 . 由此可见,水体 R _rs(807nm)的二向性受 C _s的影响较大 . 因此在反演太湖等较浑浊水体的 C _s并采用近红波段时,需要重点对待反演模型中的二向性因子 f/Q,会直接影响到 C _s的反演精度 .

叶绿素a质量浓度 C _Chla从1 ~1000μg/L变化时,同时假定浮游植物色素单位吸收系数、浮游植物色素单位散射系数、叶绿素后向散射概率都不变, Q (678nm)和 Q (807nm)的变异系数分别3 .60 %和0 .02 %, f/Q(678nm)和 f/Q(807nm)的变异系数分别为14 .88 %和2 .63 %. 总体来说,叶绿素a质量浓度1000μg/L是非常极端的情况,一般地,太湖较高叶绿素a质量浓度能够达到几百mg/L . 当 C _Chla在1 ~100μg/L变化时, Q (678nm)和 f/Q (678nm)的变异系数分别是1 .53 %和6 .60 %. 由此可见,水体 R _rs(678nm)的二向性受 C _Chla的影响较大,同时 R _rs(807nm)的二向性受 C _Chla的影响较小 . 在反演太湖等较浑浊水体的 C _Chla并采用红波段时,不能忽视反演模型中的二向性因子 f/Q,它会直接影响到 C _Chla的反演精度 .

a _CDOM是从蓝光到近红波段呈负指数衰减的,因此CDOM对蓝光波段要比对红和近红波段的 Q、 f/Q影响会更大些 . 因此针对要素 a _CDOM,研究 f/Q(442nm)要比研究 f/Q(807nm)更有意义一些 . a _CDOM在0 .2 ~3m ^{- 1}变化时, Q(442nm)和 f/Q(442nm)的变异系数分别为0 .02 %和0 .08 %. 由此可见,水体 R _rs(442nm)的二向性受 a _CDOM的影响较小 .

叶绿素后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$ 为0 .001 ~0 .010时,假设服从Fournier-Forand散射相函数的分布, Q(678nm)和 Q(807nm)的变异系数分别是0 .05 %和0 .02 %, f/Q(678nm)和 f/Q(807nm) 的变异系数分别为0 .60 %和0 .61 %. 由此可见,叶绿素后向散射概率对 Q或 f/Q的影响不大 .

悬浮物后向散射概率 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ 为0 .010 ~0 .040时,假设服从Fournier-Forand散射相函数的分布, Q(807nm)的变异系数是3 .68 %, f/Q(807nm) 的变异系数是5 .63 %. 随着 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ 增大, Q不断减小, f/Q不断增大 . 可见,悬浮物后向散射概率对 Q或 f/Q的影响较大 .

漫总比 F _dif随波段变化,从蓝光波段向长波波段呈负指数递减 . 因此这里考察了蓝光波段的 F _dif . Hydrolight的天空模型是按照每个特征波段所在的波段区间积分计算得到 F _dif,即

F _dif = $\begin{array}{c}\frac{{\int }_{\lambda }^2{E}_{\mathit{dif}}\left(\lambda \right)\mathit{d\lambda }}{{\int }_{\lambda }^2{E}_{\mathit{dif}}\left(\lambda \right)\mathit{d\lambda }+{\int }_{\lambda }^2{E}_{\mathit{dir}}\left(\lambda \right)\mathit{d\lambda }}\end{array}$ = $\begin{array}{c}\frac{E_{\mathit{dif}}}{E_{\mathit{dif}}+E_{\mathit{dir}}}\end{array}$ = $\begin{array}{c}\frac{E_{\mathit{dif}}}{E_{\mathit{total}}}\end{array}$

这里选择了430 ~454nm(中心波长442nm)作为 F _dif的积分区间 . 同时选择了15km和8km能见度,通过改变不同的气溶胶光学厚度来改变 F _dif,分别对应的 F _dif(430 ~454nm)为36 %和52 %. 当 F _dif从36 %变化到52 %时, Q(442nm)相对增加了0 .148 %, f/Q(442nm)相对增加了1 .866 %. 可见, F _dif对 Q或 f/Q的影响不大 .

云量为0 %~100 %时, Q的变异系数为3 .69 %, f/Q的变异系数为3 .51 %. 可见,云量对 Q或 f/Q的影响较大 . 一般地,常用的遥感图像往往是晴空条件获取的,因为有云的情况太过复杂,目前还没有统一的模型来研究,Hydrolight也仅仅是采用非常简化的模型 ^{[ 21]} 来校正直射和漫射天空光,因此本文对云量的分析仅限于对Hydrolight模拟结果的探讨,不具有普遍意义 .

风速为0 ~15m/s时, Q的变异系数为0 .37 %, f/Q的变异系数为0 .53 %. 可以看出风速对光场的影响较小 . 这与Morel ^{[ 4]} 和Gordon ^{[ 3]} 的结论一致,小于10m/s的风速对水体二向性的模拟可以忽略 . Park等 ^{[ 29]} 曾给出风速(0, 5、10m/s)对于二向性反射率的影响非常小 . 值得注意的是,Hydrolight考虑风速的影响时,只是将该参量代入到水表面粗糙模型中进行修正,并没有考虑到风扰动水体内部的情况 . 事实上对于太湖这样的水体,风速大于5m/s,就会使湖底悬浮物再悬浮,从而影响水下光场,扰乱了水体光场的二向性分析 .

综上, θ _s、 C _s、 C _Chla、 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ 、云量对水体光场的二向性影响较大,是影响水体光场二向性的主要影响因子,在反演浑浊类水体的水质参数时以上这些模型参量需要慎重对待,会对水质参数的反演精度产生较大的影响 . a _CDOM、 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$ 、 F _dif、风速对 Q或 f/Q的影响不大,可以忽略 .

3 结论

1) 二向性因子 f、 Q是内陆水质参数反演分析模型中的输入参数,它的取值会对水质参数反演结果产生影响 . 本文研究二向性因子随观测方向、波段等要素的变化规律如下:

① f/Q随波段的变化大于随观测天顶角和观测方位角的变化, f/Q随观测天顶角变化大于随观测方位角的变化 .

② 观测方向对不同波长的 f/Q影响不同,对蓝光和近红波段 f/Q的影响大于对绿光和红光 f/Q的影响 .

③ 当观测天顶角的变化范围越大,观测方向对于 f/Q的影响越大 .

④ 当观测方位角在90 °~270 °内,尤其在150 °~210 °范围内,观测方向对于 f/Q的影响较大 .

2) 该规律有助于选择更合理的观测方向和波段,降低二向性因子对于水质参数反演的影响:

① 仅考虑二向性影响,水质参数遥感反演时尽量选用绿光和红光波段的遥感反射率,可以适当减小方向性观测引入的误差 .

② 应尽量选择观测天顶角在40 °范围内,观测方位角在0 °~150 °和210 °~360 °内的反射率数据,如果观测天顶角大于40 °或观测方位角在150 °~210 °内,应考虑对遥感反射率进行角度归一化较正 .

③ 应将 f/Q看作随波段变化的参数代入反演模型 .

3) 本文研究了驱动要素对于二向性因子的影响规律,明确了 θ _s、 C _s、 C _Chla、 $\begin{array}{c}{\dot{b}}_{\mathit{bp}}\end{array}$ 、云量是是影响水体光场二向性的主导要素,尤其在反演浑浊类水体水质参数时需要慎重对待 . a _CDOM、 $\begin{array}{c}{\dot{b}}_{\mathit{bph}}\end{array}$ 、 F _dif、风速对 Q或 f/Q的影响不大,可以忽略 .

致谢:感谢李俊生博士、张运林博士等在2006年1月、2006年7月、2006年10月、2007年1月和2007年4月太湖5次水体光学试验数据采集中所作的贡献 . 感谢黄昌春博士对本文提出的宝贵意见 .