Different Strategies in Solving Arithmetic Calculation Problems
-
摘要:
为了清楚人脑进行加法计算和减法计算的神经机制,探索加法计算和减法计算的不同策略引起对应脑区激活差异,采用思维的自适应控制-理性(adaptive control of thought-rational,ACT-R)建模结合行为实验的方法从更细时间微粒对人类进行加法计算和减法计算的脑区协同工作原理进行研究. 行为实验结果反应时,加法运算的真实反应时为(1812.14±224.14)ms;减法运算的真实反应时为(2328.14±287.36)ms;加法运算的正确率为97.92%±2.67%,减法运算的正确率为74.38%±11.3%. ACT-R仿真实验结果为:ACT-R模拟反应时,加法运算为1813.96ms;减法运算为2314.53ms;模拟结果和真实结果的血氧水平依赖(blood oxygen level dependent,BOLD)信号变化率在左侧前额皮层(left prefrontal cortex,LPFC)脑区拟合结果为96%,在后顶叶(posterior parietal cortex,PPC)脑区拟合结果为98%. 实验结果表明:人脑完成减法计算比完成加法计算更为复杂.
-
关键词:
- 加法计算 /
- 减法计算 /
- 神经机制 /
- 自适应控制-理性(ACT-R)
Abstract:To make the brain neural mechanism of the addition and subtraction calculation clear and explore different strategies of the addition and subtraction calculations corresponding to the activating differences of the brain regions. An ACT - R model of meeting behavior experiment method was adopted to study the cognitive processing mechanism of the addition and subtraction calculations in finer time particles. The behavioral experiment results show that the the reaction time of the addition is (1812.14±224.14)ms and the subtraction is (2328.14±287.36)ms. And the accuracy of the addition is 97.92%±2.67%, while the subtraction is 74.38%±11.3%. The ACT - R model results show that when in ACT-R simulation, the addition is 1813.96ms, while the subtraction is 2314.53ms. And the fitting result between the model result and the real result of BOLD response in LPFC is 96%, while in PPC is 98%. Results show that the subtraction is much more complex than the addition.
-
Keywords:
- addition /
- subtraction /
- neural mechanism /
- ACT-R
-
加减法计算的认知加工过程传统上是人工智能最重要的组成部分,采用不同任务研究人类认知加工的神经基础包含判断任务、比喻任务、数字任务 [ 1] . 这些研究结果都显示了额顶叶区域有左侧偏侧化现象,但是不同实验任务内容的激活模式具体细节不同. 由于人类认知计算加工过程的神经关系目前还不清楚,因此需要更多的实验设计对其进行研究. 一些当代心理学理论根据认知加工过程的认知架构特征提出了关于认知架构的2种理论 [ 2] . 模块化理论认为人脑包含专门的提取与计算模块,激活对应的脑区,执行模块进行认知加工和信息封装. 通用理论观点认为,人脑包含一般的认知加工系统. 双处理加工过程理论基于通用系统即关联系统和基于规则系统 [ 3] 提出加减法计算实验范式. 双加工过程模型预测不同认知计算需要不同的神经系统参与,主要和认知任务设计内容相关. 当任务简单时,进行认知计算的响应脑区得以充分调用以得出正确的结果,主要参与脑区包含额下回、后顶叶与颞叶. 当处理较困难的任务时需要基于规则的系统来进行正确的认知计算,包含前额叶以及进行规则调用的腹外侧前额叶皮层 [ 4] . 但仍需要更多的功能磁共振成像技术(functional magnetic resonance imaging,fMRI)实验研究来验证这些理论.
1 相关研究内容
1.1 算术计算任务
算术计算是一种典型的认知计算加工任务,经常被用来研究人工智能测试 [ 5] ,包含加法计算(12+13=25)和减法计算(25-13=12). 加法计算和减法计算采用不同的计算方法. 证据显示加法计算与减法计算采用不同的策略(策略是被试者经过深思熟虑后一个有目的的加工过程),每个计算等式之间又有共同的原理,相对于减法计算,加法运算更加容易. 其结果已经被笔者团队的行为研究与fMRI研究所证实 [ 6] ,被试要求在统一规则下完成2种算术计算任务. 在加法计算时采用提取策略,加数与被加数的关系可以从长时间记忆对应的算术知识库中直接获得(例如,12+13=25: 2+3=5, 1+1=2,所以结果等25). 减法计算则采用混合计算策略,被试需要进行多次计算才能找出减数与被减数之间的关系(例如, 25-13=12:2+3=5,因此5-3=2; 1+1=2,因此2-1=1). 从影像学角度进行策略调查研究有助于丰富人们理解认知计算激活脑区位置、强度与持续时间的神经机制. 本研究目标是研究人类进行认知计算加工过程中的“独立策略”与“策略依赖”脑区(“独立策略”脑区表示2种认知计算都有共同激活的脑区;“策略依赖”脑区表示2种策略各自特有的激活脑区).
提取策略和混合策略进行认知计算加工时包含相同的激活脑区(陈述性记忆的提取被用来探测处理对象之间的关系、内部表征,保持以及输出响应),但是2种策略对工作记忆的需求程度不同. 在提取策略中(例如, 12+13=25),被试可以直接从对应的算术知识库中(例如, 2+3=5,1+1=2)直接提取他们的结果;在混合策略中,被试需要进行2次计算(例如, 25-13=12:2+3=5,因此5-3=2;1+1=2,因此2-1=1),以及2次内部计数的保持和更新. 因此相对于提取策略,混合策略需要更多的工作记忆参与. 2种策略由于对工作记忆负荷需求不同而需要不同的参与脑区. 可以预测2种策略的差异是由于相同脑区内部激活程度不同,包括负责记忆提取的左前额叶和负责心理表征的后顶叶 [ 7] .
1.2 ACT-R建模
本研究的第2个目标是采用认知计算模型对不同的策略进行预测. 基于上面的说明,期望解释以相同脑区参与程度的不同来区分不同的策略. 为了使预测更加准确(行为数据和激活程度),采用自适应控制-理性(adaptive control of thought-rational, ACT-R)建立实验任务的计算模型 [ 8] .
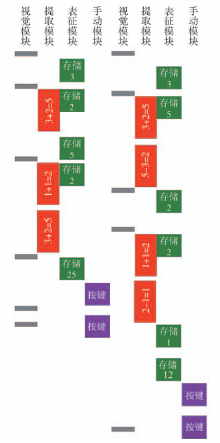
根据ACT-R理论,认知过程是产生式系统中不同外围/内部模块的激活结果 [ 9] . 外围模块包括用来感知的视觉和听觉模块以及与外部世界进行交互的手动和口动模块. 主要的认知模块包含执行核心产生式系统的产生式规则以及用来信息提取的陈述性记忆模块,目标模块负责状态控制,映像表征模块负责问题状态表征,陈述性记忆模块负责信息提取. 模块之间的相互作用依赖于对应的缓冲器模块. ACT-R的知识表征包含陈述性知识和程序性知识2种. 陈述性知识对应于已经知道的以及经常向他人描述的知识. 程序性知识是不能意识到,但可以用行为表达的知识. 在ACT-R中,用结构表达陈述性知识被称为块,采用规则表示程序性知识称为产生式. 这样块和产生式成为构建ACT-R模型的基本模块.
ACT-R中的一些参数能够被预测,包括视觉注意的时间参数、陈述性知识提取的时间,映像表征模块的内容改变时间等是为了准确预测血氧水平依赖(blood oxygen level dependent,BOLD)变化率的时间变化过程,采用伽玛函数来表达ACT-R的模块激活程度. 一旦模块参与就会产生一个BOLD 变化的延迟时间 t对应的函数 [ 9] ,即
H( t) =m( t/s) α e - ( t/s )(1)
式中: m为决定函数曲线高度的级参数; s为决定时间标度的尺度参数; α为决定函数形状宽窄的形状参数. 特定模块的累计BOLD响应是各个模块激活对应的BOLD响应之和. 采用血液动力学响应函数 H( t)与需求函数 D( t)的卷积方式模拟累计BOLD变化率. 当与脑区对应的模块激活时,预测值为1;否则为0.
H( t) =αm( t/s) α e - ( t/s )(2)
一旦设定好缓冲器行动时间,可以通过各个脑区对应的级参数 m、形状参数 α和延迟尺度参数 s来预测BOLD信号变化率. 可以发现,ACT-R模型能够解释行为绩效,同时能够知道与脑区相关的激活模式是否能够预测.
本任务的表现不同主要是由于2种策略的提取和保持需求不同 [ 10] . 2个模块在研究中有特定的意义:主要负责陈述性记忆提取的外侧前额叶脑区对应的陈述性记忆提取模块,以及主要负责问题编码和保持的后顶叶脑区对应的映像表征模块. 由于采用混合策略时需要更多的提取和保持,因此相对于提取策略(加法计算),采用混合策略(减法计算)时期望前额叶与后顶叶脑区的激活更加强烈. 同时,从经验和计算模型角度验证2种理论.
2 材料和方法
2.1 道德声明
本实验中的被试由首都医科大学安定医院道德委员会认定. 实验开始之前,被试签署告知书后对其进行实验内容的解释. fMRI实验在首都医科大学宣武医院完成.
2.2 被试
22名(男14名,女8名)来自北京工业大学在校本科生及研究生参与并完成该实验,采用DSM-IV的MINI6.0. PHQ-9和QIDS对被试进行测评判定. 被试的人口统计学与临床特征如 表1所示. 剔除标准:1)不是右利手;2)没有精神类及神经类疾病;3)
表 1 被试人口统计学及临床特征Table 1. Clinical features and demographic of health controls特征 正常被试(22名) P值 性别比例(男:女) 14:8 1.00 平均年龄/岁 24.3 ± 3.2 0.91 受教育时间/a 14.2 ± 3.8 0.93 以往头部没有创伤;4)无酒精滥用及依赖;5)非幽闭症患者.
2.3 实验设计
所有被试在任务实验开始之前有5min的休息,休息及任务实验过程保持眼睛睁开. 实验设计是结合前期相关实验范式并进行修改得到 [ 11] ,每个块设计包含4个相同的任务. 被试先休息后开始心算任务. 休息和任务交替呈现,任务包含没有进位与退位的两位数加减法运算等式. 实验前已经对算术运算等式的难易程度进行了验证.
每个BLOK有4个相同事件构成,每个事件持续6s. 当任务出现时,被试将注意力转移到算术问题,然后判断屏幕上显示的运算等式结果是否正确,并按相应按键(正确按左键,错误按右键),同时记录每个响应的反应时和正确率. 每个计算等式结果正误率各50%,偏离答案程度±1或者±10. 每个数字出现的概率是一样的,每个数字被操作的可能性为50%. 不采用重复或者结果等于0的计算等式(例如,23+23、36-36). 整个任务包含8个块设计,当任务执行时得到相应的任务数据.
2.4 数据预处理
采用SPM8 (http://www.fil.ion.ucl.ac.uk)软件对数据进行预处理,采用REST软件的功能连接提取相应的BOLD数据 [ 9] ,运行环境是Matlab2010b开发平台. 剔除任务态的前2个数据以均匀磁场. 采用时间校正和空间校正对人体移动进行校正. 剔除头动平移超过3mm、旋转超过3°的被试数据. 高分辨率的解剖图像通过EPI序列的平均图像处理,然后空间标准化到蒙特神经研究院(Montreal neurological institute,MNI)模板上. 然后采用标准化处理EPI映像数据,体积设置为3mm×3mm×3mm. 采用8mm等方向的高斯函数对标准化后的任务态数据进行高斯平滑处理.
2.5 功能数据分析
2.5.1 确定性分析
仅对正确的数据进行分析(错误响应事件超过一半和干扰事件大于要求的数据不进行分析). 响应时间是从计算等式呈现到按键响应之间持续的时间. 采用带有时间导数的标准HRF记录BOLD信号,反应时(response time,RT)表示每个事件持续的时间. 根据一般线性模型估算每个体素的刺激影响程度,采用线性对比方法比较特定脑区的激活程度. 每次对比产生一个 t统计的参数统计图,接着参数统计图被转换成统一的标准 z分布. 采用随机效应分析每个被试的对比映像数据以确定采用 t检验模板得到被试激活最强的脑区.
2.5.2 探索性分析
感兴趣脑区(region of interest, ROI)分析主要关注ACT-R中2个预定义脑区即外侧前额叶和后顶叶脑区. 采用SPM8中的一般线性模型得到2个ROIs脑区平均 β值的统计结果.
为了使本研究与以往研究具有相关性,研究了加法计算与减法计算任务的相应脑区激活差异. 可以通过以下2步得到共同激活图:首先输出加法计算激活图作为标记,然后在此标记中分析减法计算激活脑图. 采用内容对比的交互方式(加法计算-减法计算和减法计算-加法计算)分析每个策略的特定脑区. 激活结果显示体素水平密度阀值 p<0.05下的整个脑区错误发现率(false discovery rate,FDR).
2.6 ACT-R分析
对实验结果进行分析,在ACT-R理论框架下对实验结果进行解释. 构建的模型主要依赖视觉感知刺激,手动模块响应刺激,提取模块从记忆库中提取知识,映像表征模块编译和更新存储表征. 通过程序模块调用这些模块之间的交互 [ 12] . 例如以下假设为加法计算的产生式规则:
如果目标为解决数字计算问题
问题形式为“数字1,数字2,数字3”
“数字1 + 数字2 = 数字4”
然后判断屏幕显示结果数字3是否等于计算结果数字4前额叶脑网络特定感兴趣脑区对应的提取模块和映像表征模块在认知计算研究中起着非常重要的作用. 解释2个模块的BOLD响应的预测过程. 图1以加法计算(13+12=25)和减法计算(25-13=12)为例解释ACT-R四个相关缓冲器激活的结果. 每个方块反映缓冲器激活的时间范围,方块的垂直高度表示缓冲器的持续时间长短. 根据 图1的加工过程与其响应时间,验证前额叶区域的BOLD信号响应可以被预测.
3 结论
3.1 行为数据分析结果
从2个角度对变量进行分析:加法计算和减法计算的反应时和正确率. 行为结果显示被试以期望方式解决任务(如 表2所示). 加法计算和减法计算的主要作用在RT和正确率方面比较显著:相对于加法计算,减法计算的响应显著较大( F(1,21)=93.24, p<0.001),正确率较低( F(1,21)=59.61, p<0.001);说明这种显著的交互作用主要由策略的不同引起.
表 2 行为结果Table 2. Behavioral scores计算 反应时/ms 正确率 /% 加法 1812±224.14 97.92±2.67 减法 2328±287.36 74.38±11.3 3.2 功能数据分析结果
3.2.1 确定性分析结果
采用加减法计算方式对2个ROIs脑区做反复实验分析. 2个ROIs脑区显示同一模式. 加法计算对应的主要激活脑区及T检验结果为(左侧前额叶(left prefrontal cortex,LPFC): F(1,21)=34.26, p<0.001; PPC: F(1,21)=13.07, p<0.01),减法计算为(LPFC: F(1, 21)=71.02, p<0.001; 后顶叶(posterior parietal cortex,PPC): F(1,21)=28.92, p<0.001). 比较显示,策略不同导致交互作用效应不同,例如减法计算任务和加法计算任务不同(LPCF: F(1,21)=47.36, p<0.001; PPC: F(1,21)=9.97, p<0.001).
3.2.2 探索性分析结果
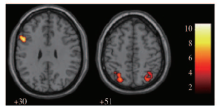
加法计算和减法计算2个任务的2个主效应具有相似的激活模式 [ 10] . 加法计算和减法计算共同激活了腹外侧前额叶皮层(left dorsolateral prefrontal cortex,DLPFC)即BA46/9,与双侧顶叶(bilateral superior parietal lobe,SPL)即BA7,以及左侧顶下小叶(left inferior parietal lobe,IPL)即BA40,如 表3、 图2所示. 减法计算-加法计算发现激活的脑区有双侧额上回(bilateral superior frontal gyrus,SFG)即BA6/8、脑岛(insula) 即BA13、双侧额下回(bilateral inferior frontal gyrus,IFG)即BA46/47、顶上小叶(superior parietal lobule,SPL)即BA7等,如 表4所示.
表 3 2种策略共同激活脑区Table 3. Regions activated commonly to both strategies脑区 BA分区 簇大小 坐标 T值 x y z 左额中回 46 71 -48 27 21 12.03 左额下回 9 -51 12 30 10.82 右额中回 6 -51 3 45 7.34 左顶上小叶 7 26 -27 -63 45 8.01 -24 -69 51 7.43 右顶上小叶 7 63 30 -72 51 5.94 27 -63 48 6.02 表 4 混合策略激活脑区Table 4. Regions specific to mixed strategy脑区 BA分区 簇大小 MNI坐标 T值 x y z 左额上回 6 1356 -3 12 54 9.85 -9 3 60 8.09 左脑岛 13 -30 24 3 7.75 右额下回 47 374 30 21 -6 8.06 46 45 18 27 4.61 右额上回 8 507 3 15 54 7.45 右扣带回 32 9 24 33 6.48 右额内侧回 9 3 39 36 6.11 左额下回 47 16 -33 30 -3 7.43 右额下回 47 13 33 30 -3 6.02 左顶上小叶 7 344 -12 -57 48 4.08 右顶上小叶 7 250 36 -75 45 4.38 右楔前叶 7 12 -66 51 4.05 左丘脑 256 -9 -12 3 4.88 左苍白球 -12 3 6 4.53 右尾状核 178 9 6 6 5.08 右壳核 15 0 9 4.87 采用RT作为变量对加法计算和减法计算任务的难易程度进行研究. 发现完成加法计算任务时对应DLPCF和PPC脑区有激活但是体素个数较少. 同时发现解决减法计算时由很多额叶脑区激活例如额中回(medifrontal gyri,MeFG)和额下回(inferiorfrontal gyri,IFG)脑区,但是在加法计算时没有发现这2个脑区有激活.
3.3 ACT-R仿真结果
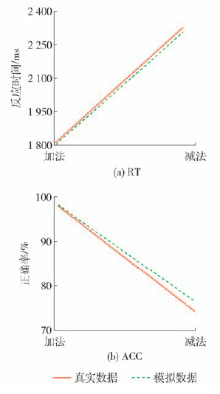
假设模型对RT和正确率(accurate rate,ACC)的预测结果如 图3所示. 设置的行为数据评估参数:陈述性记忆提取时间设置为0.4s,映像表征模块时间参数设置为0.2s. 数据的偏差说明模型做了统一的预测. 由此可知对行为数据建立的假设模型具有合理性.
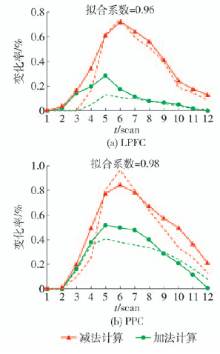
设置 a=2, s=2s. 一旦缓冲器的时间参数设置好,可以通过调整BOLD响应的 m级参数对每个脑区的BOLD信号变化率进行预测 [ 13] . 假设模型中的参数设置及模拟结果如 表5、 图4所示. 其中MΓ为 α的下一次脑区运算的组合参数,*为扫描层次.
表 5 BOLD函数预测参数Table 5. Parameters and the quality of the BOLD function prediction参数 表征模块 检索模块 指数( α) 2 2 级数( s) 3 3 MΓ( α+1) * 6.10 4.26 4 讨论
探索加法计算与减法计算2种认知策略的神经机制,例如加法计算任务的提取策略和减法计算的混合策略. 确定性分型和探索性分析说明DLPFC(左侧>右侧),2种计算任务有共同的激活脑区PPC,但激活的强度不同. 同时发现在混合策略有激活但在提取策略时没有激活的脑区包含背内侧前额叶皮层(dorsomedial prefrontal cortex,DMPFC)和腹外侧前额叶皮层(ventrolateral prefrontal cortex,VLPFC),如 表4所示. 这些结果说明策略的某些行为特征可能可以从功能数据中发现.构建计算假设模型来仿真被试的行为数据,结果显示采用模型预测实验数据有一定合理性,如 图4所示(实线为真实数据,虚线为模拟数据).
结果也说明左侧DLPFC和双边PPC显著激活被认为是独立策略. 这些结果已被本团队最近关于算术计算的fMRI所证实 [ 9] ,与先前有关算术运算的研究结果一致 [ 3] . 这说明对算术计算而言这2个脑区是主要激活脑区. 进行方程求解时左侧DLPFC激活程度相对减小 [ 3] . 有的研究结果显示DLPFC激活呈现右侧化 [ 4] ,但是有的研究以及本研究结果显示左侧化 [ 9] ,结果差异可能是由于实验设计内容不同(加减计算、解方程式). 算术计算是人工智能的一个重要研究领域 [ 11] ,算术计算被广泛应用于人工智能领域. 利用当前研究结果结合先前有关人工智能任务的神经影像学研究结果进行对比. 发现采用独立策略时前额叶区域有激活,这与以往相关的fMRI实验研究结果相一致 [ 13] ,同时也得到了新的有关人工智能理论的支持.
关于DLPFC和PPC的功能作用有不同的解释. 在算术计算领域左侧DLPFC与假设的评估与产生的过程相关 [ 1] ,额顶叶网络与算术计算策略有关 [ 9] . 文献 [ 11] 认为双边海马体与算术计算采用的策略有关,右侧框体皮层与任务的难易程度有关. 先前的研究被解释为异常刺激的语义编码,然后进行假设选择. DLPFC(左侧<右侧)与双边PPC被认为是认知计算的加工过程基线而非功能作用. 同时在智能领域,PPC与特征、抽象、阐述解释相关,DLPFC以及额叶脑区与测试假设相关 [ 6] . 对不同领域不同内容有不同的解释也很正常.
对与ACT-R模块对应的DLPFC、PPC脑区在探索性分析中已做了详细的解释. 因此推断左侧DLPFC与语义/知识的记忆性提取有关,PPC与问题状态的心理表征相关 [ 10] . 尽管混合策略与提取策略在左侧DLPFC与双边PPC都有激活,但是这些区域的激活程度可以区分不同策略. 相对于提取策略,混合策略对工作记忆的激活更大(提取与状态保持需求更多). ACT-R模型非常适合预测、解释行为实验数据与功能影像数据结果,对结果的具体加工过程解释更加合理.
当前研究结果可能还说明算术计算理论更适合解释认知架构的潜在推理. 本研究以及先前研究结果显示DLPFC与PPC在算术计算中有重要作用,有关算术计算的其他研究 [ 6] 额顶叶区域有共同的激活. 本研究同样支持了双处理理论的认知假设,该理论预测算术计算需要依赖认知需求的不同神经系统. 本研究发现越困难的任务(混合策略的减法计算)在VLPFC与DMPFC脑区的激活程度越强、激活范围越大. 该结果同样进一步支持了算术计算的双处理理论. ACT-R更适合预测被试的行为数据与功能映像数据,是一个通用认知理论. 这说明认知架构更适合解释实验结果. 双处理理论已经被以往实验所验证 [ 8] .
总之,fMRI实验设计结合ACT-R建模研究了不同算术计算任务(加法计算与减法计算)的神经基础. 这些研究结果进一步支持了认知计算的双处理理论.
The authors have declared that no competing interests exist. -
表 1 被试人口统计学及临床特征
Table 1 Clinical features and demographic of health controls
特征 正常被试(22名) P值 性别比例(男:女) 14:8 1.00 平均年龄/岁 24.3 ± 3.2 0.91 受教育时间/a 14.2 ± 3.8 0.93 表 2 行为结果
Table 2 Behavioral scores
计算 反应时/ms 正确率 /% 加法 1812±224.14 97.92±2.67 减法 2328±287.36 74.38±11.3 表 3 2种策略共同激活脑区
Table 3 Regions activated commonly to both strategies
脑区 BA分区 簇大小 坐标 T值 x y z 左额中回 46 71 -48 27 21 12.03 左额下回 9 -51 12 30 10.82 右额中回 6 -51 3 45 7.34 左顶上小叶 7 26 -27 -63 45 8.01 -24 -69 51 7.43 右顶上小叶 7 63 30 -72 51 5.94 27 -63 48 6.02 表 4 混合策略激活脑区
Table 4 Regions specific to mixed strategy
脑区 BA分区 簇大小 MNI坐标 T值 x y z 左额上回 6 1356 -3 12 54 9.85 -9 3 60 8.09 左脑岛 13 -30 24 3 7.75 右额下回 47 374 30 21 -6 8.06 46 45 18 27 4.61 右额上回 8 507 3 15 54 7.45 右扣带回 32 9 24 33 6.48 右额内侧回 9 3 39 36 6.11 左额下回 47 16 -33 30 -3 7.43 右额下回 47 13 33 30 -3 6.02 左顶上小叶 7 344 -12 -57 48 4.08 右顶上小叶 7 250 36 -75 45 4.38 右楔前叶 7 12 -66 51 4.05 左丘脑 256 -9 -12 3 4.88 左苍白球 -12 3 6 4.53 右尾状核 178 9 6 6 5.08 右壳核 15 0 9 4.87 表 5 BOLD函数预测参数
Table 5 Parameters and the quality of the BOLD function prediction
参数 表征模块 检索模块 指数( α) 2 2 级数( s) 3 3 MΓ( α+1) * 6.10 4.26 -
[1] CHRISTOFFK,PRABHAKARANV,DORFMANJ,et al.Rostrolateral prefrontal cortex involvement in relational integration during reasoning[J].Neuroimage,2001,30(14):1136-1149. [2] GOELV,GOLDB,HOULES.The seats of reason: a localization study of deductive & inductive reasoning using PET (O15) blood flow technique[J].Neuro Report,1997,102(8):1305-1310. [3] GOELV,DOLANR.Differential involvement of left prefrontal cortex in inductive and deductive reasoning[J].Cognition,2004,8(93):B109-B121. [4] GOELV,DOLANR.Anatomical segregation of component processes in an inductive inference task[J].J Cogn Neurosci,2000,203(12):1-10. [5] EVANS JS.In two minds: dual-process accounts of reasoning[J].Trends Cogn Sci,2003(10):454-459. [6] STARKEY P. COOPER R C.Perception of numbers by human infants[J].Science,1980,21(65):1033-1035. [7] PIAGETJ.The child's conception of number[J].Routledge,1997,3(19):175-202. [8] PESENTIM,ZAGOL,CRIVELLOF.Mental calculation in aprodigy is sustained by right prefrontal and medial temporal areas[J].Nat Neurosci,2001,67(4):103-107. [9] DYALL- SMITHM,DYALL- SMITHD.Recovering DNA from pathology specimens: a new life for old tissues[J].Mol Biol Rep,1988,84(16):1-2. [10] RUECKERTL,LANGEN,PARTIOTA.Visualizing cortical activation during mental calculation with functional MRI[J].Neuroimage,1996,102(3):97-103. [11] RYPMAB,ESPOSTIOM.The roles of prefrontal brain regions in components of working memory: effects of memory load and individual differences[J].Proc Natl Acad Sci USA,1999,96(3):6549-6558. [12] MENONV,RIVERA SM,WHITE CD,et al.Dissociating prefrontal and parietal cortex activation during arithmetic processing[J].Neuroimage,2000,115(12):351-357. [13] BURBAUDP,DEGREZEP,LAFONP,et al.Lateralization of prefrontal activation during internal mental calculation: a functional magnetic resonance imaging study[J].J Neurophysiol,1995,74(24):2188-2194.



 下载:
下载: