Thermal Characteristics of a Single Emitter Diode Laser Optical System
-
摘要:
激光器光学系统的热效应会影响激光的传输和激光器的使用，为了研究热效应对半导体激光器光学系统的影响，利用ANSYS有限元软件对多单管激光器单元模块进行了热应力分析.模拟分析了光学器件对应输出功率的热特性，并通过Matlab软件利用Zernike多项式进一步拟合分析了输出功率对应系统光学器件的光学特性.结果表明：光学元件在热效应的影响下像差主要为像散，为后续像差补偿方式的设计提供指导.
Abstract:The thermal effect of a laser optical system will affect the transmission of the light and the use of laser. To study the influence of thermal effect of the laser optical system, the finite element analysis software of ANSYS was used to build a thermal-stress analysis about single emitter laser unit module system in this paper. The thermal characteristics of the device corresponding for different output powers were studied, and the optical properties of optical device was analyzed by the software of Matlab using Zernike polynomial further. Results show that the main aberration of optical element under the influence of thermal is astigmatism, which provides a guidance for design of aberration compensation mode later.
-
Keywords:
- ANSYS /
- thermal-stress analysis /
- diode laser /
- thermal-characteristics
-
半导体激光器具有体积小、功率高、使用寿命长等优点，其在生产和生活中应用广泛，但是由于其电光转化效率的缘故及外光路中光学元件的对光的吸收作用，会产生大量热，这些热不仅会引起激光波长漂移，降低激光器的工作效率，而且还会引起光学系统热畸变，影响输出激光的光束质量[1].
在一般的光学热特性研究中，热特性、光学特性和结构特性是相互分离的，通常只分析激光器的热分布情况或者只分析光学元件局部受热造成热畸变的光学特性.对于一个系统而言，可能需要考虑多种因素或载荷对系统的作用结果，这也就是集成分析的思想. 1981年，美国的Jacob Miller等提出了光机热集成分析的思想，并首次将其应用于光电传感器的分析.其后集成分析的思想被广泛应用于导弹的红外跟踪镜头、卫星上的光学成像相机等国防和科技的多种领域.现在，光机热集成分析的方法也被广泛应用于激光器光学系统的设计、研制中[2].国外的Sigmadyne公司推出的SigFit软件采用了干涉检验接口技术，利用Zernike多项式对光学元件的表面形变进行处理，实现了有限元分析与光学分析的有机联系[3]. Bendow等对受激光辐照的固体材料的热透镜效应进行了研究，并且得出热透镜效应与激光的辐照强度、照射时间及材料的几何形状和热物性参数有关[4-5].中国虽然在光学系统的热效应及分析方法的研究上起步较晚，但是近年来也取得了较大的突破.中国科学院长春光学精密机械与物理研究所对空间遥感器进行了大量细致的光机热集成分析，其主要研究方法是把Zernike多项式作为接口工具，实现了有限元分析软件与光学软件的结合[6-7].长春光学精密机械与物理研究所的张磊进行了高功率激光辐照下光学元件热畸变的研究，在研究中对水冷条件下的受激光照射的45°反射镜进行了面形拟合，验证了微通道的散热方式对减小反射镜的温度梯度和形变量有重要作用[8]，并对高功率激光远场光束质量进行了测量.这些研究大多利用各种软件的不同优势，采用光机热集成分析的思想对激光器输出光路中的光学元件进行了热特性研究[9].
现阶段对半导体激光器系统光机热集成分析较少，并且对文献中大部分是对激光反射镜的分析，对激光投射也较少.
本文主要基于Zernike多项式，利用有限元分析软件计算系统在工作情况下的热、应变分布情况，并提取光学元件表面的形变数据，然后在Matlab软件中用Zernike多项式对形变数据进行拟合，对镜面面形数据进行处理，比较精确地拟合光学元件的畸变表面，分析了光学元件表面热畸变对系统输出激光光束质量的影响.激光器系统的光机热研究，对评估光学元件的表面畸变对系统像差的影响，以及对改进、提高激光器系统的光束质量有重要意义.
1. 系统介绍
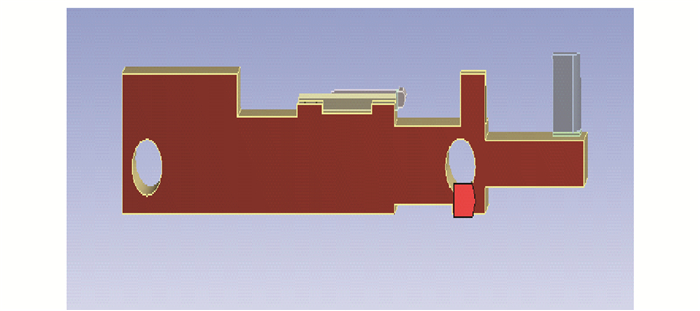
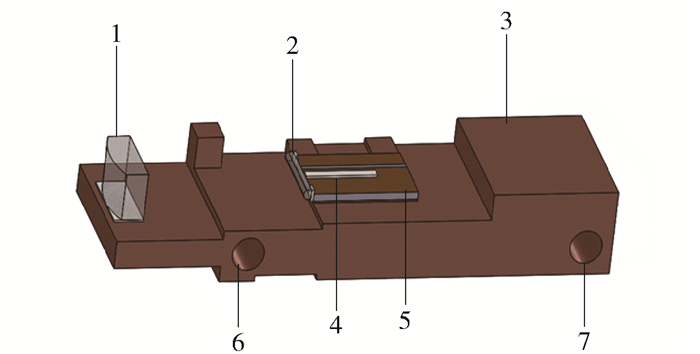
本文采用耦合系统单元模块，包括发光芯片和氮化铝热沉组成的COS(chip on sub mount)，以及对光束进行整形的快、慢轴准直镜.快轴准直镜的材料为S-TIH53玻璃，慢轴准直镜的材料为K9玻璃.单元结构如图 1所示.
![]()
图 1 单元模块三维图1—慢轴准直镜；2—快轴准直镜；3—铜基底热沉；4—发光芯片；5—氮化铝次级热沉；6、7—铜热沉定位孔.Figure 1. Three-dimensional figure of unit module芯片发光单元的尺寸为1 μm×100 μm，其发出的光先经过2对快轴方向约26°的发散角进行压缩准直，后经过1对慢轴方向约8°的发散角进行准直光学系统置于一个次级铜热沉上，其在未受热应变影响时的光学结构如图 2所示.
2. 热应力分析
2.1 热分析
多单管半导体激光器单元模块主要采用热传导方式进行散热，即可用傅里叶定律表示为
$$ q=-k\frac{\partial T}{\partial x} $$ (1) 式中：q为x方向上单位时间内通过单位面积内的热流量；k为x方向上的热导率，负号表示热流从温度高的部分向温度低的部分流动.
对模块进行热效应分析，首先就是求解模块的温度场函数，通过热力学第一定律和傅里叶定律可以得出描述光学元件内部热传导过程的热传导偏微分方程，也即可以求解温度场函数.热力学第一定律的表达式为
$$ \Delta U=Q+W $$ (2) 式中：ΔU为单位时间内物体内能的变化；Q为单位时间内物体从外界吸收的总热量；W为外界对环境做的功，对于稳态热分析ΔU=Q.
根据热传导偏微分方程
$$ \begin{align} & \frac{\partial }{\partial x}\left[ k\left( T \right)\frac{\partial T}{\partial x} \right]+\text{ }\frac{\partial }{\partial y}\left[ k\left( T \right)\frac{\partial T}{\partial y} \right]+\text{ }\frac{\partial }{\partial z}\left[ k\left( T \right)\frac{\partial T}{\partial z} \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ q\left( x,y,z,t \right)=\rho \left( T \right){{c}_{P}}\left( T \right)\frac{\partial T}{\partial t} \\ \end{align} $$ (3) 式中：左边三项为单位体积物体在三维空间坐标x、y、z方向上吸收的热能；q(x，y，z，t)为单位体积物体内热源产生的热能；右边为单位体积物体温度随时间的变化率，其中：K(T)为物体的热导率；ρ(T)为物体的密度；CP(T)为定压比热.
由于是稳态热分析，温度场不随时间变化，所以式(3) 可变为
$$ \begin{align} & \frac{\partial }{\partial x}\left[ k\left( T \right)\frac{\partial T}{\partial x} \right]+\text{ }\frac{\partial }{\partial y}\left[ k\left( T \right)\frac{\partial T}{\partial y} \right]+\text{ } \\ & \ \ \ \ \frac{\partial }{\partial z}\left[ k\left( T \right)\frac{\partial T}{\partial z} \right]=-q\left( x,y,z, \right) \\ \end{align} $$ (4) 根据式(4)，再结合边界条件就可以求出整个模块的温度场.
模拟采用的COS的芯片，其电光转化效率为50%.将芯片、快轴方向准直镜通光部分、慢轴方向准直镜通光部分设置为体热源.次级热沉为铜，其底面作为恒温面如图 3所示.
对于快轴准直镜(fast axis collimator, FAC)和慢轴准直镜(slow axis collimator, SAC)的热源设定，根据K9和T-IH53的玻璃手册，得出其950~1 000 nm的内部透过率在通过5 mm是99.9%, 通过10 mm是99.8%.光强与吸收系数为
$$ I={{I}_{0}}{{\text{e}}^{-\alpha l}} $$ (5) 式中：I和I0为入射面处激光的光强；α为透射光学元件材料对相应波长激光的吸收系数；l为光传播的距离.
根据式(5)，可得
$$ \phi ={{\phi }_{0}}{{\text{e}}^{-\alpha l}} $$ (6) 通过待定系数法可得出玻璃材料的吸收系数α为2×10-4 mm-1.分别求出在电光转换效率相同的条件下不同功率激光通过FAC和SAC内部所产生的热功率，进一步可求的其内部的不同的功率密度.功率密度作为求解温度场的热载荷.
2.2 应力分析
对于大多数材料，都具有热胀冷缩的特性，即在受热温度升高时体积会发生变化，产生热应变.根据Hooke定律，热应力的产生一部分是由于热膨胀的产生受到约束，另一部分是与温度变化成比例，在各个方向上的大小相同，与此对应热应变也是由这2种应力产生的，即一部分是应力产生应变，另一部分是温度变化产生应变.这2种应力和应变分别会产生叠加.
本文进行的热应力分析中，材料的热物性是线性的，应力应变关系是线性关系，热畸变是可恢复的且发生的畸变是微小的应变，所以可认为本文所进行的研究为线性研究.
物体的热应力和热畸变由几何方程、物理方程及力平衡方程表示[8, 10].
应力和应变的几何方程可表示为
$$ \left\{ \begin{align} & {{\varepsilon }_{x}}=\frac{\partial {{u}_{x}}}{\partial x},\text{ }{{\varepsilon }_{y}}=\frac{\partial {{u}_{y}}}{\partial y},\text{ }{{\varepsilon }_{z}}=\frac{\partial {{u}_{z}}}{\partial z} \\ & {{\varepsilon }_{xy}}=\frac{{{\gamma }_{xy}}}{2}=\frac{1}{2}\left( \frac{\partial {{u}_{x}}}{\partial y}+\frac{\partial {{u}_{y}}}{\partial x} \right) \\ & {{\varepsilon }_{yz}}=\frac{{{\gamma }_{yz}}}{2}=\frac{1}{2}\left( \frac{\partial {{u}_{y}}}{\partial z}+\frac{\partial {{u}_{z}}}{\partial y} \right) \\ & {{\varepsilon }_{zx}}=\frac{{{\gamma }_{zx}}}{2}=\frac{1}{2}\left( \frac{\partial {{u}_{x}}}{\partial z}+\frac{\partial {{u}_{z}}}{\partial x} \right) \\ \end{align} \right. $$ (7) 物理方程是描述应力和应变的一组方程，即
$$ \left\{ \begin{align} & {{\sigma }_{x}}=\zeta ({{\varepsilon }_{x}}+{{\varepsilon }_{y}}+{{\varepsilon }_{z}})+2G{{\varepsilon }_{x}}-\left( 3\zeta +2G \right)\alpha T \\ & {{\sigma }_{y}}=\zeta ({{\varepsilon }_{x}}+{{\varepsilon }_{y}}+{{\varepsilon }_{z}})+2G{{\varepsilon }_{y}}-\left( 3\zeta +2G \right)\alpha T \\ & {{\sigma }_{Z}}=\zeta ({{\varepsilon }_{x}}+{{\varepsilon }_{y}}+{{\varepsilon }_{z}})+2G{{\varepsilon }_{z}}-\left( 3\zeta +2G \right)\alpha T \\ & {{\tau }_{xy}}=2G{{\varepsilon }_{xy}},{{\tau }_{yz}}=2G{{\varepsilon }_{yz}},{{\tau }_{zx}}=2G{{\varepsilon }_{zx}}~ \\ \end{align} \right. $$ (8) 式中：ζ=Eμ/(1+μ)(1-2μ)；G=E/2(1+μ)；α为热膨胀系数；E为拉弹性模量；G为剪切弹性模量；μ为泊松比.
平衡方程可表示为
$$ \begin{align} & \sum{X}=\sum{Y}=\sum{Z}=\sum{{{M}_{x}}}= \\ & \ \ \ \ \ \ \ \ \ \sum{{{M}_{y}}}=\sum{{{M}_{Z}}}=0 \\ \end{align} $$ (9) 当x方向微小体积内有微小的形变时，根据平衡条件∑X=0可得到x方向的平衡方程
$$ \begin{align} & \left( {{\sigma }_{x}}+\frac{\partial {{\sigma }_{x}}}{\partial x}\text{d}x \right)\text{d}y\text{d}z-{{\sigma }_{x}}\text{d}y\text{d}z+ \\ & \left( {{\tau }_{yx}}+\frac{\partial {{\tau }_{yx}}}{\partial y}\text{d}y \right)\text{d}x\text{d}z-{{\tau }_{yx}}\text{d}x\text{d}z+ \\ & \left( {{\tau }_{zx}}+\frac{\partial {{\tau }_{zx}}}{{{\partial }_{z}}}\text{d}z \right)\text{d}x\text{d}y-{{\tau }_{zx}}\text{d}x\text{d}y+{{F}_{x}}\text{d}x\text{d}y\text{d}z=0 \\ \end{align} $$ (10) 将式(10) 进一步化解可得
$$ \frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}+\frac{\partial {{\tau }_{zx}}}{{{\partial }_{z}}}+{{F}_{x}}=0 $$ (11) 同理可得，y方向和z方向有相同的形式，所以平衡方程组可写为
$$ \left\{ \begin{align} & \frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}+\frac{\partial {{\tau }_{zx}}}{\partial z}+{{F}_{x}}=0 \\ & \frac{\partial {{\sigma }_{y}}}{\partial y}+\frac{\partial {{\tau }_{zy}}}{\partial z}+\frac{\partial {{\tau }_{xy}}}{\partial x}+{{F}_{y}}=0 \\ & \frac{\partial {{\sigma }_{z}}}{\partial z}+\frac{\partial {{\tau }_{xz}}}{\partial x}+\frac{\partial {{\tau }_{yz}}}{\partial y}+{{F}_{z}}=0 \\ \end{align} \right. $$ (12) F为物体受到的约束力，式(12) 即为力平衡方程.对于热应力的计算，除了上述3类方程还需要设定边界条件，根据边界条件结合方程就可以求出系统的热应变.
为了计算方便，将几何方程和物理方程写成
$$ \mathit{\boldsymbol{\varepsilon '}} = \mathit{\boldsymbol{BU}} $$ (13) $$ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{D\varepsilon }} $$ (14) $$ \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{\varepsilon '}} - {\mathit{\boldsymbol{\varepsilon }}_0} $$ (15) 式中:ε为应变向量; B为几何矩阵; ε0为初应变向量; U为位移向量; D为弹性矩阵.
根据虚功原理，可求出刚度矩阵[8].虚功原理可表示为
$$ {W_F} + {W_\sigma } = 0 $$ (16) 式中：WF为单元节点力的虚功；Wσ为内力虚功.
结合刚度矩阵，根据载荷列向量和位移线性方程组可求得位移向量，从而可以求得应力和应变.
在软件计算过程中，做如下处理：
1) 由于在热稳态环境下模拟，考虑到实际器件的温升较小，假定各材料的热物性参数不随温度变化.
2) 除制冷恒温面设置恒定温度外，由于系统实际在工作中没有强制对流，而光学元件的体积较小，所以不考虑热对流和热辐射，其余表面都设置绝热条件.
3) 由于激光束在FAC处损失的能量较小，在计算SAC吸收的光功率时认为输出总功率没有改变.
本文计算时，虽然做了如上近似处理，但是对结果影响较小，满足实际激光器工作的中的环境条件.
本文仿真所用的次级热沉及主要光学元件材料热物性参数如表 1所示.
表 1 主要材料热物性参数表Table 1. Main material parameters in thermal and physical properties密度/(kg·m-3) 热导率/(W·(m·K)-1) 热膨胀系数/K-1 杨氏模量/Pa 泊松比 铜 8 933 400.00 1.76×10-5 1.20×1011 0.340 氮化铝 3 280 180.00 4.3×10-6 3.10×1011 0.200 砷化镓 5 316 40.00 5.7×10-6 8.59×1011 0.310 K9玻璃 2 500 1.50 8.6×10-6 7.80×1010 0.208 T-IH53玻璃 3 530 0.99 9.9×10-6 9.60×1010 0.260 2.3 热应力分析后处理
激光器光学系统的光学元件在热应力的作用下发生了微小的形变，光学系统的传输特性就会受到影响.使用波面误差来分析柱面镜等光学元件在受温度影响后的光学传输性能是一种有效的进行集成分析的手段. Zernike多项式是一种进行波面误差分析的重要方法，也是一种有效的处理有限元计算结果的工具[11].
Zernike多项式不仅可以描述光学元件镜面面形，而且其多项式各项之间是正交和独立的[12]，多项式前几项与光学系统的初级像差相对应[13].所以可以通过计算Zernike多项式前几项的值来分析光学元件的像差情况.
Zernike多项式在实际使用过程中，使用较多的是其极坐标形式，其各项可表示为
$$ {U_{k(l,n)}}\left( {\rho ,\theta } \right) = U_n^l\left( {\rho ,\theta } \right) = R_n^l\left( \rho \right)\Theta _n^l\left( \theta \right) $$ (17) 式中：Rnl(ρ)为与归一化径向长度ρ有关的表达式；Θnl(θ)为与角度θ有关的表达式；n为多项式的阶数；l为与n具有相同的奇偶性但是绝对值小于等于n.
当进行面形拟合时一般采用
$$ \mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) = \sum\limits_{k = 0}^\infty {{Q_k}{U_{ik}}({\rho _i},{\theta _i})} = {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}} $$ (18) $$ \Delta \mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) = \sum\limits_{k = 0}^\infty {{Q_k}{U_{ik}}({\rho _i},{\theta _i})} ({\rho _i},{\theta _i}) = {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}} $$ (19) 式中：ΔS(ρi，θi)为光学元件表面各节点沿光轴方向的移动量；S(ρi，θi)为各光学元件表面节点移动后的坐标，i为节点序号；Q为所求的Zernike多项式系数矩阵.
在Zernike面型拟合算法中，有Gram-Schimdt正交化方法和最小二乘法，本文使用最小二乘法.
式(18) 所确定的是一系列具有相同形式的方程，且方程组中方程的数量一般多于未知数的个数，所以方程组没有精确解.
根据最小二乘法，
$$ \sigma = {\left\| {{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}} - \mathit{\boldsymbol{S}}({\rho _i},{\theta _i})} \right\|^2} $$ (20) 值最小时，就是所求的最接近真实情况的解.将式(20) 进一步化简，采用矩阵运算变形
$$ \sigma = {(\mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) - {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}})^{\rm{T}}}(\mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) - {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}}) $$ (21) 对式(21) 求Q的偏导数，当σ最小时
$$ \frac{{\partial \sigma }}{{\partial \mathit{\boldsymbol{Q}}}} = - 2\mathit{\boldsymbol{U}}_i^{\rm{T}}\mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) + 2\mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}} = 0 $$ (22) 由式(22) 可得
$$ \mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{U}}_i^{\rm{T}}\mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) $$ (23) 所以Zernike系数矩阵Q可表示为
$$ \mathit{\boldsymbol{Q}} = {(\mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{U}}_i})^{ - 1}}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{S}}({\rho _i},{\theta _i}) $$ (24) 式中Ui、Q、S(ρi，θi)均为矩阵形式.从而可以拟合出光学镜片的热致像差.
3. 结果分析
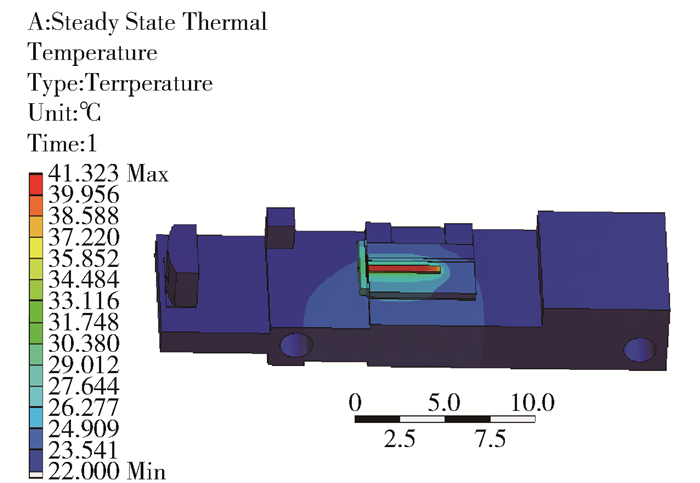
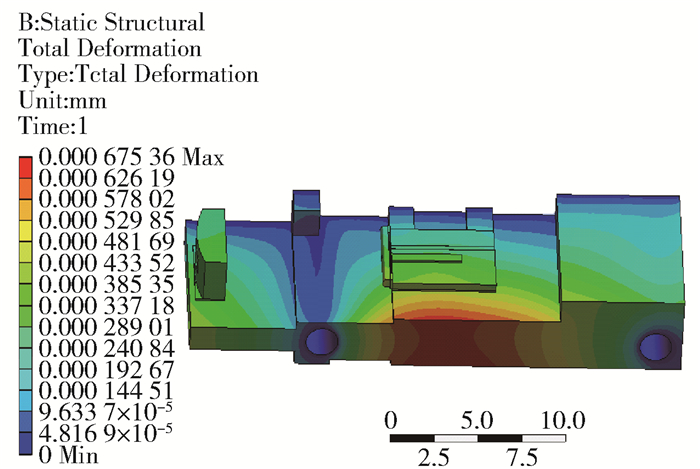
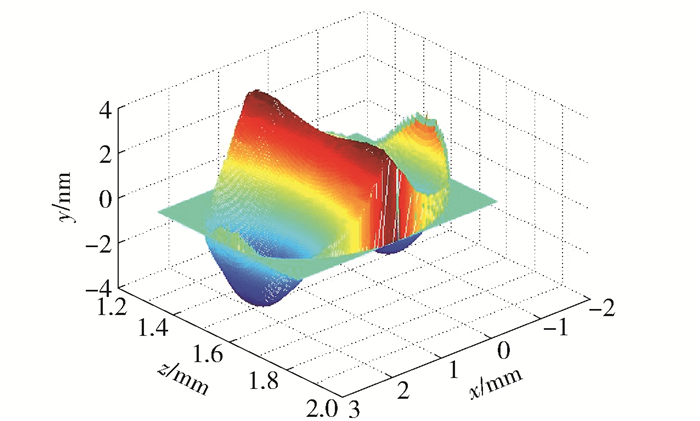
图 4~5为系统冷却温度为22 ℃、输出功率为10 W时的系统温度云图和热应变.
本文主要分析热对系统光学性能的影响，所以主要分析系统中快、慢轴准直镜受热的形变及其影响光束质量的情况.首先通过有限元分析软件计算出的镜面形变并将形变结果导出，然后采用Zernike多项式对有限元计算结果进行处理. Zernike多项式的前9项对应于低阶像差，分析中占主要因素，故高阶像差忽略不考虑.前0项分别对应平移、x方向倾斜、y方向倾斜、离焦、与轴成0°或90°的像散、与轴成45°的像散、x轴的三级彗差、y轴的三级彗差、三级球差等[14].由于处理后的平移对激光输出影响较小，所以主要考虑不同功率情况下的其他像差.
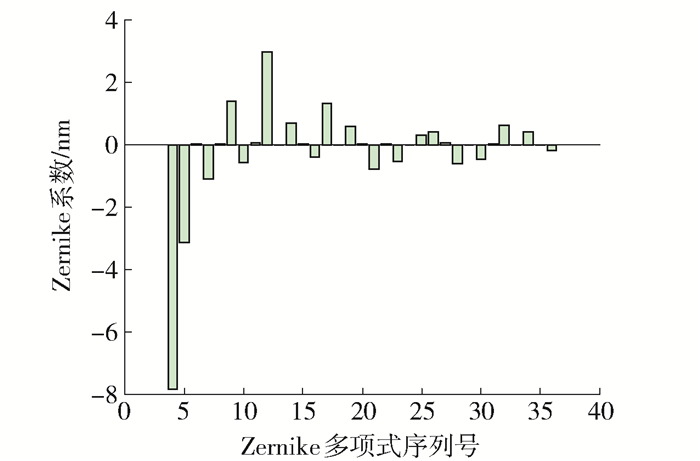
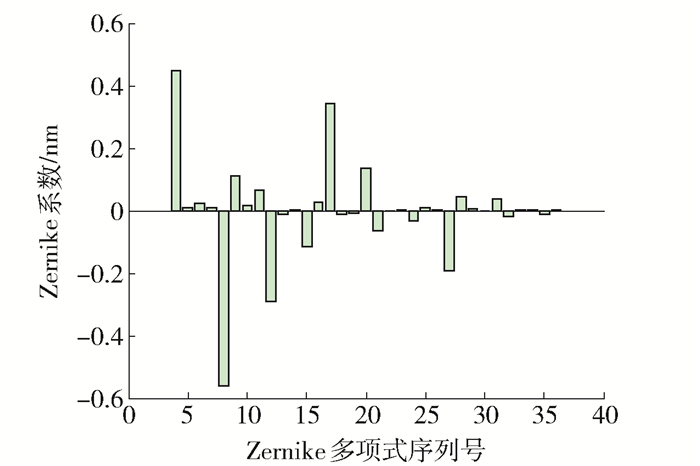
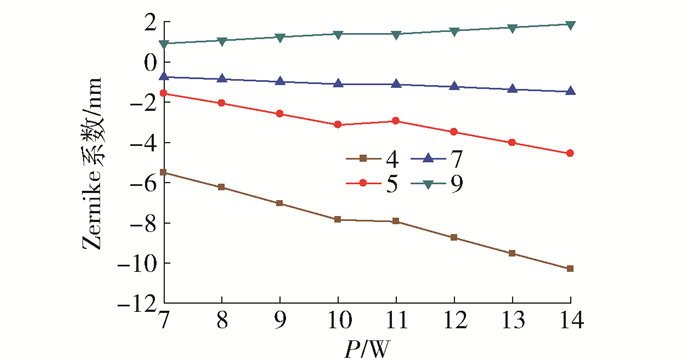
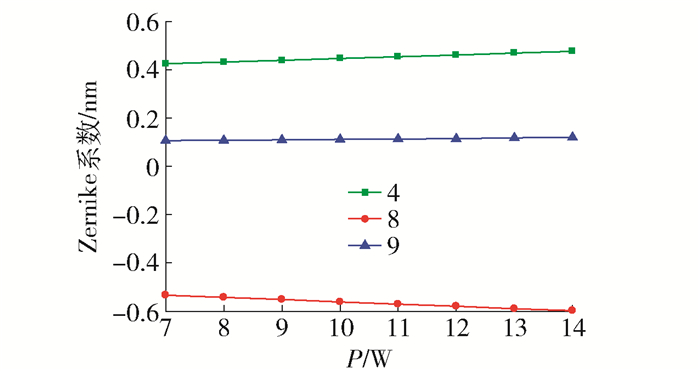
可以看出，温度对部分Zernike多项式的系数有较大的影响，在相同的条件下，本系统中FAC和SAC的热效应不同，如图 6、7所示. FAC像差图如图 8所示.
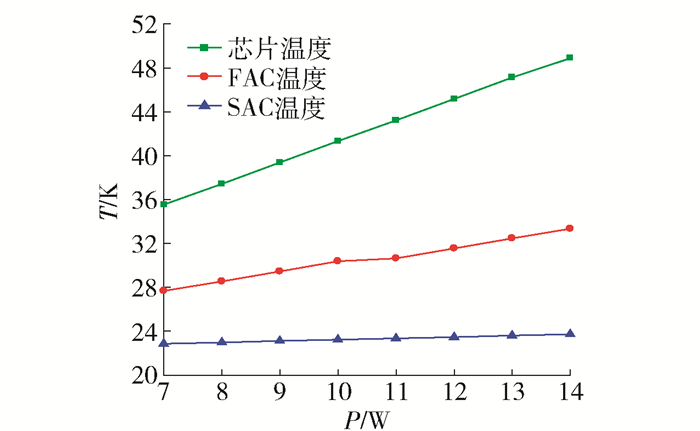
图 9~11分别是系统光学元件的温度及FAC和SAC的Zernike拟合系数随不同输出功率的变化情况.
![]()
图 9 体热源的温度与输出功率的关系Figure 9. Relationship between body heat source temperature and output power![]()
图 10 FAC的Zernike系数与输出功率的关系Figure 10. Relationship between the Zernike coefficient and output power of FAC![]()
图 11 SAC的Zernike系数与输出功率的关系Figure 11. Relationship between the Zernike coefficient and output power of the SAC当系统的冷却温度为22 ℃时，芯片、FAC和SAC随功率的变化情况不同，芯片的温度受功率变化更为明显，其从35.5 ℃上升到48.9 ℃. SAC的温度受功率变化影响较小，其从22.9 ℃上升到23.7 ℃.
图 10显示FAC在光传播方向上2个镜面的Zernike拟合系数的绝对值随输出功率的增大而增大；Zernike多项式系数4和系数5恰好对应离焦和象散，所以随功率的增大FAC温度升高，在光传播方向上离焦和象散也增大；其他像差的高阶Zernike拟合系数受功率影响的变化较小.
图 11显示SAC在光传播方向上2个镜面的Zernike拟合系数的绝对值随输出功率的增大而增大；由于SAC的整体温差较小，其不同部分的温度梯度较小，所以热效应所产生的像差较小；由于SAC温度受输出功率的变化影响较小，所以其主要表征像差的Zernike拟合系数变化受功率的影响较小，即其随输出功率的增加增长平缓.
4. 结论
1) 本文建立大功率半导体激光器的有限元热模型，并对具有快慢轴准直的单管芯大功率半导体激光器进行了热致像差分析，在转化效率一定时，系统受输出功率的影响，当输出功率升高时.
2) FAC由于距芯片较近，温升较为明显，热效应所引起的像差也较为明显，SAC由于在系统中的分布，温升较小，由热效应所引起的像差较小，且随输出功率的变化较小，模拟结果表明像差主要以像散为主，并包含少量高阶像差.
3) 在后续的设计中引入像散补偿方式以获得更好的光束传输效果.
-
![]()
图 1 单元模块三维图
1—慢轴准直镜；2—快轴准直镜；3—铜基底热沉；4—发光芯片；5—氮化铝次级热沉；6、7—铜热沉定位孔.
Figure 1. Three-dimensional figure of unit module
![]()
图 9 体热源的温度与输出功率的关系
Figure 9. Relationship between body heat source temperature and output power
![]()
图 10 FAC的Zernike系数与输出功率的关系
Figure 10. Relationship between the Zernike coefficient and output power of FAC
![]()
图 11 SAC的Zernike系数与输出功率的关系
Figure 11. Relationship between the Zernike coefficient and output power of the SAC
表 1 主要材料热物性参数表
Table 1 Main material parameters in thermal and physical properties
密度/(kg·m-3) 热导率/(W·(m·K)-1) 热膨胀系数/K-1 杨氏模量/Pa 泊松比 铜 8 933 400.00 1.76×10-5 1.20×1011 0.340 氮化铝 3 280 180.00 4.3×10-6 3.10×1011 0.200 砷化镓 5 316 40.00 5.7×10-6 8.59×1011 0.310 K9玻璃 2 500 1.50 8.6×10-6 7.80×1010 0.208 T-IH53玻璃 3 530 0.99 9.9×10-6 9.60×1010 0.260 
下载: 导出CSV
-
[1] 王文, 褚金雷, 高欣, 等.基于多芯片封装的半导体激光器热特性[J].强激光与粒子束, 2014(1):86-91 http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY201401020.htm WANG W, CHU J L, GAO X, et al. Thermal characteristics of semiconductor laser based on muti-chip packaging[J]. High Power Laser and Particle Beams, 2014(1):86-91. http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY201401020.htm
[2] 温敬阳. 光机热集成分析方法与技术研究[D]. 西安: 西安电子科技大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10701-2008056049.htm WEN J Y. Research on methods and techniques of optomechanical integrated analysis[D]. Xian:Xidian University, 2008:1-8. http://cdmd.cnki.com.cn/Article/CDMD-10701-2008056049.htm
[3] DOYLE K B, GENBERG V L, MICHELS G J, et al. Optical modeling of finite element surface displacements using commercial software[C]//Proceedings of SPIE, Optical Modeling and Performance Predictions Ⅱ. San Diego:Mark A Kahan, 2005, 5867:1-12.
[4] BENDOW B, GIANINO P D. Optics of Thermal Lensing in Solids[J]. Applied Optics, 1973, 12(4):710-718. doi: 10.1364/AO.12.000710
[5] KLEIN C A. Optical distortion coefficients of high-power laser windows[J]. Opitical Engnieering. 1990, 29(4):343-350. https://www.researchgate.net/publication/252947151_Optical_distortion_coefficients_of_high-power_laser_windows
[6] 李贤辉, 吴清文, 杨洪波.光学工程分析中的镜面面形处理新方法[J].光学技术, 2003, 29(6):752-756. http://www.cnki.com.cn/Article/CJFDTOTAL-GXJS200306036.htm LI X H, WU Q W, YANG H B. New method of mirror surface figure treatment in optical engineering analysis[J]. Optical Technique, 2003, 29(6):752-756. http://www.cnki.com.cn/Article/CJFDTOTAL-GXJS200306036.htm
[7] 李贤辉. 光机集成有限元分析光学面形后处理研究与实现[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2004. http://www.lunwentianxia.com/product.sf.3633227.1/ LI X H. Study on the integrated optomechanical analysis optical surface post-process system[D]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2004. http://www.lunwentianxia.com/product.sf.3633227.1/
[8] 张磊. 高功率激光辐照下光学元件热畸变及远场效能研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2012: 22-25. http://d.wanfangdata.com.cn/Thesis/Y2368099 ZHANG L. Study on the thermal distortion and the efficiency of far field of the reflectors irradiated by the high power laser[D]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2012:22-25. http://d.wanfangdata.com.cn/Thesis/Y2368099
[9] 杨霄. 光学玻璃在激光作用过程中的热力效应研究[D]. 长春: 长春理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10186-2009198438.htm YANG X. Research on thermal and mechanical damage in optical glass induced by laser[D]. Changchun:Changchun University of Science and Technology, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10186-2009198438.htm
[10] 孙毅. 多波段高功率激光合束技术及热效应研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2015: 77-83. http://d.g.wanfangdata.com.cn/Thesis_Y2955421.aspx SUN Y. Research on multi-wavelength laser beam combination technology and thermal effect[D]. Changchun:Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2015:77-83. http://d.g.wanfangdata.com.cn/Thesis_Y2955421.aspx
[11] WANG J Y, SILVA D E. Wave-front interpretation with Zernike polynomials[J]. Appl Opt, 1980, 19:1510-1518. doi: 10.1364/AO.19.001510
[12] GENBERG V L, MICHELS G J, DOYLE K B. Orthogonality of Zernike polynomials[C]//Proceedings of SPIE, Optomechanical Design and Engineering. Seattle:Alson E Hatheway, 2002, 4771:276-286.
[13] MALACARA D. Optical shop testing[M]. 3rd ed. Hoboken:John Wiley & Sons Inc Publication, 2007:538.
[14] BORN M, WOLF E. Principles of optics[M]. Cambridge:Cambridge University Press, 1999:905-910.
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
