预测路面使用性能衰变规律,可以作为公路养护管理的重要依据,不仅可以对现有路面结构的服务能力进行判断,而且可以指导路面维修改造设计 ^{[ 1- 3]} . 公路路面使用性能衰变预测主要有多种方法:力学经验法、力学法、经验回归法 ^{[ 4]} 、时间序列法 ^{[ 5]} 、灰色预测法 ^{[ 6]} 、遗传算法 ^{[ 7]} 等. 现有的路面使用性能预测方法各有优势,但也有其局限性. 力学经验法、力学法的理论成熟,预估准确度高,反映了路面使用性能的衰变实质,但需要大量的数据积累,采集统计工作量极大. 经验回归法、时间序列法只能就每个路面样本逐一分析,需要累计多年的检测数据,对数据要求高. 灰色预测法、遗传算法计算非常复杂,不确定性大. 但是当数据样本积累年份不足时,以上方法预测的准确性降低,或难以满足要求 ^{[ 8- 9]} .

同时各影响因素的变异性较大,因此,路面使用性能衰变规律不确定性较大,确定型模型不足以描述这种特性,但是在同一区域、路面结构参数相近、交通量等级相同时路面性能衰变规律具有相似性. 面板数据法是把时间序列沿空间方向扩展,或把截面数据按照时间轴扩展成为二维数据的集合 ^{[ 10]} ;马尔可夫模型属于概率型预测法的一种,可以很好地描述路面使用性能的不确定性变化,在路面数据积累不足时,马尔可夫模型可推测变化趋势 ^{[ 11]} . 当单一样本路段的样本数量少于25时,传统的预测方法的预测精度难以保证,而面板数据马尔科夫法适用于解决该问题,因此,本文据此研究数据样本积累年份不足条件下的沥青路面性能预测问题. 研究的基础数据为辽宁省普通公路路面性能检测数据,样本数量共69段,采集时间2011—2013年.

1 面板数据马尔可夫模型

1.1 面板数据模型

面板数据是将时间序列按空间方向进行延伸与扩展,或由沿时间扩展构成的二维截面数据集合 ^{[ 7]} . 时间序列数据(单一路段历年数据)是变量按时间得到的一维数据,截面数据(路段样本的数据)是变量在固定时点的一维数据,而面板数据是同时在时间和截面上取得的二维数据集合. 根据此方法,可以将独立路段样本的时间序列一维数据扩展为二维数据集合.

面板数据模型是建立在面板数据的基础上,可对变量之间的相互关系进行分析的计量模型,模型的解析表达式为

y _it=α _it+x _it · β _it+μ _it , i=1,2,…, N; j=1,2,…, T(1)

式中: y _it 为被解释变量; x _it= ( $\begin{array}{c}{x}_{\mathit{it}}^1\end{array}$ , $\begin{array}{c}{x}_{\mathit{it}}^2\end{array}$ ,…, $\begin{array}{c}{x}_{\mathit{it}}^k\end{array}$ )为1 ×k维变量向量; β _it= ( $\begin{array}{c}{\beta }_{\mathit{it}}^1\end{array}$ , $\begin{array}{c}{\beta }_{\mathit{it}}^2\end{array}$ ,…, $\begin{array}{c}{\beta }_{\mathit{it}}^k\end{array}$ )为 k×1维参数向量; t表示不同时间; i表示不同个体; μ _it 表示随机扰动项,符合 μ _it~ IIDN(0, $\begin{array}{c}{\sigma }_{\mu }^2\end{array}$ ). 根据模型中参数的假设不同,本文的参数为确定值,截矩项随时间和个体不同而改变. 在不同个体上固定系数模型的截距和斜率都相等 ^{[ 7]} ,其解析表达式为

y _it=α+x _itβ+μ _it (2)

模型原假设为

H ₀₁: α _i=α _j ; β _i=β _j ; i, j=1,2,…, N

参数的最小二乘估计为

β ^∧ = $\begin{array}{c}{T}_{\mathit{xx}}^{-1}\end{array}$ T _xy , α ^∧ = $\begin{array}{c}\overline{y}\end{array}$ - $\begin{array}{c}\overline{x}\end{array}$ β ^∧(3)

式中

$\begin{array}{c}\overline{x}\end{array}$ = $\begin{array}{c}\stackrel{N}{\sum _{i=1}}\stackrel{T}{\sum _{t=1}}\end{array}$ x _it , $\begin{array}{c}\overline{y}\end{array}$ = $\begin{array}{c}\stackrel{N}{\sum _{i=1}}\stackrel{T}{\sum _{t=1}}\end{array}$ y _it

T _xx= $\begin{array}{c}\stackrel{N}{\sum _{i=1}}\stackrel{T}{\sum _{t=1}}\end{array}$ ( x _it- $\begin{array}{c}\overline{x}\end{array}$ ) '( x _it- $\begin{array}{c}\overline{x}\end{array}$ )

T _xy= $\begin{array}{c}\stackrel{N}{\sum _{i=1}}\stackrel{T}{\sum _{t=1}}\end{array}$ ( x _it- $\begin{array}{c}\overline{x}\end{array}$ ) '( y _it- $\begin{array}{c}\overline{y}\end{array}$ )

T _yy= $\begin{array}{c}\stackrel{N}{\sum _{i=1}}\stackrel{T}{\sum _{t=1}}\end{array}$ ( y _it- $\begin{array}{c}\overline{y}\end{array}$ ) ²

模型估计残差平方和为

S ₁ =T _yy-T' _xy $\begin{array}{c}{T}_{\mathit{xx}}^{-1}\end{array}$ T _xy (4)

为检验仅与个体有关的省略变量的显著性,可以对样本进行 F检验 ^{[ 6]}

F= $\begin{array}{c}\frac{({\overline{S}}_2-S_2)/N-1}{S_2/(\mathit{NT}-N-K\left.\text{'}\right)}\end{array}$ (5)

式中 S ₂为残差平方和, S ₂ =W _yy-W' _xy $\begin{array}{c}{W}_{\mathit{xx}}^{-1}\end{array}$ W _xy ,即表示 y _it=α _i+x _it · β+μ _n 的残差平方和. 如果 F是显著的,则拒绝零假设,可认为备择假设是成立的.

1.2 马尔可夫转移概率模型

马尔可夫是随机过程的一种,具有普遍性和显著的无后效性. 马尔可夫链是一种随机事件序列{ X( n), n=0,1,2,…},对于任意 n( n=1,2,3,…), X( n)取整数或子集;对于任意 r+1个非负整数0≤ n ₁≤ n ₂≤…≤ n _{r+ 1}≤ m和任意正整数 k,及状态 i ₁, i ₂, i ₃,…, i _r ∈ I, I是 X( n)的子集,有

P{ X( n ₁) =i ₁, X( n ₂) =i ₂,…, X( n _i ) =i _r , X( m) =i} >0 P{ X( m+k) =j|X( n ₁) =i ₁, X( n ₂) =i ₂,…, X( n _r ) =i _r , X( m) =i} =P{ X( m+k) =j|X( m) =i}(6)

成立. 随机序列{ X( n), n=0,1,2,…}具有马尔可夫性(无后效性). 条件概率 P{ X( m+k) =j|X( m) =i}为马尔可夫链, P _ij ( m, m+k)为{ X( n), n=0,1,2,…}在 m时刻从状态 i出发,在 m+k时刻转移到状态 j的转移概率, I为马尔可夫链{ X( n), n=0,1,2,…}的状态空间 ^{[12 - 15]} .

马尔可夫描述了对路面使用性能转移前后处于各状态的概率,在上述假设的前提下,转移矩阵能够准确模拟出路网内同组路面总体使用性能情况. 依据路面养护的要求和条件可以确定路面使用性能变量. 本文采用路面使用性能指数PQI作为评定指标. 例如:将PCI分为优、良、中、次、差5种状态等级 ^{[ 16]} ,此时状态矢量阵是指某时段的处于不同状态的路段的概率. 第 t年的转移概率是指对于使用 t年处于 i状态的路段,第 t年后转变成 j状态的概率 P' _ij ,该路段的转移矩阵 P'=( P' _ij ). 设该路段在第1年的状态矢量为 P( t ₀),则 t年后,该路段的状态矢量阵为 P( t+t ₀),则有

P( t+t ₀) =P( t ₀) × $\begin{array}{c}{P}^{t_0+1}\end{array}$ × $\begin{array}{c}{P}^{t_0+2}\end{array}$ ×… × $\begin{array}{c}{P}^{t_0+t-1}\end{array}$ =P( t ₀) × $\begin{array}{c}\stackrel{t-1}{\prod _{t=1}}\end{array}\begin{array}{c}{P}^{t_0+t}\end{array}$ (7)

如果转移矩阵是静态的,则可以简化为

P( t+t ₀) =P( t ₀) ×P ^t (8)

由此可知,马尔可夫模型的关键与核心就是转移概率矩阵.

2 面板数据马尔可夫路面性能预测过程

状态转移概率矩阵作为马尔可夫模型的核心部分 ^{[ 7]} ,它是指路网内一组具有相同属性(交通等级、路面结构、环境因素、使用年限等)的路面的使用性能指数在一定的时段内,从某一状态转移成为另一状态的概率. 为使路面使用性能变化能够与马尔可夫过程相适应,马尔可夫模型必须遵循以下假定 ^{[ 8]} :路面使用性能存在有限个状态;路面使用性能从某一状态转移到另一状态的概率与以前状态无关,只与当前状态有关;转移概率不随时间改变 ^{[ 9]} .

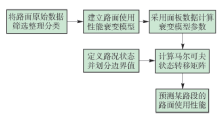
本文引入面板数据模型,用于计算路面使用性能衰变模型的参数,之后再计算马尔可夫状态转移矩阵. 概括起来,该计算过程分为5个步骤,具体计算流程见 图1.

图  1  面板数据马尔可夫模型预测路面使用性能流程图

Figure  1.  Prediction flow chart of pavement performance based on panel data Markov model

下载: 全尺寸图片 幻灯片

2.1 定义路况状态并划分状态边界值

在不同场合时,路面使用性能可采用不同的额度量指标,这些额度量指标具有不同的含义. 在项目级系统中,可采用开裂、车辙等单项损坏指标对路面使用性能予以定义,或可采用行驶质量指数RQI、抗滑能力SRI、路面状况指数PCI等指标定义,本文选用PCI和RQI为预测指标,结果可以为路面养护管理与决策提供支持. 对于普通公路而言,PCI和RQI是影响路面使用性能指数PQI的最主要指标,一级公路占75%权重,二级以下占100%. PCI和RQI划分为优、良、中、次、差5个等级 ^{[ 16]} ,划分状态边界值和中值见 表1.

表  1  沥青路面状态边界值和中值

Table  1.  Boundary value and mid-value of asphalt pavement

状态等级	PCI		RQI
	边界值	中值	边界值	中值
优	≥90,<100	95	≥90,<100	95
良	≥80,<90	85	≥80,<90	85
中	≥70,<80	75	≥70,<80	75
次	≥60,<70	65	≥60,<70	65
差	≥0,<60	30	≥0,<60	30

下载: 导出CSV 

| 显示表格

2.2 建立路面使用性能衰变模型

本文选用的沥青路面使用性能标准衰变方程 ^{[ 17]} 为

PPI =PPI ₀{1-exp[- $\begin{array}{c}{\left(\frac{\alpha }{T}\right)}^{\beta }\end{array}$ ]}(9)

式中:PPI为使用性能指数(PCI、RQI或其综合);PPI ₀为初始使用性能指数; T为道路通车年限; α、 β为模型参数, α, β=f(交通轴载、结构强度、材料类型、面层厚度、基层类型、环境状况).

2.3 采用面板数据法计算衰变模型参数

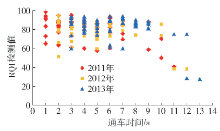
本文收集辽宁省多条国省道的69段路面检测数据,检测时间分别为2011、2012、2013年. 通过分析数据,发现其中涉及多种交通量等级和不同的路面结构. 数据见 图2、 图3.

图  2  PCI检测样本基础数据

Figure  2.  Essential test data of Pavement Condition Index

下载: 全尺寸图片 幻灯片

图  3  RQI检测样本基础数据

Figure  3.  Essential test data of Riding Quality Index

下载: 全尺寸图片 幻灯片

在同地区的路网内,因为路面结构、交通等级的不同,路面使用性能衰变过程可能不同,因此,概率转移矩阵也不同. 所以,为进一步提高马尔可夫模型预测的准确性,应将具有一定程度共性(相同的路面结构、交通量类型和相同的地区)的某些路面划分为路网子集,再根据路网子集建立相应的转移概率矩阵 ^{[ 10]} . 交通荷载是影响路面使用性能衰变的决定性因素. 交通荷载对于路面使用性能衰变规律的影响机理较为复杂 ^{[ 11]} . 根据平均日交通量,可将交通量分为5种等级;同时,结合路面结构分为40种不同的组合形式 ^{[ 17]} . 待考查的69个路段样本的路面结构和交通量均不相同. 根据路面结构厚度和交通量等级,将各路段样本归类,共计20类,见 表2.

表  2  各子集的交通量及路面结构

Table  2.  Traffic volume and pavement structure of each subnet

面层厚度/cm	基层厚度/cm	轻交通AADT<600ESAL<500	中等交通600≤AADT<1500500≤ESAL<2000	重交通1500≤AADT<30002000≤ESAL<4300	特重交通AADT≥3000ESAL≥4300
≤3	≤20	子集1	子集5	子集9	子集13
4~8	20~30	子集2	子集6	子集10	子集14
8~11	30~40	子集3	子集7	子集11	子集15
≥12	≥40	子集4	子集8	子集12	子集16
注:1) 该表分类方法仅适用于沥青面层、水泥稳定类基层(水泥稳定类底基层)的结构组合;2) 基层厚度为推荐范围,参考使用,不是绝对限制值;3) AADT指年平均日交通量,这里表示每车道、每日平均大型客车及中型以上各种货车交通量,单位:辆/(d·车道);4) ESAL指当日量轴载(BZZ-100)的作用次数,可根据相关标准进行转换,单位:次/(日·车道).

下载: 导出CSV 

| 显示表格

根据 表2的子集划分标准,将样本基础数据整理归类. 69个路段样本中,共涉及5个网,分别为:子集14包括34个样本,子集15包括4个样本、子集10包括20个样本、子集11包括2个样本、子集6包括9个样本. 由于子集15、子集11的样本过少,不具备代表性,故不作为重点研究. 下面主要研究子集14(中等厚度+特重交通)、子集10(中等厚度+重交通)、子集6(中等厚度+中等交通)的PCI和RQI的衰变规律. 并且以子集14的PCI指标为例详细说明计算过程,子集14的检测数据见 图4、 图5.

图  4  子集14的PCI样本数据

Figure  4.  Essential test data of Pavement Condition Index within subnet 14

下载: 全尺寸图片 幻灯片

图  5  子集14的RQI样本数据

Figure  5.  Essential test data of Riding Quality Index within subnet 14

下载: 全尺寸图片 幻灯片

现在利用子集14的PCI样本数据,运用面板数据法,计算孙立军 ^{[ 17]} 提出的沥青路面使用性能标准衰变模型参数,在计算PCI的参数时,可以将式(9)改写为

PCI =100{1-exp[- $\begin{array}{c}{\left(\frac{\alpha }{T}\right)}^{\beta }\end{array}$ ]} (10)

首先,因为面板数据一般采用线性求解,而式(10)为非线性的形式,可以通过取对数法,将式(10)转换为线性形式,即

Ln[-ln(1- $\begin{array}{c}\frac{\mathit{PCI}}{100}\end{array}$ )] =βln α-βln T(11)

其次,利用 表3中数据计算式(11)的参数 α、 β值. 将 表3数据写入E-Views软件进行计算,得到参数值,解得

Ln[-ln(1- $\begin{array}{c}\frac{\mathit{PCI}}{100}\end{array}$ )] =1.4758-0.8794ln TR ² =0.9834, F=117.0036(12)

表  3  子集14的路面PCI数据(有省略)

Table  3.  Pavement PCI data of subnet 14(choose the representative data)

序号	路线代码及路段起点终点	检测时间	PCI	Ln[-ln(1- $\begin{array}{c}\frac{\mathit{PCI}}{100}\end{array}$ )]	ln T
1	京哈线(G102)K365+200~K371+000	2011	75.21	4	1.3863
		2012	68.46	5	1.6094
		2013	54.75	6	1.7918
2	庄林线(G305)K129+300~K145+700	2011	95.89	3	1.0986
		2012	82.88	4	1.3863
		2013	78.47	5	1.6094
3	沈盘线(S102)K116+375~K123+474	2011	90.98	3	1.0986
		2012	54.87	4	1.3863
		2013	42.50	5	1.6094
4	中新线(S210)K43+744~K45+330	2011	45.12	11	2.3979
		2012	30.29	12	2.4849
		2013	27.28	13	2.5649
5	大锦线(S308)K93+450~K98+000	2011	71.78	3	1.0986
		2012	39.42	4	1.3863
		2013	67.70	5	1.6094
6	黑大线(G202)K1507+533~K1518+888	2011	92.53	1	0.0000
		2012	87.83	2	0.6931
		2013	79.20	3	1.0986
7	京沈线(G101)K524+000~K528+400	2011	78.69	2	0.6931
		2012	74.32	3	1.0986
		2013	75.15	4	1.3863
8	奈广线(S205)K66+914~K69+846	2011	66.75	5	1.6094
		2012	60.40	6	1.7918
		2013	55.96	7	1.9459
9	朝青线(S206)K116+000~K120+990	2011	62.82	7	1.9459
		2012	57.73	8	2.0794
		2013	51.35	9	2.1972
10	阜锦线(S204)K53+400~K58+900	2011	66.68	4	1.3863
		2012	60.92	5	1.6094
		2013	58.92	6	1.7918
11	十大线(S107)K69+891~K78+117	2011	80.38	6	1.7918
		2012	75.02	7	1.9459
		2013	69.62	8	2.0794
12	昌法线(S302)K0+000~K8+145	2011	82.85	6	1.7918
		2012	78.27	7	1.9459
		2013	69.28	8	2.0794
13	彰桓线(S303)K157+313~K159+313	2011	77.15	6	1.7918
		2012	58.24	7	1.9459
		2013	41.09	8	2.0794
14	明沈线(G203)K603+400~K614+400	2011	76.86	4	1.3863
		2012	56.41	5	1.6094
		2013	41.11	6	1.7918

下载: 导出CSV 

| 显示表格

然后,再对结果进行分析. 各回归系数的 t统计量均通过检验,调整后的 R ²值为0.9834,说明模型的拟合程度较好 . F值为117.0036,说明整个模型的线性关系是显著的 ^{[18 - 19]} .

最终得

$\begin{array}{c}\left\{\begin{array}{c}\beta =0.8794\\ \alpha =5.3558\end{array}\right.\end{array}$

即

PCI =100{1-exp[-( $\begin{array}{c}\frac{5.3558}{T}\end{array}$ )0.8794]}(13)

2.4 计算马尔可夫状态转移矩阵

根据 表1划分标准,将 PCI(或 RQI)离散为优、良、中、次、差5个状态,并组成各自状态区间. PCI:I ₁={100~90,90~80,80~70,70~60,60~0}为各状态边界值; PCI: M ₁={95,85,75,65,30}为各状态中值 ^{[ 20- 21]} .

路面状况 PCI(或 RQI)的调查检测和养护决策一般情况下为每年1次,参数空间T={0,1,2,…}是以年为基本单位构成 ^{[ 22- 25]} . 通过状态空间、参数空间,可利用得出的回归方程形成转移概率矩阵 ^{[ 26]} . 回归公式由2.3节计算得到系数α、β. 将 PCI状态空间的状态中值M ₁代入到路面状况指数 PCI的回归方程式. 反算得到T ₁={1.6626, 2.6168, 3.5729, 4.7086, 3.7509},再以T ₁+1代入回归方程式(9),计算得出下一年的路面状况 PCI(或 RQI)的期望值μ={84.4983, 74.5728, 66.0809, 57.8823, 28.2746},以μ作为概率分布的数学期望值,并按式(14)计算概率分布的标准差σ,结果见 表4.

表  4  马尔可夫模型计算参数

Table  4.  Calculated parameters of Markov model

计算项目	模型参数值
回归方程	PCI =100{1-e ∧[- $\begin{array}{c}{\left(\frac{5.3558}{T}\right)}^{0.8794}\end{array}$ ]}
系数 α			5.3558
系数 β			0.8794
标准差 σ			11.0887
马尔可夫中值	95.0000	85.0000	75.0000	65.0000	30.0000
T 1	1.5381	2.5858	3.6942	5.0677	17.2963
T 1 +1	2.5381	3.5858	4.6942	6.0677	18.2963
μ=PCI( T+1)	85.4627	75.9028	67.4681	59.1824	28.7855

下载: 导出CSV 

| 显示表格

σ= $\begin{array}{c}\sqrt[]{\frac{\stackrel{n}{\sum _{i=1}}(y_i-x_i{)}^2}{n-1}}\end{array}$ (14)

式中: y _i 为回归方程的拟合值; x _i 为路况检测的真实值; n为样本个数.

在此基础上,再分别以各状态的数学期望值 μ={85.4627, 75.9028, 67.4681, 59.1824, 28.7855}和回归方程精度 σ=11.0887作为正态分布函数的标准差,计算落在各状态上的概率 P _ij ( P _ij 表示路面性能从状态 i转移到状态 j的概率). 例如,以(85.4627,11.0887 ²)为参数,按

X~f( x) = $\begin{array}{c}\frac{1}{\sqrt[]{2\mathit{\pi \sigma }}}\end{array}\begin{array}{c}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}\end{array}$ (15)

得到正态分布函数,经过计算得到路面使用性能指标状态转移的概率分布函数. 式中: P _{1 j}= { P ₁₁, P ₁₂, P ₁₃, P ₁₄, P ₁₅)( j=1,2,3,4,5),表示路面性能从1状态转移到 j状态的概率值.

P ₁₁ =P(90 <X<100) = $\begin{array}{c}{\int }_{90}^{100}\end{array}\begin{array}{c}\frac{1}{\sqrt[]{2\mathit{\pi \sigma }}}\end{array}\begin{array}{c}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}\end{array}$ =Φ( $\begin{array}{c}\frac{90-\mu }{\sigma }\end{array}$ <x< $\begin{array}{c}\frac{0-\mu }{\sigma }\end{array}$ ) =ϕ(0.4918 <x<7.7072) =ϕ(7.7072) -ϕ(0.4918) =0.2463

同理,可得

P ₁₁ =0.2463, P ₁₂ =0.3477

P ₁₃ =0.2295, P ₁₄ =0.0708, P ₁₅ =0.0108

即得到

P _{1 j}= { P ₁₁, P ₁₂, P ₁₃, P ₁₄, P ₁₅}

按上述方式取路面性能的期望值作为正态分布的期望值 μ,进而得到正态分布的标准差 σ=11.0887,再计算落在各个状态上的转移概率值. 按上述算法,得到PCI的马尔可夫转移概率矩阵

P _ij= $\begin{array}{c}\left[\begin{array}{ccccc}0.2463& 0.3477& 0.2295& 0.0708& 0.0108\\ 0.0869& 0.2541& 0.3469& 0.2215& 0.0758\\ 0.0194& 0.1081& 0.2805& 0.3400& 0.2503\\ 0.0026& 0.0275& 0.1344& 0.3060& 0.5294\\ 0.0000& 0.0000& 0.0001& 0.0023& 0.9928\end{array}\right]\end{array}$

2.5 预测待估路面技术状况

在确定转移概率矩阵后,就可以通过当前状态矢量矩阵 P( t ₀)预估 t年后的路况状态 P( t ₀ +t), P( t ₀ +t) =P( t ₀) ×P ^t. 比如某路段位于该子集内,2011年检测其PCI为85,即2011年路面状态概率 P(0) ={0,1,0,0,0},后1年路面PCI的期望值 =0.0869 ×95 +0.2541 ×85 +0.3469 ×75 +0.2215 ×65 +0.0758 ×30 =72.5384,后2年的路面PCI期望值 =0.0508 ×95 +0.1384 ×85 +0.2630 ×75 +0.2483 ×65 +0.2995 ×30 =61.4395,即该路面2013年的PCI预测值为61.4395.

3 预测精度分析

为了检验该预测方法的预测精度,将2014年预测数据与2014年实测数据相对比,误差均不超过±5,说明检验样本满足精度要求,数据见 表5. 因此,使用该方法可以比较准确地预测具有相近特征(路面结构、交通量类型、所在地区)的路面指标的衰变规律.

表  5  PCI预测精度检验样本

Table  5.  Accuracy test samples of PCI

数据来源	京哈线(G102)K347+200~K365+100	黑大线(G202)K1507+533~K1518+888	庄林线(G305)K129+300~K145+700	中新线(S210)K75+000~K83+000	京沈线(G101)K649+500~K659+500	奈广线(S205)K60+012~K66+914	锦赤线(S306)K68+746~K83+146
2014年预测数据	48.73	65.46	64.21	58.28	61.97	51.86	51.03
2014年实测数据	45.51	68.20	69.07	60.31	66.76	55.21	47.62
误差值	3.22	2.74	4.86	2.03	4.79	3.35	3.41

下载: 导出CSV 

| 显示表格

4 不同子集的路面性能衰变规律比较

2.4、2.5节已经完成子集14的 PCI衰变规律预测. 使用上述同样方法,对子集14的 RQI衰变规律进行计算研究,并对数据充足的子集(子集10、子集6)进行计算研究,计算结果见 表6、7.

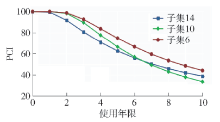
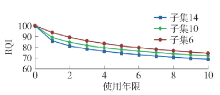
表  6  各子集PCI衰变参数

Table  6.  Decay parameters of PCI of each subnet

子集	系数 α	系数 β	标准差 σ	概率转移矩阵
子集14	5.3558	0.8794	11.0887	$\begin{array}{c}\left[\begin{array}{ccccc}0.2463& 0.3477& 0.2295& 0.0708& 0.0108\\ 0.0869& 0.2541& 0.3469& 0.2215& 0.0758\\ 0.0194& 0.1081& 0.2805& 0.3400& 0.2503\\ 0.0026& 0.0275& 0.1344& 0.3060& 0.5294\\ 0.0000& 0.0000& 0.0001& 0.0023& 0.9928\end{array}\right]\end{array}$
子集10	5.3358	1.4166	24.0055	$\begin{array}{c}\left[\begin{array}{ccccc}0.1494& 0.1649& 0.1534& 0.1202& 0.1561\\ 0.1098& 0.1464& 0.1645& 0.1558& 0.2903\\ 0.0732& 0.1139& 0.1493& 0.1649& 0.4270\\ 0.0444& 0.0796& 0.1204& 0.1535& 0.5592\\ 0.0032& 0.0093& 0.0231& 0.0482& 0.7852\end{array}\right]\end{array}$
子集6	6.4820	1.2423	9.5535	$\begin{array}{c}\left[\begin{array}{ccccc}0.2839& 0.3933& 0.2004& 0.0373& 0.0026\\ 0.0651& 0.2657& 0.3974& 0.2186& 0.0473\\ 0.0075& 0.0768& 0.2868& 0.3924& 0.2362\\ 0.0004& 0.0109& 0.0974& 0.3172& 0.5741\\ 0.0000& 0.0000& 0.0000& 0.0004& 0.9979\end{array}\right]\end{array}$

下载: 导出CSV 

| 显示表格

表  7  各子集RQI衰变参数

Table  7.  Decay parameters of RQI of each subnet

子集	系数 α	系数 β	标准差 σ	概率转移矩阵
子集14	19.1133	0.2281	13.7347	$\begin{array}{c}\left[\begin{array}{ccccc}0.2204& 0.2842& 0.2206& 0.1031& 0.0344\\ 0.1693& 0.2712& 0.2617& 0.1520& 0.0658\\ 0.0872& 0.2023& 0.2824& 0.2374& 0.1642\\ 0.0267& 0.0976& 0.2146& 0.2840& 0.3723\\ 0.0000& 0.0001& 0.0017& 0.0127& 0.9711\end{array}\right]\end{array}$
子集10	26.4225	0.2428	14.3003	$\begin{array}{c}\left[\begin{array}{ccccc}0.2399& 0.2693& 0.1890& 0.0830& 0.0271\\ 0.1832& 0.2674& 0.2442& 0.1394& 0.0625\\ 0.0957& 0.2042& 0.2725& 0.2275& 0.1664\\ 0.0312& 0.1029& 0.2121& 0.2733& 0.3739\\ 0.0000& 0.0002& 0.0023& 0.0154& 0.9641\end{array}\right]\end{array}$
子集6	26.3669	0.3108	5.3911	$\begin{array}{c}\left[\begin{array}{ccccc}0.4752& 0.4611& 0.0302& 0.0001& 0.0000\\ 0.0847& 0.6008& 0.3042& 0.0096& 0.0000\\ 0.0014& 0.1269& 0.6361& 0.2306& 0.0050\\ 0.0000& 0.0020& 0.1520& 0.6443& 0.2017\\ 0.0000& 0.0000& 0.0000& 0.0000& 1.0000\end{array}\right]\end{array}$

下载: 导出CSV 

| 显示表格

根据 表6、7中的概率转移矩阵,计算得到各子集的PCI、RQI衰变预测曲线图,见 图6、7. 反映了各子集PCI和RQI性能逐年衰变的期望值,3个子网的PCI衰变曲线为凹形,RQI衰变曲线为反S形,子集6的PCI与RQI的衰变速率均低于子集10与子集14,该区域内路面PCI与RQI的衰变存在相关性.

图  6  各子集PCI的相对衰变速率对比

Figure  6.  Comparison of PCI relative decay velocity of each subnet

下载: 全尺寸图片 幻灯片

图  7  各子集RQI的相对衰变速率对比

Figure  7.  Comparison of RQI relative decay velocity of each subnet

下载: 全尺寸图片 幻灯片

5 结论

1) 本文用面板数据马尔可夫转移概率模型预测路面性能的衰变过程. 根据沥青路面使用性能评价指标(PCI、RQI)及评价标准,确定路面状态5个等级及边界值. 通过面板数据法计算出路面性能衰变函数,再利用该函数计算出路面状态恶化的马尔可夫转移概率. 为了检验该预测方法的预测精度,将2014年预测数据与2014年实测数据相对比,误差均不超过±5,说明检验样本满足精度要求,该模型具有较高的路面使用性能预测的能力.

2) 以辽宁省69条公路3a的使用性能检测数据为基础,选定马尔可夫预测模型,并利用E-View计算模型参数,然后用MATLAB计算概率转移矩阵. 提出面板数据马尔可夫预测模型,该方法对于缺少历史年限、样本数量足够的数据库是合适的.

3) 本文计算出普通公路沥青面层厚度6cm(±2cm)+水稳基层厚度25cm(±5cm)的路面结构,在中等交通、重交通和特重交通荷载作用下的路面PCI和RQI的衰变规律,主要采用了辽宁中北部地区的沥青路面使用性能的预测,其他地区可参考该方法进行预测.