Control Measurements of Crossing Pedestrian Flows in Rail Transit
-
摘要:
为了探究轨道交通十字客流管控策略,对北京市轨道站点的客流组织现状开展调查分析. 明确十字客流冲突的形成过程,解析冲突客流基本特征. 提出基于可接受间隙理论和环流现象的客流管控优化方法,并采用行人实验的方法开展了2类管控措施的优化效果验证. 结果表明:间隙控制方法可有效避免主-次客流冲突,环岛设置方法可有效避免主-主客流冲突;分别从冲突持续时间、客流速度、通行效率方面进行了2类优化措施的效果量化.
Abstract:To investigate control measurements of crossing pedestrian flows, a field survey was carried out to learn the current conflict situation of Beijing rail transit stations. The conflict process and the characteristics of passenger flow under the conflict were analyzed. Then, optimized measures were presented based on gap acceptance theory and roundabout traffic. To verify the effects of the two measures, a pedestrian experiment was carried out. Validation results show that the gap control measure are capable of decreasing main-minor flows conflict severity, and setting roundabout can decrease the main-main flows conflict severity. As quantification indexes, conflict continuous time, passenger velocity and through efficiency are introduced to analyze the effects of the two measures.
-
客流冲突是指因流向不同的2组或多组客流交织,而发生流速变化或行进方向改变的现象 [ 1] . 十字冲突作为轨道交通站点中最为常见的冲突形式,严重影响客流组织效率,降低出行舒适度,甚至诱发踩踏事故,形成安全隐患. 在早期定性分析的基础上, 国内外学者通过开展实地观测,发现并定义了十字客流冲突中的自组织分层现象 [ 2- 3] 和环流现象 [ 4- 5] . 其中分层现象是指行人自发形成组群,以层的形式整体前进,并且同一层中行人的行走方向和速度基本一致. 环流现象是指在客流交织区域由于乘客减速、停止及避让所出现的临时性、不稳定的客流环形自组织行走现象. 由于冲突过程的短暂性和多变性,实地观测方法逐渐难以满足行人行为参数的精细化量化分析,部分学者开始采用场景实验和视频跟踪的方式获取更为高效、精准的速度、密度等行人行为数据 [ 6- 8] .
结合上述冲突客流自组织现象,部分学者研究了可能的客流管控措施. Helbing等 [ 5] 提出了在交织区域中心摆放圆形障碍物以促进环流的产生及稳定的思路. 葛世平 [ 9] 研究了不同条件下轨道站点设施位置优化的可能性,以达到缓解客流冲突的目的. 陈然等 [ 10] 和胡春平等 [ 11] 从冲突流线优化角度,探讨了冲突客流的疏解措施.
综合而言,国内外学者在十字冲突客流特性及管控措施方面已开展了部分工作,但对于十字冲突客流规律性认识仍不深刻,提出的管控措施亦有待进一步深化论证. 通过解析十字客流的冲突特性,提出有针对性的管控措施,对于轨道交通的客流组织优化和安全性提升具有十分重要的理论价值和实际意义.
1 十字客流冲突特性
为了全面、准确地获取地铁冲突客流的行为数据,对北京地铁1、2、4、6、10号线等15个轨道站点的十字客流冲突现象开展调查与特性分析.
1.1 数据采集
在工作日的早高峰时段,通过架设数码摄像机的方式,对轨道站点内选取的20个十字冲突客流多发位置进行冲突视频采集. 每个冲突位置采集6次连续完整的十字客流冲突,共计120次. 利用视频标定软件,对冲突客流流量、速度、冲突时刻等特征数据进行标定提取. 视频及检测效果如 图1所示.
1.2 特性分析
地铁客流流线设计中会尽量避免2条主流线交织. 因此现状的地铁十字客流冲突中存在较大客流量差异的流线冲突(主-次冲突)较为常见,在本次调查中约占75%,而客流量相当的流线冲突(主-主冲突)约占25%. 其中主-次客流冲突中以换乘客流和进站客流冲突最为常见,且呈现较为明显的间断特性,主-主客流冲突中则呈现较为明显的环流特性.
1.2.1 主-次客流冲突的间断特性
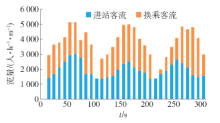
对主-次冲突客流的调查数据分析发现,由于受到列车到发间隔的影响,换乘客流会呈现明显的周期性波动且客流量峰值较大,是冲突中的主要客流. 进站客流虽然也会呈现波动特点,但客流量相对较小,是冲突中的次要客流,如 图2所示.
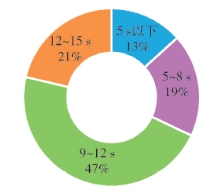
针对换乘客流的周期性波动特点,统计得到相邻2次换乘客流的到达间隔,其中9~12s间隔所占比例最大,达到47%,如 图3所示.
1.2.2 主-主客流冲突的环流特性
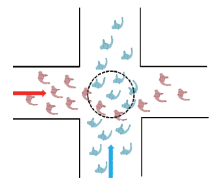
对主-主冲突客流的调查数据分析发现,冲突流线的客流量多分布在4000~6000人/(h·m),且行人在通过冲突区域时会形成自组织弧形环流行进,如 图4所示. 这种环流状态的持续时间与客流量的大小相关,一般介于2~5s.
2 客流管理控制措施
针对上述2类主要客流的冲突特性,本研究分别提出可接受间隙限流和环岛设计的管控方案,探索降低冲突干扰的可能措施.
2.1 基于可接受间隙的主-次客流冲突管控
可接受间隙理论目前主要应用于无信号交叉口的机动车冲突分析,即通过调查主要车流在交叉口冲突区的通过特性,分析次要车流穿越主要车流的临界间隙 [ 12] .
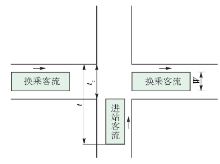
在轨道站点站厅内,当主(换乘客流)-次(进站客流)2股客流行进路径相交,由于不存在任何控制和引导,客流自主通过,与无信号交叉口的情景类似,如 图5所示. 此时,可充分利用主客流的间断特性对次要客流进行间歇放行,以确保大部分的次要客流可在主要客流的间隙通过,达到降低冲突强度的目的. 目前自动放行隔离栏或安全门在行人组织管理中已有尝试应用,真实环境中可采用该方式实现对次要客流的间歇放行,并通过视频行为采集进行效果评测优化.
2.2 基于环流现象的主-主客流冲突流线优化
由于主-主冲突中各流线的客流量相当且较大,难以通过限制某单方面客流的模式进行优化管控. 为此,结合主-主冲突客流中的环流特性,提出在客流冲突区域中心设置环岛,促进环流的产生与稳定,达到通过行人绕行降低冲突强度的目的.
3 行人实验设计
由于在实际的轨道交通运营空间中存在客流组成复杂、空间受限、干扰正常运营等问题,往往难以实现冲突管控方案效果的准确评估. 因此,选取在空旷的实验场地,搭建实地场景并开展行人实验的方法进行客流冲突管控优化的模拟分析.
3.1 可接受间隙限流的行人实验
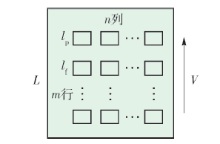
为了方便计算每个换乘客流间隙可通过的进站客流理论人数,将进站客流简化为由 m行、 n列行人组成的矩阵,如 图6所示.
根据可接受间隙理论,临界间隙 t c为允许次要行人流-进站客流一排人通过冲突区域的临界时间,其计算公式为
t c =
式中: W为换乘客流宽度,m; V为进站客流速度,m/s.
因此,可供 m行进站客流通过的冲突区域的时间为
式中: L为进站客流长度,m; l f为人与人之间纵向间距,m; l p为每人所占的空间长度,m.
由式(2)推导出
于是,在一个换乘客流间隙 t内,允许进站客流可通行的理论人数为
式中: t为换乘客流间隙,s; n为进站客流列数,列.
结合实际调查数据,选取高峰时段换乘客流间隙 t为10s;进站客流速度 V取1m/s;换乘客流宽度 W设为3m;进站客流宽度为3m;考虑到单个行人的基本行走宽度为0.75m [ 13] ,同时人与人之间会保持一定的横向距离,因此 n取3;行人静止时体宽约为0.45 ~0.46m [ 13] ,每个人所占空间长度 l p取0.5m;考虑到行人行走时前后的安全距离,人与人之间纵向间距 l f取1m. 将上述参数值代入式(4),可知当换乘客流间隙为10s时,可一次理论通过的进站客流为16人.
![]()
图 7 基于可接受间隙管控的行人实验设计Figure 7. Pedestrian experiment design based on gap acceptance theory在本实验中,将选定的100名实验者分为2组,一组为换乘客流,即为A客流,佩戴红色帽子;另一组为进站客流,即为B客流,佩戴黑色帽子. 实验场地、设备及实验过程如 图7所示. 其中,摄像机位于实验区域的正上方. 为明确客流可接受间隙控制的管控效果,结合理论计算值,分别在换乘客流的10s间隙内对进站客流进行4个对比实验控制: 1) 持续放行; 2) 放行13人; 3)放行16人; 4) 放行19人,其中实验2/3/4的放行人数分别为少于/等于/多于20%的理论推导人数.
结合实际调查数据,换乘客流(A客流)流量取4000人/(h·m),进站客流(B客流)流量取2000人/(h·m). 具体实验方案如 表1所示.
表 1 可接受间隙管控实验方案设计Table 1. Experimental scheme design of gap acceptance theory control步骤 实验1 实验2 实验3 实验4 无可接受间隙控制 完全可接受间隙控制 完全可接受间隙控制 部分可接受间隙控制 1 放行A1客流(30人) 2 A1客流放行时,B客流持续放行 A1客流通过时,放行B客流13人 A1客流通过时,放行B客流16人 A1客流通过时,放行B客流19人 3 A1客流通过后10s,放行A2客流(30人) 3.2 环岛流线优化的行人实验
将实验人员平均分为2组,结合实际调查数据,分别选取4000、5000、6000人/(h·m)的流量进行主-主冲突中的2股客流模拟. 为确保与客流出入口宽度一致,设置环岛直径为标准的2m. 实验区域与实验场景设计如 图8所示. 实验设计方案如 表2所示.
![]()
图 8 环岛流线优化的行人实验设计Figure 8. Pedestrian experiment design based on flow line optimization of roundabout表 2 环岛设置的实验方案设计Table 2. Experimental scheme design of roundabout setting流量/(人·h -1·m -1) 环岛 实验1 4000 无 实验2 4000 有 实验3 5000 无 实验4 5000 有 实验5 6000 无 实验6 6000 有 4 实验结果分析
对2类行人实验获取的视频进行行为标定,获取冲突持续时间、客流速度、通行效率等关键指标,以明确可接受间隙和环岛流线优化的十字冲突的管控效果.
4.1 可接受间隙限流效果分析
4.1.1 冲突持续时间
冲突持续时间是指在冲突区域内,客流平均速度保持在最大速度的70%以下的持续时间 [ 14] . 受可接受间隙控制的影响,4组实验的冲突持续时间各不相同,如 表3所示. 在采取可接受间隙策略控制进站客流之后,平均冲突持续时间降低约43%~81%. 同时实验2中,虽然进站客流人数比实验3少20%,但冲突时间相同,这是由于当穿越的人较少时,前导行人缺乏通过紧迫感,导致跟随客流与到达的换乘客流发生冲突. 实验4的冲突持续时间尽管是实验3的3倍,但与不设置可接受间隙管控相比,仍然有所降低. 总之,从冲突持续时间这一评价指标来看,当采取可接受间隙管控措施,且控制进站客流为理论推导的人数时,效果最佳.
表 3 可接受间隙管控的冲突持续时间分析Table 3. Conflict continuous time analysis of gap acceptance theory control实验编号 1 2 3 4 冲突时间/s 16 3 3 9 4.1.2 客流速度
对速度数据的分析发现,采取可接受间隙控制后进站客流和换乘客流的平均速度升高,速度标准差降低,冲突区域内部的客流平均速度提高18%~44%,如 表4所示. 实验2、3的客流速度平均值相当,而实验3的进站客流比实验2的通行人数高20%,这再次表明控制进站客流人数为理论推导值时客流的通行效果更好.
表 4 可接受间隙管控的行人流速度Table 4. Passenger's velocity analysis of gap acceptance theory control实验编号 平均速度/(m·s -1) 标准差 冲突区内平均速度/(m·s -1) 1 换乘客流 0.765 0.296 0.644 进站客流 0.942 0.214 2 换乘客流 1.161 0.142 1.002 进站客流 1.134 0.138 3 换乘客流 1.159 0.141 0.929 进站客流 1.093 0.158 4 换乘客流 1.057 0.152 0.760 进站客流 1.086 0.207 4.1.3 通行效率
通行效率是用来反映行人对交通设施资源的占用情况,可以表示为某一道路断面上,特定时间内单位宽度的设施所能通过的最大个体数,单位为人/(h·m) [ 15] ,计算式为
E=
式中: i为行人总数; t i 为第 i个行人通过出口的时间,s; w为设施宽度,m.
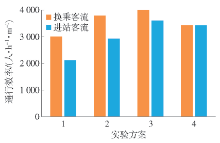
分别对进站客流和换乘客流的实验通行效率进行分析,如 图9所示. 对比发现,不进行限流管控时,两股客流的通行效率最低;采用可接受间隙措施进行放流后,通行效率提升14%~70%,其中控制进站客流为理论推导的人数时,通行效率最高.
![]()
图 9 可接受间隙管控的通行效率对比分析Figure 9. Through efficiency analysis based on the gap acceptance theory总之,当进站客流与换乘客流(主次客流)发生冲突,在对进站客流采用可接受间隙控制措施后,整体冲突持续时间缩短43%~81%,冲突区内平均速度提升18%~44%,客流通行效率提高14%~70%. 因此,可接受间隙控制可有效减少十字客流冲突,且当控制进站客流为理论推导人数时,效果最佳.
4.2 环岛流线优化的结果分析
4.2.1 冲突持续时间
对设置环岛前后的客流冲突持续时间进行标定统计,数据如 表5所示. 实验编号为1、2、3、4、5、6的冲突持续时间分别为11、9、11、8、10、7s. 设置环岛后,各流量下冲突持续时间均有不同程度的减少,分别减少18%、27%、30%,表明环岛的设置在一定程度上减缓了客流冲突. 同时流量越大冲突持续时间的减少越显著,说明环岛对大客流冲突的缓解效果更为明显.
4.2.2 客流速度
对设置环岛前后的客流速度数据进行标定统计,数据如 表5所示. 同一环岛设置下,随着流量的增加,客流的平均速度降低,标准差升高,冲突区域内客流速度降低,说明流量越大对客流的通行影响越大. 同时,对比环岛设置前后客流的速度变化可知,设置环岛后客流的平均速度提高9%~21%,速度标准差降低20%~41%. 冲突区域内的速度提升最为突出,提高11%~30%,并且当流量大于5000人/(h·m)时,提升比例在20%以上. 考虑到5000人/(h·m)正好是枢纽内单向通道的通行能力 [ 16] ,表明环岛的设置对客流行进速度提高与稳定具有一定的促进作用,并且流量大于或等于通行能力时效果最为明显.
表 5 环岛优化的行人流速度分析Table 5. Passenger's velocity analysis of roundabout setting optimizing实验编号 平均速度/(m·s -1) 标准差 冲突区内平均速度/(m·s -1) 1 1.18 0.40 1.04 2 1.29 0.32 1.16 3 1.09 0.47 0.92 4 1.23 0.30 1.13 5 0.89 0.49 0.76 6 1.08 0.29 0.99 4.2.3 通行效率
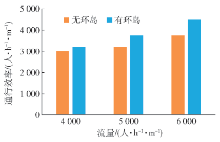
对设置环岛前后不同流量下的通行效率进行计算,结果如 图10所示. 由于客流发生冲突,各实验的通行效率都小于初始放行的流率. 对比发现,设置环岛后通行能力均有提升,提升程度7%~20%不等. 并且随着流量的增加,提升的比例增加. 这表明客流量越大,环岛的设置对通行效率的提升越明显. 因此,在人流量较大的冲突区域,可以通过设置环岛来缓解客流冲突,提高通行效率.
总之,当流量较大且相当的客流发生冲突时,设置环岛可使冲突持续时间缩短18%~30%,冲突区内平均速度提升11%~30%,通行效率提高7%~20%. 流量越大提升效果越明显,尤其当流量大于通行能力时,效果最为显著. 因此,当2股大客流相遇时,可通过在冲突区域设置环岛减缓客流冲突.
5 结论
1) 以进站客流和换乘客流相交,及2股大客流相交2类典型冲突为例,研究了轨道十字客流冲突现象,分析明确了十字冲突客流的间断特性和环流特性.
2) 提出了基于可接受间隙理论的主-次客流冲突管控方法,将行人流进行矩阵简化,构建了换乘客流间隙可通过的进站客流理论人数模型,并通过行人实验进行了优化效果验证,结果表明间隙控制方法可有效避免主-次客流冲突,且控制进站客流为理论推导的人数时效果最佳.
3) 提出了基于环流现象的主-主客流冲突流线优化方法,并通过行人实验进行了优化效果验证,结果表明设置环岛可有效促进环流的产生与稳定,显著缓解主-主客流冲突.
4) 轨道站点中的客流冲突现象存在形式多样、复杂多变的特点,未来可针对不同量级的2股交叉人流进行更多样本的研究,使成果具有普遍适用性. 同时可开展实际运营中十字冲突客流管控的效果检验工作,并进一步探讨其他冲突类型的典型规律,提出管控措施.
The authors have declared that no competing interests exist. -
![]()
图 7 基于可接受间隙管控的行人实验设计
Figure 7. Pedestrian experiment design based on gap acceptance theory
![]()
图 8 环岛流线优化的行人实验设计
Figure 8. Pedestrian experiment design based on flow line optimization of roundabout
![]()
图 9 可接受间隙管控的通行效率对比分析
Figure 9. Through efficiency analysis based on the gap acceptance theory
表 1 可接受间隙管控实验方案设计
Table 1 Experimental scheme design of gap acceptance theory control
步骤 实验1 实验2 实验3 实验4 无可接受间隙控制 完全可接受间隙控制 完全可接受间隙控制 部分可接受间隙控制 1 放行A1客流(30人) 2 A1客流放行时,B客流持续放行 A1客流通过时,放行B客流13人 A1客流通过时,放行B客流16人 A1客流通过时,放行B客流19人 3 A1客流通过后10s,放行A2客流(30人) 
下载: 导出CSV
表 2 环岛设置的实验方案设计
Table 2 Experimental scheme design of roundabout setting
流量/(人·h -1·m -1) 环岛 实验1 4000 无 实验2 4000 有 实验3 5000 无 实验4 5000 有 实验5 6000 无 实验6 6000 有
下载: 导出CSV
表 3 可接受间隙管控的冲突持续时间分析
Table 3 Conflict continuous time analysis of gap acceptance theory control
实验编号 1 2 3 4 冲突时间/s 16 3 3 9
下载: 导出CSV
表 4 可接受间隙管控的行人流速度
Table 4 Passenger's velocity analysis of gap acceptance theory control
实验编号 平均速度/(m·s -1) 标准差 冲突区内平均速度/(m·s -1) 1 换乘客流 0.765 0.296 0.644 进站客流 0.942 0.214 2 换乘客流 1.161 0.142 1.002 进站客流 1.134 0.138 3 换乘客流 1.159 0.141 0.929 进站客流 1.093 0.158 4 换乘客流 1.057 0.152 0.760 进站客流 1.086 0.207
下载: 导出CSV
表 5 环岛优化的行人流速度分析
Table 5 Passenger's velocity analysis of roundabout setting optimizing
实验编号 平均速度/(m·s -1) 标准差 冲突区内平均速度/(m·s -1) 1 1.18 0.40 1.04 2 1.29 0.32 1.16 3 1.09 0.47 0.92 4 1.23 0.30 1.13 5 0.89 0.49 0.76 6 1.08 0.29 0.99
下载: 导出CSV
-
[1] 陆奕婧,邹晓磊.城市轨道交通车站客运组织评价[J].交通科技与经济,2009,11(1):67-69. LU YJ,ZOU XL.Study on evaluation of passenger organization in urban rail transit station[J].Technology & Economy in Areas of Communications,2009,11(1):67-69. (in Chinese)
[2] HELBINGD,MOLNARP.Self-organization phenomena in pedestrian crowds[J].Self-organization of Complex Structures: From Individual to Collective Dynamics,1998,10(3):569-577. [3] HOOGENDOORNS,DAAMENW.Traffic and granular flow '03[M].New York: Springer,2005:373-382. [4] HELBINGD.A mathematical model for the behavior of individuals in a social field[J].Journal of Mathematical Sociology,1994,19(3):189-219. [5] HELBINGD,MOLNARP,FARKAS IJ,et al.Self-organizing pedestrian movement[J].Environment and Planning B,2001,28(3):361-384. [6] COFFINA,MORRALLJ.Walking speeds of elderly pedestrians at crosswalks[J].Transportation Research Record,1995,1487:63-67. [7] HELBINGD,BUZNAL,JOHANSSONA,et al.Self-organized pedestrian crowd dynamics: experiments, simulations, and design solutions[J].Transportation Science,2005,39(1):1-24. [8] GUO RY,WONG SC,HUANG HJ,et al.A microscopic pedestrian-simulation model and its application to intersecting flows[J].Physica a Statistical Mechanics & Its Applications,2010,389(3):515-526. [9] 葛世平.从大客流运营角度谈地铁车站的建筑布置优化设计[J].城市轨道交通研究,2010,13(4):1-7. GE SP.Talking about the building layout optimization design of metro station form huge flow operation[J].Urban Mass Transit,2010,13(4):1-7. (in Chinese)
[10] 陈然,李翔,董力耘.地铁站内交织行人流的简化模型和数值模拟[J].物理学报,2012,61(14):265-273. CHENR,LIX,DONG LY.Modeling and simulation of weaving pedestrian flow in subway stations[J].Acta Physica Sinica,2012,61(14):265-273. (in Chinese)
[11] 胡春平,毛保华,朱宇婷.综合客运枢纽旅客全过程流线优化模型[J].交通运输系统工程与信息,2012(3):159-164, 186. HU CP,MAO BH,ZHU YT.Streamline design and optimization for whole process of passenger transfer in integrated transportation hubs[J].Journal of Transportation Systems Engineering and Information Technology,2012(3):159-164, 186. (in Chinese)
[12] 李文权,王炜.无信号交叉口主车流服从移位负指数分别下支路多车型混合车流的通行能力[J].系统工程理论与实践,2001,21(2):122-128. LI WQ,WANGW.Capacity of minor multi-vehicle-types mixed traffic flow under major stream with shifted negative exponential distribution on unsignalized intersection[J].Systems Engineering-theory & Practice,2001,21(2):122-128. (in Chinese)
[13] 李得伟,韩宝明.行人交通[M].北京:人民交通出版社,2011:32,35. [14] WUJ,LUS.Feature analysis and operation evaluation of pedestrian weaving zone[J].Transportation Research Record: Journal of the Transportation Research Board,2013(2393):66-74. [15] 李晓蔚.城市道路通行效率及其影响因素的量化分析[D].北京: 北京交通大学,2012. LI XW.Quantitative analysis of traffic efficiency and its influencing factors[D].Beijing: Beijing Jiaotong University,2012. (in Chinese)
[16] Transit Cooperative Research Program (TCRP).Transit capacity and quality of service manual[M].Washington: Federal Transit Administration,2003:23-67.
计量
- 文章访问数: 17
- HTML全文浏览量: 2
- PDF下载量: 6
