近年来全国各地内涝灾害频发,根据2010年住房与城乡建设部对全国32个省351个城市的内涝灾害情况调查结果显示,2008—2010年,调查省市中发生过不同程度内涝灾害城市共有213个,占全部调查城市数量的61 %,其中137个城市的内涝灾害发生次数在3次及以上 ^{[ 1]} . 而解决城市内涝问题的基本依据是暴雨强度公式的推求计算问题 . 随着社会经济和计算机技术的不断发展,暴雨强度公式基础理论研究的不断深入,发现暴雨强度公式在推求过程中尚存在一些问题亟待解决 . 暴雨强度公式推求的基本步骤包括:资料收集、样本选取、频率分析、公式推求和误差分析等 . 其中样本选取方法的选择和频率分析方法的选择是决定暴雨强度公式精度至关重要的步骤,直接影响了公式的可靠性 ^{[2 - 3]} .

编制暴雨强度公式所用的数据资料是具有自记雨量记录的气象站所累积的降雨资料 . 降雨资料样本选取的方法主要有年最大值法 ^{[ 4]} 和非年最大值法 . 非年最大值法又包括年超大值法、超定量法和年多个样法 . 20世纪70年代开始,一些西方发达国家,由于降雨资料年限较长并且城市排水设计标准的重现期要求也比较高,已经使用年最大值法进行暴雨强度公式的推求 ^{[ 5]} . 90年代开始,国外在一些研究应用中也曾使用过年超大值法选样 ^{[ 6]} ;当时国内由于雨量资料缺乏及当时计算机技术的落后等众多原因,应用最多的是年多个样法 . 随着我国各地降雨资料的不断累积完善,2014年修编的室外排水设计规范规定在具有20a以上自记雨量记录的地区暴雨样本选样方法宜采用年最大值法 .

目前,我国在编制城市暴雨强度公式时经常采用的频率分布曲线主要有以下4种 ^{[ 7]} :经验频率曲线、皮尔逊 Ⅲ(P -Ⅲ)型分布曲线、指数分布曲线和Gumbel(耿贝尔)分布曲线 . 后3种理论频率分析方法各有优劣,在编制暴雨强度公式时应用较为广泛,至于在实际工程中选取的样本序列究竟更适合哪种频率分析曲线,目前尚无定论 . 各地根据经验选用的频率分析方法不尽相同,学术界对此一直没有统一的认识 ^{[8 - 11]} . 理论上指数分布和Gumbel分布都是P -Ⅲ型分布在特定参数条件下的分布曲线,指数分布曲线全部的参数都是采用数解法求得 ^{[12 - 13]} ,由于具有可免去P -Ⅲ型分布曲线人工适线不必要的烦琐步骤,计算较为简便等优点,之前在我国的很多城市得到应用,但指数分布曲线对不同降雨样本的适用性却有待研究 . 鉴于以上情况,本文着重对选取样本系列和指数分布曲线之间的适用情况进行了分析研究 .

1 指数分布的理论基础

指数分布仅是P-Ⅲ型分布曲线当偏态系数 C _s =2时的特例 ^{[ 14]} ,是P-Ⅲ型分布曲线偏态分布下的“捺”形部分 . 该分布只含有2个参数,2参数均采用数解法求得,无须适线,计算简便 .

1.1 P-Ⅲ型分布

P-Ⅲ型分布具有如下的概率密度函数 ^{[ 15]} :

f( x) = $\begin{array}{c}\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}\end{array}$ ( x-b) ^{α- 1}e ^{-β ( x-b )} ( b≤ x) (1)

式中: Γ( α)为 α的伽玛函数; α、 β、 b分别为P -Ⅲ型分布的形状、尺度和位置参数, α, β>0 .

本分布的特征函数为

φ( t) =e ^ibt ( - $\begin{array}{c}\frac{\mathit{it}}{\beta }\end{array}$ ) ^-α (2)

展开得

φ( t) = $\begin{array}{c}\stackrel{\infty }{\sum _{r=0}}\end{array}\begin{array}{c}\frac{{\left(\mathit{it}\right)}^r}{r!}\end{array}\begin{array}{c}\stackrel{r}{\sum _{j=0}}\end{array}\begin{array}{c}\left(\begin{array}{c}r\\ j\end{array}\right)\end{array}\begin{array}{c}\frac{\Gamma (\alpha +j)}{\Gamma \left(\alpha \right)}\end{array}\begin{array}{c}\frac{b^{r-j}}{{\beta }^j}\end{array}$

故 r阶原点矩

v _r= $\begin{array}{c}\stackrel{r}{\sum _{j=0}}\end{array}\begin{array}{c}\left(\begin{array}{c}r\\ j\end{array}\right)\end{array}\begin{array}{c}\frac{\Gamma (a+j)}{\Gamma \left(a\right)}\end{array}\begin{array}{c}\frac{b^{r-j}}{{\beta }^j}\end{array}$ , r=1,2,…(3)

令 r=1,得均值

$\begin{array}{c}\overline{X}\end{array}$ =v ₁ = $\begin{array}{c}\frac{\alpha }{\beta }\end{array}$ +b

由此可得各阶中心距

DX=μ ₂ =σ ² = $\begin{array}{c}\frac{\alpha }{{\beta }^2}\end{array}$

μ ₃ = $\begin{array}{c}\frac{2\alpha }{{\beta }^3}\end{array}$

︙

故

σ= $\begin{array}{c}\frac{\sqrt[]{\alpha }}{\beta }\end{array}$

C _v = $\begin{array}{c}\frac{\sqrt[]{\alpha }}{\alpha +\mathit{\beta b}}\end{array}$

C _s = $\begin{array}{c}\frac{2}{\sqrt[]{\alpha }}\end{array}$

由此,3个原始参数 α、 β、 b可以用基本参数 $\begin{array}{c}\overline{X}\end{array}$ 均值、 C _v变差系数、 C _s偏态系数表示如下:

α= $\begin{array}{c}\frac{4}{C_s^2}\end{array}$ (4)

β= $\begin{array}{c}\frac{2}{\overline{X}{C}_v{C}_s}\end{array}$ (5)

b= $\begin{array}{c}\overline{X}\end{array}$ (1 - $\begin{array}{c}\frac{2C_v}{C_s}\end{array}$ )(6)

X的分布函数为

F( x) = $\begin{array}{c}\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}\end{array}\begin{array}{c}{\int }_b^x\end{array}$ ( x-b) ^{α- 1}e ^{-β ( x-b )}d x(7)

或用超过概率形式

F ₁( x) =1 -F( x) = $\begin{array}{c}\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}\end{array}\begin{array}{c}{\int }_x^{\infty }\end{array}$ ( x-b) ^{α- 1}e ^{-β ( x-b )}d x(8)

对随机变数 X进行标准化,标准化形式为

t= $\begin{array}{c}\frac{x-\overline{X}}{\sigma }\end{array}$

则

x=tσ+ $\begin{array}{c}\overline{X}\end{array}$ =tσ+b+ $\begin{array}{c}\frac{\alpha }{\beta }\end{array}$

或

x-b=tσ+ $\begin{array}{c}\frac{\alpha }{\beta }\end{array}$

又

| $\begin{array}{c}\frac{\mathit{dx}}{\mathit{dt}}\end{array}$ | =σ

以及 σβ= $\begin{array}{c}\sqrt[]{\alpha }\end{array}$ ,可得

F ₁( x) = $\begin{array}{c}\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}\end{array}\begin{array}{c}{\int }_t^{\infty }\end{array}$ ( tσ+ $\begin{array}{c}\frac{\alpha }{\beta }\end{array}$ ) ^{α- 1} $\begin{array}{c}{e}^{-\beta (\mathit{t\sigma }+\frac{\alpha }{\beta })}\end{array}$ σd t= $\begin{array}{c}\frac{{\alpha }^{\frac{\alpha }{2}}}{\Gamma \left(\alpha \right)}\end{array}\begin{array}{c}{\int }_t^{\infty }\end{array}$ ( t+ $\begin{array}{c}\sqrt[]{\alpha }\end{array}$ ) ^{α- 1} $\begin{array}{c}{e}^{-\sqrt[]{\alpha }(t+\sqrt[]{\alpha })}\end{array}$ d t( t≥ - $\begin{array}{c}\sqrt[]{\alpha }\end{array}$ )(9)

经标准化后,分布函数仅含有单独一个待定参数 C _s,即 α= $\begin{array}{c}\frac{4}{C_s^2}\end{array}$ .

P -Ⅲ型分布参数,特别是 C _s(或 α)决定着密度曲线的形状,可以区分为以下几种形状:

图  1  P-Ⅲ型曲线的不同形状

Figure  1.  Different shapes of Pearson-Ⅲ curve

下载: 全尺寸图片 幻灯片

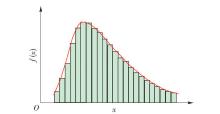
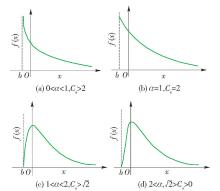
1) 当0 <α<1,即 C _s >2时,密度曲线呈“捺”形,以 x轴和 x=b直线为渐近线,见 图1(a) .

2) 当 α=1,即 C _s =2时,密度曲线退化为指数曲线,仍然呈“捺”形 . 但左端截止在曲线的起点,该处密度有限 . 右端仍延伸到无限,见 图1(b) .

3) 当1 <α<2,即2 >C _s > $\begin{array}{c}\sqrt[]{2}\end{array}$ 时,密度曲线呈“铃”形 . 左端截止在曲线起点,在该处与直线 x=b相切,右端无限,见 图1(c) .

4) 当2 <α,即 $\begin{array}{c}\sqrt[]{2}\end{array}$ >C _s >0时,密度曲线呈“铃”形 . 起点处曲线与 x轴相切,右端无限,见 图1(d) .

以上各种形状的曲线都是正偏态的 C _s >0,如果将 x轴倒转180 °,可得到对应负偏 C _s <0的P -Ⅲ型曲线,但是负偏曲线在水文上较少应用 .

1.2 指数分布

当P-Ⅲ型分布偏态系数 C _s =2的概率密度函数运用到暴雨强度公式的指数频率分析时,其数学形式的简化表达式可写为

f( x) =ae ^{-a ( x-b )}, x≥ b(10)

式中 a、 b是统计分布参数 . a表示离散程度, a>0; b为分布的下限 .

又

f'( x) =-a ²e ^{-a ( x-b )} <0

f″( x) =a ³e ^{-a ( x-b )} >0

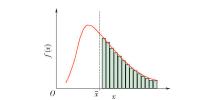
可知指数分布密度曲线是一条一端有限另一端无限的单调减凹曲线, 是P -Ⅲ型分布偏态分布下的“捺”形部分,如 图1(b)所示 .

若已知指数分布的概率密度函数,则可求得指数分布的概率分布函数式

F( x) = $\begin{array}{c}{\int }_b^{x_{}}\end{array}$ f( x)d x=1 -e ^{-a ( x-b )}(11)

则重现期

P= $\begin{array}{c}\frac{1}{f}\end{array}$ = $\begin{array}{c}\frac{1}{1-F\left(x\right)}\end{array}$ =e ^{a ( x-b )}(12)

式(12)两边取对数可得

x=alg P+b

采用最小二乘法可求得参数 a和 b

$\begin{array}{c}\left\{\begin{array}{c}a=\frac{n\sum (i_p\mathit{lnP})-\sum i_p\sum \mathit{lnP}}{(\sum \mathit{lnP}){}^2-n\sum {\left(\mathit{lnP}\right)}^2}\\ b=\frac{\sum i_p-a\sum \mathit{lnP}}{n}\end{array}\right.\end{array}$ (13)

2 指数分布的适用性分析

通过对选取的降雨样本系列进行概率密度分布研究,将不同选样方法得到的样本概率密度曲线与指数分布曲线进行分析对比,即可初步判定选取的样本系列是否可以用指数分布曲线进行下一步的频率分析 .

2.1 不同选样方法的样本系列特点

就目前来看,我国在推求暴雨强度公式过程中,常用的自记雨量资料统计降雨强度的选样方法有年最大值法和年多个样法 .

年最大值法是从暴雨强度资料中每年各历时选取一个最大的雨量值,即在连续的 N年资料中选出 N组最大值 . 此选样方法无论丰水年或枯水年,每年都有一组资料被选入总降雨时间序列,合理地考虑了气象特点,它意味着一年发生一次的年频率 . 由此方法选取的样本符合极值分布特点,按照极值理论,当降雨资料年限足够长时,它近似于全部降雨资料选样的统计结果 . 按此方法选出的降雨时间序列资料独立性最强,选样方法简单 ^{[ 7]} .

年多个样法是将全部 N年降雨资料按照不同的降雨历时,每年每个历时选取6 ~8个最大值雨样组成统计样本,然后不论年次,将每个历时子样本按大小次序排列,再从中选择资料年数的3 ~4倍的最大值,作为统计的基础资料 ^{[ 16]} . 此方法是从大量的原始降雨资料中考虑其发生年,能弥补降雨资料年限的不足,其意义是一年发生多次降雨的平均期待值 . 年多个样法选取的降雨样本较多,在进行样本重新排序后选择3 ~4倍年份降雨时,选取原始降雨系列的独立性发生了一定的改变 .

2.2 降雨样本概率密度的理论分析

随机变量的取值总是伴随相应的概率,而概率的大小总是随着随机变量的取值而变化,这种随机变量与其概率一一对应的关系,称为随机变量的概率分布规律 . 由于连续型随机变量的取值是无限多个,个别值的概率几乎为零,因而只能以区间的概率密度来分析其分布规律,即以一定区间的降雨强度为横坐标,以相应降雨强度所对应的概率密度作为纵坐标做出二维柱状图,以直方图的趋势判定与选取频率分布曲线是否走势一致 . 负偏曲线在水文上较少应用,因此暂不考虑降雨样本负偏的情况,只分析降雨样本正偏态下与指数分布曲线的拟合情况 .

从数理统计上来讲,选取的年最大值样本系列和年最大8个样的降雨强度样本值均为相互独立的随机变量值,年最大值样本系列和年多个样总样本系列均属于第一型极值分布,选取样本的概率密度曲线绝大部分是类似“铃”形的曲线 ^{[ 17]} . 对于年最大值样本系列的概率密度曲线,如 图2所示,其绝大部分为正偏“铃”形,显然与指数分布曲线的“捺”形不匹配 .

图  2  年最大值法样本系列概率密度直方图

Figure  2.  Probability density histogram of annual maximum value method

下载: 全尺寸图片 幻灯片

而对于年多个样的样本而言,选取的总样本系列的概率密度曲线基本与年最大值法样本直方图曲线一致,但是在总体样本系列去掉总样本半数强度较小的样本值后得到最终的年多个样样本系列,其概率密度曲线呈单调的“捺”形分布,如 图3所示,与指数分布曲线走势大致相同 .

图  3  年多个样法样本系列概率密度直方图

Figure  3.  Probability density histogram of multiple sample method

下载: 全尺寸图片 幻灯片

2.3 实例样本系列与指数分布曲线的拟合

本研究根据广东省气候中心提供的广州市五山站连续52a(1961—2012)的实测降雨数据进行样本采集,年最大值法采样每年每个历时挑选出一个最大值,然后不论年次由大到小排序,降雨强度样本系列长度为52;年多个样法选取每年每个历时最大8场雨,不论年次由大到小排序,总样本系列长度为416,最终选取4倍年份雨强值样本长度为208 . 采用2种不同取样方法分别得出各历时降雨样本系列,见 表1、2 .

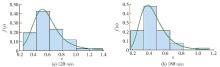
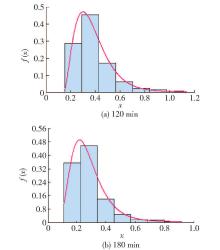
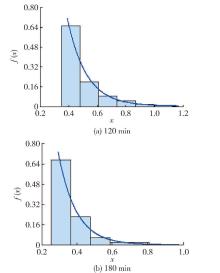
将不同采样方法下各历时降雨样本系列,以一定区间的降雨强度为横坐标,以相应降雨强度所对应的频率密度作为纵坐标做出样本系列的频率密度直方图 . 根据广州市实测降雨样本系列频率密度直方图趋势线与指数分布曲线进行对比分析,进而判定指数分布曲线是否适用于样本系列 . 图4 ~6分别给出历时120、180min下不同选样方法样本系列的直方图拟合结果曲线 .

结合实例样本系列直方图的拟合曲线图和指数分布曲线的特点进行分析:实例样本年最大值法得到的降雨样本系列频率直方图拟合线为“铃”形或部分“铃”形,如 图4所示,显然与指数分布的单调性不相符 .

对于年多个样法选取的8倍年份降雨总样本系列频率直方图拟合曲线与年最大值法得出的曲线走势基本一致,如 图5所示,不同历时下总样本拟合曲线为“铃”形. 而对于年多个样法最终选定的4倍年份降雨样本系列,由于截断了50%较小的样本数据,从而可以导致频率直方图呈“捺”形分布,也有可能呈部分“铃”形分布,其中当样本系列直方图呈“捺”形分布时,指数分布曲线几乎能穿过每个小块直方图上限的中点位置,如 图6所示,样本系列拟合曲线与指数“捺”形分布曲线相似.

表  1  不同历时下年最大值法降雨强度样本系列

Table  1.  Rain intensity samples of annual maximum value method

序号	5min	10min	15min	20min	30min	45min	60min	90min	120min	150min	180min
1	4.040	3.516	3.179	2.938	2.555	1.909	1.717	1.474	1.385	1.251	1.139
2	3.918	3.180	2.667	2.428	2.283	1.898	1.639	1.242	1.036	0.916	0.786
3	3.660	2.839	2.582	2.335	2.203	1.894	1.517	1.082	0.993	0.906	0.776
4	3.162	2.750	2.514	2.286	2.080	1.817	1.508	1.062	0.930	0.825	0.732
5	3.120	2.736	2.456	2.240	2.023	1.777	1.421	1.028	0.867	0.767	0.657
︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙
48	2.002	1.731	1.477	1.277	0.959	0.789	0.657	0.470	0.362	0.308	0.296
49	1.984	1.696	1.415	1.220	0.955	0.759	0.633	0.446	0.349	0.308	0.293
50	1.910	1.599	1.390	1.204	0.886	0.658	0.546	0.370	0.309	0.306	0.256
51	1.818	1.585	1.343	1.204	0.861	0.578	0.499	0.335	0.288	0.231	0.206
52	1.778	1.345	1.290	1.066	0.787	0.542	0.409	0.325	0.252	0.206	0.174

下载: 导出CSV 

| 显示表格

表  2  不同历时下年多个样法降雨强度样本系列

Table  2.  Rain intensity samples of multiple sample method

序号	5min	10min	15min	20min	30min	45min	60min	90min	120min	150min	180min
1	4.040	3.516	3.179	2.938	2.555	1.909	1.717	1.474	1.385	1.251	1.139
2	3.918	3.180	2.667	2.428	2.283	1.898	1.639	1.242	1.036	0.916	0.786
3	3.660	2.839	2.582	2.335	2.203	1.894	1.517	1.082	0.993	0.906	0.776
4	3.162	2.750	2.514	2.286	2.080	1.817	1.508	1.062	0.930	0.825	0.739
5	3.120	2.736	2.456	2.240	2.034	1.777	1.421	1.028	0.910	0.816	0.732
︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙
204	1.822	1.552	1.350	1.180	0.937	0.740	0.613	0.445	0.351	0.295	0.256
205	1.820	1.549	1.343	1.180	0.937	0.740	0.613	0.444	0.350	0.295	0.256
206	1.820	1.543	1.343	1.178	0.937	0.739	0.612	0.443	0.349	0.294	0.256
207	1.820	1.543	1.341	1.178	0.937	0.739	0.611	0.443	0.349	0.293	0.256
208	1.818	1.539	1.341	1.176	0.933	0.737	0.609	0.442	0.349	0.293	0.255

下载: 导出CSV 

| 显示表格

图  4  五山站年最大值法样本直方图拟合曲线

Figure  4.  Sample histogram curve of annual maximum value method in Wushan station

下载: 全尺寸图片 幻灯片

图  5  五山站年多个样法总样本系列直方图拟合曲线

Figure  5.  Sample histogram curve of total sample series in Wushan station

下载: 全尺寸图片 幻灯片

图  6  五山站年多个样法样本直方图拟合曲线

Figure  6.  Sample histogram curve of multiple sample method in Wushan station

下载: 全尺寸图片 幻灯片

3 结论

在编制城市暴雨强度公式过程中,对于不同选样方法得出的样本系列,并不是都适宜采用指数分布曲线进行频率分析. 指数分布曲线是单调的“捺”形分布,通过理论分析年最大值法选样的概率密度曲线一般是呈正偏“铃”形分布的,显然,采用年最大值法推求暴雨强度公式时是不适宜用指数分布曲线进行频率分析的. 而对于年多个样法选取的样本系列,只有当截取的50%较大样本数据的频率直方图拟合曲线呈现单调的“捺”形分布时,才可以考虑应用指数分布曲线作下一步的频率分析工作,否则不宜采用.

因此,对降雨样本进行频率分析工作之前,应先对选取的样本系列进行初步的概率密度分析,进而初步选定与样本相吻合的频率分析曲线进行降雨样本的频率分析.