A Study on the Impacts of Scientific and Technological Innovations on the Coordinated Development of Urban Clusters——An Analysis Based on the Urban Sustainable Competitiveness
-
摘要:
城市群在新时代中国区域协调发展中具有关键作用。从城市可持续竞争力的视角,在利用齐普夫法则测算中国14个主要城市群发展协调度的基础上,识别出了不同城市群的发展阶段,并进一步检验了科技创新对城市群协调发展的影响。研究发现:中国城市群的可持续竞争力分布呈现失衡状态,城市群中可持续竞争力过低的城市数量过多;在发展阶段上所有城市群仍然处于极化期,尚没有城市群进入高可持续竞争力与高协调度的阶段;城市群内单个城市的科技创新水平与城市群发展协调度呈现倒U关系。指出实施创新驱动战略、提高科技创新水平是促进城市群协调发展的重要途径。
Abstract:Urban cluster plays a key role in the regional coordinated development of China in the new era. Using the Zipf's law to calculate the coordination degree of 14 major urban clusters in China, this paper identifies the development stages of different urban clusters from the perspective of urban sustainable competitiveness, and further tests the impacts of scientific and technological innovations on the coordinated development of urban clusters. The study finds the distribution of urban sustainable competitiveness in China is unbalanced, and the number of cities with too low sustainable competitiveness in urban clusters is large. In terms of development stages, all urban clusters are still in a polarized period, and no urban clusters have yet entered the stage with high sustainable competitiveness and high degree of coordination. In addition, the level of scientific and technological innovation of individual cities within the urban cluster and the coordination degree of urban cluster development show an inverted U relationship. Therefore, implementing the innovation-driven strategy and promoting scientific and technological innovation is an important way to promote the coordinated development of urban clusters.
-
中国实施区域协调发展战略是新时代建设现代化经济体系的重要组成部分,特别是中共中央、国务院在《关于建立更加有效的区域协调发展新机制的意见》中指出:“建立以中心城市引领城市群发展、城市群带动区域发展新模式,推动区域板块之间融合互动发展。”这表明城市群在中国区域协调发展中发挥的作用将越来越重要。
目前,中国已经形成了一个以城市群体系为中间环节的城市体系[1],但城市群发展中不平衡、不协调的问题仍然非常突出。一方面,我国城市群发展过程中的区域差异仍然非常明显,东部地区城市群的规模效率要明显高于中西部地区城市群[2];另一方面,城市群内部发展的不协调问题也仍然存在,城市群作为集聚经济发展到较高阶段的结果,其空间范围往往打破了现有的省级行政区划,这使得城市群内部的协调成本更高。因而,中国城市群内部的协调机制仍然有待完善,特别是城市群中心城市与其他城市间的关系不协调,在一些城市群内部表现的非常突出,而对影响中国城市群协调发展的关键因素进行研究,具有重要的理论与现实意义。
一. 文献综述
城市群协调发展具有多方面的内涵,但从城市经济学的理论来看,由于同一个城市群内的城市形成了一个相对完整的城市体系,因此城市群内部不同城市的规模——位序分布是描述城市群内部发展协调程度的一个重要指标。在理想状态下,城市群中所有城市的规模——位序分布符合齐普夫法则所描述的分布[3]。学界针对中国城市的研究表明,中国城市分布虽然基本上符合齐普夫法则[4],但与幂律为1的齐普夫分布仍存在一定差异[5],往往呈现出扁平化趋势。李松林和刘修岩(2017)利用夜间灯光数据来测度城市规模,发现中国城市规模分布呈现扁平化趋势[6];学者在其他利用非农人口作为城市规模测度指标的研究中,也发现了中国城市规模体系呈现出一定扁平化趋势这一结论[7-9]。扁平化趋势意味着城市体系内部中小城市过多、大城市的集聚不足[10]。这也是中国城市体系发展不协调的一个重要表现。
从理论上看,城市的最优规模分布是城市集聚过程中外部经济与外部不经济之间的权衡[11-12]。在新经济地理框架下,城市的规模分布及其演化过程则取决于各种分散力与集聚力之间的权衡。藤田和克鲁格曼(Fujita and Krugman,1995)利用市场潜力函数对城市体系的形成与演化进行了明确的理论分析[13]。在此基础上,藤田和莫里(Fujita and Mori,1997)在单个产业的分析框架下,对中心地理论模式下城市体系的演化过程进行了分析[14]。藤田等(Fujita,1999)研究了多产业的情形,认为根据不同产业价格弹性的不同,拥有低弹性产业的城市会出现在离原有城市较近的地方,而拥有高弹性产业的城市则会出现在较远的地方,从而形成城市体系中的层级结构[15]。此外,田渊和蒂斯(Tabuchi and Thisse,2011)研究了运输成本下降对城市规模和数量变化的影响,发现随着运输成本的下降,小城市会逐渐失去产业和人口,而大城市会逐渐吸引更多企业和人口[16]。
从城市规模分布的角度来看,究竟什么是影响城市群协调发展的关键因素?克鲁格曼(Krugman,1996)认为,城市规模服从齐普夫分布的主要原因在于地理等“第一自然”因素的作用[17]。张亮靓和孙斌栋(2017)的研究也表明,人口规模和国土面积越大的国家,其经济地理的分布越均衡,更倾向于多中心均衡布局[18]。除了自然地理因素外,社会政治、经济因素等也是影响城市规模分布的重要原因。享德森和王(Henderson and Wang,2007)发现,民主制度有利于小城市的发展,从而使得城市规模分布要更加均衡[19]。宋(2005)也发现政治因素对城市规模分布有显著影响[20]。王贤彬等(2014)研究发现,较强的政府管制水平是导致中国城市体系过度分散化的重要原因[21]。从经济因素来看,杨孟禹等(2018)认为,中国城市规模呈现出“大规模城市扩张快、小规模城市扩张慢”两极分化现象的根本原因是,经济增长竞争对不同层次城市规模的粗放性激励差异[22]。霍和李(Ho and Li,2009)研究发现,区域收入差距会通过影响技能劳动力流动的方式来影响中国城市的规模分布[23]。此外,经济发展水平、产业结构、房价等因素都对城市规模分布有显著的影响[24-26]。
本文认为,随着中国经济进入高质量发展阶段,科技创新在城市发展中的作用将越来越重要。从产业格局的演化来看,2007年,全球市值前十的企业主要分布在金融、石油等领域,但在2017年,全球市值前十的企业中,科技型企业已占多数。因此,科技创新在决定城市全球联系度与竞争力中发挥着关键作用[27-28]。因此,我们要实现城市群的协调发展,必须紧紧抓住科技创新这一关键因素。
本文在现有研究的基础上,认为中国实现城市群的协调发展的改进与创新之处主要体现在:(1)从城市可持续竞争力的角度对中国城市群发展的协调度进行了实证分析。城市可持续竞争力是一个城市通过提升其经济、社会、环境和技术优势,系统性实现城市最优化发展,更好、更可持续地满足城市居民复杂而挑剔的社会福利的能力[29],而提升城市群的可持续发展水平是新时代中国区域高质量发展的必然要求,从城市可持续竞争力的角度来研究城市群的协调发展要更具针对性。(2)通过分层层线性模型来测算中国14个城市群的发展协调度,并利用计量回归方法检验了科技创新对城市群发展协调度的影响。特别是本文发现科技创新与城市群发展的协调度存在非线性的倒U关系,从而表明了实施创新驱动发展战略是促进城市群协调发展的长远之计。
二. 研究设计
本文在提出文章的研究假说的基础上,介绍了基于城市可持续竞争力的城市群发展协调度测度方法,并进一步对实证模型构建进行了说明,报告了样本与数据来源。
一 研究假说
从空间经济学的理论来看,城市群发展的协调程度取决于城市群内部不同城市发展过程中集聚力与分散力之间的权衡。当城市群处于极化效应主导的阶段时,要素与产业往往集聚在少数大城市,这会导致城市群内不同城市间的发展差距变大,城市群发展的协调程度较低;而当城市群处于扩散效应主导的阶段时,城市群中心城市的要素与产业向其他城市转移,此时城市群内不同城市间的发展差距变小,其协调度也变高。根据新增长理论,科技创新具有非常显著的增长效应[30-31]。因此,科技创新强的城市经济增长要更快,在本地市场效应的作用下[32],经济增长快的城市会进一步吸引其他城市的产业与要素流入,从而使得城市间的发展进一步变大。但是,随着经济发展到一段阶段,根据经典的库兹涅茨曲线,经济增长与收入差距存在倒U关系[33-34]。因此,在城市群中心城市扩散效应的带动下,城市群内不同城市的经济发展水平将会出现收敛,从而使得空间经济的发展过程呈现倒U型的变化趋势[35]。根据此理论分析,本文提出以下研究假说。
研究假说:城市群内单个城市的科技创新水平与城市群发展的协调程度呈倒U关系。
二 城市群发展协调度测度
根据城市经济学理论,齐普夫法则描述了理想状态下城市体系的规模分布,这也为实证中判断城市群发展协调与否提供了一个良好的参照标准,齐普夫法则可用如下模型来估计:
$$ \ln ({R_{ij}}) = {\beta _{0j}} - {\beta _{1j}}\ln ({I_{ij}}) + {\varepsilon _{ij}} $$ (1) 公式(1)中,Rij表示城市群j中城市i的城市可持续竞争力得分。根据中国社会科学院财经战略研究院与联合国人居署共同发布的《全球城市竞争力报告2017—2018》,本文利用城市青年人口占比与高收入人口规模(年收入高于2万美元)两个指标的算术加权平均值来测算城市的可持续竞争力得分。Iij表示城市群j中城市i可持续竞争力的排名。其中,ln(Ii)前面系数的绝对值如果越接近于1,表明城市群中城市的分布符合齐普夫法则,那么城市群的发展也就越协调;如果小于1,表明城市群内部不同城市间可持续竞争力的分布不均匀,大部分城市的可持续竞争力较低,只有少数城市的可持续竞争力较高;如果大于1,表明城市群内部不同城市间可持续竞争力的差异相对于最优水平过小。令Δβ1j=|1-β1j|,因此,如果Δβ1j越小,表明城市群j的发展越协调。
一般而言,估计式(1)中的参数β1j有两种思路:一是直接利用不同城市群的样本分别来估计式(1),并获得参数β1j的估计值。这种思路的问题在于损失了大量的样本,特别是如果某一城市群内部的城市较少,那么会严重影响参数β1j估计的准确性。为了最大限度利用样本的信息,本文采用第二种思路,即利用分层线性模型(也称为随机系数模型)。在利用全部样本估计式(1)的同时,令截距项β0j与系数β1j随城市群而变化,也就是不同城市群拥有不同的截距项β0j与系数β1j,在此基础上,我们可计算出衡量不同城市群发展协调度的指标Δβ1j。
三 计量模型构建
为了考察科技创新对不同城市群发展协调度的影响,本文设定如下计量模型:
$$ \Delta {\beta _{1j}} = {\gamma _0} + {\gamma _1}{\rm{Tec}}{{\rm{h}}_{ij}} + {\gamma _2}{\rm{Tech}}_{ij}^2 + \lambda Z + {\varepsilon _{ij}} $$ (2) 公式(2)中Δβ1j衡量了城市群发展的协调程度,Δβ1j越大,表明城市群的发展越不协调。Techij为城市群j中城市i的科技创新水平,用标准化后的专利申请数指数与论文指数的和来衡量。根据研究假说,可以预期γ2 < 0、γ1>0。Z为其他影响城市群发展协调程度的控制变量组成的向量,具体包括:(1)经济活力,该指标利用标准化后的城市人均GDP指数以及5年GDP增量指数的和来衡量;(2)环境质量,用标准化后的二氧化碳排放量(负向指标)指数与PM2.5(负向指标)指数的和来表示;(3)社会包容,用标准化后的基尼系数(负向指标)指数与犯罪率(负向指标)指数的和来表示;(4)全球联系,用标准化后的跨国公司联系度指数与国际知名度指数的和来表示;(5)人力资本潜力,用标准化后的青年人口占比指数与大学指数的和来表示;(6)基础设施,用标准化后的航运便利度、宽度用户量以及航空便利度指数的和来表示。文中变量都标准化为0-1之间,所有数据都来源于中国社科院城市与竞争力研究中心数据库,变量的描述性统计见表 1。
表 1 变量描述性统计变量 样本量 均值 标准误 最小值 最大值 科技创新 288 0.181 0.146 0.000 0.813 经济活力 288 0.123 0.112 0.014 0.707 环境质量 288 0.482 0.052 0.320 0.859 社会包容 288 0.652 0.039 0.392 0.739 全球联系 288 0.043 0.052 0.024 0.427 人力资本潜力 288 0.365 0.148 0.000 0.830 基础设施 288 0.518 0.080 0.269 0.924 四 样本与数据来源
本文样本为中国287个城市(内地285个城市和香港、澳门)的数据,关于中国城市群的识别目前尚没有统一标准。例如,黄征学(2014)结合定量与定性方法识别出了10个城市群[36],周晓波和倪鹏飞(2018)则识别出了25个城市群[1],顾朝林和庞海峰(2008)利用城市市区非农人口构造引力模型来获取城市间的联系数据,共识别出了64个地方性城市体系[37]。本文则根据国家以及地方的相关规划,选取了粤港澳大湾区城市群、长三角城市群、呼包鄂榆城市群、山东半岛城市群、京津冀城市群、辽中南城市群、哈长城市群、长江中游城市群、成渝城市群、海峡西岸城市群、关中平原城市群、北部湾城市群、中原城市群、兰西城市群,共14个中国主要城市群作为研究对象。这14个城市群包含的城市数量为202,约占全部样本城市的70%。
三. 实证结果分析
本文分析了不同城市群可持续竞争力水平与发展协调度的测算结果,按照可持续竞争力与发展协调程度的高低划分了不同城市群的类型,报告了计量回归的结果。
一 不同城市群可持续竞争力水平与协调度
表 2报告中国14个城市群可持续竞争力的均值以及根据式(1)估计得到的各城市群参数β1j的结果,并在此基础上,进一步计算得到了用来反映各城市群内部发展协调程度的指标Δβ1j。具体来看,中国城市群中可持续竞争力得分最高的是粤港澳大湾区城市群,其得分是可持续竞争力得分最低的兰西城市群的1.4倍。同时,中国城市群可持续竞争力具有三个方面的分化特征。一是东西差异明显。东部沿海地区城市群的可持续竞争力得分明显高于中西部地区。例如,排名前五的城市群中有4个城市群属于东部沿海地区,可持续竞争力最低的5个城市群中有4个位于中西部地区。二是南北差异开始显现。得分最高的粤港澳大湾区与长三角城市群都位于南方,其中南方城市群可持续竞争力平均得分为0.64;北方城市群的平均得分为0.62,南方城市群可持续竞争力要略高于北方城市群。三是城市群内部也存在明显分化。这主要体现为城市群内部城市间可持续竞争力差异过大。从齐普夫法则参数β1j的估计结果来看,我国所有城市群都明显小于1。这意味着我国每个城市群中,仅有少数城市的可持续竞争力较高,而大部分城市的可持续竞争力较低。因此,中国城市群的可持续竞争力发展不协调,有待提升。
表 2 不同城市群可持续竞争力均值与发展协调度测算结果城市群 城市数量 可持续竞争力均值 β1j Δβ1j 粤港澳大湾区 11 0.794 -0.103 0.897 长三角城市群 26 0.694 -0.130 0.870 呼包鄂榆城市群 4 0.692 -0.164 0.836 山东半岛城市群 15 0.677 -0.158 0.842 京津冀城市群 11 0.664 -0.133 0.867 辽中南城市群 9 0.629 -0.163 0.837 哈长城市群 10 0.605 -0.181 0.819 长江中游城市群 30 0.602 -0.160 0.840 成渝城市群 16 0.594 -0.159 0.841 海峡西岸城市群 17 0.592 -0.160 0.840 关中平原城市群 11 0.587 -0.171 0.829 北部湾城市群 10 0.585 -0.180 0.820 中原城市群 29 0.579 -0.186 0.814 兰西城市群 4 0.570 -0.195 0.805 注:各城市群包含的数量是根据本文287个样本城市统计得到,个别城市群包含的城市会有重合 二 不同城市群的发展阶段分析
尽管表 2显示中国14个主要城市群可持续竞争力的内部协调度较低,但不同可持续竞争力水平的城市群其协调度也存在差异。为了揭示这一差异,本文利用聚类分析的方法,首先按照可持续竞争力平均得分的高低将我国14个城市群分为高可持续竞争力与低可持续竞争力两组。其次按照Δβ1j的大小,将我国14个城市群分为低协调度与高协调度两组,由此可将全部城市群分为四种类型。结果如表 3所示。
表 3 不同城市群的分类类型 高协调 低协调 高可持续竞争力 — 粤港澳大湾区、长三角城市群、呼包鄂榆城市群、山东半岛城市群、京津冀城市群 低可持续竞争力 哈长城市群、关中平原城市群、北部湾城市群、中原城市群、兰西城市群 辽中南城市群、长江中游城市群、成渝城市群、海峡西岸城市群 注:—表示该类型下城市群数量为0 1.属于高可持续竞争力——低协调类型的城市群有粤港澳大湾区等5个城市群。
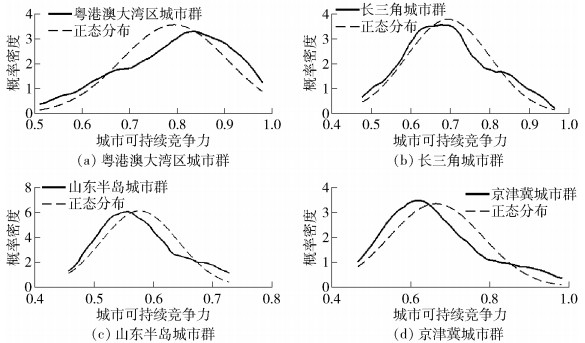
这一类型城市群的特点是尽管其可持续竞争力水平较高,但其内部差异太大,城市群中大部分城市的可持续竞争力得分都较低。本文通过对该类型城市群的核密度估计结果,可以发现,与正态分布相比,粤港澳大湾区城市群呈现一定程度的左偏分布,表明其内部差异过大主要是由少数城市可持续竞争力水平较低导致的;而长三角、山东半岛以及京津冀城市群则都呈现出了一定程度的右偏分布,这表明其内部差异过大主要是由大部分城市可持续竞争力水平较低导致的。不同城市群内部之所以差异过大的原因存在差异主要是因为,粤港澳大湾区城市群相对于其他4个城市群而言,其多中心特征要更加明显;粤港澳大湾区城市群包括香港、深圳、广州等多个中心城市,其可持续竞争力的得分分别为0.92、0.91、0.89,得分都较高且相差不大。同时,以利用可持续竞争力指数计算的5个城市群的4城市首位度来看,粤港澳大湾区的首位度最低(0.34),低于长三角城市群(0.36)、山东半岛城市群(0.35)以及京津冀城市群(0.41),而多中心的城市群结构更有利于发挥城市群中心城市对其他城市的溢出效应,从而使得粤港澳大湾区仅有少数城市的可持续竞争力较低(详见图 1)。
2.属于低可持续竞争力——高协调类型的城市群有哈长城市群等5个城市群。
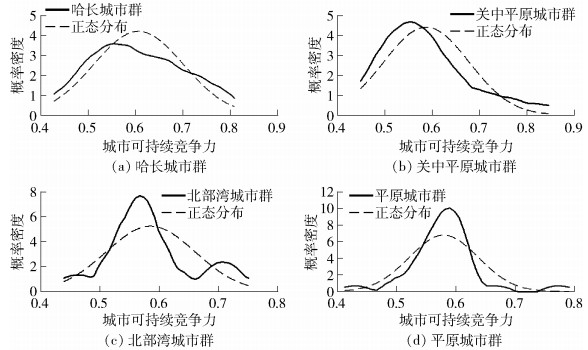
该类城市群的特点是尽管其城市群可持续竞争力水平较低,但其内部的差异较小,也就是城市群内的城市可持续竞争力普遍较低。该类型城市群的核密度详见图 2。具体来看,哈长城市群与关中平原城市群都呈现出一定的右偏分布,这与其低可持续竞争力的类型是一致的;而北部湾与中原城市群则属于“纺锤形”分布,即大部分城市的可持续竞争力都属于中等水平,因此其内部发展的协调度比较高。总体而言,属于该类型的城市群全部位于中国城市化水平相对落后的中西部地区,在全部14个城市群中属于发展相对落后的类别。
3.属于低可持续竞争力——低协调的城市群有辽中南城市群等4个城市群。
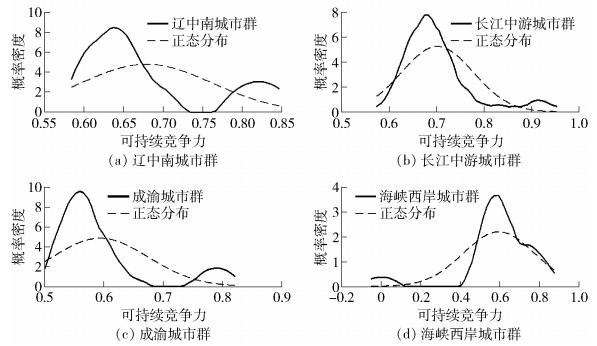
该类城市群的特征为城市群内可持续竞争力的水平普遍较低,而且内部差异较大。本文通过对该类型城市群可持续竞争力的核密度分析看,辽中南城市群与成渝城市群属于比较明显的“哑铃型”分布,即可持续竞争力属于中等水平的城市最少,城市群内两极分化现象明显,仅有个别城市的可持续竞争力较高。例如,辽中南城市群中的沈阳和大连,成渝城市群中的成都与重庆;长江中游城市群属于右偏分布,即大部分城市可持续竞争力水平过低导致了其协调度较低;海峡西岸城市群则属于明显的左偏分布,即少部分城市可持续竞争力水平明显偏低拉大了城市群内的差异,这主要是由于福建内陆城市可持续竞争力过低导致的(详见图 3)。
此外,本文通过分析发现,我国属于高可持续竞争力—高协调的城市群数量为0。这表明,我国目前尚没有城市群达到所有城市都具有较高的可持续竞争力这一阶段。那么,导致中国城市群发展出现这些分化的内在原因是什么呢?本文认为,这与城市群发展的阶段性特征是一致的。根据理论分析,城市群的发展会经历一个先极化、后扩散的过程,在这个过程中城市群的平均可持续竞争力会不断提高,但其发展的协调程度则会经历一个由协调度低向协调度高的演化过程。
本文所划分的四种类型对应了城市群发展的不同阶段。最初阶段,城市群的发展是低可持续竞争力—高协调类型,此时城市群内所有城市的可持续竞争力差异尽管较小,但处于普遍较低的状态。第二阶段,城市群的发展会进入低可持续竞争力—低协调类型,此时极化作用开始加强,资源向少数城市集聚,这会加剧城市间可持续竞争力的差距,因此城市群的协调度较低,但由于城市集聚不够充分,城市群平均的可持续竞争力水平仍然较低。第三阶段,城市群的发展是高可持续竞争力—低协调类型。尽管此时仍然是极化效应起主导作用,但已经出现了一部分发展水平较高的城市,因此城市群可持续竞争力的平均水平较高,同时城市群的协调度较低。第四个阶段,城市群的发展是高可持续竞争力—高协调类型。此时扩散效应起主导作用,城市群内所有城市的可持续竞争力都达到了较高的水平。这四种不同类型的城市群的发展阶段表明,从可持续竞争力的角度来看,中国14个主要城市群在发展阶段上仍然处于极化期,这也是导致中国城市群可持续竞争力分布失衡的重要原因。
三 回归结果分析
本文通过分析,报告了科技创新对城市群协调发展影响的回归结果(详见表 4),为了检验科技创新与城市群发展协调度之间二次关系的稳健性,模型1为仅保留科技创新变量一次项的结果,模型2则增加了二次项,模型3则在此基础上进一步添加了三次项。我们可以发现,科技创新变量的一次项显著为正,二次项显著为负,三次项不显著,这表明城市群内单个城市的科技创新水平与所在城市群发展的协调度存在显著的倒U关系,即科技创新水平的提高会先加剧城市群发展的不协调度,在超过一定水平之后则会促进城市群的协调发展,这也验证了本文的研究假说。
表 4 科技创新对城市群协调发展影响的回归结果变量名 模型1 模型2 模型3 科技创新一次项 0.053 6***
(0.018 4)0.117***
(0.032 7)0.195***
(0.060 1)科技创新二次项 -0.150**
(0.064 5)-0.477**
(0.220 7)科技创新三次项 0.329
(0.212 3)经济活力 0.034 9
(0.027 6)0.060 1**
(0.029 5)0.064 5**
(0.029 5)环境质量 0.178***
(0.038 0)0.160***
(0.038 5)0.164***
(0.038 5)社会包容 0.029 0
(0.044 8)0.010 0
(0.045 2)0.004 25
(0.045 2)全球联系 -0.207***
(0.050 3)-0.158***
(0.054 1)-0.160***
(0.054 0)人力资本潜力 0.010 1
(0.013 4)0.007 30
(0.013 3)0.009 14
(0.013 3)基础设施 0.158***
(0.037 2)0.144***
(0.037 4)0.137***
(0.037 6)常数项 0.627***
(0.042 5)0.648***
(0.043 2)0.649***
(0.043 1)样本量 287 287 287 R2 0.370 0.382 0.387 注:括号内是标准误,***、**、*分别表示在1%、5%与10%的统计水平上显著 四. 结论与启示
本文基于城市可持续竞争力的视角,利用齐普夫法则测算了中国14个主要城市群发展的协调程度并识别了不同城市群的发展阶段,在此基础上,利用计量回归方法检验了科技创新对城市群协调发展的影响。
本文主要有三方面的发现。第一,中国城市群的可持续竞争力分布呈现失衡状态,城市群中可持续竞争力过低的城市数量过多;第二,样本中所有城市群在发展阶段上仍然处于极化期,城市群中心城市对其他城市的扩散效应不足,尚没有城市群进入高可持续竞争力与高协调度的阶段;第三,城市群内单个城市的科技创新水平与城市群整体的发展协调度呈现倒U关系,即科技创新水平的提高在初始阶段不利于城市群的协调发展,只有超过一定水平之后,才有利于城市群的协调发展。
本文研究对于新时代中国城市群以及区域协调发展具有一定的启示。第一,我们要深刻认识到中国城市群可持续发展中的不平衡性。在新时代推动中国区域高质量发展的过程中,提高城市以及城市群的可持续竞争力是非常重要的一环。本文研究显示,中国城市群的可持续竞争力与齐普夫法则揭示的理想状态存在非常明显的差距,城市群内大部分城市可持续竞争力过低这一现实意味着中国城市群在高质量以及协调发展上任重道远。第二,我们要促进区域协调发展。中国未来在城市群发展中要高度重视发挥中心城市的溢出效应。目前,虽然中国已经出现了一批世界级中心城市[38],城市经济的集聚水平得到了很大提高,但城市群的发展不能一直停留在极化期,要积极加强城市群中不同城市间的合作,推动城市间产业分工、基础设施、公共服务、环境治理、对外开放、改革创新等协调联动,形成城市群内中心城市与其他城市之间在要素、产业上的双向流动格局。第三,中国城市在发展中要紧紧抓住新一轮科技革命带来的机遇,坚定实施创新驱动发展战略。由于科技创新水平与城市群发展的协调程度存在倒U关系,因此只有通过积极提高城市的科技创新水平,才能尽快越过科技创新水平的拐点,使得城市群发展进入可持续竞争力以及发展协调度“双高”的高水平均衡状态。
-
表 1 变量描述性统计
变量 样本量 均值 标准误 最小值 最大值 科技创新 288 0.181 0.146 0.000 0.813 经济活力 288 0.123 0.112 0.014 0.707 环境质量 288 0.482 0.052 0.320 0.859 社会包容 288 0.652 0.039 0.392 0.739 全球联系 288 0.043 0.052 0.024 0.427 人力资本潜力 288 0.365 0.148 0.000 0.830 基础设施 288 0.518 0.080 0.269 0.924 表 2 不同城市群可持续竞争力均值与发展协调度测算结果
城市群 城市数量 可持续竞争力均值 β1j Δβ1j 粤港澳大湾区 11 0.794 -0.103 0.897 长三角城市群 26 0.694 -0.130 0.870 呼包鄂榆城市群 4 0.692 -0.164 0.836 山东半岛城市群 15 0.677 -0.158 0.842 京津冀城市群 11 0.664 -0.133 0.867 辽中南城市群 9 0.629 -0.163 0.837 哈长城市群 10 0.605 -0.181 0.819 长江中游城市群 30 0.602 -0.160 0.840 成渝城市群 16 0.594 -0.159 0.841 海峡西岸城市群 17 0.592 -0.160 0.840 关中平原城市群 11 0.587 -0.171 0.829 北部湾城市群 10 0.585 -0.180 0.820 中原城市群 29 0.579 -0.186 0.814 兰西城市群 4 0.570 -0.195 0.805 注:各城市群包含的数量是根据本文287个样本城市统计得到,个别城市群包含的城市会有重合 表 3 不同城市群的分类
类型 高协调 低协调 高可持续竞争力 — 粤港澳大湾区、长三角城市群、呼包鄂榆城市群、山东半岛城市群、京津冀城市群 低可持续竞争力 哈长城市群、关中平原城市群、北部湾城市群、中原城市群、兰西城市群 辽中南城市群、长江中游城市群、成渝城市群、海峡西岸城市群 注:—表示该类型下城市群数量为0 表 4 科技创新对城市群协调发展影响的回归结果
变量名 模型1 模型2 模型3 科技创新一次项 0.053 6***
(0.018 4)0.117***
(0.032 7)0.195***
(0.060 1)科技创新二次项 -0.150**
(0.064 5)-0.477**
(0.220 7)科技创新三次项 0.329
(0.212 3)经济活力 0.034 9
(0.027 6)0.060 1**
(0.029 5)0.064 5**
(0.029 5)环境质量 0.178***
(0.038 0)0.160***
(0.038 5)0.164***
(0.038 5)社会包容 0.029 0
(0.044 8)0.010 0
(0.045 2)0.004 25
(0.045 2)全球联系 -0.207***
(0.050 3)-0.158***
(0.054 1)-0.160***
(0.054 0)人力资本潜力 0.010 1
(0.013 4)0.007 30
(0.013 3)0.009 14
(0.013 3)基础设施 0.158***
(0.037 2)0.144***
(0.037 4)0.137***
(0.037 6)常数项 0.627***
(0.042 5)0.648***
(0.043 2)0.649***
(0.043 1)样本量 287 287 287 R2 0.370 0.382 0.387 注:括号内是标准误,***、**、*分别表示在1%、5%与10%的统计水平上显著 -
[1] 周晓波, 倪鹏飞.城市群体系的规模分布结构及其经济增长效应[J].社会科学研究, 2018(2):64-71. doi: 10.3969/j.issn.1000-4769.2018.02.008 [2] 王德利, 杨青山.中国城市群规模结构的合理性诊断及演变特征[J].中国人口·资源与环境, 2018, 28(9):123-132. http://d.old.wanfangdata.com.cn/Periodical/zgrkzyyhj201809014 [3] ZIPF G. Human behaviour and the principle of least-effort[M]. Cambridge MA:Addison-Wesley, 1949.
[4] 魏守华, 孙宁, 姜悦. Zipf定律与Gibrat定律在中国城市规模分布中的适用性[J].世界经济, 2018, 41(9):96-120. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7000828204 [5] 梁琦, 陈强远, 王如玉.户籍改革、劳动力流动与城市层级体系优化[J].中国社会科学, 2013(12):36-59. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgshkx201312003 [6] 李松林, 刘修岩.中国城市体系规模分布扁平化:多维区域验证与经济解释[J].世界经济, 2017(11):144-169. [7] ANDERSON G, GE Y. The size distribution of Chinese cities[J]. Regional Science and Urban Economics, 2005, 35(6):756-776. doi: 10.1016/j.regsciurbeco.2005.01.003
[8] 江曼琦, 王振坡, 王丽艳.中国城市规模分布演进的实证研究及对城市发展方针的反思[J].上海经济研究, 2006(6):29-35. doi: 10.3969/j.issn.1005-1309.2006.06.005 [9] 刘学华, 张学良, 李鲁.中国城市体系规模结构:特征事实与经验阐释[J].财经研究, 2015(11):108-123. http://d.old.wanfangdata.com.cn/Periodical/cjyj201511009 [10] 陈良文, 杨开忠, 吴姣.中国城市体系演化的实证研究[J].江苏社会科学, 2007(1):81-88. doi: 10.3969/j.issn.1003-8671.2007.01.014 [11] HENDERSON J V. The sizes and types of cities[J]. American Economic Review, 1974, 64(4):640-656. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_5414976db75b429f3d95e8daf0bc4840
[12] FUJITA M, OGAWA H. Multiple equilibria and structural transition of non-monocentric urban configurations[J]. Regional Science and Urban Economics, 1982, 12(2):161-196. doi: 10.1016/0166-0462(82)90031-X
[13] FUJITA M, KRUGMAN P. When is the economy monocentric? von thünen and chamberlin unified[J]. Regional Science and Urban Economics, 1995, 25(4):505-528. doi: 10.1016/0166-0462(95)02098-F
[14] FUJITA M, MORI T. Structural stability and evolution of urban systems[J]. Regional Science and Urban Economics, 1997, 27(4-5):399-442. doi: 10.1016/S0166-0462(97)80004-X
[15] FUJITA M, KRUGMAN P, MORI T. On the evolution of hierarchical urban systems1[J]. European Economic Review, 1999, 43(2):209-251. doi: 10.1016/S0014-2921(98)00066-X
[16] TABUCHI T, THISSE J-F. A new economic geography model of central places[J]. Journal of Urban Economics, 2011, 69(2):240-252. doi: 10.1016/j.jue.2010.11.001
[17] KRUGMAN P. The self-organizing economy[M]. Oxford:Blackwell, 1996.
[18] 张亮靓, 孙斌栋.极化还是均衡:重塑大国经济地理的战略选择——城市规模分布变化和影响因素的跨国分析[J].地理学报, 2017, 72(8):1419-1431. http://d.old.wanfangdata.com.cn/Periodical/dlxb201708007 [19] HENDERSON J V, WANG H G. Urbanization and city growth:the role of institutions[J]. Regional Science and Urban Economics, 2007, 37(3):283-313. doi: 10.1016/j.regsciurbeco.2006.11.008
[20] SOO K T. Zipf's law for cities:a cross-country investigation[J]. Regional Science and Urban Economics, 2005, 35(3):239-263. doi: 10.1016/j.regsciurbeco.2004.04.004
[21] 王贤彬, 谢小平, 杨本建.国有经济与城市规模分布演进[J].经济评论, 2014(2):16-27. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jjpl201402002 [22] 杨孟禹, 梁双陆, 蔡之兵.中国城市规模为何两极分化:一个空间竞争的经验解释[J].财贸经济, 2018, 39(8):141-154. doi: 10.3969/j.issn.1005-913X.2018.08.057 [23] HO C Y, LI D. The nexus of income and size distribution of Chinese cities, 1984-2003[J]. Applied Economics Letters, 2009, 16(17):1677-1682. doi: 10.1080/13504850701675458
[24] GONZÁLEZ-VAL R. Deviations from zipf's law for American cities:an empirical examination[J]. Urban Studies, 2011, 48(5):1017-1035. doi: 10.1177/0042098010371394
[25] NAM K M, REILLY J M. City size distribution as a function of socioeconomic conditions:an eclectic approach to downscaling global population[J]. Urban Studies, 2013, 50(1):208-225. doi: 10.1177/0042098012448943
[26] 范剑勇, 邵挺.房价水平、差异化产品区位分布与城市体系[J].经济研究, 2011, 46(2):87-99. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jjyj201102007 [27] 倪鹏飞, 徐海东, 沈立, 等.城市经济竞争力:关键因素与作用机制——基于亚洲566个城市的结构方程分析[J].北京工业大学学报(社会科学版), 2019, 19(1):50-59. doi: 10.12120/bjutskxb20190150 [28] 曹清峰, 倪鹏飞, 沈立, 等.东亚主导下的亚洲城市体系——基于城市竞争力的分析[J].北京工业大学学报(社会科学版), 2018, 18(6):39-48. doi: 10.12120/bjutskxb20180639 [29] 杨晓兰, 倪鹏飞.城市可持续竞争力的起源与发展评述[J].经济学动态, 2017(9):96-110. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jjxdt201709008 [30] ROMER P M. Endogenous technological change[J]. Journal of Political Economy, 1990, 98(5):71-102. doi: 10.1086/261725
[31] GROSSMAN G M, HELPMAN E. Trade, innovation, and growth[J]. American Economic Review, 1990, 80(2):86-91. http://d.old.wanfangdata.com.cn/Periodical/zgltjj201503003
[32] KRUGMAN P. Increasing returns and economic geography[J]. Journal of Political Economy, 1991, 99(3):483-499. doi: 10.1086/261763
[33] ZHANG Z, LIU A, YAO S. Convergence of China's regional incomes:1952-1997[J]. China Economic Review, 2001, 12(2-3):243-258. doi: 10.1016/S1043-951X(01)00053-0
[34] FUJITA M, HU D. Regional disparity in China 1985-1994:the effects of globalization and economic liberalization[J]. Annals of Regional Science, 2001, 35(1):3-37. doi: 10.1007/s001680000020
[35] WILLIAMSON J G. Regional inequality and the process of national development:a description of the patterns[J]. Economic Development and Cultural Change, 1965, 13(4):1-84. doi: 10.1086/450136
[36] 黄征学.城市群界定的标准研究[J].经济问题探索, 2014(8):156-164. doi: 10.3969/j.issn.1006-2912.2014.08.024 [37] 顾朝林, 庞海峰.基于重力模型的中国城市体系空间联系与层域划分[J].地理研究, 2008(1):1-12. http://d.old.wanfangdata.com.cn/Periodical/dlyj200801001 [38] 王海波, 倪鹏飞, 龚维进, 等.从全球视角看中国城市格局、层级与类型——基于全球城市竞争力数据的研究[J].北京工业大学学报(社会科学版), 2019, 19(1):60-68. doi: 10.12120/bjutskxb20190160 -
期刊类型引用(6)
1. 姚战琪,熊琪颜. 科技服务业区域试点对我国数字贸易国际竞争力的影响与机制. 中国流通经济. 2025(02): 30-44 .  百度学术
百度学术
2. 梁军,李佳艺. 中心城市科技创新能促进城市群协调发展吗?——兼论收入房价比的调节作用. 经济经纬. 2024(04): 16-28 .  百度学术
百度学术
3. 李洪涛,王丽丽. 中心城市科技创新、学习效应对区域共同富裕的影响. 科技进步与对策. 2023(18): 33-41 .  百度学术
百度学术
4. 喻登科,黄小彦. 市域知性管理对城市可持续发展的影响. 科技进步与对策. 2022(04): 29-38 .  百度学术
百度学术
5. 刘笑男,倪鹏飞. 科技创新对中国城市金融竞争力的影响机制研究. 当代经济管理. 2021(08): 90-97 .  百度学术
百度学术
6. 张恒龙,罗唯. 基本公共服务均等化对城市群协调发展的驱动机制. 上海商学院学报. 2021(05): 55-73 .  百度学术
百度学术
其他类型引用(7)



 下载:
下载: